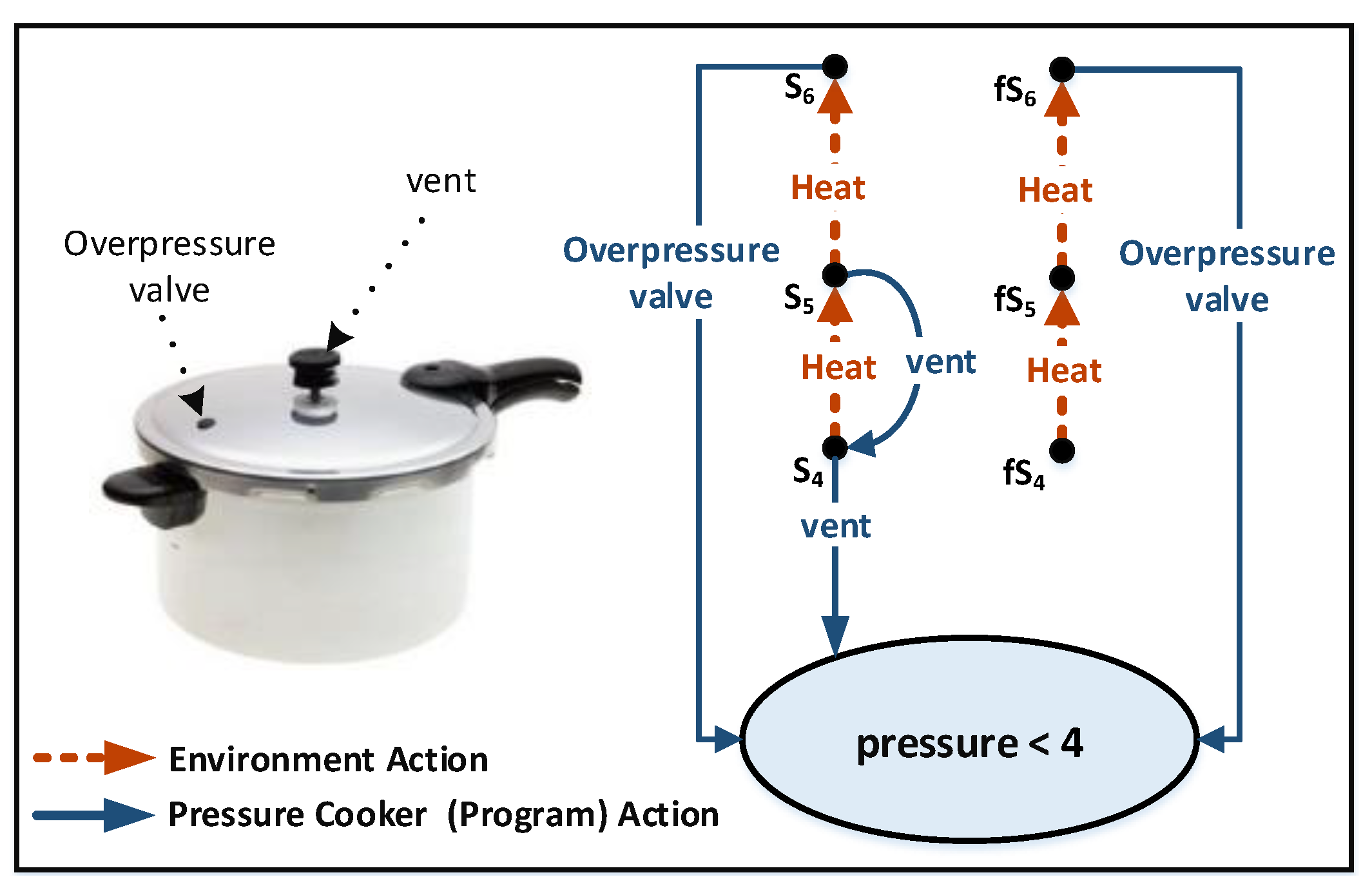
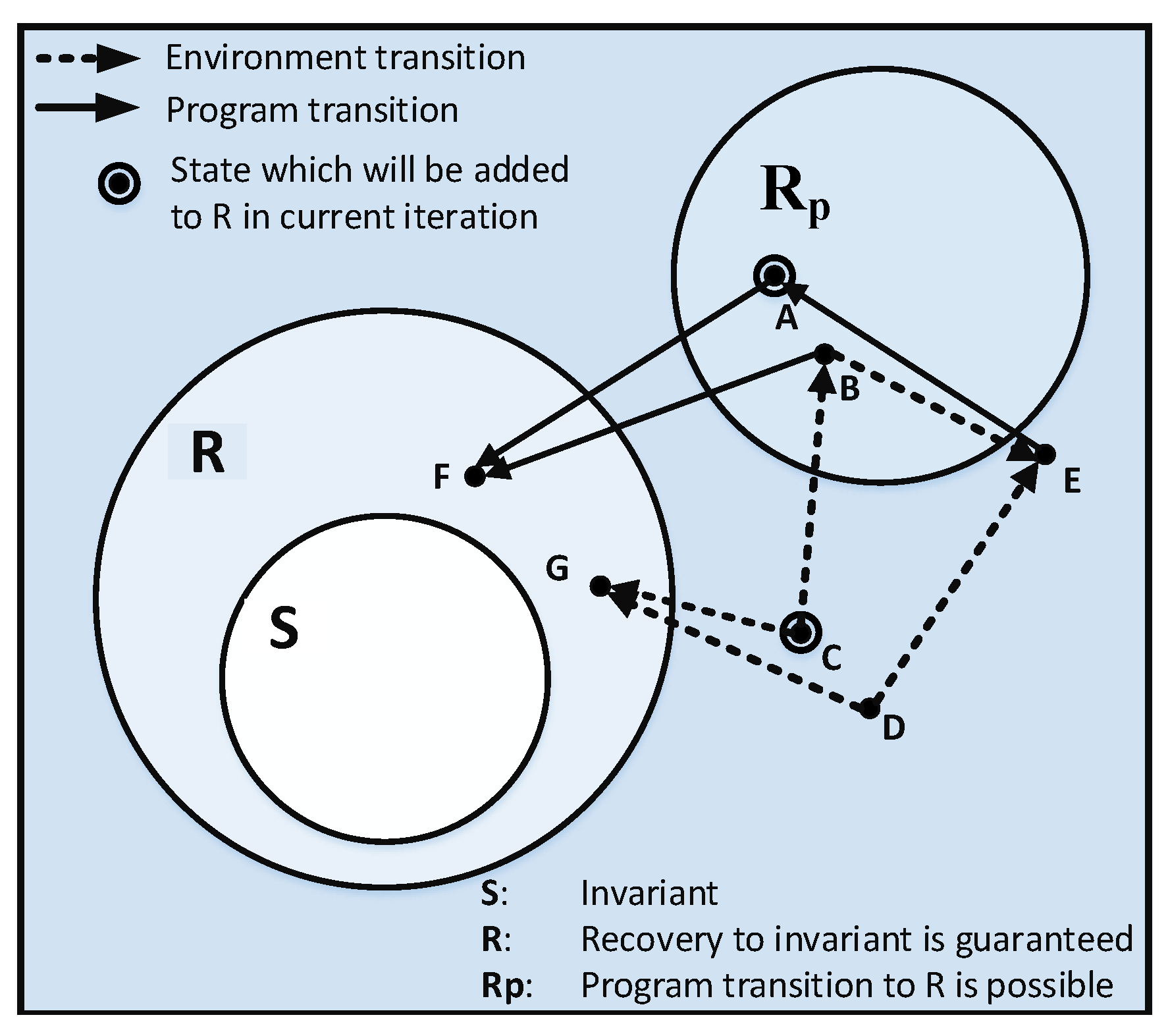
Appendix B.1. Soundness
First, we show that the program constructed by Algorithm 3 never reaches a state in . Specifically,
Lemma A5. For any computation where , there dose not exist such that is in .
Proof. Consider a computation of where . We proof by induction that for all , :
Base case:
It is clear , because and and by construction, we know (see Line 33). Also, , because otherwise that is contradiction to .
Induction hypothesis:
Induction step:
Suppose . Then, . By construction, the program does not have any transition in . Thus, we have two cases for :
Case 1:
In this case, (by Line 28) that is contradictory to the induction hypothesis.
Case 2:
In this case, . If , then that is contradiction to . If , then . By construction, the program does not have any transition in . Thus, we have two cases for
Case 2.1: :
In this case, that is contradictory to the induction hypothesis.
Case 2.2: :
In this case, as both and are in , according to the fairness assumption, there does not exist a transition starting from and it means that is added to by Line 28 which is in contradiction with the induction hypothesis. □
Since we never reach any state in starting from and since any state in is in by Line 23, we conclude we never reach . Thus, we have the following corollary:
Corollary A1. in the last iteration of loop on Lines 6–43 is a f-span for the program resulted by Algorithm 3.
The following lemma states that in every computation of the repaired program that starts from its invariant (i.e., ), if the program reaches a state in R, in the rest of the computation it will reach . Specifically,
Lemma A6. For every computation such that , for and R in the last iteration of the loop on Lines 6–43, we have:
.
Proof. We prove this lemma by induction as we expand set R:
Base case:
The proof is trivial.
Induction hypothesis: Theorem holds for current R.
Induction step:
For any state
that is added to
R we have
Thus, any environment transition either reaches R or . In the second case, since we have reached a state in by an environment transition, and since from any state in there is a program transition to R (cf. Line 17), based on the fairness assumption, the computation will reach R. Thus, in either case, we reach R. Since in the last iteration of loop on Lines 6–43, we do not change the set of transitions for states in R of the previous iteration, based on the induction hypothesis, the lemma is proved. □
The following lemma states that when the repaired program starts at its invariant , if it reaches a state in , in the rest of the its computation it will reach a state in . Specifically,
Lemma A7. For every computation such that , for , and R in the last iteration of loop on Lines 6–43, we have:
.
Proof. Let . Any state that is not in R is in . Thus, . By construction, the program does not have any transition in . Thus, . If , then that is a contradiction to Lemma A5. Thus, . Since we have reached by an environment transition and , the computation will reach R and according to Lemma A6, the computation will reach . □
Based on Lemmas A6 and A7, we have the following corollary that guarantees recovery to the invariant from .:
Corollary A2. For every computation such that , for , and R in the last iteration of loop on Lines 6–43, we have:
.
Theorem A4. Algorithm 3 is sound.
Proof. In order to show the soundness of our algorithm, we need to show that the three conditions of the problem statement are satisfied.
C1: Satisfaction of C1 for Algorithm 3 is the same as that for Algorithm 2 stated in the proof of the Theorem A1.
C2: We need to show that is a masking fault-tolerant revision for p. Thus, we need to show the constraints of Definition 16 are satisfied. From C1, , the assumption that satisfies from S, and is closed in , all constraints of Definition 10 are satisfied. Thus, 2-satisfies from .
Let . Consider prefix c of such that c starts from a state in . If c does not satisfy , there exists a prefix of c, say , such that it has a transition in . W.l.o.g., let be the smallest such prefix. It follows that . Hence, . By construction, does not contain any transition in . Thus, is a transition of f or . If it is in f then which is a contradiction to Lemma A5. If it is in then and . Again, by construction, we know that does not contain any transition in , so is either in f or . If it is in f then (contradiction to Lemma A5). If it is in , as both and are in , according to the fairness assumption, there does not exist a transition of starting from and it means that , which is again a contradiction to Lemma A5. Thus, each prefix of c does not have a transition in . Therefore, any prefix of satisfies .
As 2-satisfies from in environment , any prefix of 2-satisfies and according to Corollary A1 and Corollary A2, is masking 2-f-tolerant to from in environment with fault-span for R and in the last iteration of the loop on Lines 6–43.
C3: Any , is in . By construction, does not have any transition in , so C3 holds. □
Appendix B.2. Completeness
Like the proof of the completeness of Algorithm 2, the proof of the completeness of Algorithm 3 is based on the analysis of states that are removed from S. For Algorithm 3, we focus on the iterations of the loop on Lines 6–43.
Similar to Observation 1, we have the following observation for Algorithm 3:
Observation 5. In any given iteration i of loop on 6–43, let R, and be R, and at the end of iteration i. Then, for any such that and , we have
.
We also note the following observation:
Observation 6. For any such that , either , or .
Lemmas A8, A9, A10 and A11, Corollary A3 and Theorem A5 provided in the following, hold for any given iteration i of loop on Lines 6–43 assuming Algorithm 3 has declared failure. For these results, let with invariant be any revision for program with invariant S such that , and . Consider , and at the beginning of iteration i and , , R and at the end of the iteration. Also, let f and be a set of fault transitions and a set of environment transitions for p (i.e., ), respectively.
The following lemma focuses on the situation where a given revision reaches a state that our algorithm marks as .
Lemma A8. For every prefix such that , there exists a suffix β such that is a computation and
, or
, or
, or
.
Proof. There are two cases for :
Case 1: is environment-enabled (see Definition 18) in prefix :
According to Observation 5, there exists such that , . Any suffix that starts from s proves the theorem.
Case 2: is not environment-enabled in prefix
The proof for this case is identical to the proof of Case 2 of Lemma 2. □
Corollary A3. For every prefix such that , there exists a suffix β such that is a computation and
, or
, or
.
The following lemma focuses on states that are marked as .
Lemma A9. If α is a prefix of a computation and such that , or such that and , then, there exists a suffix β such that is a computation and
, or
, or
.
Proof. We prove this lemma by looking at lines where we expand :
Line 4:
In this case, we add to if either it is in , or it has a transition that is in . If , any computation starting from proves the theorem. Otherwise, any computation proves the theorem.
Line 24: :
According to Observation 6, there is a suffix (possibly ) that reaches . According to Corollary A3 there is a computation that either reaches , or never reaches .
Line 29:
In this case, we add state to , if is in or can reach state with an environment transition. If , any computation starting from proves the theorem. Otherwise, any computation proves the theorem. Note that, since we have started the computation from , or we have reached with a fault or program transition, even with the fairness assumption, the environment transition can execute. □
The following lemma states that reaching any state in will result in bad consequences that can be either executing a bad transition or never recovering to the invariant. Specifically,
Lemma A10. If where is a prefix of a computation, then, there exists a suffix such that is a computation and
, or
.
Proof. We prove this theorem inductively based on where we expand :
Base Case:
Let be any computation starting from . Since fault transitions can execute in any state, is a computation such that .
Induction hypothesis: Theorem holds for current .
Induction step: We look at lines where we add a state to :
Line 23:
According to Corollary A3, there is a suffix that either runs a transition in , never reaches , or reaches a state in . Thus, the theorem is proved by the induction hypothesis.
Line 28:
We add state to in three cases in this line:
Case 1
In this case according to Lemma A9, a transition in may occur, or there is a suffix that never reach , or a state in can be reached. Thus, according to the induction hypothesis, the theorem is proved.
Case 2
In this case, if according to fairness, can occur, state can be reached by and according to the induction hypothesis, the theorem is proved. However, if cannot occur, some other transition occurs. Since , we know that . By construction, contains any transition from states to R. Since , we conclude t goes to a state in (i.e., ). Thus, according to Lemma A9 either a transition in can occur, or there is a suffix that never reaches , or a state in can be reached. Thus, according to the induction hypothesis, the theorem is proved.
Case 3
In this case, if according to fairness, can occur, by its occurrence a transition in has occurred. However, if cannot occur, some other transition in should occur. Since , . Our algorithm add any possible program transition that is not and goes to a state in R to in Line 17. Since there is no such transition, any transition in either is in or goes to . In either case, we have a computation that reaches a state in starting from . Thus, according to Lemma A9, either a transition in can occur, or there is suffix that never reaches , or a state in can be reached. Thus, according to the induction hypothesis, the theorem is proved. □
Like Lemma A4 for Algorithm 2, we have following lemma for for Algorithm 3.
Lemma A11. If includes any state in in any iteration of the loop on Lines 13–21, then there is a computation that starts from that is not a .
Proof. The proof of this lemma is very similar to that of Lemma A4. □
Theorem A5. Algorithm 3 is complete.
Proof. Suppose program and invariant solve transformation problem. We show that at any point of Algorithm 3, must always be a subset of . We prove this by looking at lines where we set .
In the first iteration of the loop on Lines 6–43,
. According to constraint
C1 of the problem definition in
Section 5.1,
. Thus,
for the
at the beginning of the first iteration of the loop on Lines 6–43. According to Lemmas A9 and A10,
cannot have any transition in
in first iteration of the loop on Line 6–43, because by starting from a state in
, a computation may execute a bad transition, or reach a state outside
from which there is a computation that never reaches
(i.e., never reaches
). In addition,
must be closed in
and cannot have any deadlock state. Thus,
for
at Line 33.
According to Lemma A11, cannot include any state in in the first iteration of the loop of Lines 6–43, because otherwise there is a computation that is not (contradiction to C1). Thus, for at the end of the first iteration of the loop on Lines 6–43.
With the induction, we conclude that cannot include any states in or in next iterations of the loop of Lines 6–43. Thus, always we have . Our algorithm declares failure only when . Thus, if our algorithm does not find any solution, from , we have (contradiction to Definition 11). □