A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication
Abstract
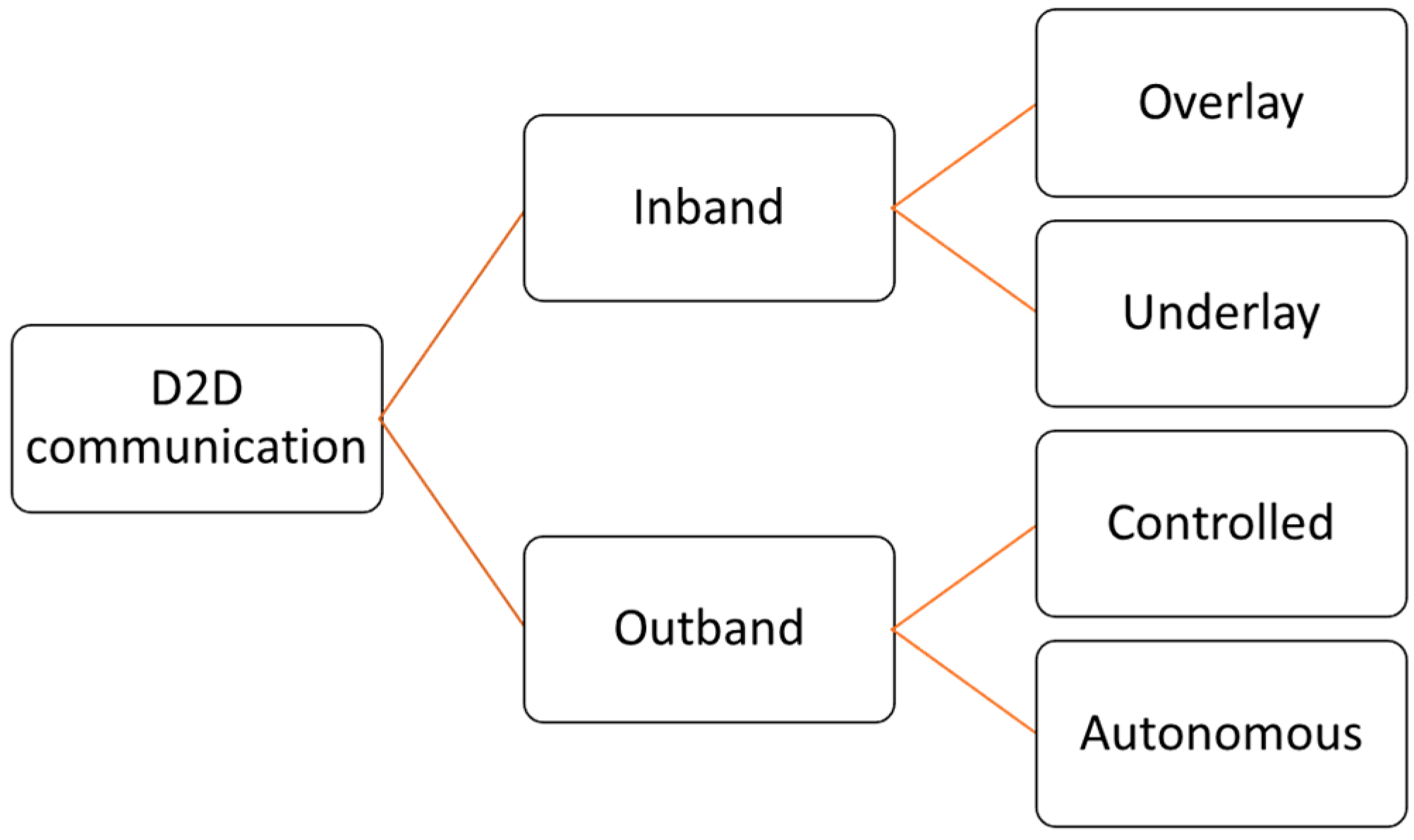
1. Introduction
2. Related Works
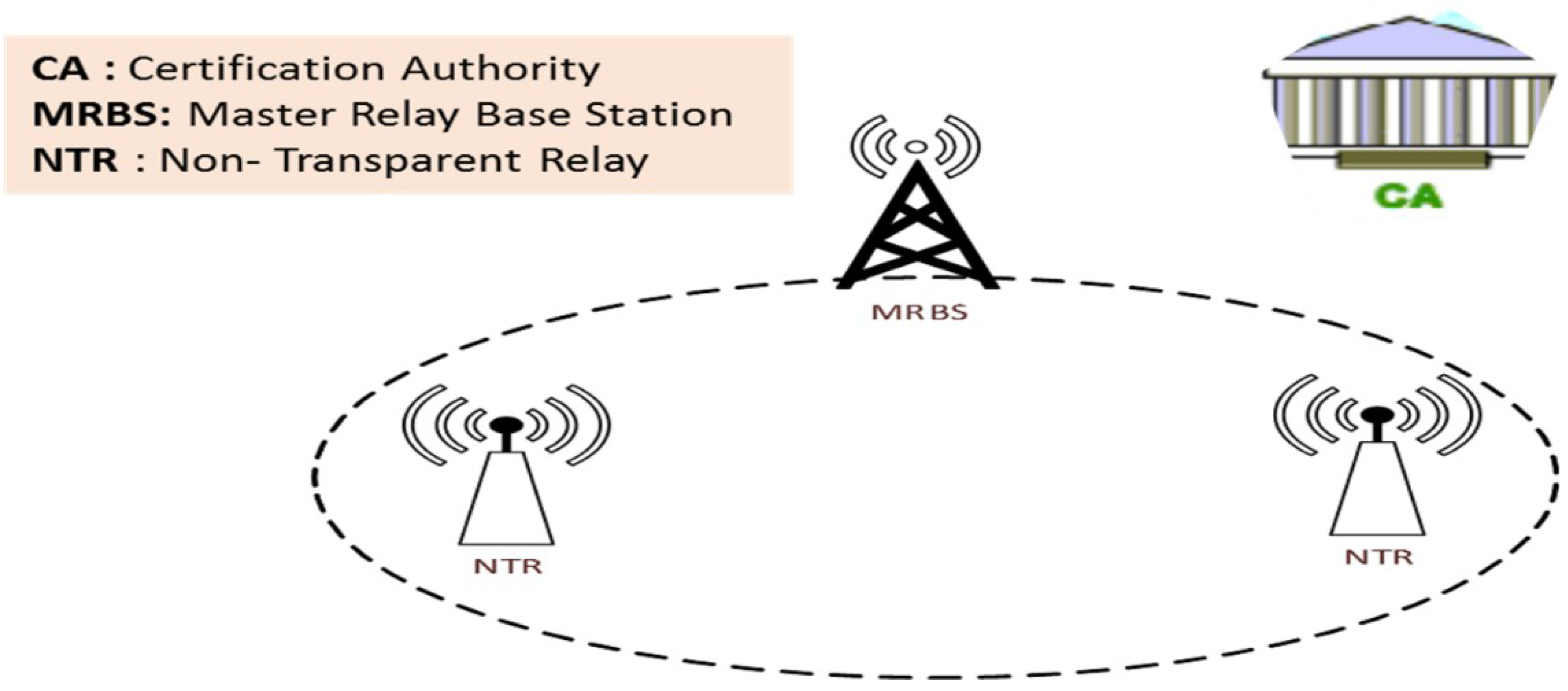
3. System Model
- Certification Authority (CA): The Certification Authority (CA) is a globally recognized and trusted entity in which all nodes can trust. Its task is to verify the authenticity of nodes and publish the public key for each node on a secured publicly available Whitelist that can be accessed by each node (‘node’ indicates MRBS or NTR).
- Master Relay Base Station (MRBS) is a node that is already registered with the CA and provides connectivity of all underlying nodes. Cellular companies deploy MRBS
- Non-Transparent Relay (NTR) is a node that provides the facility of connection, communication, and coverage to underlying devices. These relays are decode and forward and thus have limited capabilities such as MRBS. NTR is very limited in power, storage and computation.
- MRBS = {
- NTR = {
4. Our Cryptosystem
| Algorithm 1: Scheme for Encryption for Session transmission |
| AT NTR |
| Step 1: Select secret key |
| Step 2: Compute Public Key |
| Step 3: Send temporal public key to MRBS |
| AT MRBS |
| Step 4: Decrypt to get |
| Step 5: Select secret key |
| Step 6: Compute Public Key |
| Step 7: Compute the Secret key |
| Step 8: Encrypt the Message to get the Cipher |
5. Analysis and Discussion
5.1. Security Aspects
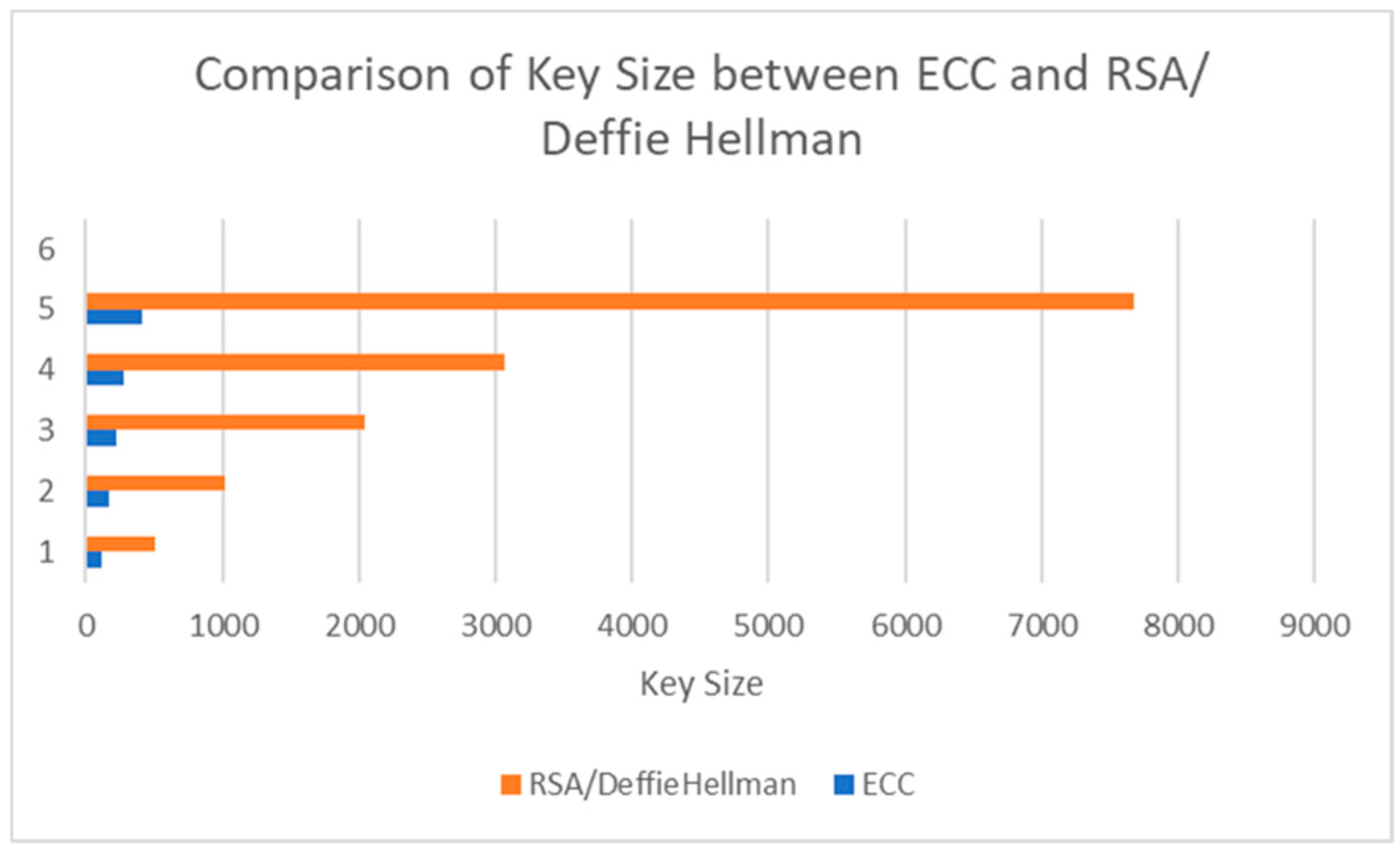
5.2. Computational Aspects
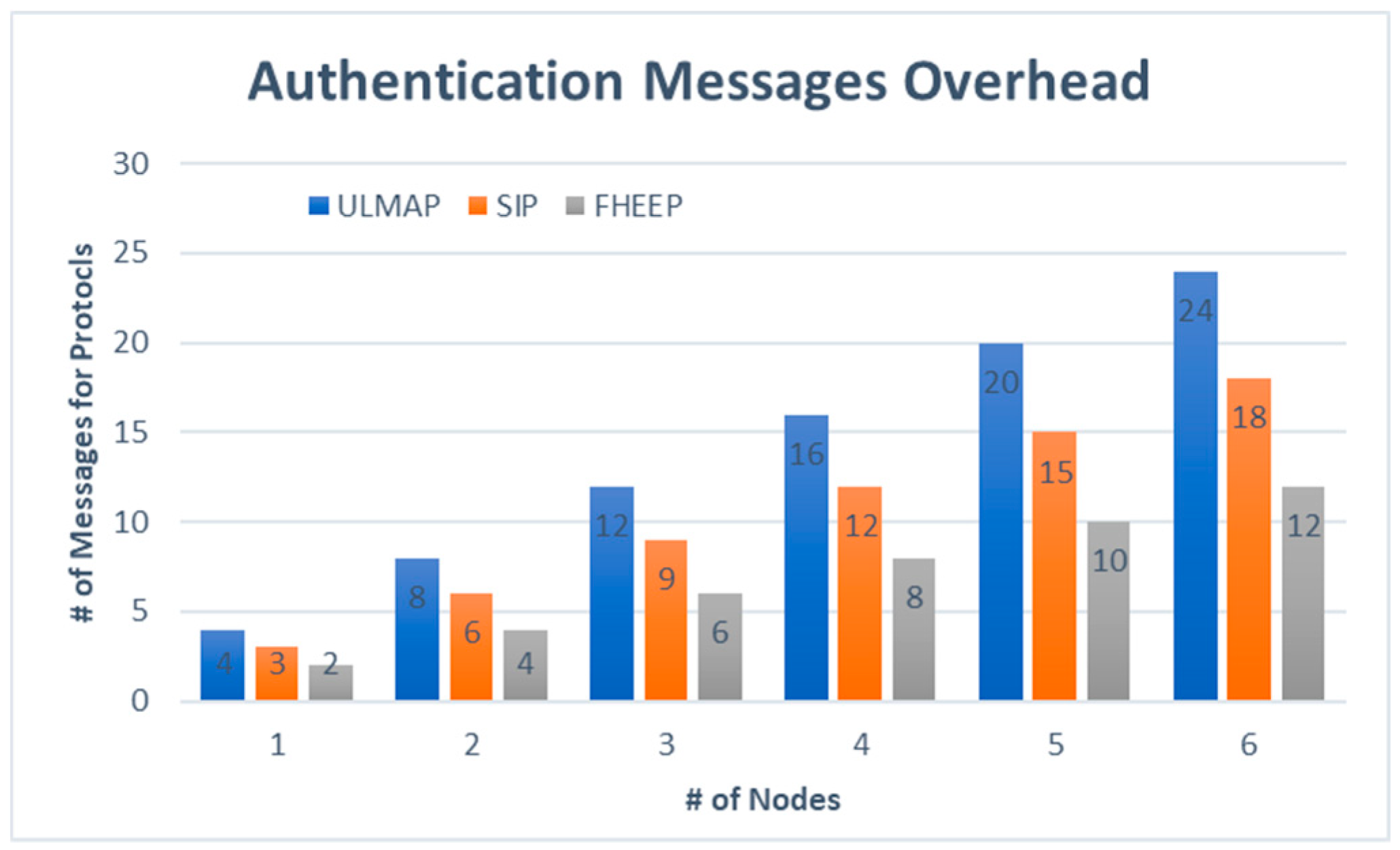
5.3. Authentication Overhead
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kato, N. On device-to-device (D2D) communication [Editor’s note]. IEEE Netw. 2016, 30, 2. [Google Scholar] [CrossRef]
- Wang, M.; Yan, Z. A Survey on Security in D2D Communications. Mob. Netw. Appl. 2017, 22, 195–208. [Google Scholar] [CrossRef]
- Alkurd, R.; Shubair, R.M.; Abualhaol, I. Survey on device-to-device communications: Challenges and design issues. In Proceedings of the IEEE 12th International New Circuits and Systems Conference (NEWCAS), Trois-Rivieres, QC, Canada, 22–25 June 2014; pp. 361–364. [Google Scholar]
- Asadi, A.; Wang, Q.; Mancuso, V. A survey on device-to-device communication in cellular networks. IEEE Commun. Surv. Tutor. 2014, 16, 1801–1819. [Google Scholar] [CrossRef]
- Liu, J.; Kato, N.; Ma, J.; Kadowaki, N. Device-to-Device Communication in LTE-Advanced Networks: A Survey. IEEE Commun. Surv. Tutor. 2015, 17, 1923–1940. [Google Scholar] [CrossRef]
- Theobald, L.M.; Wu, D.; Wang, J.; Hu, R.Q.; Cai, Y.; Zhou, L.; Laya, A.; Wang, K.K.; Widaa, A.A.; Alonso-Zarate, J.; et al. Device-to-device discovery for proximity-based service in LTE-advanced system. IEEE Commun. Mag. 2014, 16, 60–64. [Google Scholar] [CrossRef]
- 3GPP. Feasibility Study on Remote Management of USIM Application on M2M Equipment; 3GPP: Sophia Antipolis, France, 2009. [Google Scholar]
- Shiu, Y.-S.; Chang, S.-Y.; Wu, H.-C.; Huang, S.C.-H.; Chen, H.-H. Physical Layer Security in Wireless Networks: A Tutorial. IEEE Wirel. Commun. 2011, 18, 66–74. [Google Scholar] [CrossRef]
- Khan, A.S.; Javed, Y.; Abdullah, J.; Nazim, J.M.; Khan, N. Security issues in 5G device to device communication. Int. J. Comput. Sci. Netw. Secur. 2017, 17, 366–375. [Google Scholar]
- Stallings, W. Foundations of Modern Networking: SDN, NFV, QoE, IoT, and Cloud; Addison-Wesley Professional: Boston, MA, USA, 2015. [Google Scholar]
- Rahman, H.; Azad, S. Elliptic curve cryptography. In Practical Cryptography: Algorithms and Implementations Using C++; CRC Press: Boca Raton, FL, USA, 2014; pp. 147–181. [Google Scholar]
- Lazrag, H.; Chaibi, H.; Rachid, S.; Rahmani, M.D. An Optimal and Secure Routing Protocol for Wireless Sensor Networks. In Proceedings of the 2018 6th International Conference on Multimedia Computing and Systems (ICMCS), Rabat, Morocco, 10–12 May 2018; p. 13. [Google Scholar]
- Van der Meulen, R. Gartner Says 8.4 Billion Connected “Things” Will Be in Use in 2017, Up 31 Percent From 2016. Gart. Press Release 2017, 2016, 1. [Google Scholar] [CrossRef]
- Alenezi, M.; Almustafa, K.; Hussein, M. On Virtualization and Security-Awareness Performance Analysis in 5G Cellular Networks. J. Eng. Sci. Technol. Rev. 2018, 11, 199–207. [Google Scholar] [CrossRef]
- Al-Turjman, F. Information-centric framework for the Internet of Things (IoT): Traffic modeling & optimization. Future Gener. Comput. Syst. 2018, 80, 63–75. [Google Scholar] [CrossRef]
- Farris, I.; Orsino, A.; Militano, L.; Iera, A.; Araniti, G. Federated IoT services leveraging 5G technologies at the edge. Ad Hoc Networks 2018, 68, 58–69. [Google Scholar] [CrossRef]
- Habiba, U.; Hossain, E. Auction Mechanisms for Virtualization in 5G Cellular Networks: Basics, Trends, and Open Challenges. IEEE Commun. Surv. Tutor. 2018. [Google Scholar] [CrossRef]
- Ahmad, I.; Kumar, T.; Liyanage, M.; Okwuibe, J.; Ylianttila, M.; Gurtov, A. Overview of 5G Security Challenges and Solutions. IEEE Commun. Stand. Mag. 2018, 2, 36–43. [Google Scholar] [CrossRef]
- Kim, J.Y.; Hu, W.; Shafagh, H.; Jha, S. SEDA: Secure Over-The-Air CodeDissemination Protocol for the Internet of Things. IEEE Trans. Dependable Secur. Comput. 2016, 15, 1041–1054. [Google Scholar] [CrossRef]
- Laiphrakpam, D.S.; Khumanthem, M.S. A robust image encryption scheme based on chaotic system and elliptic curve over finite field. Multimed. Tools Appl. 2017, 1–24. [Google Scholar] [CrossRef]
- Ni, J.; Lin, X.; Shen, X. Efficient and Secure Service-oriented Authentication Supporting Network Slicing for 5G-enabled IoT. IEEE J. Sel. Areas Commun. 2018. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Leu, F.Y.; Atiquzzaman, M. Secure and efficient protocol for fast handover in 5G mobile Xhaul networks. J. Netw. Comput. Appl. 2018, 102, 38–57. [Google Scholar] [CrossRef]
- Karati, A.; Islam, S.H.; Karuppiah, M. Provably Secure and Lightweight Certificateless Signature Scheme for IIoT Environments. IEEE Trans. Ind. Inf. 2018. [Google Scholar] [CrossRef]
- Gritti, C.; Molva, R.; Önen, M. Lightweight Secure Bootstrap and Message Attestation in the Internet of Things. In Proceedings of the SAC 2018, 33rd ACM/SIGAPP Symposium On Applied Computing, Pau, France, 9–13 April 2018. [Google Scholar]
- Fang, D.; Qian, Y.; Hu, R.Q. Security for 5G Mobile Wireless Networks. IEEE Access 2017, PP, 1. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, B.; Weng, J.; Zhao, Z.; Cheng, Y. Attack and Countermeasure on Interlock-based Device Pairing Schemes. IEEE Trans. Inf. Forensics Secur. 2017. [Google Scholar] [CrossRef]
- Sedidi, R.; Kumar, A. Key exchange protocols for secure Device-to-Device (D2D) communication in 5G. In Proceedings of the 2016 Wireless Days (WD), Toulouse, France, 23–25 March 2016. [Google Scholar] [CrossRef]
- Ahmed, T. Securing AOMDV Protocol in Mobile Adhoc Network with Elliptic Curve Cryptography. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 539–543. [Google Scholar]
- Dake, S.S.; Ighare, R.U. A proposed ECC algorithm for smart cards cell phones and wireless networks. In Proceedings of the 2017 International Conference on Nascent Technologies in Engineering (ICNTE), Navi Mumbai, India, 27–28 January 2017. [Google Scholar]
- Khan, S.; Khan, R. Elgamal elliptic curve based secure communication architecture for microgrids. Energies 2018, 11, 759. [Google Scholar] [CrossRef]
- Javed, Y.; Khan, A.S.; Abbasi, M.A.K. Key Security Attacks and Their Remedies in D2D Communication. UBICC 2019, 13. [Google Scholar]
- Shah, S.T.; Hasan, S.F.; Seet, B.C.; Chong, P.H.J.; Chung, M.Y. Device-to-Device Communications: A Contemporary Survey. Wirel. Pers. Commun. 2018, 98, 1247–1284. [Google Scholar] [CrossRef]
- Kumar, M.; Gupta, P. A Novel and Secure Multiparty Key Exchange Scheme Using Trilinear Pairing Map Based on Elliptic Curve Cryptography. Adv. Intell. Syst. Comput. 2018, 583, 37–50. [Google Scholar] [CrossRef]
- Javed, Y.; Khan, A.S.; Qahar, A.; Abdullah, J. EEoP: A lightweight security scheme over PKI in D2D cellular networks. J. Telecommun. Electron. Comput. Eng. 2017, 9, 99–105. [Google Scholar]
- Bach, E. Toward a theory of Pollard’s rho method. Inf. Comput. 1991, 90, 139–155. [Google Scholar] [CrossRef]
- Bos, J.; Kaihara, M.; Kleinjung, T. On the Security of 1024-bit RSA and 160-bit Elliptic Curve Cryptography. Iacr Cryptol. Eprint 2009, 57, 1–19. [Google Scholar]
- Bos, J.W.; Kaihara, M.E.; Kleinjung, T.; Lenstra, A.K.; Montgomery, P.L. Solving a 112-bit prime elliptic curve discrete logarithm problem on game consoles using sloppy reduction. Int. J. Appl. Cryptogr. 2012, 2, 212. [Google Scholar] [CrossRef]
- Meadows, C. Analyzing the Needham-Schroeder public key protocol: A comparison of two approaches. Comput. Secur.—Esorics 96 1996, 1146, 351–364. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Macdonald, I.G. Introduction to commutative algebra. Am. Math. Mon. 1969, 77, ix+128. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2004. [Google Scholar]
- Vanstone, S.A. Next generation security for wireless: Elliptic curve cryptography. Comput. Secur. 2003, 22, 412–415. [Google Scholar] [CrossRef]
- Wang, Y.; Ramamurthy, B.; Zou, X. The Performance of Elliptic Curve Based Group Diffie-Hellman Protocols for Secure Group Communication over Ad Hoc Networks. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 2243–2248. [Google Scholar]
- Stajano, F.; Anderson, R. The Resurrecting Duckling: Security Issues for Ubiquitous Computing. Computer 2002, 35, supl22–supl26. [Google Scholar] [CrossRef]
- Fan, K.; Song, P.; Yang, Y. ULMAP: Ultralightweight NFC Mutual Authentication Protocol with Pseudonyms in the Tag for IoT in 5G. Mob. Inf. Syst. 2017, 2017. [Google Scholar] [CrossRef]
- Chaudhry, S.A.; Naqvi, H.; Sher, M.; Farash, M.S.; Hassan, M.U. An improved and provably secure privacy preserving authentication protocol for SIP. Peer Peer Netw. Appl. 2015, 1–15. [Google Scholar] [CrossRef]

| FHEEP | RSA/DH |
|---|---|
| 112 | 512 |
| 224 | 2048 |
| 571 | 15,360 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abro, A.; Deng, Z.; Memon, K.A. A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication. Future Internet 2019, 11, 108. https://doi.org/10.3390/fi11050108
Abro A, Deng Z, Memon KA. A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication. Future Internet. 2019; 11(5):108. https://doi.org/10.3390/fi11050108
Chicago/Turabian StyleAbro, Adeel, Zhongliang Deng, and Kamran Ali Memon. 2019. "A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication" Future Internet 11, no. 5: 108. https://doi.org/10.3390/fi11050108
APA StyleAbro, A., Deng, Z., & Memon, K. A. (2019). A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication. Future Internet, 11(5), 108. https://doi.org/10.3390/fi11050108






