Epidemic Spreading in Urban Areas Using Agent-Based Transportation Models
Abstract
:1. Introduction
- Using a large-scale agent-based transport simulation model, it is feasible to describe individual behavior throughout an epidemic outbreak. Not only can the locations, the person-to-person interaction time, and the activities of each individual be simulated, but also the interactions between household members and their behavior changes can be taken into account.
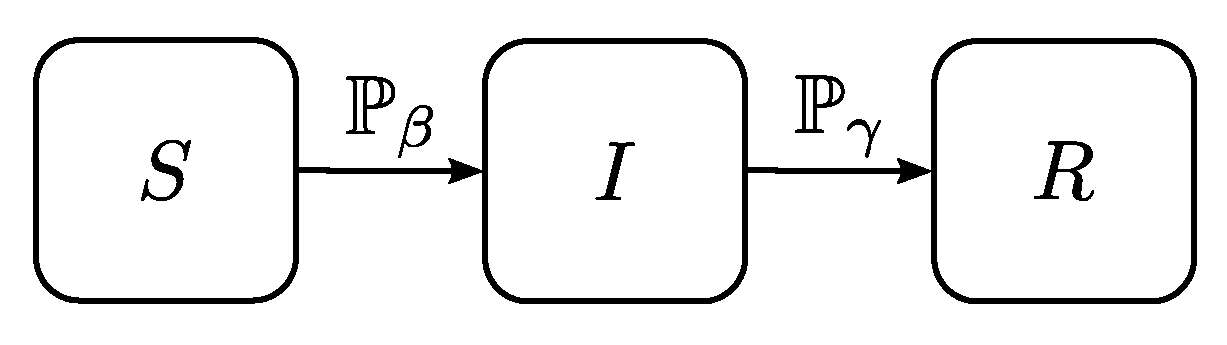
- Because each person is represented individually, it is possible to directly assign infection and recovery probabilities to them, which provides a more realistic representation than the parameter-based approach of classical epidemic spread models.
- The proposed approach allows the recreation of historical events of epidemic outbreaks. Using the metropolitan area of Zurich, Switzerland, it is shown that even with simple assumptions the agent-based model gives a good approximation of the seasonal influenza outbreak observed in 2016/2017.
2. Background
2.1. Classical Epidemic Spread Models
2.2. Complex Network Epidemic Spread Models
2.3. Agent-Based Epidemic Spread Models
3. Methods
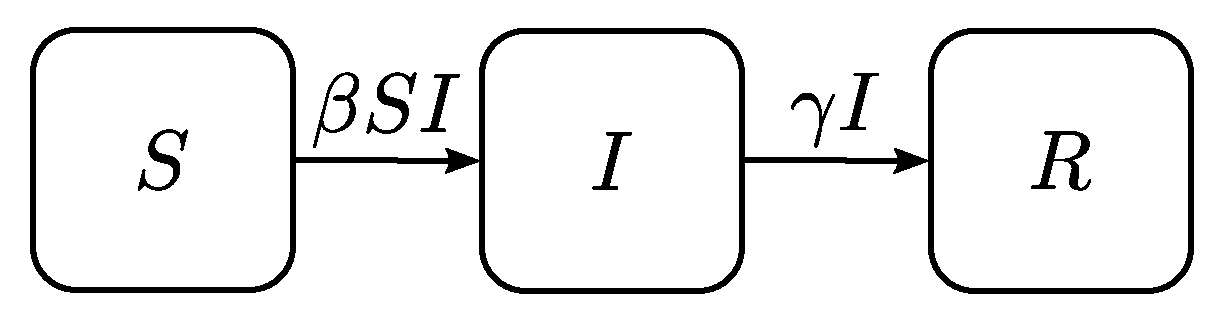
3.1. Generic Epidemic Spread Model
- A constant and closed population is assumed meaning that although the number of individuals in each disease state changes over time, the sum of all states is always equal to the population size. Demographic turnovers and fatalities due to the virus are not considered.
- Every agent has the same probability to get infected, even though children are much more infectious than adults and shed virus from just before they develop symptoms until two weeks after infection. Additionally, every susceptible agent in a facility has the probability of getting infected, even if there is no direct contact with an infected agent.
- It is assumed that infected agents do not change their daily activities, i.e., they continue with their original plans.
- Every agent has the same probability of getting recovered.
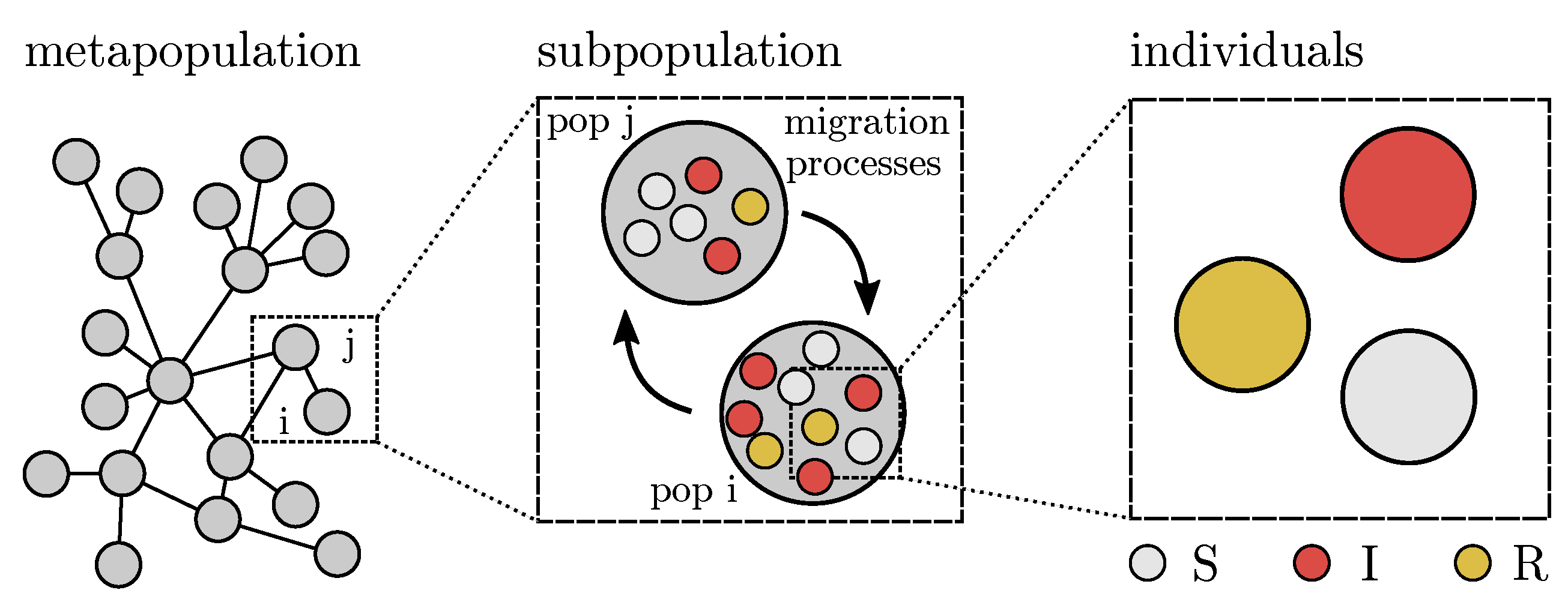
3.2. Agent-Based Model
3.3. Model Calibration and Validation
- Defining the agents in terms of basic socio-demographic data and home location
- Assigning an activity schedule to each of these agents.
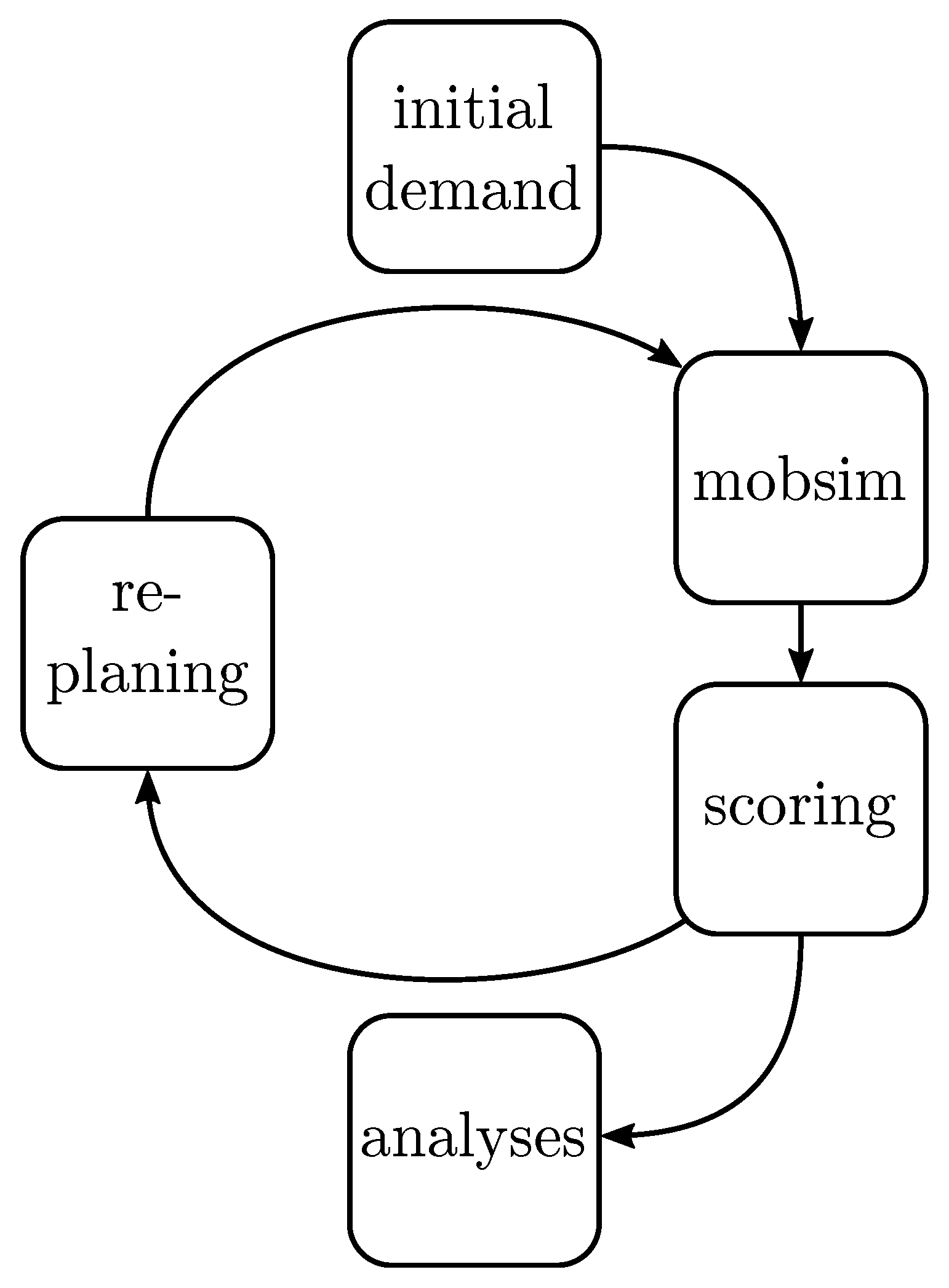
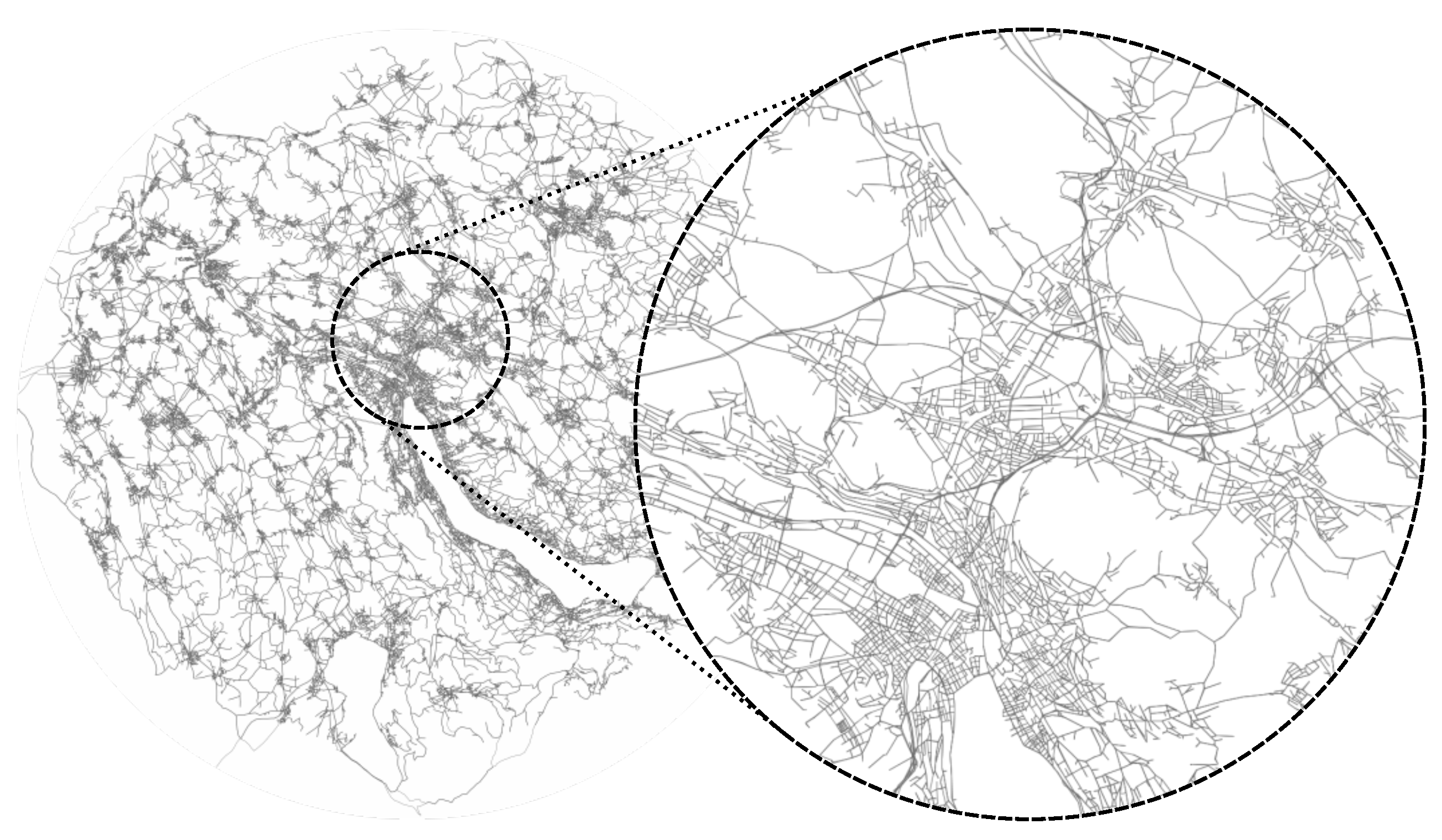
3.4. Implementation
- Numerical study: The first example is a numerical study where a series of simulations are performed with varying input parameters , and . The aim is to test the variability of the model and to investigate the sensitivity of the individual parameters. Furthermore, it serves as a basis for the second example and the identification of further research priorities.
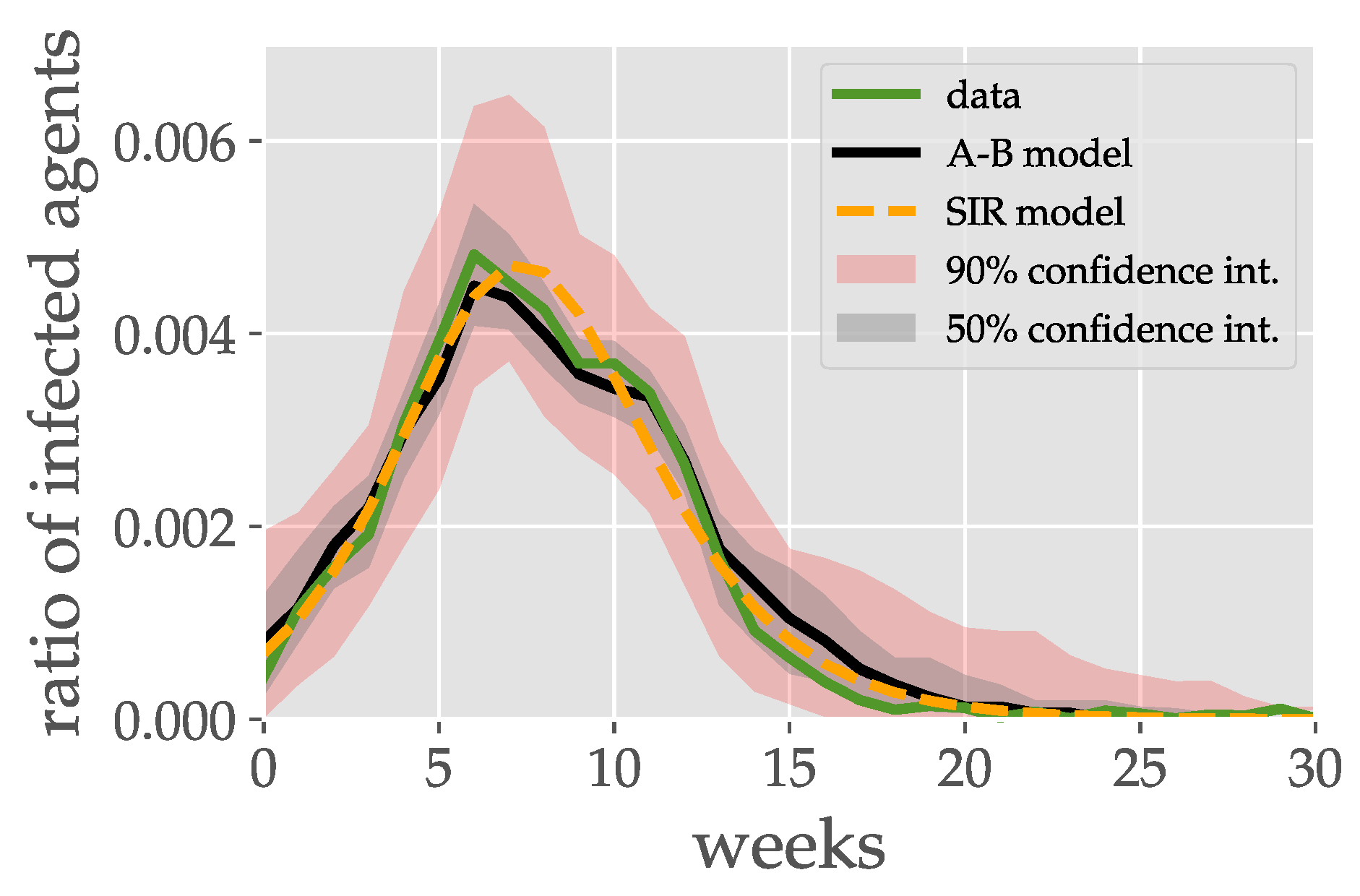
- Historical event: While the first example gives a general insight into the model, this example aims at the best possible reproduction of a historical event with the gained knowledge. To achieve this, the agent-based epidemic spread model and the classical compartment SIR model are fitted to real data of seasonal influenza in the season 2016/2017 observed in the Zurich area [35].
4. Result and Discussion
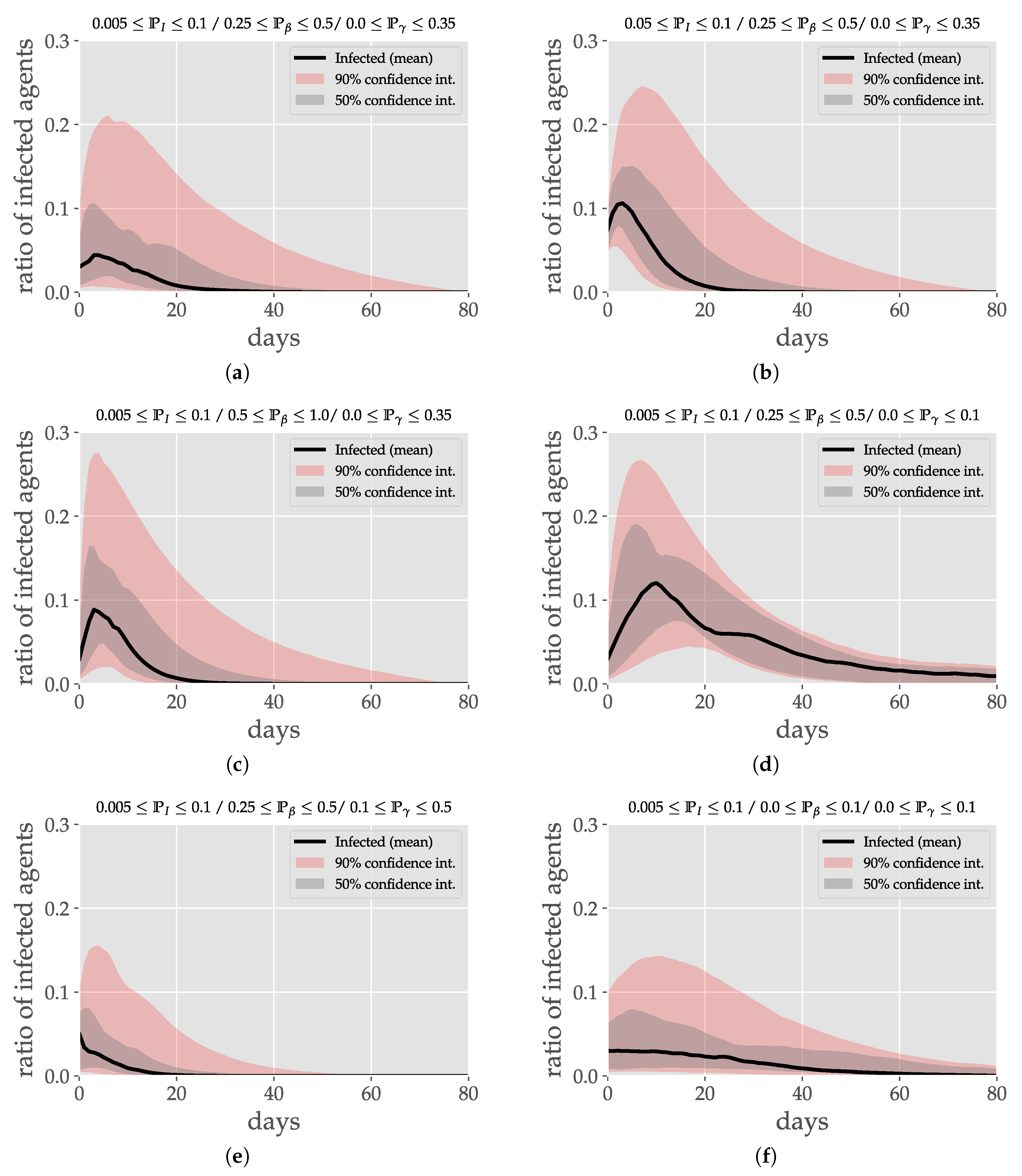
4.1. Numerical Study
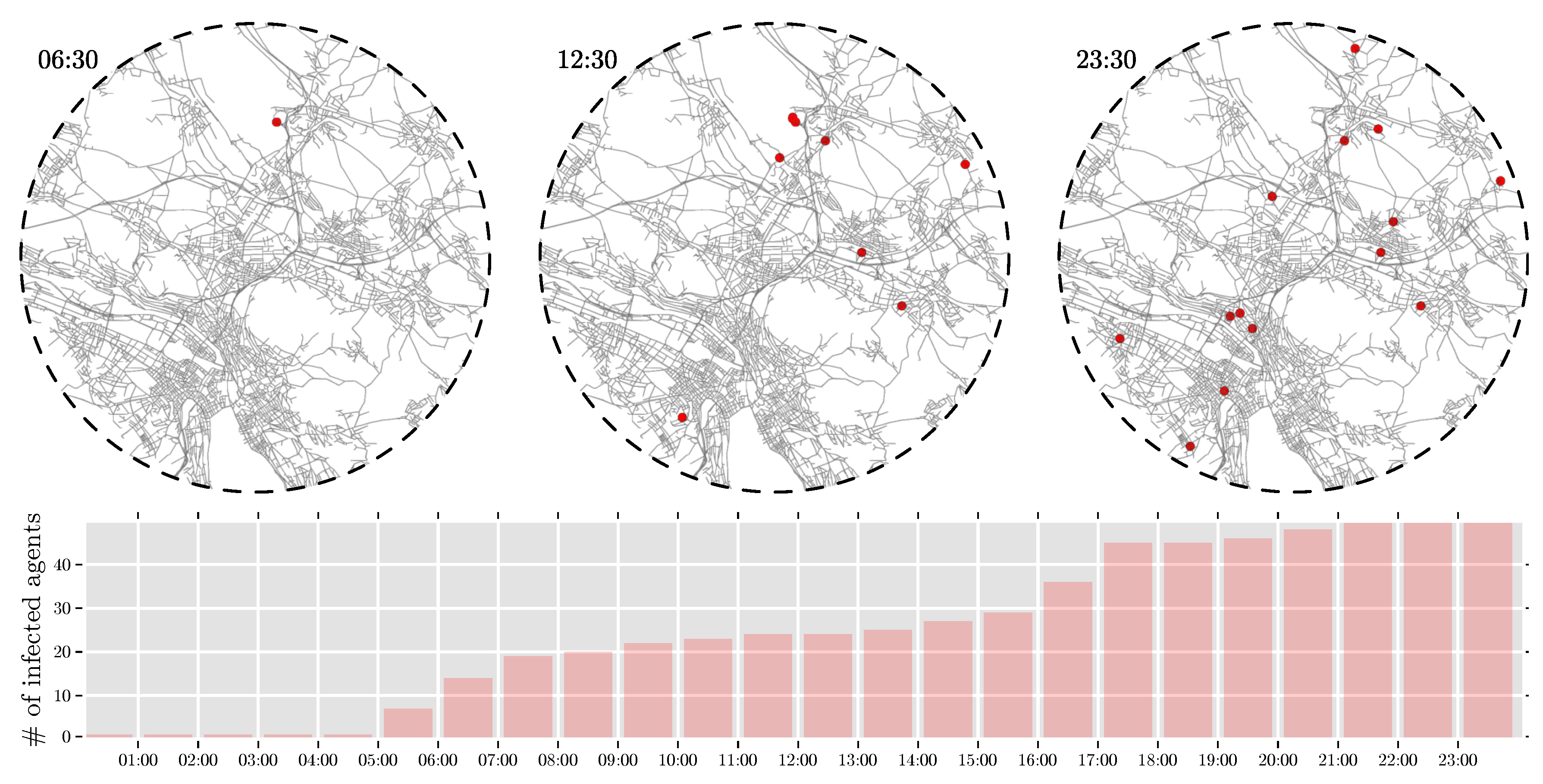
4.1.1. Temporal-Spatial Resolution
4.1.2. Varying Parameters
4.2. Historical Event
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| S | Susceptible |
| I | Infected |
| R | Recoveredthree |
| MATSim | Multi-Agent Transport Simulation |
References
- Hackl, J.; Dubernet, T. Modelling epidemic spreading in urban areas with large-scale agent-based transport simulations. In Complex Networks and Their Applications—Volume 2, Proceedings the 7th International Conference on Complex Networks and Their Applications, Cambridge, UK, 11–13 December 2018; Cherifi, H., Aiello, L.M., Cherifi, C., Lio, P., Lambiotte, R., Rocha, L.M., Eds.; University of Cambridge: Cambridge, UK, 2018; pp. 85–87. [Google Scholar]
- Brockmann, D. Human Mobility and Spatial Disease Dynamics. Rev. Nonlinear Dyn. Complex. 2010, 2, 1–24. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361–367. [Google Scholar] [CrossRef]
- Balcan, D.; Colizza, V.; Gonclaves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale mobility networks and the spatial. Proc. Natl. Acad. Sci. USA 2009, 106, 21484–21489. [Google Scholar] [CrossRef]
- Bajardi, P.; Poletto, C.; Ramasco, J.J.; Tizzoni, M.; Colizza, V.; Vespignani, A. Human mobility networks, travel restrictions, and the global spread of 2009 H1N1 pandemic. PLoS ONE 2011, 6, e16591. [Google Scholar] [CrossRef]
- Connell, R.; Dawson, P.; Skvortsov, A. Comparison of an Agent-Based Model of Disease Propagation with the Generalised SIR Epidemic Model; DSTO-TR-23; Defense Science and Technology Organisation: Canberra, Australia, 2009; pp. 1–22.
- Balcan, D.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Colizza, V.; Vespignani, A. Modeling the spatial spread of infectious diseases: The global epidemic and mobility computational model. J. Comput. Sci. 2010, 1, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Frias-Martinez, E.; Williamson, G.; Frias-Martinez, V. An Agent-Based Model of Epidemic Spread using Human Mobility and Social Network Information. In Proceedings of the 3rd International Conference on Social Computing (SocialCom’11), Boston, MA, USA, 9–11 October 2011; pp. 49–56. [Google Scholar] [CrossRef]
- Smieszek, T.; Balmer, M.; Hattendorf, J.; Axhausen, K.W.; Zinsstag, J.; Scholz, R.W. Reconstructing the 2003/2004 H3N2 influenza epidemic in Switzerland with a spatially explicit, individual-based model. BMC Infect. Dis. 2011, 11, 115. [Google Scholar] [CrossRef] [PubMed]
- García-Magariño, I. Practical multi-agent system application for simulation of tourists in Madrid routes with INGENIAS. In Advances in Practical Applications of Heterogeneous Multi-Agent Systems. The PAAMS Collection, Proceedings of the 12th International Conference, PAAMS 2014, Salamanca, Spain, 4–6 June 2014; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); 8473 LNAI; Springer: Berlin, Germany, 2014; pp. 122–133. [Google Scholar] [CrossRef]
- García-Magariño, I. ABSTUR: An Agent-based Simulator for Tourist Urban Routes. Expert Syst. Appl. 2015, 42, 5287–5302. [Google Scholar] [CrossRef]
- Nicholls, S.; Amelung, B.; Student, J. Agent-Based Modeling. J. Travel Res. 2017, 56, 3–15. [Google Scholar] [CrossRef]
- García-Magariño, I.; Gutiérrez, C.; Fuentes-Fernández, R. The INGENIAS Development Kit: A Practical Application for Crisis-Management. In Bio-Inspired Systems: Computational and Ambient Intelligence IWANN 2009; Lecture Notes in Computer Science; Cabestany, J., Sandoval, F., Prieto, A., Corchado, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5517, pp. 537–544. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Lee, S. An evacuation route choice model based on multi-agent simulation in order to prepare Tsunami disasters. Transp. B Transp. Dyn. 2017, 5, 385–401. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, K.; Ozbay, K.; Yang, H. Hurricane Evacuation Modeling Using Behavior Models and Scenario-Driven Agent-based Simulations. Procedia Comput. Sci. 2018, 130, 836–843. [Google Scholar] [CrossRef]
- Horni, A.; Nagel, K.; Axhausen, K. (Eds.) The Multi-Agent Transport Simulation MATSim; Ubiquity Press: London, UK, 2016; p. 618. [Google Scholar] [CrossRef]
- Perez, L.; Dragicevic, S. An agent-based approach for modeling dynamics of contagious disease spread. Int. J. Health Geogr. 2009, 8, 1–17. [Google Scholar] [CrossRef]
- D’Onofrio, A. On pulse vaccination strategy in the SIR epidemic model with vertical transmission. Appl. Math. Lett. 2005, 18, 729–732. [Google Scholar] [CrossRef] [Green Version]
- Makinde, O. Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 2007, 184, 842–848. [Google Scholar] [CrossRef]
- Shang, Y. A lie algebra approach to susceptible-infected-susceptible epidemics. Electron. J. Differ. Equ. 2012, 2012, 1–7. [Google Scholar]
- Shang, Y. Analytical Solution for an In-host Viral Infection Model with Time-inhomogeneous Rates. Acta Phys. Pol. B 2015, 46, 1567. [Google Scholar] [CrossRef]
- Shang, Y. Modeling epidemic spread with awareness and heterogeneous transmission rates in networks. J. Biol. Phys. 2013, 39, 489–500. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, Y. Degree distribution dynamics for disease spreading with individual awareness. J. Syst. Sci. Complex. 2015, 28, 96–104. [Google Scholar] [CrossRef]
- Colizza, V.; Vespignani, A. Epidemic modeling in metapopulation systems with heterogeneous coupling pattern: Theory and simulations. J. Theor. Biol. 2008, 251, 450–467. [Google Scholar] [CrossRef] [Green Version]
- Helbing, D.; Balietti, S. Agent-Based Modeling. In Social Self-Organization; Helbing, D., Ed.; Understanding Complex Systems, Springer: Berlin/Heidelberg, Germany, 2012; Chapter 2; pp. 25–70. [Google Scholar] [CrossRef]
- Eubank, S.; Guclu, H.; Anil Kumar, V.S.; Marathe, M.V.; Srinivasan, A.; Toroczkai, Z.; Wang, N. Modelling disease outbreaks in realistic urban social networks. Nature 2004, 429, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Song, Z.; Sheng, K.; Duan, H.; Qiu, X. The Design of a Small-Scale Epidemic Spreading Simulation System. In Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems, Proceedings of the 16th Asia Simulation Conference and SCS Autumn Simulation Multi-Conference, AsiaSim/SCS AutumnSim 2016, Beijing, China, 8–11 October 2016; Zhang, L., Song, X., Wu, Y., Eds.; Springer: Singapore, 2016; pp. 201–215. [Google Scholar] [CrossRef]
- Müller, K. A Generalized Approach to Population Synthesis. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2017. [Google Scholar] [CrossRef]
- Bösch, P.M.; Müller, K.; Ciari, F. The IVT 2015 Baseline Scenario. In Proceedings of the 16th Swiss Transport Research Conference, Monte Verità, Switzerland, 18–20 May 2016. [Google Scholar] [CrossRef]
- Ruch, C.; Horl, S.; Frazzoli, E. AMoDeus, a Simulation-Based Testbed for Autonomous Mobility-on-Demand Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3639–3644. [Google Scholar] [CrossRef]
- Rieser, M.; Métrailler, D.; Lieberherr, J. Adding Realism and Efficiency to Public Transportation in MATSim. In Proceedings of the 18th Swiss Transport Research Conference, Ascona, Switzerland, 16–18 May 2018; pp. 1–21. [Google Scholar]
- Wardrop, J.G. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Chakirov, A.; Fourie, P.J. Enriched Sioux Falls Scenario with Dynamic and Disaggregate Demand; Technical Report; IVT, ETH Zurich: Zurich, Switherland, 2014. [Google Scholar]
- FOPH. Saisonbericht Grippe 2016 / 2017. BAG-Bulletin 31; Federal Office of Public Health (FOPH): Bern, Switzerland, 2017.
- Troko, J.; Myles, P.; Gibson, J.; Hashim, A.; Enstone, J.; Kingdon, S.; Packham, C.; Amin, S.; Hayward, A.; Van-Tam, J.N. Is public transport a risk factor for acute respiratory infection? BMC Infect. Dis. 2011, 11, 2–7. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hackl, J.; Dubernet, T. Epidemic Spreading in Urban Areas Using Agent-Based Transportation Models. Future Internet 2019, 11, 92. https://doi.org/10.3390/fi11040092
Hackl J, Dubernet T. Epidemic Spreading in Urban Areas Using Agent-Based Transportation Models. Future Internet. 2019; 11(4):92. https://doi.org/10.3390/fi11040092
Chicago/Turabian StyleHackl, Jürgen, and Thibaut Dubernet. 2019. "Epidemic Spreading in Urban Areas Using Agent-Based Transportation Models" Future Internet 11, no. 4: 92. https://doi.org/10.3390/fi11040092
APA StyleHackl, J., & Dubernet, T. (2019). Epidemic Spreading in Urban Areas Using Agent-Based Transportation Models. Future Internet, 11(4), 92. https://doi.org/10.3390/fi11040092




