Abstract
One of the most important research topics nowadays is human action recognition, which is of significant interest to the computer vision and machine learning communities. Some of the factors that hamper it include changes in postures and shapes and the memory space and time required to gather, store, label, and process the pictures. During our research, we noted a considerable complexity to recognize human actions from different viewpoints, and this can be explained by the position and orientation of the viewer related to the position of the subject. We attempted to address this issue in this paper by learning different special view-invariant facets that are robust to view variations. Moreover, we focused on providing a solution to this challenge by exploring view-specific as well as view-shared facets utilizing a novel deep model called the sample-affinity matrix (SAM). These models can accurately determine the similarities among samples of videos in diverse angles of the camera and enable us to precisely fine-tune transfer between various views and learn more detailed shared facets found in cross-view action identification. Additionally, we proposed a novel view-invariant facets algorithm that enabled us to better comprehend the internal processes of our project. Using a series of experiments applied on INRIA Xmas Motion Acquisition Sequences (IXMAS) and the Northwestern–UCLA Multi-view Action 3D (NUMA) datasets, we were able to show that our technique performs much better than state-of-the-art techniques.
1. Introduction
Human action data are all-encompassing, which is why such data are of significant interest to the computer vision [1,2] as well as machine learning communities [3,4]. There are various views through which we can study human action data. One example is a group of dynamic actions captured by different views of the camera, as shown in Figure 1. Classifying this kind of data is quite difficult in a cross-view situation because the raw data are captured at varying locations by different cameras and, thus, could look completely different. A perfect example is represented in Figure 1a, where the action captured from a top view appears different from the one captured from a side view. This implies that features obtained from a single camera view cannot provide enough discriminative aspects to classify actions in another camera view. Many studies concentrate on ways of developing view-invariant pictures for action recognition [5,6], where all the actions captured on video are treated as frame time series. Many approaches have utilized a self-similarity matrix (SSM) descriptor [5,7] to replay actions and have proven to be robust in cross-view outlines. Information shared among camera views are each kept and transferred to all the views [7,8]. It is assumed that the shared features contribute equally with samples from different views. Through our research, we found that this assumption is not true because the discriminative parameters of one of the views could be very far away from the parameters of other views. Therefore, this may result in a misunderstanding by classifiers, as they do not control the sharing of data between action categories, which would result in an incorrect model result.
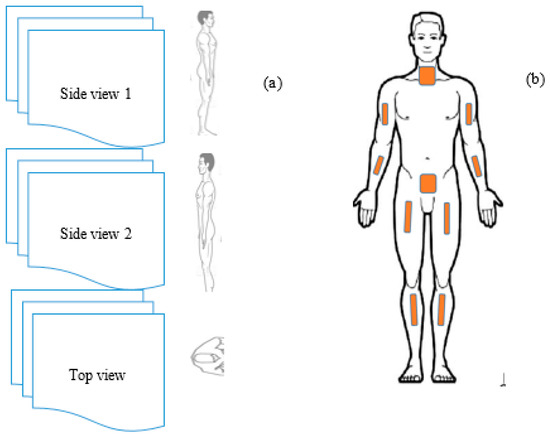
Figure 1.
The figure shows a multi-view situation where (a) shows how human actions are captured from different perspectives, while (b) shows how various sensors are connected on the body of a human being so as to gather enough action data (images from Google Images).
As a response to the assumption of the equal contribution of share features, in this paper, we put forward original networks that can learn view-invariant features for cross-view action categorization, and we have introduced a novel sample-affinity matrix (SAM) that can accurately determine similarities of video samples. By encouraging incoherence between shared and private features, we learned discriminative view-invariant information. Our approaches retain two types of features—strong private features as well as shared features across views acquired by a single autoencoder. SAM focuses on the resemblance between samples, but SSM concentrates on the video frames. The vanity between these facets was achieved by strengthening the coherence between the mapping matrices. In addition, in a layer-wise fashion, we piled several layers of features in order to learn them. After a set of experiments was carried out on three multi-view sets of data, we found out that our method performs much better than state-of-the-art methods. The following pieces of information are covered in the next sections of this paper. We first analyze works related to our topic and follow this with an analysis of view-invariant features. Then, we present a detailed description of the structure of our method together with the algorithm used. Finally, through a set of experiments, we show that our method performs much better than state-of-the-art methods.
2. Research Problem Definition
It is difficult for various view-invariant methods to find similarity among various frames captured from different RGB camera (standard CMOS sensor camera) views at the same time. However, with an RGB-D camera (depth sensor added), this is not an issue because the camera provides a powerful feature that allows for easy extraction of the required feature from the plan (Figure 2). The only challenge is generating artificial views that have all the facets necessary for understanding the action. In this paper, we also introduce a novel algorithm based on sample affine matrix (SAM) and various powerful autoencoders that allows for extraction of shared and unshared facets needed for identifying human action.
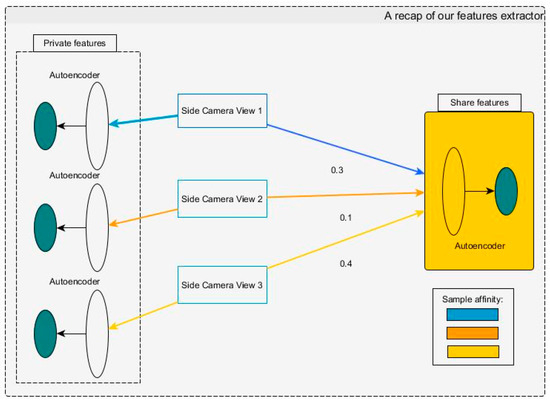
Figure 2.
The figure shows a recap of our features extractor.
3. Related Research
A multi-view study, as cited in [4], establishes the similarities between two different views. There are several other published methods used to serve the same purpose. These methods have been published with the intention of concentrating their interest on expressive as well as discriminative facets from low-level observations [9,10,11,12,13,14]. Similarly, [15] entirely used the intrinsic characteristics extracted from the views by combining color and depth information, which resulted in the improvement of their perspective-invariant feature transform (PIFT) for RGB-D images. However, [15] focused on the combined used of the RGB and depth component and gave less attention to the features (shared and global) to be extracted from each viewpoint. Zhang et al. [16] obtained a dictionary that can be used to convert 2D video to a view-invariant sparse representation, as well as a classifier to recognize actions with an arbitrary view by using an end-to-end framework to learn view invariance jointly. The authors of [16] also introduced a 3D trajectory which can describe the action better; however, it does not emphasize the percentage of contribution of each view to that trajectory. Kerola et al. [17] took a temporal sequence of graphs as an illustration of a graph representation action and used that to create a feature descriptor by applying a spectral graph wavelet transform. The authors of [17] also emphasized two well-known types of view-invariant graphs—key point-based and skeleton-based graphs. Rahmani et al. [18] devised a histogram of oriented principal components (HOPC) that is robust to noise. Unlike several articles, [18] obtained cloud points by directly dealing with point clouds for cross-view action recognition from unknown and unseen views. Also, [19] proposed a different approach when extracted functionality is needed. Hsu et al. [19] used the Euclidean distance between the spatiotemporal characteristic vectors represented in a spatiotemporal matrix (STM). Daumé and Kumar [20] presented a cotraining technique that trains various learning algorithms for every view and determines a certain correlation between two pairs of information among various views. Zhang et al. [21] and He et al. [22] introduced another approach called canonical correlation analysis (CCA) that helps in monitoring a common space among various views. Moreover, in [23], a challenge was encountered when studying an incomplete view owing to an assumption that multiple views are created from a shared space. Kumar et al. [24] provided another approach called generalized multi-view analysis (GMA). According to Liu et al. [11], which found that matrix factorization was applicable in the clustering of multiple views, [10] was introduced alongside the collective matrix factorization (CMF) method, which learns relationships between feature matrices. Similarly, Ding et al. [14] came up with a low-rank controlled matrix factorization model that provides a solution to the challenge faced in the multi-view learning. Various studies have tried to provide solutions to the challenges associated with view-invariant action recognition. One of these challenges is related to the generation of action labels in a scenario where multiple views are involved. Özuysal et al. [25] introduced an approach that offers a structured categorization of the 3D histogram of oriented gradients (HOG) and local separation with an intention to represent successive images. Dexter and colleagues [5,26] showed an SSM-based approach that extracts view-invariant descriptors in a log-polar block of the matrix by determining a frame-wise resemblance matrix in a video. However, a multitask learning technique can be used to enhance the SSM power of the representation [7]. This technique comprises shared facets among different views as examined in [6,8,27,28], where more explicit approaches exist. Gao et al. [6] used an MRM-Lasso method to keep latent adjustment through various views. This was achieved by examining a lowly ranked matrix comprising weights of specific patterns. However, Jiang et al. [8] and Jiang and Zheng [29] introduced handy dictionary pairs that support the sparse common feature space. Compared to other methods [20,22,23,30], our approach enables us to keep multiple layers of learners and to examine view-invariant facets more effectively. In addition, it enables us to record complicated movements that exist in certain views. Our approach uses private facets and supports the inconsistencies among shared as well as private facets. Compared to other methods of sharing knowledge [6,8,27,31,32], our approach achieves the sharing of information among different views as per sample similarities. Since samples of data can appear the same in some views, our method provides a solution that enables us to distinguish different classes. While [30] calculated between and within classes of Laplacian matrices, SAM Z approach takes directly within and between classes. Moreover, the space between two views of one sample is determined using SAM Z. Such a distance cannot be encoded by [30].
4. Sharp Study of View-Invariant Features
4.1. Sample-Affinity Matrix (SAM)
SAM is used here to determine the similarities among views (a pair of videos). Assume we have as input two training videos with N views: {Xt,yt}tN=1, where the data of the view frame at the interval of time t, Xt has of N actions videos Xt = [x1t, ···, xtN] ∈ Rd×N with their associate labels yt = [yt1, ···, ytN]. SAM Z ∈ RV N×V N shows as a block diagonal matrix:
NB: dial(.) generates a diagonal matrix, and shows the space between two view frames in the ith sample obtained by ) parameterized by c. In different views within one class, the appearance of variations is characterized by the block Zi in Z. This illustrates clearly how an action might be seen differently from different viewpoints and allows us to share information between views that results in the construction of robust cross-view features. Furthermore, the presence of 0 on the off-diagonal blocks in our SAM Z limits the transfer of information between classes in the same view, with the direct impact of encouraging the distance between the features from various classes having the same view frame. It also gives us the possibility of differentiating multiple action categories if they seem similar in some view frames.
4.2. Preliminary on Autoencoders
Based on popular deep learning approaches [33,34,35], we have built an autoencoder (AE) that links the raw input X to hidden unit H using a powerful “encoder” e1(.): H = e1(X) and uses the “decoder” e2(.): O = e2(H) to connect the concealed units to outputs. The objective of studying AE is to strengthen matching or related input and output pairs where the restoration failure is decreased once decoding is over:
where N is the number of training samples. As the process of reconstruction keeps track of incoming information, neurons in the latent layer represent the inputs. On the other hand, the two-phase coding and decoding in autoencoders [33] is emphasized on the marginalized stacked denoising autoencoder (mSDA), which is used to reap the ruined information by use of one mapping W:
where represents the corrupted version of our Yi and computes by assigning 0 to each feature with a given probability p. Regarding the mSDA method, let us understand that for achieving a better result, it needs to pass n times over the training set with a different corruption each time. This causes a nonconformity regularization [36]. In the objective to achieve a robust transformation matrix W, n is set as n → ∞ so that mSDA will effectively use an infinite number of noisy data copies. Furthermore, mSDA is solved in closed form and is also stackable.
4.3. Single-Layer Feature Learning
As mentioned so far, our proposed method is based on mSDA. We aimed to get the shared facets among private features, especially those that belong to a single view frame and multiple view frames for cross-view action recognition categorization. Furthermore, in order to construct more robust features that are aware of the very large motion difference in diverse view frames, we introduced SAM Z to learn shared facets with the objective of equating information among view frames.
By the help of the objective function below, we have learned private and shared features:
where W and {Gv}Vv=1 are, respectively, the mapping matrix used to learn shared features and a collection of mapping matrices used to learn private features of each view frame, and pv can be expressed as pv = (W;Gv). Equation (4) Consists of four expressions: = is used to learn shared features (SF) among view frames. SF view is particularly used in the reconstruction process of the action data taken from a single view frame with the help of the data extracted from other view frames. To ascertain certain unshared facets that seem similar to shared features, the second terms is φv = . Nevertheless, = , the third term, minimizes redundancies between the mapping matrices, and = Tr (Pv Xv LXvT PvT), as the fourth term, emphasizes the similarity of the private and shared features belonging to the same class and view frame. The parameters α, β, and γ are discussed below. However, we can introduce them as elements used to balance the components discussed beforehand. It is important to note that data obtained from all view frames in cross-view action recognition are availed in training so that our model can learn private and shared features. However, with the testing phase, data collected from some view frames are not present.
4.3.1. Shared Features
The action recognition ability found in humans is easily understood from a single view, but does how the action appear if observed from multiple views? This is possible, since we regularly observe the same action from several views. This problem is one of the reasons why we tried to restore the action data view from one point with the help of action data from multiple views. Considering , the disparity between the data of all the V source views and the data of the target view can be expressed as:
where represents the value measuring the endowment of the u-th view action in the remodeling of the sample of the view frame. Also, W is a single linear mapping for the corrupted input of all the views frames with W ∈ . From the sample-affinity matrix, which encodes all the values {}, also called weights, we have Z ∈ . It is good to mention that the corrupted version of X matrices, which is ∈ [33], performs a drop out regularization on the model [33,36]. Furthermore, to accurately regulate the information transfer among view frames and learn more easily discriminative shared features, SAM Z is used. As an alternative of using equal values (weights) [8], all the samples are used, so that we remodel the i-th training sample taking from the view. Let us note, by the help of Figure 3, a greater similarity will be found between a sample of side view frame (S1) and side view t (which is the target view) compared to the one found between S1 and top view frame (S2). These result in the increase of weight for S1 with the objective to learn more expressive features for t.
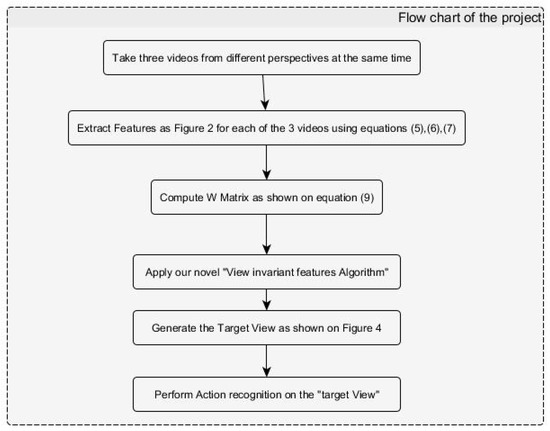
Figure 3.
Flow chart of the project.
4.3.2. Private Features
Selective information can still be found in each view despite the information shared across view frames. By improving the robustness of that information, in [33], we have used robust feature learning, and by using a matrix ∈ , we have “learned view specific private features” for the samples in view frame:
where the feature matrix has for corrupted version of the view. Using associate inputs of different view frames, we obtained the V mapping matrices . We should take into consideration that Equation (6) can keep some redundant shared information from view, but by promoting the inconsistency among the view-specific mapping matrix and view-shared mapping matrix W, we reduce some redundancy in our project:
4.3.3. Label Information
We should keep in mind that action data collected from different viewpoints may come with a considerable proportion of posture and motion variations. Thus, features (private and shared) collected by applying Equations (5) and (7) could appear not sufficiently selective for classifying action with considerable variation. Facing this issue, our approach leads to the same view and the same class to enforce similarity between private and shared features. To normalize view-specific mapping matrix and view-shared mapping matrix W, we have defined a “within class” and “within view frame” variance as:
where L ∈ and L = D − A is label view the Laplacian matrix with degree matrix D(i,j) = and the adjacent matrix A. Note that the (i,j)-th element: a(i,j) in A is 1 if . As we have implicitly required facets from various view frames to be similar in Equation (5), we do not need it here. Furthermore, by using facets from different view frames of a given sample, we can better illustrate expected facets of a given sample. This can be possible due to the mapping function (based on mapping matrix W) applied on the shared features (SF) so that the SF is mapped to a new space. Base on label information results obtained from Equation (8), in a supervised approach (SA) and by considering γ = 0, we can derive an unsupervised equation. In the following lines, a supervised approach is renaming.
4.4. Learning Process
Using a coordinate convergent algorithm, we are able to optimize parameters W and the V mapping matrices . Our process resolves the optimization problem in Equation (5). Furthermore, after determining the derivative of Δw.r.t to the parameter and allocating 0 to it, one parameter matrix within every step is updated by setting the others. First of all, we update W by fixing the derivative, as:
Keep in mind that in updating W, matrices are fixed; also by performing m → times the corruption, we obtain after computation F1 and F2 for and XZ, respectively. As referred to in [33], the weak law of large numbers applied on and XZ gave us the computation values: F1 = Ep () and F2 = Ep (XZ), where p is the corruption probability.
Similar to the previous update schema, by fixing the derivative , parameter is updated with and W sets with default value. Furthermore, computation values are obtained by applying Ep (expectation with corruption p):
As a resolution approach of Equation (1)’s problem, let us subdivide it into V + 1 subproblems, where by considering one variable, each one is a convex problem. Thus, an optimal solution to each subproblem is surely found by using the learning algorithm which will consequently converge to a local solution.
Every mentioned method has some advantages and disadvantages where need to be taken into account when designing solution as shown in table (Table 1). We are also defining our own approach as the alternative.

Table 1.
Advantages and disadvantages of used approaches.
5. The Design of the Proposed Approach—Deep Architecture
From the papers [33,37], we find a deep model developed by piling multiple layers facets discussed earlier in single layer feature learning where we utilized the nonlinear feature mapping function on the output of every layer, so that for and , the outcome is a series of matrices of latent features. We utilized a “layer wise” training approach to train the networks and that have K layers. It is imperative to note that the input of the (k + 1)th layer is the output of the nth layer This gives the input of our matrix and . Moreover, since k = 0 (implying layer 1 because there are layers), X and have for raw features in that order.
5.1. Flow Chart of our Project
Figure 3 shows the steps of our project. These steps are described below:
- Take three videos from different perspectives at the same time: Here, we try to capture images of a person from varying angles.
- We then obtain key features from the captured pictures by utilizing Equations (5)–(7): The pictures obviously have various features in common because they belong to one subject and they were taken at the same time. These features are called shared features, while the unique features that every picture has are called private features. We submit these two types of features to the next component as input.
- Applying a novel invariant feature algorithm: This step is a learning point pertinent for the process.
- Create the target views: In this step, we solve the sample-affinity matrix Z for every arrow. We also solve the W mapping matrix and create the target view having all the relevant features that will help in understanding the action.
- Allocate a label and an explanation of the action taking place.
5.2. Novel View-Invariant Features Algorithm
While in this paper we are targeting to present a powerful view-invariant feature, considering two subjects acting in the same environment as shown in figure (Figure 4a), our algorithm selects the zone of interest, extracts share, and private features as shown in figure (Figure 4b). It uses SAM to determine the similarities among views (a pair of videos). Additionally, figure (Figure 4c) shows a Clear mapping among view as described by our computed W mapping matrix.
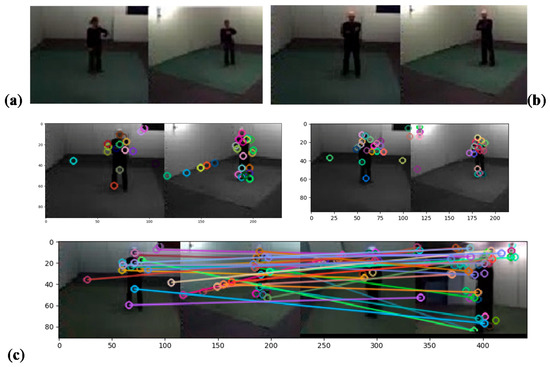
Figure 4.
(a) Powerful view-invariant feature for two subjects acting in the same environment; (b) our algorithm selects the zone of interest, extracts share; and private features; and (c) clear mapping among views.
Using our supervising technique, we determined the similarity between our target view and source views (Figure 5). A view shared mapping matrix W can be used to accomplish this process. The matrix is incorporated into Equation (5) to calculate weight value (Z) and get the shared feature. The arrow with the largest weight is the one situated between our target view and source view.
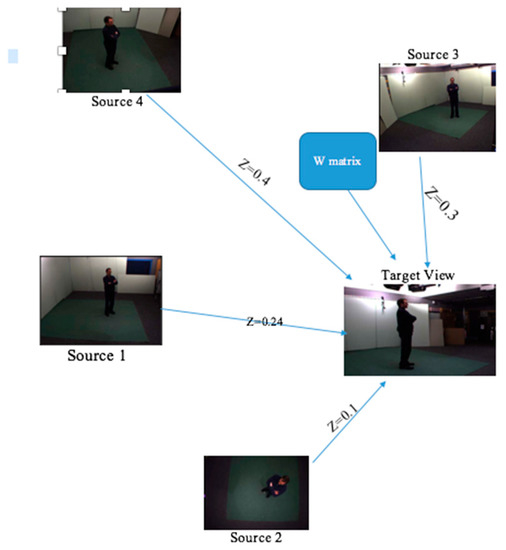
Figure 5.
Extracting the features from source pictures and creating the target view (image retrieved from the public dataset IXMAS).
Here (Figure 6), we derived a supervised approach from our previous one. W is the mapping matrix updated through several iterations (as show in our algorithm), while the shared and private features are determined. We aimed through our approach to determine or generate a target view (obtained from several viewpoints after applying W matrix) accurate enough so that the weight (Z) of the arrow will be same as the one obtained after applying Equation (5):
| Input: |
| Output: , |
| i 0 |
| While Layer i ≤ k do |
| Input for learning Wk. |
| Input for learning |
| Do |
| Update Wk applying (9); |
| Update applying (10); |
| While converge |
| Compute . |
| Compute by: . |
| i |
| end while |
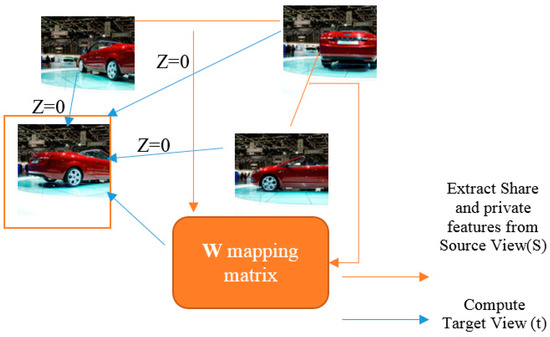
Figure 6.
Extraction of features of sources view followed by the computation of the mapping matrix (W) as well as the target view (t) (image obtained from a public dataset [38]).
In opposite of [3,6,8,27,28] where features extracted from views are used individually, we further process those features, and we derive a target view which contends the combined relevant features.
6. Experiment
We evaluated our method using three multi-view datasets and the Daily and Sports Activities (DSA) dataset [3], multi-view IXMAS dataset [39], and the Northwestern–UCLA Multi-view Action 3D (NUMA) dataset [40]). It is important to note that the datasets we used were also used in many studies, such as [3,6,8,27,28]. Many-to-one and one-to-one were treated here as two cross-view categorization situations. The first was trained on one view and examined another view, but the second was trained on V-1 views and examined the remaining views. The corresponding in Equation (5) was used for the vth view meant for testing. In addition, we employed the intersection kernel support vector machine (IKSVM) as our classifier with parameters C = 1. γ = 1, β = 1, α = 1, p = 0, and K = 1 were default parameters with the default number of layers being 1. We also took into consideration NUMA and IXMAS. These are datasets for multiple camera view video. We acquired the first from three Kinect sensors in five scenarios comprising 10 human actions, while the second was taken from one top-view camera, and four side-view cameras. In addition, we employed a k-means clustering approach to create video words and quantize the descriptors. This led to the likelihood of using a histogram of the feature to represent a given video. As a further contribution, we were curious to see how our model would react if the recording was not done continuously for the performing action; that is, will it be possible for our model to keep the same accuracy if we remove some frame of the video? As described in Section 4.1, for an interval of time t, we have N actions. If we pause the recording during a small period (p << t), we can still see a flow described by feature points of the target view, as shown in Figure 7.
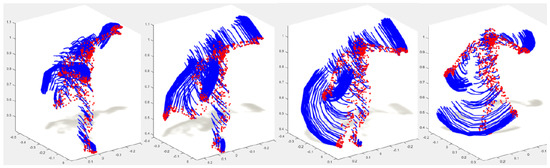
Figure 7.
Three-dimensional dense trajectories of the target view obtained by following each feature point during the interval of time t. This can be further interpreted as the set of positions occupied by each feature point of the target view [16].
It is also worth noting that V feature vectors constituted a representation of an action taken from V camera angles.
6.1. Using the IXMAS Dataset
Just like in [33], we obtained a histogram of intense trajectory and slanting optical flow and a dictionary for every feature was obtained by making use of k-means. In addition, a bag-of-words model was used to turn every video into a feature and encode each of the features. A “leave one action class out” training scheme was used to obtain a reasonable concurrence, just like in [8] and [28]. A single action class was used every time we needed to test. Moreover, we removed all videos from the feature steps of learning in order to examine the ability of our method to transfer information, and we introduced a fifth component, which was the result of our method when we performed several p pauses (p << t) (Table 2).

Table 2.
One-to-one cross-view recognition outcome for different controlled methods on the IXMAS dataset. The values enclosed in brackets are the recognition accuracies for [8,29,41,42] and our supervised method (with and without the p pause).
6.1.1. Many-to-One Cross-View Action Recognition
A single view was used in our experiment as a test view, while all other views were used for training. The experiment enabled us to evaluate our method of learning shared and private features.
The renowned methods in [5,25,28,29] were compared with our method and it was found that approximately 99.9% was achieved by our method, as shown in Table 3. Our method Seb1 achieved a better performance compared to the other approaches, which illustrates the benefit of using our private and shared feature approach in our paper. To determine the resemblance among video samples across camera views, our method implements the sample-affinity matrix with the direct consequence of accurate characterization of the similitude across views by the learned shared features. Furthermore, the learned private features become more edifying for categorization, as the redundancy between private and shared features is reduced.

Table 3.
One-to-one cross-view recognition results of various unsupervised approaches on the IXMAS dataset. The results in brackets are the recognition accuracies of [8,27,28,29,43], and our unsupervised approach, respectively.
6.1.2. One-to-One View Action Recognition
In this experiment, we trained our model with information from a single camera view and we performed the test based on the data extracted from another view. The private features were discarded here and only learned shared features were utilized since private features of one view do not suffice.
By doing a comparison between our approach (Seb1) and the reported recognition results in Table 4 of [8,29,44], we can say that our method performed best in 18 out of 20 combinations, which is considerably better than all the other methods. Again, our approach reached 99.8% in 16 instances, showing the potency of the learned shared features. Due to the importance of discriminative information obtained from the label information and the learned shared features, our approach is resistant enough to viewpoint variation and demonstrates high performance that is cross-view invariant.

Table 4.
Many-to-one cross-view action recognition results on the IXMAS dataset, where each column corresponds to a test view.
6.2. Use of NUMA 3D Dataset
6.2.1. Many-to-One Cross-View Action Recognition
It is good to keep in mind that the features used here are similar to those of the IXMAS dataset. As mentioned in [40], many-to-one cross-view recognition accuracy in three cross-view scenarios can be expressed as cross-camera view, cross-subject, and cross-environment. Following [40], our approach is compared with [31,40,45,46,47].
Table 5 shows that our approach is better than [40] Low-resolution visual features (LowR) by 10.4% and 3.9% in cross-environment and cross-view scenario, respectively. Furthermore, in the cross-subject scenario, it reaches an incredible performance with LowR added to [40]. A close look at the different comparison shows that the most important gain of performance of Seb1 in cross-environment, cross-subject, and cross-view scenarios are, respectively, 62.3% (over [48]), 30.4% (over [48]), and 32.0% (over [31]). This shows an incredible gain of performance obtained by the Seb1 approach due to the use of SAM to determine similarities of samples in different views and shared and private facts for modeling cross-view data.

Table 5.
Cross-view, cross-environment, and cross-subject action recognition outcomes on the NUMA dataset.
6.2.2. Parameter Analysis
Let us evaluate the sensibility of our method when we applied α, β, and γ parameters, as shown in Figure 8. We can observe the mean performance of many-to-one cross-view action recognition given values of 0.001, 0.01, 0.1, 1, 10, and 100 of parameters α, β, and γ. We concluded that our approach is insensible to that variation (parameter values). Despite the 2% observed as the large performance gap when parameters α, β, and γ were set, we came again to the conclusion that our method is robust.
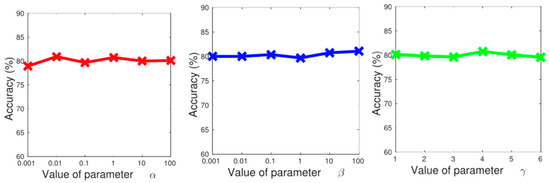
Figure 8.
Robustness evaluation of our approach by applying different values of α, β, and γ.
7. Conclusions
In this paper, we proposed an approach that can label human actions from cross views. Our research focuses on two new methods using unshared and shared facets to precisely classify human action with varying appearances and viewpoints. We have introduced a sample-affinity matrix that is used to determine similarities across views. This matrix has also been used in the monitoring of shared features as well as in controlling the transfer of information so that the contribution of every sample can be measured accurately. Our methods can keep several layers of learners to study view-invariant features more efficiently. It equipoises the sharing of information among views as per sample similarities and can measure the distance between two views using SAM Z. We also found that our method is robust to some variation in the recording time, as shown in Table 2. However, we noticed during our experiments that our approach required the use of various computer resources. We will further improve our model so that it uses fewer computational resources. To also help in measuring the contribution of every sample precisely, we carried out a series of experiments in NUMA and IXMAS, where we found out that our methods performed well when it came to the categorization of cross-view actions. We have also seen the potentials of our approach, and we now intend to handle image extract flow and space-time instead of taking it during a time t in order to handle activities. We also intend to adjust our model and algorithm in a way based on our previous projects [49] so that they enable us to capture many activities in a more accurate manner.
Funding
The work and the contribution were supported by the SPEV project “Smart Solutions in Ubiquitous Computing Environments 2018”, Faculty of Informatics and Management, University of Hradec Kralove, Czech Republic.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kong, Y.; Fu, Y. Bilinear heterogeneous information machine for RGB-D action recognition. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1054–1062. [Google Scholar]
- Kong, Y.; Fu, Y. Max-margin action prediction machine. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1844–1858. [Google Scholar] [CrossRef] [PubMed]
- Altun, K.; Barshan, B.; Tunçel, O. Comparative study on classifying human activities with miniature inertial and magnetic sensors. Pattern Recognit. 2010, 43, 3605–3620. [Google Scholar] [CrossRef]
- Grabocka, J.; Nanopoulos, A.; Schmidt-Thieme, L. Categorization of sparse time series via supervised matrix factorization. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; pp. 928–934. [Google Scholar]
- Junejo, I.N.; Dexter, E.; Laptev, I.; Pérez, P. Crossview action recognition from temporal self-similarities. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 293–306. [Google Scholar]
- Yang, W.; Gao, Y.; Shi, Y.; Cao, L. MRM-lasso: A sparse multiview feature selection method via low-rank analysis. IEEE Trans. Neural Netw. 2015, 26, 2801–2815. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Ricci, E.; Subramanian, S.; Liu, G.; Sebe, N. Multitask linear discriminant analysis for view invariant action recognition. IEEE Trans. Image Process. 2014, 23, 5599–5611. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Zheng, J.; Phillips, J.; Chellappa, R. Cross-view action recognition via a transferable dictionary pair. In Proceedings of the British Machine Vision Conference, Surrey, UK, 10–12 September 2012; pp. 125.1–125.11. [Google Scholar]
- Ding, G.; Guo, Y.; Zhou, J. Collective matrix factorization hashing for multimodal data. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2075–2082. [Google Scholar]
- Singh, A.P.; Gordon, G.J. Relational learning via collective matrix factorization. In Proceedings of the 14th ACM International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 650–658. [Google Scholar]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. In Proceedings of the SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 252–260. [Google Scholar]
- Liu, L.; Shao, L. Learning discriminative representations from RGB-D video data. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 1493–1500. [Google Scholar]
- Argyriou, A.; Evgeniou, T.; Pontil, M. Convex multi-task feature learning. Mach. Learn. 2008, 73, 243–272. [Google Scholar] [CrossRef]
- Ding, Z.; Fu, Y. Low-rank common subspace for multi-view learning. In Proceedings of the IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 110–119. [Google Scholar]
- Yu, Q.; Liang, J.; Xiao, J.; Lu, H.; Zheng, Z. A Novel perspective invariant feature transform for RGB-D images. Comput. Vis. Image Understand. 2018, 167, 109–120. [Google Scholar] [CrossRef]
- Zhang, J.; Shum, H.P.H.; Han, J.; Shao, L. Action Recognition from Arbitrary Views Using Transferable Dictionary Learning. IEEE Trans. Image Process. 2018, 27, 4709–4723. [Google Scholar] [CrossRef] [PubMed]
- Kerola, T.; Inoue, N.; Shinoda, K. Cross-view human action recognition from depth maps using spectral graph sequences. Comput. Vis. Image Understand. 2017, 154, 108–126. [Google Scholar] [CrossRef]
- Rahmani, H.; Mahmood, A.; Huynh, D.; Mian, A. Histogram of Oriented Principal Components for Cross-View Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2430–2443. [Google Scholar] [CrossRef] [PubMed]
- Hsu, Y.P.; Liu, C.; Chen, T.Y.; Fu, L.C. Online view-invariant human action recognition using rgb-d spatio-temporal matrix. Pattern Recognit. 2016, 60, 215–226. [Google Scholar] [CrossRef]
- Kumar, A.; Daumé, H. A co-training approach for multi-view spectral clustering. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 393–400. [Google Scholar]
- Zhang, W.; Zhang, K.; Gu, P.; Xue, X. Multi-view embedding learning for incompletely labeled data. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 1910–1916. [Google Scholar]
- Wang, K.; He, R.; Wang, W.; Wang, L.; Tan, T. Learning coupled feature spaces for cross-modal matching. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2088–2095. [Google Scholar]
- Xu, C.; Tao, D.; Xu, C. Multi-view learning with incomplete views. IEEE Trans. Image Process. 2015, 24, 5812–5825. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Kumar, A.; Daume, H.; Jacobs, D.W. Generalized multiview analysis: A discriminative latent space. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2160–2167. [Google Scholar]
- Weinland, D.; Özuysal, M.; Fua, P. Making action recognition robust to occlusions and viewpoint changes. In Proceedings of the European Conference on Computer Vision, Grete, Greece, 5–11 September 2010; pp. 635–648. [Google Scholar]
- Junejo, I.; Dexter, E.; Laptev, I.; Perez, P. View-independent action recognition from temporal self-similarities. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 172–185. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, H.; Mian, A. Learning a non-linear knowledge transfer model for crossview action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2458–2466. [Google Scholar]
- Liu, J.; Shah, M.; Kuipers, B.; Savarese, S. Crossview Action Recognition via View Knowledge Transfer. Available online: https://web.eecs.umich.edu/~kuipers/papers/Liu-cvpr-11_cross_view_action.pdf (accessed on 12 September 2018).
- Jiang, Z.; Zheng, J. Learning view invariant sparse representations for crossview action recognition. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3176–3183. [Google Scholar]
- Kan, M.; Shan, S.; Zhang, H.; Lao, S.; Chen, X. Multi-view discriminant analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Camps, O.I.; Sznaier, M. Crossview activity recognition using Hankelets. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1362–1369. [Google Scholar]
- Zhang, Z.; Wang, C.; Xiao, B.; Zhou, W.; Liu, S.; Shi, C. Cross-view action recognition via a continuous virtual path. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2690–2697. [Google Scholar]
- Chen, M.; Xu, Z.; Weinberger, K.; Sha, F. Marginalized denoising autoencoders for domain adaptation. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 1627–1634. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, T.; Luo, W.; Yang, J.; Yuan, X.; Zhang, J. Sparseness analysis in the pretraining of deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1425–1438. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Weinberger, K.; Sha, F.; Bengio, Y. Marginalized denoising auto-encoders for nonlinear representations. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1476–1484. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Polytechique, E.A. Computer Vision Laboratory CVLAB. Available online: https://cvlab.epfl.ch/data/pose (accessed on 12 September 2018).
- Weinland, D.; Ronfard, R.; Boyer, E. Free viewpoint action recognition using motion history volumes. Comput. Vis. Image Understand. 2006, 104, 249–257. [Google Scholar] [CrossRef]
- Wang, J.; Nie, X.; Xia, Y.; Wu, Y.; Zhu, S.C. Crossview action modeling, learning and recognition. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2649–2656. [Google Scholar]
- Farhadi, A.; Tabrizi, M.K.; Endres, I.; Forsyth, D.A. A latent model of discriminative aspect. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 948–955. [Google Scholar]
- Zhang, C.; Zheng, H.; Lai, J. Cross-View Action Recognition Based on Hierarchical View-Shared Dictionary Learning. IEEE Access 2018, 6, 16855–16868. [Google Scholar] [CrossRef]
- Gupta, A.; Martinez, J.; Little, J.J.; Woodham, R.J. 3D pose from motion for crossview action recognition via non-linear circulant temporal encoding. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2601–2608. [Google Scholar]
- Liu, J.; Shah, M. Learning human actions via information maxi-mization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Sadanand, S.; Corso, J.J. Action bank: A high-level representation of activity in video. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1234–1241. [Google Scholar]
- Maji, S.; Bourdev, L.; Malik, J. Action recognition from a distributed representation of pose and appearance. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3177–3184. [Google Scholar]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zickle, T. Discriminative virtual views for crossview action recognition. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2855–2862. [Google Scholar]
- Sobeslav, V.; Maresova, P.; Krejcar, O.; Franca, T.C.C.; Kuca, K. Use of cloud computing in biomedicine. J. Biomol. Struct. Dyn. 2016, 34, 2688–2697. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).