On the Security of Rotation Operation Based Ultra-Lightweight Authentication Protocols for RFID Systems
Abstract
1. Introduction
- We show that the ULRAS protocol [24], a protocol which has been designed based on rotation function, is not secure and fixing the security problem by any particular mode of rotation function may not be possible.
- An improved protocol named UEAP has also been proposed using lightweight encryption functions in which the ULRAS protocol’s security pitfalls are solved.
- The security proof of the UEAP protocol has been done through an informal way and also a formal way through Scyther tool.
2. Preliminaries
2.1. The Adversary Model
2.2. Related Work
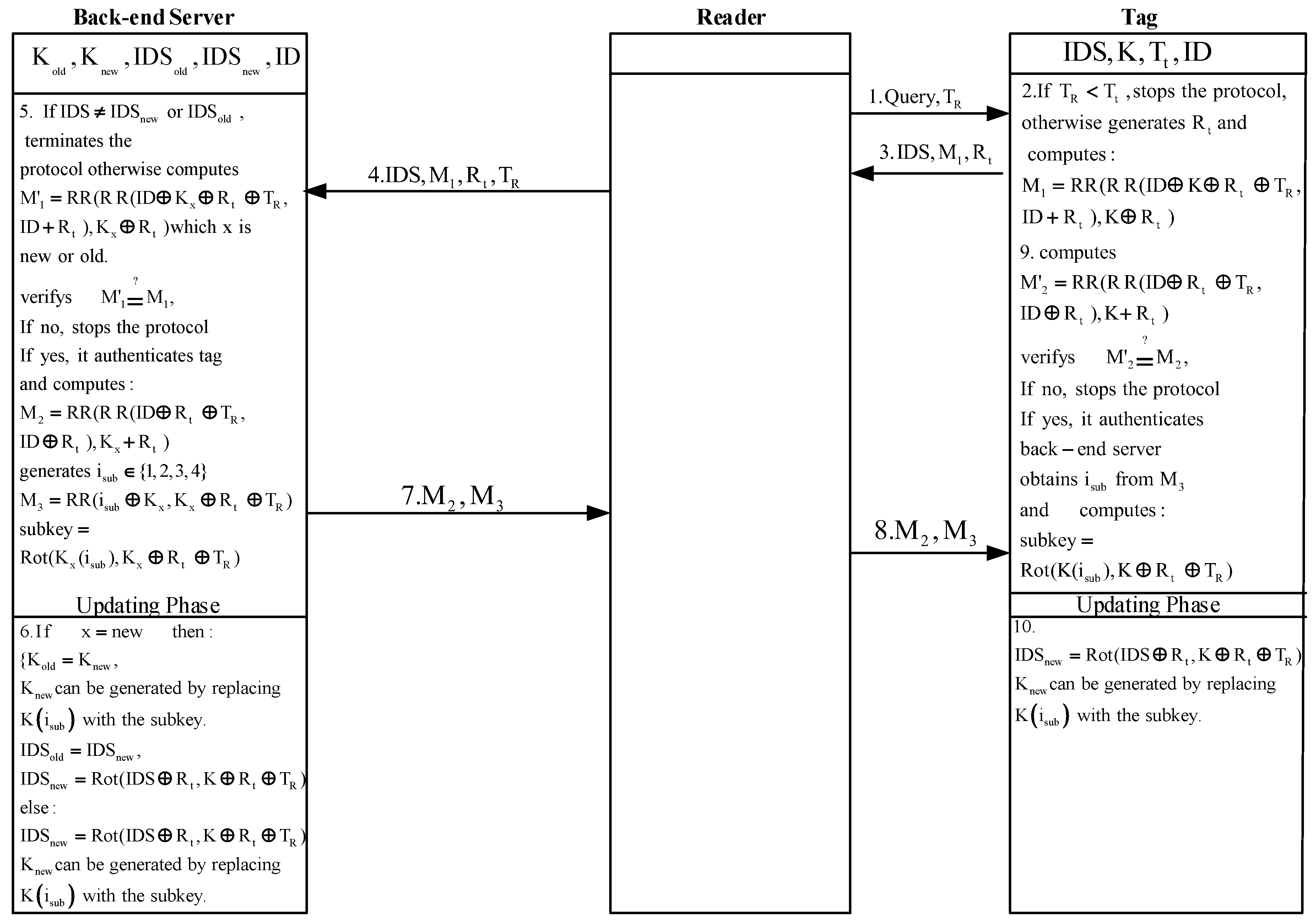
2.3. The ULRAS Protocol
- presents X and Y in their binary forms;
- computes , which inverses only those bits of X for which their correspondence bit-place in Y are “1”;
- computes as which is the left rotation of by amount of , where L is the length of X and Y.
- The reader starts the protocol by generating and sending a random time stamp and Query to the tag.
- The tag, once received the message, verifies whether . If , the tag:
- generates a random number ;
- calculates as below:;
- and sends , and to the reader.
- Upon reception of the message, the reader sends , , and to the back-end database.
- Once the back-end database receives the message, it verifies whether the received matches with or . If the back-end database does not find any match, stops the protocol; otherwise, the database:
- calculates which X is or . Then it verifies whether . If , the back-end database stops the protocol; otherwise, it does as follows:
- -
- authenticates the tag;
- -
- generates and computes and as below:;;
- -
- generates sub-key as below:;
- -
- updates its values as below:;;;is generated by replacing ;
- -
- and sends and through reader to the tag.
- Upon receipt of the messages, the tag calculates with its local values and then verifies whether . If , the tag:
- successfully authenticates the back-end server;
- extracts from ;
- generates new sub-key as ;
- and finally updates its and as below:;is generated by replacing .
3. Security Analysis of ULRAS Protocol
3.1. De-Synchronization Attack
- The reader sends and Query to the tag.
- The tag verifies whether , generates , calculates , and sends and to the reader.
- The reader sends , , and to the back-end database.
- The back-end database verifies the received , authenticates the tag, generates and computes and and sends them to the reader. It then generates and updates the tag’s parameters as below:;;;generated by replacing ;
- The adversary, who has eavesdropped , , and , manipulates as follows:
- Assuming and given that , because , the adversary can determine and also x by knowing as below:
- -
- Given that the adversary already has eavesdropped and , she can calculate . On the other hand, has only three bits. Hence, given and , it would be easy to determine the values of x and , exclude that the value of is rotation invariant which has no high probability and we omit it here for simplicity.
- Adversary selects and calculates .
- The adversary sends and to the tag.
- Upon receipt of the messages, the tag calculates with its local values and then verifies whether , which it is because the adversary has not changed . Hence, the tag:
- successfully authenticates the back-end server;
- gets , where .
- generates a new sub-key as ;
- and finally updates its and as below:;generated by replacing ;
3.2. Traceability Attack
| Algorithm 1: The algorithm of proposed traceability attack against ULRAS protocol |
| Data: , |
| Result: decides whether where is an adversary’s target tag. |
| 1. Eavesdrops a session between reader and and stores ; |
| 2. Obtains and by using , and and this fact ; |
| 3. Retrieves bits information from by using x; |
| 4. Eavesdrops a session between and the reader; |
| 5. Obtains and by using , and and this fact ; |
| 6. Retrieves bits information from by using ; |
| 7. Compares the retrieved bits of with to decide whether . |
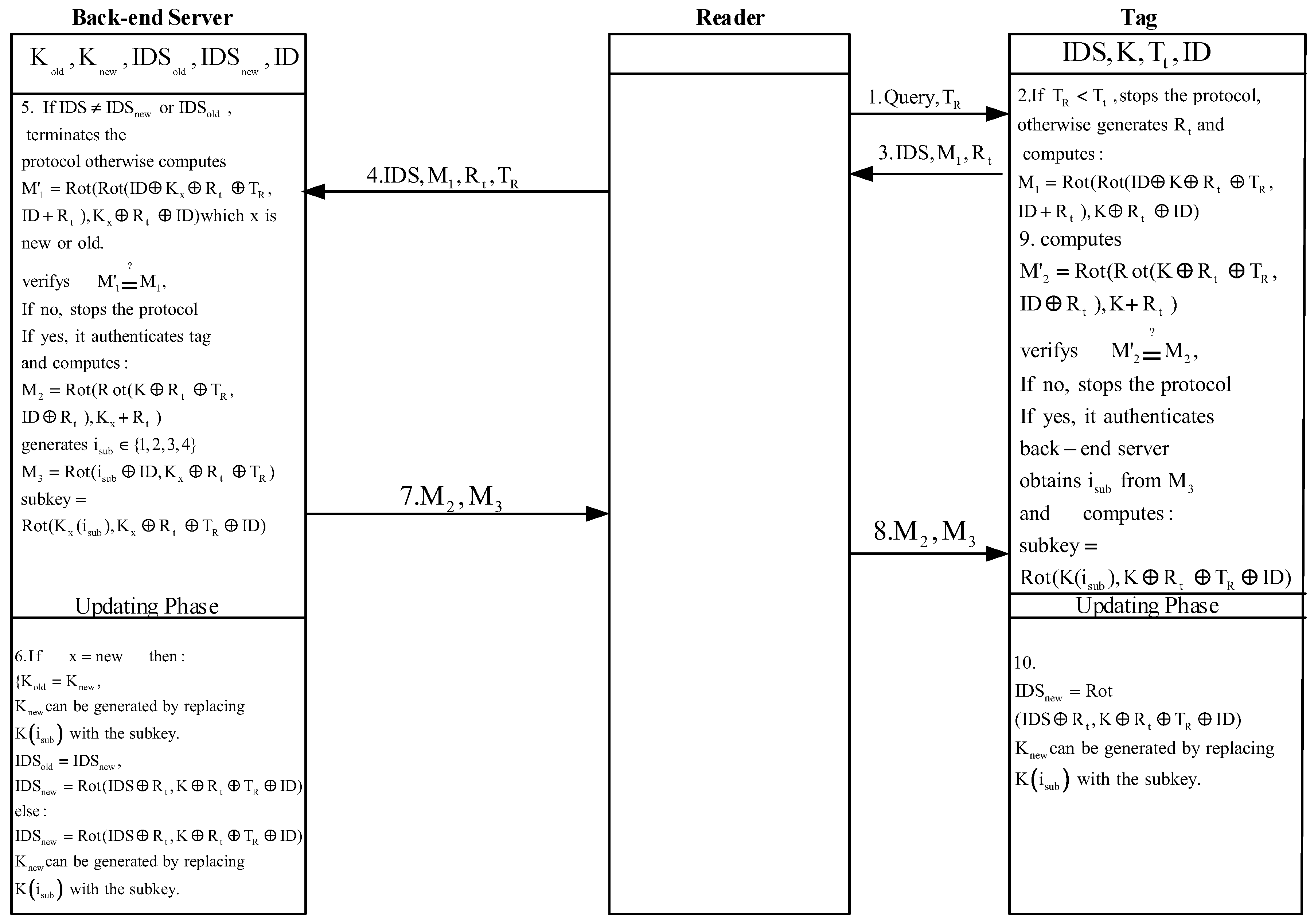
3.3. Security Analysis of Aghili and Mala Improvement to ULRAS
- The use of a rotation operation several times is like using one rotation i.e., in the Aghili and Mala improvement equals with where i is a value between 0 to L. The same point applies to message.
- Based on this fact given and X, if we rotate right M for and comparing the result with X, one can determine Y, the adversary with eavesdropping two sessions of protocol messages without completion of protocol sessions which leads to not updating secret values, can conduct secret disclosure attack which reveals and K. Precisely, given and , , , , , and , the adversary for verifies whether to retrieve K as . Similarly, for the adversary verifies whether to retrieve as . Given that K has already been acquired, the adversary can get and can verify the correctness of the obtained values by using other protocol’s messages.
- Since all the secret values of the protocol are revealed, it is easy to do a variety of attacks including impersonation attacks, traceability attacks, de-synchronization attacks, etc.
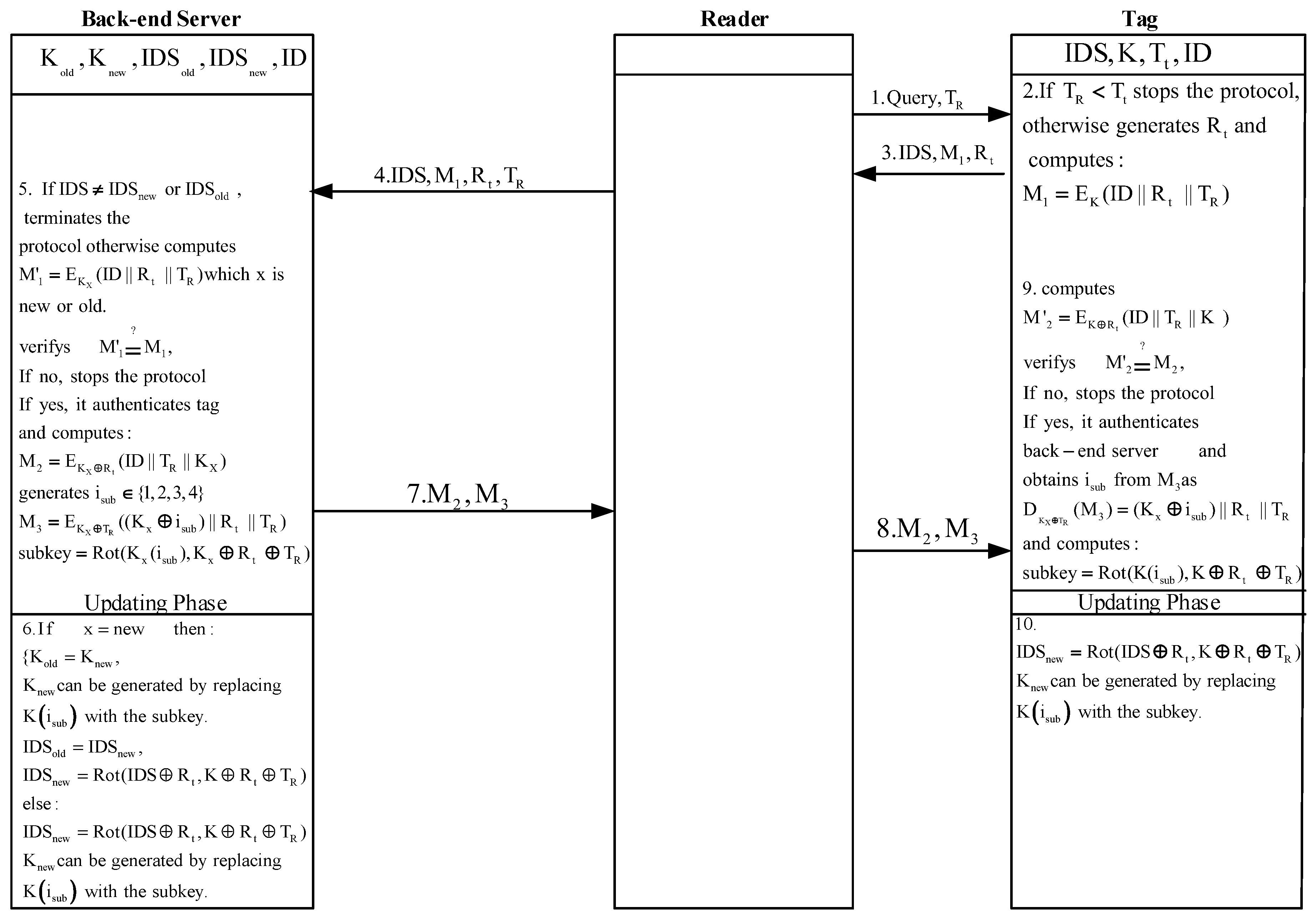
4. UEAP-Our Proposed Protocol
- The reader starts the protocol by generating and sending a random time stamp and to the tag.
- The tag, once it receives the message, verifies whether . If , the tag:
- generates a random number ;
- calculates as ;
- and sends , and to the reader.
- Upon reception the message, the reader sends , , and to the back-end database.
- Once the back-end database received the message, verifies whether the received matches with or . If the back-end database does not find any match, stops the protocol; otherwise, the database:
- calculates which X is or . Then it verifies whether . If , the back-end database stops the protocol; otherwise, it does as follows:
- -
- authenticates the tag;
- -
- generates and computes and as below:;;
- -
- generates sub-key as below:;
- -
- updates its values as below:;;;is generated by replacing ;
- -
- and sends and through the reader to the tag.
- Upon receipt of the messages, the tag calculates by its local values and then verifies whether . If , the tag:
- successfully authenticates the back-end server;
- extracts from ;
- generates new sub-key as ;
- and finally updates its and as below:;is generated by replacing .
4.1. Security Evaluation of UEAP
4.1.1. Informal Security Proof
4.1.2. Formal Security Proof
4.2. Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arjona, L.; Landaluce, H.; Perallos, A.; Onieva, E. Timing-Aware RFID Anti-Collision Protocol to Increase the Tag Identification Rate. IEEE Access 2018, 6, 33529–33541. [Google Scholar] [CrossRef]
- Saadi, H.; Touhami, R.; Yagoub, M.C.E. TDMA-SDMA-based RFID algorithm for fast detection and efficient collision avoidance. Int. J. Commun. Syst. 2018, 31, e3392. [Google Scholar] [CrossRef]
- Liu, B.; Su, X. An Anti-Collision Algorithm for RFID Based on an Array and Encoding Scheme. Information 2018, 9, 63. [Google Scholar] [CrossRef]
- Arjona, L.; Landaluce, H.; Perallos, A. Energy-Aware RFID Anti-Collision Protocol. Sensors 2018, 18, 1904. [Google Scholar] [CrossRef] [PubMed]
- Memon, M.Q.; He, J.; Yasir, M.A.; Memon, A. Improving Efficiency of Passive RFID Tag Anti-Collision Protocol Using Dynamic Frame Adjustment and Optimal Splitting. Sensors 2018, 18, 1185. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Wang, H.; Fu, L.; Wang, J.; Min, H.; Engels, D.W. Collision Detection and Signal Recovery for UHF RFID Systems. IEEE Trans. Autom. Sci. Eng. 2018, 15, 239–250. [Google Scholar] [CrossRef]
- Zhang, L.; Xiang, W.; Tang, X.; Li, Q.; Yan, Q. A Time- and Energy-Aware Collision Tree Protocol for Efficient Large-Scale RFID Tag Identification. IEEE Trans. Ind. Inform. 2018, 14, 2406–2417. [Google Scholar] [CrossRef]
- Rezaie, H.; Golsorkhtabaramiri, M. A fair reader collision avoidance protocol for RFID dense reader environments. Wirel. Netw. 2018, 24, 1953–1964. [Google Scholar] [CrossRef]
- Su, J.; Sheng, Z.; Xie, L. A Collision-Tolerant-Based Anti-Collision Algorithm for Large Scale RFID System. IEEE Commun. Lett. 2017, 21, 1517–1520. [Google Scholar] [CrossRef]
- Liu, B.H.; Nguyen, N.T.; Pham, V.T.; Yeh, Y.H. A maximum-weight-independent-set-based algorithm for reader-coverage collision avoidance arrangement in rfid networks. IEEE Sens. J. 2016, 16, 1342–1350. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Liu, B.H.; Pham, V.T. A dynamic-range-based algorithm for reader-tag collision avoidance deployment in rfid networks. In Proceedings of the 2016 International Conference on Electronics, Information, and Communications (ICEIC), Danang, Vietnam, 27–30 January 2016; pp. 1–4. [Google Scholar]
- Chien, H.Y. Sasi: A new ultralightweight rfid authentication protocol providing strong authentication and strong integrity. IEEE Trans. Dependable Secur. Comput. 2007, 4, 337–340. [Google Scholar] [CrossRef]
- Peris-Lopez, P.; Hernandez-Castro, J.C.; Tapiador, J.M.E.; Ribagorda, A. Advances in Ultralightweight Cryptography for Low-Cost RFID Tags: Gossamer Protoco. In Information Security Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 56–68. [Google Scholar]
- Tewari, A.; Gupta, B.B. Cryptanalysis of a novel ultra-lightweight mutual authentication protocol for IoT devices using RFID tags. J. Supercomput. 2017, 73, 1085–1102. [Google Scholar] [CrossRef]
- Fan, K.; Gong, Y.; Liang, C.; Li, H.; Yang, Y. Lightweight and ultralightweight RFID mutual authentication protocol with cache in the reader for IoT in 5G. Secur. Commun. Netw. 2016, 9, 3095–3104. [Google Scholar] [CrossRef]
- Phan, R.C.W. Cryptanalysis of a new ultralightweight RFID authentication protocol—SASI. IEEE Trans. Dependable Secur. Comput. 2009, 6, 316–320. [Google Scholar] [CrossRef]
- Cao, T.; Bertino, E.; Lei, H. Security analysis of the SASI protocol. IEEE Trans. Dependable secur. Comput. 2009, 6, 73–77. [Google Scholar]
- Hernandez-Castro, J.C.; Tapiador, J.M.E.; Peris-Lopez, P.; Quisquater, J.J. Cryptanalysis of the SASI ultralightweight RFID authentication protocol with modular rotations. arXiv, 2008; arXiv:0811.4257. [Google Scholar]
- Sun, H.M.; Ting, W.C.; Wang, K.H. On the security of Chien’s ultralightweight RFID authentication protocol. IEEE Trans. Dependable Secur. Comput. 2011, 8, 315–317. [Google Scholar] [CrossRef]
- Bilal, Z.; Masood, A.; Kausar, F. Security analysis of ultra-lightweight cryptographic protocol for low-cost RFID tags: Gossamer protocol. In Proceedings of the 2009 International Conference on Network-Based Information Systems, Indianapolis, IN, USA, 19–21 August 2009; pp. 260–267. [Google Scholar]
- Safkhani, M.; Bagheri, N. Passive secret disclosure attack on an ultralightweight authentication protocol for Internet of Things. J. Supercomput. 2017, 73, 3579–3585. [Google Scholar] [CrossRef]
- Wang, K.H.; Chen, C.M.; Fang, W.; Wu, T.Y. On the security of a new ultra-lightweight authentication protocol in IoT environment for RFID tags. J. Supercomput. 2018, 74, 65–70. [Google Scholar] [CrossRef]
- Aghili, S.F.; Ashouri-Talouki, M.; Mala, H. DoS, impersonation and de-synchronization attacks against an ultra-lightweight RFID mutual authentication protocol for IoT. J. Supercomput. 2018, 74, 509–525. [Google Scholar] [CrossRef]
- Fan, K.; Ge, N.; Gong, Y.; Li, H.; Su, R.; Yang, Y. An ultra-lightweight RFID authentication scheme for mobile commerce. Peer-to-Peer Netw. Appl. 2016, 10, 1–9. [Google Scholar] [CrossRef]
- Aghili, S.F.; Mala, H. Security Analysis of an Ultra-lightweight RFID Authentication Protocol for M-commerce. IACR Cryptol. ePr. Archiv. 2017, 2017, 547. [Google Scholar]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK lightweight block ciphers. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; p. 175. [Google Scholar]
- Beierle, C.; Jean, J.; Kölbl, S.; Leander, G.; Moradi, A.; Peyrin, T.; Sasaki, Y.; Sasdrich, P.; Sim, S.M. The SKINNY family of block ciphers and its low-latency variant MANTIS. In Advances in Cryptology—CRYPTO 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 123–153. [Google Scholar]
- Beaulieu, R.; Treatman-Clark, S.; Shors, D.; Weeks, B.; Smith, J.; Wingers, L. The SIMON and SPECK lightweight block ciphers. In Proceedings of the 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- Cremers, C.J.F. The Scyther Tool: Verification, Falsification, and Analysis of Security Protocols. In Computer Aided Verification; Springer: Berlin/Heidelberg, Germany, 2008; pp. 414–418. [Google Scholar]
- Avoine, G.; Carpent, X.; Martin, B. Strong authentication and strong. In Radio Frequency Identification: Security and Privacy Issues; Springer: Berlin/Heidelberg, Germany, 2010; pp. 50–64. [Google Scholar]

| Notation | Description |
|---|---|
| RFID | Radio Frequency Identification |
| IoT | Internet of Things |
| SD | Secret Disclosure |
| DA | De-synchronization Attack |
| IA | Impersonation Attack |
| TA | Traceability Attack |
| The last time used index number | |
| This time successful used of index number | |
| K | The tag’s key which is divided to four sub-keys indexed by |
| The last successful tag’s session key | |
| The current tag’s session key | |
| The last successful sub-key indexed by | |
| The number which is used for sub-keys index | |
| The random time stamp generated by the reader | |
| The last used time stamp | |
| The random number that is generated by the tag | |
| The binary representation of X | |
| The binary representation of Y | |
| ⋘ | Left rotation operation |
| The left rotation of X by amount of where X and Y are of the same length L | |
| The right rotation of X by amount of where X and Y are of the same length L | |
| L | The length of protocol parameters |
| The inverse of X | |
| The inverse operation of X, where for any bit-place in Y that is “1”, | |
| the corresponding bit in X is inverted | |
| This is RR method which has been presented in [24] to do rotation operation as | |
| An RFID tag | |
| / | The Encryption /Decryption function respectively with the key of K |
| X | Y | ||
|---|---|---|---|
| 0000 | 1011 | 1011 | 1011 |
| 0001 | 1011 | 1010 | 1010 |
| 0010 | 1011 | 1001 | 1001 |
| 0011 | 1011 | 1000 | 1000 |
| 0100 | 1011 | 1111 | 1111 |
| 0101 | 1011 | 1110 | 1110 |
| 0110 | 1011 | 1101 | 1101 |
| 0111 | 1011 | 1100 | 1100 |
| 1000 | 1011 | 0011 | 0011 |
| 1001 | 1011 | 0010 | 0010 |
| 1010 | 1011 | 0001 | 0001 |
| 1011 | 1011 | 0000 | 0000 |
| 1100 | 1011 | 0111 | 0111 |
| 1101 | 1011 | 0110 | 0110 |
| 1110 | 1011 | 0101 | 0101 |
| 1111 | 1011 | 0100 | 0100 |
| Protocol | SD | DA | IA | TA |
|---|---|---|---|---|
| SASI [12] | × [18,30] | × [19] | × [18,30] | × [16] |
| Gossamer [13] | ✓ | × [20] | × [20] | × [20] |
| ULRMAPC [15] | × [23] | ✓ | ×[23] | ×[23] |
| Tewari and Gupta [14] | × [21,22] | ×[21,22] | × [21,22] | ×[21,22] |
| ULRAS [24] | ×(in this paper,[25] ) | ✓ | ×[25] | ×(in this paper) |
| Aghili and Mala [25] | ×(in this paper) | ×(in this paper) | ×(in this paper) | ×(in this paper) |
| UEAP | ✓ | ✓ | ✓ | ✓ |
| Protocol | ♯ of ⊕ | ♯ of | ♯ of | ♯ of Transferred Bits |
|---|---|---|---|---|
| SASI [12] | 20 L | 4 | - | 6 L |
| Gossamer [13] | 12 L | 36 | - | 6 L |
| Tewari and Gupta [14] | 24 L | 12 | - | 7 L |
| ULRMAPC [15] | 34 L | 14 | - | 11 L |
| ULRAS [24] | 30 L | 14 | - | 13 L |
| Aghili and Mala [25] | 36 L | 14 | - | 13 L |
| UEAP | 16 L | 4 | 6 | 13 L |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safkhani, M.; Bagheri, N.; Shariat, M. On the Security of Rotation Operation Based Ultra-Lightweight Authentication Protocols for RFID Systems. Future Internet 2018, 10, 82. https://doi.org/10.3390/fi10090082
Safkhani M, Bagheri N, Shariat M. On the Security of Rotation Operation Based Ultra-Lightweight Authentication Protocols for RFID Systems. Future Internet. 2018; 10(9):82. https://doi.org/10.3390/fi10090082
Chicago/Turabian StyleSafkhani, Masoumeh, Nasour Bagheri, and Mahyar Shariat. 2018. "On the Security of Rotation Operation Based Ultra-Lightweight Authentication Protocols for RFID Systems" Future Internet 10, no. 9: 82. https://doi.org/10.3390/fi10090082
APA StyleSafkhani, M., Bagheri, N., & Shariat, M. (2018). On the Security of Rotation Operation Based Ultra-Lightweight Authentication Protocols for RFID Systems. Future Internet, 10(9), 82. https://doi.org/10.3390/fi10090082






