Clock Recovery Challenges in DSP-Based Coherent Single-Mode and Multi-Mode Optical Systems
Abstract
1. Introduction
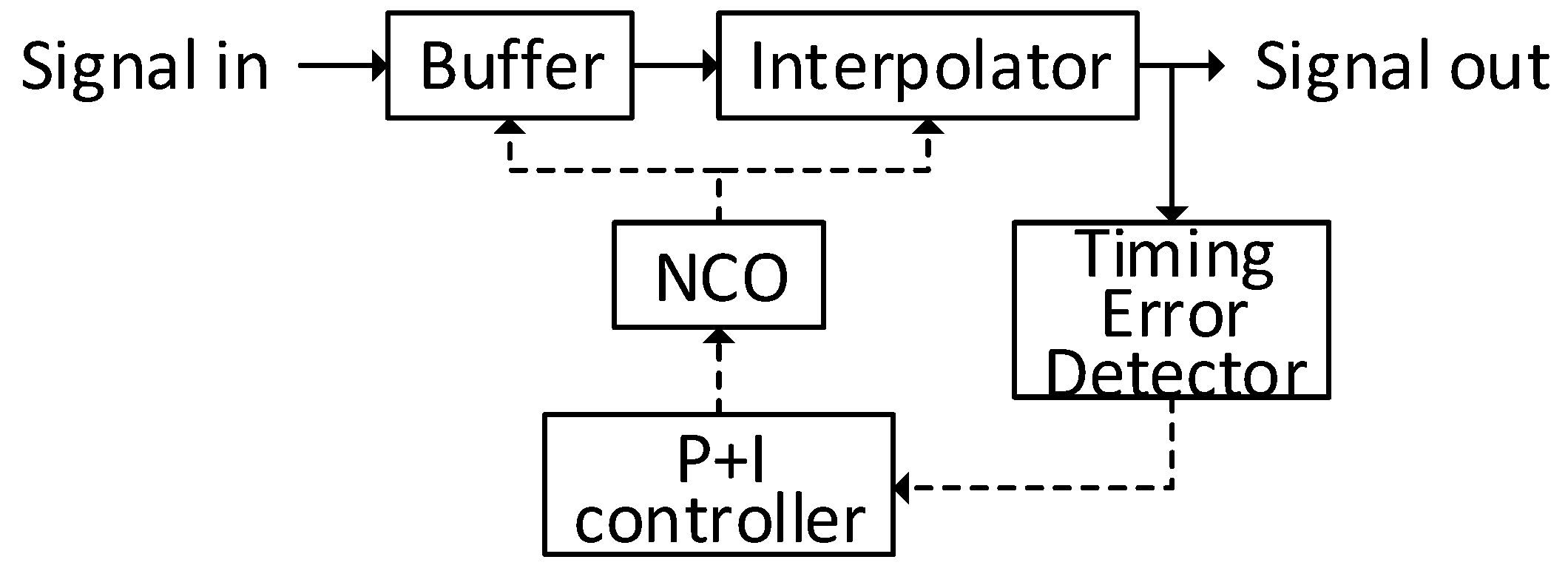
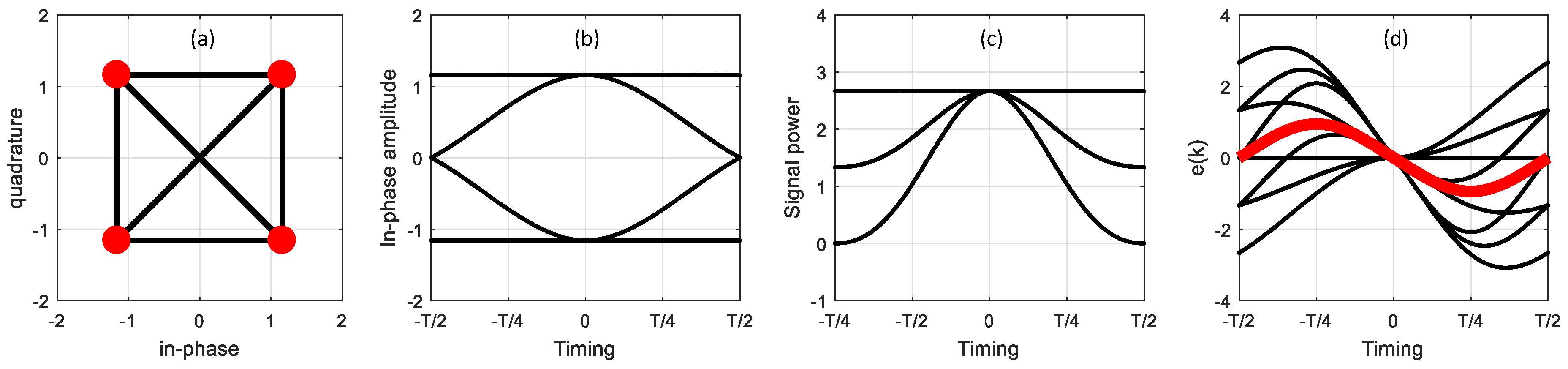
2. Clock Recovery in Coherent Optical Receivers
Feedback Timing Synchronization Method
3. Matrix Propagation Model for Optical Fibers
3.1. Single-Mode Fibers without Coupling between Polarizations
3.2. Single-Mode Fibers with Strong Coupling between Polarizations
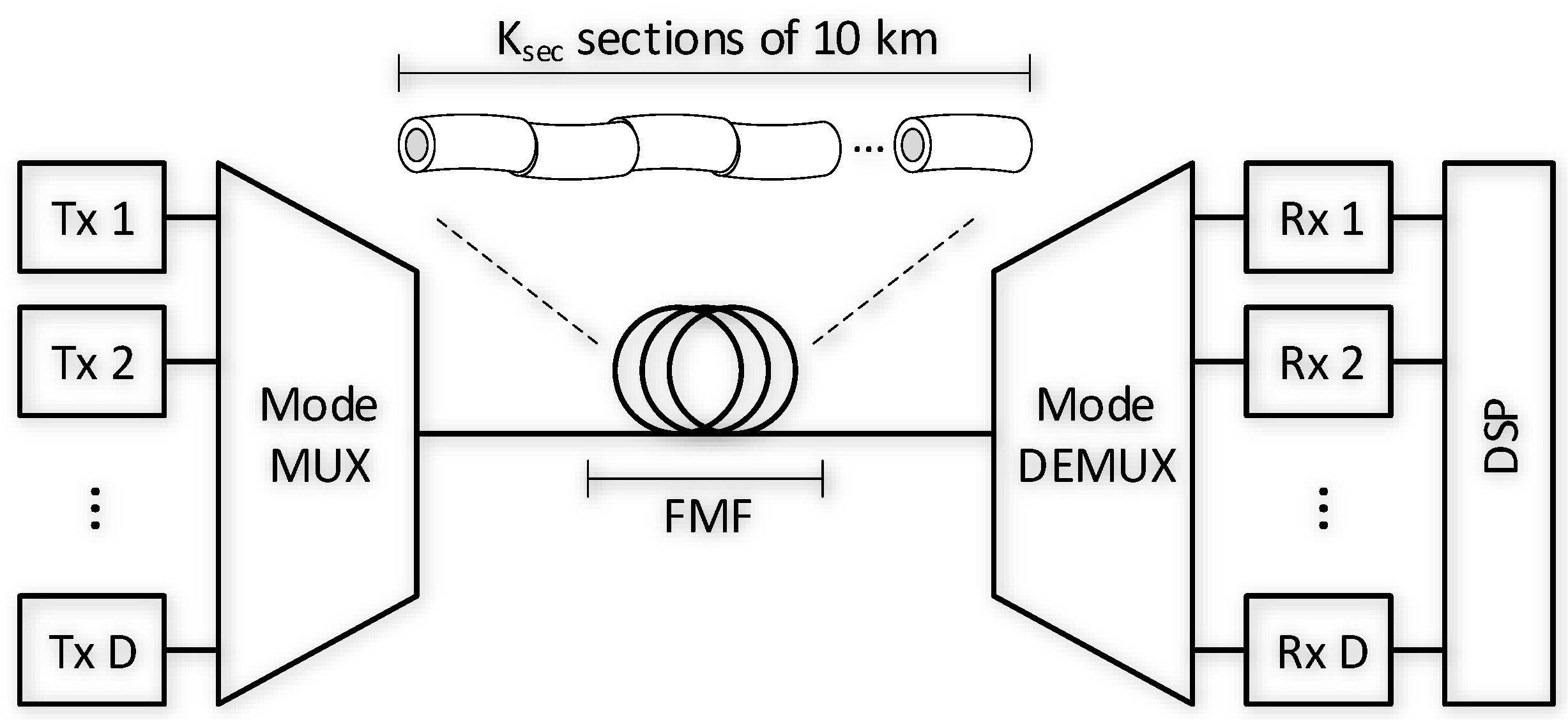
3.3. Multi-Mode and Multi-Core Fibers
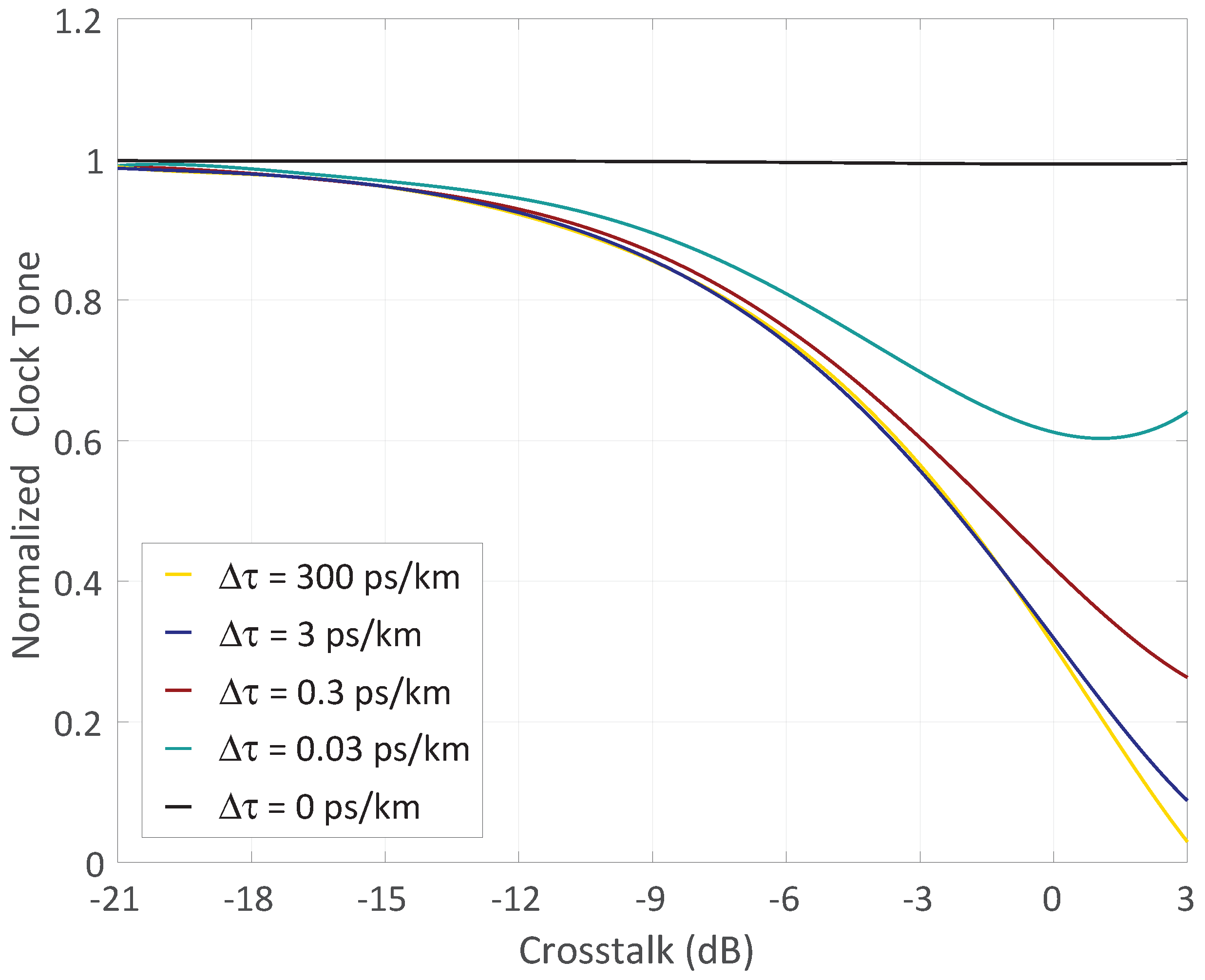
3.4. Time Skew between Polarizations and Modes
4. Clock Recovery Performance in Single-Mode Fibers
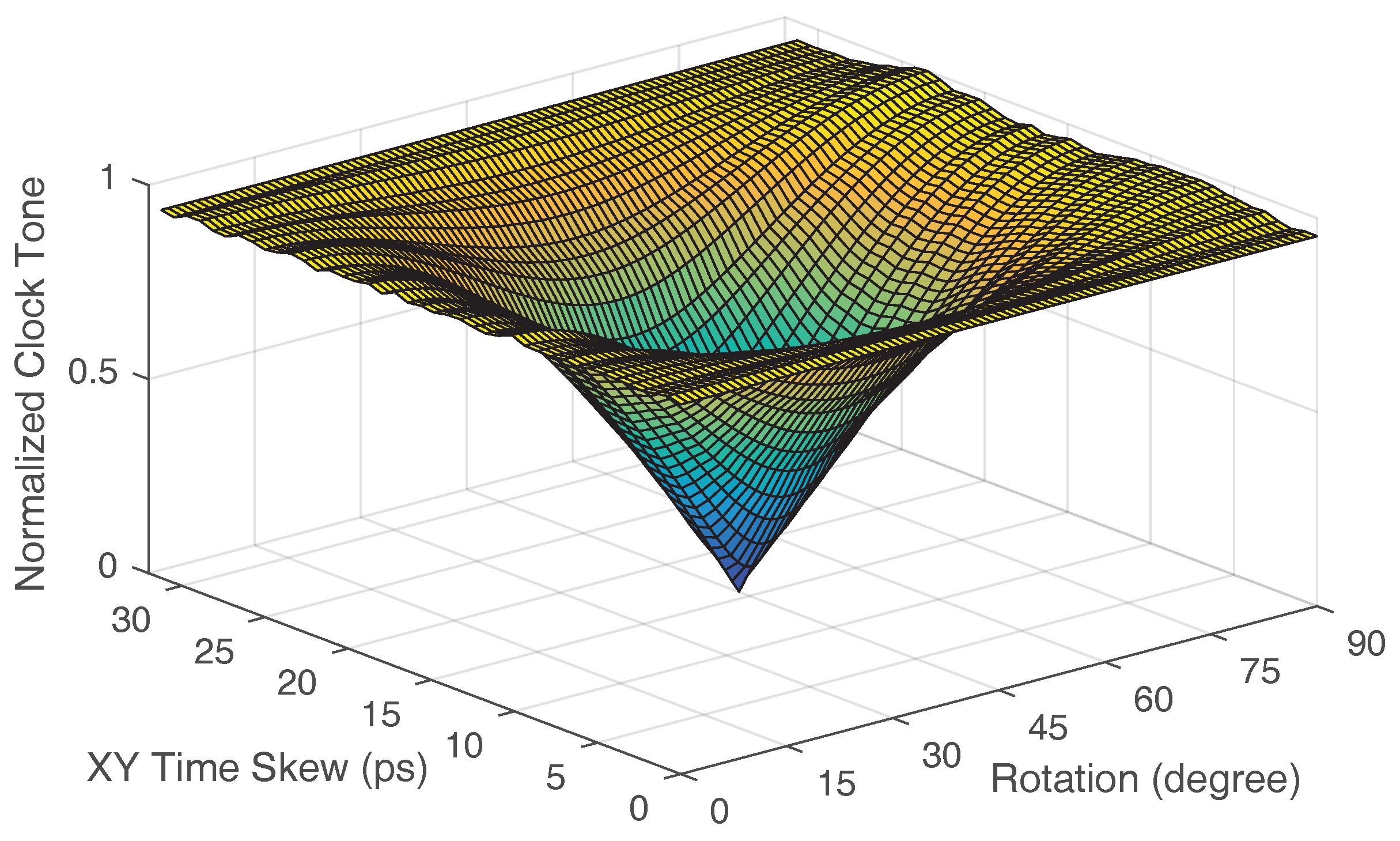
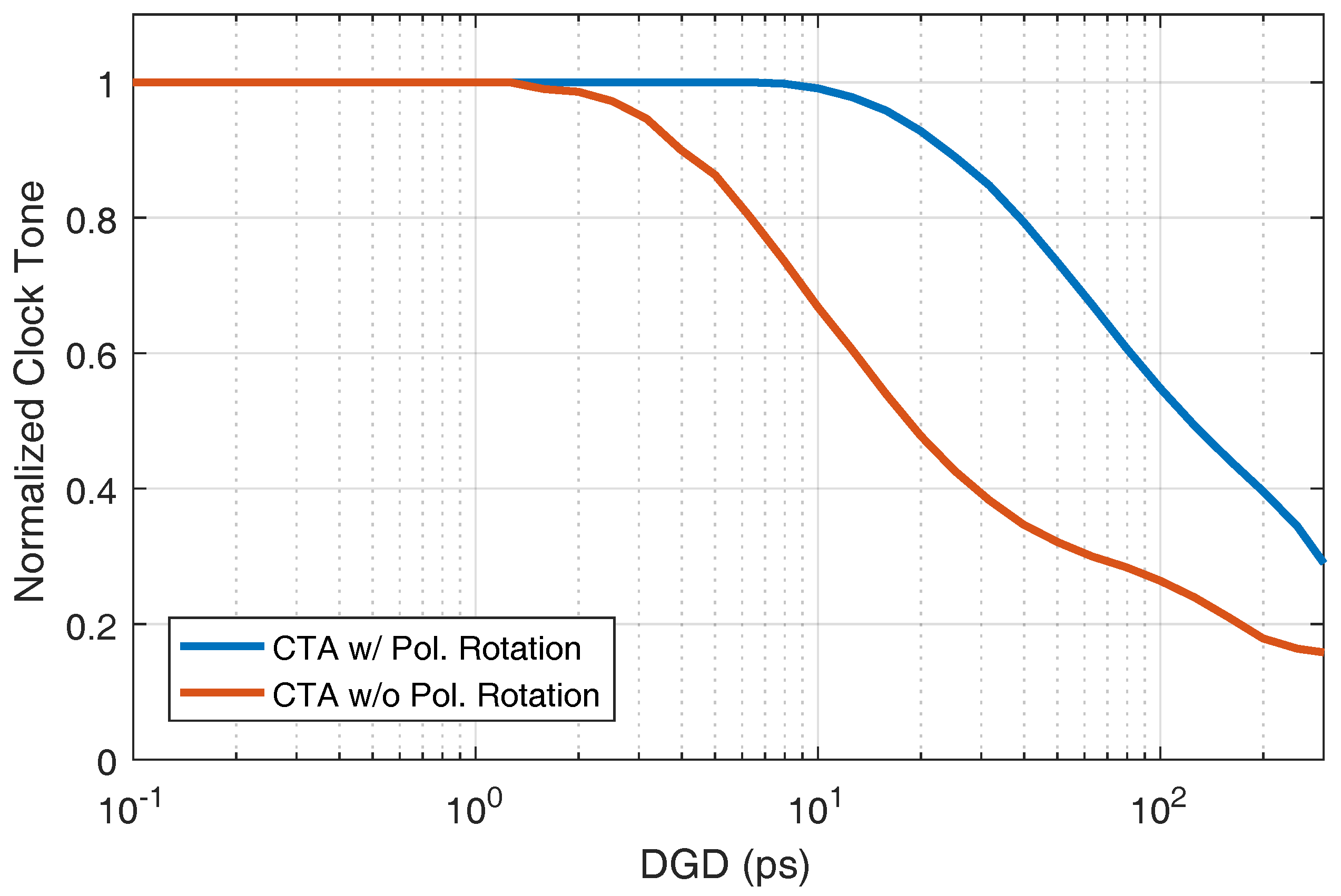
4.1. Time Skew between Polarizations
4.2. Polarization Mode Dispersion
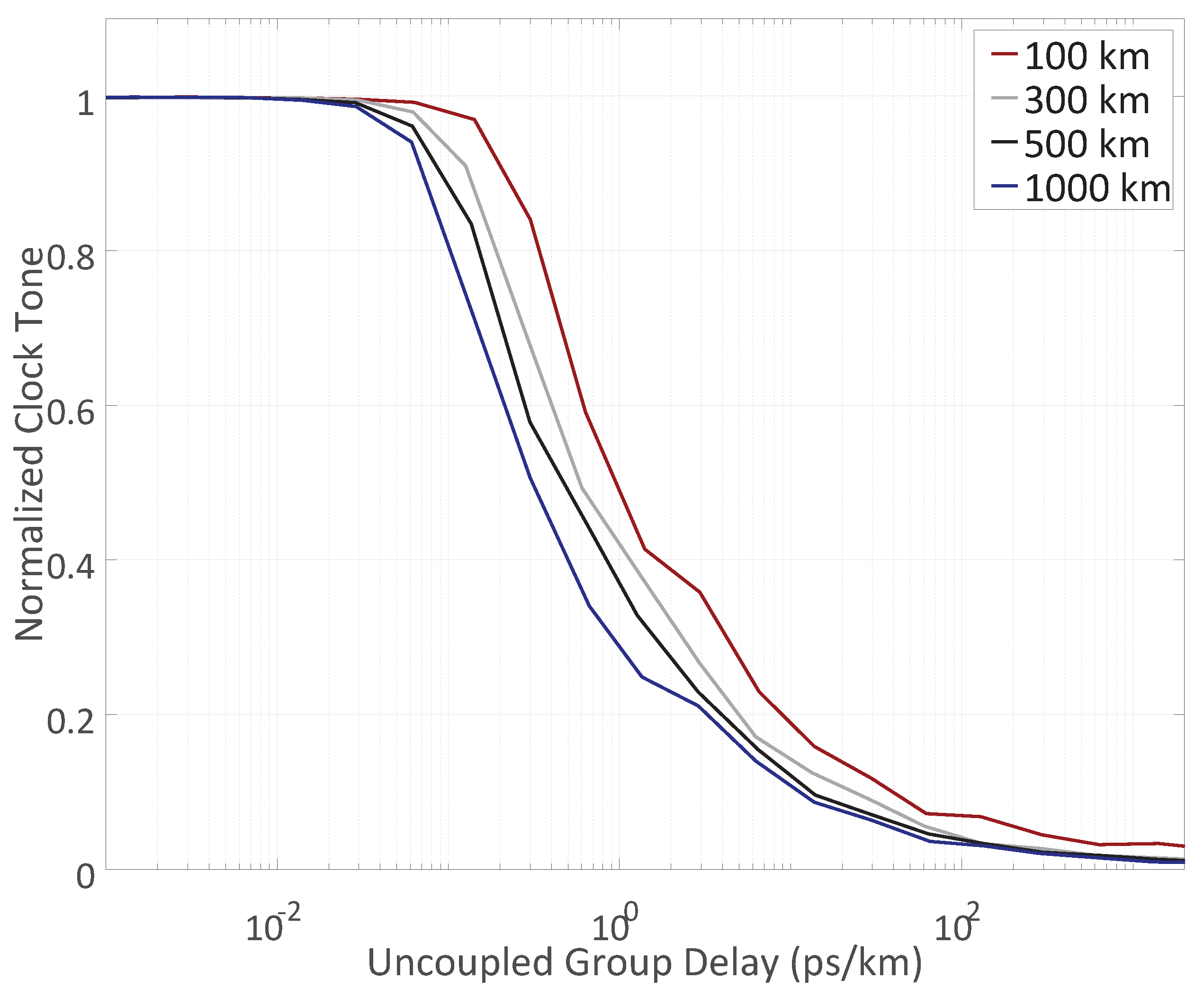
5. Clock Recovery Performance in Multi-Mode Fibers
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CD | Chromatic dispersion |
| CTA | Clock tone amplitude |
| DGD | Differential group delay |
| DSP | Digital signal processing |
| IM-DD | Intensity modulation/direct detection |
| FMF | Few mode fiber |
| MCF | Multi-core fiber |
| MD | Mode delay |
| MDL | Mode-dependent loss |
| MDM | Mode division multiplexing |
| MIMO | Multiple-input multiple-output |
| M-PSK | m-ary phase shift keying |
| M-QAM | m-ary quadrature amplitude modulation |
| NCO | Numeric controlled oscillator |
| NRZ | Non-return-to-zero |
| PDM | Polarization division multiplexing |
| PDL | Polarization dependent loss |
| PMD | Polarization mode dispersion |
| PSK | Phase shift keying |
| P+I | Proportional-plus-integral controller |
| QPSK | Quadriphase shift keying |
| SDM | Space-division multiplexing |
| SMF | Single-mode fiber |
| WDM | Wavelength division multiplexing |
References
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J.; et al. Roadmap of optical communications. J. Opt. 2016, 18, 063002. [Google Scholar] [CrossRef]
- Savory, S.J. Digital Coherent Optical Receivers: Algorithms and Subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Zibar, D.; Bianciotto, A.; Wang, Z.; Napoli, A.; Spinnler, B. Analysis and Dimensioning of Fully Digital Clock Recovery for 112 Gb/s Coherent Polmux QPSK Systems. In Proceedings of the 2009 35th European Conference on Optical Communication (ECOC), Vienna, Austria, 20–24 September 2009. [Google Scholar]
- Sun, H.; Wu, K.T. A novel dispersion and PMD tolerant clock phase detector for coherent transmission systems. In Proceedings of the Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 6–10 March 2011. [Google Scholar]
- Zibar, D.; de Oliviera, J.C.R.; Ribeiro, V.B.; Paradisi, A.; Diniz, J.C.; Larsen, K.J.; Monroy, I.T. Experimental Investigation of Digital Compensation of DGD for 112 Gb/s PDM-QPSK Clock Recovery. In Proceedings of the European Conference on Optical Communication (ECOC), Geneva, Switzerland, 18–22 Septmner 2011. [Google Scholar]
- Zibar, D.; de Olivera, J.C.R.F.; Ribeiro, V.B.; Paradisi, A.; Diniz, J.C.; Larsen, K.J.; Monroy, I.T. Experimental investigation and digital compensation of DGD for 112 Gb/s PDM-QPSK clock recovery. Opt. Express 2011, 19, B429–B439. [Google Scholar] [CrossRef] [PubMed]
- Stojanović, N.; Xie, C.; Zhao, Y.; Mao, B.; Guerrero Gonzalez, N. A Circuit enabling Clock Extraction in Coherent Receivers. In Proceedings of the European Conference on Optical Communication (ECOC), Amsterdam, Netherlands, 16–20 September 2012. [Google Scholar]
- Birk, M.; Gerard, P.; Curto, R.; Nelson, L.E.; Zhou, X.; Magill, P.; Schmidt, T.J.; Malouin, C.; Zhang, B.; Ibragimov, E.; et al. Coherent 100 Gb/s PM-QPSK field trial. IEEE Commun. Mag. 2010, 48, 52–60. [Google Scholar] [CrossRef]
- Winzer, P. Spatial Multiplexing: The Next Frontier in Network Capacity Scaling. In Proceedings of the European Conference on Optical Communication (ECOC), London, UK, 22–26 September 2013. [Google Scholar]
- Winzer, P.J.; Neilson, D.T. From Scaling Disparities to Integrated Parallelism: A Decathlon for a Decade. J. Lightwave Technol. 2017, 35, 1099–1115. [Google Scholar] [CrossRef]
- Arik, S.O.; Ho, K.P.; Kahn, J.M. Group Delay Management and Multiinput Multioutput Signal Processing in Mode-Division Multiplexing Systems. J. Lightwave Technol. 2016, 34, 2867–2880. [Google Scholar] [CrossRef]
- Randel, S.; Ryf, R.; Sierra, A.; Winzer, P.J.; Gnauck, A.H.; Bolle, C.A.; Essiambre, R.J.; Peckham, D.W.; McCurdy, A.; Lingle, R. 6×56-Gb/s mode-division multiplexed transmission over 33-km few-mode fiber enabled by 6 × 6 MIMO equalization. Opt. Express 2011, 19, 16697–16707. [Google Scholar] [CrossRef] [PubMed]
- Randel, S.; Sierra, A.; Mumtaz, S.; Tulino, A.; Ryf, R.; Winzer, P.; Schmidt, C.; Essiambre, R. Adaptive MIMO signal processing for mode-division multiplexing. In Proceedings of the Optical Fiber Communication Conference and Exposition (OFC), Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar]
- Randel, S.; Winzer, P. DSP for mode division multiplexing. In Proceedings of the OptoElectronics and Communications Conference/Photonics in Switching (OECC/PS), Kyoto, Japan, 30 June–4 July 2013. [Google Scholar]
- Arik, S.O.; Askarov, D.; Kahn, J.M. Adaptive Frequency-Domain Equalization in Mode-Division Multiplexing Systems. J. Lightwave Technol. 2014, 32, 1841–1852. [Google Scholar] [CrossRef]
- Asif, R.; Ye, F.; Morioka, T. Equalizer complexity for 6-LP mode 112 Gbit/s m-ary DP-QAM space division multiplexed transmission in strongly coupled Few-Mode-Fibers. In Proceedings of the 2015 European Conference on Networks and Communications (EuCNC), Paris, France, 29 June–2 July 2015. [Google Scholar]
- Shi, K.; Thomsen, B.C. Sparse Adaptive Frequency Domain Equalizers for Mode-Group Division Multiplexing. J. Lightwave Technol. 2015, 33, 311–317. [Google Scholar] [CrossRef]
- Lee, D.; Shibahara, K.; Kobayashi, T.; Mizuno, T.; Takara, H.; Sano, A.; Kawakami, H.; Nakagawa, T.; Miyamoto, Y. A Sparsity Managed Adaptive MIMO Equalization for Few-Mode Fiber Transmission with Various Differential Mode Delays. J. Lightwave Technol. 2016, 34, 1754–1761. [Google Scholar] [CrossRef]
- Ferreira, F.; Suibhne, N.M.; Sánchez, C.; Sygletos, S.; Ellis, A.D. Advantages of Strong Mode Coupling for Suppression of Nonlinear Distortion in Few-Mode Fibers. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–22 March 2016. [Google Scholar]
- Antonelli, C.; Mecozzi, A.; Shtaif, M. Scaling of inter-channel nonlinear interference noise and capacity with the number of strongly coupled modes in SDM systems. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–22 March 2016; pp. 1–3. [Google Scholar]
- Diniz, J.C.M.; Piels, M.; Zibar, D. Performance Evaluation of Clock Recovery for Coherent Mode Division Multiplexed Systems. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Diniz, J.C.M.; Da Ros, F.; da Silva, E.P.; Jones, R.T.; Zibar, D. Optimization of DP-M-QAM Transmitter Using Cooperative Coevolutionary Genetic Algorithm. J. Lightwave Technol. 2018, 36, 2450–2462. [Google Scholar] [CrossRef]
- Mueller, K.; Muller, M. Timing Recovery in Digital Synchronous Data Receivers. IEEE Trans. Commun. 1976, 24, 516–531. [Google Scholar] [CrossRef]
- Gardner, F. A BPSK/QPSK Timing-Error Detector for Sampled Receivers. IEEE Trans. Commun. 1986, 34, 423–429. [Google Scholar] [CrossRef]
- Godard, D. Passband Timing Recovery in an All-Digital Modem Receiver. IEEE Trans. Commun. 1978, 26, 517–523. [Google Scholar] [CrossRef]
- Huang, L.; Wang, D.; Lau, A.P.T.; Lu, C.; He, S. Performance analysis of blind timing phase estimators for digital coherent receivers. Opt. Express 2014, 22, 6749–6763. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Ho, K.P.; Kahn, J.M. Mode Coupling and its Impact on Spatially Multiplexed Systems. In Optical Fiber Telecommunications; Kaminow, I., Li, T., Willner, A., Eds.; Academic Press: Cambridge, MA, USA, 2013; Volume VIB, Chapter 11; pp. 491–568. [Google Scholar]
- Givens, W. Computation of Plain Unitary Rotations Transforming a General Matrix to Triangular Form. J. Soc. Ind. Appl. Math. 1958, 6, 26–50. [Google Scholar] [CrossRef]
- Ip, E.; Kahn, J.M. Power spectra of return-to-zero optical signals. J. Lightwave Technol. 2006, 24, 1610–1618. [Google Scholar] [CrossRef]
- Colavolpe, G.; Foggi, T.; Forestieri, E.; Secondini, M. Impact of Phase Noise and Compensation Techniques in Coherent Optical Systems. J. Lightwave Technol. 2011, 29, 2790–2800. [Google Scholar] [CrossRef]
- Czegledi, C.B.; Liga, G.; Lavery, D.; Karlsson, M.; Agrell, E.; Savory, S.J.; Bayvel, P. Digital backpropagation accounting for polarization-mode dispersion. Opt. Express 2017, 25, 1903. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value |
|---|---|
| Modulation format | NRZ-QPSK |
| Symbol rate | 32 GBd |
| Rotation angle interval | |
| Rotation angle step size | |
| Transmitter time skew interval | ps |
| Transmitter time skew step size | fs |
| Receiver time skew | 0 |
| Parameter | Value |
|---|---|
| Modulation format | NRZ-QPSK |
| Symbol rate | 32 GBd |
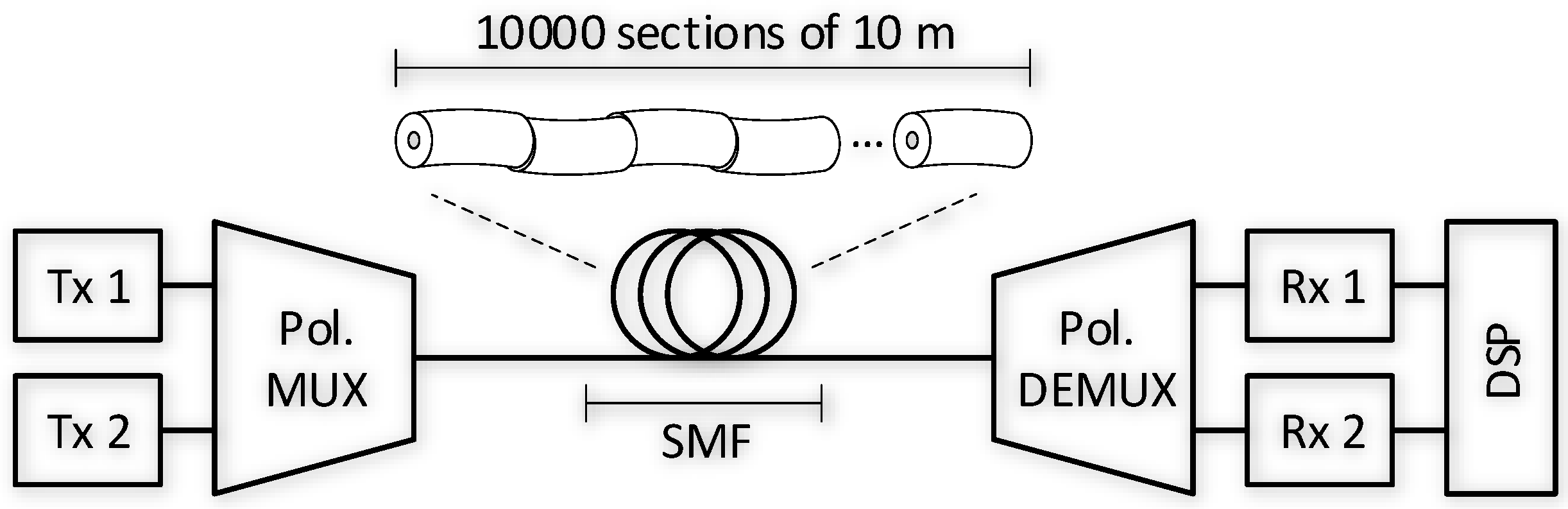
| Number of fiber sections | 10,000 |
| Fiber length per section | 10 m |
| Total fiber length | 100 km |
| Rotation angle per section | uniform distribution |
| Uncoupled DGD interval | ps/km |
| Uncoupled DGD step size | greater every iteration |
| Transmitter time skew | 0 |
| Receiver time skew | 0 |
| Parameter | Value |
|---|---|
| Modulation format | NRZ-QPSK |
| Symbol rate | 32 GBd |
| Number of degrees of freedom | 6 |
| Fiber length per section | 10 km |
| Total fiber length (Figure 8) | 1000 km |
| Total fiber length (Figure 9) | 100, 300, 500 and 1000 km |
| Uncoupled group delay (Figure 8) | 0, 0.03, 0.3, 3 and 300 ps/km |
| Uncoupled group delay interval (Figure 9) | ps/km |
| Rotation angle per section | zero-mean normal distribution |
| Rotation angle variance interval | |
| Transmitter time skew | 0 |
| Receiver time skew | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diniz, J.C.M.; Da Ros, F.; Zibar, D. Clock Recovery Challenges in DSP-Based Coherent Single-Mode and Multi-Mode Optical Systems. Future Internet 2018, 10, 59. https://doi.org/10.3390/fi10070059
Diniz JCM, Da Ros F, Zibar D. Clock Recovery Challenges in DSP-Based Coherent Single-Mode and Multi-Mode Optical Systems. Future Internet. 2018; 10(7):59. https://doi.org/10.3390/fi10070059
Chicago/Turabian StyleDiniz, Júlio César Medeiros, Francesco Da Ros, and Darko Zibar. 2018. "Clock Recovery Challenges in DSP-Based Coherent Single-Mode and Multi-Mode Optical Systems" Future Internet 10, no. 7: 59. https://doi.org/10.3390/fi10070059
APA StyleDiniz, J. C. M., Da Ros, F., & Zibar, D. (2018). Clock Recovery Challenges in DSP-Based Coherent Single-Mode and Multi-Mode Optical Systems. Future Internet, 10(7), 59. https://doi.org/10.3390/fi10070059







