Abstract
Mobile devices could augment their ability via cloud resources in mobile cloud computing environments. This paper developed a novel two-layered reinforcement learning (TLRL) algorithm to consider task offloading for resource-constrained mobile devices. As opposed to existing literature, the utilization rate of the physical machine and the delay for offloaded tasks are taken into account simultaneously by introducing a weighted reward. The high dimensionality of the state space and action space might affect the speed of convergence. Therefore, a novel reinforcement learning algorithm with a two-layered structure is presented to address this problem. First, clusters of the physical machines are generated based on the k-nearest neighbors algorithm (k-NN). The first layer of TLRL is implemented by a deep reinforcement learning to determine the cluster to be assigned for the offloaded tasks. On this basis, the second layer intends to further specify a physical machine for task execution. Finally, simulation examples are carried out to verify that the proposed TLRL algorithm is able to speed up the optimal policy learning and can deal with the tradeoff between physical machine utilization rate and delay.
1. Introduction
Internet of things (IoT) [1] connects mobile devices to the internet and makes it possible for objects to connect. However, due to their limited memory, storage, CPU, and battery life, mobile devices need to offload computing-intensive or energy-consuming tasks to cloud computing infrastructure via the internet. Mobile cloud computing (MCC) [2] is a new paradigm for augmenting devices via remote cloud resource, which can overcome resource constraints for mobile devices. It is a hotspot for research on how to run applications on mobile devices by utilizing cloud resource effectively in an MCC environment.
Offloading the tasks that require considerable computational power and energy to the remote cloud server is the best way to augment ability and reduce the energy consumption for mobile devices. Many different offloading methods have been proposed in recent research. The offloading strategy is based on many factors such as the energy consumption of mobile devices, the network bandwidth, latency, the capacity of cloud servers, and the application structures that save bandwidth or speed up the execution, etc. Considering these factors, the offloading strategy compares the cost of local and remote execution in order to decide which tasks should be offloaded. The cloud computing [3] makes task offloading possible which is adopted in MCC environment. One of its core techniques is virtualization, which is used to run multiple operating systems and applications based on maintaining isolation. The virtual machines (VMs) run on physical machines (PMs) in the remote cloud. By offloading tasks to the remote cloud, the energy consumption of mobile devices can be reduced [4,5]. The offloaded tasks run on corresponding VMs that are commonly deployed in distributed cloud centers. Offloading tasks to different PMs may lead to a different delay for mobile devices. Moreover, the utilization rate of PM in a cloud center should be considered as this could cause the waste of physical machine resources if it is at a lower level.
The main contributions of this paper are as follows:
First, we take into account utilization rate of PM and delay for task offloading simultaneously. Then, based on theoretical analysis, we find that a higher utilization rate of PM and a lower delay are conflicting commonly with each other. In order to trade off between utilization rate of PM and delay, we use deep reinforcement learning (DRL) to find optimal PM to execute the offloaded tasks by introducing a weighted reward. Moreover, a novel two-layered reinforcement learning algorithm is presented to address the problem, in which the high dimensionality of the state space and action space might affect the speed of learning optimal policy.
This paper is organized as follows: Section 2 introduces the related works. We propose the problem that our paper focuses on and give the definition of the utilization rate of PM and delay in Section 3. Section 4 introduces the deep reinforcement learning. In Section 5, we formulate our problem using DRL and propose an algorithm for task offloading based on DRL. Moreover, a two-layered reinforcement learning (TLRL) structure for task offloading is proposed to improve the speed of learning optimal policy. We show the advantage of our proposed algorithm for task offloading through simulation experiments in Section 6. In Section 7, we conclude our paper.
2. Related Works
Much research has studied the task offloading in MCC environment. They propose many different methods for different optimization objects. Zhang et al. [6] provides a theoretical framework for energy-optimal MCC under stochastic wireless channel. They focus on conserving energy for the mobile device, by executing tasks in the local device or offloading to the remote cloud. The scheduling problem is formulated as a constrained optimization problem in their study. The paper [7] proposed a scheduling algorithm based on Lyapunov optimizing problem, which schedules the tasks for the remote server or local execution dynamically. It aims at balancing the energy consumption and delay between the device and remote server according to the current network condition and task queue backlogs. Liu et al. [8] formulate the delay minimization problem under power-constrained using Markov chain. An efficient one–dimensional search algorithm is proposed to find the optimal task offloading policy. Their experimental results show that proposed task scheduling policy could achieve a shorter average delay than the baseline policies. Considering the total execution time of tasks. Kim et al. [9] considered the situation that the cloud server is not smooth and large-scale jobs are needed to process in MCC. They proposed an adaptive mobile resource offloading to balance the processing large-scale jobs by using mobile resources, where jobs could be offloaded to other mobile resources instead of the cloud. Shahzad and Szymanski [10] proposed an offloading algorithm called dynamic programming with hamming distance termination. They try to offload as many tasks as possible to the cloud server when the bandwidth is high. Their algorithm can minimize the energy cost of the mobile device while meeting a task’s execution time constraints.
There are also some studies focused on resource management for task offloading. Wang et al. [11] proposed a framework named ENORM for resource management in fog computing environment. A novel auto-scaling mechanism for managing the edge resources is studied, which can reduce the latency of target applications and improve the QoS. Lyu et al. [12] considered the limited resource in the proximate cloud and studied the optimization for resource utilization and offloading decision. They try to optimize the resource utilization for an offloading decision, according to the user preferences on task completion time and energy consumption. They regard the resource of proximate clouds as a whole with limited resource. They proposed a heuristic offloading decision algorithm in order to optimize the offloading decision, and computation resources to maximize system utility. Ciobanu et al. [13] introduced a Drop Computing paradigm that employs the mobile crowd formed of devices in close proximity for quicker and more efficient access. It was different from traditional method, where every data or computation request going directly to the cloud. This paper mainly proposed the decentralized computing over multilayered networks for mobile devices. This new paradigm could reduce the costs of employing a cloud platform without affecting the user experience. Chae et al. [14] proposed a cost-effective mobile-to-cloud offloading platform, which aimed at minimizing the server costs and the user service fee. Based on ensuring the performance of target applications, the platform offloaded as many applications to the same server as possible.
Machine learning technologies have been applied for offloading decision. Liu et al. [15] developed a mobile cloud platform to boost the general performance and application quality for mobile devices. The platform optimized computation partitioning scheme and tunable parameter setting for getting a higher comprehensive performance, based on history-based platform-learned knowledge, developer-provided information and the platform-monitored environment conditions. Eom et al. [16] proposed a framework for mobile offloading scheduling based on online machine learning. The framework provided an online training mechanism for the machine learning-based runtime scheduler, which supported a flexible policy. Through the observation of previous offloading decisions and their correctness, it can adapt scheduling decisions dynamically. Crutcher et al. [17] focused on reducing overall resource consumption for computing offloading in mobile edge networks. They obtained features composed of a “hyperprofile” and position nodes by predicting costs of offloading a particular task. Then a hyperprofile-based solution was formalized and a machine learning techniques based to predict metrics for computation offloading was explored in this paper.
However, existing researches have some limitations. Papers [6,7,8,10] only consider the energy and delay as optimization objects that ignore the management of cloud resources. Moreover, some works [11,12,14] focus on resource management for task offloading, which do not consider utilization rate of cloud resources. These works rarely consider utilization rate of PM in cloud server and delay caused by arranging the offloaded task to different PMs in the cloud simultaneously. They do not consider the detail of the remote cloud, which has an impact on offloaded tasks. The bandwidth between the different PMs of the cloud and mobile devices are different because PMs of the cloud are distributed geographically in a real environment. This can affect the transmission time that a task is offloaded from mobile device to the PM. Moreover, a waiting time in the cloud for the offloaded task will be taken into consideration. Besides, the resources of the cloud are also limited. If the number of offloaded tasks is too large due to the popularity of mobile devices, the utilization rate of cloud resources should be considered to avoid waste of cloud resources. Our paper intends to study scheduling the offloaded tasks to optimal PM by trading off between utilization rate of physical machine and delay, in which the delay comprises of the waiting time, the execution time of offloaded task and data transmission time. We model the problem using DRL to obtain an optimal policy for task offloading, which is more effective than traditional reinforcement learning when facing to high-dimension state space and action space. Different from existing studies [15,16,17] that applied machine learning technologies for offloading based on related historical data, we intend to study an online learning method based on DRL where a weighted reward is introduced for tradeoff between utilization rate of PM and delay. Furthermore, we propose a two-layered reinforcement learning (TLRL) algorithm for task offloading to improve learning speed, where the dimensions of state space and action space are reduced by utilizing the k-NN [18] to classify the PMs in the remote cloud.
3. Problem Statement
Previous works for task offloading focus on whether to offload corresponding tasks to a cloud server in order to optimize a certain parameter. They regard the cloud resource as a whole and make decisions for task offloading according to resource availability, energy consumption etc. They do not consider improving the utilization rate of cloud resource, which may lead to a waste of cloud resources. A dedicated cloud resource manager is in charge of optimal resource allocation following its optimization objects, such as saving energy, decreasing the waste of computing resource etc. It does not consider the impact on mobile devices in mobile cloud computing environment. In our paper, we intend to improve the utilization rate of cloud resource and reduce the latency when the cloud resource is applied to augment mobile devices, which is seldom considered by other studies on the issue of task offloading. Moreover, the selection of physical machines that an offloaded task runs in can affect the delay of offloaded tasks. Therefore, it is necessary to make sure a high utilization rate of PM and a low delay for offloaded tasks when offloading tasks to the cloud. We will mainly study the tradeoff between the optimal utilization of cloud resource and the delay for offloaded tasks in our paper.
We consider the real cloud environment where all tasks run on the virtual machines and a physical machine could deploy several virtual machines. The proximity cloud may reduce data transmission time between the mobile device and cloud. In our paper, we consider the bandwidth between mobile devices and the PMs. As shown in Figure 1, represents the physical machine (PM) in cloud center that is used to run VMs. We can see that the number of VMs running in each PM are different. The is not in a running state that there are no VMs running in. The bandwidth between mobile devices and the PM is denoted as correspondingly. Suppose that the number of current running PMs is and the max number of VMs that PMs could run is . The number of current running VMs on these PMs is and the max number of VMs each PM can run is . We defined utilization rate of PM as follow
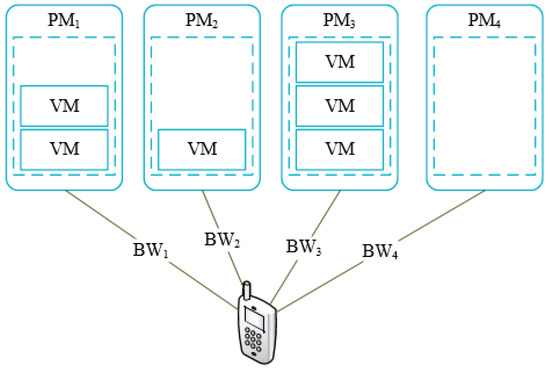
Figure 1.
Allocation of physical machine.
We can see that proposed algorithm should decrease the and increase the in order to get larger when offloading tasks to cloud server. Therefore, offloaded tasks should be assigned to those PMs that have run VMs preferentially than being assigned to a new PM. However, it may lead to a higher delay than offloading tasks to a new PM.
We define the delay caused by an offloading task as follow:
where is the execution time of offloaded tasks in cloud server, and is the amount of data to be transferred between the mobile device and the cloud server. is the waiting time when an offloaded task is assigned to the VM that existing another task is running in. As shown in Figure 2, the Task1 is running on in the time among 0 and , and only one VM is running in current PM during that period time. The of Task1 is . If an offloaded task Task2 arrives at , then there are two ways to choose for running the offloaded task Task2. One way is that the Task2 is assigned to , it will be executed at when the Task1 is completed. Therefore the waiting time caused by this way is . Another way is that the Task2 is offloaded to a new running VM that no task is running on. The Task2 can be executed in at and there is no need to wait, . Moreover, the VMs from different PMs are in different running states, which could lead to different waiting time for offloaded tasks. Meanwhile, the bandwidths between mobile devices and the PMs are also different. We need choosing the optimal PM for offloaded tasks to make the delay lower according to Formula (3).
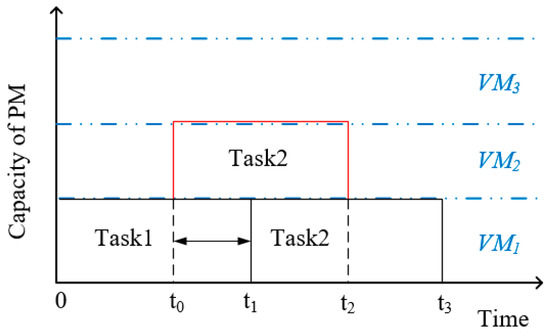
Figure 2.
Waiting time for offloaded tasks.
Through this analysis above, we find that choosing different physical machines to run offloaded tasks may affect the latency and the utilization rate of physical machines. In this paper, we mainly focus on assigning the offloaded tasks to an optimal PM for making sure a higher utilization rate of PM and a lower delay .
Our proposed algorithms will be deployed in the remote cloud, and the process of offloading tasks to the remote cloud is illustrated in Figure 3. Fist, the information of offloaded tasks will be sent to Proposed Algorithms in step 1. According to the information, the module of Proposed Algorithms can select an optimal physical machine for executing the offloaded tasks. Therefore, the ID of the obtained optimal physical machine from the module of Proposed Algorithms will be sent back to the corresponding mobile devices in step 2. Moreover, the offloaded task and the ID of the optimal physical machine will be sent to the module of Resource Management. Finally, the module of Resource Management arrange the offloaded tasks to corresponding physical machines.
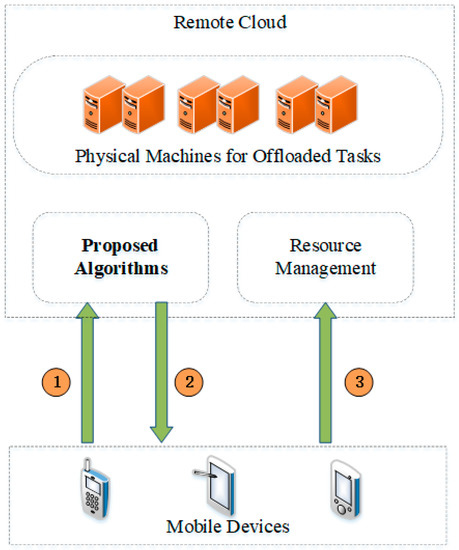
Figure 3.
The process of offloading tasks to remote cloud.
4. Deep Reinforcement Learning
Reinforcement learning (RL) is a subfield in machine learning, in which the agent can learn from trial and error by interacting with the environment and observing reward [19]. As shown in Figure 4, the agent, also referred to as the decision-maker, obtains an immediate reward from the environment according to the current action when its current state is . Moreover, the agent’s state transits to after executing the action . The goal of RL is to lean an optimal policy for an agent that can make it choose the best action according to current state.
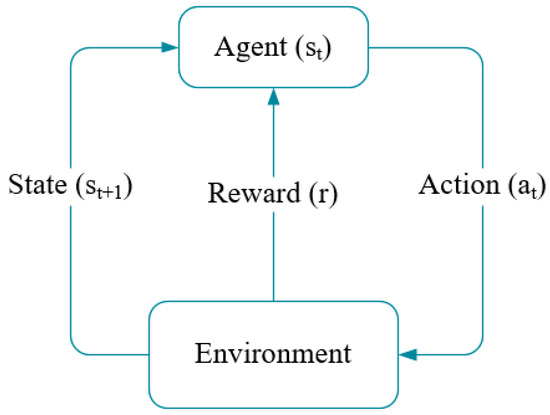
Figure 4.
The progress of an agent interacts with the environment.
We can use a tuple to present the RL, the action an agent can choose is and the state an agent can reach is . R represents the space of reward value.
Q learning is a model-free algorithm [20] for RL, which can be used to get the optimal policy. The evaluation function represents the maximum discount cumulative reward when the agent starts with state and uses as the first action. Therefore, the optimal policy could be denoted as:
According to the Formula (4), in order to obtain the optimal policy , an agent needs to select the action that maximizes when agent is in state . In general, could be iteratively updated by the following Formula:
where represents immediate reward when the agent is in state and selects action to execute. is a constant that determines the discount value of a delayed reward. is learning rate, a larger value of α will lead to a faster convergence for Q function.
However, when the state space and the action space are too large, it is very hard to make converge by traversing all states and actions. DRL can handle the complicated problems with large state space and action space [21]. It has been successfully applied to Alpha Go [22] and playing Atari [23].
When facing high-dimension state space and action space, it is difficult to obtain according to the original method. Suppose that if could be represented by a function, it will be regarded as a value function approximation problem for obtaining . Therefore, we can approximate the function by using function , where represents related parameters.
The loss function was defined by using the mean-square error for DRL that was proposed in paper [24]. Therefore, we follow their definition about the loss function in our paper:
Then, the gradient of is:
In Formula (8), could be calculated by a deep neural network (DNN) [25]. Therefore, the DRL is composed of an offline DNN phase and an online Q-learning progress. Different from RL, a DNN for estimating the value is constructed according to each state-action pair and corresponding value. Therefore, all the Q value cloud be estimated by the DNN in each decision step, which makes algorithm not need to traverse all states and actions. The related training data is usually obtained from actual measurement [22], where the experience memory defined with capacity is used to store state transition profiles and values. Then, the weight set of the DNN could be trained by these training data. In the progress of online Q-learning, the DRL also adopts the -greedy policy for selecting action to update the value. Take a decision step as an example, the agent is in the state . By using the constructed DNN, the agent can estimates the corresponding for all possible actions. The agent can select the maximum value estimate with probability , and select a random action with probability . When the selected action is executed, the agent observes corresponding reward that is used to update the value according to Formula (5). After this decision, the DNN will be updated by the latest observed value.
5. Proposed Methods
5.1. Deep Reinforcement Learning for Task Offloading
Task offloading in MCC environment tries to offload computing-intensive or energy-consuming tasks to cloud servers. As described in Section 3, we should select the optimal PM to execute offloaded tasks by trading off the utilization rate of PM and delay. Existing machine learning methods [15,16,17] for task offloading belong to supervised learning. They need to learn the optimal policy through amount of historical data, in which the selection of historical data will affect the effectiveness of the corresponding algorithm. In order to learn the optimal task offloading policy from real-time data, we mode this problem using DRL in which action space is the set of PMs in the cloud. This method can update policy constantly according to real-time data until it converges. Usually, these PMs are distributed geographically and large scale in order to meet the needs of a large number of devices. This can lead to a large action space.
We define state space according to the waiting time and the number of VMs that run in PMs that are introduced in Section 3. Suppose that, there are PMs in cloud for task offloading and the PM is denoted as . The number of VMs that run in the PM is at current decision step . We use to denote the waiting time that a task is offloaded to the PM in the cloud. Therefore, we could define the state for task offloading as follow:
The dimension of state in our proposed problem is , where is always lager in real cloud infrastructure. Therefore, our proposed problem has a high-dimension state space.
We define the reward value according to the utilization rate of PM and delay which are also the goal of optimization. However, the highest utilization rate of PM and the lowest delay often cannot be met at the same time. If the action is selected and the task is offloaded to the PM correspondingly, then the reward is defined as follow:
The first part is current utilization rate of PM in the cloud, and the second part is the delay caused by task offloading. Then is a weight factor that is used to trade off the utilization rate of PM and delay. If is larger, it means that the utilization rate of PM is preferred than the delay and vice versa. In order to trade off between and efficiently by adjusting the weight factor , we need to normalize the two metric. The Min-Max normalization is used to the two metric. Because the value of is between 0 and 1, we only normalize the in general. In Formula (10), function represents the normalization of the .
In DRL, before the process of online learning, we construct the DNN by learning from the related training data or initializing parameters randomly. The construction and updating of the DNN are based on experience replay [26,27]. The experience M consists of a tuple at each time step in this paper. The input of DNN is the state of PMs in cloud according to Formula (9) and the output of DNN is the corresponding value for selecting each PMs. Therefore, the dimension of input is , and the dimension of output is .
The Figure 5 shows the process of our proposed task offloading algorithm based on DRL that focuses on the online Q learning. When the offloaded task arrives at time step , the algorithm obtains current states and decides how to select the action that represents the PM in cloud that the offloaded task executes on. It will select a random action with probability as shown in step 3 and select a PM that has a large value through the estimation of DNN with probability as shown in step 2. In step 4, the system offloads the task to selected PM and calculates the reward value according to Formula (10). Moreover, the system updates the current state with in step 5 and updates the current value according to Formula (6). Store the transition profiles in experience memory for experience replay in step 6. Finally, update the parameter of DNN according to experience memory . The details of our proposed algorithm are shown in Algorithm 1.
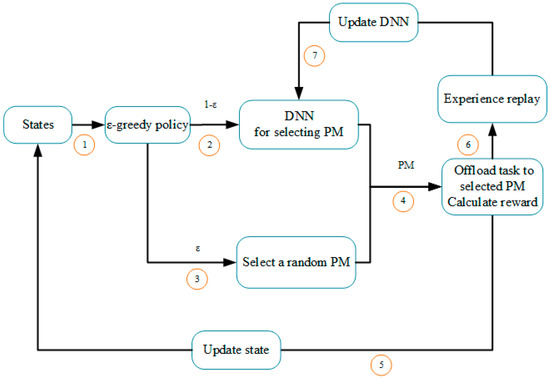
Figure 5.
Flow diagram of task offloading algorithm based on deep reinforcement learning (DRL).
As mentioned above, the dimension of state, the input of DNN, is . The dimension of action is and the action is the output of DNN. If the number of PMs in cloud is large, it will lead to a high dimension of state and action. Therefore, in each decision step, the DNN will estimate value of every possible action in the current state. Moreover, the high dimensional input of the DNN requires a greater number of neurons in hidden layers, which could lead to high computational complexity. We try to reduce both the dimension of state and action for decreasing the computational complexity in order to speed up the optimal policy learning.
| Algorithm 1. Task offloading algorithm based on deep reinforcement learning |
|
5.2. Two-Layered Reinforcement Learning for Task Offloading
In this subsection, we propose a two-layered reinforcement learning (TLRL) algorithm for task offloading to address above problem. First, we divide the PMs into clusters according to the bandwidth between PMs and devices using the k-NN algorithm where the cluster contains PMs. The structure diagram of proposed TLRL algorithm is shown as Figure 6.
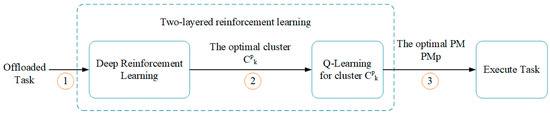
Figure 6.
The structure diagram of two-layered reinforcement learning (TLRL) algorithm.
Our proposed two-layered reinforcement learning structure comprises of DRL and RL. Different from DRL for task offloading, TLRL gives a current optimal cluster of PMs according to the current state first by using DRL first. Then the optimal PM is obtained by using Q-Learning for the cluster . The detailed flow of task offloading algorithm based on TLRL is shown in Figure 7.
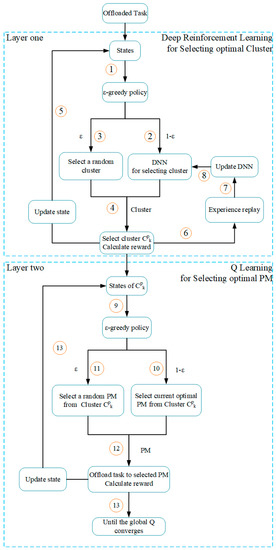
Figure 7.
Flow diagram of task offloading algorithm based on TLRL.
The first layer of TLRL is implemented by DRL, which is used to get an optimal cluster for offloaded tasks. We define the waiting time of the cluster as:
where is the waiting time of the PM. The total number of VMs that run in the cluster is at decision . The state for clusters is denoted as follow:
and
where represents the state of layer one and is its action space. Then we define the reward value when the action is selected and the task is offloaded to the cluster:
where the bandwidth of the cluster is denoted as , which is equal to the bandwidth of center PM of cluster. The evaluation function corresponds to is denoted as , which can be updated according to Formula (5).
The second layer of TLRL is implemented by Q-learning, which is used to get an optimal PM for offloaded tasks. We need to build a Q-learning model for each cluster separately. After the DRL of TLRL selects the cluster, the RL of TLRL will select a PM for executing current offloaded task further by using Q-learning in the cluster. In the cluster, we define the total number of VMs that run in the PM is at episode . The state for clusters is denoted as follow:
and
where represents the state of layer two and is its action space. The reward is denoted as:
where is max number of VMs that run in the cluster. Similarly, the evaluation function corresponds to is denoted as which can be updated according to Formula (5). Besides, we define the global Q-function for TLRL algorithm given by Formula (18), which indicates the convergence of Algorithm 2.
| Algorithm 2. Task offloading algorithm based on two-layered reinforcement learning |
|
6. Simulation Study
In this section, we evaluate the performance of proposed algorithms for offloading tasks through simulations. First, we evaluate the utilization rate of physical machine and delay for 200 offloaded tasks by using three different methods, TLRL algorithm, DRL algorithm and random algorithm. Moreover, we compare our proposed TLRL algorithm with DRL algorithm and Q-learning for offloading tasks, observe convergence times and discounted cumulative reward. Finally, we show the validity of trading off between utilization rate of physical machine and delay for task offloading by using TLRL algorithm and adjust the weight factor .
In this simulation, we set the number of PMs in the remote cloud is 100. According to Section 5, we know that the dimension of state in this simulation is 200 that is a high dimensional state space problem for RL. The bandwidths between these PMs and mobile devices are generated randomly among the interval (500 kbps, 10 Mbps). We suppose all PMs have almost the same hardware configuration. Each PMs could run three VMs at most for executing offloaded tasks. We consider multiple devices in our paper where different devices may contain the same tasks. Therefore, our proposed algorithm makes a decision according to the difference of tasks. In our experiments, we take 6 different tasks and the corresponding parameters are displayed in Table 1. We set , -greedy strategy and reward discount for our proposed algorithms.

Table 1.
The parameters of offloaded tasks in following experiments.
In order to evaluate the TLRL algorithm, we divide the 100 PMs into 20 clusters using k-NN algorithm where the k is equal to 20. Therefore, the dimension of state belonging to RL of TLRL is decreased to 20 × 2 and the number of corresponding actions is 20 according to Section 5. Comparing with DRL algorithm, both the dimension of state and the number of actions have a significant reduction.
Before these experiments, we construct two full-connected CNNs with an input layer, an output layer, and two hidden layers. The details of the two full-connected CNNs are displayed in the Table 2.

Table 2.
The setting of CNN in following experiments.
According to the Table 2, we can see that our proposed TLRL contains less number of input and output compared with DRL by classifying the PMs into 20 clusters via k-NN algorithm. Correspondingly, the hidden layers also contain less number of neurons than DRL.
6.1. The Comparison of Different Algorithms
In this experiment, we compare our proposed TLRL algorithm and DRL algorithm with the random policy for task offloading. The random algorithm arranges the offloaded tasks to the PM randomly and ignores the utilization rate of PMs and delay. The beginning state is initialized randomly, and = 0.5 is selected for the weight factor of reward. We observe the change of utilization rate of PMs and delay through simulating offloading tasks, where the number of offloaded tasks increases from 1 to 200. We will compare the obtained optimal policy after learning process for DRL and TLRL with a random policy. We track the utilization rate of PMs and delay for 200 offloaded tasks by following the learned optimal policy for task offloading.
These results are shown in Figure 8. It is shown that the random algorithm results in severe fluctuation, in terms of the utilization rate of PMs and delay, compared to the cases of DRL and TLRL. First, in Figure 8a, both the DRL and TLRL, the utilization rate of PMs is maintained at the level around 60%, whereas the random algorithm leads to an inferior level around 23% for the utilization rate of PMs, which may lead to the waste of cloud resources. Second, in Figure 8b, it can be seen that based on DRL and TLRL, a lower delay for each offloaded task can be obtained. It changes between 9 s and 15 s. However, frequent changes in the delay for the offloaded task by using the random algorithm, where the max delay is around 27 s. This is because the random approach selects a PM to execute the offloaded task randomly. According to the definition of delay in Formula (3), if is larger and is smaller, it will lead to a higher delay correspondingly. On the contrary, if is smaller and is larger, a lower delay is obtained. Therefore, this random selection approach for PMs can lead to a random delay in each decision step, which may cause the high jitter in the delay for offloaded tasks. We can conclude that our proposed algorithms based on DRL can get a better performance for increasing the utilization rate of PMs and decreasing the delay caused by task offloading than random policy.
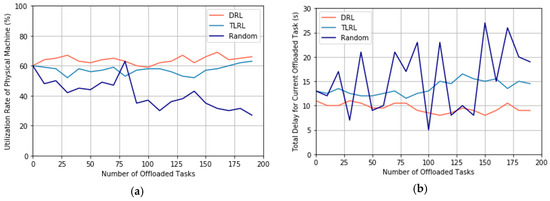
Figure 8.
It shows the comparison of different algorithms for task offloading. (a) shows the change for utilization rate of physical machine; (b) shows the change for the delay of offloaded tasks.
From the above results, one can observe that the policy learned by DRL can achieve better results than the policy learned by TLRL. This is because we reduce both the dimension of state and action for decreasing the computational complex by proposing the TLRL algorithm, where we assume the PMs from the same cluster are similar. Then we assume the waiting time and bandwidth of PMs from the same cluster are equal to the cluster according to Section 5, which may lead to a bias of learning optimal policy. However, our proposed TLRL algorithm could find the optimal policy than other methods when facing to high-dimension state space and action space.
To discuss above problem, we start from a randomly initialized state for DRL, TLRL, and Q-learning. We compare convergence speed of the three algorithms for task offloading. The results are given in Figure 9.
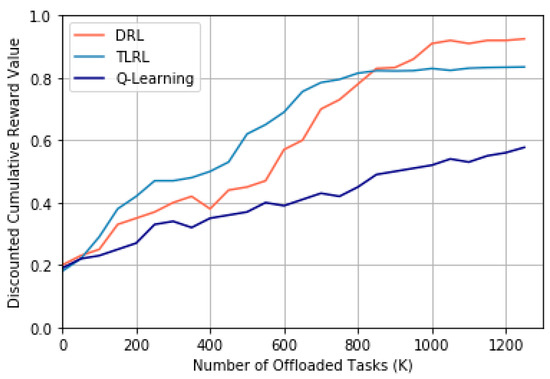
Figure 9.
Comparison of convergence speed between different algorithms.
Through observing the experimental results, it can be shown that both the DRL and TLRL can converge through a period learning process that is represented by the number of offloaded tasks. However, the traditional Q-learning algorithm does not converge. This indicates that the algorithms based on DRL for task offloading are more suitable to the problem with high-dimension state space and action space than traditional Q-learning. In addition, our proposed TLRL algorithm can converge faster than DRL owing to dimension reduction for the input and output of DNN and less number of needed neurons in hidden layers of DNN than DRL according to Table 2. Therefore, our proposed TLRL could obtain a faster convergence speed than DRL.
6.2. The Verification of Tradeoff
In this experiment, we will show the trading off between utilization rate of PMs and delay for task offloading by using our proposed TLRL algorithm. We evaluate these two indicators by simulating offloading tasks that are selected from Table 1 randomly. We record these two indicators after each decision of TLRL for offloading tasks. We adjust the weight factor from 0.1 to 0.9 to do experiments separately and observe the change of the two indicators.
From these results, we can conclude that our proposed TLRL algorithm can trade off the utilization rate of PMs and delay by adjusting the weight in the reward effectively. According to Formula (10), the weights for the utilization rate of PMs and delay are and respectively. The experimental results in Figure 10 show the process of online learning optimal policy when β takes different values and track the changes of the utilization rate of PMs and delay during the learning process. We assume that the number of needed offloaded tasks is more than 800 in a real MCC environment and our proposed algorithm could converge. Therefore, our proposed algorithm will lean an optimal policy, which make the utilization rate of PM and delay keep stable in an interval. In Figure 10a–e, we can see that the utilization rate of PMs converges to a larger value when the weight factor is set to a larger value. Correspondingly, the weight of delay for current offloaded task becomes smaller, which lead to a larger delay. Therefore, if the utilization rate of PM is preferred, then a larger β is chosen and vice versa. Moreover, the TLRL algorithm can learn the optimal policy for task offloading with the increase of offloading tasks. This is because the TLRL comprises with DRL in layer one and Q learning in layer two, both of the two methods can converge according to Bellman Equation. We define the global Q-function for TLRL algorithm given by Formula (18), which indicates the convergence of TLRL algorithm. We can see that is composed of the Q values from above two algorithms. Therefore, TLRL algorithm can also converge which indicates that it can learn the optimal policy. Therefore, the two indicators will become stable in a certain interval that is related to the value of .
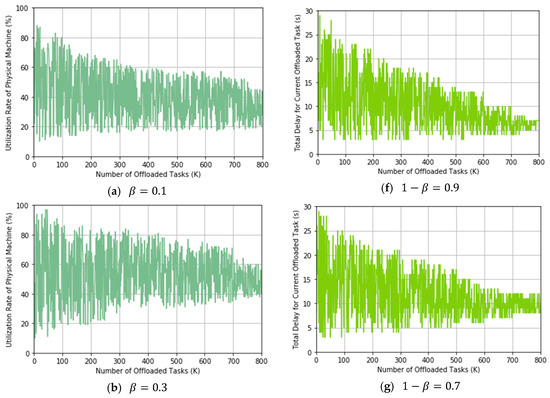
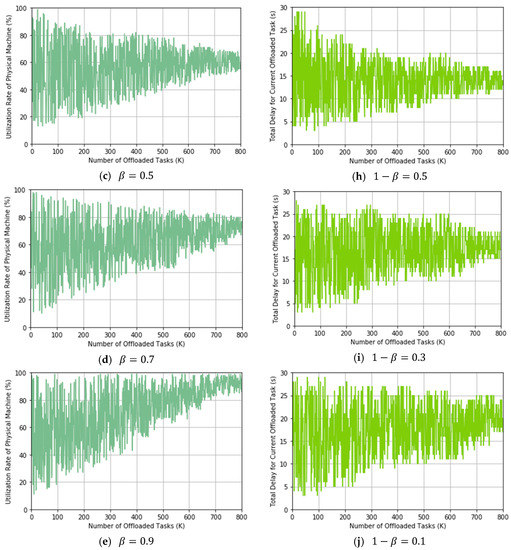
Figure 10.
(a–e) shows the change for the utilization rate of physical machines (PMs) with the weight increasing from 0.1 to 0.9. (f–j) shows the change of delay for the current offloaded task with the weight decreasing from 0.9 to 0.1 correspondingly.
7. Conclusions
In this paper, we solve the problem of task offloading in order to decrease the delay for offloaded tasks and increase the utilization rate of physical machine in the cloud. Different from the traditional Q-learning algorithm, the DRL can be suited to the problem with high-dimension state space. Moreover, in order to improve the speed of learning optimal policy, we propose a novel TLRL algorithm for task offloading, where the k-NN algorithm is applied to divide the PMs into several clusters. With the reduced dimension of state space and action space, the DRL layer aims at learning the optimal policy to choose a cluster. Then, the Q-learning layer learns an optimal policy to select the optimal PM to execute the current offloaded task. The experiments show that the TLRL algorithm is faster than the DRL algorithm when learning the optimal policy for task offloading. By adjusting the weight factor , our proposed algorithms for task offloading can trade off between utilization rate of physical machine and delay effectively.
Our proposed algorithms intend to find the optimal PM for executing offloaded tasks by considering utilization rate of PM and delay for task offloading simultaneously. We simulate 100 PMs with different bandwidths and six different target applications to verify our proposed algorithms. Moreover, this paper is mainly focused on developing novel RL-based algorithms to solve the offloading problem. We verify the effectiveness of the proposed algorithms in theory, which can trade off between utilization rate of PM and delay effectively by designing a weighted reward. In the future study, we will verify our proposed algorithms in a real environment where the running environments of offloaded tasks are deployed on PMs. Besides, simulated tasks will be replaced by the real applications running on smartphones. Moreover, Different tasks have different attributes, which also cloud have different delay requirement. However, we mainly focus on the effective tradeoff between the utilization rate of PM and delay and try to decrease the delay as possible ignoring the delay requirement for different tasks. Take task 1 for example, if it requires that the delay cannot exceed a given time t, then the algorithm could choose a β that makes the utilization rate of PM larger before meeting its delay requirement. Therefore, we can find the relation between the value of β and the delay requirement for different tasks through analyzing the obtained real data. Therefore, we will research on choosing the adaptive value β according to offloading tasks conditions by using the prediction model in our future work.
Author Contributions
The work presented in this paper represents a collaborative effort by all authors, whereas L.Q. wrote the main paper. Z.W. and F.R. discussed the proposed main problem and algorithms. Both authors have read and approved the final manuscript.
Funding
This paper is supported by National Natural Science Foundation of China (Key Project, No. 61432004): Mental Health Cognition and Computing Based on Emotional Interactions. National Key Research and Development Program of China (No. 2016YFB1001404): Multimodal Data Interaction Intention Understanding in Cloud Fusion. National Key Research and Development Program of China (No. 2017YFB1002804) and National Key Research and Development Program of China (No. 2017YFB1401200).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Fernando, N.; Loke, S.W.; Rahayu, W. Mobile cloud computing: A survey. Future Gener. Comput. Syst. 2013, 29, 84–106. [Google Scholar] [CrossRef]
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.D.; Katz, R.H.; Konwinski, A.; Lee, G.; Patterson, D.A.; Rabkin, A.; Stoica, I.; Zaharia, M. Above the Clouds: A Berkeley View of Cloud Computing; Eecs Department University of California Berkeley: Berkeley, CA, USA, 2009; Volume 53, pp. 50–58. [Google Scholar]
- Kumar, K.; Lu, Y.H. Cloud computing for mobile users: Can offloading computation save energy? Computer 2010, 43, 51–56. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Xu, R. Computation offloading to save energy on handheld devices:A partition scheme. In Proceedings of the 2001 International Conference on Compilers, Architecture, and Synthesis for Embedded Systems (CASES’01), Atlanta, GA, USA, 16–17 November 2001; pp. 238–246. [Google Scholar]
- Zhang, W.; Wen, Y.; Guan, K.; Dan, K.; Luo, H.; Wu, D.O. Energy-optimal mobile cloud computing under stochastic wireless channel. IEEE Trans. Wirel. Commun. 2013, 12, 4569–4581. [Google Scholar] [CrossRef]
- Jiang, Z.; Mao, S. Energy delay tradeoff in cloud offloading for mutli-core mobile devices. IEEE Access 2015, 3, 2306–2316. [Google Scholar] [CrossRef]
- Liu, J.; Mao, Y.; Zhang, J.; Letaief, K.B. Delay-optimal computation task scheduling for mobile-edge computing systems. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1451–1455. [Google Scholar]
- Kim, B.; Byun, H.; Heo, Y.-A.; Jeong, Y.-S. Adaptive job load balancing scheme on mobile cloud computing with collaborative architecture. Symmetry 2017, 9, 65. [Google Scholar] [CrossRef]
- Shahzad, H.; Szymanski, T.H. A dynamic programming offloading algorithm for mobile cloud computing. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016. [Google Scholar]
- Wang, N.; Varghese, B.; Matthaiou, M.; Nikolopoulos, D.S. Enorm: A framework for edge node resource management. IEEE Trans. Serv. Comput. 2017. [Google Scholar] [CrossRef]
- Lyu, X.; Tian, H.; Sengul, C.; Zhang, P. Multiuser joint task offloading and resource optimization in proximate clouds. IEEE Trans. Veh. Technol. 2017, 66, 3435–3447. [Google Scholar] [CrossRef]
- Ciobanu, R.I.; Negru, C.; Pop, F.; Dobre, C.; Mavromoustakis, C.X.; Mastorakis, G. Drop computing: Ad-hoc dynamic collaborative computing. Future Gener. Comput. Syst. 2017. [Google Scholar] [CrossRef]
- Chae, D.; Kim, J.; Kim, J.; Kim, J.; Yang, S.; Cho, Y.; Kwon, Y.; Paek, Y. In Cmcloud: Cloud platform for cost-effective offloading of mobile applications. In Proceedings of the 2014 14th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Chicago, IL, USA, 26–29 May 2014; pp. 434–444. [Google Scholar]
- Liu, W.; Cao, J.; Yang, L.; Xu, L.; Qiu, X.; Li, J. Appbooster: Boosting the performance of interactive mobile applications with computation offloading and parameter tuning. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1593–1606. [Google Scholar] [CrossRef]
- Eom, H.; Figueiredo, R.; Cai, H.; Zhang, Y.; Huang, G. Malmos: Machine learning-based mobile offloading scheduler with online training. In Proceedings of the 2015 3rd IEEE International Conference on Mobile Cloud Computing, Services, and Engineering, San Francisco, CA, USA, 30 March–3 April 2015; pp. 51–60. [Google Scholar]
- Crutcher, A.; Koch, C.; Coleman, K.; Patman, J.; Esposito, F.; Calyam, P. Hyperprofile-based computation offloading for mobile edge networks. arXiv, 2017; 525–529arXiv:1707.09422. [Google Scholar]
- Zhan, Y.; Chen, H.; Zhang, G.C. An optimization algorithm of k-nn classification. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 2246–2251. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 2005, 16, 285–286. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Li, Y. Deep reinforcement learning: An overview. arXiv, 2017; arXiv:1701.07274 2 017. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Driessche, G.V.D.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M. Mastering the game of go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. Comput. Sci. 2013, arXiv:1312.5602. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2016, 234, 11–26. [Google Scholar] [CrossRef]
- Hansen, S. Using deep q-learning to control optimization hyperparameters. arXiv, 2016; arXiv:1602.04062 2016. [Google Scholar]
- Lin, L.-J. Reinforcement Learning for Robots Using Neural Networks; Carnegie-Mellon Univ Pittsburgh PA School of Computer Science: Pittsburgh, PA, USA, 1993. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).