Certificateless Provable Group Shared Data Possession with Comprehensive Privacy Preservation for Cloud Storage
Abstract
:1. Introduction
- First, we propose a new PDP protocol (CL-PGSDP) for group shared data by utilizing certificateless cryptography [31], which eliminates the problems of certificate management and key escrow.
- Second, by making use of the idea of zero-knowledge proof protocol, the equality of discrete logarithm [32,33,34], and randomization method, we construct a privacy-preserving CL-PGSDP protocol. On the one hand, our protocol leaks no information of the group shared data to the TPA. On the other hand, all the data blocks are signed by group users to get corresponding authentication tags, and the TPA cannot learn any identity information from the challenged data block during the auditing process.
- Third, based on CDH and DL assumptions, we provide detailed security proofs of our new protocol. Additionally, our protocol supports efficient group user revocation. We perform some experiments and show the practicality of our protocol.
2. Preliminaries
2.1. Bilinear Pairing
- Bilinearity: For all . and , holds.
- Non-Degeneracy: , in which is the identity of .
- Efficient Computation: can be computed efficiently for all. .
2.2. Certificateless Cryptography
- Setup: This algorithm takes security parameter k as input and returns the system parameters and master-key.
- Partial-Private-Key-Extract: This algorithm takes , master-key, and entity’s ID as inputs and returns a partial private key for the entity.
- Set-Secret-Value: This algorithm takes and entity’s ID as inputs and outputs this entity’s secret value .
- Set-Private-Key: This algorithm takes , entity’s ID, partial private key , and secret value as inputs and outputs private key .
- Set-Public-Key: This algorithm takes and secret value as inputs and outputs public key .
- Encrypt: This algorithm takes , message m, and public key as inputs and entity’s ID and generates ciphertext of the message m if success.
- Decrypt: This algorithm takes , , and as inputs and returns message m.
2.3. Zero-Knowledge Proof
- P randomly chooses , and computes , then sends to V.
- V also randomly chooses and sends to P.
- P computes , in which is the secret key of P, and returns to V.
- V accepts the proof if and only if and .
2.4. Security Assumption
3. System Model and Security Model
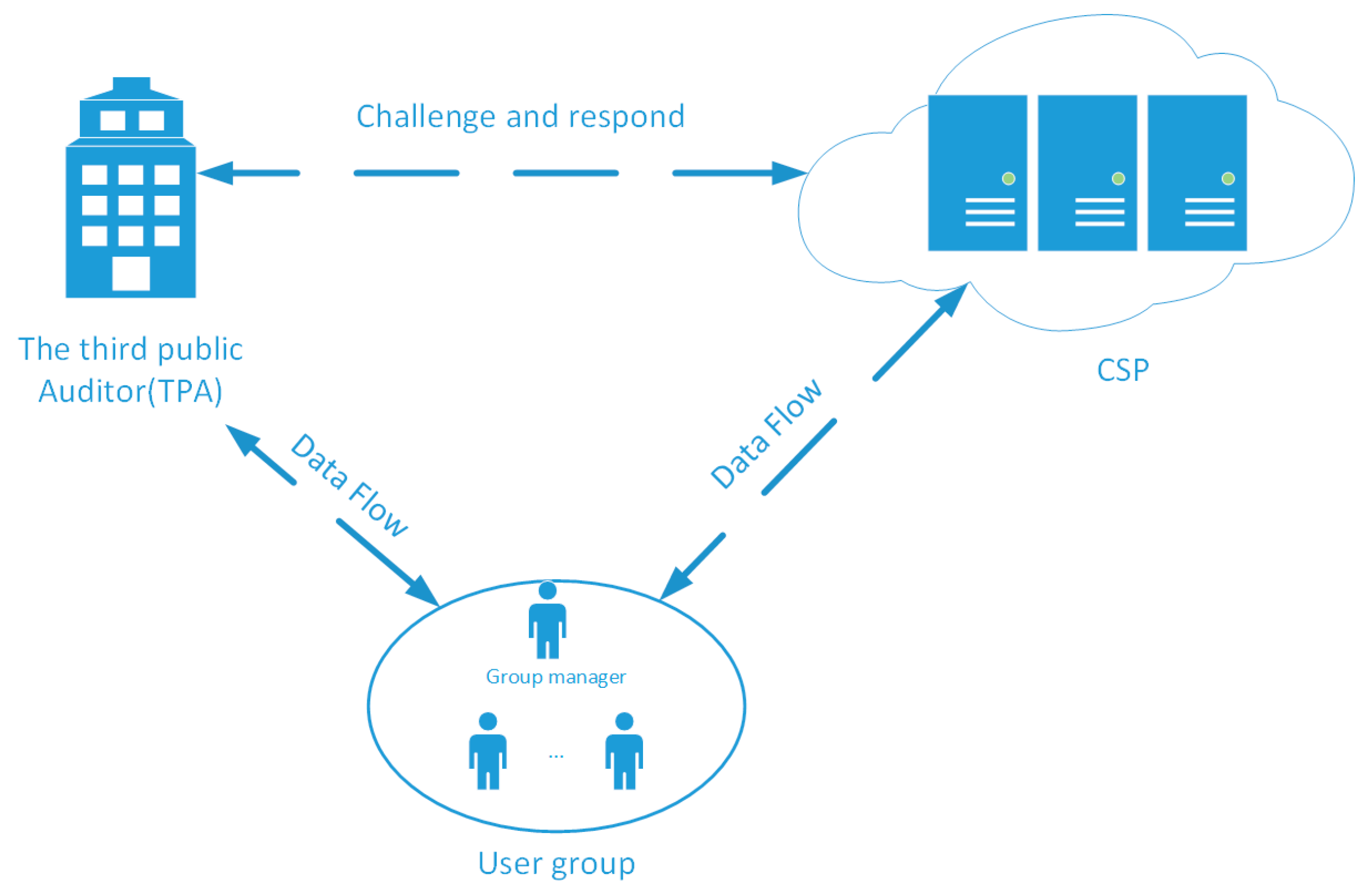
3.1. CL-PGSDP System
3.2. System Components
- Setup is a probabilistic algorithm run by the group manager. It takes a security parameter λ as input and outputs the system parameters and the master key .
- Partial-Private-Key-Gen is a probabilistic algorithm run by the group manager. It takes the master key , a random value , and the identity of the user as inputs, and outputs the ’s partial private key .
- Secret-Value-Gen is a probabilistic algorithm run by the group user who randomly selects as the secret value. Thus, the private key of the group user contains two parts: secret value and partial private key .
- Public-Key-Gen is a probabilistic algorithm performed by the group user to compute the public key. It inputs the ’s secret value and outputs the ’s public key .
- Tag-Gen is a probabilistic algorithm executed by the group user to generate authentication tags for data blocks. It takes the ’s partial private key , the secret value , and the data block as inputs, and outputs the tag of .
- Challenge is a randomized algorithm run by the TPA. It takes the system parameters , a unique file name, and the count of the challenged data blocks as inputs, and outputs the challenge information .
- Proof-Gen is a probabilistic algorithm run by cloud server to obtain a data possession proof P of the challenged blocks. The inputs include , the challenged data blocks and tags of the challenged data blocks.
- Proof-Check is a deterministic algorithm run by the TPA. It inputs the proof P, the challenge information , and the user’s public key. If P is correct, this algorithm outputs 1, otherwise it outputs 0.
3.3. System Security
- Completeness means the cloud server can pass the possession checking procedure as long as the cloud server properly stores the group shared data.
- Comprehensive privacy preservation means that the TPA achieves no information on the data blocks and the user’s identity during the integrity checking procedure.
- Soundness states that whenever the cloud server convinces a TPA to accept its proof, the cloud server should actually store the challenged data blocks. According to certificateless cryptography [30,31], we consider three types of probabilistic polynomial-time (PPT) adversaries, namely, A1, A2, A3, and a challenger C in our security model and define the security of our protocol by three games. The details are as follows:
- (1)
- Hash Query. A1 makes hash function queries to C for any identity ID, and C responds to the hash values to A1.
- (2)
- Partial Private Key Query. A1 adaptively chooses different ID and summits it to C for querying the partial private key of the ID. C executes the Partial-Private-Key-Gen algorithm to obtain the partial private key for the ID and sends it to A1.
- (3)
- Secret Value Query. A1 adaptively chooses different ID and summits it to C for querying the secret value of the ID. C runs the Secret-value-Gen algorithm to generate the secret value for the ID and sends it to A1.
- (4)
- Public Key Query. A1 adaptively chooses different ID and summits it to C for querying the public key of the ID. C performs the algorithm Public-key-Gen to compute the public key for the ID and sends it to A1.
- (5)
- Public Key Replacement. A1 can repeatedly select a value to replace the public key of any ID.
- (6)
- Tag Query. A1 adaptively chooses the tuple (ID, ) and submits it to C for querying the tag of the data block . C runs Tag-Gen algorithm to generate the tag of data block and sends it to A1.
- (1)
- Hash Query. A2 makes hash function queries to C for any identity ID, and C responds the hash values to A2.
- (2)
- Secret Value Query. A2 adaptively chooses different ID and summits it to C for querying the secret value of the ID. C runs the Secret-value-Gen algorithm to generate the secret value for the ID and sends it to A2.
- (3)
- Public Key Query. A2 adaptively chooses different ID and summits it to C for querying the public key of the ID. C performs the algorithm Public-key-Gen to compute the public key for the ID and sends it to A2.
- (4)
- Tag Query. A2 adaptively chooses the tuple (ID, ) and submits it to C for querying the tag of the data block generated by the ID. C runs Tag-Gen algorithm to generate the tag of data block and sends it to A2.
4. Our Construction
- Setup. This algorithm is run by . On input of security parameter , chooses two cyclic multiplicative groups, and , with prime order , . is a generator of . There exists a bilinear map . selects three secure hash functions , , a pseudo-random permutation (PRP) , and a pseudo-random function (PRF) . initializes a public log file , which is used to record the information of the indexes of the data blocks and the information of the corresponding tag generators. randomly chooses as master secret key and as secret value, and computes . keeps the master secret key and privately, and publishes the system parameters .
- Partial-Private-Key-Gen. This algorithm is run by . When receiving the identity of the user , computes the ’s partial private key and sends and to .
- Secret-Value-Gen. This algorithm is run by group user. randomly selects as the secret value and keeps it privately.
- Public-Key-Gen. This algorithm is run by group user. uses the secret value to compute the public key .
- Tag-Gen. Each user in group can generate tags of data blocks using partial private key and secret value. Suppose user generates an authentication tag for data block . It takes ’s partial private key , the secret value , and the data block as inputs and outputs the tag of . The equation for computing tag is , in which , is the index of data block , and denotes the unique identity of data block . Each time the generates a tag for data block , will update the information in public log file with the index of , , and . Actually, is a table, and one line of it can be showed as follows:
j - The user uploads the data blocks and its tags to the CSP. The CSP can check the validation of each tag using the following equation:
- Challenge. This algorithm is run by the TPA, who randomly picks c-element subset of the set by pseudo-random permutation (PRP) ; each element in denotes the index of the challenged data block. The TPA chooses a random element for each element in by pseudo-random function (PRF) . Let be the set . To generate a challenge, the TPA will search the log file according the set to get the information . The TPA picks a random value as secret value and computes , . Let . The TPA sends the to the server.
- Proof-Gen. Upon receiving the , the CSP computes , and , then sends as a response to the from the TPA.
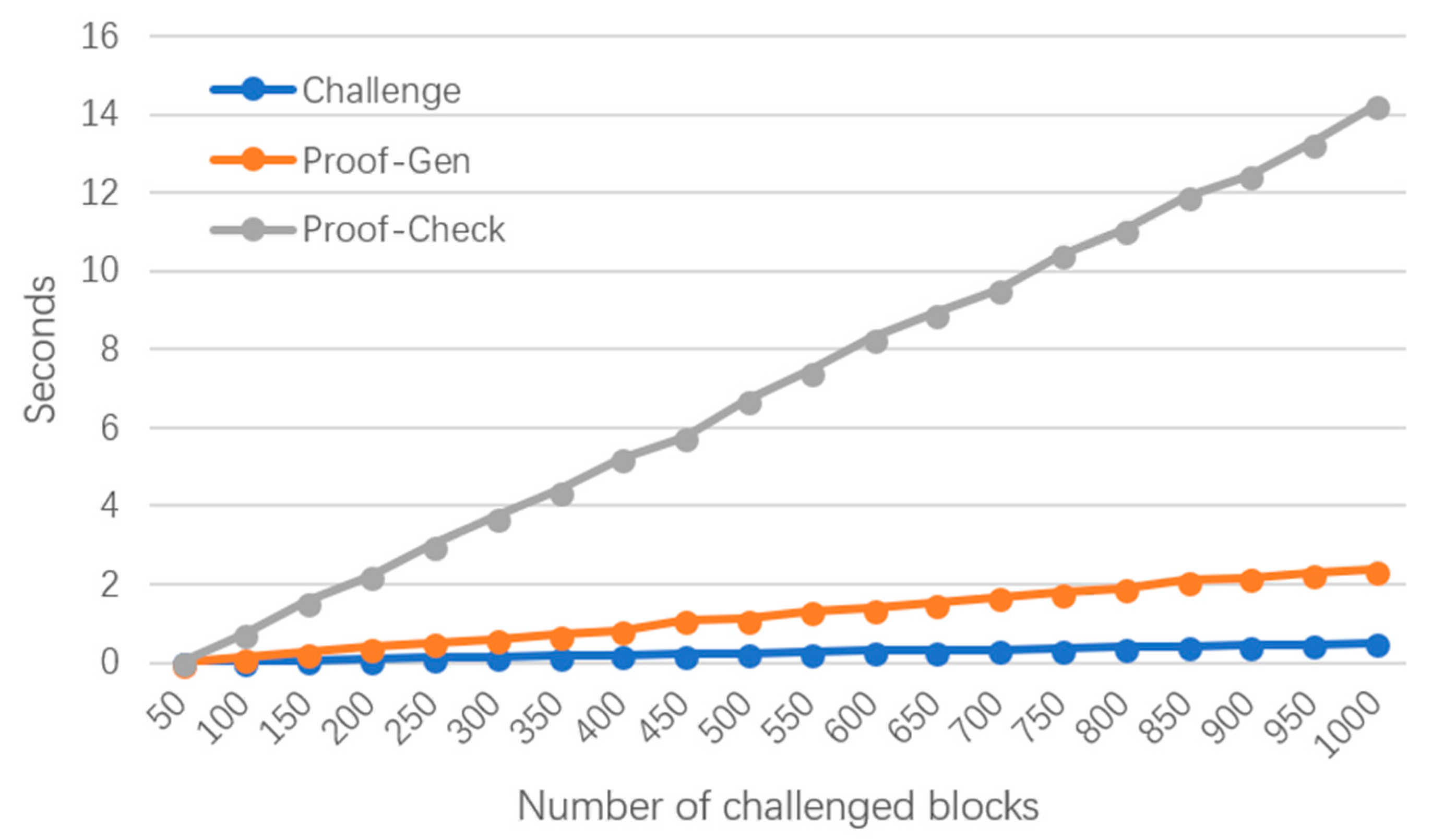
- Proof-Check. Upon receiving the from the CSP, the TPA first searches the publish log file to get the information and checks the equation:in which means the information of can be find from public log file by the index of data block . If the equation holds, the TPA accepts the proof; otherwise, the proof is invalid. The process of Challenge, Proof-Gen, and Proof-Check are summarized as Figure 2.
- Revocation-Tag-Gen. If user , leaves the group, and user will be the successor of . The following procedure will efficiently update the tags generated by . It needs , and the CSP online simultaneously.
- (1)
- The CSP randomly selects , and sends it to .
- (2)
- Upon receiving , computes and sends to .
- (3)
- computes and sends it to the CSP.
- (4)
- When receiving , the CSP computes . The CSP will update the tag of the data block by computing the equation , in which is the tag generated by . The proof of the correctness of algorithm Revocation-Tag-Gen is as follows:
5. Security Analysis of the New Protocol
5.1. Completeness
5.2. Soundness
- (1)
- If , then algorithm retrieves the tuple and responds with to A1.
- (2)
- Otherwise, picks a random and computes . Then, it adds the tuple to Tab1 and responds with to A1.
- (1)
- If , then algorithm retrieves the tuple and responds to A1.
- (2)
- Otherwise, computes . Then, it adds the tuple to Tab2 and responds to A1.
- (1)
- If , then algorithm retrieves the tuple and responds with to A2.
- (2)
- Otherwise, picks a random and computes . Then, it adds the tuple to Tab1 and responds with to A2.
- (1)
- If , then algorithm retrieves the tuple and responds with to A2.
- (2)
- Otherwise, randomly selects and makes . Then, it adds the tuple to Tab2 and responds with to A2.
5.3. Comprehensive Privacy Preservation
5.3.1. Data Privacy Preservation
5.3.2. User Identity Privacy Preservation
6. Performance and Implementation
6.1. Performance Analysis
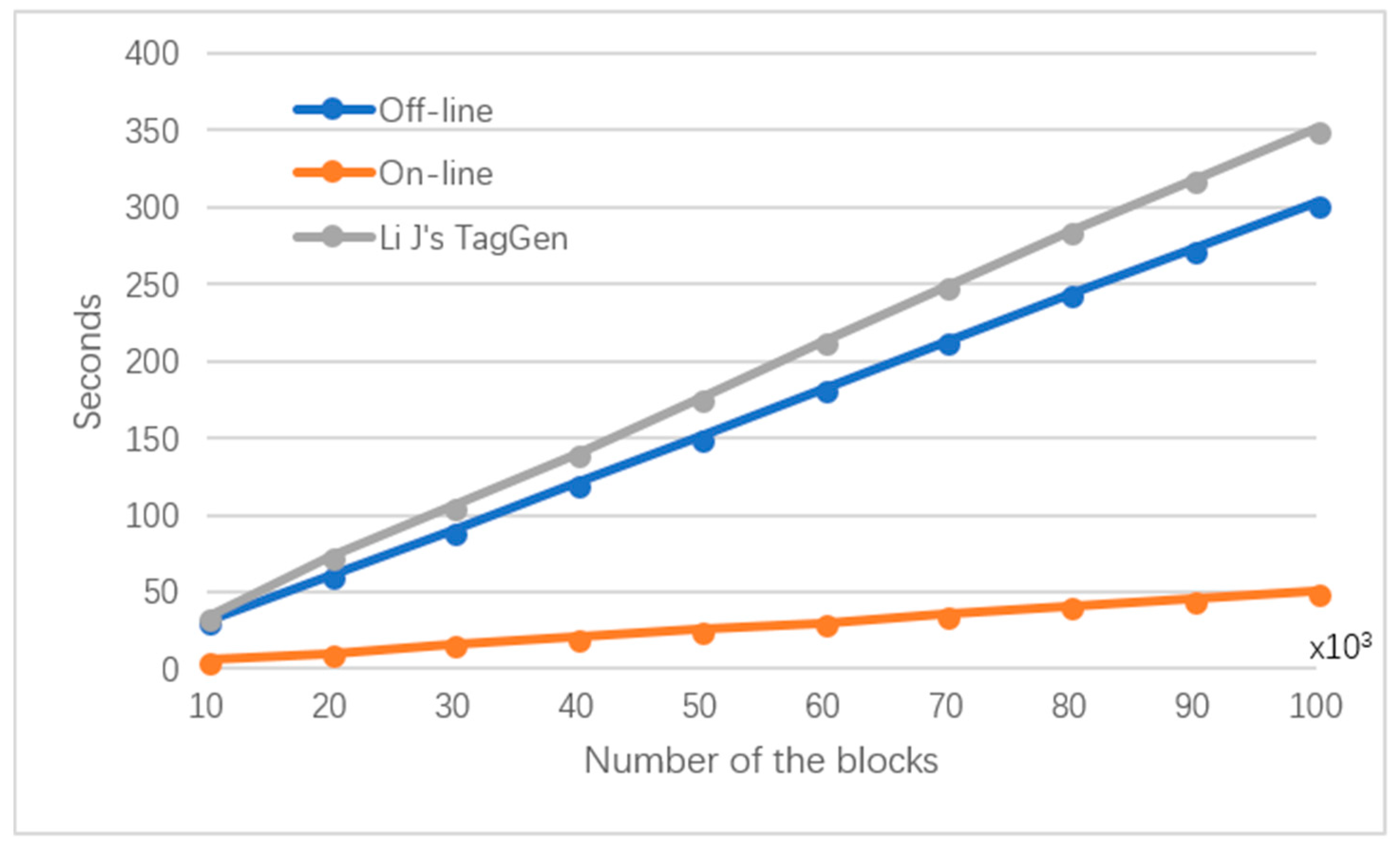
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; Florida Entomological Society: Gaithersburg, MD, USA, 2011. [Google Scholar]
- Antonis, M.; Paladi, N.; Gehrmann, C. Security aspects of e-health systems migration to the cloud. In Proceedings of the IEEE 16th International Conference on e-Health Networking, Applications and Services (Healthcom), Natal, Brazil, 15–18 October 2014. [Google Scholar]
- Santos, N.; Gummadi, K.P.; Rodrigues, R. Towards Trusted Cloud Computing. In Proceedings of the Conference on Hot Topics in Cloud Computing, San Diego, CA, USA, 14–19 June 2009. [Google Scholar]
- Paladi, N.; Gehrmann, C.; Michalas, A. Providing user security guarantees in public infrastructure clouds. IEEE Trans. Cloud Comput. 2017, 5, 405–419. [Google Scholar] [CrossRef]
- Chu, C.; Zhu, W.; Han, J.; Liu, J.K.; Xu, J.; Zhou, J. Security concerns in popular cloud storage services. IEEE Pervasive Comput. 2013, 12, 50–57. [Google Scholar] [CrossRef]
- Miller, R. Amazon Addresses EC2 Power Outages. Available online: http://www.datacenterknowledge.com/archives/2010/05/10/amazon-addresses-ec2-power-outages (accessed on 6 June 2018).
- Yang, K.; Jia, X. Data storage auditing service in cloud computing: Challenges, methods and opportunities. World Wide Web 2012, 15, 409–428. [Google Scholar] [CrossRef]
- Kaufman, L.M. Data security in the world of cloud computing. IEEE Secur. Privacy 2009, 7, 61–64. [Google Scholar] [CrossRef]
- Ateniese, G.; Burns, R.; Curtmola, R.; Herring, J.; Kissner, L.; Peterson, Z.; Song, D. Provable data possession at untrusted stores. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007; pp. 598–609. [Google Scholar]
- Juels, A.; Kaliski, B.S., Jr. PORs: Proofs of retrievability for large files. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007. [Google Scholar]
- Shacham, H.; Waters, B. Compact proofs of retrievability. In Proceedings of the 14th Annual International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008; pp. 90–107. [Google Scholar]
- Boneh, D.; Lynn, B.; Shacham, H. Short signatures from the Weil pairing. In Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001; pp. 514–532. [Google Scholar]
- Ateniese, G.; di Pietro, R.; Mancini, L.V.; Tsudik, G. Scalable and efficient provable data possession. In Proceedings of the 4th International Conference on Security and Privacy in Communication Networks, Istanbul, Turkey, 22–25 September 2008; p. 9. [Google Scholar]
- Erway, C.; Küpçü, A.; Papamanthou, C.; Tamassia, R. Dynamic provable data possession. In Proceedings of the ACM Transactions on Information and System Security (TISSEC), Chicago, IL, USA, 9–13 November 2009; p. 15. [Google Scholar]
- David, C.; Küpçü, A.; Wichs, D. Dynamic proofs of retrievability via oblivious RAM. J. Cryptol. 2017, 30, 22–57. [Google Scholar]
- Wang, Q.; Wang, C.; Li, J.; Ren, K.; Lou, W. Enabling public verifiability and data dynamics for storage security in cloud computing. In Proceedings of the European Symposium on Research in Computer Security, Saint-Malo, France, 21–23 September 2009; pp. 355–370. [Google Scholar]
- Liu, C.; Ranjan, R.; Yang, C.; Zhang, X.; Wang, L.; Chen, J. MuR-DPA: Top-down levelled multi-replica merkle hash tree based secure public auditing for dynamic big data storage on cloud. IEEE Trans. Comput. 2015, 64, 2609–2622. [Google Scholar] [CrossRef]
- Yuan, J.; Yu, S. Proofs of retrievability with public verifiability and constant communication cost in cloud. In Proceedings of the International Workshop on Security in Cloud Computing, Hangzhou, China, 8 May 2013; pp. 19–26. [Google Scholar]
- Wang, H. Proxy provable data possession in public clouds. IEEE Trans. Ser. Comput. 2013, 6, 551–559. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Q.; Ren, K.; Lou, W. Privacy-preserving public auditing for data storage security in cloud computing. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Wang, C.; Chow, S.S.M.; Wang, Q.; Ren, K.; Lou, W. Privacy-preserving public auditing for secure cloud storage. IEEE Trans. Comput. 2013, 62, 362–375. [Google Scholar] [CrossRef]
- Yu, Y.; Au, M.H.; Mu, Y.; Tang, S.; Ren, J.; Susilo, W.; Dong, L. Enhanced privacy of a remote data integrity-checking protocol for secure cloud storage. Int. J. Inf. Secur. 2015, 14, 307–318. [Google Scholar] [CrossRef]
- Cooper, D.; Santesson, S.; Farrell, S.; Boeyen, S.; Housley, R.; Polk, W. Internet X.509 Public Key Infrastructure Certificate and Certificate Revocation List (CRL) Profile. Available online: https://tools.ietf.org/html/rfc5280 (accessed on 6 June 2018).
- Yu, Y.; Au, M.H.; Ateniese, G.; Huang, X.; Susilo, W.; Dai, Y.; Min, G. Identity-based remote data integrity checking with perfect data privacy preserving for cloud storage. IEEE Trans. Inf. Forensics Secur. 2017, 12, 767–778. [Google Scholar] [CrossRef]
- Wang, H. Identity-based distributed provable data possession in multicloud storage. IEEE Trans. Ser. Comput. 2015, 8, 328–340. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Q.; Qin, B.; Domingo-Ferrer, J. Identity-based remote data possession checking in public clouds. IET Inf. Secur. 2013, 8, 114–121. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, Q. Efficient ID-based public auditing for the outsourced data in cloud storage. Inf. Sci. 2016, 343, 1–14. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; pp. 213–229. [Google Scholar]
- Wang, B.; Li, B.; Li, H.; Li, F. Certificateless public auditing for data integrity in the cloud. In Proceedings of the IEEE Conference on IEEE Communications and Network Security (CNS), National Harbor, MD, USA, 14–16 October 2013; pp. 136–144. [Google Scholar]
- Li, J.; Yan, H.; Zhang, Y. Certificateless public integrity checking of group shared data on cloud storage. IEEE Trans. Serv. Comput. 2018. [Google Scholar] [CrossRef]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 30 November–4 December 2003; pp. 452–473. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rackoff, C. The knowledge complexity of interactive proof systems. SIAM J. Comput. 1989, 18, 186–208. [Google Scholar] [CrossRef]
- Feige, U.; Fiat, A.; Shamir, A. Zero-knowledge proofs of identity. J. Cryptol. 1988, 1, 77–94. [Google Scholar] [CrossRef]
- Chaum, D.; Pedersen, T.P. Wallet databases with observers. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 1992; pp. 89–105. [Google Scholar]
- Nyberg, K.; Rueppel, R.A. Message recovery for signature schemes based on the discrete logarithm problem. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Perugia, Italy, 9–12 May 1997; pp. 182–193. [Google Scholar]
- Bao, F.; Deng, R.H.; Zhu, H. Variations of diffie-hellman problem. In Proceedings of the 5th International Conference on Information and Communications Security, Huhehaote, China, 10–13 October 2003; pp. 301–312. [Google Scholar]
- Lynn, B. The Pairing-Based Cryptography Library (0.5.14), 2017. Available online: https://crypto.stanford.edu/pbc/ (accessed on 6 June 2018).
- Free Software Foundation. The GNU Multiple Precision Arithmetic Library. Available online: https://gmplib.org/ (accessed on 6 June 2018).

| Li [30] | Our CL-PGSDP | |
|---|---|---|
| Tag Generation cost | 2nExpG1 + nH | 2nExpG1 + nH |
| Challenge cost | Negligible cost | zP + zExpG2 + ExpG1 |
| Proof Generation cost | cExpG1 + (c − z) MultG1 | (2c − 1) MultG1 + cMultG2 + cExpG2 + cExpG1 + P |
| Proof-Check cost | (z + 2) P + (c + d) ExpG1 + (c + 2d) MultG1 + dMultG2 | 2cExpG1 + cPG1 + cH + (c − 1) ExpG2 |
| Working scenario | Group data | Group data |
| Support data privacy-preserving | No | Yes |
| Support user identity privacy-preserving | No | Yes |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Jiang, S.; Shen, W.; Lei, Z. Certificateless Provable Group Shared Data Possession with Comprehensive Privacy Preservation for Cloud Storage. Future Internet 2018, 10, 49. https://doi.org/10.3390/fi10060049
Yang H, Jiang S, Shen W, Lei Z. Certificateless Provable Group Shared Data Possession with Comprehensive Privacy Preservation for Cloud Storage. Future Internet. 2018; 10(6):49. https://doi.org/10.3390/fi10060049
Chicago/Turabian StyleYang, Hongbin, Shuxiong Jiang, Wenfeng Shen, and Zhou Lei. 2018. "Certificateless Provable Group Shared Data Possession with Comprehensive Privacy Preservation for Cloud Storage" Future Internet 10, no. 6: 49. https://doi.org/10.3390/fi10060049
APA StyleYang, H., Jiang, S., Shen, W., & Lei, Z. (2018). Certificateless Provable Group Shared Data Possession with Comprehensive Privacy Preservation for Cloud Storage. Future Internet, 10(6), 49. https://doi.org/10.3390/fi10060049





