1. Introduction
Radio Frequency Identification (RFID) is a wireless technology that uses radio waves to collect and transfer data from an RFID tag or (transponder) attached to an object linked to an RFID reader or (interrogator) for the purpose of identification, tracking, and data capturing. It is expected to be the next generation mutation in auto identification technologies, and the future seems very auspicious for this technology [
1]. The reason behind using RFID instead of other auto identification techniques, such as barcode and smart cards, relates to its advantages of disregarding the line of sight, working for a long range between tags and the reader (over 100 m long), capability of writing on tags, simultaneous reading of multiple tags, immunity against harsh weather conditions such as rain and fog, and susceptibility to being integrated using sensors [
2]. Despite these advantages, RFID technology has the limitation of tags collision when multiple tags existing in the reader interrogation zone respond to its request simultaneously. Therefore, many anti-collision protocols have been proposed by researchers to overcome the collision problem and ensure a full read rate when the capture effect phenomenon exists with good identification efficiency and a low time delay. However, they experienced drawbacks, including the influence of interference and a lack of the blocking technique [
3,
4,
5]. Anti-collision protocols are mainly categorized into three classes: aloha-based (probabilistic), tree-based (deterministic), and hybrid protocols [
6]. In aloha-based protocols, such as dynamic frame slotted aloha (DFSA), the time is divided into several frames by the reader, and each frame consists of several slots, such that the
i-th slot belongs to the frame length F, which is from 0 to F−1. At the beginning of the identification process, the reader broadcasts the frame length to the tags that exist in its interrogation zone, and then each tag randomly selects a time slot to respond. If multiple tags respond to the same slot, a collision slot would occur. Alternatively, if no tag responds to a specific slot, an idle slot would result. Intuitively, a readable slot occurs when only one tag responds to a slot. At the end of the frame, the reader estimates the number of collided tags in order to adjust the frame length F of the next reading cycle. Aloha protocols have simple implementation but suffer from the problem of “tags starvation”, in which some tags might not be identified (recognized), even after a long identification period [
7]. In addition, the throughput of aloha protocols depends on the tags estimation methods and has a peak efficiency of 37% for dynamic frame slotted aloha (DFSA) and 43% for tree slotted aloha (TSA), accompanied by complex implementation and a high identification delay [
6,
8]. Secondly, tree-based protocols are mainly divided into binary tree (memory based protocols) and query tree (memoryless based protocols). In both classes, the collided tags are recursively divided into two disjoint subsets from root to leaves, until there is one tag or no tag in each leaf. The root of the tree represents the beginning of the identification process. The intermediate nodes denote the collided tags, and the leaves of the tree indicate the readable and idle cycles [
9]. Moreover, tree-based protocols have shown better performance and efficiency compared to aloha protocols. However, they suffer from many collisions at the beginning of the identification process, with a system efficiency below 50% [
6]. Moreover, the identification efficiency of deterministic protocols is affected by the length and distribution of the tag IDs and the population size [
7]. Furthermore, to enhance the identification efficiency, the adaptive query splitting protocol (AQS) and adaptive binary splitting protocol (ABS) have been proposed to reduce the identification time and collision cycles by recalling the success prefixes of the past identification frame (for AQS) and maintaining tags states of the past frame (in other words, by remembering the allocated slot counter (ASCs) values (for ABS) [
10]). Lastly, hybrid protocols are anti-collision protocols that possess the advantages of both classes, i.e., aloha and tree-based protocols. Furthermore, the BA protocol has shown the best identification efficiency amongst the protocols that do not employ bit tracking technology [
11]. In practical implementation, the deviation in tags responses increases as the number of tags increases. Therefore, the position of the collided bit cannot be detected accurately, and bit-tracking technology is difficult to employ [
12]. GQT1 and GQT2 are enhanced query tree protocols for coping with the capture effect. However, they have the shortcomings of low identification efficiency (especially for non-uniform distribution of tag IDs) and sensitivity to the type of tags distribution and the length of the tag IDs. Moreover, GBT and TBT protocols have utilized the capture-effect treatment; however, they experienced many collision cycles, even when the tags motion was slow (they do not employ the blocking technique). Moreover, these protocols are sizably affected (in many collision and idle cycles) by interference signals, even when the tags motion is slow, since they cannot recognize between the staying and arriving tags and the staying tags alone (i.e., they cannot separate between collision and interference signals for the period of staying tags). Consequently, we improve the BA to deal with the capture effect (C.E) in order to avoid losing tags when the reader decodes the tag with the strongest signal during the simultaneous response of tags. Furthermore, the improvements include distinguishing between the interference response resulting from the signal distortion (due to noise) of one tag response and the collision response caused by the multiple tags responses at one time during the period of staying tags.
In this paper,
Section 2 shows the basic principle of the BA anti-collision protocol.
Section 3 introduces the modified BA protocol and its analytical analysis.
Section 4 introduces the performance and simulation results of the modified protocol and other protocols under the impact of various parameters including the capture effect probability, interference probability, total number of tags, length of tags, and distributions of tag IDs. At the end,
Section 5 concludes this paper.
2. The Basic Principle of BA
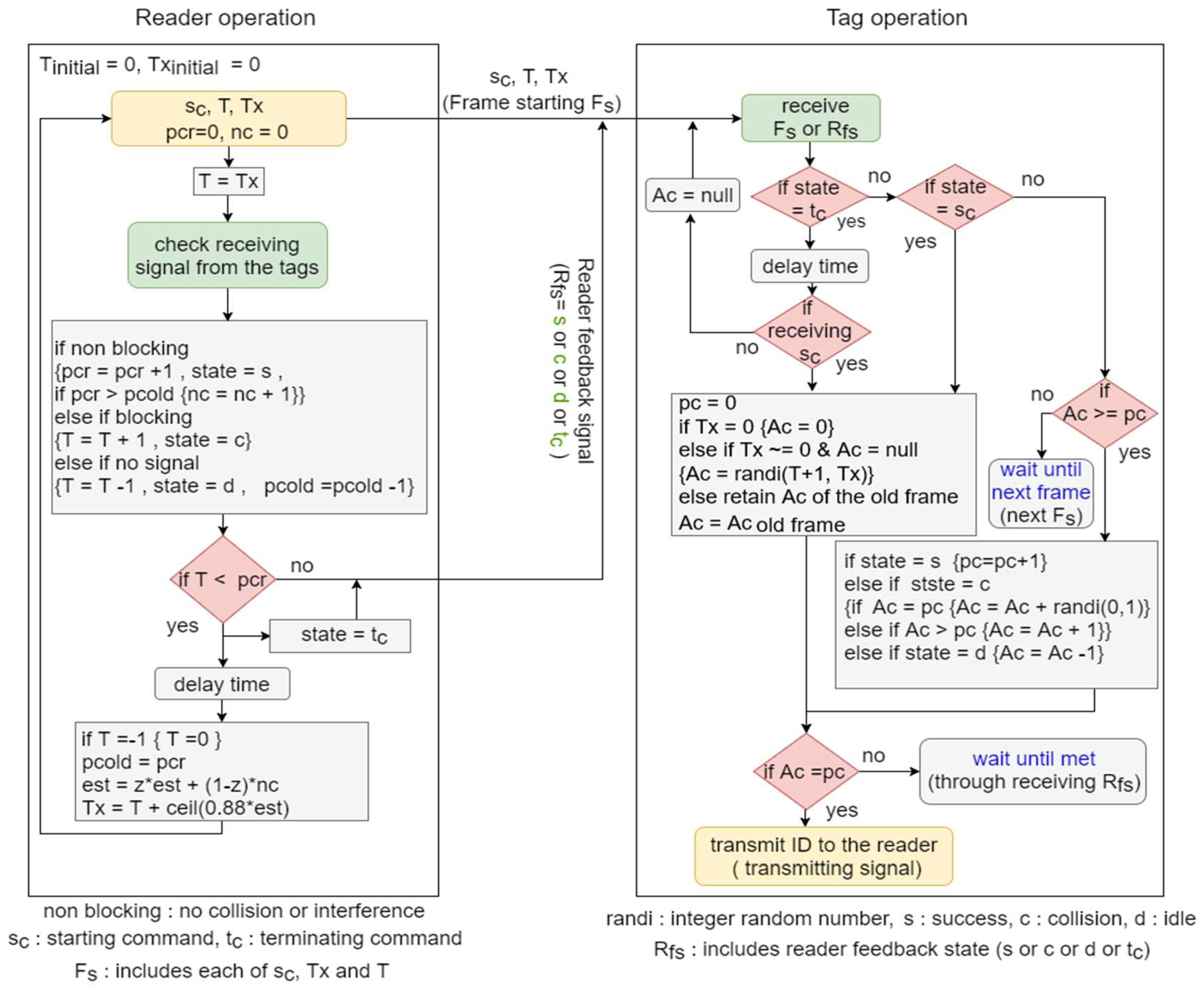
In this section, the principle of the blocking anti-collision protocol (BA) is presented. BA protocol was proposed as an improvement to the adaptive binary splitting protocol (ABS). Before delving into the principle of BA, some other definitions should be introduced first. The cycle is the time duration from the transmission of the reader signal till the reception of the tags’ responses, while the collision cycle is the simultaneous response of multiple tags or the response of one tag with an interference signal and no distinction between collision and interference response. The frame is the duration from the moment of reading the first tag to the last tag in the reader interrogation zone.
The ABS protocol surpasses the binary tree (BT) protocol through less collision cycles and through memorizing the cycles in which each tag has responded during the past identification frame in the tags counter. However, ABS protocol cannot separate between the arriving and staying tags, as well as the tags that were not executed in the past frame but executed in the current frame, and the tags that were executed in the past and current frame, respectively. Thus, the arriving tags may take the same of values stored by the staying tags. Therefore, BA protocol was proposed to separate the arriving and staying tags through assigning different values for the arriving tags to avoid colliding responses between the arriving and staying tags. Moreover, BA protocol uses two counters for the tags, and , in which is initialized to zero at the beginning of each frame and represents the number of the recognized (identified) tags through the frame, i.e., it is increased by one for all tags that have still not been recognized after each successful response, whilst represents the cycle through which each tag responds. In addition, the reader owns three counters: , , and . has the same operation as pc, in which it is increased by one after each success cycle (success cycle: one tag response with successful reader decoding). represents the number of the initial allocated cycles in each frame and is utilized to end the ongoing frame when . Lastly, is used to calculate the number of arriving tags for the purpose of tags estimation.
The operation of BA protocol is shown in
Figure 1 and is summarized in the following steps:
Step 1: The reader transmits a starting command () to start a new frame by transmitting T and Tx; then, they reset its counters and to zero and set .
Step 2: When receiving the , the tags reset their counter pc to zero and set the other counter (denoted by ) as follows:
If (the starting frame)
▪
If & (arriving tag)
▪
If & (staying tag)
▪ , i.e., retain of the old frame
Step 3: After the transmission of the reader signal (starting frame or feedback signal), its counters , , and are adjusted according to the detected received signal as follows:
If the received signal is a non-blocking signal, i.e., there is no collision or interference:
▪ , state (reader feedback signal) = (success cycle) & { if }
If the received signal is a blocking signal:
▪ state = (collision cycle) &
If no signal is detected (after a certain time delay):
▪
Step 4: Each tag, which received the starting command , adjusts its counters and if (not recognized/identified tag), according to the reader feedback signal (state) as follows:
If state =
▪
If state =
▪ If yields
▪ If yields
If state =
▪
Then, each tag transmits its response to the reader only if , or once the condition is met during the next cycle (if not identified yet) or next frame (if it is already identified).
Step 5: The reader checks if in order to terminate the ongoing frame:
If the condition is true, the frame is terminated as follows:
- ▪
State = terminating command (), if , (the number of the identified tags in the past frame) =, (the estimated number of the tags for the next frame) = (reader weight factor) and , in which ceil () is the nearest upper integer of .
If the condition is false
- ▪
The reader transmits its feedback signal (state) to the tags and repeats steps 3 and 4 until condition met.
Step 6: When receiving , the tags wait for a certain time (the duration consumed by the reader between the end of a frame to the starting of the new frame) to receive a new starting command . Hence, they adjust their counter as follows:
If receiving of the new frame (staying tags)
▪ of the old frame
If not receiving of the new frame (leaving tags)
▪
3. The Modified BA Protocol (MBA)
In this section, the modified BA anti-collision protocol (MBA) is introduced. The BA protocol does not take the capture effect into consideration, and its design supposes that the reader can decode the tag signal only when there is just one tag that responds to its request at one time. Therefore, when the capture effect indecent exists according to the relative attenuation between the tags [
4], and the reader decodes one tag response from multiple tags respond simultaneously, the rest of the tags will not be identified. Then, the reader will not guarantee full read rate of the tags located in their interrogation zone. In addition, radio frequency signals behave differently when various objects or materials are presented in the environment. In addition, one tag response cannot be successfully detected under interfering environments [
13]. Therefore, the interference factor in tag detection must be taken into account, which is neglected in the BA protocol and treated as collision, when tag collision detection is directly related to tag signal strength detected by the reader or cyclic redundancy check (
)-based method [
14]. MBA has been proposed to overcome these two drawbacks in BA protocol. Firstly, to avoid killing tags through capture effect phenomenon, the modified protocol does not terminate the ongoing frame until it ensures the identification of all tags in the range. By recognizing the hiding tags (the unrecognized/unidentified due to capture effect) during some rounds following the main identification process, the modified protocol will guarantee full read rate of the tags in the range. Secondly, since the modified protocol uses the blocking technique to separate the arriving and staying tags, it remembers
of the staying tags (as same as BA) and assigns different
values for the arriving tags, and it also treats the capture effect. Consequently, it ensures the arriving tags do not collide with the staying tags, and that the staying tags do not collide with another. Thus, to reduce the total cycles consumed by BA protocol, i.e., enhancing the identification efficiency, when interference existed, the modified protocol can distinguish between collision and interference responses for the period of staying tags (the period that guarantees no collisions between tags responses). As a result, any corrupted signal detected by the reader for this period will be considered as interference detection (interference cycle), and the reader will request the tag to repeat its transmission without increasing its
counter, i.e., it consumes just one more cycle. Moreover, the reader requests the tag that participated in the interference response to repeat its transmission and never be treated as success cycle in spite of the reader’s prior knowledge about the one tag that was being responded, because the tag’s ID sent is not recognized during the interference response. However, for BA protocol, any corrupted signal (one tag response with interference signal) detected by the reader is considered as a collision detection (collision cycle) for the entire period of identification. Thus, the participated tag will add one or zero to its
counter, and the remaining unrecognized tags will increase their
counter by one, according to
As a result, if the tag that participated in the collision detection increases its counter by one according to Equation (1), the next cycle will be an idle cycle, since is greater than pc by one for the participated tag and by two for some of the other unrecognized tags. Then, the participated tag decreases its value by one (as same as the remaining unrecognized tags) and repeats its transmission in the next cycle. Consequently, BA consumes one more cycle than the modified protocol. Also, if the participated tag in the collision detection does not increase its counter by one according to Equation (1), it will repeat its transmission in the next cycle, since is equal to for the participated tag and is twice for some other unrecognized tags. Thus, after the tag’s success response (conduct success cycle), the remaining unrecognized tags increase their by one. Consequently, is still greater than pc by one. Therefore, the unrecognized tags consume one idle cycle to make equal to for some tags. As a result, BA consumes one more cycle compared to MBA for both cases in the period of the staying tags.
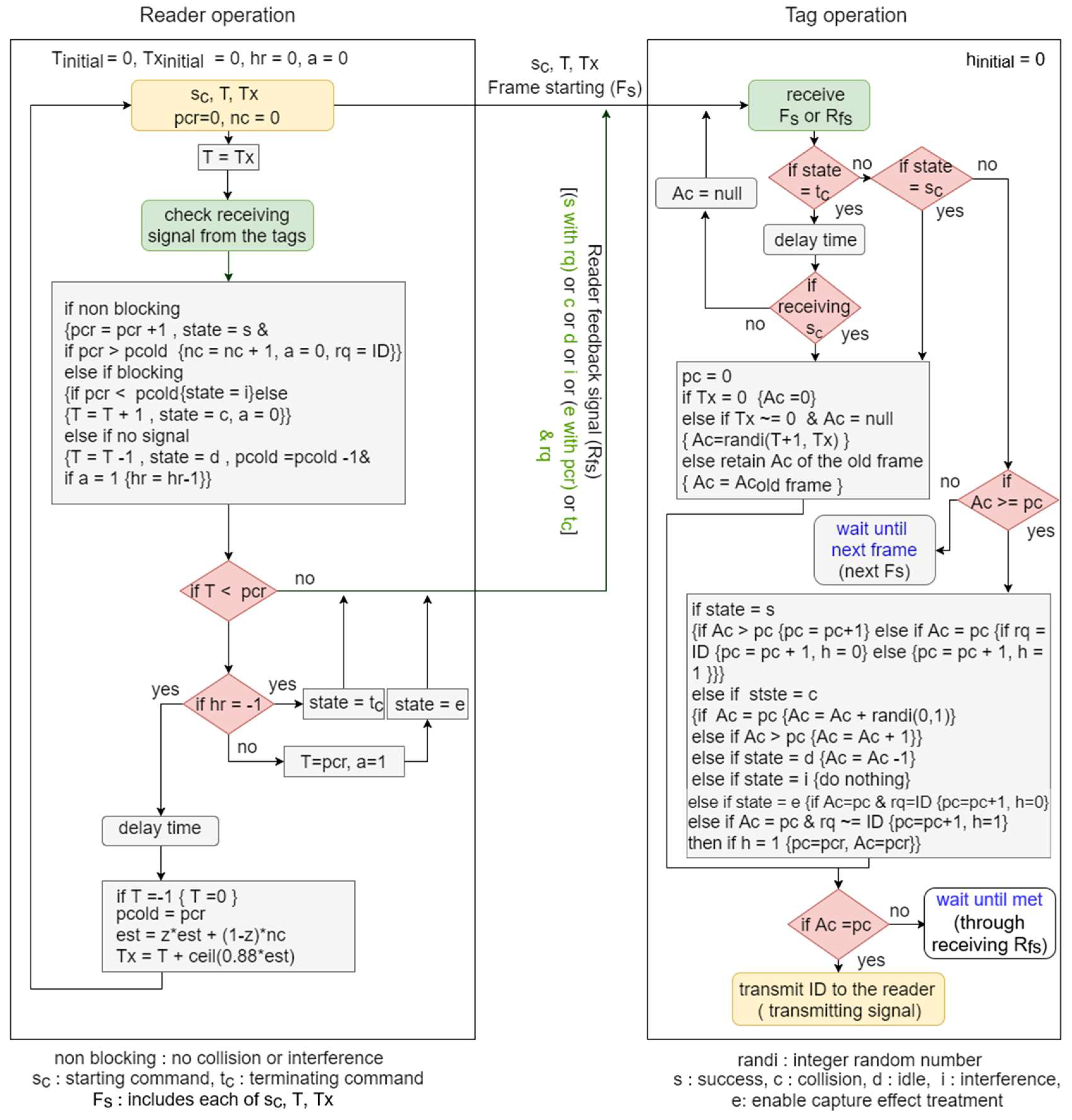
To handle the capture-effect treatment, and the separation between collision and interference responses for the period of the staying tags, MBA protocol replaces steps 3, 4, and 5 of BA protocol with the following three steps, and its operation is shown in
Figure 2.
Step 1: After the transmission of the reader signal (starting frame or feedback signal), its counters , and , and the new flag () is adjusted as follows according to the detected received signal:
If the received signal is a non-blocking signal:
▪ , state = , (new parmeter) = & { if }
If the received signal is a blocking signal:
▪ If yields state = (interference cycle)
▪ If yields state = , = , = 0
If no signal detected (after a certain time delay):
▪ state = , , & { if }
Step 2: Each tag, which received the starting command , adjusts its counters and and the hidden new flag () if (not recognized/identified tag) according to the reader feedback signal (state), as follows:
If state =
▪ If yields
▪ If & yields ,
▪ If & yields ,
If state =
▪ If yields
▪ If yields
If state =
▪ Ac = Ac − 1
If state =
▪ do nothing
If state =
▪ If & yields ,
▪ If & yields ,
Then, if yields (,
Then, each tag transmits its response to the reader only if Ac = pc or waits until the condition is met.
Step 3: The reader checks if in order to terminate the ongoing frame
If the condition is true
▪ If , the frame is terminating as follows:
State=terminating command (),
if , ,
and
- ▪
If , , , state = (new parameter), and the reader transmits its feedback signal () to the tags and repeat steps 1 and 2 until condition met.
If the condition is false
- ▪
The reader transmits its feedback signal (state) to the tags and repeats steps 1 and 2 until condition met.
Analytical Analysis of MBA Protocol
The identification delay of tag anti-collision protocols is defined as the number of slots from multiple cycles as discussed in BT and GBT analysis, or the number of cycles from multiple rounds as discussed in MBA analysis and the rest of paper for all protocols; the reader needs to identify all the tags in its interrogation zone. The identification delay of GBT protocol (the multiple cycles protocol without blocking and interference distinguish) was analyzed under the hypothesis that the capture effect probability is
α [
4]. GBT consists of multiple BT cycles. Thus,
indicates the number of consumed slots for one BT cycle under C.E probability of
α and unrecognized tags (
) located in reader zone. When C.E happens at
α probability of one, the number of consumed slots in each BT cycle is one. Due to this, BT does not expand the corresponding node. On the contrary, when C.E does not happen at a slot, the unrecognized
tags will collide, and these tags are randomly divided into two subsets. Consequently,
can be formulated as follows:
in which
and
= 1.
Similarly, the number of readable slots,
, can be found by the recursive equation:
in which
= 0 and
= 1.
Furthermore, to calculate the identification delay of GBT, the number of unrecognized tags participated in the beginning of
j-th BT cycle,
, must be known. Let
indicate the number of recognized tags in the
j-th cycle. Thus,
and
are obtained as follows:
Alternatively, from Equations (5) and (6), , , , , , , …, , are obtained, in which = and = .
Lastly, the identification delay of GBT is the sum of the slots of all BT cycles plus one as follows:
The term (1) in represents the last cycle in GBT, which consists of one idle slot to ensure that all the tags in reader zone have been identified.
According to [
15], the number of slots required to identified
tags in j-th cycle,
, is equal to
in which
denotes the number of collision slots required to identify
tags in
j-th cycle. Thus, substituting (8) in (7) yields
Now, let
denote the number of cycles required to recognize
tags (
) by GBT, so
in which
(
denotes the total collision slots required to identify
tags through (
r − 1) cycles of GBT, and
which is calculated according to [
15] as follows:
in which
is the number of collision slots at
k-th tree level of BT
j-th cycle.
Moreover, at
α = 0 (C.E probability of zero), the number of GBT cycles (
r) is two only. Therefore,
as
α increases the collision slots of each BT cycle are reduced, and thus the identification delay is reduced.
In fact, MBA protocol consists of two phases. In phase I, the staying tags are identified without colliding with each other through number of successful (for staying tags) and idle (for leaving) cycles (denoted by slots in BT and GBT). Whilst, in phase II, the arriving tags are identified without colliding with the staying tags through multiple rounds (denoted by cycles in BT and GBT), in which the first round is executed by ABS protocol (for , initial allocated cycles determined by tags exponential average estimation method and equal to 0.88γ, in the steady state, in which γ is the number of arriving tags in the -th frame , and the number of staying tags is zero), and each round consists of multiple cycles.
Now, let the number of the tags in the -th frame () be , and the number of arriving and leaving tags in the -th frame () be γ and β, respectively.
Since ABS does not estimate the number of tags, its initial allocated cycles in the
-th frame are equal to
when the number of tags in the
-th frame is
. Thus, according to the identification delay analysis of ABS [
16], the first round of MBA in phase II can be formulated as follows:
and
in
were replaced by
and
in
, respectively, since the number of allocated cycles of
was replaced by 0.88
γ, and the number of staying tags in
is zero.
For GBT, from Equation (10), we obtain
while for MBA in
frame in phase I, the number of cycles equals the sum of the number of staying and leaving tags (blocking protocol). In phase II, only the arriving tags collide with each other according to Equation (13) in the first round and with BT protocol in the remaining rounds; Therefore,
When
α is equal to zero, i.e.,
, the third term in Equation (15) will be eliminated, and
is equal to
γ. The first term represents one idle cycle consumed in the last round, i.e.,
, to ensure that all the tags have been identified. We notice, from Equations (14) and (15), when
, MBA outperforms GBT and TBT (since
=
, according to [
5]) significantly in consuming a lower total number of cycles when
is equal to or less than
. MBA also enhances the identification efficiency when
decreases, but the identification delay is not affected.
As explained previously, the former protocols, GQT1, GQT2, GBT, and TBT, do not use blocking technique, and thus there is no ability to distinguish between collision and interference signals (responses of tags) for the entire identification delay period, while MBA recognizes between collision and interference responses for the period of staying tags. Thus, the identification delay of GBT is much more affected than MBA when interference signals exist according to the following equations:
The last term in Equation (16) and last two terms in Equation (17) denote the number of the additional cycles () when interference signals exist. The last term in both equations is equal to the number of interference responses multiplied by 2, since GBT and MBA consume two additional cycles (one collision and one idle) for each interference response without the distinguishing from collision response (the entire period for GBT, and the arriving tags period for MBA). However, the term prior to the last one in Equation (17) is equal to the number of interference responses, since MBA consumes only one additional cycle (interference cycle) for each interference response as opposed to each collision response in GBT (staying tags period). Consequently, when interference occurs, MBA expends fewer additional cycles than GBT, since the period of consuming two additional cycles for each interference response in MBA is smaller than the period of GBT and depends on .
4. Performance and Simulation Results
This section demonstrates the performance and simulation results of the original BA protocol and the MBA. Then, MBA performance is compared with the existing protocols in the same field, which are GQT1, GQT2, GBT, and TBT, under various influences such as capture effect probability, interference probability, total number of tags, and tag IDs length (for query tree protocols GQT1 and GQT2). Moreover, to evaluate the performance of tags identification, two metrics are considered:
- ❖
The total number of cycles (Identification delay)
The number of the cycles consumed for identifying all the tags in reader range. These cycles are divided into the following categories:
- ▪
Readable/success cycles (): the reader can decode one tag signal.
- ▪
Collision cycles (): multiple tags respond simultaneously, and the reader detects collision tags signal. Or, one tag responds with interference influence and no distinction is made between collision and interference responses.
- ▪
Interference cycles (): one tag responds to the reader request, and the reader cannot decode the tag signal due to the interference influence, but a distinction is made between collision and interference responses.
- ▪
Idle/empty cycles (): No tag responds to the reader request.
- ❖
Identification efficiency
The number of the success cycles to the total number of cycles consumed for identifying all the tags in reader range.
in which
,
and
are success, collision, and idle cycles without the cycles that resulted from interference responses. Additionally, € is the number of additional cycles (
c and
d) for non-blocking protocols, or (
i,
c, and
d) for blocking MBA protocol, produced due to interference responses.
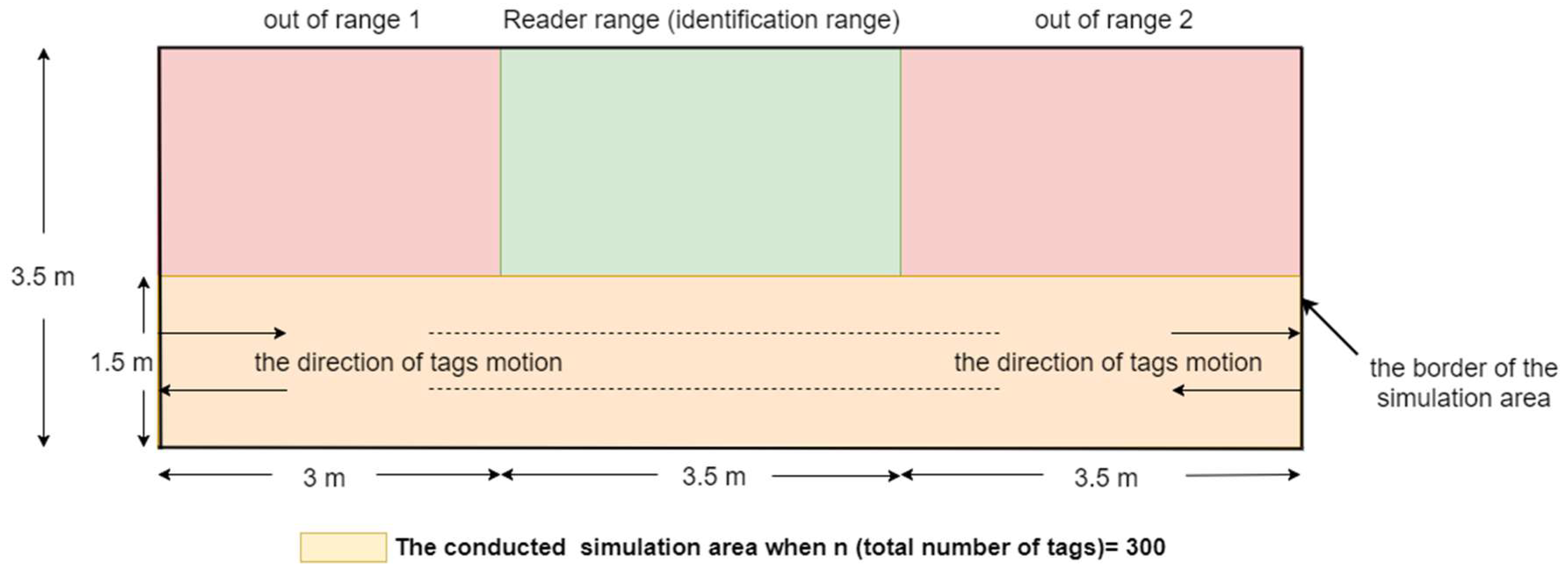
4.1. Actual Simulation Environment
To evaluate the performance of MBA protocol, simulation area dimensions of 3.5 m × 10 m is taken in which 3.5 m × 3.5 m area is the reader identification zone, as shown in
Figure 3. Within this area, the tags are moving at a specific velocity (
v) from border to border so that some tags will enter the reader zone as arriving tags (which did not exist in the past frame but are executed in the current frame), and other tags leaving reader zone as leaving tags (which are executed in the current frame but will not be executed in the next frame). On the other hand, staying tags are those tags that do not leave reader zone after the duration of one frame (executed in the past and current frame). To compare the proposed protocol with the other protocols, the parameters of the simulation are illustrated in
Table 1. So, there are a number of tags (
) moving in a simulated area of 3.5 m × 10 m with a stationary probability; the probability of whether the tag will move or not during the period of one frame; (
) equal to zero (moving constantly) and the tags velocity (
); the distance that each tag moves during a period of one frame when it moves; of 1 m/frame blocking velocity and 3.5 m/frame non-blocking velocity. Finally, the reader weight factor (
), which is responsible for estimating the number of the tags in the reader zone, was taken as 0.5. Each simulation has been conducted for 1000 frames by Matlab software to simulate the proposed protocol and the other older protocols, and to represent the area in which the tags move for the purpose of comparing and showing our big improvements in dealing with RFID problems.
4.2. The Original BA Protocol
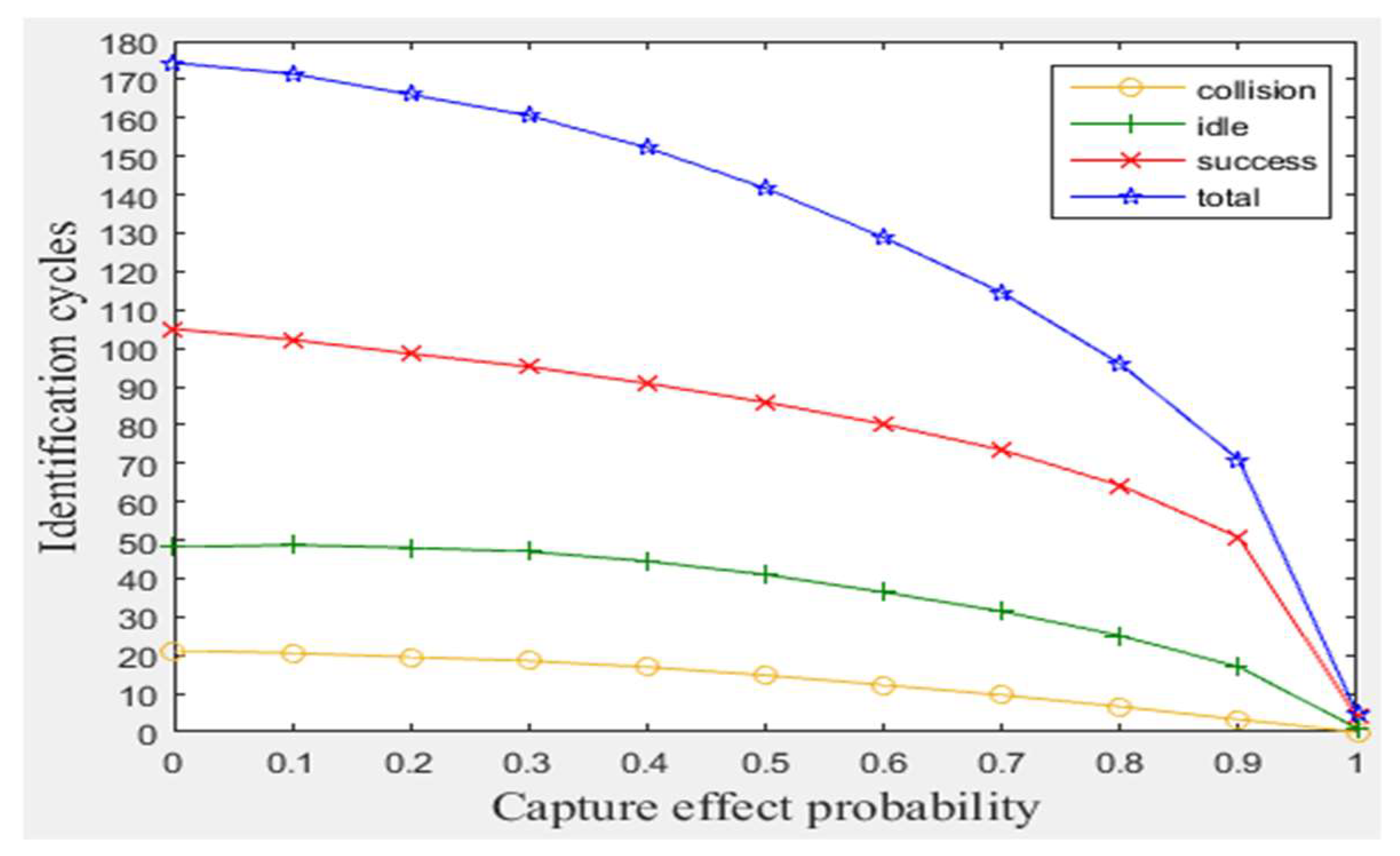
As explained before, the proposed modifications of BA anti-collision protocol can handle the capture effect phenomenon and ensure that the full read rate of the tags existed in reader interrogation zone. Moreover, the distinction between collision and interference signals for the period of staying tags can be obtained. Before showing our modifications improvements, a simulation of the original BA protocol was conducted with varying capture effect probability
from zero (no tag has stronger signal than other tag) to one (one tag has the strongest signal), as shown in
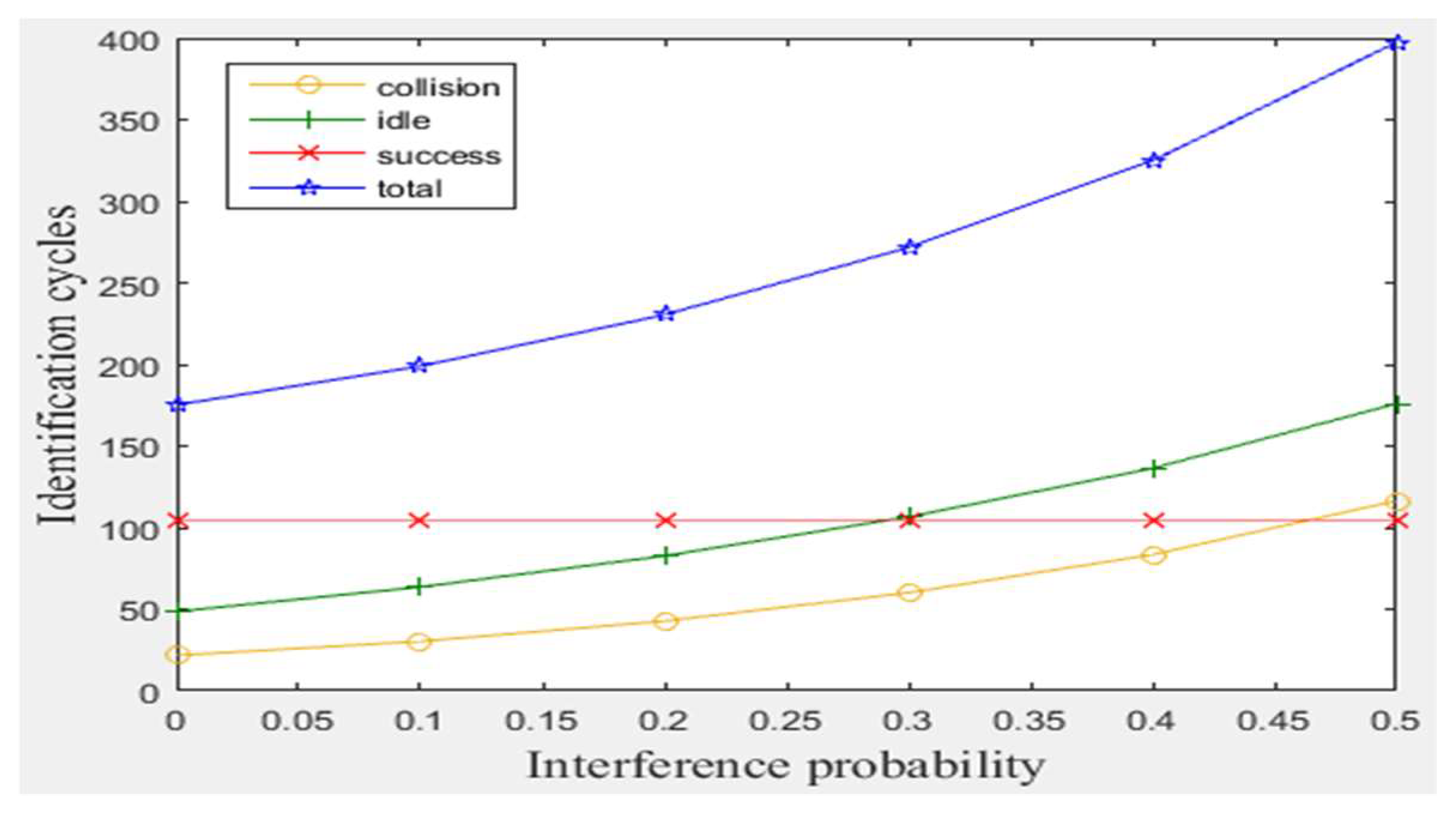
Figure 4. The results indicate that a number of tags will be killed (not identified) increasingly as C.E probability increases. Also, as interference probability increases, the consumed total number of cycles will increase significantly, even when the number of staying tags is large (for 1 m/frame velocity), as shown in
Figure 5. Consequently, MBA attempts to solve these two drawbacks in the following subsections.
4.3. The Modified BA Protocol, MBA
Contrary to the original BA protocol, the modified protocol ensures that the entire number of the tags in reader interrogation zone will be recognized (identified) whatever C.E probability is. Moreover, it recognizes between the collision and the interference (affected one tag response) responses for the period of staying tags. Thus, enhanced identification efficiency is obtained by consuming a lower total number of cycles than the original BA protocol for the same value of probability of interference.
Furthermore, a simulation of each protocol existed to treat the capture effect until the present time was conducted (without using bit-tracking technology, which is used in GQT1, GQT2, GBT, and TBT). Our proposed modified protocol, MBA, has shown better performance and efficiency (a lower number of consumed total cycles) when the number of staying tags is high (the tags move at low velocity, for blocking purposes). Finally, the impact of C.E probability, interference probability, the total number of tags existed in simulation area, and the length and distributions of tag IDs were measured to compare the modified protocol with the other existing protocols.
4.3.1. MBA Performance and the Impact of Capture Effect
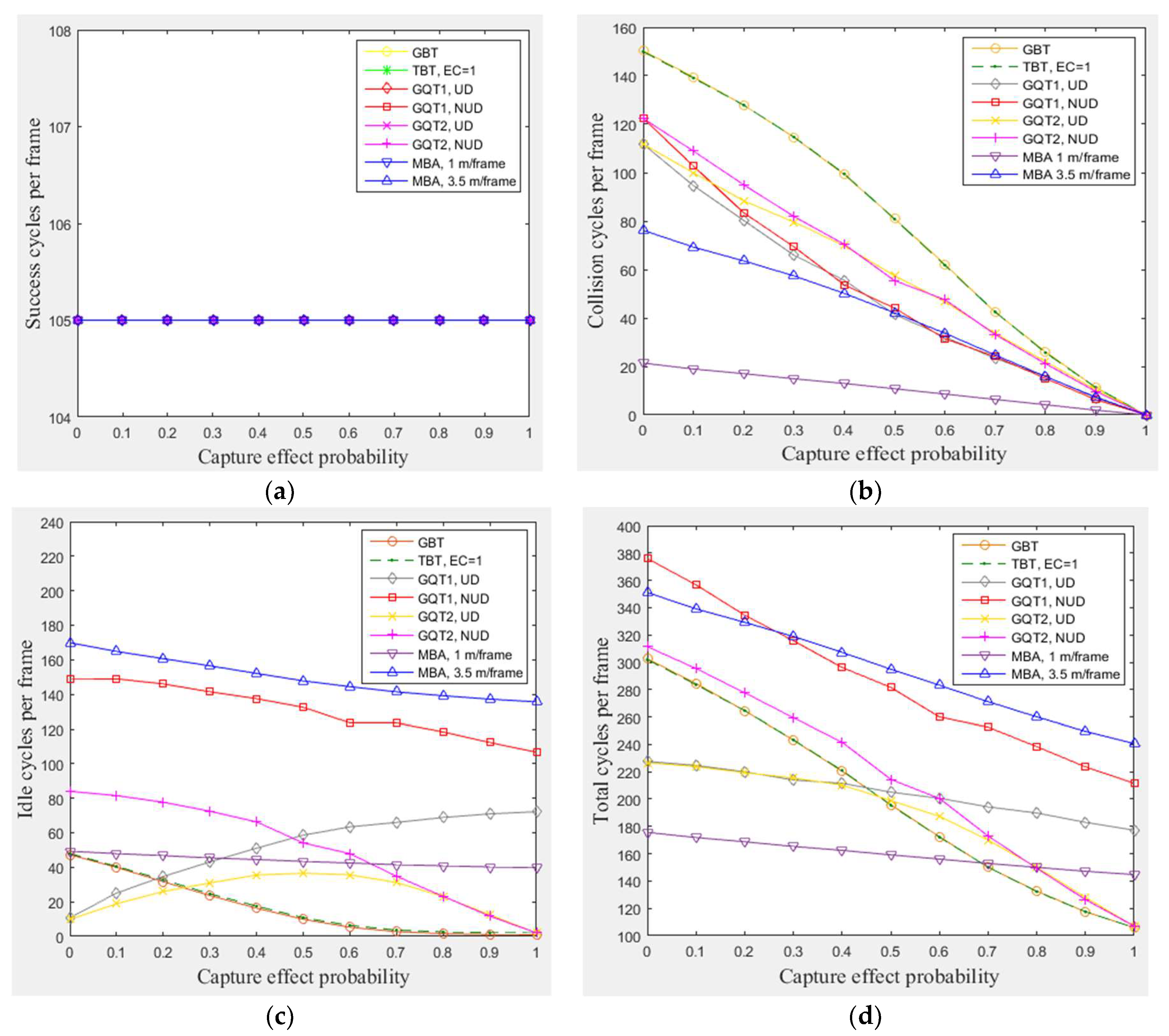
In this subsection, a simulation of 300 tags existed in the entire zone of
Figure 3 (105 tags in reader interrogation zone) moving at any velocity for GBT, TBT, GQT1, and GQT2 protocols, and velocities of 1 m/frame (blocking velocity) and 3.5 m/frame (non-blocking velocity) for the MBA were conducted, with varying
α from 0 to 1. Since all of the simulated protocols deal with C.E, the results presented in
Figure 6a show the full read rate of the tags that existed in reader zone, which is 105 (the number of the tags existed in the green region of the simulated area) regardless of what the C.E probability is, while the results in
Figure 6b show that the highest number of collision cycles was taken by GBT and TBT protocols. This is because they are non-blocking protocols, and the process of separating collided tags is done by the tags themselves (not by reader prefixes and independent of the tag IDs), with probabilistic (random) separation of collided tags. In
Figure 6c, the results indicate that GBT and TBT consume the lowest number of idle cycles, except for the interval from 0 to 0.25 of
α in which GQT1 and GQT2 with uniform distribution of tags IDs exceed them, since they do not use either the blocking technique (MBA) or expanding or repeating the success prefixes (GQT1 and GQT2 respectively). For GQT1 and GQT2,
Figure 6b, the number of collision cycles is reduced when the distribution of tag IDs is uniform, since reducing the common prefixes of tag IDs for QT protocols yields reduces the number of collision cycles [
9]. For instance, the number of collision cycles for two tags with IDs 1000 and 0000 (shortest common prefix, null prefix) is one, while the number of collision cycles for 0001 and 0000 tags (longest common prefix, 000) is four. Thus, when the uniform distribution is obtained in the entire simulation area (
, in which
is reader interrogation zone) as shown in
Figure 3, the tags in reader zone will have IDs with shorter common prefixes than those when using the non-uniform distribution in the entire simulation area. In addition, for both GQT1 and GQT2, the number of collision cycles is the same for uniform and non-uniform distribution when C.E probability (
α) is about 0.4 or more. Besides, for both distributions, GQT1 exceeds GQT2 in small number of collision cycles for
α probability from about 0.1 to about 0.9. Moreover, both GQT1 and GQT2 beat GBT and TBT at consuming a lower number of collision cycles. In adverse, for idle cycles shown in
Figure 6c, GQT2 uniform or non-uniform distribution always beats GQT1 uniform or non-uniform distribution, respectively, in consuming fewer idle cycles at any value of
α (except
α = 0 for uniform distribution). This happens because GQT2 uses repetition of success prefixes instead of expanding prefixes that used in GQT1. GQT2 (the both distributions) also consumes fewer idle cycles than any distribution of GQT1, as
probability increases more than 0.5, and the number of idle cycles is only equal to two cycles when
α is equal to one. For total cycles,
Figure 6d, GQT2 equals GQT1 (for uniform distribution and
α from 0 to 0.4) and surpasses GQT1 (for uniform distributions or non-uniform distributions, for both protocols, with
α larger than 0.4), and any distribution of GQT2 exceeds both distributions of GQT1 for
from 0.6 to 1 in a lower total number of cycles. In addition, both GBT and TBT consume a lower total number of cycles than GQT1 and GQT2 for both distributions for the period of
α between 0.5 and 1. Lastly, the MBA, surpasses all of the previous protocols at consuming fewer collision and total cycles for the period of
α from 0 to 0.7 and blocking velocity of 1 m/frame.
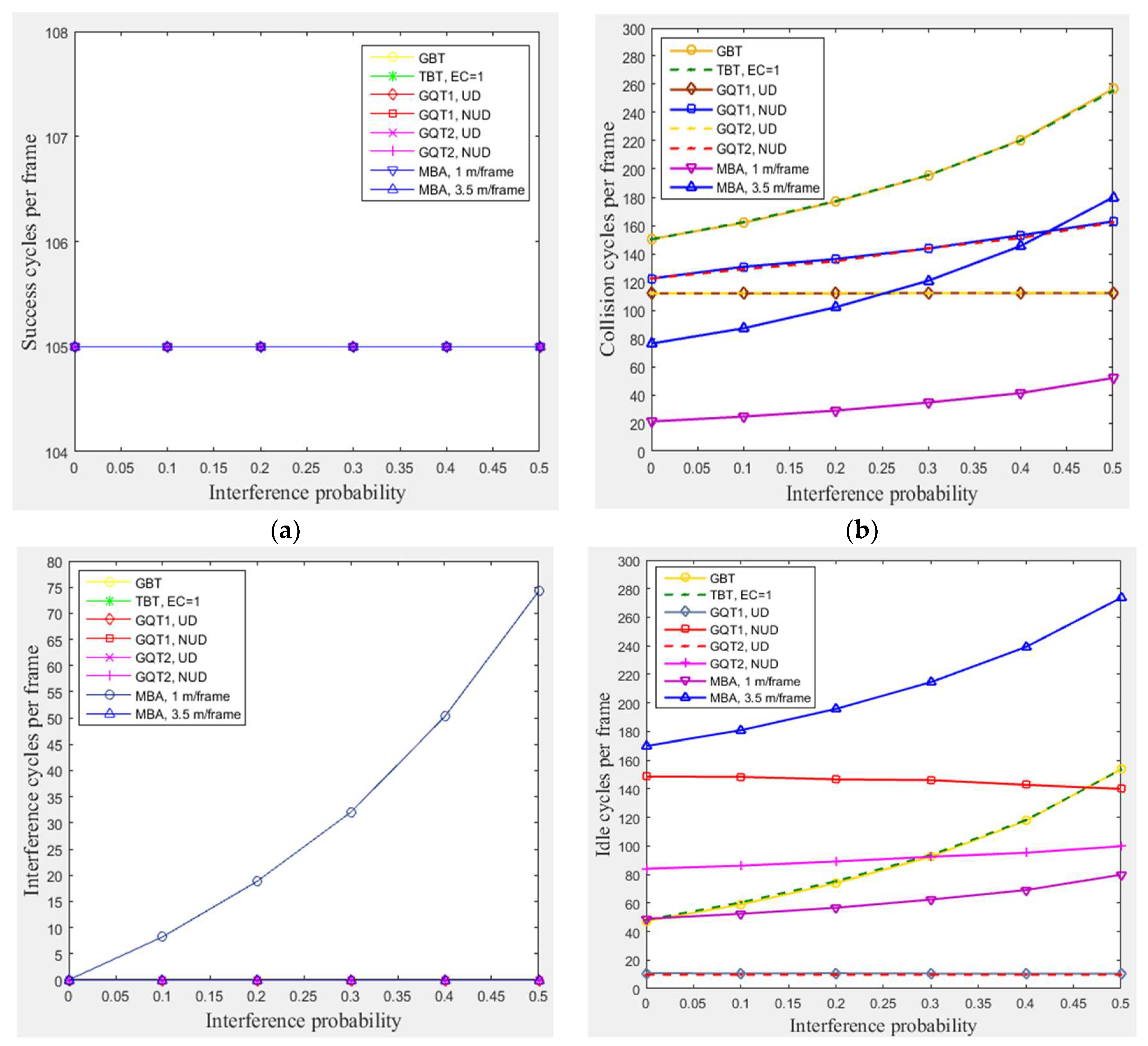
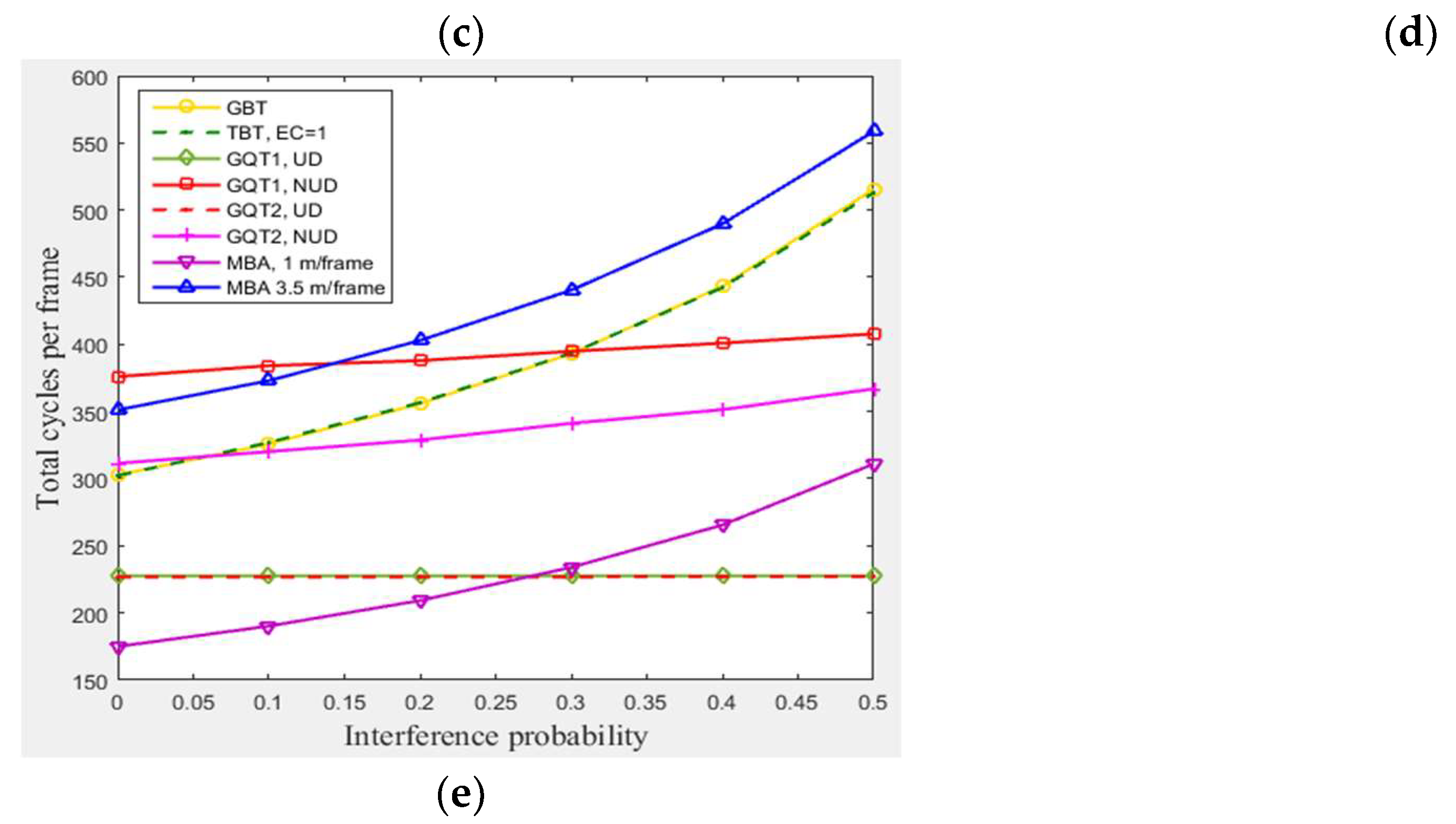
4.3.2. The Impact of Interference
In this subsection, a simulation of 300 tags existed in the entire zone of
Figure 3 moving at any velocity for GBT, TBT, GQT1, and GQT2 protocols was conducted with varying interference probabilities (
) from 0 to 0.5 under the following conditions: velocities of 1 m/frame (blocking velocity) and 3.5 m/frame (non-blocking velocity) for the MBA. All of the simulated protocols (except the modified protocol, MBA) do not distinguish between collision and interference signals, because the blocking technique is not employed. Thus, the efficiency of identification process is reduced, as the probability of interference is increased due to consuming more cycles. The exception to this lack is in the uniform distributions of GQT1 and GQT2 shown in
Figure 7e, since success or interference cycles never happen except for in the full-length of ID reader prefix, in which the interference response can be distinguished as success cycle. Consequently, GBT and TBT consumes more collision, idle, and total cycles, as shown in
Figure 7b, d, and e, as interference probability increases due to the branching of the tree of identification process through one tag response. On the other hand, for GQT1 and GQT2 with uniform distributions, the success response (one tag matches reader prefix) never happens until full ID prefix is prepared by the reader. In this case, even the collision response is detected by the reader (due to interference signals). The reader can deduce that there is only one tag responds to its query (there is only one tag ID matches reader full prefix), and thus the response is considered as success without consuming more of collision and idle cycles due to the tree branching, see
Figure 7b and d. In contrary, for GQT1 and GQT2 with non-uniform distribution, the collision cycles increase as interference probability rises due to the tree branching through collision response, when only one tag responds with signal corrupted (due to interference signals). Besides, the idle cycles for GQT1 decrease as interference probability rises. Because the success prefixes are nearly equal, there are full prefixes for large number of tags. Therefore, the collision response due to interference signals of
reader’s query length branches the tree to [
] and [
]; one of these two queries will be success cycle without branching (full prefix length), and the other query will be idle cycle. If the response is successful due to
length, the reader will consume two idle cycles instead of one through tree branching. In adverse, GQT2 consumes more idle cycles as interference probability rises, since the reader repeats its prefix (consumes only one idle cycle) instead of tree branching in GQT1 for successful response. As a result, the total cycles are increased for non-uniform distribution of GQT1 and GQT2, and remain constant for uniform distribution, as illustrated in
Figure 7e. Finally, for the modified protocol, MBA, the collision, idle, and total cycles are increased as interference probability rises but without tree branching for the period of staying tags, because MBA separates the collision and interference responses for the mentioned period while BA does not. Thus, MBA outperforms the other protocols, including BA and the non-uniform distributions for GQT1 and GQT2 (practical case), in consuming less total number of cycles for pi from 0 to 0.5. For pi from 0 to 0.25 when comparing with GQT1 and GQT2 with uniform distributions (unpractical case), see
Figure 7e. For instance (at 1 m/frame velocity), at pi equals 0.5 and 105 of success cycles (identified tags), BA protocol consumes 120, 175, and 400, collision, idle, and total cycles, respectively, whereas MBA protocol consumes only 51, 74, 80, and 310, collision, interference, idle, and total cycles, respectively.
4.3.3. The Impact of Total Number of Tags
In this subsection, a simulation of n tags that existed in the entire zone of
Figure 3 moving at any velocity for GBT, TBT, GQT1, and GQT2 protocols was conducted at the following conditions: velocities of 1 m/frame (blocking velocity) and 3.5 m/frame (non-blocking velocity) for the modified BA protocol MBA
. Figure 8a shows that the number of success cycles (the identified tags) increases when the total number of tags rises from 100 to 500. The increasing of the total number of tags in the simulated area yields an increasing number of tags located in the reader zone.
Figure 8b,c show that the collision and idle cycles increase (except the idle cycles for the uniform distributions of GQT1 and GQT2) as the total number of tags rises, because the number of tags located in the reader zone increase, but with a different ratio of increasing for each protocol. For GQT1 and GQT2 with uniform distributions, the idle cycles never increase when changing the total number of tags, since the empty leaves are nearly constant, because the success cycles never branches the identification tree for full reader prefixes. As a result, GBT, TBT, and MBA in
Figure 8d have constant efficiencies when changing n from 100 to 500, which are 30% (MBA with 3.5 m/frame), 35% (GBT & TBT), and 60% (MBA with 1 m/frame). Adversely, the efficiencies for GQT1 and GQT2 are increased when n is increased, so that GQT1 and GQT2 with uniform distribution have an efficiency of 48% when n is 500 but only 41% for n equals 100. GQT1 with non-uniform distribution has also an efficiency of 28% when n is 500 but only 22% for n equals 100. Moreover, GQT2 with non-uniform distribution has an efficiency of 34% when n is 500 but only 28% for n equals 100. As a result, MBA outperforms the other protocols in consuming fewer total number of cycles with constant high efficiency when changing n from 100 to 500 with low tag mobility.
4.3.4. The Impact of Length and Distributions of Tags IDs
In this subsection, a simulation of 300 tags that existed in the entire zone of
Figure 3 moving at any velocity for GQT1 and GQT2 protocols was conducted with varying tag ID lengths from 9 to 11 bits and applying three different types of non-uniform distributions (one type for each length of tag ID).
Figure 9a shows the number of success cycles for any length of tag ID.
Figure 9b and c show that GQT1 and GQT2 with uniform distributions consumed more of collision and idle cycles to identify the same number of tags when tag IDs were lengthened. This happens because they take longer path to reach success prefixes (one more collision cycle and one more idle cycle for each bit appended), whereas the number of collision and idle cycles for non-uniform distributions is nearly neglected affected by the lengthening of the IDs when compared with the influence of the manner in which the non-uniform distributed tags are spread (the type of the non-uniform distribution). As a result,
Figure 9d shows that GQT1 and GQT2 with uniform distributions consume more total cycles when tag IDs are lengthened (two more cycles for each one bit appended). However, for the non-uniform distributions, the length of tag IDs is not noticeably affected especially for few appended bits. When the number of appended bits is one (changing tag IDs bit length from 9 to 10) and another type of non-uniform distribution is used, the total number of cycles of GQT1 and GQT2 increases significantly from 420 and 337 to 463 and 367, respectively. Furthermore, when changing tag IDs bits length from 10 to 11 (with one appended bit too) and third type of non-uniform distribution is used, the number of total cycles for GQT1 and GQT2 increases slightly from 463 and 367 to 471 and 370, respectively. As a result, the type of the non-uniform distribution has much greater influence than tag IDs’ length. Thus, MBA outperforms the former protocols, since it does not use IDs to identify tags. Therefore, MBA consumes a constant total number of cycles for specific interference probability, C.E probability, and total number of tags.