Integrating In Vitro BE Checker with In Silico Physiologically Based Biopharmaceutics Modeling to Predict the Pharmacokinetic Profiles of Oral Drug Products
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals and Reagents
2.2. Structure and Parameters of the BE Checker System
2.3. Solubility Measurement
2.4. Apparent Membrane Permeability Coefficient (Papp) Measurement
2.5. In Vitro BE Checker Data
2.6. In Vivo Pharmacokinetic Data
2.7. Parameters Estimation Using the “BE Checker Model”
2.7.1. “BE Checker Model” for Simulating the Dissolution and Permeation of Metoprolol from Seloken® Tablets
2.7.2. “BE Checker Model” for Simulating the Dissolution, Precipitation, and Permeation of Dipyridamole from Persantin® Tablets
2.8. PBBM for Predicting PK Profiles in Humans
2.8.1. Structure of the PBBM
2.8.2. Calculation of Prediction Errors for Human PK Parameters
3. Results and Discussion
3.1. Solubility
3.2. Apparent Membrane Permeability Coefficient (Papp)
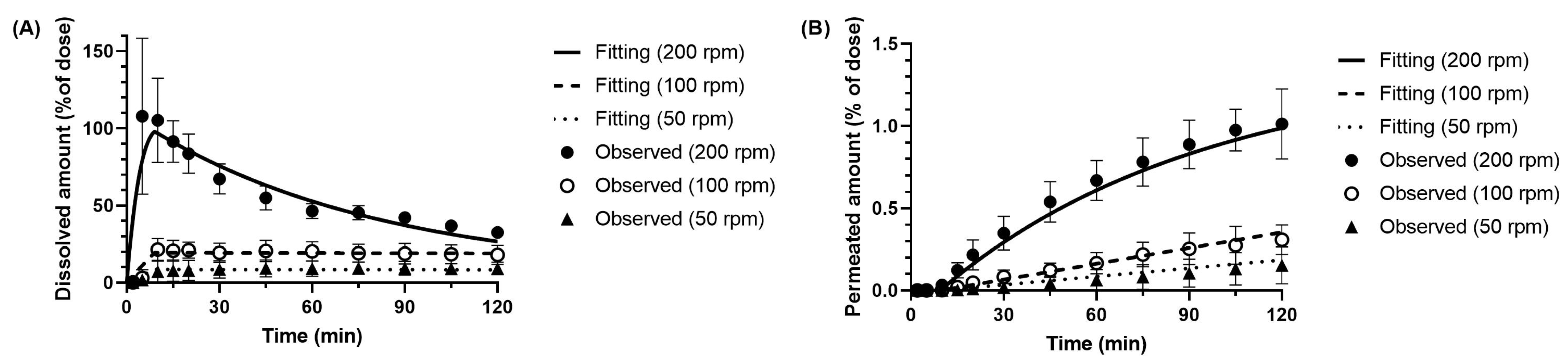
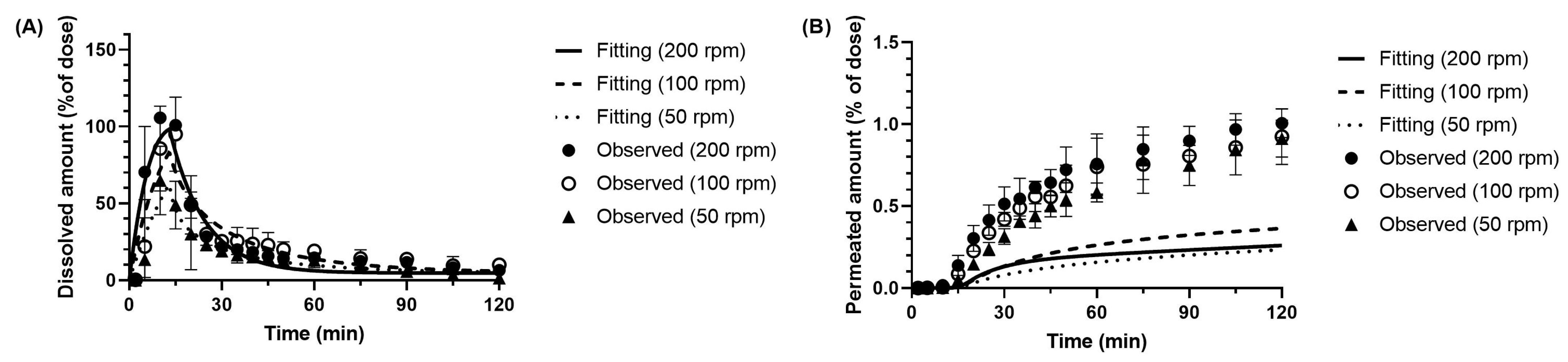
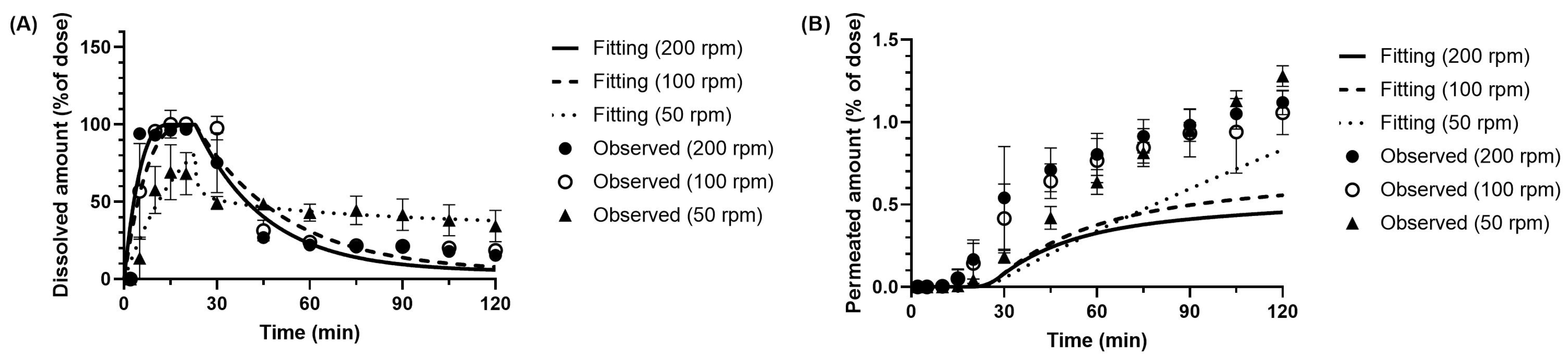
3.3. Parameter Estimation from the BE Checker Model
3.3.1. Dissolution Parameter of Metoprolol in the BE Checker Model
3.3.2. Dissolution and Precipitation Parameters of Dipyridamole in the BE Checker Model
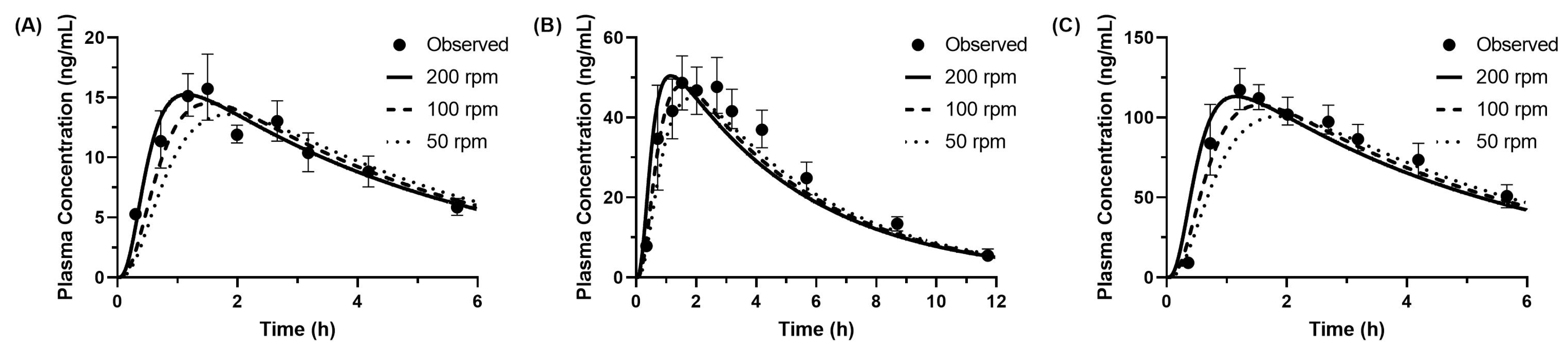
3.4. Predicted Pharmacokinetic Profiles in Humans
3.4.1. Predicted PK Profiles of Metoprolol
3.4.2. Predicted PK Profiles of Dipyridamole (Model 1)
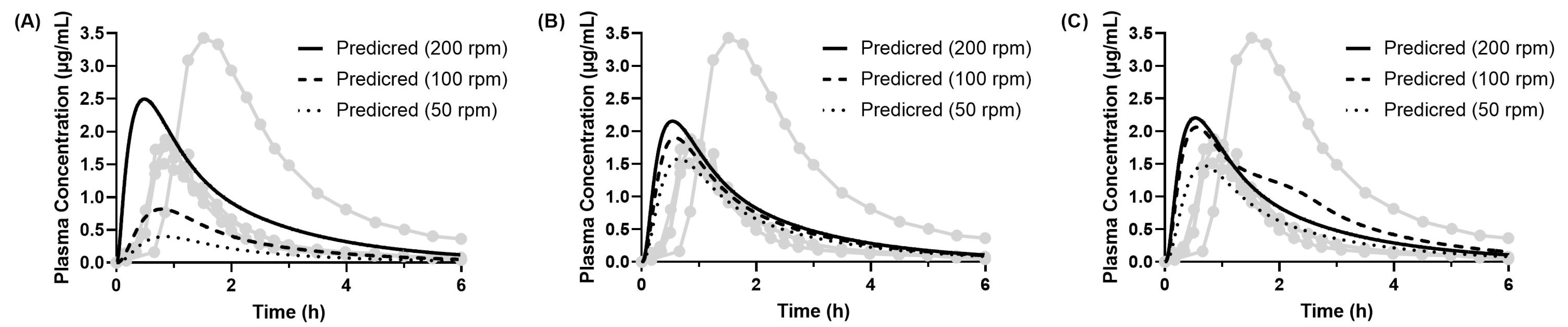
3.4.3. Predicted PK Profiles of Dipyridamole (Model 2)
3.5. Discussion Based on the Overall Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Takagi, T.; Masada, T.; Minami, K.; Kataoka, M.; Yamashita, S. Development of an In Vitro Methodology to Assess the Bioequivalence of Orally Disintegrating Tablets Taken without Water. Pharmaceutics 2023, 15, 2192. [Google Scholar] [CrossRef] [PubMed]
- Masada, T.; Takagi, T.; Minami, K.; Kataoka, M.; Izutsu, K.; Matsui, K.; Yamashita, S. Bioequivalence of Oral Drug Products in the Healthy and Special Populations: Assessment and Prediction Using a Newly Developed In Vitro System “BE Checker”. Pharmaceutics 2021, 13, 1136. [Google Scholar] [CrossRef]
- Riedmaier, A.E.; DeMent, K.; Huckle, J.; Bransford, P.; Stillhart, C.; Lloyd, R.; Alluri, R.; Basu, S.; Chen, Y.; Dhamankar, V.; et al. Use of Physiologically Based Pharmacokinetic (PBPK) Modeling for Predicting Drug-Food Interactions: An Industry Perspective. AAPS J. 2020, 22, 123. [Google Scholar] [CrossRef]
- Heimbach, T.; Kesisoglou, F.; Novakovic, J.; Tistaert, C.; Mueller-Zsigmondy, M.; Kollipara, S.; Ahmed, T.; Mitra, A.; Suarez-Sharp, S. Establishing the Bioequivalence Safe Space for Immediate-Release Oral Dosage Forms Using Physiologically Based Biopharmaceutics Modeling (PBBM): Case Studies. J. Pharm. Sci. 2021, 110, 3896–3906. [Google Scholar] [CrossRef] [PubMed]
- Kollipara, S.; Martins, F.S.; Sanghavi, M.; Santos, G.M.L.; Saini, A.; Ahmed, T. Role of Physiologically Based Biopharmaceutics Modeling (PBBM) in Fed Bioequivalence Study Waivers: Regulatory Outlook, Case Studies and Future Perspectives. J. Pharm. Sci. 2024, 113, 345–358. [Google Scholar] [CrossRef] [PubMed]
- Kato, T.; Mikkaichi, T.; Yoshigae, Y.; Okudaira, N.; Shimizu, T.; Izumi, T.; Ando, S.; Matsumoto, Y. Quantitative Analysis of an Impact of P-Glycoprotein on Edoxaban’s Disposition Using a Human Physiologically Based Pharmacokinetic (PBPK) Model. Int. J. Pharm. 2021, 597, 120349. [Google Scholar] [CrossRef]
- Pepin, X.J.H.; Moir, A.J.; Mann, J.C.; Sanderson, N.J.; Barker, R.; Meehan, E.; Plumb, A.P.; Bailey, G.R.; Murphy, D.S.; Krejsa, C.M.; et al. Bridging in Vitro Dissolution and in Vivo Exposure for Acalabrutinib. Part II. A Mechanistic PBPK Model for IR Formulation Comparison, Proton Pump Inhibitor Drug Interactions, and Administration with Acidic Juices. Eur. J. Pharm. Biopharm. 2019, 142, 435–448. [Google Scholar] [CrossRef]
- Heikkinen, A.T.; Baneyx, G.; Caruso, A.; Parrott, N. Application of PBPK Modeling to Predict Human Intestinal Metabolism of CYP3A Substrates—An Evaluation and Case Study Using GastroPlusTM. Eur. J. Pharm. Sci. 2012, 47, 375–386. [Google Scholar] [CrossRef]
- Kambayashi, A. In Silico Modeling Approaches Coupled with In Vitro Characterization in Predicting In Vivo Performance of Drug Delivery System Formulations. Mol. Pharm. 2023, 20, 4344–4353. [Google Scholar] [CrossRef]
- Li, J.; Spivey, N.; Silchenko, S.; Gonzalez-Alvarez, I.; Bermejo, M.; Hidalgo, I.J. A Differential Equation Based Modelling Approach to Predict Supersaturation and in Vivo Absorption from in Vitro Dissolution-Absorption System (Idas2) Data. Eur. J. Pharm. Biopharm. 2021, 165, 1–12. [Google Scholar] [CrossRef]
- McFarland, J.W.; Avdeef, A.; Berger, C.M.; Raevsky, O.A. Estimating the Water Solubilities of Crystalline Compounds from Their Chemical Structures Alone. J. Chem. Inf. Comput. Sci. 2001, 41, 1355–1359. [Google Scholar] [CrossRef] [PubMed]
- Vertzoni, M.; Dressman, J.; Butler, J.; Hempenstall, J.; Reppas, C. Simulation of Fasting Gastric Conditions and Its Importance for the In Vivo Dissolution of Lipophilic Compounds. Eur. J. Pharm. Biopharm. 2005, 60, 413–417. [Google Scholar] [CrossRef]
- Jantratid, E.; Janssen, N.; Reppas, C.; Dressman, J.B. Dissolution Media Simulating Conditions in the Proximal Human Gastrointestinal Tract: An Update. Pharm. Res. 2008, 25, 1663–1676. [Google Scholar] [CrossRef] [PubMed]
- Johnsson, G.; Regärdh, C.; Sölvell, L. Combined Pharmacokinetic and Pharmacodynamic Studies in Man of the Adrenergic β 1 -receptor Antagonist Metoprolol. Acta Pharmacol. Toxicol. 1975, 36, 31–44. [Google Scholar] [CrossRef]
- Nielsen-Kudsk, F.; Pedersen, A.K. Pharmacokinetics of Dipyridamole. Acta Pharmacol. Toxicol. 1979, 44, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Bukhtiyarov, Y.; Spivey, N.; Force, C.; Hidalgo, C.; Huang, Y.; Owen, A.J.; Hidalgo, I.J. In Vitro and In Vivo Assessment of the Potential of Supersaturation to Enhance the Absorption of Poorly Soluble Basic Drugs. J. Pharm. Innov. 2020, 15, 591–602. [Google Scholar] [CrossRef]
- Noyes, A.A.; Whitney, W.R. The Rate of Solution of Solid Substances in Their Own Solutions. J. Am. Chem. Soc. 1897, 19, 930–934. [Google Scholar] [CrossRef]
- Takano, R.; Sugano, K.; Higashida, A.; Hayashi, Y.; Machida, M.; Aso, Y.; Yamashita, S. Oral Absorption of Poorly Water-Soluble Drugs: Computer Simulation of Fraction Absorbed in Humans from a Miniscale Dissolution Test. Pharm. Res. 2006, 23, 1144–1156. [Google Scholar] [CrossRef]
- Jakubiak, P.; Wagner, B.; Grimm, H.P.; Petrig-Schaffland, J.; Schuler, F.; Alvarez-Sánchez, R. Development of a Unified Dissolution and Precipitation Model and Its Use for the Prediction of Oral Drug Absorption. Mol. Pharm. 2016, 13, 586–598. [Google Scholar] [CrossRef] [PubMed]
- Hofsäss, M.A.; Dressman, J. Suitability of the Z-Factor for Dissolution Simulation of Solid Oral Dosage Forms: Potential Pitfalls and Refinements. J. Pharm. Sci. 2020, 109, 2735–2745. [Google Scholar] [CrossRef] [PubMed]
- Yano, K.; Masaoka, Y.; Kataoka, M.; Sakuma, S.; Yamashita, S. Mechanisms of Membrane Transport of Poorly Soluble Drugs: Role of Micelles in Oral Absorption Processes. J. Pharm. Sci. 2010, 99, 1336–1345. [Google Scholar] [CrossRef]
- Kataoka, M.; Yano, K.; Hamatsu, Y.; Masaoka, Y.; Sakuma, S.; Yamashita, S. Assessment of Absorption Potential of Poorly Water-Soluble Drugs by Using the Dissolution/Permeation System. Eur. J. Pharm. Biopharm. 2013, 85, 1317–1324. [Google Scholar] [CrossRef] [PubMed]
- Katneni, K.; Charman, S.A.; Porter, C.J.H. Permeability Assessment of Poorly Water-soluble Compounds under Solubilizing Conditions: The Reciprocal Permeability Approach. J. Pharm. Sci. 2006, 95, 2170–2185. [Google Scholar] [CrossRef] [PubMed]
- Poelma, F.G.J.; Breäs, R.; Tukker, J.J.; Crommelin, D.J.A. Intestinal Absorption of Drugs. The Influence of Mixed Micelles on on the Disappearance Kinetics of Drugs from the Small Intestine of the Rat. J. Pharm. Pharmacol. 1991, 43, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Kambayashi, A.; Yasuji, T.; Dressman, J.B. Prediction of the Precipitation Profiles of Weak Base Drugs in the Small Intestine Using a Simplified Transfer (“Dumping”) Model Coupled with In Silico Modeling and Simulation Approach. Eur. J. Pharm. Biopharm. 2016, 103, 95–103. [Google Scholar] [CrossRef]
- Grimm, M.; Koziolek, M.; Saleh, M.; Schneider, F.; Garbacz, G.; Kühn, J.-P.; Weitschies, W. Gastric Emptying and Small Bowel Water Content after Administration of Grapefruit Juice Compared to Water and Isocaloric Solutions of Glucose and Fructose: A Four-Way Crossover MRI Pilot Study in Healthy Subjects. Mol. Pharm. 2018, 15, 548–559. [Google Scholar] [CrossRef]
- Grimm, M.; Scholz, E.; Koziolek, M.; Kühn, J.-P.; Weitschies, W. Gastric Water Emptying under Fed State Clinical Trial Conditions Is as Fast as under Fasted Conditions. Mol. Pharm. 2017, 14, 4262–4271. [Google Scholar] [CrossRef]
- Mudie, D.M.; Murray, K.; Hoad, C.L.; Pritchard, S.E.; Garnett, M.C.; Amidon, G.L.; Gowland, P.A.; Spiller, R.C.; Amidon, G.E.; Marciani, L. Quantification of Gastrointestinal Liquid Volumes and Distribution Following a 240 ML Dose of Water in the Fasted State. Mol. Pharm. 2014, 11, 3039–3047. [Google Scholar] [CrossRef]
- US FDA. Guidance for Industry: Bioavailability and Bioequivalence Studies Submitted in NDAs or INDs—General Considerations; DRAFT GUIDANCE. 2014. Available online: https://www.fda.gov/media/88254/download (accessed on 29 May 2025).
- Macheras, P.; Reppas, C.; Dressman, J. Biopharmaceutics of Orally Administered Drugs; CRC Press: Boca Raton, FL, USA, 1995; ISBN 9780203022849. [Google Scholar]
- Basit, A.W.; Newton, J.M.; Short, M.D.; Waddington, W.A.; Ell, P.J.; Lacey, L.F. The Effect of Polyethylene Glycol 400 on Gastrointestinal Transit: Implications for the Formulation of Poorly-Water Soluble Drugs. Pharm. Res. 2001, 18, 1146–1150. [Google Scholar] [CrossRef]
- Yu, L.X. An Integrated Model for Determining Causes of Poor Oral Drug Absorption. Pharm. Res. 1999, 16, 1883–1887. [Google Scholar] [CrossRef]
- Lennernäs, H. Intestinal Permeability and Its Relevance for Absorption and Elimination. Xenobiotica 2007, 37, 1015–1051. [Google Scholar] [CrossRef]
- Higashino, H.; Hasegawa, T.; Yamamoto, M.; Matsui, R.; Masaoka, Y.; Kataoka, M.; Sakuma, S.; Yamashita, S. In Vitro—In Vivo Correlation of the Effect of Supersaturation on the Intestinal Absorption of BCS Class 2 Drugs. Mol. Pharm. 2014, 11, 746–754. [Google Scholar] [CrossRef] [PubMed]
- Matsui, K.; Tsume, Y.; Amidon, G.E.; Amidon, G.L. In Vitro Dissolution of Fluconazole and Dipyridamole in Gastrointestinal Simulator (GIS), Predicting in Vivo Dissolution and Drug–Drug Interaction Caused by Acid-Reducing Agents. Mol. Pharm. 2015, 12, 2418–2428. [Google Scholar] [CrossRef] [PubMed]
- de Stoppelaar, F.M.; Stolk, L.M.L.; Beysens, A.J.; Stappers, J.L.M.; Gorgels, A.P.M. The Relative Bioavailability of Metoprolol Following Oral and Rectal Administration to Volunteers and Patients. Pharm. World Sci. 1999, 21, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Galia, E.; Nicolaides, E.; Hörter, D.; Löbenberg, R.; Reppas, C.; Dressman, J.B. Evaluation of Various Dissolution Media for Predicting In Vivo Performance of Class I and II Drugs. Pharm. Res. 1998, 15, 698–705. [Google Scholar] [CrossRef]
- Incecayir, T.; Tsume, Y.; Amidon, G.L. Comparison of the Permeability of Metoprolol and Labetalol in Rat, Mouse, and Caco-2 Cells: Use as a Reference Standard for BCS Classification. Mol. Pharm. 2013, 10, 958–966. [Google Scholar] [CrossRef]
- Masada, T.; Takagi, T.; Minami, K.; Kataoka, M.; Takeyama, S.; Fujii, Y.; Takahashi, M.; Yamashita, S. New Biphasic System in Side-by-Side Chambers for Testing Drug Dissolution and Permeation in Vitro (BiDP System). J. Drug Deliv. Sci. Technol. 2021, 65, 102747. [Google Scholar] [CrossRef]
- Girdhar, A.; Thakur, P.S.; Sheokand, S.; Bansal, A.K. Permeability Behavior of Nanocrystalline Solid Dispersion of Dipyridamole Generated Using NanoCrySP Technology. Pharmaceutics 2018, 10, 160. [Google Scholar] [CrossRef]
- Artursson, P. Epithelial Transport Of Drugs In Cell Culture. I: A Model For Studying The Passive Diffusion Of Drugs Over Intestinal Absorbtive (Caco-2) Cells. J. Pharm. Sci. 1990, 79, 476–482. [Google Scholar] [CrossRef]
- Segregur, D.; Barker, R.; Mann, J.; Moir, A.; Karlsson, E.M.; Turner, D.B.; Arora, S.; Dressman, J. Evaluating the Impact of Acid-Reducing Agents on Drug Absorption Using Biorelevant in Vitro Tools and PBPK Modeling—Case Example Dipyridamole. Eur. J. Pharm. Sci. 2021, 160, 105750. [Google Scholar] [CrossRef]
- Psachoulias, D.; Vertzoni, M.; Goumas, K.; Kalioras, V.; Beato, S.; Butler, J.; Reppas, C. Precipitation in and Supersaturation of Contents of the Upper Small Intestine After Administration of Two Weak Bases to Fasted Adults. Pharm. Res. 2011, 28, 3145–3158. [Google Scholar] [CrossRef] [PubMed]
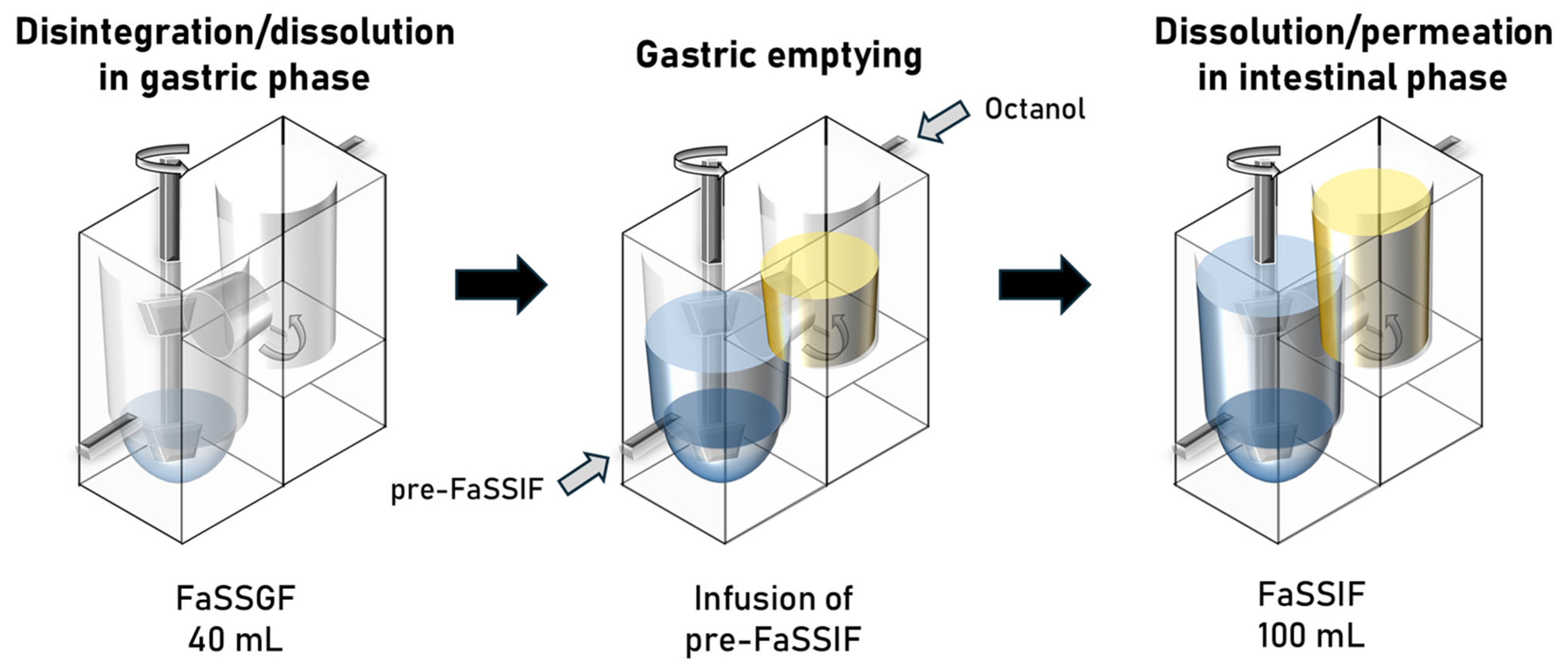
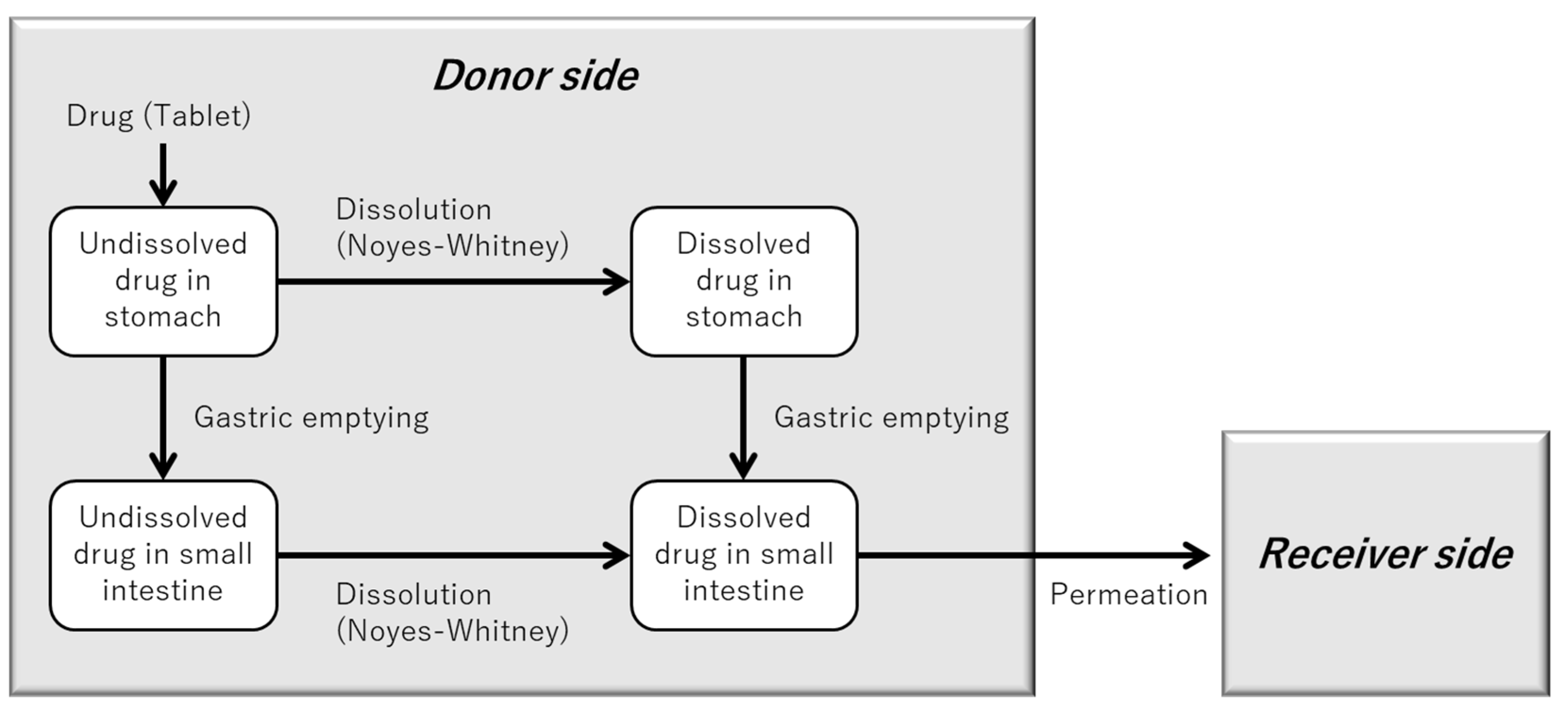

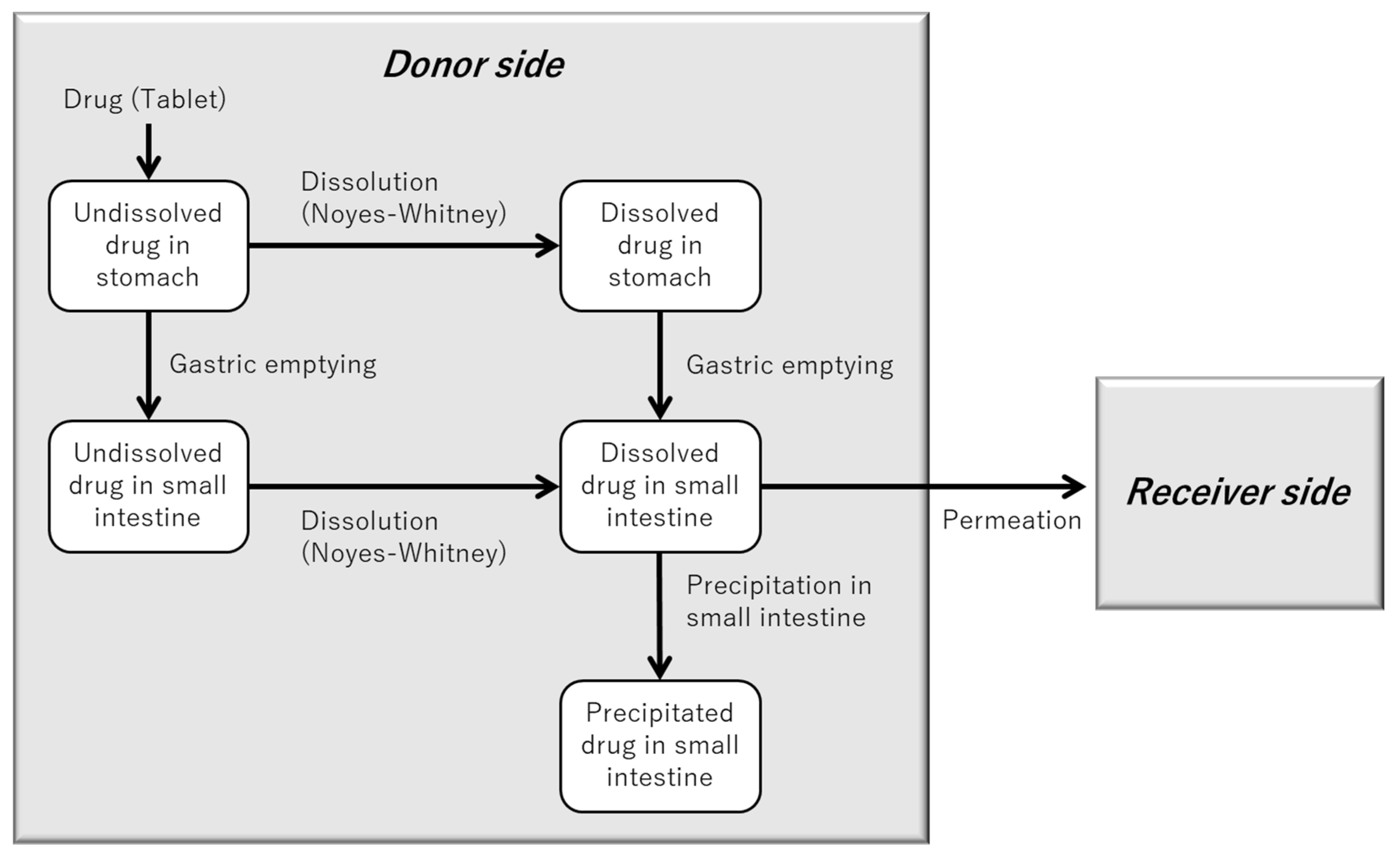
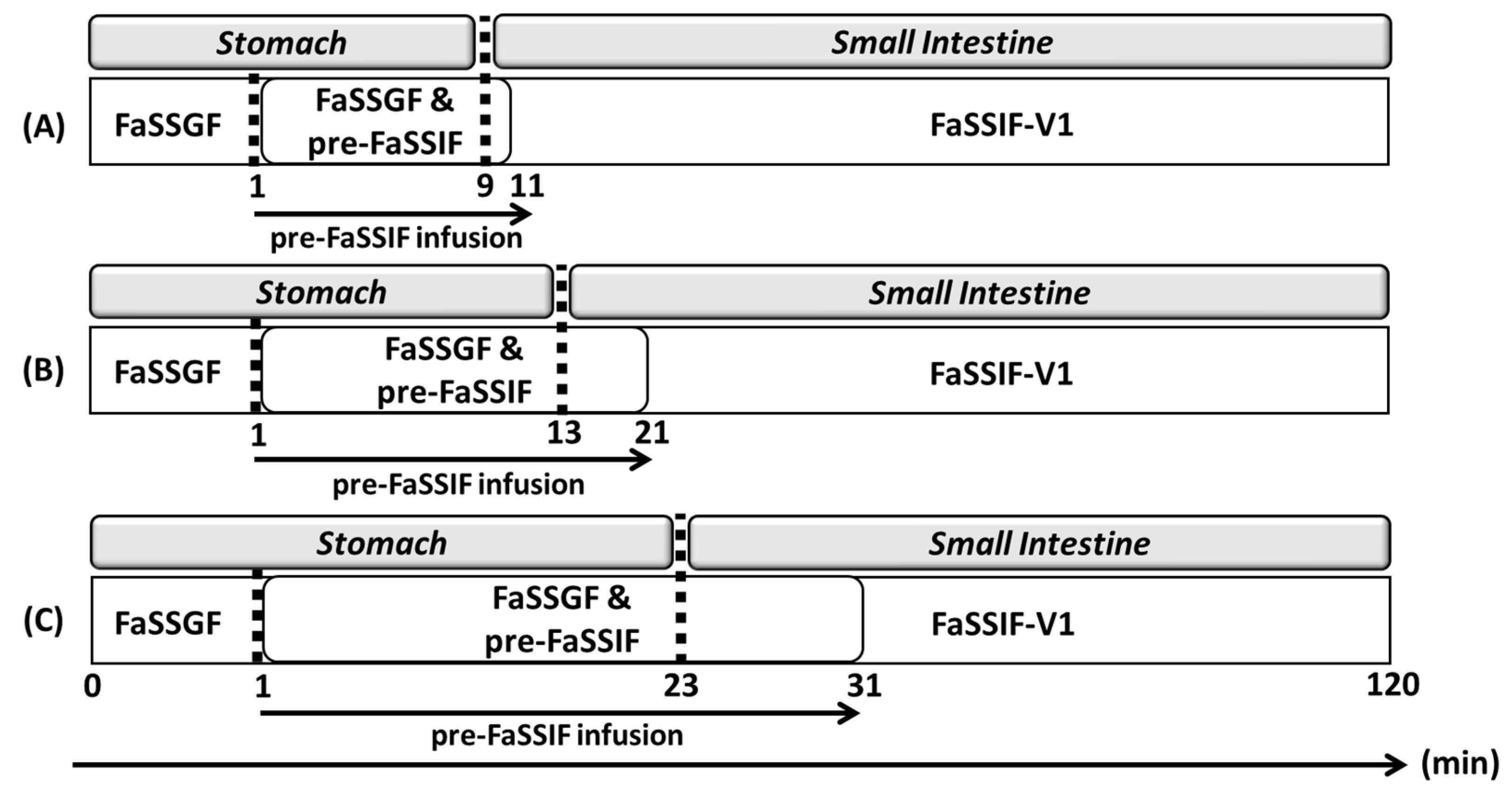



| Drug | Biorelevant Media | Solubility (Mean ± SD) |
|---|---|---|
| Metoprolol tartrate | SGF and FaSSIF (pH 1.6~pH 6.5) | >2 mg/mL [11,16] |
| Dipyridamole | FaSSGF (pH 1.6) | 11.16 ± 0.15 mg/mL |
| FaSSGF (pH 3.0) | 0.304 ± 0.063 mg/mL | |
| FaSSGF (pH 5.0) | 0.0072 ± 0.0015 mg/mL | |
| FaSSGF (pH 6.5) | 0.0043 ± 0.0005 mg/mL | |
| FaSSIF-V1 (pH 6.5) | 0.0118 ± 0.0002 mg/mL |
| BE Checker Condition (Pre-FaSSIF Infusion Time, Stirring Speeds) | z Factor (mL·mg−1·min−1) | |
|---|---|---|
| 10 min, 50 rpm | Stomach | 3.74 × 10−4 |
| Small intestine | 1.60 × 10−3 | |
| 10 min, 100 rpm | Stomach | 3.54 × 10−4 |
| Small intestine | 2.69 × 10−3 | |
| 10 min, 200 rpm | Stomach | 2.89 × 10−3 |
| Small intestine | 3.79 × 10−3 | |
| BE Checker Condition (Pre-FaSSIF Infusion Time, Stirring Speeds) | z Factor (mL·mg−1·min−1) | k0 (min−1) | X (mL/mg) | |
|---|---|---|---|---|
| 10 min, 50 rpm | Stomach | 8.77 × 10−4 | 8.67 × 10−19 | 4.24 |
| Small intestine | 3.94 × 10−13 | |||
| 10 min, 100 rpm | Stomach | 2.07 × 10−3 | 1.34 × 10−18 | 1.83 × 10−13 |
| Small intestine | 9.17 × 10−15 | |||
| 10 min, 200 rpm | Stomach | 6.52 × 10−2 | 1.28 × 10−2 | 6.64 × 10−13 |
| Small intestine | 6.17 × 10−16 | |||
| 20 min, 50 rpm | Stomach | 5.85 × 10−3 | 2.64 × 10−2 | 10.8 |
| Small intestine | 1.16 × 10−11 | |||
| 20 min, 100 rpm | Stomach | 9.44 × 10−3 | 3.03 × 10−2 | 4.42 |
| Small intestine | 1.00 × 10−14 | |||
| 20 min, 200 rpm | Stomach | 1.58 × 10−2 | 8.75 × 10−2 | 1.85 × 10−21 |
| Small intestine | 6.32 × 10−14 | |||
| 30 min, 50 rpm | Stomach | 5.09 × 10−3 | 1.85 × 10−5 | 48.5 |
| Small intestine | 1.61 × 10−9 | |||
| 30 min, 100 rpm | Stomach | 1.27 × 10−2 | 3.46 × 10−2 | 2.63 × 10−13 |
| Small intestine | 8.82 | |||
| 30 min, 200 rpm | Stomach | 1.79 × 10−2 | 4.43 × 10−2 | 6.60 × 10−14 |
| Small intestine | 3.38 × 10−15 | |||
| Dose (mg) | Observed | Predicted (50 rpm) | Predicted (100 rpm) | Predicted (200 rpm) | |
|---|---|---|---|---|---|
| 20 | Tmax (h) | 1.53 | 1.86 (+0.33 h) | 1.53 (+0.00 h) | 1.15 (−0.38 h) |
| Cmax (ng/mL) | 16.0 | 13.6 (−15%) | 14.5 (−9%) | 15.3 (−5%) | |
| AUCinf (ng·h/mL) | 79.9 | 85.7 (+7%) | 85.4 (+7%) | 85.4 (+7%) | |
| 50 | Tmax (h) | 1.59 | 1.86 (+0.28 h) | 1.54 (−0.05 h) | 1.15 (−0.44 h) |
| Cmax (ng/mL) | 49.2 | 44.9 (−9%) | 48.0 (−3%) | 50.4 (+2%) | |
| AUCinf (ng·h/mL) | 318 | 282 (−11%) | 282 (−11%) | 282 (−11%) | |
| 100 | Tmax (h) | 1.22 | 1.87 (+0.66 h) | 1.54 (+0.32 h) | 1.15 (−0.06 h) |
| Cmax (ng/mL) | 117 | 101 (−14%) | 108 (−8%) | 113 (−3%) | |
| AUCinf (ng·h/mL) | 677 | 636 (−6%) | 634 (−6%) | 633 (−6%) |
| Observed (Mean ± SD) | Predicted | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 min | 20 min | 30 min | ||||||||
| 50 rpm | 100 rpm | 200 rpm | 50 rpm | 100 rpm | 200 rpm | 50 rpm | 100 rpm | 200 rpm | ||
| Tmax (h) | 1.03 ± 0.33 | 0.86 (−0.18 h) | 0.79 (−0.24 h) | 0.49 (−0.55 h) | 0.66 (−0.37 h) | 0.59 (−0.44 h) | 0.55 (−0.48 h) | 0.68 (−0.36 h) | 0.56 (−0.47 h) | 0.54 (−0.50 h) |
| Cmax (μg/mL) | 2.18 ± 0.85 | 0.40 (−82%) | 0.82 (−62%) | 2.46 (+13%) | 1.52 (−30%) | 1.82 (−16%) | 1.96 (−10%) | 1.47 (−32%) | 1.98 (−9%) | 2.09 (−4%) |
| AUCinf (μg·h/mL) | 4.25 ± 2.73 | 0.96 (−77%) | 1.89 (−56%) | 4.98 (+17%) | 3.23 (−24%) | 3.78 (−11%) | 4.05 (−5%) | 3.14 (−26%) | 5.16 (+22%) | 4.29 (+1%) |
| Observed (Mean ± SD) | Predicted | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 min | 20 min | 30 min | ||||||||
| 50 rpm | 100 rpm | 200 rpm | 50 rpm | 100 rpm | 200 rpm | 50 rpm | 100 rpm | 200 rpm | ||
| Tmax (h) | 1.03 ± 0.33 | 0.86 (−0.18 h) | 0.79 (−0.24 h) | 0.49 (−0.55 h) | 0.66 (−0.38 h) | 0.59 (−0.45 h) | 0.54 (−0.49 h) | 0.68 (−0.36 h) | 0.56 (−0.48 h) | 0.53 (−0.50 h) |
| Cmax (μg/mL) | 2.18 ± 0.85 | 0.40 (−82%) | 0.82 (−62%) | 2.50 (+15%) | 1.58 (−28%) | 1.90 (−13%) | 2.15 (−1%) | 1.47 (−32%) | 2.06 (−5%) | 2.20 (+1%) |
| AUCinf (μg·h/mL) | 4.25 ± 2.73 | 0.96 (−77%) | 1.89 (−56%) | 5.04 (+19%) | 3.32 (−22%) | 3.90 (−8%) | 4.38 (+3%) | 3.14 (−26%) | 5.29 (+25%) | 4.47 (+5%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niino, T.; Masada, T.; Takagi, T.; Kataoka, M.; Yoshida, H.; Yamashita, S.; Kambayashi, A. Integrating In Vitro BE Checker with In Silico Physiologically Based Biopharmaceutics Modeling to Predict the Pharmacokinetic Profiles of Oral Drug Products. Pharmaceutics 2025, 17, 1222. https://doi.org/10.3390/pharmaceutics17091222
Niino T, Masada T, Takagi T, Kataoka M, Yoshida H, Yamashita S, Kambayashi A. Integrating In Vitro BE Checker with In Silico Physiologically Based Biopharmaceutics Modeling to Predict the Pharmacokinetic Profiles of Oral Drug Products. Pharmaceutics. 2025; 17(9):1222. https://doi.org/10.3390/pharmaceutics17091222
Chicago/Turabian StyleNiino, Takuto, Takato Masada, Toshihide Takagi, Makoto Kataoka, Hiroyuki Yoshida, Shinji Yamashita, and Atsushi Kambayashi. 2025. "Integrating In Vitro BE Checker with In Silico Physiologically Based Biopharmaceutics Modeling to Predict the Pharmacokinetic Profiles of Oral Drug Products" Pharmaceutics 17, no. 9: 1222. https://doi.org/10.3390/pharmaceutics17091222
APA StyleNiino, T., Masada, T., Takagi, T., Kataoka, M., Yoshida, H., Yamashita, S., & Kambayashi, A. (2025). Integrating In Vitro BE Checker with In Silico Physiologically Based Biopharmaceutics Modeling to Predict the Pharmacokinetic Profiles of Oral Drug Products. Pharmaceutics, 17(9), 1222. https://doi.org/10.3390/pharmaceutics17091222






