PBPK/PD Model of Vancomycin in Sepsis: Linking Interstitial Exposure in Perfusion-Limited Tissues to MRSA Infection
Abstract
1. Introduction
2. Materials and Methods
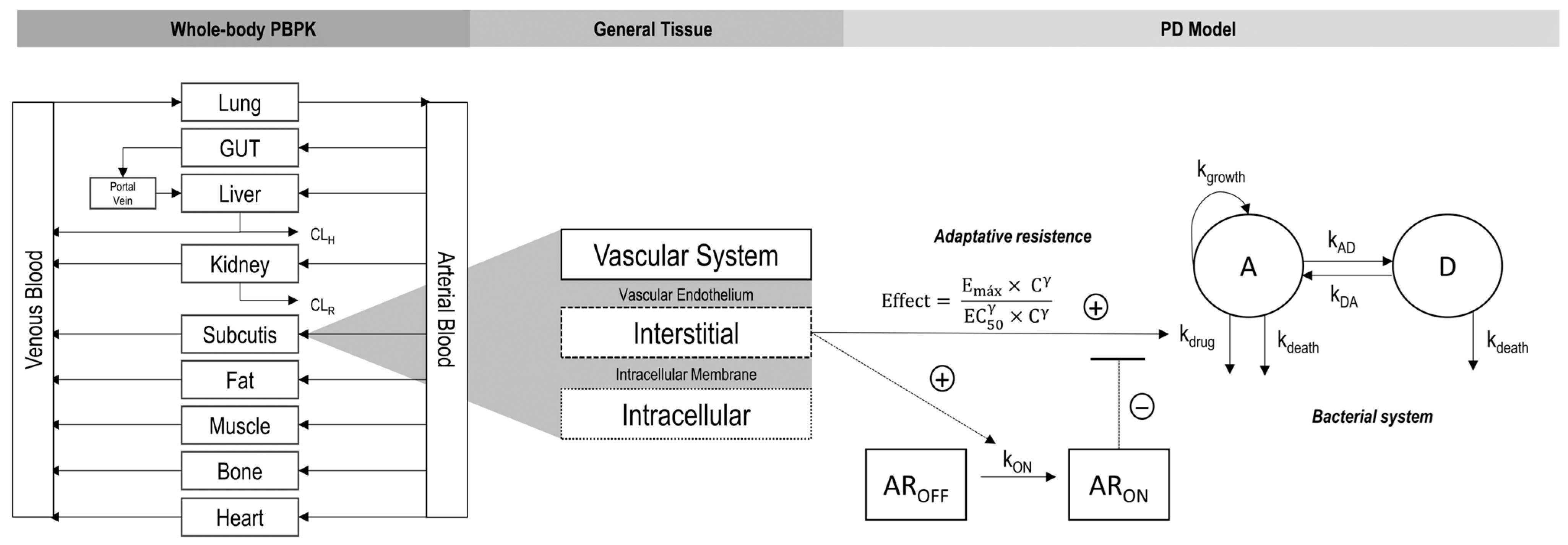
2.1. PBPK Model Building
2.1.1. Software Platforms
2.1.2. Healthy Volunteers
2.1.3. Septic Patients
2.2. Pharmacodynamic Model Building
Methicillin-Resistant Staphylococcus aureus (MRSA)
2.3. PBPK/PD Model Building
3. Results
3.1. Healthy Volunteers PBPK Model
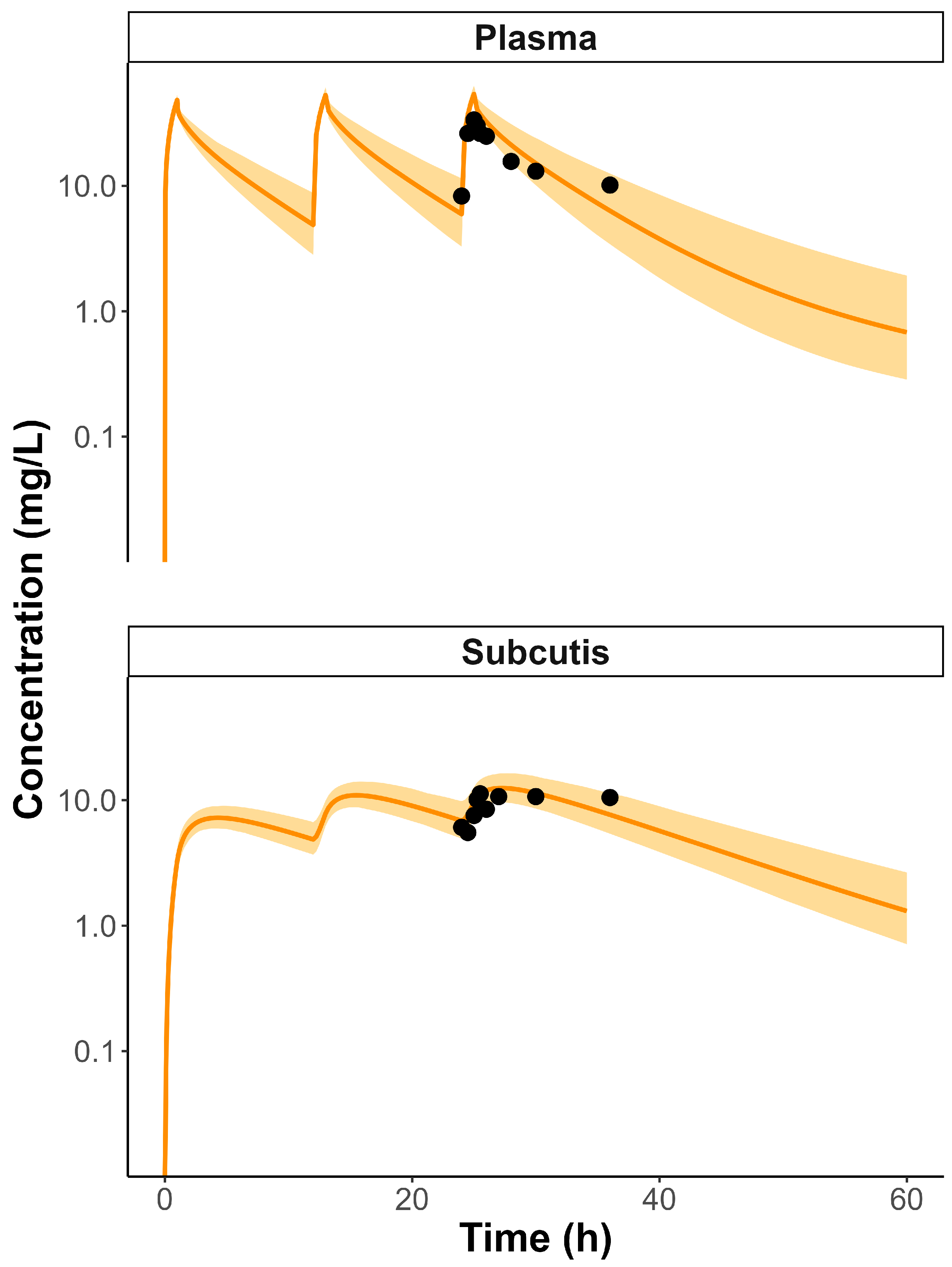
3.2. Septic Patients PBPK Model
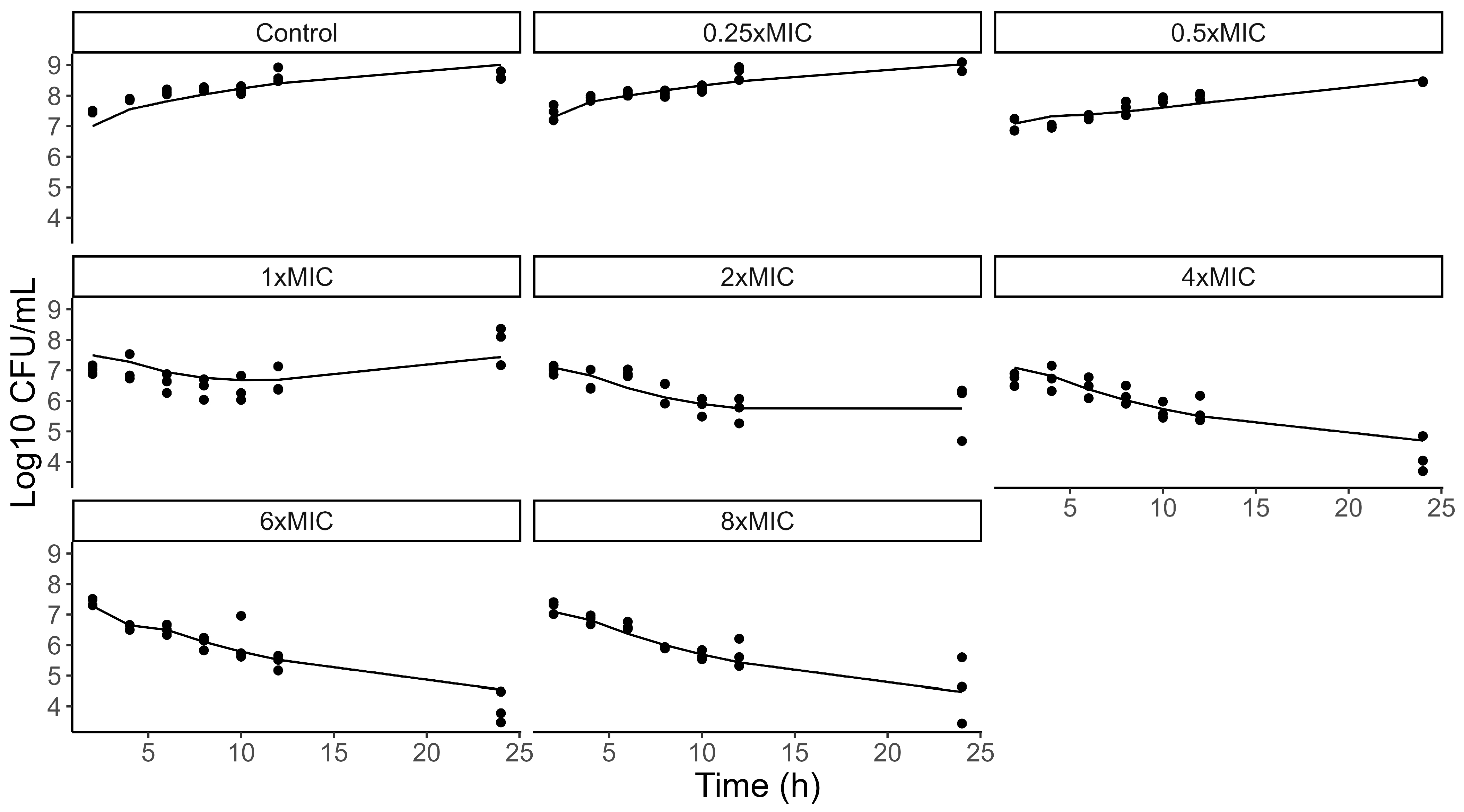
3.3. PD Model
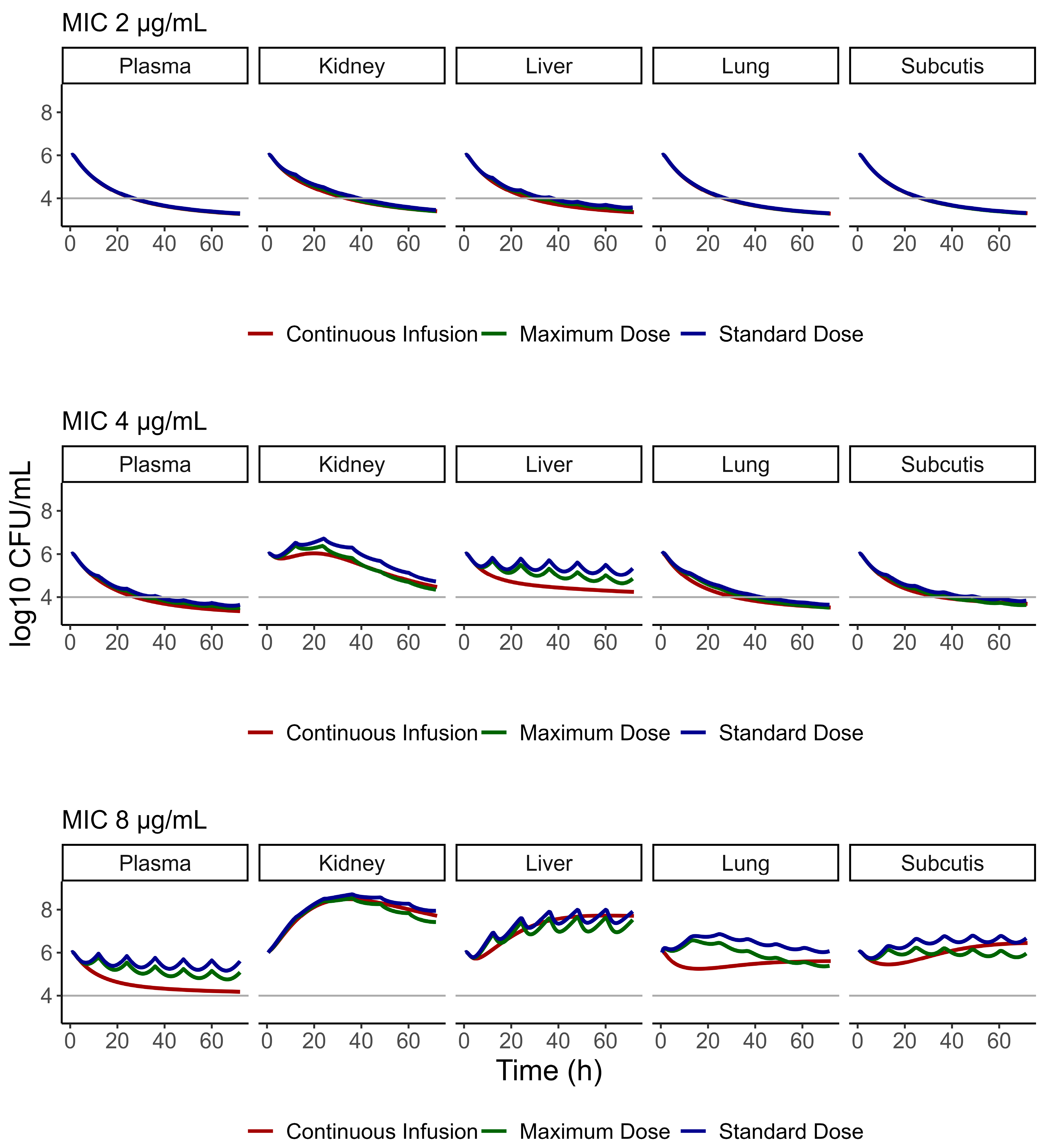
3.4. PBPK/PD Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brasil. Ministério da Saúde. Secretaria de Vigilância em Saúde. Doenças infecciosas e parasitárias: Guia de Bolso. 8. ed. Brasília, DF. 2010. Available online: https://www.gov.br/saude/pt-br/centrais-de-conteudo/publicacoes/svsa/doencas-diarreicas-agudas/doencas-infecciosas-e-parasitarias_-guia-de-bolso.pdf/view (accessed on 4 June 2025).
- da Silva, E.L.M.; dos Santos, S.; Torquati, A.; Araújo, C.; Brandão, F. Why are infectious and parasitic diseases among the leading causes of death in Brazil? Res. Soc. Dev. 2022, 11, e453111537370. [Google Scholar] [CrossRef]
- Santos-Borges, K.T.; Henz, P.; de Araújo, B.V. The influence of sepsis on antimicrobials tissue penetration: The use of microdialysis technique to access free drug distribution. Braz. J. Pharm. Sci. 2023, 59, e22982. [Google Scholar] [CrossRef]
- Strich, J.R.; Heil, E.L.; Masur, H. Considerations for Empiric Antimicrobial Therapy in Sepsis and Septic Shock in an Era of Antimicrobial Resistance. J. Infect. Dis. 2020, 222, S119–S131. [Google Scholar] [CrossRef]
- Latin American Sepsis Institute. Practical Guide to Antimicrobial Therapy in Sepsis, 2nd ed.; Latin American Sepsis Institute: São Paulo, Brazil, 2022. [Google Scholar]
- Stanford Health Care. SHC Vancomycin Dosing Guide [S. l.]. 2023. Available online: https://med.stanford.edu/content/dam/sm/bugsanddrugs/documents/antimicrobial-dosing-protocols/SHC%20Vancomycin%20Dosing%20Guide.pdf (accessed on 4 June 2025).
- Meibohm, B.; Derendorf, H. Basic concepts of pharmacokinetic/pharmacodynamic (PK/PD) modelling. International J. Clin. Pharmacol. Ther. 1997, 35, 401–413. [Google Scholar] [PubMed]
- Girdwood, S.T.; Tang, P.; Fenchel, M.; Dong, M.; Stoneman, E.; Jones, R.; Ostermeier, A.; Curry, C.; Forton, M.; Hail, T.; et al. Pharmacokinetic parameters over time during sepsis and the association of target attainment and outcomes in critically ill children and young adults receiving ceftriaxone. Pharmacotherapy 2023, 43, 609–621. [Google Scholar] [CrossRef]
- Kuepfer, L.; Niederalt, C.; Wendl, T.; Schlender, J.; Willmann, S.; Lippert, J.; Block, M.; Eissing, T.; Teutonico, D. Applied Concepts in PBPK Modeling: How to Build a PBPK/PD Model. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Sinnollareddy, M.G.; Roberts, M.S.; Williams, P.; Peake, S.L.; Lipman, J.; Roberts, J.A. Plasma and interstitial fluid population pharmacokinetics of vancomycin in critically ill patients with sepsis. Int. J. Antimicrob. Agents 2019, 53, 137–142. [Google Scholar] [CrossRef]
- Radke, C.; Horn, D.; Lanckohr, C.; Ellger, B.; Meyer, M.; Eissing, T.; Hempel, G. Development of a Physiologically Based Pharmacokinetic Modelling Approach to Predict the Pharmacokinetics of Vancomycin in Critically Ill Septic Patients. Clin. Pharmacokinet. 2017, 56, 759–779. [Google Scholar] [CrossRef] [PubMed]
- Automeris. WebPlotDigitalizer (Version 4.5). 2023. Available online: https://apps.automeris.io/wpd/ (accessed on 15 January 2025).
- A Blouin, R.; A Bauer, L.; Miller, D.D.; E Record, K.; O Griffen, W. Vancomycin pharmacokinetics in normal and morbidly obese subjects. Antimicrob. Agents Chemother. 1982, 21, 575–580. [Google Scholar] [CrossRef]
- Boeckh, M.; Lode, H.; Borner, K.; Höffken, G.; Wagner, J.; Koeppe, P. Pharmacokinetics and serum bactericidal activity of vancomycin alone and in combination with ceftazidime in healthy volunteers. Antimicrob. Agents Chemother. 1988, 32, 92–95. [Google Scholar] [CrossRef]
- Cutler, N.R.; Narang, P.K.; Lesko, L.J.; Ninos, M.; Power, M. Vancomycin disposition: The importance of age. Clin. Pharmacol. Ther. 1984, 36, 803–810. [Google Scholar] [CrossRef] [PubMed]
- Healy, D.P.; E Polk, R.; Garson, M.L.; Rock, D.T.; Comstock, T.J. Comparison of steady-state pharmacokinetics of two dosage regimens of vancomycin in normal volunteers. Antimicrob. Agents Chemother. 1987, 31, 393–397. [Google Scholar] [CrossRef]
- Krogstad, D.J.; Moellering, R.C.; Greenrlatt, D.J. Single-dose kinetics of intravenous vancomycin. J. Clin. Pharmacol. 1980, 20, 197–201. [Google Scholar] [CrossRef]
- Schmitt, W. General approach for the calculation of tissue to plasma partition coefficients. Toxicol. Vitr. 2008, 22, 457–467. [Google Scholar] [CrossRef]
- De Cock, P.A.J.G.; Desmet, S.; De Jaeger, A.; Biarent, D.; Dhont, E.; Herck, I.; Vens, D.; Colman, S.; Stove, V.; Commeyne, S.; et al. Impact of vancomycin protein binding on target attainment in critically ill children: Back to the drawing board? J. Antimicrob. Chemother. 2017, 72, 801–804. [Google Scholar] [CrossRef] [PubMed]
- Matzke, G.; Kovarik, J.; Rybak, M.; Boike, S. Evaluation of the vancomycin-clearance:creatinine-clearance relationship for predicting vancomycin dosage. Clin. Pharm. 1985, 4, 311–315. [Google Scholar]
- Levenberg, K. A method for the solution of certain problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Lana, D.F.D.; Kaminski, T.F.A.; Lavorato, S.N.; Merkel, S.; Zanette, R.A.; da Rosa, P.D.; Staudt, K.J.; de Araújo, B.V.; da Costa, B.; Quatrin, P.M.; et al. In vitro pharmacokinetics/pharmacodynamics modeling and efficacy against systemic candidiasis in Drosophila melanogaster of a bisaryloxypropanamine derivative. Med. Mycol. 2021, 59, 58–66. [Google Scholar] [CrossRef]
- Menezes, B.; Alves, I.; Staudt, K.; Beltrame, B.; Michelin, L.; de Araújo, B.V.; Tasso, L. PK/PD modeling of daptomycin against MRSA and MRSE and Monte Carlo simulation for bacteremia treatment. Braz. J. Microbiol. 2021, 52, 1967–1979. [Google Scholar] [CrossRef] [PubMed]
- Vera-Yunca, D.; Matias, C.; Lundberg, C.V.; E Friberg, L. Model-based translation of the PKPD-relationship for linezolid and vancomycin on methicillin-resistant Staphylococcus aureus: From in vitro time–kill experiments to a mouse pneumonia model. J. Antimicrob. Chemother. 2025, 80, 1860–1868. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Schuck, E.; Kumar, V.; Burkhardt, O.; Derendorf, H. Integration of pharmacokinetic/pharmacodynamic modeling and simulation in the development of new anti-infective agents—Minimum inhibitory concentration versus time-kill curves. Expert Opin. Drug Discov. 2007, 2, 849–860. [Google Scholar] [CrossRef]
- Bahnasawy, A.M.; Parrott, N.J.; Gijsen, M.; Spriet, I.; Friberg, L.E.; Nielsen, E.I. Physiologically-based pharmacokinetic modelling in sepsis: A tool to elucidate how pathophysiology affects meropenem pharmacokinetics. Int. J. Antimicrob Agents. 2024, 64, 107352. [Google Scholar] [CrossRef]
- Rybak, M.J.; Le, J.; Lodise, T.P.; Levine, D.P.; Bradley, J.S.; Liu, C.; Mueller, B.A.; Pai, M.P.; Wong-Beringer, A.; Rotschafer, J.C.; et al. Therapeutic monitoring of vancomycin for serious methicillin-resistant Staphylococcus aureus infections: A revised consensus guideline and review by the American Society of Health-System Pharmacists, the Infectious Diseases Society of America, the Pediatric Infectious Diseases Society, and the Society of Infectious Diseases Pharmacists. Am. J. Health Syst. Pharm. 2020, 77, 835–864. [Google Scholar] [CrossRef]
- Evans, L.; Rhodes, A.; Alhazzani, W.; Antonelli, M.; Coopersmith, C.M.; French, C.; Machado, F.R.; Mcintyre, L.; Ostermann, M.; Prescott, H.C.; et al. Surviving sepsis campaign: International guidelines for management of sepsis and septic shock. Intensive Care Med. 2021, 47, 1181–1247. [Google Scholar] [CrossRef]
- Nejtek, T.; Müller, M.; Moravec, M.; Průcha, M.; Zazula, R. Bacteremia in Patients with Sepsis in the ICU: Does It Make a Difference? Microorganisms 2023, 11, 2357. [Google Scholar] [CrossRef]
- Mi, K.; Zhou, K.; Sun, L.; Hou, Y.; Ma, W.; Xu, X.; Huo, M.; Liu, Z.; Huang, L. Application of Semi-Mechanistic Pharmacokinetic and Pharmacodynamic Model in Antimicrobial Resistance. Pharmaceutics 2022, 14, 246. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, M.; Schneider, T.R.; Sheldrick, G.M. Crystal structure of vancomycin. Structure 1996, 4, 1509–1515. [Google Scholar] [CrossRef]
- Jia, Z.; O’MAra, M.L.; Zuegg, J.; Cooper, M.A.; Mark, A.E. Vancomycin: Ligand recognition, dimerization and super-complex formation. FEBS J. 2013, 280, 1294–1307. [Google Scholar] [CrossRef] [PubMed]

| Healthy Volunteers | Septic Patients | ||
|---|---|---|---|
| Parameter | Value | Value | Reference |
| Molecular weight (g/mol) | 1449.30 | 1449.30 | PK-Sim database |
| Log P | 2.23 | 2.23 | PK-Sim database |
| pKa | 2.18 (acid), 7.75 (base), 8.89 (base) | 2.18 (acid), 7.75 (base), 8.89 (base) | PK-Sim database |
| Solubility at pH 7 (mg/L) | 225 | 225 | PK-Sim database |
| Fraction unbound | 0.67 | 0.72 | [19] |
| Binding protein | Albumin | Albumin | PK-Sim database |
| Has halogens | No | No | PK-Sim database |
| Partition coefficients | Schmitt | Schmitt | PK-Sim [18] |
| Cellular permeabilities | Charge dependent Schmitt | Charge dependent Schmitt | PK-Sim [18] |
| P plasma ↔ interstitial (cm/s) | 100 # | 6.00 × 10−7 | Optimized by PK-Sim |
| Renal CL (mL/min/kg) | 0.91 * | 0.80 | [20] |
| Hepatic CL (mL/min/kg) | 0.07 | 0.07 | [11] |
| Protocol | Loading Dose (mg/kg) | Maintenance Dose (mg/kg) | Time of Infusion (h) [Frequency] | Treatment Duration (Days) |
|---|---|---|---|---|
| Continuous infusion | 27.5 | 35 | 24 [continuous] | 10 |
| Typical sepsis dose | 27.5 | 17.5 | 1 [q12h] | 10 |
| Highest sepsis dose | 30 | 20 | 1 [q12h] | 10 |
| Study | Dose | AFE Value |
|---|---|---|
| Blouin et al. [13] | 1000 mg | 0.9798 |
| Boeckh et al. [14] | 500 mg | 1.1468 |
| Cutler et al. [15] | 6 mg/kg | 1.2989 |
| Healy et al. [16] | 500 mg | 1.0282 |
| Healy et al. [16] | 1000 mg | 1.0322 |
| Krogstad et al. [17] | 500 mg (patient 1) | 1.3674 |
| Krogstad et al. [17] | 500 mg (patient 2) | 1.1475 |
| Krogstad et al. [17] | 700 mg | 1.2503 |
| Krogstad et al. [17] | 1000 mg | 1.1581 |
| Effect Parameter | Unit | Value | RSE (%) | SIR (95% CI) |
|---|---|---|---|---|
| kgrowth | h−1 | 1.96 | 1.8 | 1.95 (1.89–2.01) |
| Hill factor | 5.74 | 3.4 | 5.72 (5.41–6.05) | |
| Maximum effect | h−1 | 0.061 | 0.5 | 0.062 (0.060–0.065) |
| EC50 in absence of AR | mg/L | 1.05 | 0.7 | 1.05 (1.03–1.06) |
| Maximum bacteria | Log CFU/mL | 8.94 | 1.8 | 8.93 (8.66–9.21) |
| kON | h−1 | 0.021 | 3.7 | 0.022 (0.021–0.023) |
| kDA | h−1 | 0.022 | 3.7 | 0.022 (0.020–0.023) |
| kdeath | h−1 | 1.85 | 1.4 | 1.85 (1.80–1.89) |
| Slope | 3.24 | 1.4 | 3.23 (3.17–3.31) | |
| Proportional error | % | 0.16 | 13.6 | 0.16 (0.13–0.19) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivo, L.B.; de Lemos, J.L.S.; Rodrigues, V.J.; Kretschmer, D.B.; Cruz, W.d.A.; Staudt, K.J.; Annaert, P.; de Araújo, B.V. PBPK/PD Model of Vancomycin in Sepsis: Linking Interstitial Exposure in Perfusion-Limited Tissues to MRSA Infection. Pharmaceutics 2025, 17, 1111. https://doi.org/10.3390/pharmaceutics17091111
Olivo LB, de Lemos JLS, Rodrigues VJ, Kretschmer DB, Cruz WdA, Staudt KJ, Annaert P, de Araújo BV. PBPK/PD Model of Vancomycin in Sepsis: Linking Interstitial Exposure in Perfusion-Limited Tissues to MRSA Infection. Pharmaceutics. 2025; 17(9):1111. https://doi.org/10.3390/pharmaceutics17091111
Chicago/Turabian StyleOlivo, Laura Ben, Jéssica Luísa Silva de Lemos, Vinicius Jardim Rodrigues, Dúnia Batirola Kretschmer, William de Avila Cruz, Keli Jaqueline Staudt, Pieter Annaert, and Bibiana Verlindo de Araújo. 2025. "PBPK/PD Model of Vancomycin in Sepsis: Linking Interstitial Exposure in Perfusion-Limited Tissues to MRSA Infection" Pharmaceutics 17, no. 9: 1111. https://doi.org/10.3390/pharmaceutics17091111
APA StyleOlivo, L. B., de Lemos, J. L. S., Rodrigues, V. J., Kretschmer, D. B., Cruz, W. d. A., Staudt, K. J., Annaert, P., & de Araújo, B. V. (2025). PBPK/PD Model of Vancomycin in Sepsis: Linking Interstitial Exposure in Perfusion-Limited Tissues to MRSA Infection. Pharmaceutics, 17(9), 1111. https://doi.org/10.3390/pharmaceutics17091111






