Adaptive Closed-Loop Control System for the Optimization of Tablet Manufacturing Processes
Abstract
1. Introduction
2. Basic Theory of Iterative Learning Predictive Control
2.1. Model Predictive Control with Iterative Learning Constraints
2.2. Real-Time Adaptive Model Predictive Control
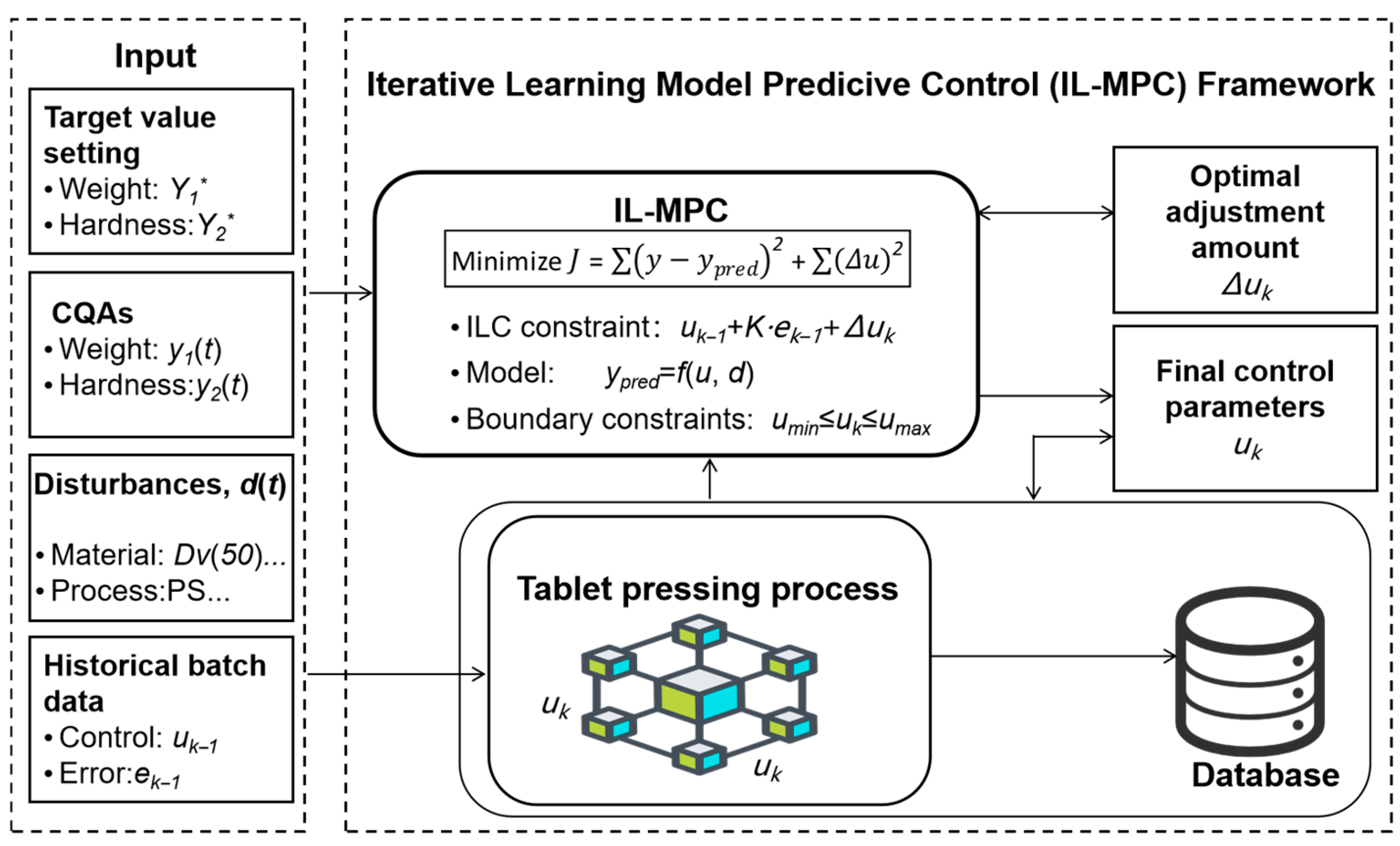
3. MPC-ILC Strategy for Tablet Quality Assurance
3.1. Integrated Predictive Controller Design
3.2. Real-Time Learning and Adaptation
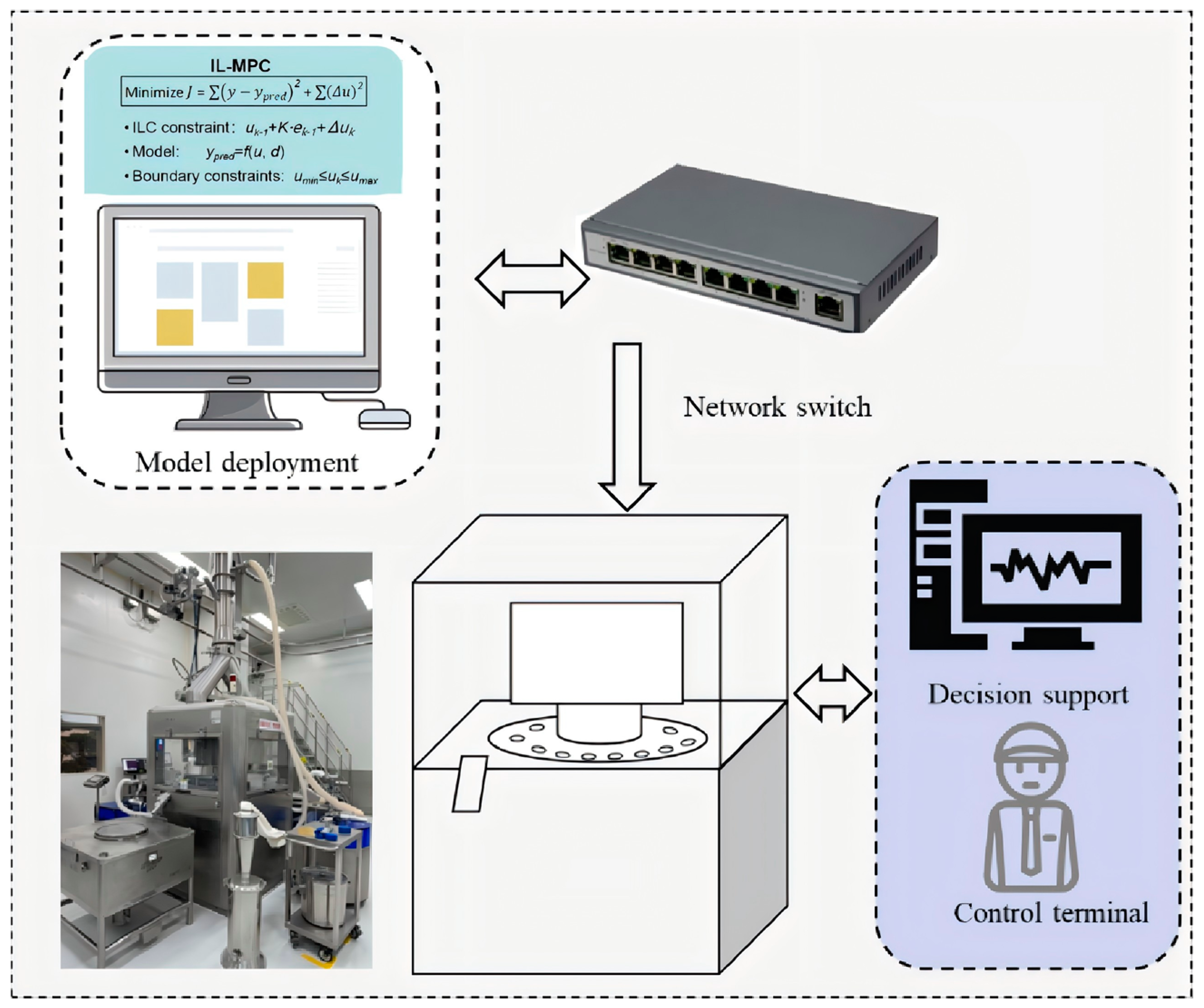
3.3. Online Implementation Architecture
- Real-time sensing: Online sensors continuously monitor material attributes (moisture, particle size) and process parameters.
- MPC optimization: The controller computes optimal adjustments to fill position and compression wheel position.
- Quality monitoring: Tablet weight and hardness are measured at regular intervals.
- ILC learning: After each batch, model parameters are updated based on performance errors.
- Constraint enforcement: The ILC-updated model is embedded as a constraint in the next MPC optimization cycle.
4. Materials and Methods
4.1. Experimental Design
4.2. Data Analysis of Particle Size Distribution
4.3. Identifying Critical Variables for Closed-Loop Regulatory Model
4.4. Control Performance Evaluation Index
5. Results and Discussion
5.1. Principal Component Analysis of Particle Size Distribution
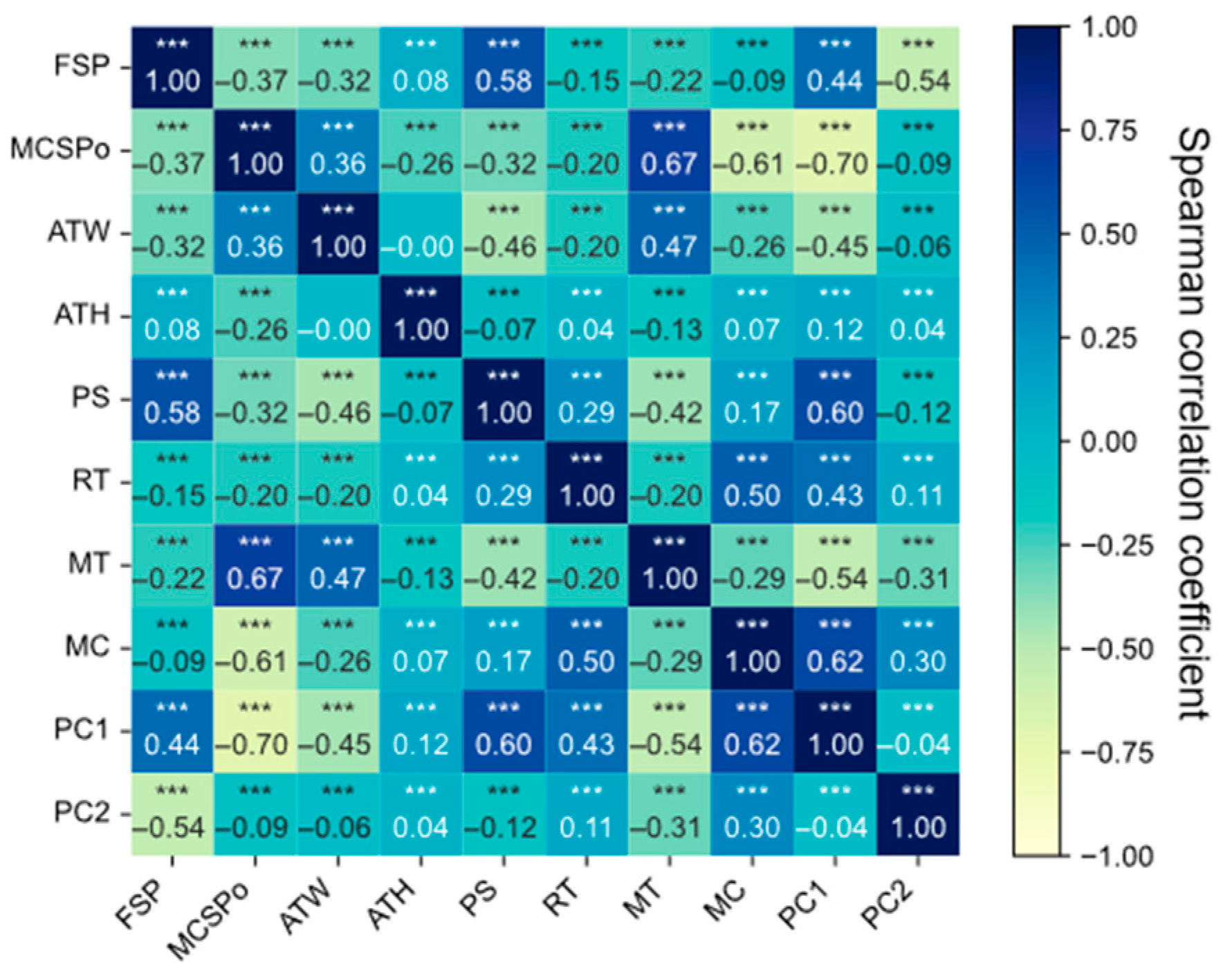
5.2. Feature Selection Based on Spearman’s Rank Correlation
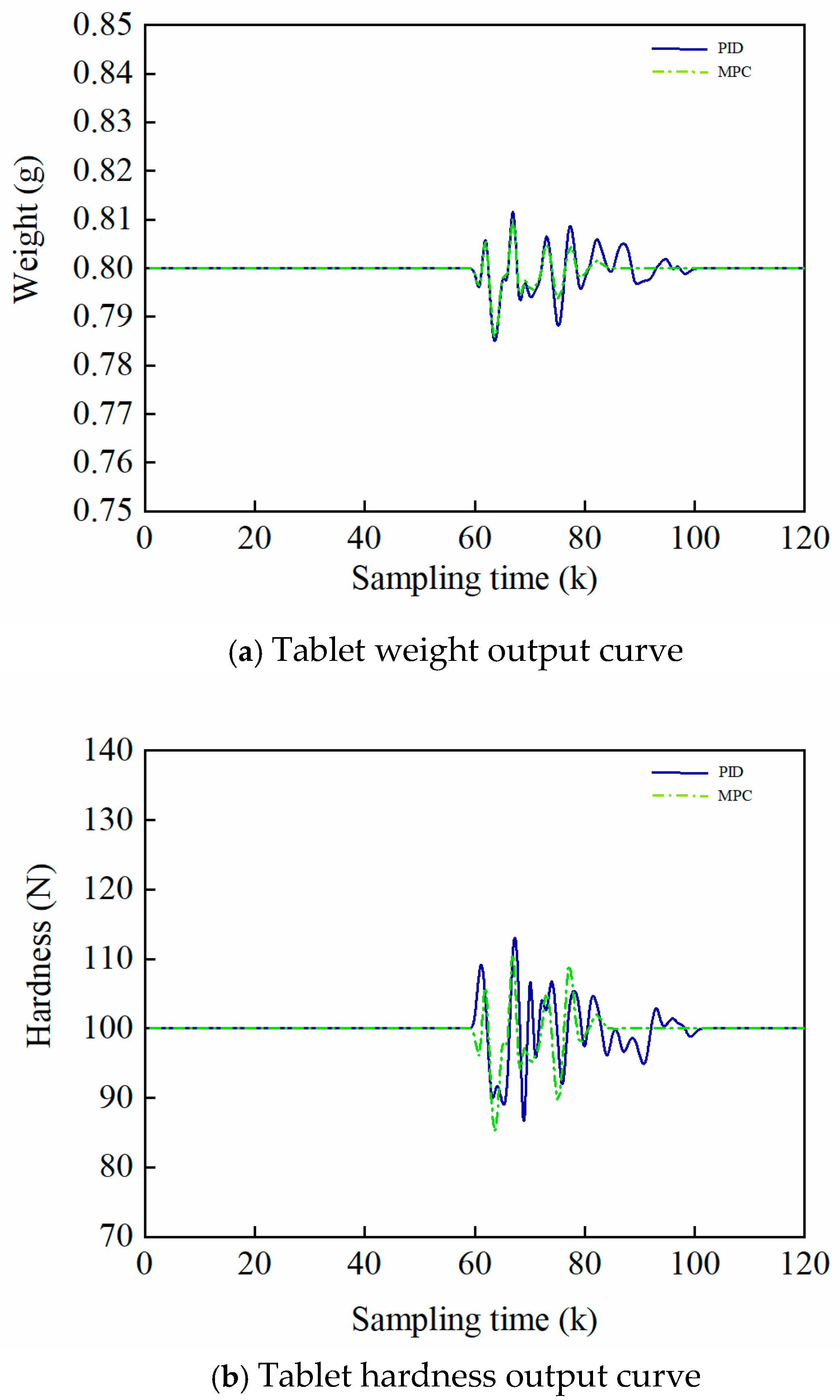
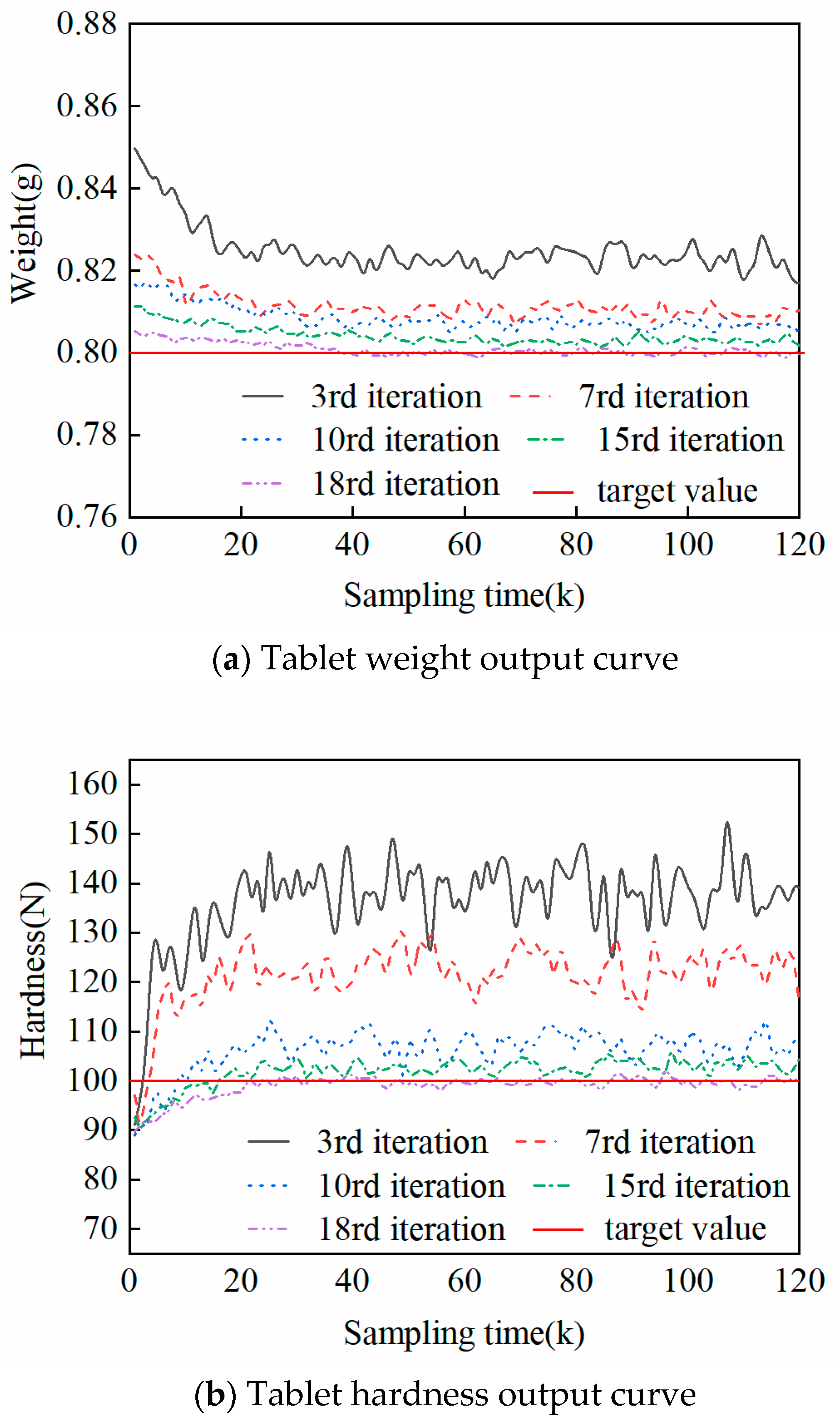
5.3. Experiments on In-Batch Control of the Tableting Process
5.4. Inter-Batch Control Experiment for Tableting Process
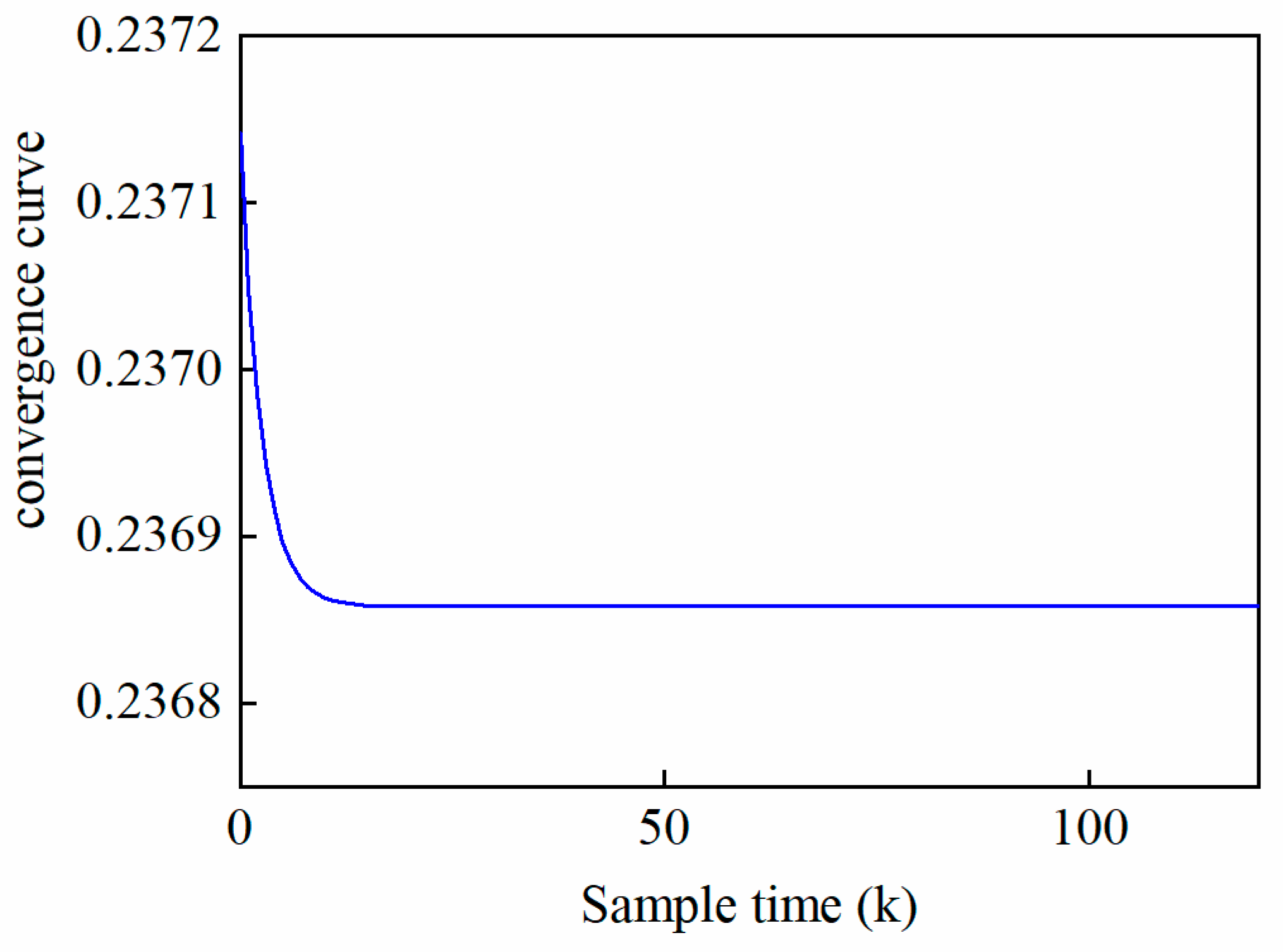
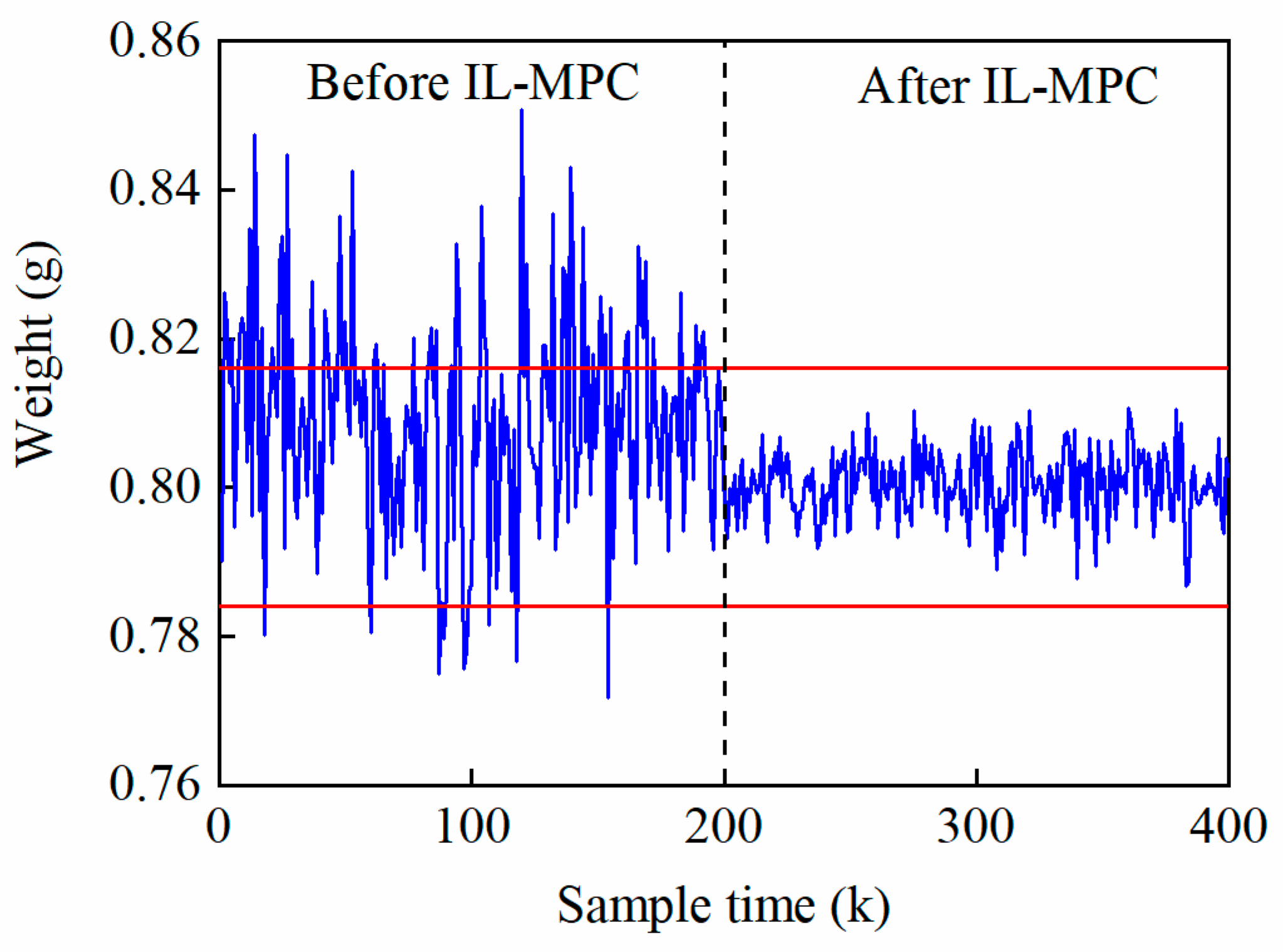
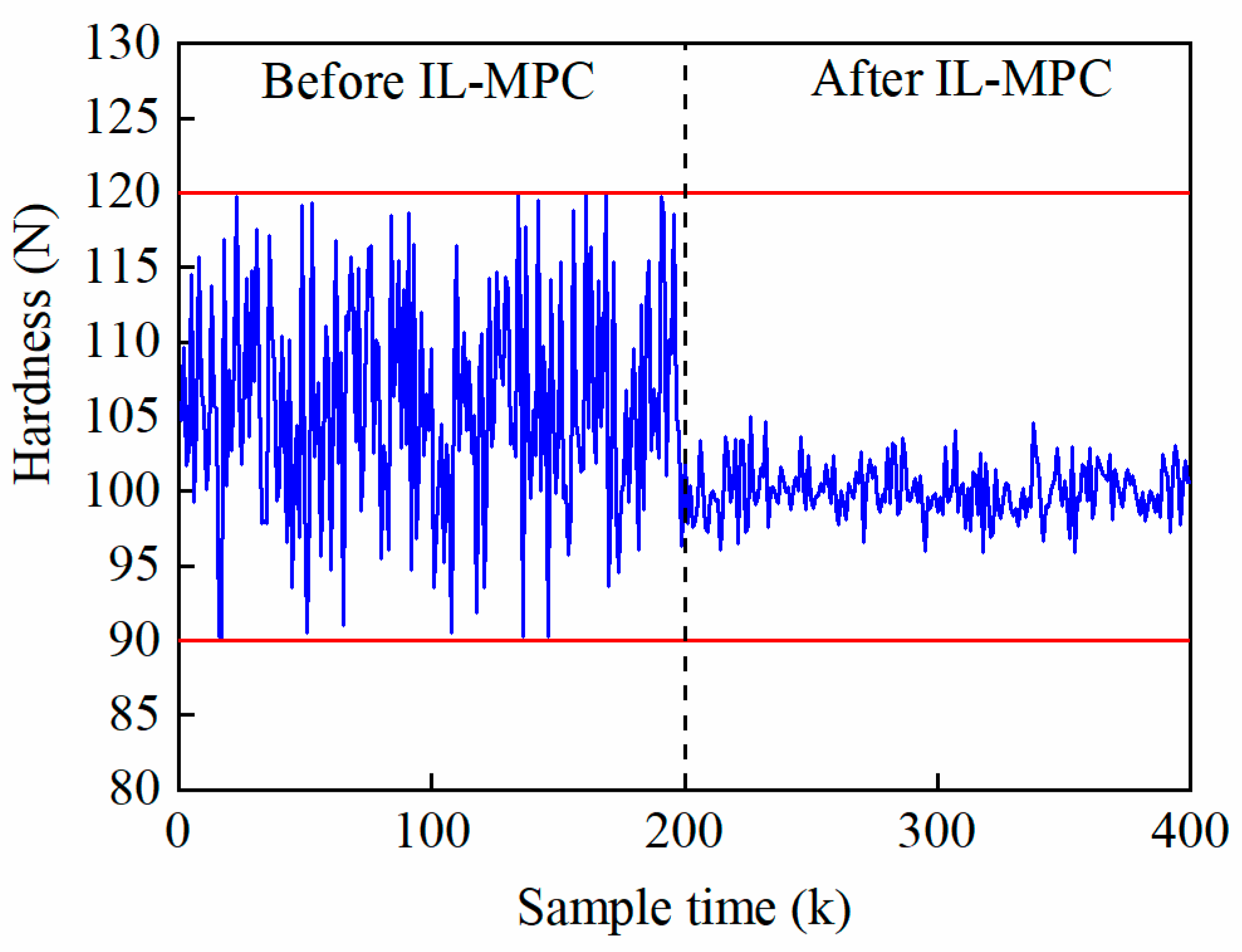
5.5. IL-MPC Model Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Xiong, H.; Li, Q.; Naeem, A.; Yang, L.; Zhu, W.; Wu, Y.; Jin, Z.; Ming, L. Advancements in the application of numerical simulation during tablet compaction. Pharmaceutics 2025, 17, 220. [Google Scholar] [CrossRef] [PubMed]
- Schomberg, A.K.; Kwade, A.; Finke, J.H. Modeling gravity filling of dies on a rotary tablet press. Powder Technol. 2023, 413, 117998. [Google Scholar] [CrossRef]
- Liu, Z.; Bruwer, M.-J.; MacGregor, J.F.; Rathore, S.S.S.; Reed, D.E.; Champagne, M.J. Modeling and Optimization of a Tablet Manufacturing Line. J. Pharm. Innov. 2011, 6, 170–180. [Google Scholar] [CrossRef]
- Destro, F.; Barolo, M. A review on the modernization of pharmaceutical development and manufacturing—Trends, perspectives, and the role of mathematical modeling. Int. J. Pharm. 2022, 620, 121715. [Google Scholar] [CrossRef]
- Singh, R.; Sahay, A.; Muzzio, F.; Ierapetritou, M.; Ramachandran, R. A systematic framework for onsite design and implementation of a control system in a continuous tablet manufacturing process. Comput. Chem. Eng. 2014, 66, 186–200. [Google Scholar] [CrossRef]
- Jelsch, M.; Roggo, Y.; Kleinebudde, P.; Krumme, M. Model predictive control in pharmaceutical continuous manufacturing: A review from a user’s perspective. Eur. J. Pharm. Biopharm. 2021, 159, 137–142. [Google Scholar] [CrossRef]
- Nașcu, I.; Diangelakis, N.A.; Muñoz, S.G.; Pistikopoulos, E.N. Advanced model predictive control strategies for evaporation processes in the pharmaceutical industries. Comput. Chem. Eng. 2023, 173, 108212. [Google Scholar] [CrossRef]
- Nașcu, I.; Diangelakis, N.A.; Pistikopoulos, E.N. Multi-parametric Model Predictive Control Strategies for Evaporation Processes in Pharmaceutical Industries. Comput. Aided Chem. Eng. 2022, 51, 1159–1164. [Google Scholar]
- Vega-Zambrano, C.; Diangelakis, N.A.; Charitopoulos, V.M. Data-driven model predictive control for continuous pharmaceutical manufacturing. Int. J. Pharm. 2025, 672, 125322. [Google Scholar] [CrossRef]
- Mesbah, A.; Paulson, J.A.; Lakerveld, R.; Braatz, R.D. Plant-wide model predictive control for a continuous pharmaceutical process. In Proceedings of the American Control Conference Chicago, Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Talavera, A.G.; Tupac, Y.J.; Vellasco, M.M.B.R. Controlling oil production in smart wells by MPC strategy with reinforcement learning. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Lima, Peru, 1–3 December 2010. [Google Scholar]
- Willersrud, A.; Imsland, L.; Hauger, S.O.; Kittilsen, P. Short-term production optimization of offshore oil and gas production using nonlinear model predictive control. J. Process Control 2011, 44, 10851–10856. [Google Scholar] [CrossRef]
- Rehrl, J.; Kruisz, J.; Sacher, S.; Khinast, J.; Horn, M. Optimized continuous pharmaceutical manufacturing via model-predictive control. Int. J. Pharm. 2016, 510, 100–115. [Google Scholar] [CrossRef] [PubMed]
- Celikovic, S.; Kirchengast, M.; Rehrl, J.; Kruisz, J.; Sacher, S.; Khinast, J.; Horn, M. Model predictive control for continuous pharmaceutical feeding blending units. Chem. Eng. Res. Des. 2020, 154, 101–114. [Google Scholar] [CrossRef]
- Haas, N.T.; Ierapetritou, M.; Singh, R. Advanced Model Predictive Feedforward/Feedback Control of a Tablet Press. J. Pharm. Innov. 2017, 12, 110–123. [Google Scholar] [CrossRef]
- Natarajan, S.; Lee, J.H. Repetitive model predictive control applied to a simulated moving bed chromatography system. Comput. Chem. Eng. 2000, 24, 1127–1133. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zhao, Z. Robust stability analysis for an enhanced ILC-based PI controller. J. Process Control 2013, 23, 201–214. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X.Z.; Chen, J. Robust PID based indirect-type iterative learning control for batch processes with time-varying uncertainties. J. Process Control 2014, 24, 95–106. [Google Scholar] [CrossRef]
- Sanzida, N.; Nagy, Z.K. Iterative learning control for the systematic design of supersaturation controlled batch cooling crystallisation processes. Comput. Chem. Eng. 2013, 59, 111–121. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, J.; Wang, X.; Xu, Y. Tracking control for batch processes through integrating batch-to-batch iterative learning control and within-batch on-line control. Ind. Eng. Chem. Res. 2005, 44, 3983–3992. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Zhang, J.; Wang, X.; Xu, Y.M. Integrated tracking control strategy for batch processes using a batch-wise linear time-varying perturbation model. IET Control Theory Appl. 2007, 1, 178–188. [Google Scholar] [CrossRef]
- Wan, Y.; Liu, D.; Ren, J.C. Iterative Learning-Based Predictive Control Method for Electronic Grade Silicon Single Crystal Batch Process. IEEE Trans. Semicond. Manuf. 2023, 36, 677–693. [Google Scholar] [CrossRef]
- Meindl, M.; Bachhuber, S.; Seel, T. Iterative Model Learning and Dual Iterative Learning Control: A Unified Framework for Data-Driven Iterative Learning Control. TechRxiv 2025, 1–10. [Google Scholar] [CrossRef]
- Karime, P.; Angela, P.S. Adaptive model predictive control for high-accuracy trajectory tracking in changing conditions. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7831–7837. [Google Scholar]
- Honti, B.; Farkas, A.; Nagy, Z.K.; Pataki, H.; Nagy, B. Explainable deep recurrent neural networks for the batch analysis of a pharmaceutical tableting process in the spirit of Pharma 4.0. Int. J. Pharm. 2024, 662, 124509. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Yu, Y.; Zhao, J.; Miao, P.; Xue, Q.; Liu, C.; Li, Z. Hyperspectral imaging combined with artificial intelligence techniques to explore the drying behavior of natural Lonicerae Japonicae Flos extracts. Measurement 2023, 218, 113246. [Google Scholar] [CrossRef]
- Eden, S.; Li, C.; Shepherd, B. Nonparametric estimation of Spearman’s rank correlation with bivariate survival data. Biometrics 2022, 78, 421–434. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Min | Median | Max | Unit | Abbreviation |
|---|---|---|---|---|---|
| Moisture Content | 2.00 | 2.59 | 4.54 | % | MC |
| Material Temperature | 16.95 | 29.84 | 63.95 | °C | MT |
| Dv(10) | 0.0087 | 10.0700 | 23.0399 | μm | Dv(10) |
| Dv(20) | 10.4702 | 26.4192 | 42.1990 | μm | Dv(20) |
| Dv(30) | 17.4036 | 38.2016 | 60.4698 | μm | Dv(30) |
| Dv(40) | 27.2277 | 49.2379 | 76.7750 | μm | Dv(40) |
| Dv(50) | 38.1602 | 59.6753 | 94.6714 | μm | Dv(50) |
| Dv(60) | 53.4553 | 72.3098 | 114.6689 | μm | Dv(60) |
| Dv(70) | 63.7003 | 88.4150 | 147.3606 | μm | Dv(70) |
| Dv(80) | 92.0202 | 120.4006 | 189.5668 | μm | Dv(80) |
| Dv(90) | 111.1426 | 153.1794 | 258.8265 | μm | Dv(90) |
| Filling set position | 5.20 | 5.92 | 6.95 | mm | FSP |
| Main compression set Position | 5.47 | 5.93 | 6.56 | mm | MCSPo |
| Production speed | 14.96 | 18.01 | 19.03 | 10000 tablets/h | PS |
| Rail Temperature | 2.540 | 34.215 | 194.610 | °C | RT |
| Average tablet weight | 0.778 | 0.802 | 0.823 | g | ATW |
| Average tablet hardness | 80.0978 | 107.376 | 119.974 | N | ATH |
| Evaluation Indicators | Formula |
|---|---|
| MSE | |
| IAE | |
| ITAE |
| Particle Size | PC1 | PC2 |
|---|---|---|
| Dv(10) | 0.252 | 0.385 |
| Dv(20) | 0.261 | 0.321 |
| Dv(30) | 0.249 | 0.156 |
| Dv(40) | 0.265 | 0.082 |
| Dv(50) | 0.258 | 0.023 |
| Dv(60) | 0.263 | −0.057 |
| Dv(70) | 0.255 | −0.183 |
| Dv(80) | 0.246 | −0.316 |
| Dv(90) | 0.269 | −0.405 |
| Iterations | 3rd Iteration | 7th Iteration | 10th Iteration | 15th Iteration | 18th Iteration | |
|---|---|---|---|---|---|---|
| MSE | Weight (g2) | 6.55698 × 10−4 | 1.4287 × 10−4 | 8.0393 × 10−5 | 2.2121 × 10−5 | 3.2448 × 10−6 |
| Hardness (N2) | 1.4331 × 103 | 508.1883 | 59.0167 | 13.1855 | 6.1626 | |
| IAE | Weight (g) | 3.0105 | 1.3826 | 1.0211 | 0.5007 | 0.1593 |
| Hardness (N) | 4.4397 × 103 | 2.6338 × 103 | 850.7811 | 373.9173 | 184.2277 | |
| ITAE | Weight (g∙s) | 170.1868 | 75.8181 | 53.6621 | 23.6157 | 6.1641 |
| Hardness (N∙s) | 2.8363 × 105 | 1.6811 × 105 | 5.3681 × 104 | 2.2641 × 104 | 6.7289 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Zhong, Z.; Deng, P.; Fei, Y.; Cui, P.; Zhu, W.; Xiao, Z.; Wang, T.; Li, L. Adaptive Closed-Loop Control System for the Optimization of Tablet Manufacturing Processes. Pharmaceutics 2025, 17, 1510. https://doi.org/10.3390/pharmaceutics17121510
Luo X, Zhong Z, Deng P, Fei Y, Cui P, Zhu W, Xiao Z, Wang T, Li L. Adaptive Closed-Loop Control System for the Optimization of Tablet Manufacturing Processes. Pharmaceutics. 2025; 17(12):1510. https://doi.org/10.3390/pharmaceutics17121510
Chicago/Turabian StyleLuo, Xiaorong, Zhijian Zhong, Pan Deng, Yicheng Fei, Pengdi Cui, Weifeng Zhu, Zhiqiang Xiao, Ting Wang, and Liying Li. 2025. "Adaptive Closed-Loop Control System for the Optimization of Tablet Manufacturing Processes" Pharmaceutics 17, no. 12: 1510. https://doi.org/10.3390/pharmaceutics17121510
APA StyleLuo, X., Zhong, Z., Deng, P., Fei, Y., Cui, P., Zhu, W., Xiao, Z., Wang, T., & Li, L. (2025). Adaptive Closed-Loop Control System for the Optimization of Tablet Manufacturing Processes. Pharmaceutics, 17(12), 1510. https://doi.org/10.3390/pharmaceutics17121510






