Quantitative Analysis of Photothermal Therapy of Tumor Tissue Using Various Gold Nanoparticle Injection Schemes
Abstract
1. Introduction
2. Material Properties and Numerical Methods
2.1. Optical Properties of Gold Nanoparticles and Biological Tissues
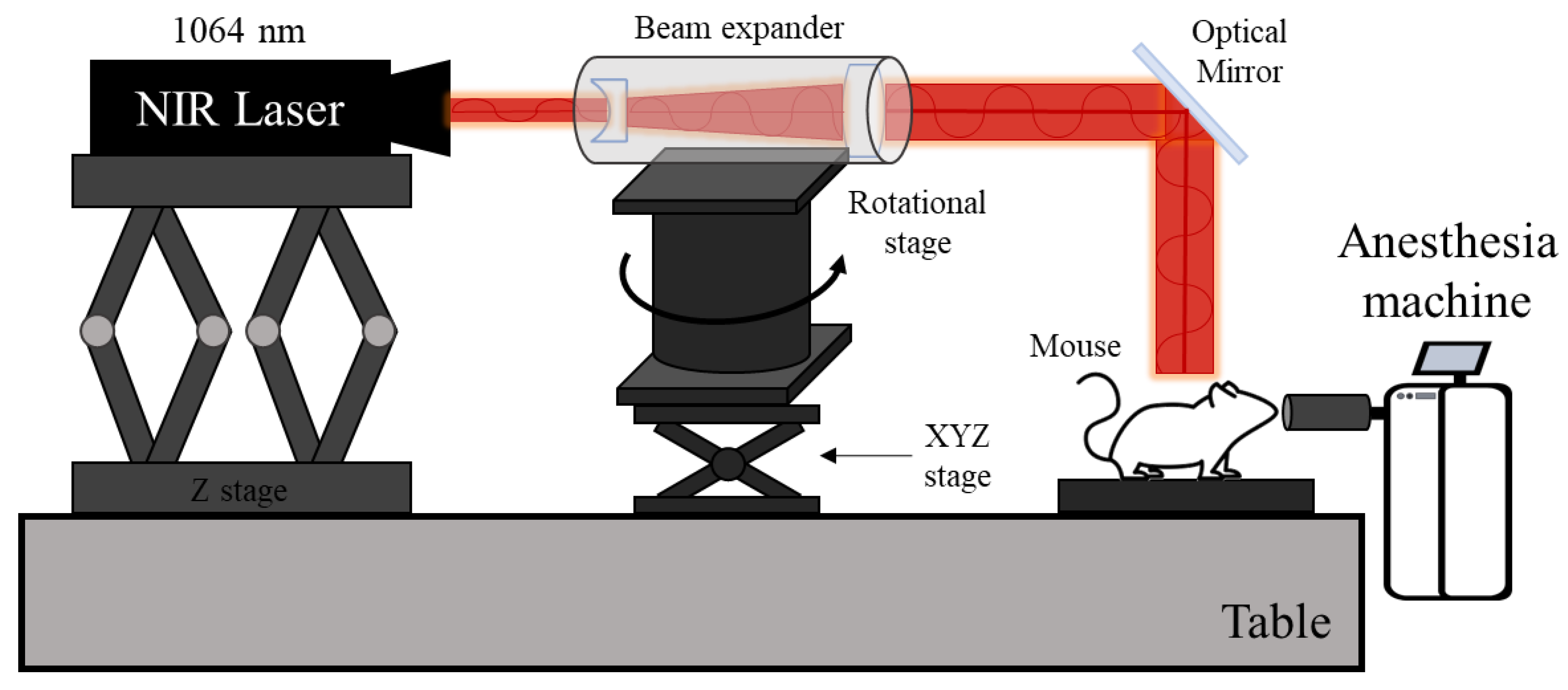
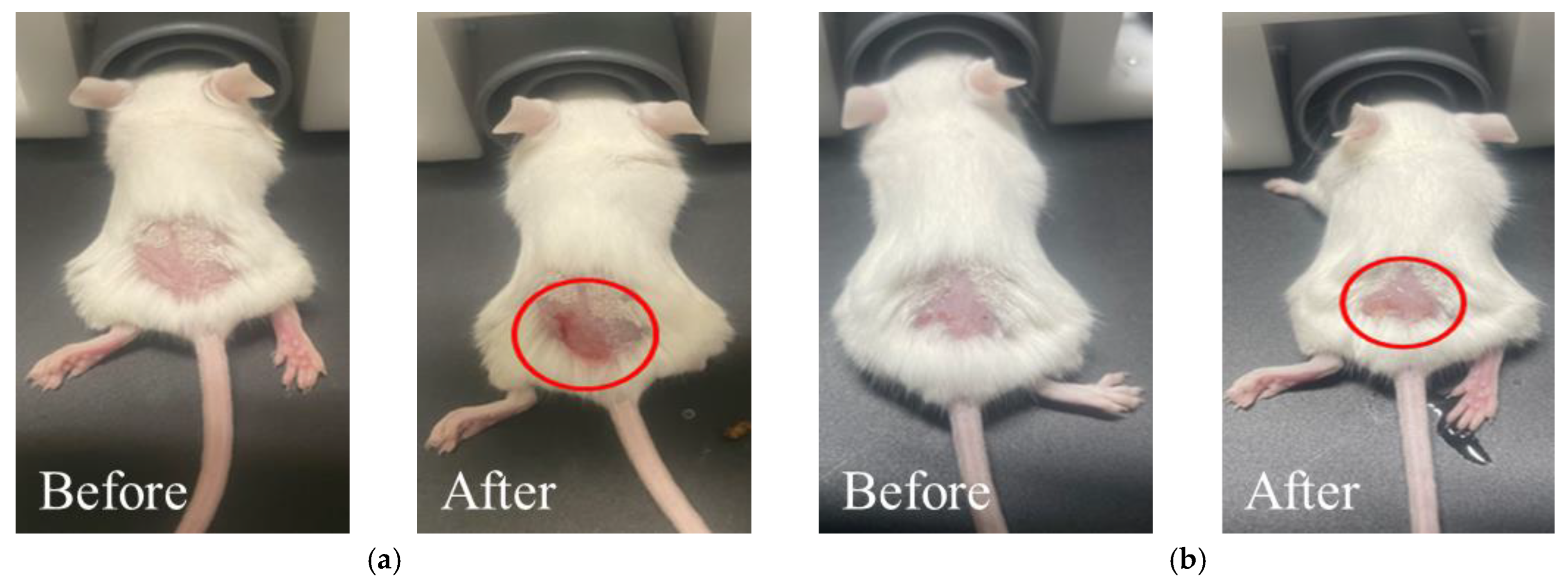
2.2. Validation of Numerical Process
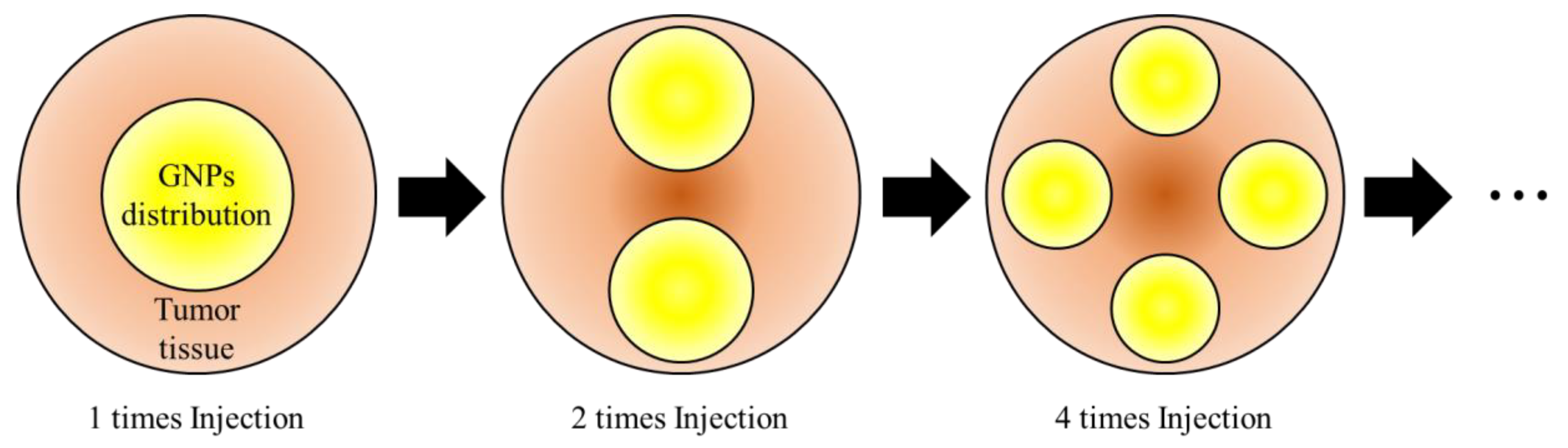
2.3. Numerical Investigation
3. Results and Discussion
3.1. Temperature Distribution of Biological Tissues
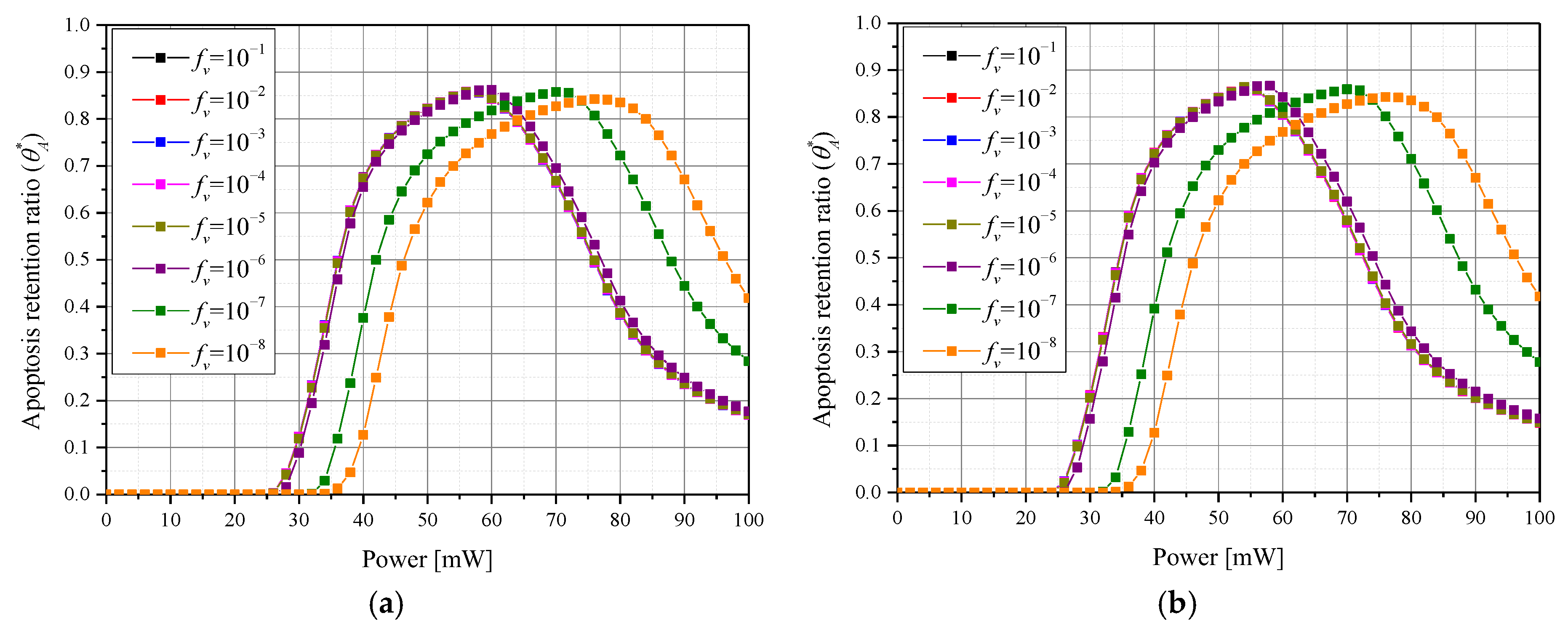
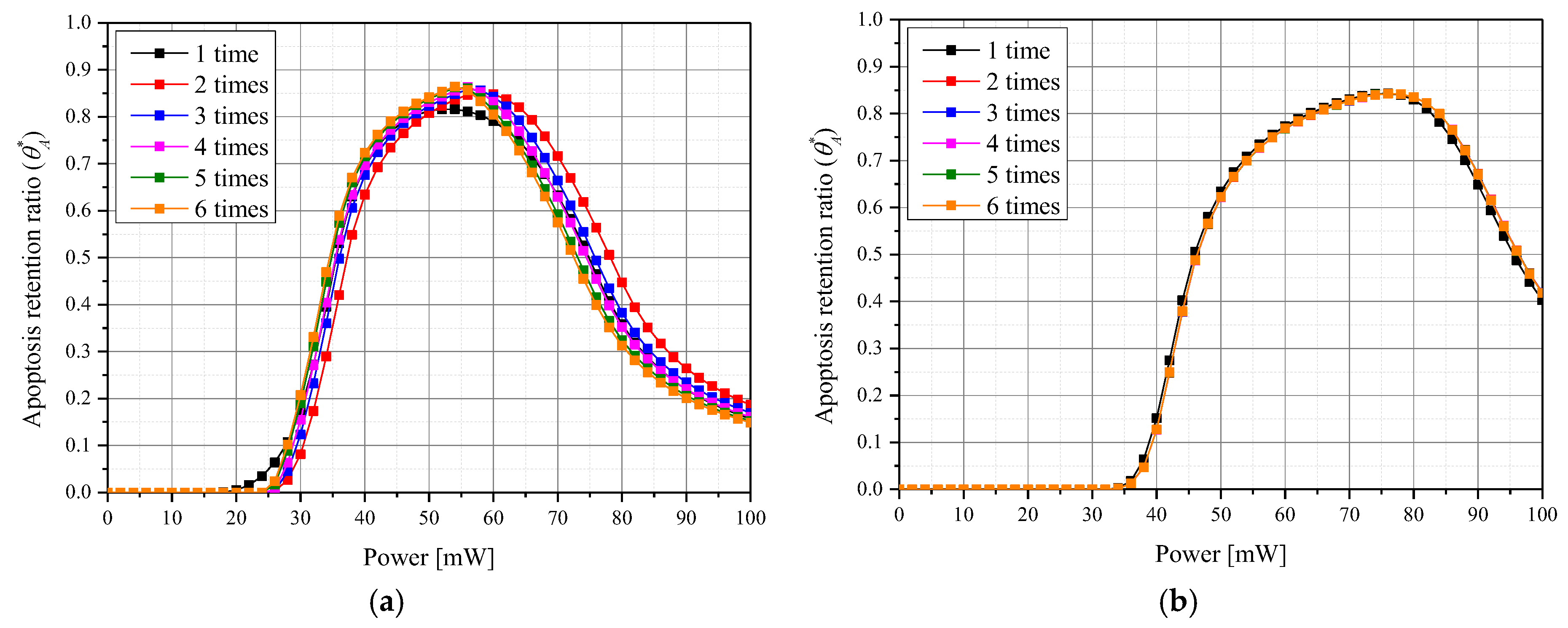
3.2. Apoptosis Occurrence Amount in Tumor Tissue
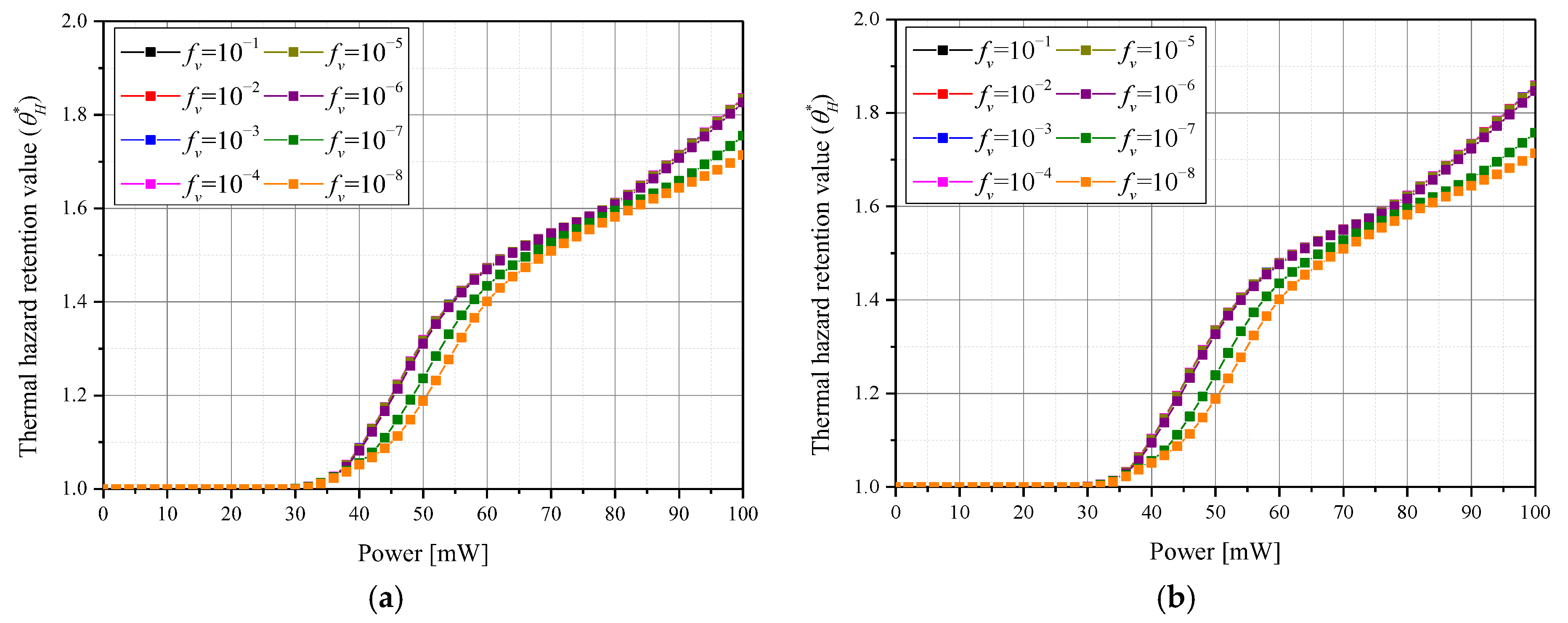
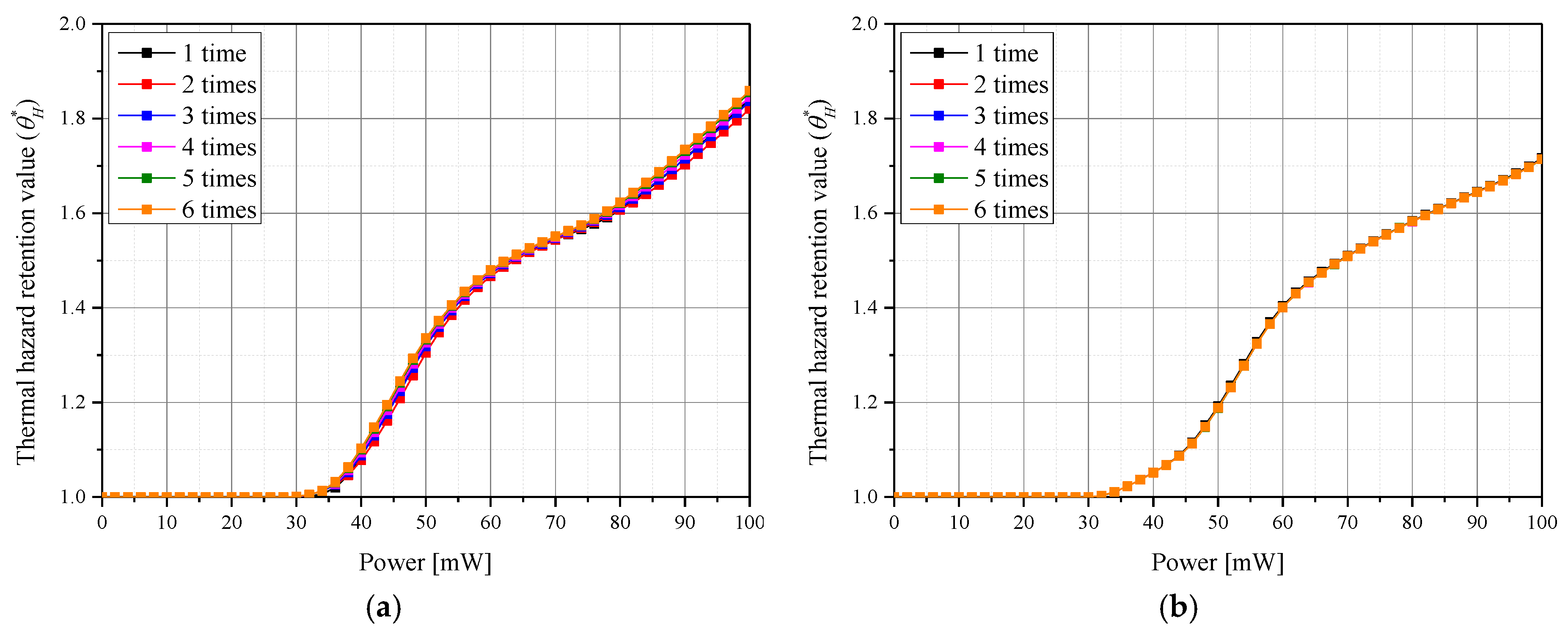
3.3. Thermal Damage of Surrounding Normal Tissues
3.4. Quantitative Analysis of Photothermal Therapy Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| C | ) |
| cv | ) |
| E | Electric field () |
| fv | Volume fraction of GNPs |
| F | ) |
| g | Anisotropy factor |
| k | ) |
| km | ) |
| P | Polarization vector () |
| Pl | Intensity of laser (W) |
| Q | Dimensionless efficiency factor |
| r | Position vector |
| reff | Effective radius of nanoparticle (m) |
| t | Thickness (m) |
| T | Temperature (K) |
| Greek symbols | |
| ) | |
| Apoptosis retention ratio | |
| Effective apoptosis retention ratio | |
| Thermal hazard retention value | |
| Absorption coefficient (1/m) | |
| Scattering coefficient (1/m) | |
| ) | |
| Time (s) | |
| Subscripts | |
| abs | Absorption |
| m | Medium |
| np | Nanoparticle |
| sca | Scattering |
| x, y, z | Notation of direction |
| Superscripts | |
| + | Next element |
| − | Previous element |
References
- Almond, D.P.; Patel, P.; Patel, P. Photothermal Science and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Huang, X.; El-Sayed, I.H.; Qian, W.; El-Sayed, M.A. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J. Am. Chem. Soc. 2006, 128, 2115–2120. [Google Scholar] [CrossRef]
- Liu, Y.; Bhattarai, P.; Dai, Z.; Chen, X. Photothermal therapy and photoacoustic imaging via nanotheranostics in fighting cancer. Chem. Soc. Rev. 2019, 48, 2053–2108. [Google Scholar] [CrossRef]
- Abbas, M.; Zou, Q.; Li, S.; Yan, X. Self-assembled peptide-and protein-based nanomaterials for antitumor photodynamic and photothermal therapy. Adv. Mater. 2017, 29, 1605021. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.; Serpell, J. Wound infection after abdominal incision with scalpel or diathermy. Scalpel 1990, 130, 18–95. [Google Scholar] [CrossRef]
- Verrier, E.D.; Bossart, K.J.; Heer, F.W. Reduction of infection rates in abdominal incisions by delayed wound closure techniques. Am. J. Surg. 1979, 138, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.S.; Kong, W.H.; Sung, D.K.; Lee, M.-Y.; Beack, S.E.; Keum, D.H.; Kim, K.S.; Yun, S.H.; Hahn, S.K. Nanographene oxide–hyaluronic acid conjugate for photothermal ablation therapy of skin cancer. ACS Nano 2014, 8, 260–268. [Google Scholar] [CrossRef]
- Abo-Elfadl, M.T.; Gamal-Eldeen, A.M.; Elshafey, M.M.; Abdalla, G.M.; Ali, S.S.; Ali, M.R.; Zawrah, M.F. Photothermal therapeutic effect of PEGylated gold nano-semicubes in chemically-induced skin cancer in mice. J. Photochem. Photobiol. B Biol. 2016, 164, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, F.; Jaafar, M. Comparison of wavelength-dependent penetration depths of lasers in different types of skin in photodynamic therapy. Indian J. Phys. 2013, 87, 203–209. [Google Scholar] [CrossRef]
- Ash, C.; Dubec, M.; Donne, K.; Bashford, T. Effect of wavelength and beam width on penetration in light-tissue interaction using computational methods. Lasers Med. Sci. 2017, 32, 1909–1918. [Google Scholar] [CrossRef]
- Salomatina, E.V.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.; Chen, Y.; Liu, L.; Mo, A.; Peng, Q. Nanomaterials-based photothermal therapy and its potentials in antibacterial treatment. J. Control. Release 2020, 328, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.S.; Verwilst, P.; Sharma, A.; Shin, J.; Sessler, J.L.; Kim, J.S. Organic molecule-based photothermal agents: An expanding photothermal therapy universe. Chem. Soc. Rev. 2018, 47, 2280–2297. [Google Scholar] [CrossRef]
- Song, X.; Chen, Q.; Liu, Z. Recent advances in the development of organic photothermal nano-agents. Nano Res. 2015, 8, 340–354. [Google Scholar] [CrossRef]
- Hutter, E.; Fendler, J.H. Exploitation of localized surface plasmon resonance. Adv. Mater. 2004, 16, 1685–1706. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef]
- El-Sayed, I.H.; Huang, X.; El-Sayed, M.A. Selective laser photo-thermal therapy of epithelial carcinoma using anti-EGFR antibody conjugated gold nanoparticles. Cancer Lett. 2006, 239, 129–135. [Google Scholar] [CrossRef]
- Huang, X.; El-Sayed, M.A. Gold nanoparticles: Optical properties and implementations in cancer diagnosis and photothermal therapy. J. Adv. Res. 2010, 1, 13–28. [Google Scholar] [CrossRef]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Determination of the minimum temperature required for selective photothermal destruction of cancer cells with the use of immunotargeted gold nanoparticles. Photochem. Photobiol. 2006, 82, 412–417. [Google Scholar] [CrossRef] [PubMed]
- Hawes, M.C.; Wheeler, H. Factors affecting victorin-induced root cap cell death: Temperature and plasmolysist. Physiol. Plant Pathol. 1982, 20, 137–144. [Google Scholar] [CrossRef]
- Kerr, J.F.; Wyllie, A.H.; Currie, A.R. Apoptosis: A basic biological phenomenon with wideranging implications in tissue kinetics. Br. J. Cancer 1972, 26, 239–257. [Google Scholar] [CrossRef]
- Wyllie, A.H. Cell death. Cytol. Cell Physiol. 1987, 361, 755–785. [Google Scholar]
- Muzzi, B.; Albino, M.; Gabbani, A.; Omelyanchik, A.; Kozenkova, E.; Petrecca, M.; Innocenti, C.; Balica, E.; Lavacchi, A.; Scavone, F. Star-Shaped Magnetic-Plasmonic Au@ Fe3O4 Nano-Heterostructures for Photothermal Therapy. ACS Appl. Mater. Interfaces 2022, 14, 29087–29098. [Google Scholar] [CrossRef]
- Bi, X.; Bai, Q.; Liang, M.; Yang, D.; Li, S.; Wang, L.; Liu, J.; Yu, W.W.; Sui, N.; Zhu, Z. Silver peroxide nanoparticles for combined antibacterial sonodynamic and photothermal therapy. Small 2022, 18, 2104160. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-L.; Qi, H.; Ren, Y.-T.; Chen, Q.; Ruan, L.-M. Optimal temperature control of tissue embedded with gold nanoparticles for enhanced thermal therapy based on two-energy equation model. J. Therm. Biol. 2018, 74, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Ren, Y.; Li, H.; Qi, H. Characteristic analysis of light and heat transfer in photothermal therapy using multiple-light-source heating strategy. Int. J. Therm. Sci. 2020, 158, 106533. [Google Scholar] [CrossRef]
- Guglielmelli, A.; Rosa, P.; Contardi, M.; Prato, M.; Mangino, G.; Miglietta, S.; Petrozza, V.; Pani, R.; Calogero, A.; Athanassiou, A.; et al. Biomimetic keratin gold nanoparticle-mediated in vitro photothermal therapy on glioblastoma multiforme. Nanomedicine 2020, 16, 121–138. [Google Scholar] [CrossRef]
- Annesi, F.; Pane, A.; Losso, M.A.; Guglielmelli, A.; Lucente, F.; Petronella, F.; Placido, T.; Comparelli, R.; Guzzo, M.G.; Curri, M.L.; et al. Thermo-plasmonic killing of Escherichia coli TG1 bacteria. Materials 2019, 12, 1530. [Google Scholar] [CrossRef]
- Candreva, A.; De Rose, R.; Perrotta, I.D.; Guglielmelli, A.; La Deda, M. Light-Induced Clusterization of Gold Nanoparticles: A New Photo-Triggered Antibacterial against E. coli Proliferation. Nanomaterials 2023, 13, 746. [Google Scholar] [CrossRef] [PubMed]
- Terentyuk, G.S.; Maslyakova, G.N.; Suleymanova, L.V.; Khlebtsov, B.N.; Kogan, B.Y.; Akchurin, G.G.; Shantrocha, A.V.; Maksimova, I.L.; Khlebtsov, N.G.; Tuchin, V.V. Circulation and distribution of gold nanoparticles and induced alterations of tissue morphology at intravenous particle delivery. J. Biophotonics 2009, 2, 292–302. [Google Scholar] [CrossRef]
- Ko, W.-K.; Lee, S.J.; Kim, S.J.; Han, G.H.; Han, I.-b.; Hong, J.B.; Sheen, S.H.; Sohn, S. Direct injection of hydrogels embedding gold nanoparticles for local therapy after spinal cord injury. Biomacromolecules 2021, 22, 2887–2901. [Google Scholar] [CrossRef] [PubMed]
- Dimitriou, N.M.; Tsekenis, G.; Balanikas, E.C.; Pavlopoulou, A.; Mitsiogianni, M.; Mantso, T.; Pashos, G.; Boudouvis, A.G.; Lykakis, L.N.; Tsigaridas, G.; et al. Gold nanoparticles, radiations and the immune system: Current insights into the physical mechanisms and the biological interactions of this new alliance towards cancer therapy. Pharmacol. Ther. 2017, 178, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, H. Induction of apoptotic temperature in photothermal therapy under various heating conditions in multi-layered skin structure. Int. J. Mol. Sci. 2021, 22, 11091. [Google Scholar] [CrossRef] [PubMed]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for scattering calculations. Josa A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for periodic targets: Theory and tests. Josa A 2008, 25, 2693–2703. [Google Scholar] [CrossRef]
- Mie, G. Contributions to the optics of turbid media, particularly of colloidal metal solutions. Contrib. Opt. Turbid. Media 1976, 25, 377–445. [Google Scholar]
- Dombrovsky, L.A.; Timchenko, V.; Jackson, M.; Yeoh, G.H. A combined transient thermal model for laser hyperthermia of tumors with embedded gold nanoshells. Int. J. Heat Mass Transf. 2011, 54, 5459–5469. [Google Scholar] [CrossRef]
- Vera, J.; Bayazitoglu, Y. Gold nanoshell density variation with laser power for induced hyperthermia. Int. J. Heat Mass Transf. 2009, 52, 564–573. [Google Scholar] [CrossRef]
- Vähätupa, M.; Pemmari, T.; Junttila, I.; Pesu, M.; Järvinen, T.A. Chemical-induced skin carcinogenesis model using dimethylbenz [a] anthracene and 12-o-tetradecanoyl phorbol-13-acetate (DMBA-TPA). J. Vis. Exp. 2019, 154, e60445. [Google Scholar] [CrossRef] [PubMed]
- Stoll, A.M.; Chianta, M.A. Heat transfer through fabrics as related to thermal injury. Trans. N. Y. Acad. Sci. 1971, 33, 649–670. [Google Scholar] [CrossRef]
- Leach, E.; Peters, R.; Rossiter, R. Experimental thermal burns, especially the moderate temperature burn. Q. J. Exp. Physiol. Cogn. Med. Sci. Transl. Integr. 1943, 32, 67–86. [Google Scholar] [CrossRef]
- Mi, Y.; Yao, C.; Li, C.; Sun, C.; Tang, J.; Yang, F.; Wen, Y. Caspase-3 activation by exponential decay nanosecond pulsed electric fields on tumor-bearing BALB/c nude mice in vivo. IEEE Trans. Plasma Sci. 2010, 38, 1963–1971. [Google Scholar]
- Krainov, A.; Mokeeva, A.; Sergeeva, E.; Agrba, P.; Kirillin, M.Y. Optical properties of mouse biotissues and their optical phantoms. Opt. Spectrosc. 2013, 115, 193–200. [Google Scholar] [CrossRef]
- Gananathan, P.; Rao, A.P.; Singaravelu, G.; Manickam, E. Review of laser in nanophotonics–a literature study for cellular mechanism. J. Cancer Biol. Res. 2017, 5, 1094. [Google Scholar]
- Çetingül, M.P.; Herman, C. A heat transfer model of skin tissue for the detection of lesions: Sensitivity analysis. Phys. Med. Biol. 2010, 55, 5933. [Google Scholar] [CrossRef] [PubMed]
- Çetingül, M.P.; Herman, C. Quantification of the thermal signature of a melanoma lesion. Int. J. Therm. Sci. 2011, 50, 421–431. [Google Scholar] [CrossRef]
- Holmer, C.; Lehmann, K.-S.; Wanken, J.; Reissfelder, C.; Roggan, A.; Müller, G.J.; Buhr, H.-J.; Ritz, J.-P. Optical properties of adenocarcinoma and squamous cell carcinoma of the gastroesophageal junction. J. Biomed. Opt. 2007, 12, 014025. [Google Scholar] [CrossRef]
- Jiang, S.; Ma, N.; Li, H.; Zhang, X. Effects of thermal properties and geometrical dimensions on skin burn injuries. Burns 2002, 28, 713–717. [Google Scholar] [CrossRef] [PubMed]
- Prasad, B.; Kim, S.; Cho, W.; Kim, S.; Kim, J.K. Effect of tumor properties on energy absorption, temperature mapping, and thermal dose in 13.56-MHz radiofrequency hyperthermia. J. Therm. Biol. 2018, 74, 281–289. [Google Scholar] [CrossRef]
- Torvi, D.; Dale, J. A finite element model of skin subjected to a flash fire. J. Biomech. Eng. 1994, 116, 250–255. [Google Scholar] [CrossRef]
- Wilson, S.B.; Spence, V.A. A tissue heat transfer model for relating dynamic skin temperature changes to physiological parameters. Phys. Med. Biol. 1988, 33, 895. [Google Scholar] [CrossRef]
- Kim, D.; Kim, H. Numerical Study on Death of Squamous Cell Carcinoma Based on Various Shapes of Gold Nanoparticles Using Photothermal Therapy. Sensors 2022, 22, 1671. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Marti, D.; Aasbjerg, R.N.; Andersen, P.E.; Hansen, A.K. MCmatlab: An open-source, user-friendly, MATLAB-integrated three-dimensional Monte Carlo light transport solver with heat diffusion and tissue damage. J. Biomed. Opt. 2018, 23, 121622. [Google Scholar] [CrossRef] [PubMed]




| Thermal conductivity km (W/mK) | 0.34 |
| (kg/m3) | 1000 |
| Specific heat cv (J/kgK) | 3000 |
| (1/mm) | 6.1 |
| (1/mm) | 40.65 |
| Anisotropy factor g | 0.8 |
(mm) | km (W/mK) | (kg/m3) | cv (J/kgK) | (1/mm) | (1/mm) | ||
|---|---|---|---|---|---|---|---|
| Epidermis | 0.08 | 0.235 | 1200 | 3589 | 0.8 | 0.4 | 45 |
| Papillary dermis | 0.5 | 0.445 | 1200 | 3300 | 0.9 | 0.38 | 30 |
| Reticular dermis | 0.6 | 0.445 | 1200 | 3300 | 0.8 | 0.48 | 25 |
| Subcutaneous fat | 18.82 | 0.19 | 1000 | 2500 | 0.75 | 0.43 | 5 |
| Tumor | 2 | 0.495 | 1070 | 3421 | 0.8 | 0.047 | 0.883 |
| Parameter | Case | Number | Remarks |
|---|---|---|---|
| Laser power (Pl) | 0 to 100 mW | 51 | Intv: 2 mW |
| Volume fraction of GNPs (fv) | 10−1 to 10−8 | 8 | Intv: 10−1 |
| Number of injected GNPs | 1 to 6 | 6 | Intv: 1 |
| fv | 10−1 | 10−2 | 10−3 | 10−4 | 10−5 | 10−6 | 10−7 | 10−8 |
|---|---|---|---|---|---|---|---|---|
| (cm−1) | 5,016,309.16 | 501,631.34 | 50,163.55 | 5016.78 | 502.10 | 50.63 | 5.48 | 0.97 |
| (cm−1) | 1,059,239.60 | 105,931.91 | 10,601.14 | 1068.06 | 114.75 | 19.42 | 9.89 | 8.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Kim, H. Quantitative Analysis of Photothermal Therapy of Tumor Tissue Using Various Gold Nanoparticle Injection Schemes. Pharmaceutics 2023, 15, 911. https://doi.org/10.3390/pharmaceutics15030911
Kim D, Kim H. Quantitative Analysis of Photothermal Therapy of Tumor Tissue Using Various Gold Nanoparticle Injection Schemes. Pharmaceutics. 2023; 15(3):911. https://doi.org/10.3390/pharmaceutics15030911
Chicago/Turabian StyleKim, Donghyuk, and Hyunjung Kim. 2023. "Quantitative Analysis of Photothermal Therapy of Tumor Tissue Using Various Gold Nanoparticle Injection Schemes" Pharmaceutics 15, no. 3: 911. https://doi.org/10.3390/pharmaceutics15030911
APA StyleKim, D., & Kim, H. (2023). Quantitative Analysis of Photothermal Therapy of Tumor Tissue Using Various Gold Nanoparticle Injection Schemes. Pharmaceutics, 15(3), 911. https://doi.org/10.3390/pharmaceutics15030911






