Effect of Copolymer Properties on the Phase Behavior of Ibuprofen–PLA/PLGA Mixtures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Methods
2.2.1. Differential Scanning Calorimetry
2.2.2. Calorimetric Determination of SLE Curve and Mapping of LLE Region
2.3. Modeling Approaches
2.3.1. Modeling of Glass-Transition Temperature
2.3.2. SLE and LLE Modeling Using PC-SAFT EOS
3. Results
3.1. Physicochemical Properties of Pure Components
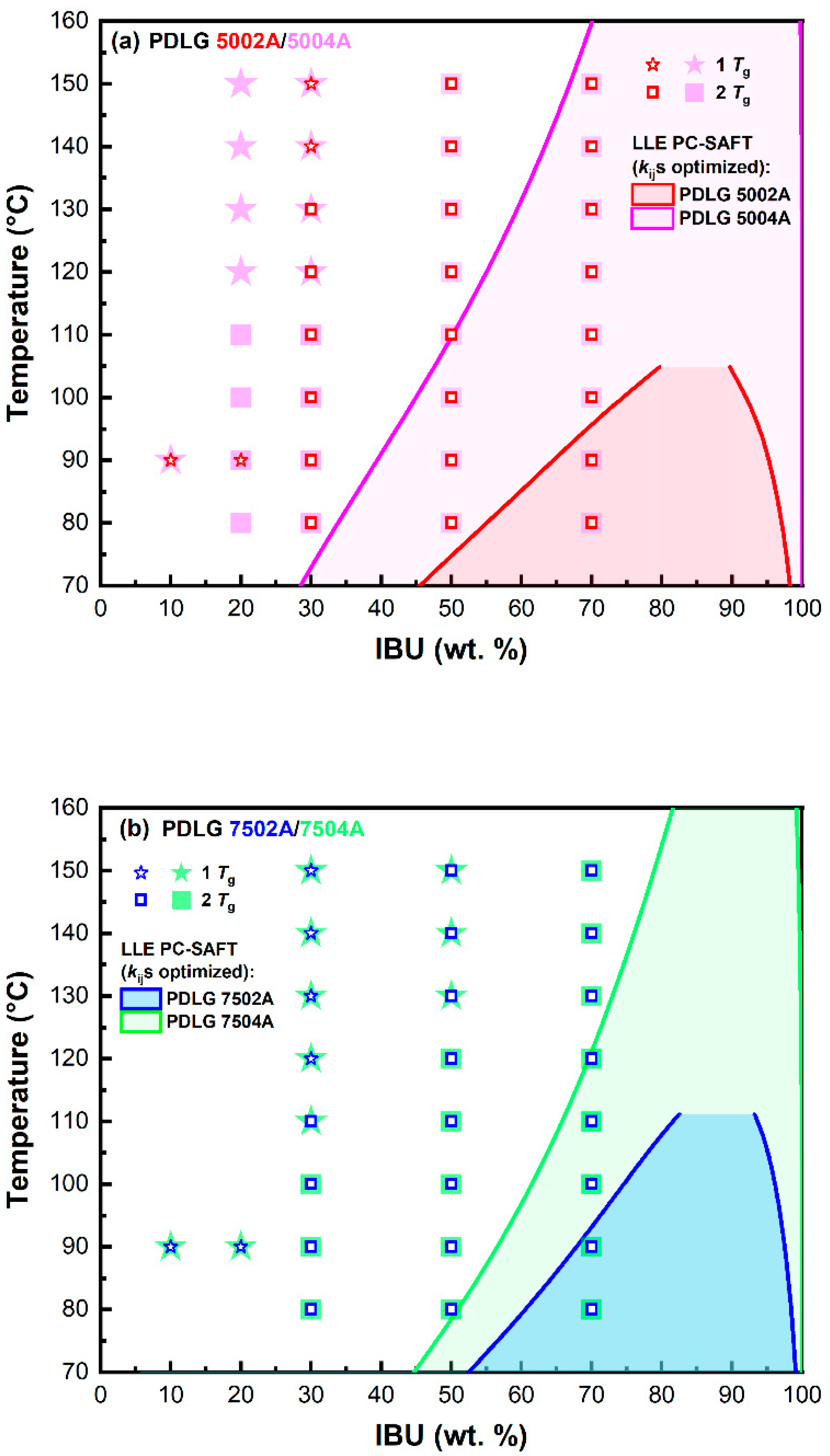
3.2. IBU–PLA/PLGA Phase Diagrams
3.3. Miscibility of IBU with PLA/PLGA Polymers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savjani, K.T.; Gajjar, A.K.; Savjani, J.K. Drug Solubility: Importance and Enhancement Techniques. ISRN Pharm. 2012, 2012, 195727. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Ho, C. Amorphous Solid Dispersions: Utilization and Challenges in Drug Discovery and Development. J. Pharm. Sci. 2015, 104, 3237–3258. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.U.; Minhas, M.U.; Badshah, S.F.; Suhail, M.; Ahmad, A.; Ijaz, S. Overview of nanoparticulate strategies for solubility enhancement of poorly soluble drugs. Life Sci. 2022, 291, 120301. [Google Scholar] [CrossRef] [PubMed]
- Makadia, H.K.; Siegel, S.J. Poly Lactic-co-Glycolic Acid (PLGA) as Biodegradable Controlled Drug Delivery Carrier. Polymers 2011, 3, 1377–1397. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Qu, W.; Choi, S.H. FDA’s Regulatory Science Program for Generic PLA/PLGA-Based Drug Products. Am. Pharm. Rev. 2016, 20. Available online: https://www.americanpharmaceuticalreview.com/Featured-Articles/188841-FDA-s-Regulatory-Science-Program-for-Generic-PLA-PLGA-Based-Drug-Products/ (accessed on 19 December 2022).
- Erbetta, C. Synthesis and Characterization of Poly(D,L-Lactide-co-Glycolide) Copolymer. J. Biomater. Nanobiotechnol. 2012, 3, 208–225. [Google Scholar] [CrossRef]
- Nieto, K.; Mallery, S.; Schwendeman, S. Microencapsulation of Amorphous Solid Dispersions of Fenretinide Enhances Drug Solubility and Release from PLGA in vitro and in vivo. Int. J. Pharm. 2020, 586, 119475. [Google Scholar] [CrossRef]
- Bohr, A.; Kristensen, J.; Stride, E.; Dyas, M.; Edirisinghe, M. Preparation of microspheres containing low solubility drug compound by electrohydrodynamic spraying. Int. J. Pharm. 2011, 412, 59–67. [Google Scholar] [CrossRef]
- Bala, I.; Hariharan, S.; Kumar, M.N.V.R. PLGA Nanoparticles in Drug Delivery: The State of the Art. Crit. Rev. Ther. Drug Carr. Syst. 2004, 21, 387–422. [Google Scholar] [CrossRef] [PubMed]
- Panyam, J.; Williams, D.; Dash, A.; Leslie-Pelecky, D.; Labhasetwar, V. Solid-state solubility influences encapsulation and release of hydrophobic drugs from PLGA/PLA nanoparticles. J. Pharm. Sci. 2004, 93, 1804–1814. [Google Scholar] [CrossRef] [PubMed]
- Blasi, P. Poly(lactic acid)/poly(lactic-co-glycolic acid)-based microparticles: An overview. J. Pharm. Investig. 2019, 49, 337–346. [Google Scholar] [CrossRef]
- Zumaya, A.L.V.; Ulbrich, P.; Vilčáková, J.; Dendisová, M.; Fulem, M.; Šoóš, M.; Hassouna, F. Comparison between two multicomponent drug delivery systems based on PEGylated-poly (l-lactide-co-glycolide) and superparamagnetic nanoparticles: Nanoparticulate versus nanocluster systems. J. Drug Deliv. Sci. Technol. 2021, 64, 102643. [Google Scholar] [CrossRef]
- Zumaya, A.L.V.; Martynek, D.; Bautkinová, T.; Šoóš, M.; Ulbrich, P.; Raquez, J.-M.; Dendisová, M.; Merna, J.; Vilčáková, J.; Kopecký, D.; et al. Self-assembly of poly(L-lactide-co-glycolide) and magnetic nanoparticles into nanoclusters for controlled drug delivery. Eur. Polym. J. 2020, 133, 109795. [Google Scholar] [CrossRef]
- Iemtsev, A.; Hassouna, F.; Klajmon, M.; Mathers, A.; Fulem, M. Compatibility of selected active pharmaceutical ingredients with poly(D, L-lactide-co-glycolide): Computational and experimental study. Eur. J. Pharm. Biopharm. 2022, 179, 232–245. [Google Scholar] [CrossRef]
- Mahieu, A.; Willart, J.-F.; Dudognon, E.; Danède, F.; Descamps, M. A New Protocol To Determine the Solubility of Drugs into Polymer Matrixes. Mol. Pharm. 2013, 10, 560–566. [Google Scholar] [CrossRef]
- Marsac, P.J.; Shamblin, S.L.; Taylor, L.S. Theoretical and Practical Approaches for Prediction of Drug–Polymer Miscibility and Solubility. Pharm. Res. 2006, 23, 2417. [Google Scholar] [CrossRef]
- Sun, Y.; Tao, J.; Zhang, G.G.Z.; Yu, L. Solubilities of Crystalline Drugs in Polymers: An Improved Analytical Method and Comparison of Solubilities of Indomethacin and Nifedipine in PVP, PVP/VA, and PVAc. J. Pharm. Sci. 2010, 99, 4023–4031. [Google Scholar] [CrossRef] [PubMed]
- Gill, P.; Moghadam, T.T.; Ranjbar, B. Differential scanning calorimetry techniques: Applications in biology and nanoscience. J. Biomol. Tech. 2010, 21, 167–193. [Google Scholar]
- Mathers, A.; Hassouna, F.; Klajmon, M.; Fulem, M. Comparative Study of DSC-Based Protocols for API–Polymer Solubility Determination. Mol. Pharm. 2021, 18, 1742–1757. [Google Scholar] [CrossRef] [PubMed]
- Höhne, G.W.H.; Hemminger, W.; Flammersheim, H.-J. Differential Scanning Calorimetry; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2. [Google Scholar]
- Kwei, T.K. The effect of hydrogen bonding on the glass transition temperatures of polymer mixtures. J. Polym. Sci. Polym. Lett. Ed. 1984, 22, 307–313. [Google Scholar] [CrossRef]
- Simha, R.; Boyer, R.F. On a General Relation Involving the Glass Temperature and Coefficients of Expansion of Polymers. J. Chem. Phys. 1962, 37, 1003–1007. [Google Scholar] [CrossRef]
- Iemtsev, A.; Hassouna, F.; Mathers, A.; Klajmon, M.; Dendisová, M.; Malinová, L.; Školáková, T.; Fulem, M. Physical stability of hydroxypropyl methylcellulose-based amorphous solid dispersions: Experimental and computational study. Int. J. Pharm. 2020, 589, 119845. [Google Scholar] [CrossRef]
- Von Solms, N.; Kouskoumvekaki, I.A.; Lindvig, T.; Michelsen, M.L.; Kontogeorgis, G.M. A novel approach to liquid-liquid equilibrium in polymer systems with application to simplified PC-SAFT. Fluid Phase Equilib. 2004, 222, 87–93. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Application of the Perturbed-Chain SAFT Equation of State to Associating Systems. Ind. Eng. Chem. Res. 2002, 41, 5510–5515. [Google Scholar] [CrossRef]
- Gross, J.; Spuhl, O.; Tumakaka, F.; Sadowski, G. Modeling copolymer systems using the perturbed-chain SAFT equation of state. Ind. Eng. Chem. Res. 2003, 42, 1266–1274. [Google Scholar] [CrossRef]
- Klajmon, M. Investigating Various Parametrization Strategies for Pharmaceuticals within the PC-SAFT Equation of State. J. Chem. Eng. Data. 2020, 65, 5753–5767. [Google Scholar] [CrossRef]
- Prudic, A.; Lesniak, A.K.; Ji, Y.H.; Sadowski, G. Thermodynamic phase behaviour of indomethacin/PLGA formulations. Eur. J. Pharm. Biopharm. 2015, 93, 88–94. [Google Scholar] [CrossRef]
- Cocchi, G.; Angelis, M.G.D.; Sadowski, G.; Doghieri, F. Modelling polylactide/water/dioxane systems for TIPS scaffold fabrication. Fluid Phase Equilib. 2014, 374, 1–8. [Google Scholar] [CrossRef]
- Štejfa, V.; Pokorný, V.; Mathers, A.; Růžička, K.; Fulem, M. Heat capacities of selected active pharmaceutical ingredients. J. Chem. Thermodyn. 2021, 163, 106585. [Google Scholar] [CrossRef]
- In Pyo Park, P.; Jonnalagadda, S. Predictors of glass transition in the biodegradable poly-lactide and poly-lactide-co-glycolide polymers. J. Appl. Polym. Sci. 2006, 100, 1983–1987. [Google Scholar] [CrossRef]
- Lee, J.; Chae, G.; Khang, G.; Kim, M.; Cho, S.; Lee, H. The effect of gamma irradiation on PLGA and release behavior of BCNU from PLGA wafer. Macromol. Res. 2003, 11, 352–356. [Google Scholar] [CrossRef]
- Luebbert, C.; Huxoll, F.; Sadowski, G. Amorphous-Amorphous Phase Separation in API/Polymer Formulations. Molecules 2017, 22, 296. [Google Scholar] [CrossRef] [PubMed]




| Compound | (Å) | (K) | (K) | a | ||
|---|---|---|---|---|---|---|
| API | ||||||
| IBU b | 0.02636 | 4.0179 | 309.40 | 516.469 | 0.08946 | 4 (2, 2) |
| PLGA c | ||||||
| PLLA d | 0.04545 | 2.920 | 230.0 | 0 | 0 | 0 (0, 0) |
| PDLA d | 0.03699 | 3.120 | 240.0 | 0 | 0 | 0 (0, 0) |
| PGA e | 0.03130 | 2.860 | 233.9 | 0 | 0 | 0 (0, 0) |
| Polymer | wLLA = wDLA | wGA |
|---|---|---|
| PDLG 5002A/PDLG 5004A | 0.277 | 0.446 |
| PDLG 7502A/PDLG 7504A | 0.394 | 0.212 |
| PDL 02A/PDL 04A | 0.500 | 0 |
| Compound | Mwa (g·mol−1) | Tgb (°C) | Tmb (°C) | ΔHfus b (kJ·mol−1) | ΔCp,fus c (J·K−1·mol−1) |
|---|---|---|---|---|---|
| IBU | 206.3 | −45.0 ± 0.3 | 75.6 ± 0.3 | 26.4 ± 0.8 | 176.16440 − 0.3449480·(T/K) |
| PDLG 5002A | 9877 | 39.6 ± 0.3 | - | - | - |
| PDLG 5004A | 35,900 | 46.7 ± 0.3 | - | - | - |
| PDLG 7502A | 12,900 | 38.7 ± 0.3 | - | - | - |
| PDLG 7504A | 38,800 | 48.8 ± 0.3 | - | - | - |
| PDL 02A | 16,400 | 47.8 ± 0.3 | - | - | - |
| PDL 04A | 40,200 | 50.4 ± 0.3 | - | - | - |
| Polymer | Mw (g·mol−1) | LA Group (mol%) | Solubility wIBU (wt.%, kijs = 0)) | Solubility wIBU (wt.%, Optimized kijs) |
|---|---|---|---|---|
| Lower Mw polymers | ||||
| PDLG 5002A | 9877 | 50 | 21.9 | 1.4 |
| PDLG 7502A | 12,900 | 75 | 22.4 | 1.7 |
| PDL 02A | 16,400 | 100 | 22.9 | 2.1 |
| Higher Mw polymers | ||||
| PDLG 5004A | 35,900 | 50 | 21.6 | 1.2 |
| PDLG 7504A | 38,800 | 75 | 22.2 | 1.6 |
| PDL 04A | 40,200 | 100 | 22.7 | 2.0 |
| Polymer | Mw (g·mol−1) | LA Group (mol%) | APS wIBU (wt.%, kijs = 0) | APS wIBU (wt.%, Optimized kijs) |
|---|---|---|---|---|
| Lower Mw polymers | ||||
| PDLG 5002A | 9877 | 50 | - | 15.4 |
| PDLG 7502A | 12,900 | 75 | - | 19.8 |
| PDL 02A | 16,400 | 100 | - | 31.9 |
| Higher Mw polymers | ||||
| PDLG 5004A | 35,900 | 50 | - | 11.5 |
| PDLG 7504A | 38,800 | 75 | - | 18.4 |
| PDL 04A | 40,200 | 100 | - | 29.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iemtsev, A.; Klajmon, M.; Hassouna, F.; Fulem, M. Effect of Copolymer Properties on the Phase Behavior of Ibuprofen–PLA/PLGA Mixtures. Pharmaceutics 2023, 15, 645. https://doi.org/10.3390/pharmaceutics15020645
Iemtsev A, Klajmon M, Hassouna F, Fulem M. Effect of Copolymer Properties on the Phase Behavior of Ibuprofen–PLA/PLGA Mixtures. Pharmaceutics. 2023; 15(2):645. https://doi.org/10.3390/pharmaceutics15020645
Chicago/Turabian StyleIemtsev, Anton, Martin Klajmon, Fatima Hassouna, and Michal Fulem. 2023. "Effect of Copolymer Properties on the Phase Behavior of Ibuprofen–PLA/PLGA Mixtures" Pharmaceutics 15, no. 2: 645. https://doi.org/10.3390/pharmaceutics15020645
APA StyleIemtsev, A., Klajmon, M., Hassouna, F., & Fulem, M. (2023). Effect of Copolymer Properties on the Phase Behavior of Ibuprofen–PLA/PLGA Mixtures. Pharmaceutics, 15(2), 645. https://doi.org/10.3390/pharmaceutics15020645







