Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation
Abstract
1. Introduction
2. Methods
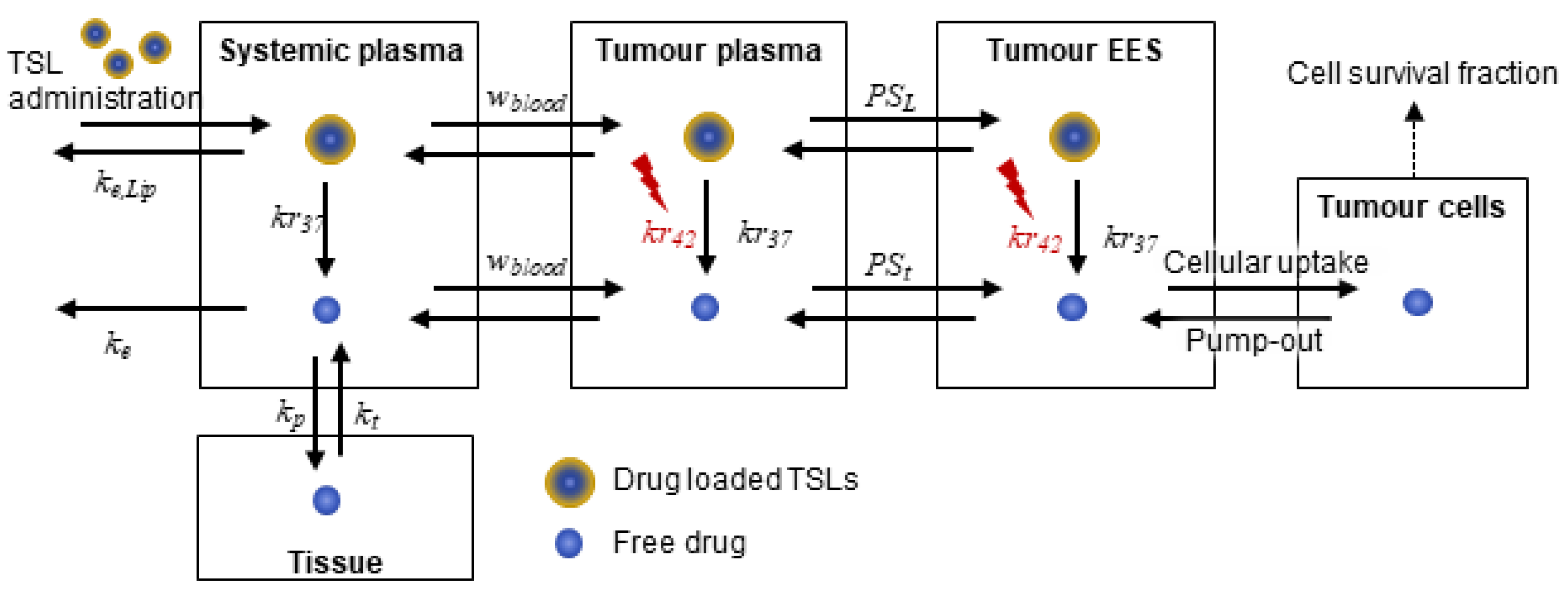
2.1. Systemic Drug Transport: Pharmacokinetics of TSLs and Anticancer Drug
2.2. Drug Transport in the Tumour Compartment
2.2.1. Transport in Tumour Plasma
2.2.2. Transport in the Tumour Interstitium
2.3. Parameterisation and Initialisation
2.4. Numerical Methods
2.5. Optimisation
3. Results and Discussion
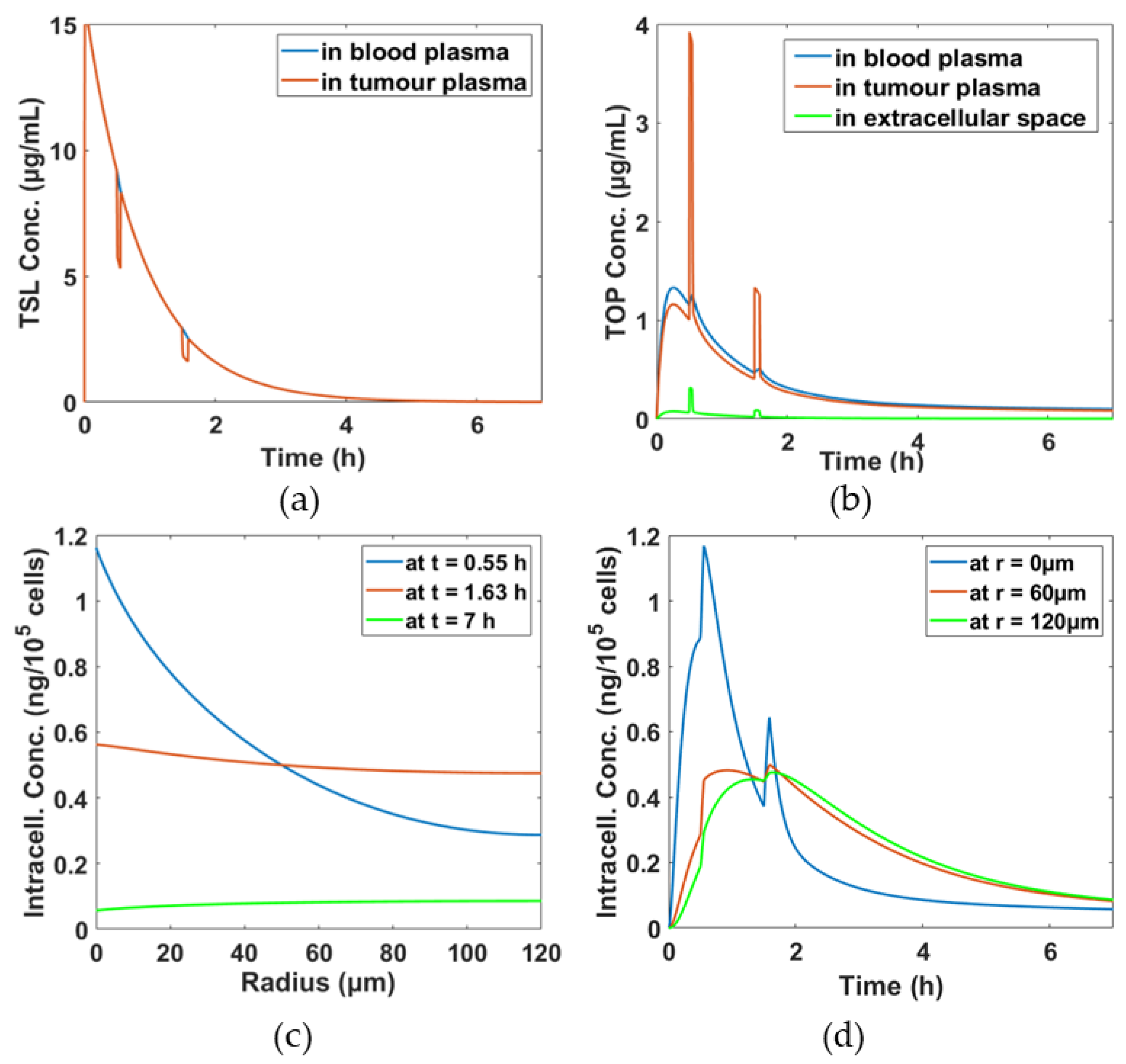
3.1. Simulation Results for the Baseline Scenario
3.2. Comparison of DOX and TOP
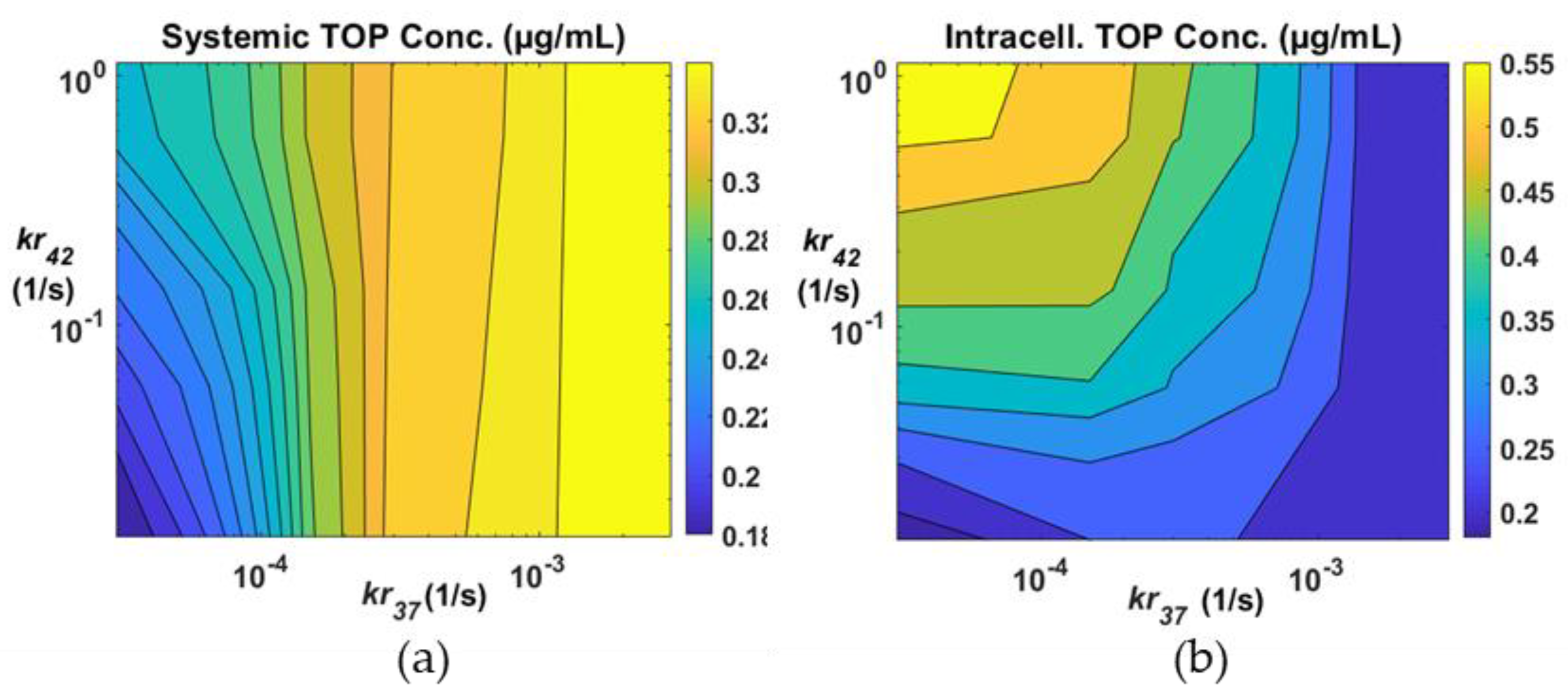
3.3. Effects of Drug Release Rates
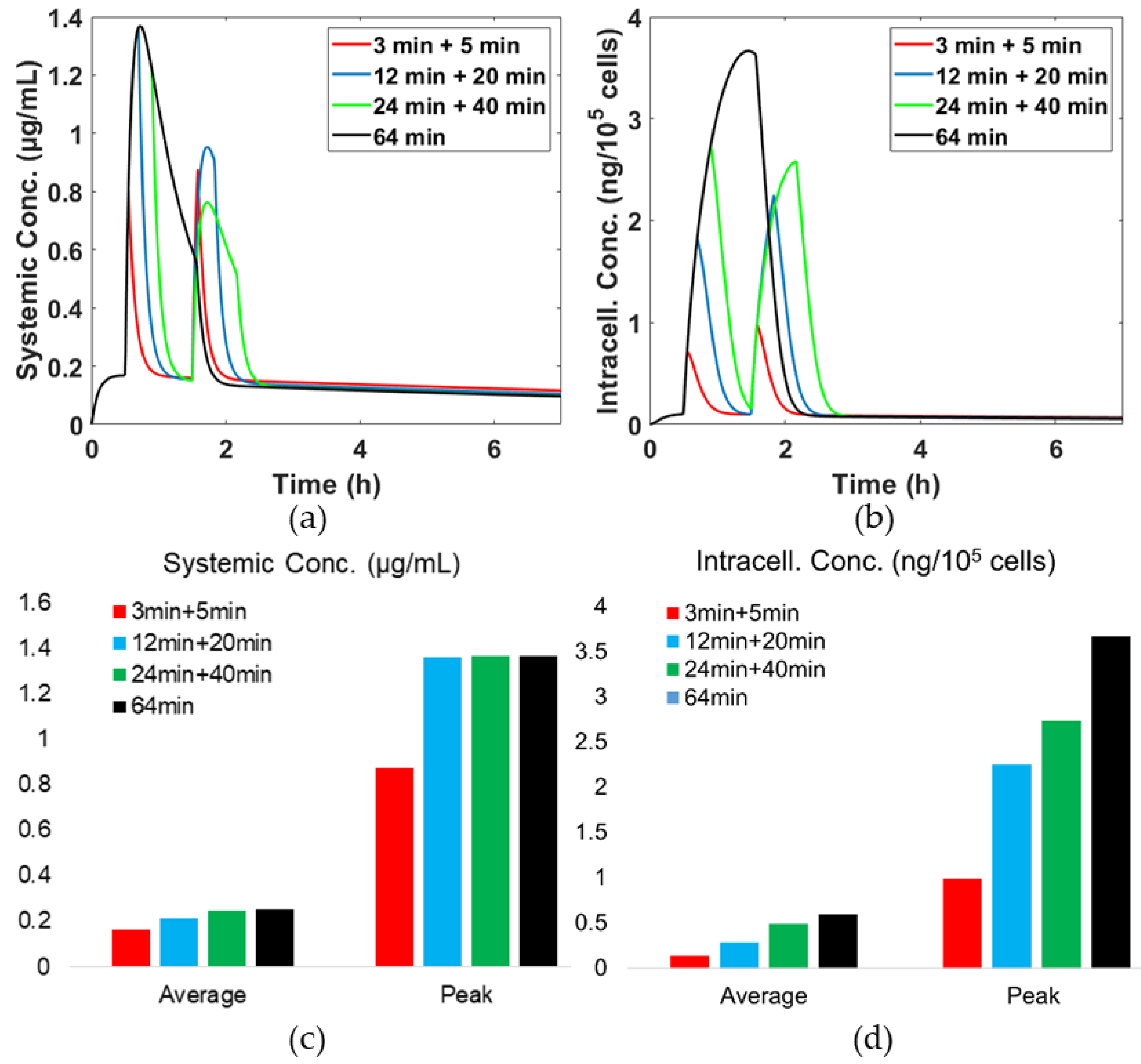
3.4. Effects of Hyperthermia (HT) Duration
3.5. Optimisation Results
4. Conclusions and Future Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Gabizon, A.; Papahadjopoulos, D. Liposome formulations with prolonged circulation time in blood and enhanced uptake by tumors. Proc. Natl. Acad. Sci. USA 1988, 85, 6949–6953. [Google Scholar] [CrossRef] [PubMed]
- Kneidl, B.; Peller, M.; Winter, G.; Lindner, L.H.; Hossann, M. Thermosensitive liposomal drug delivery systems: State of the art review. Int. J. Nanomed. 2014, 9, 4387–4398. [Google Scholar]
- Koning, G.A.; Eggermont, A.M.M.; Lindner, L.H.; Ten Hagen, T.L.M. Hyperthermia and thermosensitive liposomes for improved delivery of chemotherapeutic drugs to solid tumors. Pharm. Res. 2010, 27, 1750–1754. [Google Scholar] [CrossRef] [PubMed]
- Kirui, D.K.; Koay, E.J.; Guo, X.; Cristini, V.; Shen, H.; Ferrari, M. Tumor vascular permeabilization localized mild hyperthermia improve macromolecule transport. Nanomed. Nanotechnol. Biol. Med. 2014, 10, 1487–1496. [Google Scholar] [CrossRef]
- Popilski, H.; Stepensky, D. Mathematical modeling analysis of intratumoral disposition of anticancer agents and drug delivery systems. Expert Opin. Drug Metab. Toxicol. 2015, 11, 767–784. [Google Scholar] [CrossRef]
- Gasselhuber, A.; Dreher, M.R.; Negussie, A.; Wood, B.J.; Rattay, F.; Haemmerich, D. Mathematical spatio-temporal model of drug delivery from low temperature sensitive liposomes during radiofrequency tumour ablation. Int. J. Hyperth. 2010, 26, 499–513. [Google Scholar] [CrossRef]
- Gasselhuber, A.; Dreher, M.R.; Rattay, F.; Wood, B.J.; Haemmerich, D. Comparison of Conventional Chemotherapy, Stealth Liposomes and Temperature-Sensitive Liposomes in a Mathematical Model. PLoS ONE 2012, 7, e47453. [Google Scholar] [CrossRef]
- Liu, C.; Xu, X.Y. A systematic study of temperature sensitive liposomal delivery of doxorubicin using a mathematical model. Comput. Biol. Med. 2015, 60, 107–116. [Google Scholar] [CrossRef]
- Gasselhuber, A.; Dreher, M.R.; Partanen, A.; Yarmolenko, P.S.; Woods, D.; Wood, B.J.; Haemmerich, D. Targeted drug delivery by high intensity focused ultrasound mediated hyperthermia combined with temperature-sensitive liposomes: Computational modelling and preliminary in vivovalidation. Int. J. Hyperth. 2012, 28, 337–348. [Google Scholar] [CrossRef]
- Zhan, W.; Gedroyc, W.; Xu, X.Y. Towards a multiphysics modelling framework for thermosensitive liposomal drug delivery to solid tumour combined with focused ultrasound hyperthermia. Biophys. Rep. 2019, 5, 43–59. [Google Scholar] [CrossRef]
- Zhan, W.; Gedroyc, W.; Xu, X.Y. Effect of heterogeneous microvasculature distribution on drug delivery to solid tumour. J. Phys. D Appl. Phys. 2014, 47, 475401. [Google Scholar] [CrossRef]
- Eikenberry, S. A tumor cord model for Doxorubicin delivery and dose optimization in solid tumors. Theor. Biol. Med. Model. 2009, 6, 16. [Google Scholar] [CrossRef] [PubMed]
- Thurber, G.M.; Weissleder, R. A systems approach for tumor pharmacokinetics. PLoS ONE 2011, 6, e24696. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.Y.; Huang, C.K.; Lu, K.W.; Horng, T.L.; Lin, W.L. Investigation of the spatiotemporal responses of nanoparticles in tumor tissues with a small-scale mathematical model. PLoS ONE 2013, 8, e59135. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Krishnan, J.; Xu, X. A systems-based mathematical modelling framework for investigating the effect of drugs on solid tumours. Theor. Biol. Med. Model. 2011, 8, 45. [Google Scholar] [CrossRef]
- Centelles, M.N.; Wright, M.; So, P.W.; Amrahli, M.; Xu, X.Y.; Stebbing, J.; Miller, A.D.; Gedroyc, W.; Thanou, M. Image-guided thermosensitive liposomes for focused ultrasound drug delivery: Using NIRF-labelled lipids and topotecan to visualise the effects of hyperthermia in tumours. J. Control. Release 2018, 280, 87–98. [Google Scholar] [CrossRef]
- Heron, J.F. Topotecan: An Oncologist’s View. Oncologist 1998, 3, 390–402. [Google Scholar]
- Gabizon, A.; Shmeeda, H.; Barenholz, Y. Pharmacokinetics of pegylated liposomal doxorubicin: Review of animal and human studies. Clin. Pharmacokinet. 2003, 42, 419–436. [Google Scholar] [CrossRef]
- El-Kareh, A.W.; Secomb, T.W. A Mathematical Model for Comparison of Bolus Injection, Continuous Infusion, and Liposomal Delivery of Doxorubicin to Tumor Cells. Neoplasia 2002, 2, 325–338. [Google Scholar] [CrossRef]
- Zhan, W.; Xu, X.Y. A Mathematical Model for Thermosensitive Liposomal Delivery of Doxorubicin to Solid Tumour. J. Drug Deliv. 2013, 2013, 13. [Google Scholar]
- Rippley, R.K.; Stokes, C.L. Effects of cellular pharmacology on drug distribution in tissues. Biophys. J. 1995, 69, 825–839. [Google Scholar] [CrossRef]
- Park, K. A microfluidic system for evaluating drug delivery to solid tumors. J. Control. Release 2015, 201, 101. [Google Scholar] [CrossRef] [PubMed]
- Ozcelikkale, A.; Ghosh, S.; Han, B. Multifaceted transport characteristics of nanomedicine: Needs for characterization in dynamic environment. Mol. Pharm. 2013, 10, 2111–2126. [Google Scholar] [CrossRef] [PubMed]
- Kong, G.; Braun, R.D.; Dewhirst, M.W. Hyperthermia enables tumor-specific nanoparticle delivery: Effect of particle size. Cancer Res. 2000, 60, 4440–4445. [Google Scholar] [PubMed]
- Liu, C.; Krishnan, J.; Xu, X.Y. Towards an integrated systems-based modelling framework for drug transport and its effect on tumour cells. J. Biol. Eng. 2014, 8, 3. [Google Scholar] [CrossRef] [PubMed][Green Version]

| Symbol | Description | Value | Reference |
|---|---|---|---|
| Rate constant of TSLs clearance | 9.417 × 10−6 (1/s) | [9] | |
| Rate constant of drug clearance | 1.1 × 10−3 (1/s) | [6] | |
| Transfer constant from systemic plasma to tissue | 1.6 × 10−3 (1/s) | [6] | |
| Transfer constant from tissue to systemic plasma | 4.68 × 10−5 (1/s) | [6] | |
| Release rate constant from iTSLs at body temperature | 3 × 10−4 (1/s) | [16] | |
| Release rate constant from iTSLs during HT (at 42 °C) | 0.114 (1/s) | [16] | |
| Michaelis constant for transmembrane transport | 2.19 × 10−4 (µg/mm3) | [19] | |
| Michaelis constant for transmembrane transport | 1.37 (ng/105 cells) | [19] | |
| Maximum rate for transmembrane transport | 0.28 (ng/(105 cells·min)) | [19] | |
| Rate for passive intracellular uptake | 6.33 × 10−4 (1/s) | Fit to [6] | |
| Volume of systemic plasma | 3.04 (L) | [9] | |
| Volume of body tissue | 64.47 (L) | [9] | |
| Volume of tumour tissue | 8.82 × 10−2 (L) | Estimated based on a spherical tumour with a radius of 2.7 cm | |
| Volume fraction of tumour plasma | 0.07452 | [9] | |
| Volume fraction of tumour EES | 0.454 | [9] | |
| Volume fraction of intracellular space | 0.454 | [9] | |
| Blood perfusion rate | 0.018 (1/s) | [9] | |
| Haematocrit for tumour microvasculature | 0.19 | [9] | |
| Permeability surface area product for drugs | 2.53 × 10−3 (1/s) (TOP) 7 × 10−3 (1/s) (DOX) | Estimated based on molecular size [9] | |
| Permeability surface area product for TSL | 4.76 × 10−6 (1/s) (TOP) 2.38 × 10−5 (1/s) (DOX) | Estimated using the , and of DOX and TOP respectively | |
| Diffusive permeability for drugs | 3.61 × 10−7 (m/s) (TOP) 1 × 10−6 (m/s) (DOX) | Estimated based on molecular size [19] | |
| Diffusive permeability for TSLs and iTSLs | 3.4 × 10−9 (m/s) | [19] | |
| Diffusion coefficient | 4.123 × 10−10 (m2/s) (TOP) 1.578 × 10−10 (m2/s) (DOX) | Estimated based on molecular size [12] | |
| Diffusion coefficient for TSLs and iTSLs | 9 × 10−12 (m2/s) | [20] | |
| Tumour capillary radius | 10 () | [12] | |
| Tumour cord radius | 120 () | [12] | |
| Volume of single tumour cell | 1 × 10−6 (mm3/cell) | [19] | |
| Total dose | 49 (mg) | Calculated at a dose of 0.7 mg/kg in a 70 kg human |
| Weighting Factor, w1, for the Systemic Plasma Conc. | Weighting Factor, w2, for the Intracellular Conc. | kr37 (10−4 s−1) | kr42 (s−1) | Hyperthermia Duration (s) | Systemic Plasma Concentration (μg/mL) | Intracellular Concentration (ng/105 cells) |
|---|---|---|---|---|---|---|
| 0 | 1 | 0.3 | 1.14 | 3600 | 0.26 | 0.56 |
| 0.25 | 0.75 | 0.3 | 1.1 | 3600 | 0.25 | 0.56 |
| 0.5 | 0.5 | 0.3 | 0.7 | 3600 | 0.24 | 0.55 |
| 0.75 | 0.25 | 0.3 | 0.13 | 3600 | 0.21 | 0.48 |
| 1 | 0 | 0.3 | 0.0114 | 3600 | 0.18 | 0.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Gu, B.; Liu, C.; Stebbing, J.; Gedroyc, W.; Thanou, M.; Xu, X.Y. Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation. Pharmaceutics 2019, 11, 637. https://doi.org/10.3390/pharmaceutics11120637
Huang Y, Gu B, Liu C, Stebbing J, Gedroyc W, Thanou M, Xu XY. Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation. Pharmaceutics. 2019; 11(12):637. https://doi.org/10.3390/pharmaceutics11120637
Chicago/Turabian StyleHuang, Yu, Boram Gu, Cong Liu, Justin Stebbing, Wladyslaw Gedroyc, Maya Thanou, and Xiao Yun Xu. 2019. "Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation" Pharmaceutics 11, no. 12: 637. https://doi.org/10.3390/pharmaceutics11120637
APA StyleHuang, Y., Gu, B., Liu, C., Stebbing, J., Gedroyc, W., Thanou, M., & Xu, X. Y. (2019). Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation. Pharmaceutics, 11(12), 637. https://doi.org/10.3390/pharmaceutics11120637







