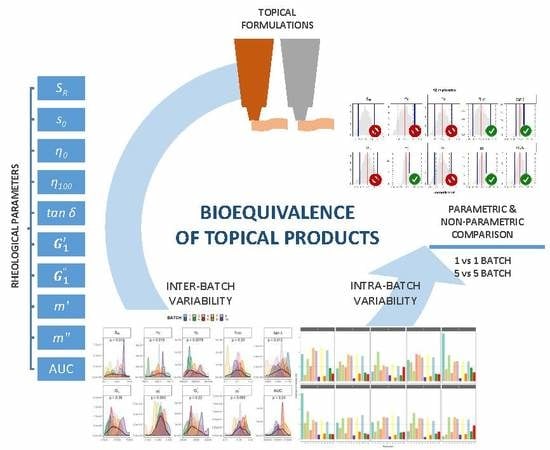
Assessment of the Inter-Batch Variability of Microstructure Parameters in Topical Semisolids and Impact on the Demonstration of Equivalence
Abstract
1. Introduction
2. Materials and Methods
2.1. Drug Products
2.2. Rheological Analysis
2.2.1. Hysteresis Loops
2.2.2. Flow Curves
2.2.3. Viscoelastic Properties from Oscillatory Tests
2.3. Spreadability Measurements
2.4. Parametric Comparison
2.4.1. Comparison of 1 Batch vs. 1 Batch
2.4.2. Comparison of 5 Batches vs. 5 Batches
2.4.3. Comparison of Median of 5 Batches vs. Median of 5 Batches
2.5. Non-Parametric Comparison
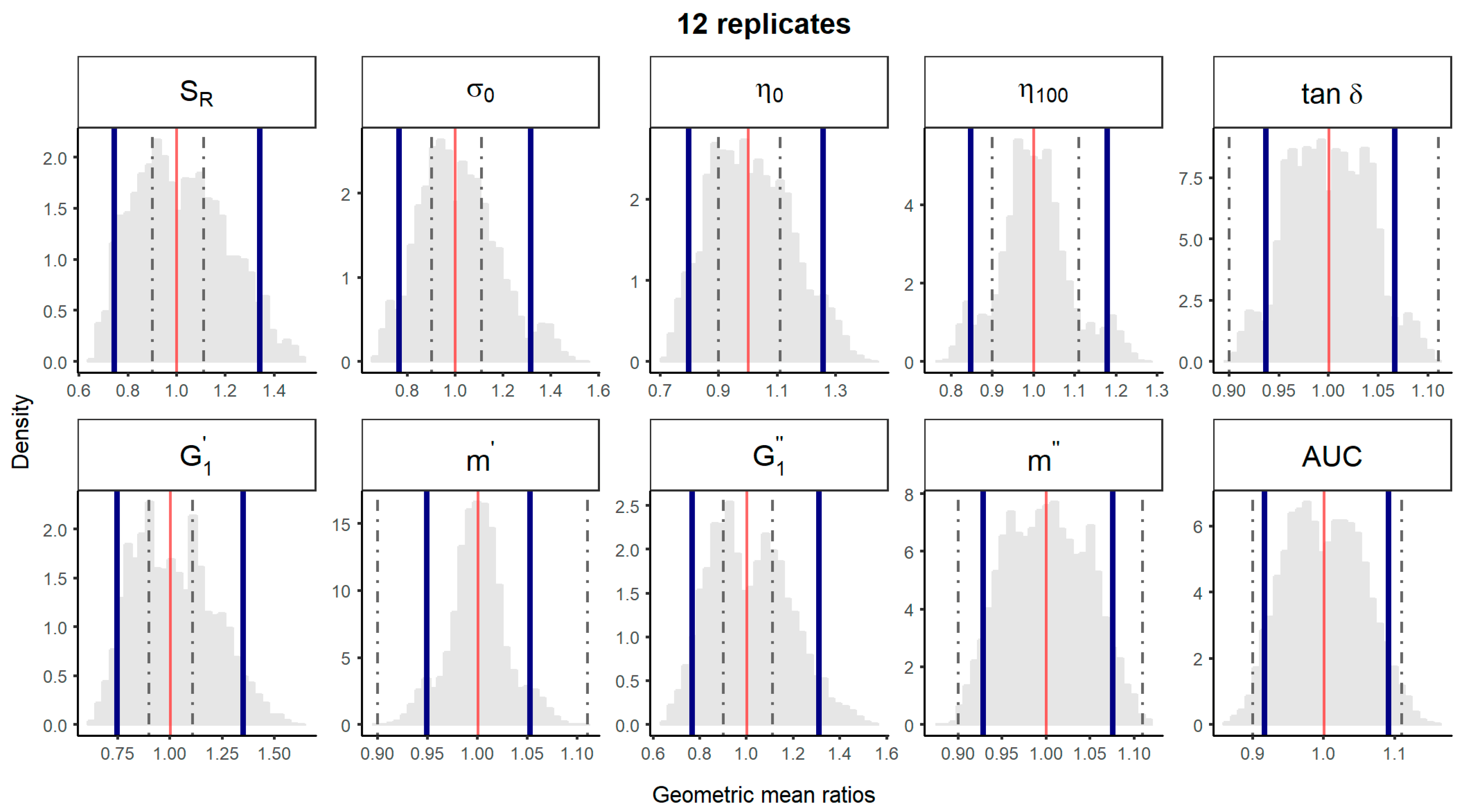
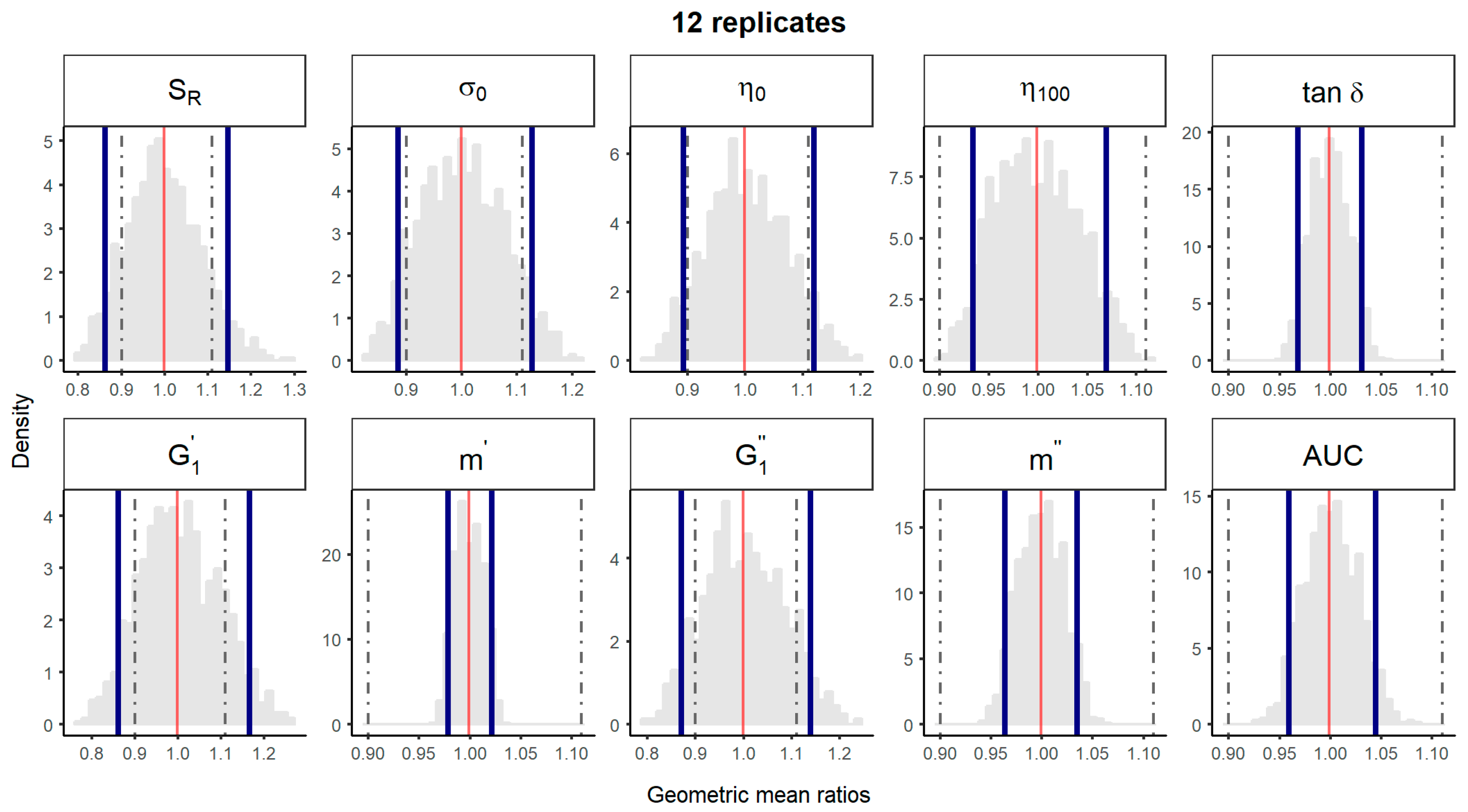
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, R.-K.; Raw, A.; Lionberger, R.; Yu, L. Generic Development of Topical Dermatologic Products, Part II: Quality by Design for Topical Semisolid Products. AAPS J. 2013, 15, 674–683. [Google Scholar] [CrossRef] [PubMed]
- Baynes, R.; Riviere, J.; Franz, T.; Monteiro-Riviere, N.; Lehman, P.; Peyrou, M.; Toutain, P.-L. Challenges obtaining a biowaiver for topical veterinary dosage forms. J. Vet. Pharmacol. Ther. 2012, 35, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Pershing, L.K.; Nelson, J.L.; Corlett, J.L.; Shrivastava, S.P.; Hare, D.B.; Shah, V.P. Assessment of dermatopharmacokinetic approach in the bioequivalence determination of topical tretinoin gel products. J. Am. Acad. Dermatol. 2003, 48, 740–751. [Google Scholar] [CrossRef] [PubMed]
- Committee for Medicinal Products for Human Use (CHMP). Draft guideline on quality and equivalence of topical product. CHMP/QWP/708282/2018. 2018. Available online: https://www.ema.europa.eu/en/documents/scientific-guideline/draft-guideline-quality-equivalence-topical-products_en.pdf (accessed on 18 October 2018).
- Dolz, M.; Hernández, M.J.; Pellicer, J.; Delegido, J. Shear Stress Synergism Index and Relative Thixotropic Area. J. Pharm. Sci. 1995, 84, 728–732. [Google Scholar] [CrossRef] [PubMed]
- Mezger, T.G. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers, 4th ed.; Vincentz Network: Hannover, Germany, 2014; ISBN 978-3-87870-174-3. [Google Scholar]
- Picó, J.A.; Peris, J.; Sánchez, A.; Hernández, M.J.; Nacher, A.; Diez-Sales, O. A comparative rheological study of several dentifrices trademarks. In The multidisciplinary science of rheology. Towards a healthy and sustainable development; GER: Valencia, Spain, 2017; pp. 164–168. [Google Scholar]
- Sanz, T.; Salvador, A.; Hernández, M.J. Creep–Recovery and Oscillatory Rheology of Flour-Based Systems. In Advances in Food Rheology and Applications; Elsevier: Amsterdam, The Netherlands, 2017; pp. 277–295. ISBN 978-0-08-100431-9. [Google Scholar]
- Bonate, P.L. Appendix: Computer Intensive Statistical Methods. In Pharmacokinetic-Pharmacodynamic Modeling and Simulation; Springer: New York, NY, USA, 2016; pp. 353–363. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Royston, J.P. An Extension of Shapiro and Wilk’s W Test for Normality to Large Samples. J. R. Stat. Soc. Ser. C Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Committee For Medicinal Products For Human Use (CHMP). Guideline on the requirements for clinical documentation for orally inhaled products (OIP) including the requirements for demonstration of therapeutic equivalence between two inhaled products for use in the treatment of asthma and chronic obstructive pulmonary disease (COPD) in adults and for use in the treatment of asthma in children and adolescents. CPMP/EWP/4151/00 Rev. 1. 2009. Available online: https://www.ema.europa.eu/en/documents/scientific-guideline/guideline-requirements-clinical-documentation-orally-inhaled-products-oip-including-requirements_en.pdf (accessed on 22 January 2009).
- Questions and Answers of the Pharmacokinetic Working Party. 3.4 Evaluation of orally inhaled medicinal products: Can I scale acceptance limits (for Cmax and perhaps AUC) to allow for variability in reference product for fine particle dose? January 2015. Available online: https://www.ema.europa.eu/en/human-regulatory/research-development/scientific-guidelines/clinical-pharmacology-pharmacokinetics/clinical-pharmacology-pharmacokinetics-questions-answers (accessed on 23 September 2019).
- Davit, B.M.; Stier, E.; Jiang, X.; Anand, O. Expectations of the US-FDA regarding dissolution data in generic drug regulatory submissions. Biopharma. Asia 2013, 2, 14–21. [Google Scholar]
- Mould, D.R.; Upton, R.N. Basic Concepts in Population Modeling, Simulation, and Model-Based Drug Development—Part 2: Introduction to Pharmacokinetic Modeling Methods. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e38. [Google Scholar] [CrossRef] [PubMed]
- Gobburu, J.V.S.; Lawrence, J. Application of Resampling Techniques to Estimate Exact Significance Levels for Covariate Selection During Nonlinear Mixed Effects Model Building: Some Inferences. Pharm. Res. 2002, 19, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Mangas-Sanjuan, V.; Pastor, J.M.; Rengelshausen, J.; Bursi, R.; Troconiz, I.F. Population pharmacokinetic/pharmacodynamic modelling of the effects of axomadol and its O-demethyl metabolite on pupil diameter and nociception in healthy subjects. Br. J. Clin. Pharmacol. 2016, 82, 92–107. [Google Scholar] [CrossRef] [PubMed]
- Committee For Medicinal Products For Human Use (CHMP). Guideline on the investigation of bioequivalence. CPMP/EWP/QWP/1401/98 Rev 1/Corr **. 2010. Available online: https://www.ema.europa.eu/en/investigation-bioequivalence (accessed on 29 January 2010).
- Kryscio, D.R.; Sathe, P.M.; Lionberger, R.; Yu, L.; Bell, M.A.; Jay, M.; Hilt, J.Z. Spreadability Measurements to Assess Structural Equivalence (Q3) of Topical Formulations—A Technical Note. AAPS Pharm. Sci. Tech. 2008, 9, 84–86. [Google Scholar] [CrossRef] [PubMed]
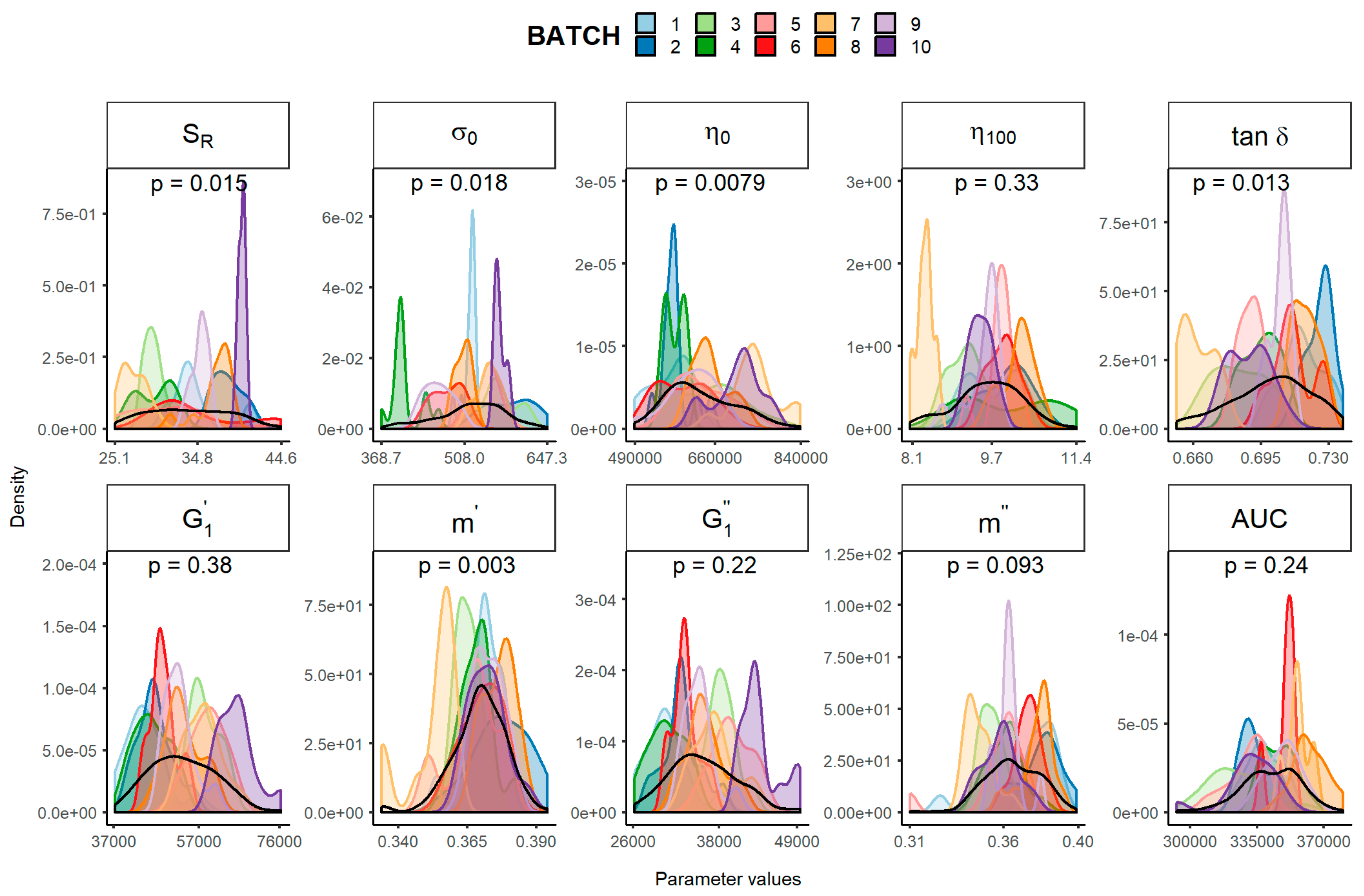
| Parameter | Mean | SD | Minimum | Maximum | Total CV (%) | Inter-Batch CV (%) | Intra-Batch CV | |
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | |||||||
| SR (%) | 33.80 | 4.82 | 25.06 | 44.56 | 14.3 | 12.2 | 1.0 | 16.4 |
| σ0 (Pa) | 519 | 57 | 369 | 647 | 11.0 | 10.6 | 1.6 | 6.8 |
| η0 (Pa·s) | 630,067 | 74,229 | 488,890 | 839,980 | 11.8 | 9.6 | 3.6 | 10.1 |
| η 100 (Pa·s) | 9.63 | 0.67 | 8.05 | 11.40 | 7.0 | 5.7 | 2.0 | 9.3 |
| tan δ | 0.700 | 0.020 | 0.651 | 0.737 | 2.9 | 2.7 | 0.8 | 2.0 |
| (Pa) | 53,255 | 7741 | 37,195 | 76,270 | 14.6 | 13.1 | 5.9 | 11.5 |
| m′ | 0.369 | 0.010 | 0.334 | 0.394 | 2.6 | 1.9 | 1.3 | 2.7 |
| (Pa) | 35,829 | 4723 | 26,149 | 49,457 | 13.2 | 11.7 | 5.2 | 10.6 |
| m″ | 0.365 | 0.015 | 0.310 | 0.399 | 4.1 | 3.1 | 1.8 | 4.6 |
| Spreadability (mm2) | 342,224 | 15,438 | 292,922 | 379,991 | 4.5 | 3.7 | 1.7 | 4.9 |
| Comparison Method | 1 Batch vs. 1 Batch | 5 Batches vs. 5 Batches | Median Batch within 5 Batches vs. Median Batch within 5 Batches | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acceptance Range | 10% | 15% | 20% | 25% | 30% | 10% | 15% | 20% | 25% | 10% | 15% | 20% | 25% |
| Parameter | |||||||||||||
| SR (%) | 7/45 (16%) | 17/45 (38%) | 27/45 (60%) | 36/45 (80%) | 43/45 (96%) | 66/126 (52%) | 100/126 (79%) | 124/126 (98%) | 126/126 (100%) | 54/126 (43%) | 60/126 (48%) | 105/126 (83%) | 126/126 (100%) |
| σ0 (Pa) | 17/45 (38%) | 26/45 (58%) | 34/45 (76%) | 39/45 (87%) | 42/45 (93%) | 83/126 (66%) | 120/126 (95%) | 126/126 (100%) | 126/126 (100%) | 90/126 (71%) | 111/126 (88%) | 126/126 (100%) | 126/126 (100%) |
| η 0 (Pa·s) | 10/45 (22%) | 25/45 (56%) | 36/45 (80%) | 41/45 (91%) | 45/45 (100%) | 96/126 (76%) | 124/126 (98%) | 126/126 (100%) | 126/126 (100%) | 0/126 (0%) | 102/126 (81%) | 117/126 (93%) | 126/126 (100%) |
| η 100 (Pa·s) | 33/45 (73%) | 39/45 (87%) | 44/45 (98%) | 45/45 (100%) | 45/45 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) |
| tan δ | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) |
| (Pa) | 7/45 (16%) | 19/45 (42%)) | 25/45 (56%) | 34/45 (76%) | 42/43 (93%) | 65/126 (52%) | 108/126 (86%) | 124/126 (98%) | 126/126 (100%) | 36/126 (29%) | 78/126 (62%) | 84/126 (67%) | 126/126 (100%) |
| m’ | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) |
| (Pa) | 7/45 (16%) | 20/45 (44%) | 31/45 (69%) | 39/45 (87%) | 43/45 (96%) | 76/126 (60%) | 117/126 (93%) | 126/126 (100%) | 126/126 (100%) | 36/126 (29%) | 84/126 (67%) | 126/126 (100%) | 126/126 (100%) |
| m″ | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) |
| Spreadability (mm2) | 41/45 (91%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 45/45 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) | 126/126 (100%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangas-Sanjuán, V.; Pleguezuelos-Villa, M.; Merino-Sanjuán, M.; Hernández, M.J.; Nácher, A.; García-Arieta, A.; Peris, D.; Hidalgo, I.; Soler, L.; Sallan, M.; et al. Assessment of the Inter-Batch Variability of Microstructure Parameters in Topical Semisolids and Impact on the Demonstration of Equivalence. Pharmaceutics 2019, 11, 503. https://doi.org/10.3390/pharmaceutics11100503
Mangas-Sanjuán V, Pleguezuelos-Villa M, Merino-Sanjuán M, Hernández MJ, Nácher A, García-Arieta A, Peris D, Hidalgo I, Soler L, Sallan M, et al. Assessment of the Inter-Batch Variability of Microstructure Parameters in Topical Semisolids and Impact on the Demonstration of Equivalence. Pharmaceutics. 2019; 11(10):503. https://doi.org/10.3390/pharmaceutics11100503
Chicago/Turabian StyleMangas-Sanjuán, Víctor, María Pleguezuelos-Villa, Matilde Merino-Sanjuán, Mª Jesús Hernández, Amparo Nácher, Alfredo García-Arieta, Daniel Peris, Irene Hidalgo, Lluís Soler, Marta Sallan, and et al. 2019. "Assessment of the Inter-Batch Variability of Microstructure Parameters in Topical Semisolids and Impact on the Demonstration of Equivalence" Pharmaceutics 11, no. 10: 503. https://doi.org/10.3390/pharmaceutics11100503
APA StyleMangas-Sanjuán, V., Pleguezuelos-Villa, M., Merino-Sanjuán, M., Hernández, M. J., Nácher, A., García-Arieta, A., Peris, D., Hidalgo, I., Soler, L., Sallan, M., & Merino, V. (2019). Assessment of the Inter-Batch Variability of Microstructure Parameters in Topical Semisolids and Impact on the Demonstration of Equivalence. Pharmaceutics, 11(10), 503. https://doi.org/10.3390/pharmaceutics11100503