1. Introduction
The hepatitis C virus (HCV) only infects human (and some higher primate) liver cells. Even though HCV-infected liver cells (hepatocytes) may initially remain viable, culminative stress to the liver following a period of about 10–20 years infection predisposes patients to develop liver cirrhosis and liver cancer. Liver damage caused by HCV infection is the main cause for liver transplantations in the Western World. Substantial efforts to understand the mechanisms underpinning HCV replication [
1,
2,
3], have culminated in the the development of effective direct acting antivirals (DAAs) [
4] against HCV, which now offer substantial cure rates for many patients infected with the virus.
However, many facets of HCV replication remain poorly understood. In particular, even though various central steps of virus genome replication could be revealed experimentally, still many processes are understood only in part and/or only qualitatively. A deeper insight into the exact molecular dynamics of HCV replication will enhance, for example, the understanding of the interplay between viral proteins, viral RNA (vRNA) replication, and cell metabolism. This knowledge will likely serve to enhance our understanding of the impact of direct antiviral agents (DAAs) upon the interplay of vRNA and viral proteins. Additionally, such understanding could be used to reveal global mechanisms involved in replication of related viruses.
Mathematical descriptions for the dynamics of biophysical processes have become better refined within the last years. In the case of virus dynamics, compartmental kinetic models based on ordinary differential equations (ODEs) now represent the state of the art [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. In fact, such ODEs represent homogenized descriptions of processes for which the spatial resolution is not accounted for. For many processes, such homogenizations are justified and useful. (In this study, the term “homogenization” refers to the averaging of the dynamics over the complete space rather then other meanings which appear in other contexts.) Therefore, ODE-based models of HCV dynamics allowed for new and important insights. However, the investigation of those effects which depend on the spatial location of the components, requires a description based on partial differential equations (PDEs) that need to be solved on computational domains that reflect realistic geometric structures. PDEs, indeed, allow to describing effects such as the spatial distribution of the agents concurring to the evolution of the vRNA, that cannot be resolved otherwise, and permit to account for the influence of geometry on the spatio-temporal evolution of the unknowns. Realistic reconstructed geometries of cell structures are often the most appropriate basis for the in silico evaluation of spatially resolved models, since they reflect best the role of the real geometry upon the modeled processes, and influence that cannot be obtained by simplified geometric objects.
In the literature, there already exist models that describe virus dynamics with the aid of PDEs, cf. [
19,
20,
21]. In [
19], the authors elaborated the global stability for a class of diffusion equations which appear in computational biology. They studied the global stability of constant steady-state solutions for several reaction-diffusion systems with and without delay. The models harbored up to one dimension in space and inherited in part time delayed coefficients. The solution techniques were based upon a variational principle: The authors constructed Lyapunov functionals for PDEs and delayed partial differential equations (DPDEs) using Lyapunov functionals for ODEs and delayed differential equations (DDEs). They applied their framework to study the global stability of several models from virology and epidemiology. We mention in particular the consideration of 1D PDE model of [
22] which described the reaction-diffusion system of infected and uninfected hepatocytes which were considered to be immobile, while viruses were consideder to move freely following the Fickian diffusion law. Moreover, the authors of [
19] constructed a Lyapunov functional and studied the stability of the model of [
22]. Indeed, the first diffusive model of [
22] was an extension of former ODE models [
23,
24,
25] to the spatial case. In detail, Wang and Wang [
22] introduced a HBV model by means of spatial dependence in such a way that viruses move freely in the liver, but healthy and infected hepatocytes (liver cells) are immobile. Hence, the original model coupled all three concentrations by means of a coupled ODE-PDE system. This model was improved within various steps [
26,
27,
28]. In [
20], the authors generalized and extended all these HBV models by means of a time-delayed coupled ODE-PDE system, i.e., they presented a hepatitis B virus (HBV) model with spatial diffusion and time delays [
20]. In particular, Hattaf and Yousfi [
20] extended and generalized various diffusive HBV models of the literature, which are based upon the first approach of [
22]. Lyapunov functionals were constructed for the analysis of the equilibrium in the cases of disease-free and chronic infection. Hattaf and Yousfi [
20] also performed the important intensive theoretical investigation for proving that there exists a unique solution of their basic equation system and that this solution remained non-negative and bounded. Constructing Lyapunov functionals, the authors investigated in detail the asymptotic stability of the disease-free case and of the chronic infection equilibrium case and derived distinct conditions for this stability. The results of the theoretical investigations were applied to the extended model which harbored homogeneous Neumann boundary conditions. They investigated the 1D system using various different parameters to test for the sensitivity of the results to the diffusion coefficient and to the time delays. They concluded that the diffusion coefficient caused different virus loads at different spatial locations and, therefore, the time scale to arrive at the chronic infection equilibrium depended upon the diffusion coefficient of the virus, even though in their case the virus diffusion showed no effect on the asymptotic properties of the equilibrium. This fits to the assumption of a unique medium where the processes take place. The results of [
20] demonstrated the importance to incorporate spatial resolution within computational virology. In [
21], the authors introduced a numerical method for coupled DPDEs which allowed for the evaluation of viral infection models similar to the previously described HBV work [
20], but now extended to HIV. The paper presented a model of 3 coupled equations which described similar biology to [
20]: Two of the equations are DDEs and one is a DPDE. (Similar to the case before, the model describes the reactive and diffusive properties of the dynamics of the densities of uninfected cells, infected cells and free virus at a spatial position and time, respectively.) The focus of that work was the introduction of numerically stable methods to solve such equation systems. The authors introduce Finite Difference (FD) schemes for the temporal and spatial derivations. They proved that the solutions of the discretized version of their delayed discrete model remained nonnegative and bounded, hence the numerical method could be applied safely. They investigated the global stability of the DPDEs system by constructing discrete Lyapunov functionals and proved the asymptotically stability of the system for the disease-free case and for the chronic infection case. They further demonstrated that the proposed method preserved the global stability of equilibria of the continuous system with no restriction on the space and time step sizes. The authors derived parameter conditions for the cases when the disease-free equilibrium was globally stable which, biologically-speaking, gave conditions for when the infection was resolved compared to chronic.
In summary, at the scale of the virus-infected patient, there exist models of the spatially resolved dynamics of different viruses corresponding to the interplay of the uninfected cells, infected cells, and free virus concentrations [
19,
20,
21] as discussed previously. The techniques corresponding to the author’s PDEs and delayed PDEs (DPDEs) are based upon Lyapunov functionals and the models are extensions of former ODE models [
23,
24,
25] to the spatially resolved case. As discussed previously, these models and methods allowed for interesting insight at the scale of the complete liver.
However, to the best of our knowledge, studies performing such analyses at the (intra)cellular scale have not been published yet. Therefore, our aim was to perform a similar approach to [
19,
20,
21], but at a (intra)cellular level. We remark that in opposite to the scale of the complete liver where single non-distinguishable hepatocytes form the basis of the medium, the inner structure of single hepatocytes shows significant non-continuous structure, hence the effects originating from the medium structure may be expected to be even stronger compared to the scale of the complete liver.
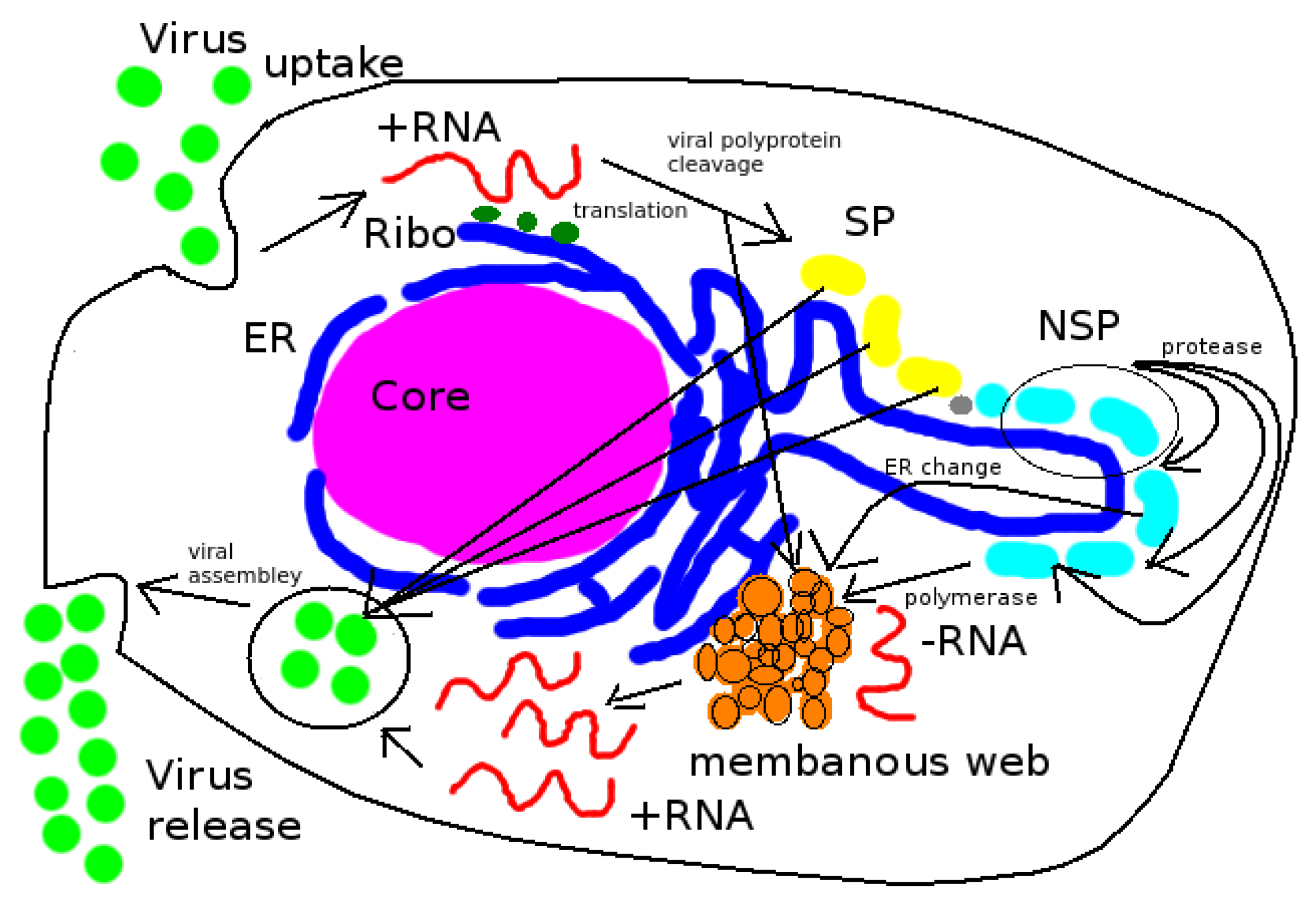
There is strong biological evidence that the spatial dependence is a crucial factor for the vRNA replication of HCV at a (intra)cellular level [
2,
29]. Such replication takes place within specialized compartments of virus-infected hepatocytes, which form from the surface of the Endoplasmatic Reticulum (ER) [
1,
2]. The subsequent remodelling of the ER membrane by HCV results in a structure termed the “membranous web”, which houses replication complexes that serve as factories for vRNA replication and bridge the virus-dependent process of genome replication and packaging. It has proven to be difficult to experimentally capture the formation of the membranous web [
30] and the trafficking of its components, namely host and viral proteins and vRNA. Trafficking of the components take place within the complex three dimensional space, which is determined by the shape of the modified ER membranes that serve to form the membranous web. An important example that demonstrated the requirement for spatial dependence of HCV components is highlighted through the behaviour of the HCV-encoded NSP NS5A in response to specific pharmacological-mediated inhibition by NS5A inhibitors [
31,
32]. Such small molecules cause a spatial redistribution of the viral protein and change its intracellular mobility patterns [
33].
Therefore, multiple levels of rationale exist for developing computational models that resolve HCV replication dynamics both in time (as ODE models do), and in space (as PDEs allow for).
HCV virus replication is based upon two basic processes [
1,
3,
18]: The vRNA gets replicated (vRNA cycle) and then combined (packaged) with structural virus proteins (SPs) to form new progeny virions (virus assembly).
The present study introduces relatively simple but fully 3D spatio-temporal resolved models of the interplay between vRNA, nonstructural viral proteins (NSP), membranous web (web) and a generic host factor (host) in order to recapitulate the basic properties of the vRNA replication cycle. The models are evaluated on a realistic geometric intracellular environment, based upon reconstructed ER surface and membranous web regions from experimentally-derived imaging data. On top of this geometric setup, we developed and implemented the models we present here.
We describe the replication cycle of the viral genome (vRNA) by means of a set of nonlinear coupled partial differential equations (PDEs). These equations are discretized by means of a Finite Volume method (FV). The arising equations are solved by employing massively parallel multigrid solvers [
34]. The computations are performed with the aid of the simulation software UG4 [
34,
35,
36] on leading supercomputers [
37].
Even though there exist already advanced quantitative data of HCV replication dynamics averaged over the entire cell [
38,
39], it is rather difficult to get exact quantitative data of the spatio-temporal behaviour of all the components of the vRNA replication cycle. Recently, we have estimated the diffusion constant of the NS5A protein of HCV. (The technical basics of the estimation are already published [
37,
40] while the parameter estimation itself based on experimental FRAP time series has not been published yet). In the present study we use heuristic values for the parameters of a new diffusion-reaction model and we restrict its evaluation to a specific (intra)cellular localisation of a realistic reconstructed cell.
Moving forward, detailed experimental setups can be developed that allow for estimating the necessary additional parameters required to develop the model further. This interdisciplinary interaction will hopefully catalyze more detailed insights into HCV replication properties. Further, approaches such as the one described by the current study may also form the basis for spatially resolved models of other viral infections.
This paper is organized as follows: First, we describe the reconstruction process of the ER surface and the web regions, and we introduce surface and volume meshes of the computational domains. Then, we introduce two spatial models, which both capture important aspects of the spatial behavior of the basic components of the vRNA cycle, i.e., a surface PDE (sPDE) model and a PDE model evaluated in the complete volume of the cell, rather than on the surface of the compartments. The sPDE model captures the fact that the NSPs anchor to the ER surface directly after their cleavage [
1], i.e., that viral nonstructural protein movement is restricted to the ER surface. Indeed, using mathematical language, the ER surface can be considered to be a curved 2D tubular manifold embedded in the three-dimensional Euclidian space. Moreover, we also introduce a “normal” PDE model within the volume, which takes into account the fact that, presumably, the other components of the vRNA cycle (like the vRNA itself or the host factor) may move within the cytosol.
In future research, we intend to combine these two approaches. Here, we present simulations and evaluations for both models separately. At the end, we discuss our results and put them into the context of current and future research.
3. Results
In the following, we present the results related to the mathematical models discussed in the previous sections. In particular, we focus on the formulations based on the set of Equations (8a)–(8c), (9a)–(9d) and (13a)–(13d). We emphasize that all the considered models are computed on realistic geometries, reconstructed on the basis of the microscopy data presented in
Section 2.2.
In the following, we will sometimes denote the viral RNA simply as RNA rather then vRNA. Since we do not refer to body-own messenger RNA at any point, this should not cause confusion.
3.1. Surface PDE Model of vRNA, webProtein and Host Factor
This model is based on Equations (8a)–(8c).
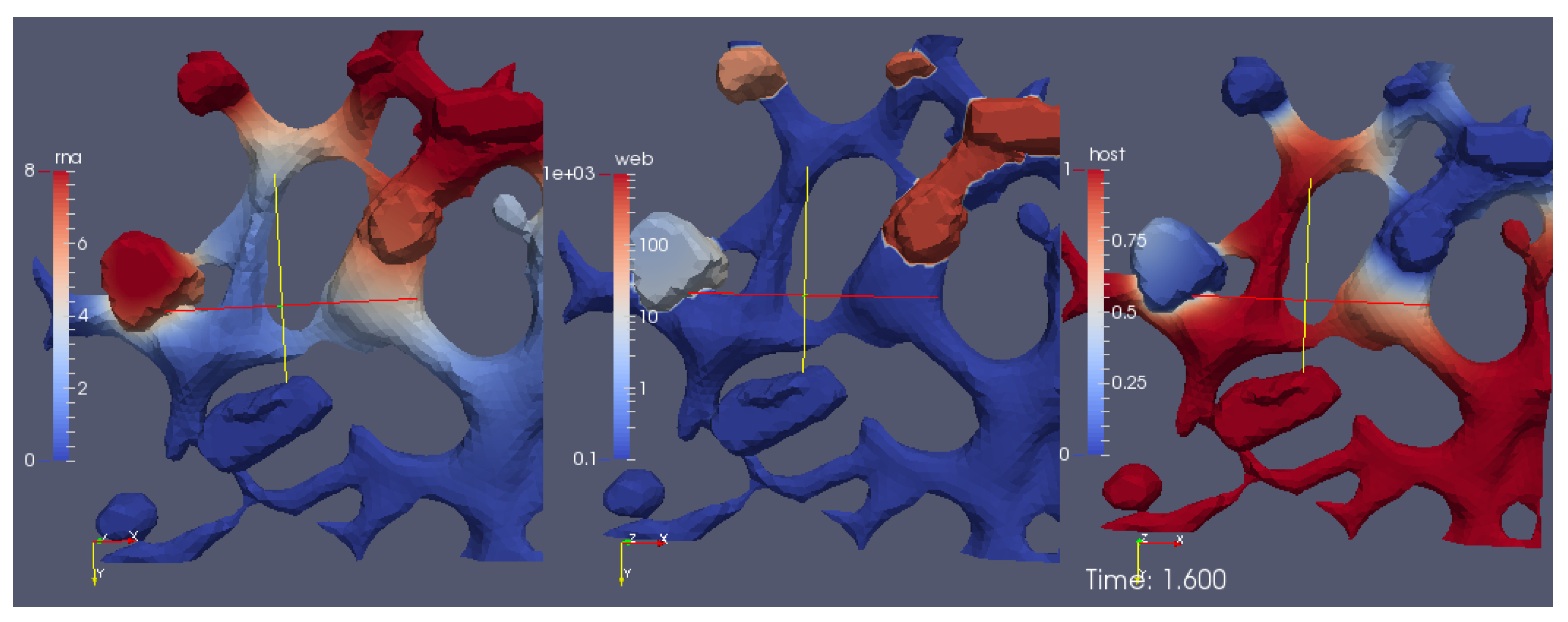
A screenshot of the
movie S1 Video in Supplementary Material reporting the evolution of the surface concentrations of the vRNA, web-protein, and host factor (denoted in the formla by
R,
W, and
H, respectively) is shown in
Figure 6. We emphasize that
R,
W, and
H are the solutions of Equations (8a)–(8c), respectively, obtained with the initial conditions Equations (5a)–(5c).
The movie depicts a portion of the computational domain obtained by cutting the domain itself by means of plane. This is done to permit the visualization of the initial concentration , which otherwise cannot be seen, since it is nonzero only at the ribosomes (i.e., at the intersections between the ER and the web regions, which are indeed hidden unless the computational domain is disclosed by a cutting plane).
With reference to
Figure 6, the concentrations are ordered in the following way: From left to right, one can see a snapshot of the spatial distribution of the concentration of the vRNA,
R, web protein,
W, and host factor,
H. (This means that the left sector of the screen represents the RNA, the middle sector the web protein, and the right sector of the movie the host factor concentration.) As soon as we start the simulations, it is possible to observe that the web protein is produced at the ribosomes (cf., middle sector). Indeed, the RNA start concentration (visible at the left sector of the simulation movie screen) causes the translation of the web protein (visible in the middle sector of the simulation movie screen). Then, the web protein moves into the web region (middle sector), which—as elsewhere recalled—has been constructed on the basis of experimental data [
29].
Since at the beginning of the simulation we watch the section of the ER from behind, we are not able to see the evolution of the concentrations inside the web regions that find themselves over the ER surface. To visualize such evolution, we rotate the perspective to see the ER from the front.
While the perspective is still rotating, we can already see that the web protein (which gets translated by to the RNA at the ribosomes) moves into the web region (cf., middle sector). We can observe this process because the color of the web protein concentration changes from blue (low concentration) to red, which indicates high concentration. However, we observe also that the RNA itself is diffusing. The RNA diffuses away into two directions: One direction of the RNA diffusion happens on the ER surface. However, the concentration gets rather small there soon. Anyhow, the other direction of RNA diffusion is into the web region. Inside the web region, the major process takes place: The RNA concentration rises up again, because the web proteins copy the RNA. By now, the camera perspective does not move any more. From now on until to the end of this simulation movie, the perspective of the view is such that we observe the processes so that we see the front of the ER and the web regions. One sees clearly in the left sector of the movie, how the RNA concentration is uprising strong within the web region. The web is already growing, cf., middle sector of the movie. At the right sector of the movie, we see the host factor which, due to the RNA production, gets consumed. By now, the web region is filled with RNA. This is visible due to the red color of the RNA sector of the three concentrations, i.e., in the left sector of the movie. Due to the diffusion, now the RNA moves strongly outside again to the ER surface. This movement is visible on the ER surface because the red color appears on the ER surface of the RNA representing sector of the scene. Once the diffusing RNA arrives at the next experimentally predefined web region, the RNA also arrives at the corresponding ribosomes which are located at the intersection of the reconstructed ER surface and the reconstructed web region. Therefore, the ribosomes are "hidden" and not visible any more from our present perspective. Now, the same game begins again as described before: The RNA produces the web proteins. In the middle sector of the clip, i.e., the web protein concentration sector, one sees that the web is growing, indicated by the change of the color from blue to red within this (second) web region. The RNA diffuses (as before at the other web) into the new web region. There, the web protein replicates the RNA as before at the other web. And as before, one observes the depletion of the host factor (right sector). The newly synthesized RNA diffuses away again and spreads itself further. The RNA reaches the next web region, translates the web protein which replicates the RNA, and so on—in this way, some sort of “wave”’propagates within the cell which causes the RNA replication, the growth of the webs, and the host factor depletion. As soon as the host factor is depleted, the RNA reproduction stops at the corresponding sites. This stop appears especially once when also the host factor of the surrounding regions is depleted and no further host factor can diffuse to the replication sites, due to the lack of the availability. In this manner, the “wave” contaminates the cell bit by bit with viral RNA and viral web regions. At the beginning, one sees clearly that the viral RNA is concentrated at the web regions. Only after when a lot of RNA is produced, after a substantial amount of time, the complete computational domain (i.e., the cutout of the cell where we evaluate the model) at the left hand side sector (the RNA part) appears to be red, i.e., filled with RNA. Indeed, in particular at this stage, the model still bears the potential to be improved. This improvement could be performed by means of the incorporation of a degradation of RNA, which should take place especially exteriorly of the web regions, i.e., at the ER surface.
As mentioned before, the simulations assume that a host factor is consumed during the reproduction of the viral RNA. Of course, this host factor will be missed at another place, namely for the normal metabolic processes of the cell. Indeed, the cell does not produce the host factor for the sake of virus reproduction but moreover for metabolic purposes. However, due to the depletion of the host factor and presumably also due to the overall appearing replication sites of the vRNA (the web regions), the cell will get into cell stress. The depletion of the host factor, the web regions and the appearance of the vRNA for sure are not beneficial for the cell and its metabolism.
To this end, our simulations recapitulate already by now the major events of the vRNA cycle as observed experimentally. Since the vRNA reproduction of our model is also proportional to the host factor, a breakdown of vRNA or NSP production cannot take place which else would appear and which would not be physically sound.
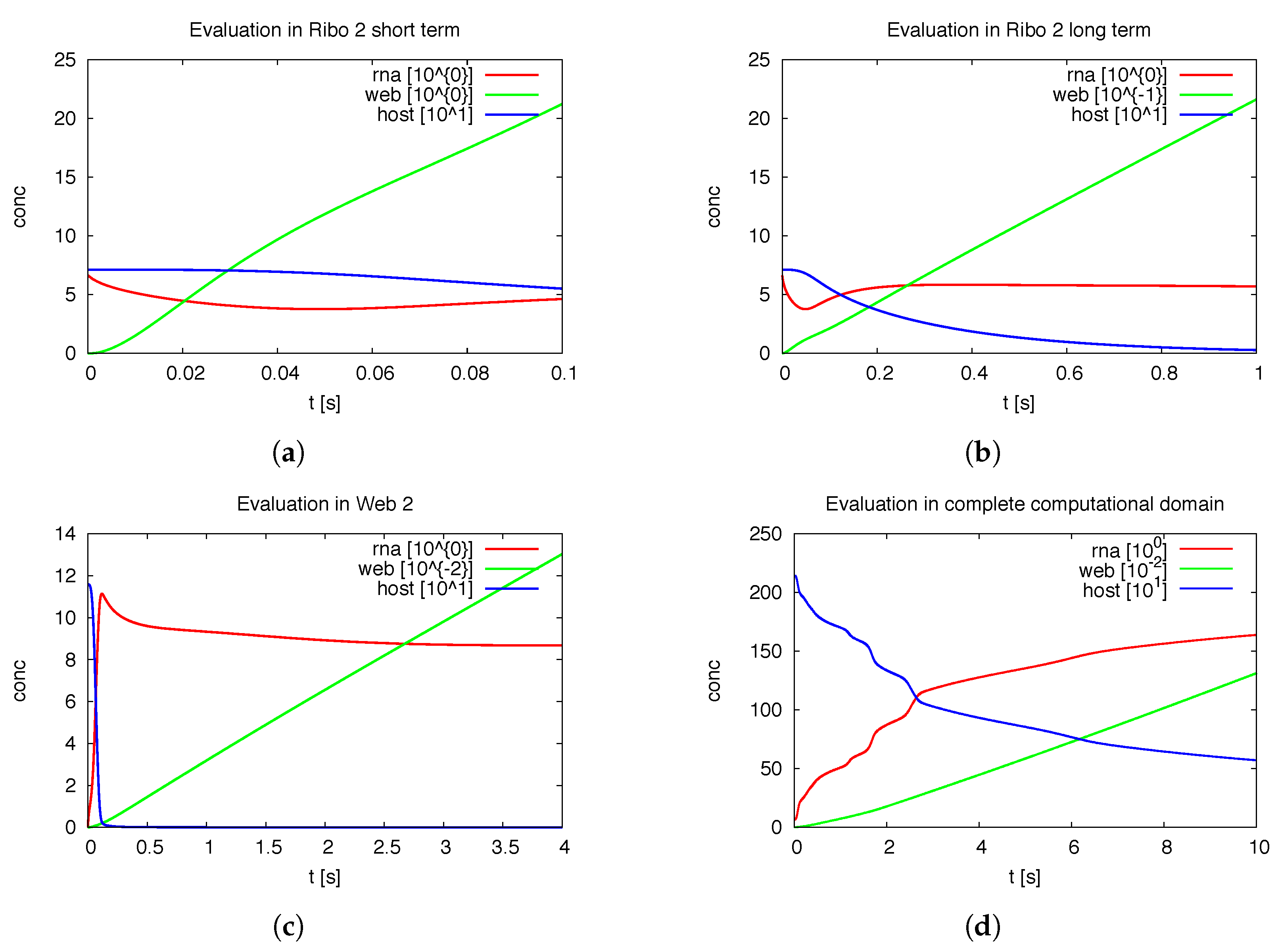
3.1.1. Quantitative Spatially Resolved Evaluation
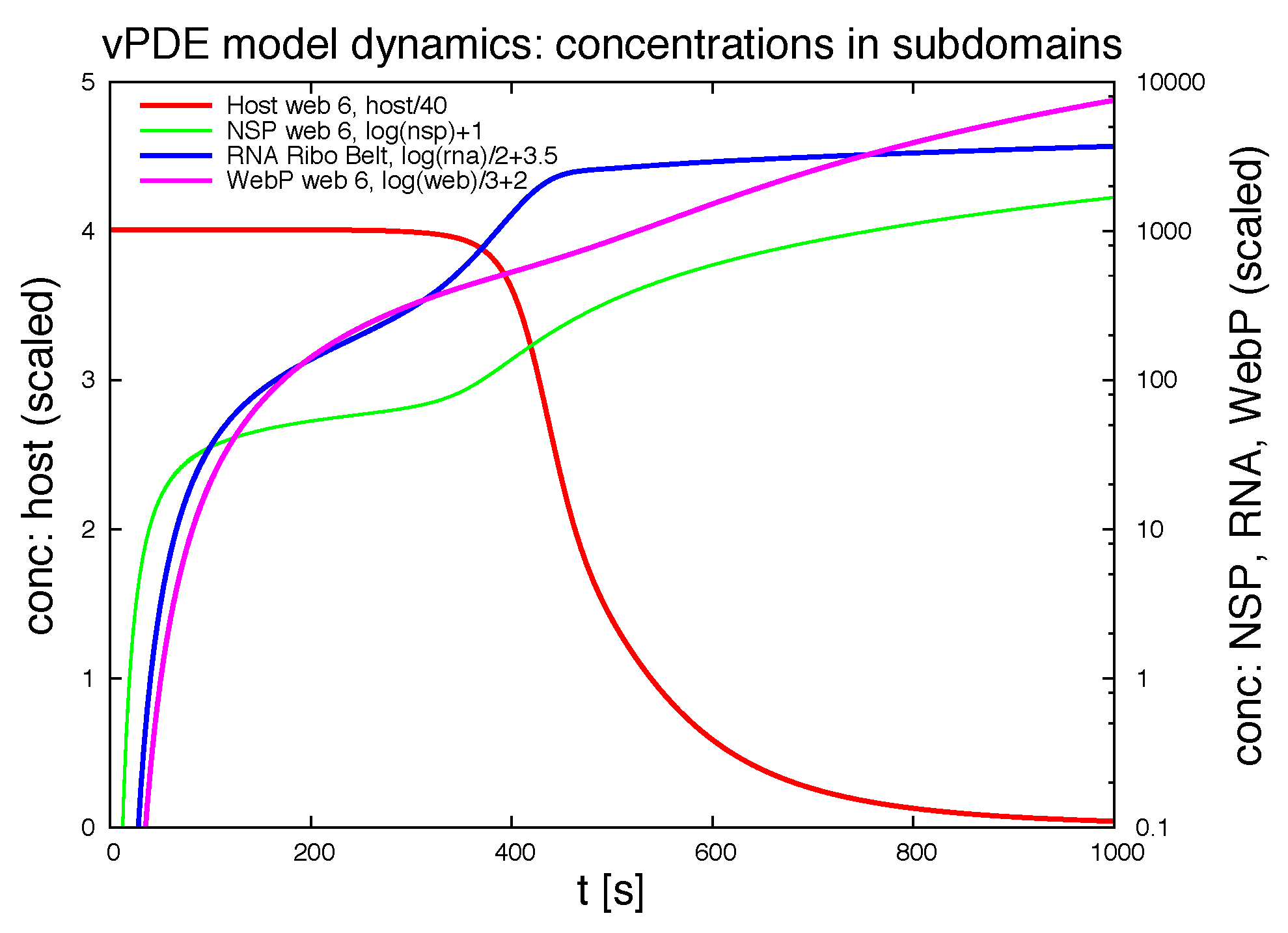
Figure 7 shows the deployment of the integrals of the concentrations within special subdomains, also resolved within different time scales. We show the development of the three concentrations of vRNA, web protein and host factor for the short time behavior at the beginning of the process within the first ribosomal region, where the vRNA is located at the very beginning. Further we depict the long time behavior at the same location. As well, we depict the deployment of the concentrations within the attached web region. Finally, we show the deployment of the integrals of the concentrations evaluated within the
complete domain of computation. In future work, our modeling framework has to be extended to complete cells and the model has to be further improved, namely also adapted to experimental values. Then, the integration of the concentrations over the complete cell will get an important benchmark test by means of the comparison to already by known known data averaged over the complete cell. For example, [
39] reported data concerning the deployment of the numbers of different viral proteins and the vRNA for single cells.
Of special interest is the observation of the step structure in the RNA dynamics as visible in
Figure 7d: Each time that the RNA reaches a new web, the overall RNA level develops some sort of step-wise increase. The “step-structure” of the RNA increase is due to the successive involvement of new web regions. Hence, the influence of the spatial distribution of the membranous web growth manifests itself trough the “staircase”-shape of the curves of the integrated concentrations of RNA and the host factor, as visible in
Figure 7d. It would bring new insight to observe such effects within fluorescence data of single cells. Anyhow such an observation will not be possible within Western/Northern-blot analysis based homogenized experiments. Spatially homogenized descriptions did not predict such structures up to now to our best knowledge.
It would be also interesting to investigate experimentally weather the propagation of the RNA through the cell causes some sort of ordered “switching on” of new webs, or if the RNA induced translation and web growth appears randomly all over different places of the cell. Fluorescence experiments presumably have the potential to investigate this property. Such research would help to justify our simple RNA diffusion approach or would ask for more involved RNA dynamics descriptions, thereby helping to resolve the so far experimentally unresolved question of the RNA movement properties.
3.1.2. Variation of the Parameters and Web Numbers
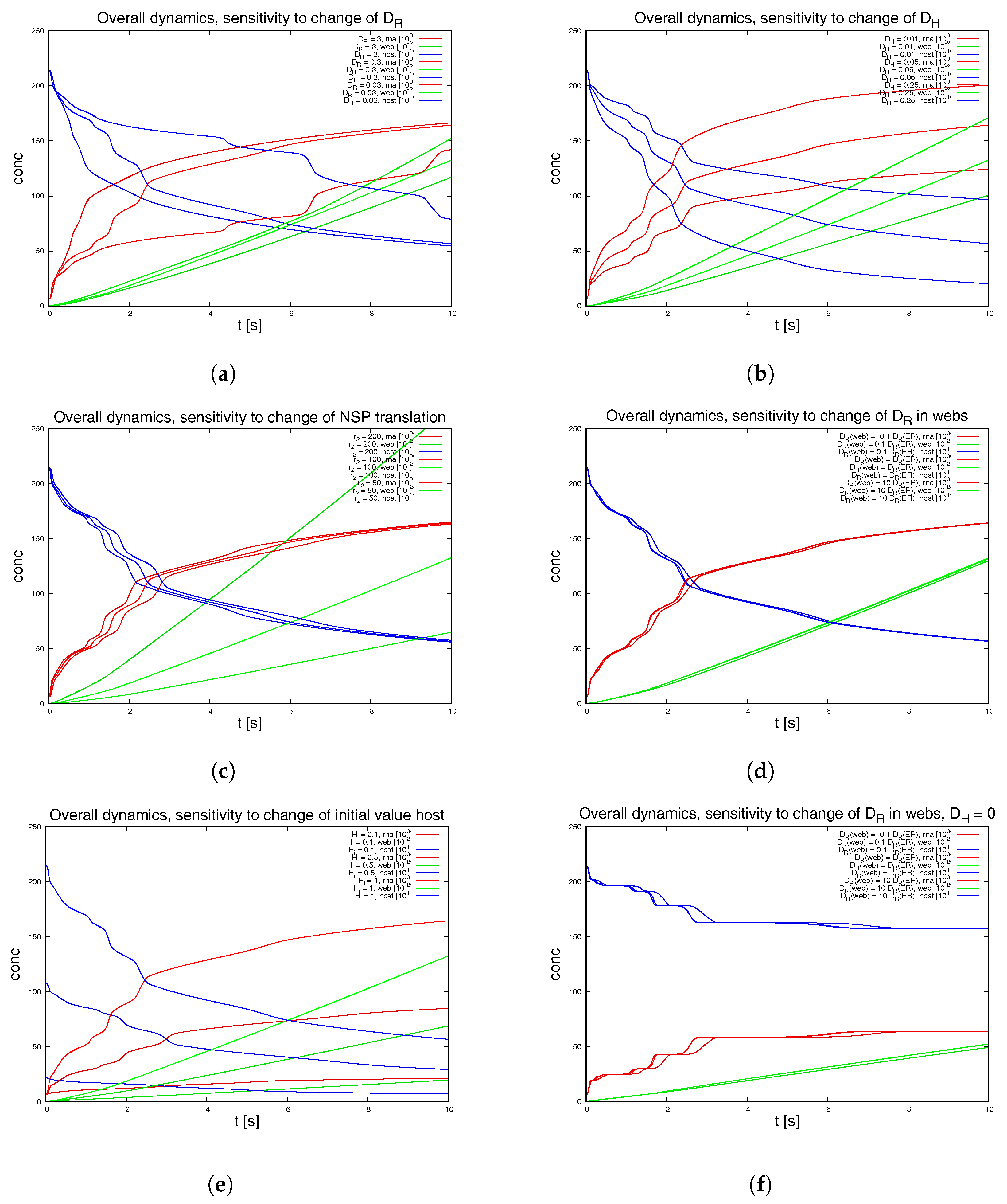
To test for the sensitivity of the model, we vary the parameters featuring in the sPDEs.
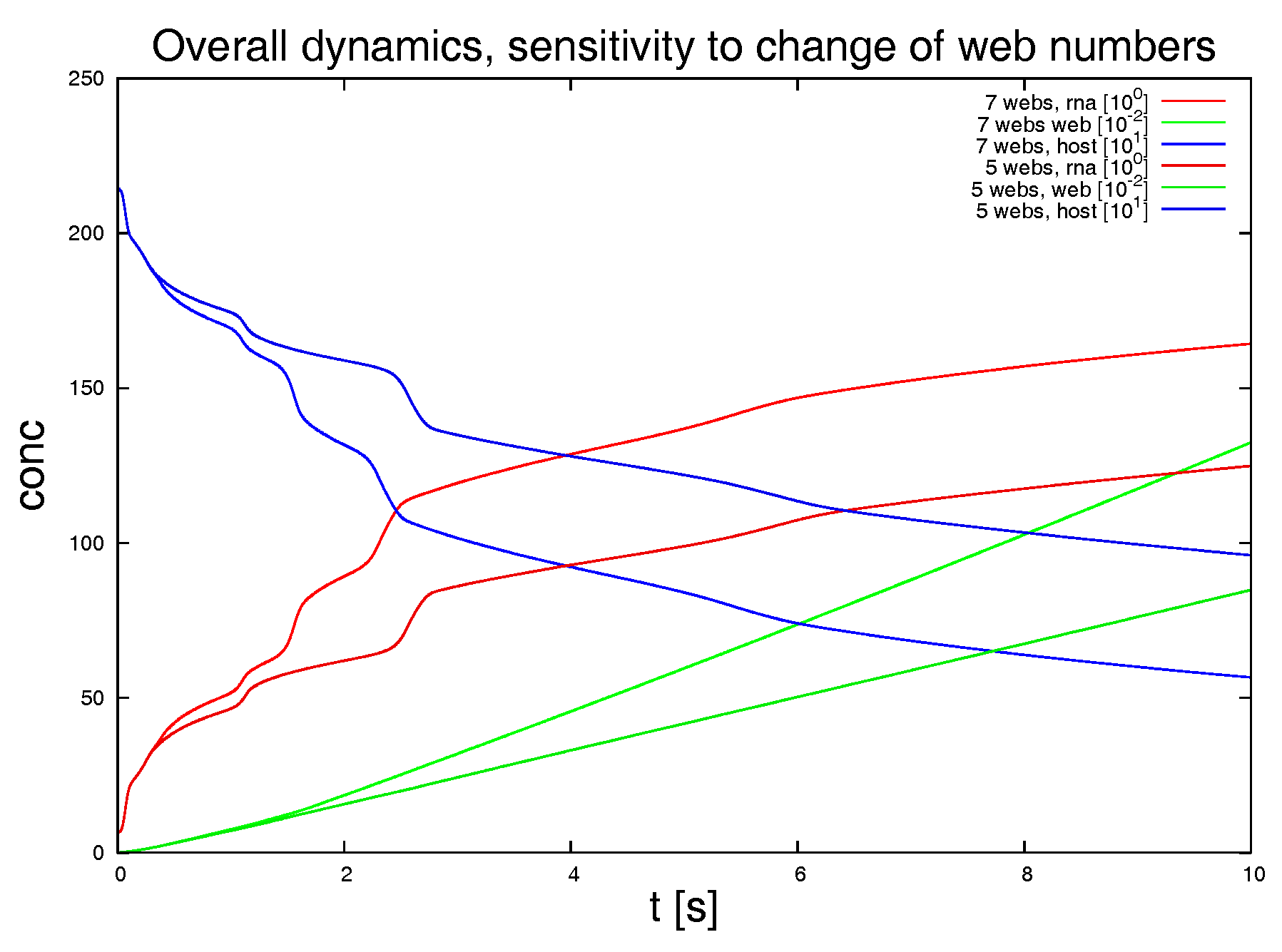
Figure 8 depicts various examples. We also switch off some of the webs in order to mimic a less dense web.
Figure 9 shows the result of this study. The latter approach is non-biological and just for test purposes, while the other variations allow for insight into the structure of the sPDE model upon the realistic reconstructed geometric structures.
The graphical representations show the integrals of the concentration of RNA, web and host factor for the complete computational domain. Hence they repeat those results of
Figure 7d which depicted the overall dynamics. These overall kinetics behaviour also gives the base for comparisons to ODE models.
We remark the following major observations:
Figure 8a: For the initial dynamical phase, the variation of the diffusion coefficient of the RNA has a major influence upon the RNA dynamics and the host factor depletion, while it has no major influence upon the long term level. The web growth however is only affected in a minor manner by the RNA diffusion coefficient.
Figure 8b: The diffusion constant of the host factor has a very important influence upon the complete kinetics.
Figure 8c: The reaction of the translation of NSPs (i.e., web protein, since intermediate polyprotein not considered) has an influence at the short term level each time that the RNA reaches a new web, but even in the middle-term level, this influence is nearly negligible.
Figure 8d: The influence of a pure change of the diffusion coefficient of the RNA inside the webs (keeping the diffusion on the ER as before) has nearly no influence upon the kinetics as long as the host factor may diffuse with a substantial diffusion coefficient.
Figure 8e: The initial value of the host factor has strong influence on the overall dynamics, but this influence may be considered to be even less important compared to the afore described influence of the transport of the host factor.
Figure 8f: Once the host factor diffusion is switched off, it is interesting to note that at a short-term level, the change of the RNA diffusion coefficient inside the webs shows substantial impact at the short term level, but not at the middle term level.
The latter observation indicates that the afore described, nearly vanishing influence of the variation of the RNA diffusion coefficient inside the webs arises from the superposed influence of the diffusion of the host factor. This argument also explains why the NSP translation rate has only minor influence upon the overall dynamics as demonstrated in
Figure 8c).
Switching off 2 of the 7 web regions, as shown in
Figure 9, demonstrates the strong influence of the density of web regions (i.e., number of web regions divided by the area of the considered volume) on the dynamics.
3.2. Surface PDE Model Incorporating the Polyprotein
In the last section, we have presented the deployment of the model with 3 concentrations (vRNA, web protein and host factor). On this way, we have neglected that the web protein does not get translated directly. Indeed, at first the polyprotein gets translated Equation (2b) and cleaves into the NSPs, namely the web protein Equation (2c).
Therefore, we consider this process again, in a complete manner including also the intermediate step of polyprotein translation and cleavage as indicated by the original full model of Equations (2a)–(2d) (respectively Equations (9a)–(9d), rewritten in a more intuitive form). This means that we describe the evaluation of the surface model of vRNA, polyprotein, web (accumulating/accumulated) protein and host factor.
The corresponding simulation
movie S2 Video in Supplementary Material shows the deployment of the concentrations of vRNA, polyprotein, web protein and host factor.
Figure 10 depicts a screenshot of this movie. Watching this movie, the dynamics is overall similar as in
Section 3.1. In contrast to before, this time the perspective is static rather then rotating. Therefore, a part of the concentrations is shown from different perspectives, i.e., some concentrations occupy more then one sector of the movie, hence are shown simultaneously from different (static) perspectives:
All three upper sectors show the deployment of the RNA, but from different perspectives. The lower three sectors depict (from left to right) the polyprotein, the web protein and the host factor.
Let us explain in detail the different perspectives of the movie sectors:
At top in the middle (one of three RNA sectors), one sees the geometry from the same perspective as shown at the beginning of the last
Section 3.1, i.e., as in
movie S2 Video in Supplementary Material: The perspective is from behind to the inner of the ER because we use again a cut plane for “opening” the ER (in the perspective, not in the simulation—the simulations are performed on the complete computational domain in all cases). This means that we may see the RNA initial concentration in the same way as we have seen it at the beginning of
movie S2 Video in Supplementary Material.
At the upper sector on the left, we observe the RNA at the same perspective which we have seen in
movie S2 Video in Supplementary Material after the rotation, i.e., we look from the front to the ER and the web regions.
At the sector to the upper right, we observe the RNA concentration from behind, but without the cut plane, i.e., from the same perspective as in the middle, but without the cut plane.
Therefore, we can observe the RNA deployment from nearly all possible directions including cut planes. The only “missing” direction would be from the front with a cut plane, but we omit this for the sake of simplicity.
At the lower left sector, we watch the polyprotein from behind with a cut plane (as the RNA upper in the middle). In the lower middle sector, we observe the web (accumulating) protein from the front view (as the upper left RNA), and on the right sector, we observe the host factor from the same front perspective.
Having described the preconditions of the simulation movie, we want to evaluate the simulation itself:
At the beginning, we see that the RNA (visible in the upper middle sector) translates the polyprotein (visible in the lower left sector) at the ribosomal region. The polyprotein cleaves immidiately into the web (accumulating) protein, causing the growth of the web (visible at the lower middle sector).
This causes the reproduction of the RNA within the web regions (visible preferably upper left, but also upper middle sectors). The RNA diffuses away and reaches the next ribosomal region (visible at the upper left sector and upper middle sector). Hence, the polyprotein gets translated also at this ribosomal region into the web (accumulating) protein (visible in the lower middle sector), the web protein diffuses into the web region and causes the reproduction of the RNA (visible preferably upper left but also upper middle sectors).
Again, as before, the RNA-“wave” propagates through the geometry and the host factor gets consumed at those places where RNA gets polymerized (visible lower right sector).
In the sector at the upper right (RNA concentration), one observes only at later time the RNA production at the corresponding web regions. This refers to the condition that those web regions which are located such that they are visible from the perspective of the upper right are not reached by RNA at the very beginning. Therefore, from the perspective of this sector, at the beginning one observes only few free diffusing RNA but no RNA which arises from reactive production. However, this changes once the RNA reaches the web regions visible form this perspective (respectively the “hidden” ribosomes corresponding to the interface of web regions and ER surface), then also there the polyprotein gets translated, cleaves into web protein, and the web protein accumulates at the web regions, forming the webs which replicate the RNA and so on.
Strikingly, only little of the polyprotein is visible over the complete passage of time. This is due to the fast decay of the polyprotein into the web protein. This observation justifies the approximation as realized within the section afore
Section 3.1, i.e., the model of only three concentrations.
Anyhow this approximation only makes sense as long as we consider only one non structural protein (NSP), which we denoted in this case as web protein (respectively sometimes web accumulating protein to be more precise). Once we extend the model thus that the polyprotein cleaves into various NSPs, we need the intermediate step of the polyprotein.
3.3. The Volume PDE Model
Like the models presented afore, the simulation of the mathematical model as described in
Section 2.4.2, i.e., Equations (10a)–(10d), capture the major events of the vRNA reproduction of HCV in a fully spatio-temporal resolving manner. In this model, we permit the dynamics within the volume of cytosol and of the web regions with the exclusion of the ER lumen. Therefore, the focus lies on different aspects compared to the surface models. The major disadvantage of this volume model is that, so far, the anchoring of the NSPs to the ER surface is neglected and replaced by a full volume movement. The latter one could be more appropriate for the host factor characteristics and maybe also for the movement characteristics of the vRNA.
We calculate the PDEs for the interplay of RNA (“
R”), NSP (“
N”), web accumulating/bound protein “
W” and a generic host factor “
H” as regulator which gets consumed when the web protein reproduces the vRNA at the membranous webs. The model is evaluated in the domain which consists of cytosol, web and ribosomes, i.e., the afore explained 3D continuum (
Section 2.3), i.e., the volume of the cytosol (with the ER lumen exclusion) and the web regions.
Figure 11 shows a screenshot of the simulation
movie S3 Video in Supplementary Material of the process using heuristic parameters. The complete movie visualizing the simulation from a cut perspective of the volume is attached as
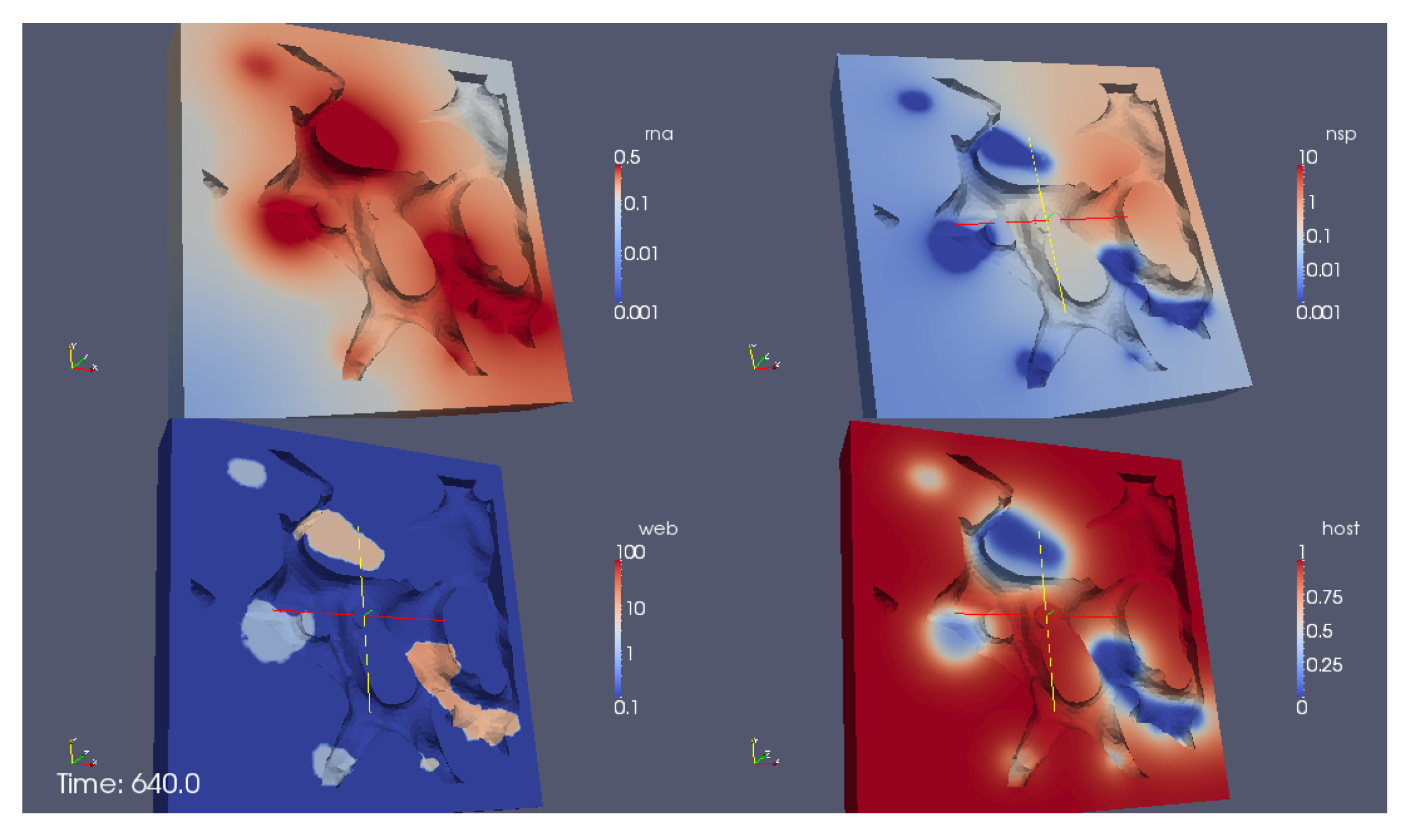
supplemental movie S3 Video in Supplementary Material. The perspective of the visualization is such that we consider the volume of computation disclosed by means of a cut plane. We visualize the RNA (upper sector at left), the NSP (upper sector right), the web protein (lower sector left) and the host factor (lower sector right).
In detail, we observe the following processes during the simulation:
The process starts directly after the uncoating of the first vRNA from the infecting virus. Therefore the simulations begin with an initial concentration of uncoated vRNA which is located originally within a sphere inside the cell close to ribosomes. The vRNA diffuses from its starting sphere and reaches the ribosomic region. (The ribosomic region has belt-like shape. It is not based on data. Moreover, we put the ribosomic belt “by hand” around a region of the ER). At the ribosomes, nonstructural viral proteins (NSPs) are translated. The NSPs diffuse away from the ribosomes and reach the experimentally predefined web regions. At these web regions, the NSPs get bound and form the membranous web complexes. The bound NSPs are denoted to be “web proteins” (web/webP). Since also the vRNA is diffusing within the cell, once vRNA reaches the membranous web complexes, vRNA gets reproduced. The new vRNA moves again to the ribosomes where the NSP translation mechanism gets enhanced. Also these NSPs diffuse away and reach the web regions. At the web regions, they get also bound as web protein. Since the web regions grow in this way, vRNA reproduction is further enhanced. A generic host factor gets consumed once vRNA gets polymerized and once the host factor is consumed, vRNA reproduction stops. (In this way, a breakdown of vRNA production is prevented, which also is biophysically sound—an unlimited production would not be realistic, and the energy which is needed to polymerize new vRNA for sure has to be strongly related to the host environment.)
Our framework allows the evaluation of the concentrations at each point in space (of the domain) and time.
Figure 12 shows the evolution of the integration of the concentrations of the ingredients within different subdomains (exemplaric values shown, evaluation possible for all ingredients at all spatital points and/or subdomains at any time point).
4. Discussion
The present state of the art with regards to HCV-specific computational virology is that models of HCV replication are represented by means of homogenized ODE models which are capable of describing a lot of important effects, cf., e.g., [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18].
However the spatial component of the dynamics plays an important role to develop a complete and well-founded understanding of HCV replication dynamics. For example, it would be important to understand why NS5A gets redistributed and changes mobility following application of NS5A inhibitors [
32], and it would be interesting to understand the role of the spatially non-homogeneous and discontinuous distributed membanous web regions [
30].
Therefore, we are developing spatially resolved models of the HCV vRNA replication cycle [
1]. In this paper, we presented the development of spatio-temporal resolved models of the vRNA replication cycle and corresponding simulations of our models. Our approaches mimic the interplay of vRNA, non structural proteins/membranous web growth and a host factor for directing the vRNA reproduction cycle in a spatio-temporal resolved manner. Our PDE models are highly related to the realistic reconstructed ER geometry (either its surface or to the cytosol as established by means of the ER surface forming its boundary, depending on the model) acknowledging the major role of the ER in plus strand RNA virus replication [
3].
Indeed, the equations we use are in principle just the extension of the state-of-the-art standard HCV ODE models which describe all processes with space-independent reaction constants, cf., e.g., [
5,
6,
17,
18], even so so far with less states. Our extension to the spatial description however gets performed from the very beginning upon highly realistic geometric environments.
Therefore, our simulations already by now capture the main events of the vRNA replication cycle as we have shown with the simulations as presented afore in
Section 3:
When a HCV virus particle enters a hepatoma cell, it uncoates its vRNA. The vRNA moves to the ribosomes. Nonstructural viral proteins get produced, create the webs where the vRNA gets replicated. The vRNA moves again to ribosomes, the vRNA cycle is closed and starts again respectively continues. Our simulations based upon the models as developed within
Section 2 and presented within
Section 3 reproduce these events based on different mathematical descriptions which leads to biologically meaningful simulations. Nevertheless, our approach is so far more qualitative and also restricted to a specific sub-part of the ER.
We created two types of models: Models which focus upon the restriction of the movement of viral components to the surfaces of the ER and the webs (motivated by the experimentally well-founded anchoring of the NSPs to the ER surface) and a model which allows for the movement of all components within the complete cytosol and and the web regions with the exclusion of the ER lumen (motivated by the assumption that the host factor and maybe also vRNA movement is not restricted to any surface but take place within the volume of cytosol and webs.)
Indeed, these approaches presumably have to be combined in the middle run in subsequent work. Nevertheless, we consider them to be a first but well-founded approach of spatially resolved HCV models.
Let us evaluate the models critically in detail:
4.1. The Suface PDE Models
Our sPDE models represent the first approach of surface bound dynamic descriptions of the major components of the vRNA replication cycle.
We presented two types of this model type: One model incorporated the polyprotein state while the other model neglected this intermediate step due to the time scale which is short in comparison to the other events of the process.
While the corresponding simulations reproduce the main effects of the vRNA cycle, the reproduction process of the vRNA is not restricted to the web surface in reality, but moreover takes place within the volume of the webs. Nevertheless we restrict the vRNA reproduction to the surface of the web regions in this model. The latter fact is of minor importance for the quality of the surface models at this model stage since the surface of the webs and their volume are comparably at similar scales within the geometric structure we analyze, thus we may use surface descriptions of the replication processes within the surface PDE based models. The same argument applies to the related dynamics of the growth of the membranous web regions by means of web protein accumulation. However, a minor disadvantage of the surface models presented here is that vRNA movement is restricted to the ER surface even though experimentally it is not clear how vRNA moves (cf., also the discussion in this paper in
Section 4.6). Eventually, the vRNA may move also in the cytosol. In particular, it is doubtful if the host factor movement should be restricted to the surfaces of ER and the web regions. Therefore, we developed also a model where all components move within the complete volume of cytosol and web regions while the ER lumen is excluded from the computational domain.
4.2. The “Volume” PDE Model
In the new volume model, the movement of the nonstructural viral proteins, vRNA and the host factor is possible within the complete cytosol volume (with the exclusion of the ER lumen as indicated also experimentally, i.e., the ER lumen does not participate in the vRNA cycle as indicated also by experiment [
1]) and the volumes of the membranous web regions. However, this model neglects the important biophysical property to restrict NSP movement to the ER surface which was clearly proved by experiment [
1], in contrast the movement of the viral proteins is possible within the complete cytosol. Therefore, we developed the afore mentioned models which take into account the attachment of the viral proteins to the ER surface.
4.3. Comparison of Our PDE Models to ODE Models—Relationship Form/Function
To the best of our knowledge and understanding, a basic ODE model of HCV replication kinetics at the cellular level has been presented in [
6], whereas an extension of this model has been recently proposed, for example, in [
17]. These models enable a description of the overall kinetics of the basic compartments of HCV replication. Dahari et.al. [
6] introduced an ODE model describing the interaction of various compartments which are separated into cytosolic and web bound parts. Basic components are RNA, translation complex, polyprotein, NSP polymerase and different states of double stranded RNA, which arise from multilinear reactions of the other constituents. The core of the model is given by the multilinear transition and production rates of RNA which is resolved by means of various intermediate steps (namely the transition rates of the constituents between the the cytosol and the webs and the afore mentioned various intermediate states of the RNA). The RNA production is based on a detailed description of different forms of intermediate replication complexes that appear in several places of the model equations in the form of multilinear reactions of NSP polymerase and web bound RNA. The latter ones form other states of replication complexes with the same characteristics, and incorporating double strand RNA. Another important feature of the RNA kinetics model presented in [
6] is that there is one unknown, corresponding to one type of RNA and NSP concentration, for each compartment
and for each aggregation state in which the constituents appear.
In part, some of the states of the RNA which intend to mimic spatial states of the RNA within the ODE models are entire part of one RNA state at different spatial locations. In our spatial model, this distinction appears more natural. Nevertheless, some of the biophysical bound states still could be resolved more finely also within our approach because in some cases, the distinction just based upon the spatial location is a rough first approach and it will be useful to introduce different states at the same spatial location, based upon different biophysical states.
The reaction terms describing the evolution of the different aggregation states of the double strand RNA are multilinear functions. These functions describe the production of new (web bound) RNA. The newly synthesized RNA forms in part new replication complexes and in part reacts into cytosolic free RNA. Degradations of various components are included. To this end, the cell is considered to be homogeneous, and those time delays which arise from transport are modeled by means of reactions which replace transport by transition rates. All in all, the reactions which describe the transitions and productions from and to different states are in various cases effective reactions which incorporate also the transport properties. The model harbored various unknown parameters that were fitted such that the steady state properties of experiment were reproduced. The fitting of the unknown parameters of the afore described multi-parameter model to experimental data as extracted from averaged samples of in vitro experiments allowed for the design of a model which was capable of describing the spatially homogenized dynamics of a sample of cells [
6].
Binder et.al extended the model of [
6] substantially [
17]. The authors of [
17] measured the homogenized RNA levels within the first hours after virus infection of the in vitro cell samples. Hence, in [
17], an ODE model in a similar style as afore [
6] but with various extensions was developed which allowed for the description of the overall dynamics of the RNA levels of the cell samples as well within the first hours after infection and also for the steady state phase. Northern blot analysis of the viral plus- and minus-strand RNA formed the experimental basis of the fit of the model to the data of [
17], i.e., all data were averaged over a sample of cells. The principle of spatial homogenization was applied and the homogenized ODE compartment model was able to capture the effects of the homogenized sample to reproduce the dynamics of the system [
17]. The authors of [
17] also introduced a host factor which was crucial for fitting their model to the dynamics of RNA replication. Therefore, we used the host factor principle of [
17] as inspiration to avoid the RNA breakdown which also else would happen within our model framework. Binder at.al [
17] also used trilinear reaction terms incorporating the host factor for RNA replication as in principle in our case. Thus, the model of [
17] allowed for a distinguishing between high and low permissive in vitro cell lines due to different host factor properties. (A cell “line” is a term of virology to denote a special cell type.)
While the ODE model of [
17] established the influence of the host factor, a spatial model could help for resolving the origin of the difference in the host factor influence for e.g., different cell lines which is beyond the potential of compartment models.
The authors of [
17] further performed a sensitivity analysis to figure out which reactions of the ODE model have the most impact onto the RNA replication, searching hence for how to break the RNA cycle the most effectively. This analysis gave insight into the sensitivity of the RNA production to various intermediate steps. Since the reaction rates of the ODE models are effective reactions which may incorporate transport phenomena, the PDE based ansatz has the potential to resolve this sensitivity analysis in more detail, for example by disabling some of the webs in the simulation environment or to change diffusion parameters to test for the influence of the interplay of transport and reaction as we have demonstrated afore in this study. Such efforts are much more difficult to perform within experimental approaches compared to our simulation framework.
Degradation effects are so far neglected in our approach due to the proof-of-concept of the qualitative model without fit to experimental values. The introduction of reactive degradations is technically easy within our framework and has to be done once experimental values available.
To this end, the ODE models of [
6,
17] enabled a lot of insight into various processes of HCV replication which may be considered at a spatially homogenized level.
Hence, the models of [
6,
17] represent approaches to model various basic effects of HCV replication by means of techniques homogenizing the concentrations over the complete space hence neglecting the spatial component. Such approaches are always useful as long as the spatial aspect may be neglected at a first approach or as long as spatial effects are negligible. This assumption holds true for the questions of [
6,
17] and their respective answers allowed for deep insight into HCV replication dynamics. However, there remain other questions which are rather difficult to solve upon a pure ODE approach which neglects the spatial aspect.
Indeed, our PDE models are in principle an extension of the ODE models of the [
6,
17] type to the spatially resolved case for acknowledging those effects which may not be resolved as long as spatial resolution is neglected and for approaching to a higher resolution with respect to the details of the underlying processes.
Therefore, while the models of type [
6,
17] are already realistic, our model approach may allow for more detailed insight. For example, the step structure of RNA replication which we have shown qualitatively once a new web starts its work has not been proposed upon ODE compartment models. Of course, it will remain to future experiments to investigate if the step-structure will be a main feature of spatial HCV models, or if other aspects will predominate based upon our new approach.
The overall kinetics of our PDE ansatz differs to basic ODE models like e.g., [
6,
17] in particular in the following way:
The reaction terms are restricted only to the regions of the interior of a cell in which it is known from biology that they are allowed to occur.
Also in the limit case of no diffusion, the spatial resolution of the reaction terms implies that the kinetics of the considered problem is not space-independent. Rather, different reactions occur in different places and, in principle, also non simultaneously. In a model based solely on ODEs, these aspects of the phenomenology cannot be resolved, and the reaction terms should thus be understood as effective. The fact that the concentration of an agent, e.g., the concentration of the viral RNA, R, features in different cellular regions (indeed, R appears both in the reaction term defined over the web-regions and in that defined over the ribosomes) means that the considered substance has to “travel” from one region to the other in order for the reactions to take place. Moreover, this travel (in fact, a transport process) is characterised by time-scales that are generally different from those associated with the reaction terms and by length-scales that require a fully spatial resolution of the kinetics. This is the main reason for justifying the introduction of diffusion in the model equations.
In particular, as stated afore, ODE approaches allow comparisons to the averaged sample of various cells evaluated together, but they do not allow, for example, detailed comparisons to spatially resolved fluorescence data where the processes are considered in detail. To understand spatially resolved observations like fluorescence microscopy data rather then e.g., Western/Northern blot analyses of samples of cells, spatially resolved models are unpreventable .
Therefore, we cite [
17] concerning the webs:
“The exact architecture and topology of these structures, and particularly their structure-function-relationship, is not fully understood yet”. It seems to be rather unlikely that an ODE model bears the potential to resolve for example this important question of the relation of form and function. However, PDE models bear the potential to resolve the relationship of form and function as we have demonstrated in [
53] for the case of presynaptic boutons within computational neuroscience. A PDE model could help for resolving, e.g., if the difference in the host factor for different cell types arises from its entire initial concentration, or from the transport properties. Our investigations as shown in
Section 3.1.1 and
Section 3.1.2 suggest that the availability of host factor in a cell line may not only depend upon its total amount within the complete cell, but moreover upon the transport mechanisms offered by the cell line.
Finally, also the switching-off of single webs is rather difficult to simulate within ODE models, while it appears natural within PDE models at realistic reconstructed geometries.
The overall behaviour as depicted in
Section 3.1.1 and investigated with respect to parameter variations in
Section 3.1.2 demonstrated an important impact of the RNA and host factor transport properties upon the global kinetics. In particular, the transport of the RNA to the next webs caused a step-like influence upon the RNA uprise kinetics. These properties have to be investigated in more detail by means of adequate new experiments, based, e.g., upon fluorescence data of single cells with high spatial and temporal resolution. If the spatial propagation of RNA will be revealed by experiments to be different from the one suggested by us, our model will need further refinement, since such a different behaviour may cause different kinetic properties. In any case, the overall kinetics of the dynamics of the levels of the concentrations within single cells presumably may have not so continuous structures as they appear within evaluations which are homogenized over the space.
To this end, our spatial framework creates, for example, a basis for the detailed investigation of the relation of form and function during HCV replication within single cells. Our virus model of this study is a first step on this way for virology purposes to resolve, e.g., questions of form and function, which of course still will need ask for a lot of forthcoming efforts on both sides, in silico and in vitro/in vivo.
4.4. Critical Summary and Potentials of Our Models
We have developed new fully 3D spatio-temporal resolved models of the HCV vRNA replication cycle. Intriguingly, these models are capable of reproducing the main events of the vRNA cycle (as known from experimental analysis) in a qualitative but spatio-temporal resolved manner. Our simulations demonstrated the potential of new directions for research, which we initiate by means of the spatial framework we introduce for mathematical modeling of viral replication cycles. Therefore, we predict that the introduction of spatial resolution could represent a significant step forward for approaches to computational virology in the future.
We present a model of HCV vRNA replication dynamics based upon a realistic reconstructed geometric environment of an immonustained hepatocyte, i.e., we developed and simulated a 3D spatio-temporal resolving PDE model mimicking the HCV vRNA replication cycle within a specific subsection of a realistic geometry based on experimentally-derived data. The parameters of the diffusion-reaction PDEs we use so far are heuristic, however it is important to fit the parameters from new experimental data.
The model is capable of covering all major steps of the vRNA replication cycle dynamics in a spatially resolved manner: vRNA uncoates, translates viral proteins, the viral proteins cause the growth of the membranous web, the vRNA gets replicated inside the membranous web. The newly synthesized vRNA moves again to the ribosomes where new NSPs are produced. Thus, the first vRNA cycle is complete and then subsequent cycles continue. During vRNA reproduction, a generic host factor gets consumed which aims the involvement of the host into the vRNA polymerization and which prevents unlimited vRNA reproduction (which would not be biophysically sound).
The state-of-the-art ODE model computations effectively perform summations of each component (like vRNA or NSPs) over the complete cell. Our simulations allow for the evaluation of the concentrations of the components of our models at each point in time and space of the computational domain. Our simulations are visualized as movies and hence allow the observation of the in silico processes in a manner similar to observations of in vivo/in vitro experiments by microscopes, however with the advantage of a much higher resolution, though with some obvious restrictions, such as:
At first, the location of the ribosomes is simplified in both approaches presented here, also due to a lack of exact experimental information. Presumably, it would be comparably easy to get experimental data concerning this aspect.
Further, it does not seem to be very realistic that the vRNA may diffuse away while it gets translated and may get, in part at the same local point, even replicated.
Therefore, to make the model more realistic, it will get necessary to distinguish between different states of the components, e.g., to treat vRNA different when it is bound to ribosomes compared to when it gets replicated inside the webs.
Also, the multilinearity of the reproduction process of the vRNA, cf., Equations (2a)–(2d) (the surface PDE model and all subsequent simplifications of this type) resp. Equations (13a)–(13d) (the volume PDE model), is valid only for small concentrations. However, we use this type of reaction since it is also state of the art of the ODE models.
Further, the coupling of surface based events and volume based events, i.e., the coupling of 3D sPDEs and 3D volume PDEs will become important, since some agents like the NSPs are bound to the ER surface, however other agents like the host factor are presumably able to move in the cytosol, the web proteins are able to move within the volume of the web regions, i.e., within a volumetric framework. Thus, in future research, forthcoming models will need to combine volume effects like host factor diffusion, and surface effects as they are proven experimentally for the NSPs (as they are realized within the afore explained surface models). Such couplings of sPDEs with volume PDEs will cause further challenges referring to modeling but also to numerical evaluation techniques.
Finally, one will also have to take into account that even though actually we call the limiting factor “host factor”, that host factor may play a different role in this context, it could even get enriched in the web regions as it was recently shown for ATP [
3].
Within future research, strong interest could refer to the question whether there any general characteristics of the ER and the web structures that can be used to generate random structures. For example, it would be interesting to evaluate the average distance between webs and the average web volume. Also the curvature structure of the ER surface and the ratio of e.g., volume to surface or the ratio of length of ER branches to volume could be of interest. Such a question could be handled with the help of e.g., SpineLab [
54] which allows for the generation of characteristic skeletons. Also we have various tools which we apply already sucesfully within spatially resolved computational neuroscience like NeuGen [
55] which could serve as basis also for creation of artificial ERs. Especially when trying to apply this modeling framework to novel experimental data it would be interesting to know if there are some specific characteristics that determine the topology of the ER and membraneous web.
To date, our work focused more upon the development of a model using geometric structures derived from real experimental data rather than artificially created geometries. In any case, the question gives rise for interesting future studies which are beyond the scope of the present paper.
The present study represents the first step of the development of a model that takes into account the geometry of the ER. To derive results which can be verified experimentally, realistic geometries are needed. Therefore, these studies could serve as basis for the identification of the crucial parameters of the geometric structure and hence serve for the randomly based creation of artificial but reality-similar geometries. This is one of the reasons why we perform 3D studies—to investigate for the influence of the geometry upon the dynamics. Therefore, future work will have to incorporate the comparison of the results of the dynamics for different realistic reconstructed cell environments. Such work we already performed for the estimation of the NS5A diffusion constant based upon experimental FRAP time series cross combined with different topologies of ERs to investigate the influence of the geometry upon the result [
40]. Our results (which are so far unpublished) demonstrate clearly the strong influence of the geometry upon the process dynamics of even one single ingredient of the vRNA cycle—depending on the geometric structure, the transport “velocity” of the NS5A spread changes strongly. The propagation velocity of NS5A over the cell depends strongly upon the ER itself, and hence also the vRNA cycle itself will change its dynamics depending on the structure of the ER.
During the way to make our model quantitative, we will include of course such checks and quantitative validations with different geometries into the project. The aim of this paper is to introduce the model framework itself and to demonstrate its potential in a qualitative manner.
To this end, our approach is based on two columns which are intended to grow together in the middle run: On the one hand, we are doing parameter estimations of single components of viral replication based on the Gauss-Newton algorithm in order for extracting e.g., the diffusion constant of basic viral proteins on the surface of the ER using experimental FRAP (fluorescence recovery after photobleaching) time series [
37,
40,
56].
On the other hand side, we are developing (as presented here) the model which mimics the interplay of all important components of virus replication, e.g., viral RNA, nonstructural viral proteins and a host factor. The estimated parameters are entering the model step by step. Therefore, the presented work is a practical application of the powerful simulation software tool UG4 [
34,
36] and its multigrid techniques in the context of modern biophysical research. The computations are performed at leading supercomputers [
37] and hence bear the potential of fast and efficient comparisons to experiment once the model gets quantitative.
4.5. Multiscale Modeling
Even though the analysis of small fractions of a cell could help for new helpful insights, we suggest that for a complete understanding, complete cells will be needed to derive a complete understanding. We suggest the extension of the model to complete cells will have to go hand in hand with the adaption of some parameters which could be based in part upon small fractions of experimental cells. However, we suggest small fractions may have special behaviour which changes too strongly from one region to the other, indicating that consideration of complete cells will become necessary in the long run. Of course, some questions could be answered by considering only small fractions of cells, while other questions will likely need to account for the whole cell.
As next steps, there are two project directions in our view: On the one hand side, we intend to extend our model from small pieces of the ER to the complete ER. The computational domain needs to be extended to complete cells once experimental data are available which allow for a fitting of all parameters of the basic PDEs. Complete ERs were already reconstructed by us for various hepatocytes represented by fluorescence z-stacks, cf. for more detail [
40]. On this way, a coupling of surface PDEs to take into account surface effects and “volume” PDEs for volume effects will get necessary for sure.
On the other hand side, the model has to get realistic quantitative parameters. In particular, we intend to use realistic parameters as far as ever possible, like e.g., the afore mentioned estimated (so far unpublished) NS5A diffusion constant.
In the other direction of scale, a future aim could be to make a more detailed model of spatially resolved webs, i.e., a single web based e.g. on electrotomography data [
2] taking into account the different vesicle types as DMV or Single or Multi Membrane vesicles (SMV and MMV) [
2].
Future models could incorporate vRNA and protein degradation. The inclusion of degradation effects is trivial within UG4, therefore we omitted this small point within our first approach.
An important milestone of the model development will be to be able to reproduce quantitative data such as [
38,
39].
Besides all restrictions as discussed above, our approaches show the potential of spatial models of virus replication at realistic reconstructed geometric structures. Since many details are still unclear even qualitatively also in experiment, our approach represents a good basis for extensions in the interplay of model extensions and new experiments.
4.6. The vRNA Transport and the Web Movement
In particular, further improvements will ask for the afore mentioned improvement of the vRNA movement. A delicate detail will be the question if indeed the vRNA “cloud” diffuses just around, causing the vRNA/NSP front to move like a wave through the ER; or if the RNA moves around and binds in a stochastic manner, causing not a wave-like spread of the webs, but moreover a spread in the way as if “lights” would be switched on randomly in a random order randomly distributed in time and space all over the ER, until the ER is filled completely. This could be a point which could be tested also experimentally and would have strong impact upon our forthcoming model improvement.
Of big interest and challenge will be the aim to model the movement of the small web particles as described at first by [
30]. The modeling/simulating of the web movements will get a technical challenge, as well with respect to the physical description on the one hand side as well as the technical realization within the FV context. Insights could be gained by experiments which we propose for this sake also in order for getting a basic idea of how the particles move spatially.
4.7. Future Perspectives of Spatial Virus Modeling
In the medium term, our model development has the potential to help contribute to a more detailed understanding of the viral replication dynamics, hence allowing for the planning of more straightforward experiments.
In the course of the afore mentioned possible model improvements, we suggest that our framework may allow for substantial input for experimental design in order for augmenting the “mechanistic”, i.e., mathematical-biophysical, understanding of the HCV replication dynamics, also in order of having a tool to give support in the context of the development of new DAAs.
In the long run, our model development has the potential to give substantial impact on the quantitative understanding of those basic virus replication properties which are dependent strongly upon spatial patterns, like, e.g., the interplay of form and function of intracellular virus replication mechanisms. Therefore, our approach may be considered as an entire interdisciplinary pathway with substantial future perspective.
4.8. Context of ER Related Research
Only few approaches so far take into account realistic ER geometries in the literature to our best knowledge at all in any biological fields. Indeed, we only could find [
57] which calculate Calcium dynamics on top of a reconstructed ER geometry based on electrotomography stacks using Finite Element (FE) methods and a tetrahedral grid representing the ER lumen. This approach remembers us to our method shown in
Section 2.2 and
Section 3.3.
Anyhow, the ER takes a major role within various fields of pathogenesis. For example, the authors of [
58] have shown recently the important role of the ER respectively its disfunction within the pathogenesis of Alzheimer. Therefore, also in such a context, spatial models could help for new insights.
To this end, our new approach opens new gates of basic research for various fields of medicine and biophysics and even for clinical applications in the long run, not only, but in particular also, for virus infections.