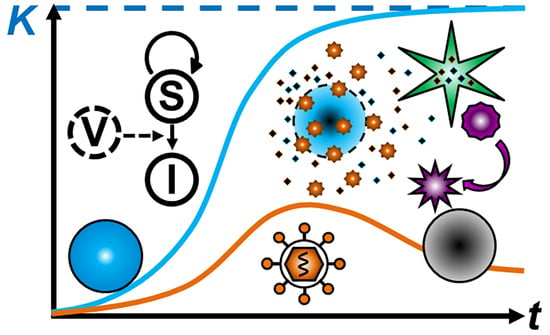
Fighting Cancer with Mathematics and Viruses
Abstract
1. Introduction
2. Mathematical Modeling of Tumor Growth
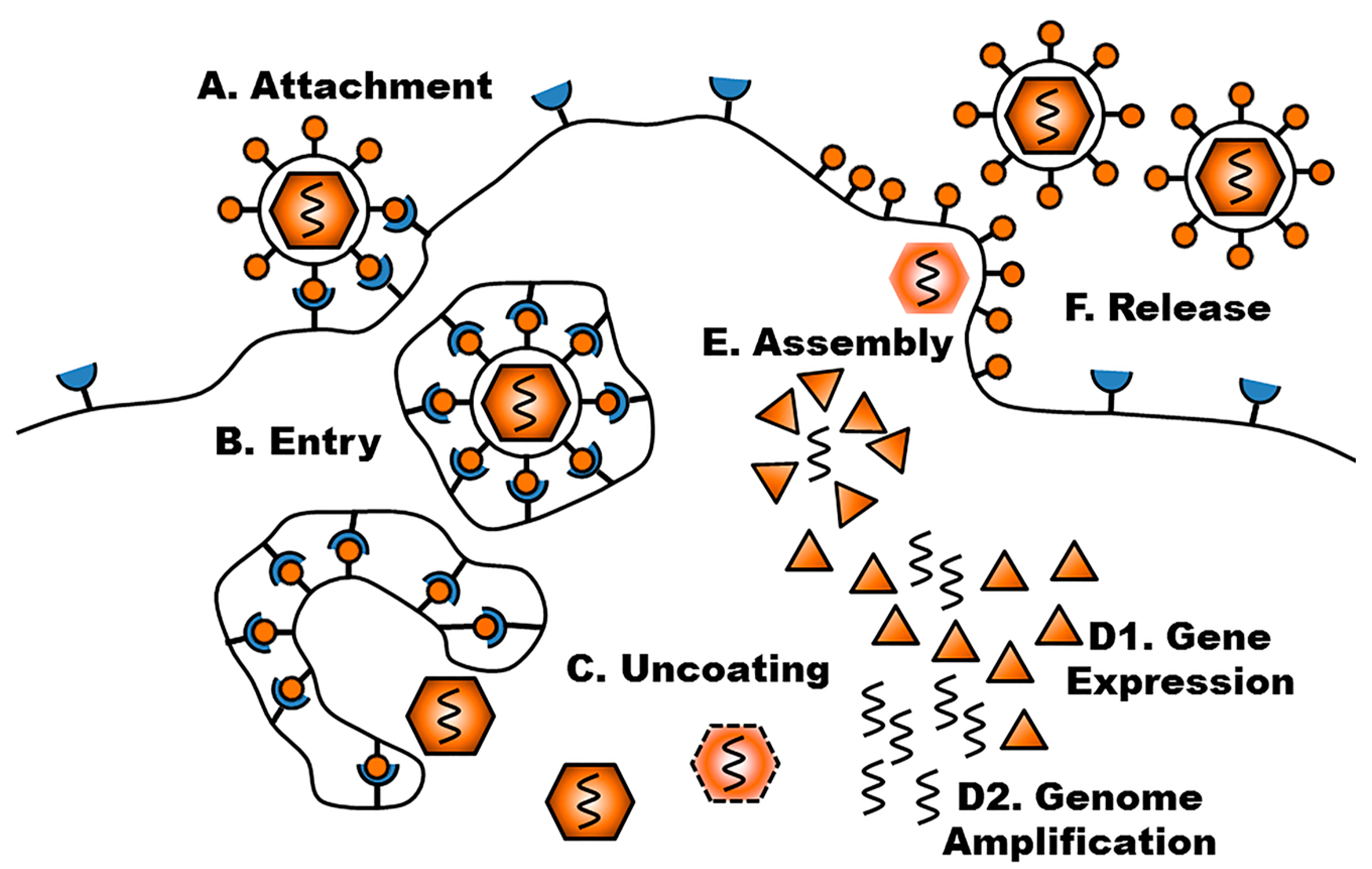
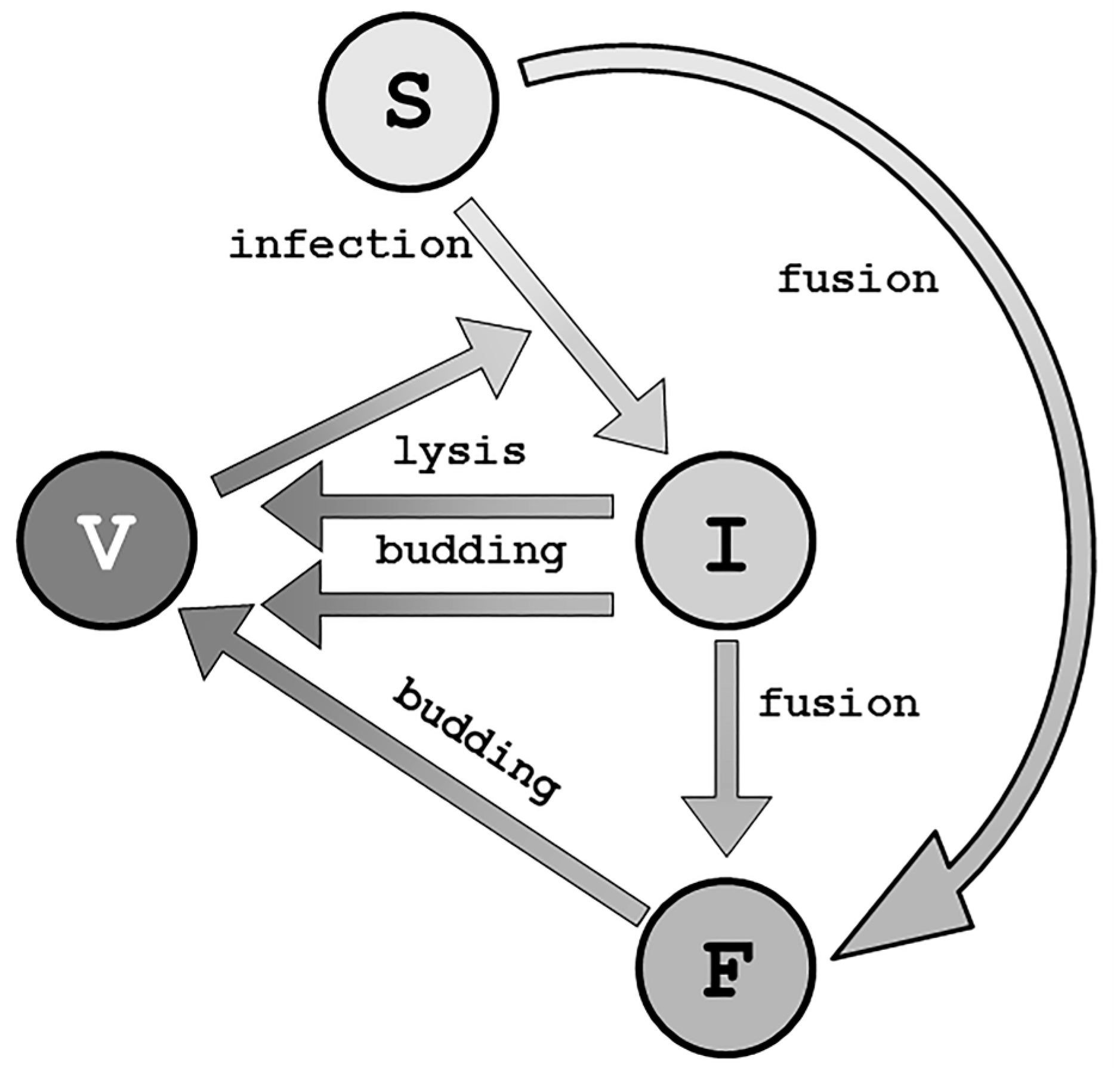
3. Viral Life Cycle
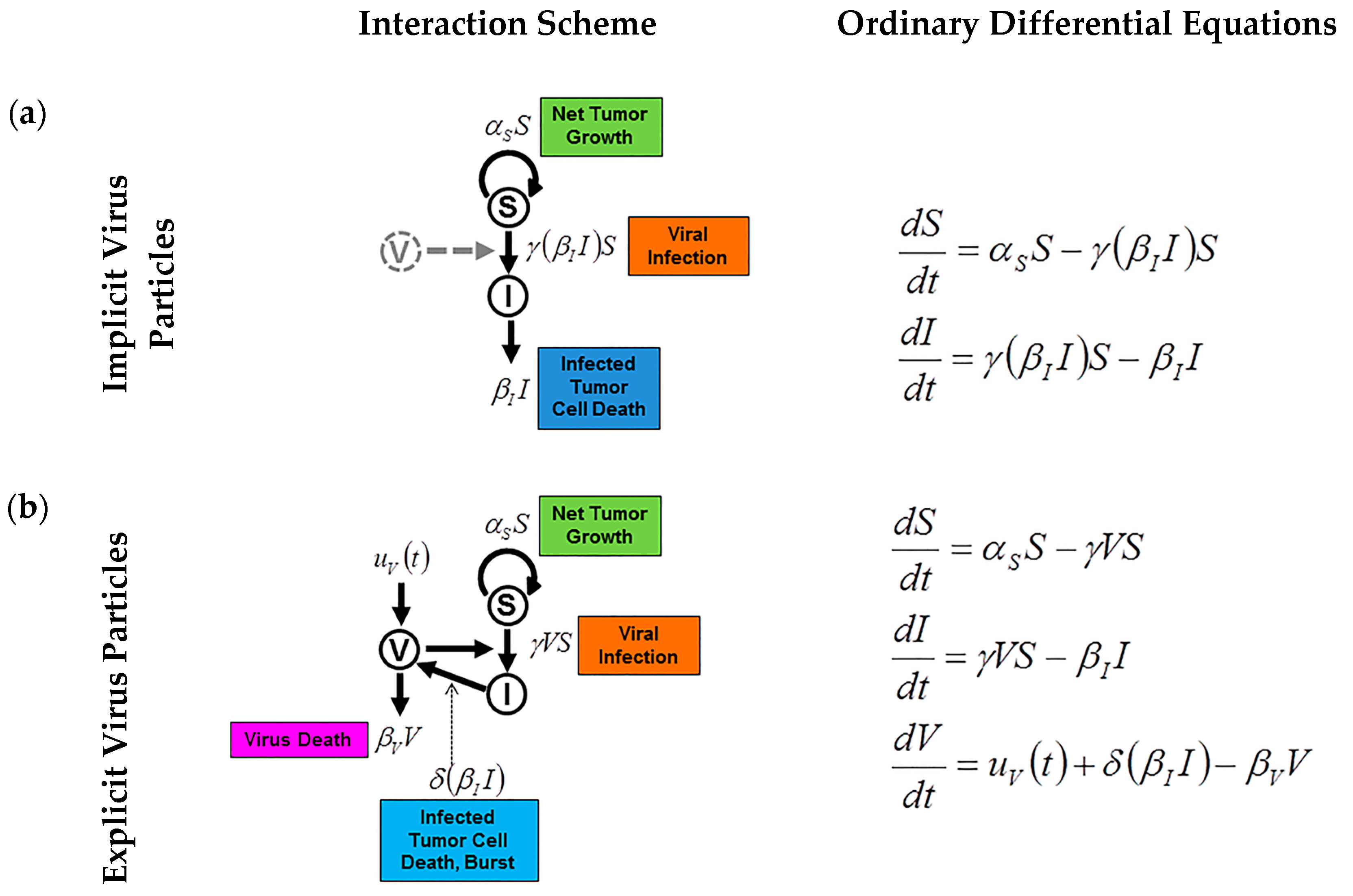
4. Mathematical Modeling of Infection: Susceptible and Infected Model
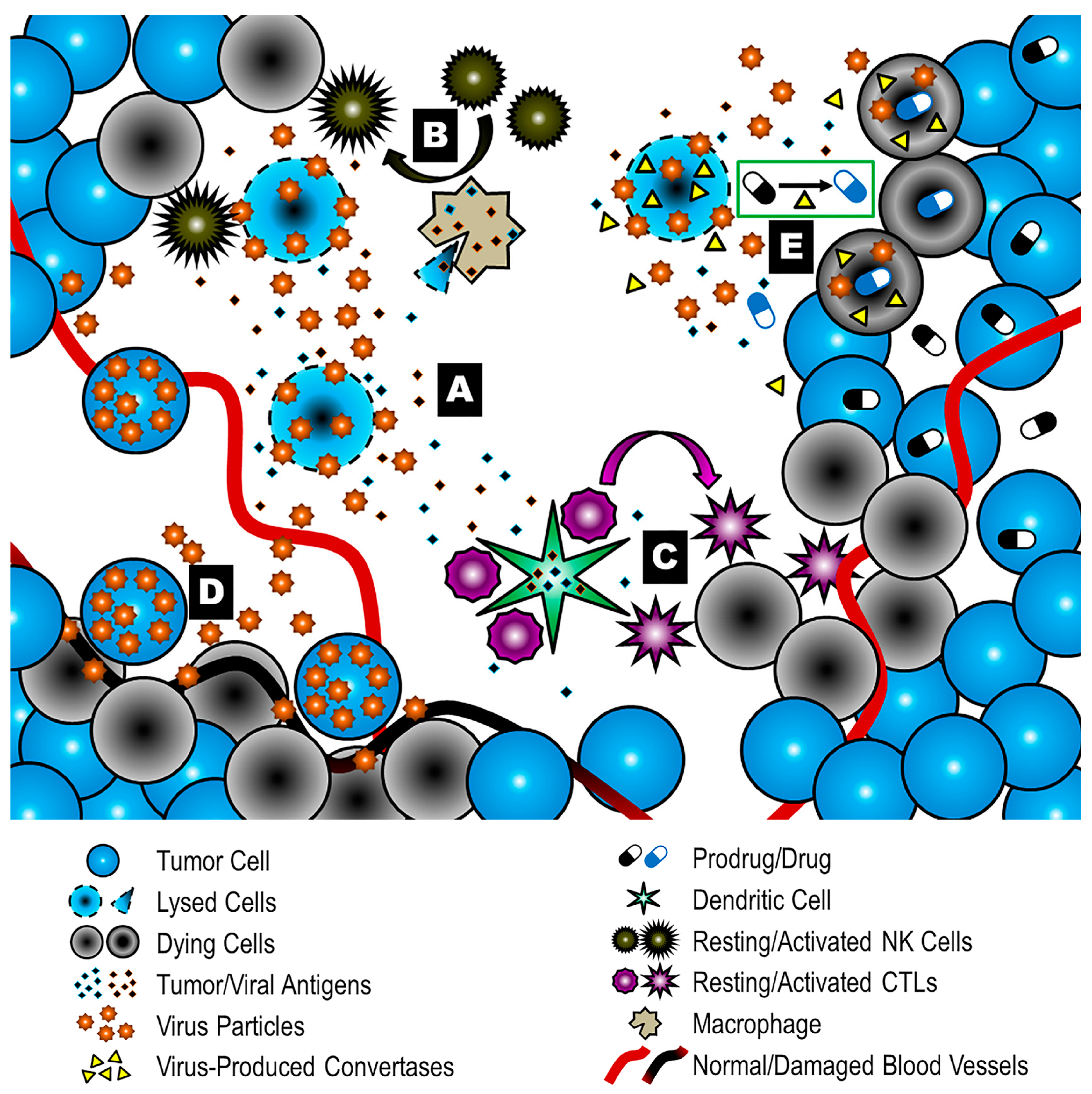
5. Modes of Action in Oncolytic Virotherapy
6. Modeling Specific Mechanisms of Action
7. Current Developments in Oncolytic Virotherapy
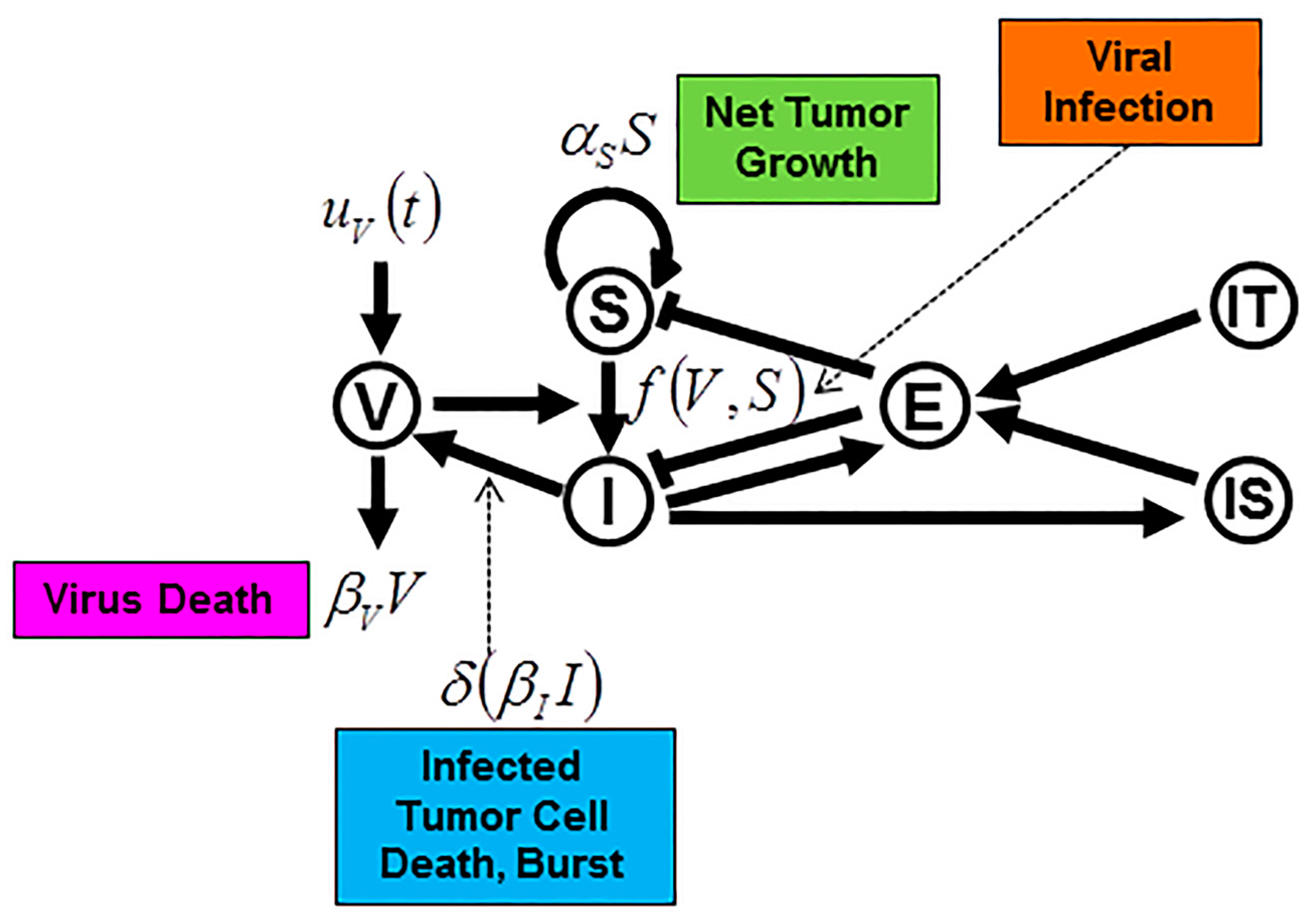
8. Mathematical Modeling of Oncolytic Virus Treatment with Immunotherapy
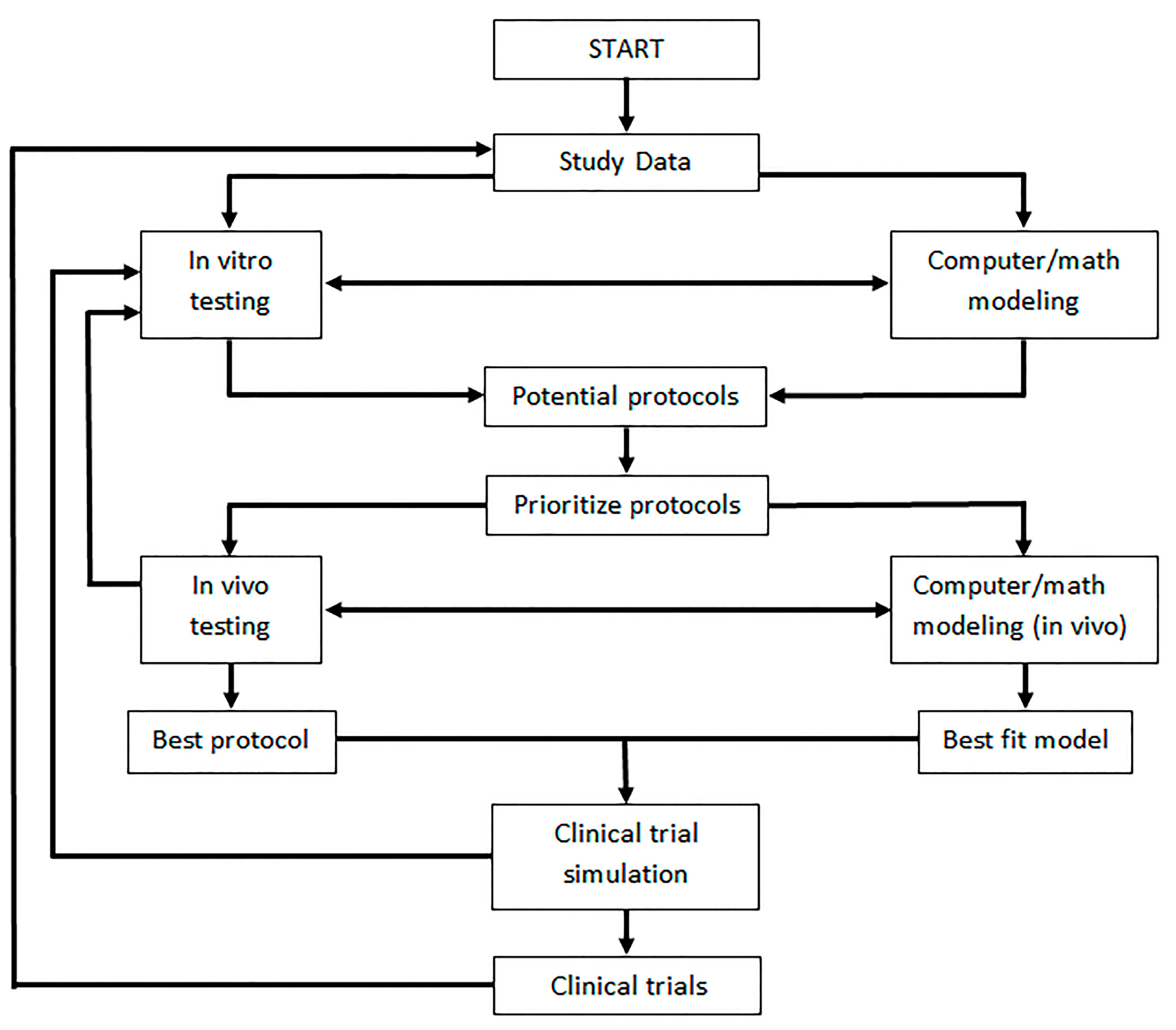
9. Discussion and Future Directions
Acknowledgments
Conflicts of Interest
References
- Anderson, A.R.; Quaranta, V. Integrative mathematical oncology. Nat. Rev. Cancer 2008, 8, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Enderling, H.; Hlatky, L.; Hahnfeldt, P. Migration rules: Tumours are conglomerates of self-metastases. Br. J. Cancer 2009, 100, 1917–1925. [Google Scholar] [CrossRef] [PubMed]
- Bajzer, Z.; Carr, T.; Josić, K.; Russell, S.J.; Dingli, D. Modeling of cancer virotherapy with recombinant measles viruses. J. Theor. Biol. 2008, 252, 109–122. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Dushoff, J.; Bridle, B.; Bramson, J.L.; Earn, D.J.D. Multi-stability and multi-instability phenomena in a mathematical model of tumor-immune-virus interactions. Bull. Math. Biol. 2011, 73, 2932–2961. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Mirmirani, M.; Oster, G.F. Optimal strategies in immunology. I. B-cell differentiation and proliferation. J. Math. Biol. 1976, 3, 325–367. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Mirmirani, M.; Oster, G.F. Optimal strategies in immunology. II. B memory cell production. J. Math. Biol. 1978, 5, 213–256. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Goldstein, B.; Rocklin, S. Optimal strategies in immunology III. The IgM-IgG switch. J. Math. Biol. 1980, 10, 209–256. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Kirschner, D.E.; De Boer, R. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Ho, D.D.; Neumann, A.U.; Perelson, A.S.; Chen, W.; Leonard, J.M.; Markowitz, M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 1995, 373, 123–126. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Neumann, A.U.; Markowitz, M.; Leonard, J.M.; Ho, D.D. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 1996, 271, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Essunger, P.; Cao, Y.; Vesanen, M.; Hurley, A.; Saksela, K.; Markowitz, M.; Ho, D.D. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 1997, 387, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; May, R. Viral Dynamics: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2001; p. 256. [Google Scholar]
- Dock, G. The influence of complicating diseases upon leukaemia. Am. J. Med. Sci. 1904, 127, 563–592. [Google Scholar] [CrossRef]
- Hoster, H.A.; Zanes, R.P.; Von Haam, E. Studies in Hodgkin’s syndrome; the association of viral hepatitis and Hodgkin’s disease; a preliminary report. Cancer Res. 1949, 9, 473–480. [Google Scholar] [PubMed]
- Southam, C.M.; Moore, A.E. Clinical studies of viruses as antineoplastic agents with particular reference to Egypt 101 virus. Cancer 1952, 5, 1025–1034. [Google Scholar] [CrossRef]
- Georgiades, J.; Zielinski, T.; Cicholska, A.; Jordan, E. Research on the oncolytic effect of APC viruses in cancer of the cervix uteri; preliminary report. Biul. Inst. Med. Mor. Gdansk 1959, 10, 49–57. [Google Scholar]
- Asada, T. Treatment of human cancer with mumps virus. Cancer 1974, 34, 1907–1928. [Google Scholar] [CrossRef]
- Cassady, K.A.; Haworth, K.B.; Jackson, J.; Markert, J.M.; Cripe, T.P. To infection and beyond: The multi-pronged anti-cancer mechanisms of oncolytic viruses. Viruses 2016, 8, 43. [Google Scholar] [CrossRef] [PubMed]
- Araujo, R.P.; McElwain, D.L. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.; Preziosi, L. Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 2003, 20, 341–366. [Google Scholar] [CrossRef] [PubMed]
- Folkman, J.; Hochberg, M. Self-regulation of growth in three dimensions. J. Exp. Med. 1973, 138, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Vaupel, P. The role of hypoxia-induced factors in tumor progression. Oncologist 2004, 9 (Suppl. 5), 10–17. [Google Scholar] [CrossRef] [PubMed]
- Vaupel, P.; Harrison, L. Tumor hypoxia: Causative factors, compensatory mechanisms, and cellular response. Oncologist 2004, 9 (Suppl. 5), 4–9. [Google Scholar] [CrossRef] [PubMed]
- Deisboeck, T.S.; Wang, Z. Cancer dissemination: A consequence of limited carrying capacity? Med. Hypotheses 2007, 69, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Hahnfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer Res. 1999, 59, 4770–4775. [Google Scholar] [PubMed]
- Gerlee, P.; Anderson, A.R. The evolution of carrying capacity in constrained and expanding tumour cell populations. Phys. Biol. 2015, 12, 056001. [Google Scholar] [CrossRef] [PubMed]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [PubMed]
- Murphy, H.; Jaafari, H.; Dobrovolny, H.M. Differences in predictions of ODE models of tumor growth: A cautionary example. BMC Cancer 2016, 16, 163. [Google Scholar] [CrossRef] [PubMed]
- Gerlee, P. The model muddle: In search of tumor growth laws. Cancer Res. 2013, 73, 2407–2411. [Google Scholar] [CrossRef] [PubMed]
- Brouwer, A.F.; Meza, R.; Eisenberg, M.C. Parameter estimation for multistage clonal expansion models from cancer incidence data: A practical identifiability analysis. PLoS Comput. Biol. 2017, 13, e1005431. [Google Scholar]
- Eisenberg, M.C.; Robertson, S.L.; Tien, J.H. Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J. Theor. Biol. 2013, 324, 84–102. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, M.C.; Hayashi, M.A. Determining identifiable parameter combinations using subset profiling. Math. Biosci. 2014, 256, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Idema, S.; Dirven, C.M.F.; van Beusechem, V.W.; Carette, J.E.; Planque, R.; Noskel, D.P.; Lamfers, M.L.M.; Vandertop, W.P. Objective determination of the oncolytic potency of conditionally-replicating adenoviruses using mathematical modeling. J. Gene Med. 2010, 12, 564–571. [Google Scholar] [CrossRef] [PubMed]
- De Pillis, L.G.; Eladdadi, A.; Radunskaya, A.E. Modeling cancer-immune responses to therapy. J. Pharmacokinet. Pharmacodyn. 2014, 41, 461–478. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Butner, J.D.; Kerketta, R.; Cristini, V.; Deisboeck, T.S. Simulating cancer growth with multiscale agent-based modeling. Semin. Cancer Biol. 2015, 30, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Wodarz, D. Computational modeling approaches to the dynamics of oncolytic viruses. Wiley Interdiscip. Rev. Syst. Biol. 2016, 8, 242–252. [Google Scholar] [CrossRef] [PubMed]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Seymour, L.W.; Fisher, K.D. Oncolytic viruses: Finally delivering. Br. J. Cancer 2016, 114, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Martin, G.S. The hunting of the Src. Nat. Rev. Mol. Cell Biol. 2001, 2, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Martin, G.S. The road to Src. Oncogene 2004, 23, 7910–7917. [Google Scholar] [CrossRef] [PubMed]
- Sefton, B.M.; Hunter, T.; Raschke, W.C. Evidence that the Abelson virus protein functions in vivo as a protein kinase that phosphorylates tyrosine. Proc. Natl. Acad. Sci. USA 1981, 78, 1552–1556. [Google Scholar] [CrossRef] [PubMed]
- Durst, M.; Gissmann, L.; Ikenberg, H.; zur Hausen, H. A papillomavirus DNA from a cervical carcinoma and its prevalence in cancer biopsy samples from different geographic regions. Proc. Natl. Acad. Sci. USA 1983, 80, 3812–3815. [Google Scholar] [CrossRef] [PubMed]
- Munger, K.; Phelps, W.C.; Bubb, V.; Howley, P.M.; Schlegel, R. The E6 and E7 genes of the human papillomavirus type 16 together are necessary and sufficient for transformation of primary human keratinocytes. J. Virol. 1989, 63, 4417–4421. [Google Scholar] [PubMed]
- Hacein-Bey-Abina, S.; Von Kalle, C.; Schmidt, M.; McCormack, M.P.; Wulffraat, N.; Leboulch, P.; Lim, A.; Osborne, C.S.; Pawliuk, R.; Morillon, E.; et al. LMO2-associated clonal T cell proliferation in two patients after gene therapy for SCID-X1. Science 2003, 302, 415–419. [Google Scholar] [CrossRef] [PubMed]
- Takeda, H.; Takai, A.; Inuzuka, T.; Marusawa, H. Genetic basis of hepatitis virus-associated hepatocellular carcinoma: Linkage between infection, inflammation, and tumorigenesis. J. Gastroenterol. 2017, 52, 26–38. [Google Scholar] [CrossRef] [PubMed]
- Bluming, A.Z.; Ziegler, J.L. Regression of Burkitt’s lymphoma in association with measles infection. Lancet 1971, 2, 105–106. [Google Scholar] [CrossRef]
- Cattaneo, R.; Miest, T.; Shashkova, E.V.; Barry, M.A. Reprogrammed viruses as cancer therapeutics: Targeted, armed and shielded. Nat. Rev. Microbiol. 2008, 6, 529–540. [Google Scholar] [CrossRef] [PubMed]
- Virgin, S. Pathogenesis of Viral Infection. In Fields’ Virology; Fields, B.N., Knipe, D.M., Howley, P.M., Eds.; Wolters Kluwer Health/Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007; Volume 1, pp. 327–388. [Google Scholar]
- Finkelshtein, D.; Werman, A.; Novick, D.; Barak, S.; Rubinstein, M. LDL receptor and its family members serve as the cellular receptors for vesicular stomatitis virus. Proc. Natl. Acad. Sci. USA 2013, 110, 7306–7311. [Google Scholar] [CrossRef] [PubMed]
- Tatsuo, H.; Ono, N.; Tanaka, K.; Yanagi, Y. SLAM (CDw150) is a cellular receptor for measles virus. Nature 2000, 406, 893–897. [Google Scholar] [PubMed]
- Noyce, R.S.; Bondre, D.G.; Ha, M.N.; Lin, L.T.; Sisson, G.; Tsao, M.S.; Richardson, C.D. Tumor cell marker PVRL4 (Nectin 4) is an epithelial cell receptor for measles virus. PLoS Pathog. 2011, 7, e1002240. [Google Scholar] [CrossRef] [PubMed]
- Bankamp, B.; Takeda, M.; Zhang, Y.; Xu, W.; Rota, P.A. Genetic characterization of measles vaccine strains. J. Infect. Dis. 2011, 204 (Suppl. 1), S533–S548. [Google Scholar] [CrossRef] [PubMed]
- Dorig, R.E.; Marcil, A.; Chopra, A.; Richardson, C.D. The human CD46 molecule is a receptor for measles virus (Edmonston strain). Cell 1993, 75, 295–305. [Google Scholar] [CrossRef]
- Naniche, D.; Varior-Krishnan, G.; Cervoni, F.; Wild, T.F.; Rossi, B.; Rabourdin-Combe, C.; Gerlier, D. Human membrane cofactor protein (CD46) acts as a cellular receptor for measles virus. J. Virol. 1993, 67, 6025–6032. [Google Scholar] [PubMed]
- Nielsen, L.; Blixenkrone-Moller, M.; Thylstrup, M.; Hansen, N.J.; Bolt, G. Adaptation of wild-type measles virus to CD46 receptor usage. Arch. Virol. 2001, 146, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Hammond, A.L.; Plemper, R.K.; Zhang, J.; Schneider, U.; Russell, S.J.; Cattaneo, R. Single-chain antibody displayed on a recombinant measles virus confers entry through the tumor-associated carcinoembryonic antigen. J. Virol. 2001, 75, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Peng, K.W.; Holler, P.D.; Orr, B.A.; Kranz, D.M.; Russell, S.J. Targeting virus entry and membrane fusion through specific peptide/MHC complexes using a high-affinity T-cell receptor. Gene Ther. 2004, 11, 1234–1239. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Peng, K.W.; Vongpunsawad, S.; Harvey, M.; Mizuguchi, H.; Hayakawa, T.; Cattaneo, R.; Russell, S.J. Antibody-targeted cell fusion. Nat. Biotechnol. 2004, 22, 331–336. [Google Scholar] [CrossRef] [PubMed]
- Cronin, J.; Zhang, X.Y.; Reiser, J. Altering the tropism of lentiviral vectors through pseudotyping. Curr. Gene Ther. 2005, 5, 387–598. [Google Scholar] [CrossRef] [PubMed]
- Funke, S.; Schneider, I.C.; Glaser, S.; Muhlebach, M.D.; Moritz, T.; Cattaneo, R.; Cichutek, K.; Buchholz, C.J. Pseudotyping lentiviral vectors with the wild-type measles virus glycoproteins improves titer and selectivity. Gene Ther. 2009, 16, 700–705. [Google Scholar] [CrossRef] [PubMed]
- Plattet, P.; Alves, L.; Herren, M.; Aguilar, H.C. Measles virus fusion protein: Structure, function and inhibition. Viruses 2016, 8, 112. [Google Scholar] [CrossRef] [PubMed]
- Lamb, R.A.; Parks, G.D. Paramyxoviridae: The Viruses and Their Replication. In Fields’ Virology; Fields, B.N., Knipe, D.M., Howley, P.M., Eds.; Wolters Kluwer Health/Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007; Volume 1, pp. 1449–1496. [Google Scholar]
- Stegmann, T.; Hoekstra, D.; Scherphof, G.; Wilschut, J. Kinetics of pH-dependent fusion between influenza virus and liposomes. Biochemistry 1985, 24, 3107–3113. [Google Scholar] [CrossRef] [PubMed]
- Van Rikxoort, M.; Michaelis, M.; Wolschek, M.; Muster, T.; Egorov, A.; Seipelt, J.; Doerr, H.W.; Cinatl, J. Oncolytic effects of a novel influenza A virus expressing interleukin-15 from the NS reading frame. PLoS ONE 2012, 7, e36506. [Google Scholar] [CrossRef] [PubMed]
- Kasloff, S.B.; Pizzuto, M.S.; Silic-Benussi, M.; Pavone, S.; Ciminale, V.; Capua, I. Oncolytic activity of avian influenza virus in human pancreatic ductal adenocarcinoma cell lines. J. Virol. 2014, 88, 9321–9334. [Google Scholar] [CrossRef] [PubMed]
- Pizzuto, M.S.; Silic-Benussi, M.; Ciminale, V.; Elderfield, R.A.; Capua, I.; Barclay, W.S. An engineered avian-origin influenza A virus for pancreatic ductal adenocarcinoma virotherapy. J. Gen. Virol. 2016, 97, 2166–2179. [Google Scholar] [CrossRef] [PubMed]
- Kalia, M.; Jameel, S. Virus entry paradigms. Amino Acids 2011, 41, 1147–1157. [Google Scholar] [CrossRef] [PubMed]
- Marchini, A.; Bonifati, S.; Scott, E.M.; Angelova, A.L.; Rommelaere, J. Oncolytic parvoviruses: From basic virology to clinical applications. Virol. J. 2015, 12, 6. [Google Scholar] [CrossRef] [PubMed]
- Kirn, D. Oncolytic Vaccinia Virus Cancer Therapy. U.S. Patent US8980246 B2, 17 March 2015. [Google Scholar]
- Weller, S.K.; Coen, D.M. Herpes simplex viruses: Mechanisms of DNA replication. Cold Spring Harb. Perspect. Biol. 2012, 4, a013011. [Google Scholar] [CrossRef] [PubMed]
- Moss, B. Poxvirus DNA replication. Cold Spring Harb. Perspect. Biol. 2013, 5, a010199. [Google Scholar] [CrossRef] [PubMed]
- Hoeben, R.C.; Uil, T.G. Adenovirus DNA replication. Cold Spring Harb. Perspect. Biol. 2013, 5, a013003. [Google Scholar] [CrossRef] [PubMed]
- Griffin, D.E. Measles Virus. In Fields’ Virology; Fields, B.N., Knipe, D.M., Howley, P.M., Eds.; Wolters Kluwer Health/Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007; Volume 1, pp. 1551–1586. [Google Scholar]
- Anacker, D.C.; Moody, C.A. Modulation of the DNA damage response during the life cycle of human papillomaviruses. Virus Res. 2017, 231, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Longworth, M.S.; Laimins, L.A. Pathogenesis of human papillomaviruses in differentiating epithelia. Microbiol. Mol. Biol. Rev. 2004, 68, 362–372. [Google Scholar] [CrossRef] [PubMed]
- Petros, P.; Panagiotis, T.; Georgios, I.; Stefanos, Z.; Zacharoula, K.; Anastasia, B.; Georgios, G.; Simona, V. Human papillomavirus’ life cycle and carcinogenesis. Maedica 2016, 11, 48–54. [Google Scholar]
- Honess, R.W.; Roizman, B. Regulation of herpesvirus macromolecular synthesis. I. Cascade regulation of the synthesis of three groups of viral proteins. J. Virol. 1974, 14, 8–19. [Google Scholar] [PubMed]
- Kakizoe, Y.; Nakaoka, S.; Beauchemin, C.A.; Morita, S.; Mori, H.; Igarashi, T.; Aihara, K.; Miura, T.; Iwami, S. A method to determine the duration of the eclipse phase for in vitro infection with a highly pathogenic SHIV strain. Sci. Rep. 2015, 5, 10371. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, A.J.; Russell, S.J. MicroRNAs and oncolytic viruses. Curr. Opin. Virol. 2015, 13, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Bofill-De Ros, X.; Villanueva, E.; Fillat, C. Late-phase miRNA-controlled oncolytic adenovirus for selective killing of cancer cells. Oncotarget 2015, 6, 6179–6190. [Google Scholar] [CrossRef] [PubMed]
- Leber, M.F.; Bossow, S.; Leonard, V.H.; Zaoui, K.; Grossardt, C.; Frenzke, M.; Miest, T.; Sawall, S.; Cattaneo, R.; von Kalle, C.; et al. MicroRNA-sensitive oncolytic measles viruses for cancer-specific vector tropism. Mol. Ther. 2011, 19, 1097–1106. [Google Scholar] [CrossRef] [PubMed]
- Springfeld, C.; von Messling, V.; Frenzke, M.; Ungerechts, G.; Buchholz, C.J.; Cattaneo, R. Oncolytic efficacy and enhanced safety of measles virus activated by tumor-secreted matrix metalloproteinases. Cancer Res. 2006, 66, 7694–7700. [Google Scholar] [CrossRef] [PubMed]
- Ketzer, P.; Kaufmann, J.K.; Engelhardt, S.; Bossow, S.; von Kalle, C.; Hartig, J.S.; Ungerechts, G.; Nettelbeck, D.M. Artificial riboswitches for gene expression and replication control of DNA and RNA viruses. Proc. Natl. Acad. Sci. USA 2014, 111, E554–E562. [Google Scholar] [CrossRef] [PubMed]
- José, A.; Rovira-Rigau, M.; Luna, J.; Giménez-Alejandre, M.; Vaquero, E.; de la García Torre, B.; Andreu, D.; Alemany, R.; Fillat, C. A genetic fiber modification to achieve matrix-metalloprotease-activated infectivity of oncolytic adenovirus. J. Control. Release 2014, 192, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Villanueva, E.; Navarro, P.; Rovira-Rigau, M.; Sibilio, A.; Méndez, R.; Fillat, C. Translational reprogramming in tumour cells can generate oncoselectivity in viral therapies. Nat. Commun. 2017, 8, 14833. [Google Scholar] [CrossRef] [PubMed]
- Doerfler, W. Beware of manipulations on the genome: Epigenetic destabilization through (foreign) DNA insertions. Epigenomics 2016, 8, 587–591. [Google Scholar] [CrossRef] [PubMed]
- Ranzani, M.; Annunziato, S.; Adams, D.J.; Montini, E. Cancer gene discovery: Exploiting insertional mutagenesis. Mol. Cancer Res. 2013, 11, 1141–1158. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.K.; Li, N.; Mark, A.C.; Mateo, M.; Cattaneo, R.; Sinn, P.L. Cell-to-cell contact and Nectin-4 govern spread of measles virus from primary human myeloid cells to primary human airway epithelial cells. J. Virol. 2016, 90, 6808–6817. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.D.; Nakamura, T.; Russell, S.J.; Peng, K.W. High CD46 receptor density determines preferential killing of tumor cells by oncolytic measles virus. Cancer Res. 2004, 64, 4919–4926. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Brenes, I.A.; Hofacre, A.; Fan, H.; Wodarz, D. Complex dynamics of virus spread from low infection multiplicities: Implications for the spread of oncolytic viruses. PLoS Comput. Biol. 2017, 13, e1005241. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.; Haque, M.; Venturino, E.; Chakravarty, S. Dynamics of a three species ratio-dependent food chain model with intra-specific competition within the top predator. Comput. Biol. Med. 2017, 85, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Bangham, C.R. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A. Models of tumor–host interaction as competing populations: Implications for tumor biology and treatment. J. Theor. Biol. 1995, 176, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Novozhilov, A.S.; Berezovskaya, F.S.; Koonin, E.V.; Karev, G.P. Mathematical modeling of tumor therapy with oncolytic viruses: Regimes with complete tumor elimination within the framework of deterministic models. Biol. Direct 2006, 1, 6. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Ribeiro, R.M. Modeling the within-host dynamics of HIV infection. BMC Biol. 2013, 11, 96. [Google Scholar] [CrossRef] [PubMed]
- Arazi, A.; Pendergraft, W.F.; Ribeiro, R.M.; Perelson, A.S.; Hacohen, N. Human systems immunology: Hypothesis-based modeling and unbiased data-driven approaches. Semin. Immunol. 2013, 25, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Canini, L.; Perelson, A.S. Viral kinetic modeling: State of the art. J. Pharmacokinet. Pharmacodyn. 2014, 41, 431–443. [Google Scholar] [CrossRef] [PubMed]
- Wodarz, D. Viruses as antitumor weapons: Defining conditions for tumor remission. Cancer Res. 2001, 61, 3501–3507. [Google Scholar] [PubMed]
- Wodarz, D. Mechanisms underlying antigen-specific CD8+ T cell homeostasis. Science 2001, 292, 595. [Google Scholar] [CrossRef] [PubMed]
- Dingli, D.; Offord, C.; Myers, R.; Peng, K.W.; Carr, T.W.; Josic, K.; Russell, S.J.; Bajzer, Z. Dynamics of multiple myeloma tumor therapy with a recombinant measles virus. Cancer Gene Ther. 2009, 16, 873–882. [Google Scholar] [CrossRef] [PubMed]
- Biesecker, M.; Kimn, J.H.; Lu, H.; Dingli, D.; Bajzer, Z. Optimization of virotherapy for cancer. Bull. Math. Biol. 2010, 72, 469–489. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.P. The replicability of oncolytic virus: Defining conditions in tumor virotherapy. Math. Biosci. Eng. 2011, 8, 841–860. [Google Scholar] [CrossRef] [PubMed]
- Wodarz, D.; Komarova, N. Towards predictive computational models of oncolytic virus therapy: Basis for experimental validation and model selection. PLoS ONE 2009, 4, e4271. [Google Scholar] [CrossRef] [PubMed]
- Wares, J.R.; Crivelli, J.J.; Yun, C.O.; Choi, I.K.; Gevertz, J.L.; Kim, P.S. Treatment strategies for combining immunostimulatory oncolytic virus therapeutics with dendritic cell injections. Math. Biosci. Eng. 2015, 12, 1237–1256. [Google Scholar] [CrossRef] [PubMed]
- Lichty, B.D.; Breitbach, C.J.; Stojdl, D.F.; Bell, J.C. Going viral with cancer immunotherapy. Nat. Rev. Cancer 2014, 14, 559–567. [Google Scholar] [CrossRef] [PubMed]
- Workenhe, S.T.; Mossman, K.L. Oncolytic virotherapy and immunogenic cancer cell death: Sharpening the sword for improved cancer treatment strategies. Mol. Ther. 2014, 22, 251–256. [Google Scholar] [CrossRef] [PubMed]
- Barik, S. What Really Rigs Up RIG-I? J. Innate Immun. 2016, 8, 429–436. [Google Scholar] [CrossRef] [PubMed]
- Beug, S.T.; Tang, V.A.; LaCasse, E.C.; Cheung, H.H.; Beauregard, C.E.; Brun, J.; Nuyens, J.P.; Earl, N.; St-Jean, M.; Holbrook, J.; et al. Smac mimetics and innate immune stimuli synergize to promote tumor death. Nat. Biotechnol. 2014, 32, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Bhat, R.; Rommelaere, J. Emerging role of natural killer cells in oncolytic virotherapy. Immunotargets Ther. 2015, 4, 65–77. [Google Scholar] [PubMed]
- Mellman, I.; Coukos, G.; Dranoff, G. Cancer immunotherapy comes of age. Nature 2011, 480, 480–489. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Clements, D.R.; Sterea, A.M.; Jang, H.W.; Gujar, S.A.; Lee, P.W. Dendritic cells in oncolytic virus-based anti-cancer therapy. Viruses 2015, 7, 6506–6525. [Google Scholar] [CrossRef] [PubMed]
- Mosmann, T.R.; Cherwinski, H.; Bond, M.W.; Giedlin, M.A.; Coffman, R.L. Two types of murine helper T cell clone. I. Definition according to profiles of lymphokine activities and secreted proteins. J. Immunol. 1986, 136, 2348–2357. [Google Scholar] [PubMed]
- Farrar, J.D.; Asnagli, H.; Murphy, K.M. T helper subset development: Roles of instruction, selection, and transcription. J. Clin. Investig. 2002, 109, 431–435. [Google Scholar] [CrossRef] [PubMed]
- Flossdorf, M.; Rossler, J.; Buchholz, V.R.; Busch, D.H.; Hofer, T. CD8+ T cell diversification by asymmetric cell division. Nat. Immunol. 2015, 16, 891–893. [Google Scholar] [CrossRef] [PubMed]
- Hand, T.W.; Kaech, S.M. Intrinsic and extrinsic control of effector T cell survival and memory T cell development. Immunol. Res. 2009, 45, 46–61. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Liang, H.; Zen, K. Molecular mechanisms that influence the macrophage M1–M2 polarization balance. Front. Immunol. 2014, 5, 614. [Google Scholar] [CrossRef] [PubMed]
- Darrasse-Jeze, G.; Deroubaix, S.; Mouquet, H.; Victora, G.D.; Eisenreich, T.; Yao, K.H.; Masilamani, R.F.; Dustin, M.L.; Rudensky, A.; Liu, K.; et al. Feedback control of regulatory T cell homeostasis by dendritic cells in vivo. J. Exp. Med. 2009, 206, 1853–1862. [Google Scholar] [CrossRef] [PubMed]
- Tuve, S.; Liu, Y.; Tragoolpua, K.; Jacobs, J.D.; Yumul, R.C.; Li, Z.Y.; Strauss, R.; Hellström, K.E.; Disis, M.L.; Roffler, S.; et al. In situ adenovirus vaccination engages T effector cells against cancer. Vaccine 2009, 27, 4225–4239. [Google Scholar] [CrossRef] [PubMed]
- Workenhe, S.T.; Pol, J.G.; Lichty, B.D.; Cummings, D.T.; Mossman, K.L. Combining oncolytic HSV-1 with immunogenic cell death-inducing drug mitoxantrone breaks cancer immune tolerance and improves therapeutic efficacy. Cancer Immunol. Res. 2013, 1, 309–319. [Google Scholar] [CrossRef] [PubMed]
- Grossardt, C.; Engeland, C.E.; Bossow, S.; Halama, N.; Zaoui, K.; Leber, M.F.; Springfeld, C.; Jaeger, D.; von Kalle, C.; Ungerechts, G. Granulocyte-macrophage colony-stimulating factor-armed oncolytic measles virus is an effective therapeutic cancer vaccine. Hum. Gene Ther. 2013, 24, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Veinalde, R.; Grossardt, C.; Hartmann, L.; Bourgeois-Daigneault, M.C.; Bell, J.C.; Jäger, D.; von Kalle, C.; Ungerechts, G.; Engeland, C.E. Oncolytic measles virus encoding interleukin-12 mediates potent antitumor effects through T cell activation. Oncoimmunology 2017, 6, e1285992. [Google Scholar] [CrossRef] [PubMed]
- Engeland, C.E.; Grossardt, C.; Veinalde, R.; Bossow, S.; Lutz, D.; Kaufmann, J.K.; Shevchenko, I.; Umansky, V.; Nettelbeck, D.M.; Weichert, W.; et al. CTLA-4 and PD-L1 checkpoint blockade enhances oncolytic measles virus therapy. Mol. Ther. 2014, 22, 1949–1959. [Google Scholar] [CrossRef] [PubMed]
- Zamarin, D.; Holmgaard, R.B.; Ricca, J.; Plitt, T.; Palese, P.; Sharma, P.; Merghoub, T.; Wolchok, J.D.; Allison, J.P. Intratumoral modulation of the inducible co-stimulator ICOS by recombinant oncolytic virus promotes systemic anti-tumour immunity. Nat. Commun. 2017, 8, 14340. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Wang, X.; Guo, Z.S.; Bartlett, D.L.; Gottschalk, S.M.; Song, X.T. T-cell engager-armed oncolytic vaccinia virus significantly enhances antitumor therapy. Mol. Ther. 2014, 22, 102–111. [Google Scholar] [CrossRef] [PubMed]
- Fajardo, C.A.; Guedan, S.; Rojas, L.A.; Moreno, R.; Arias-Badia, M.; de Sostoa, J.; June, C.H.; Alemany, R. Oncolytic adenoviral delivery of an EGFR-targeting T-cell engager improves antitumor efficacy. Cancer Res. 2017, 77, 2052–2063. [Google Scholar] [CrossRef] [PubMed]
- Freedman, J.D.; Hagel, J.; Scott, E.M.; Psallidas, I.; Gupta, A.; Spiers, L.; Miller, P.; Kanellakis, N.; Ashfield, R.; Fisher, K.D.; et al. Oncolytic adenovirus expressing bispecific antibody targets T-cell cytotoxicity in cancer biopsies. EMBO Mol. Med. 2017, 9, 1067–1087. [Google Scholar] [CrossRef] [PubMed]
- Vigil, A.; Martinez, O.; Chua, M.A.; García-Sastre, A. Recombinant Newcastle disease virus as a vaccine vector for cancer therapy. Mol. Ther. 2008, 16, 1883–1890. [Google Scholar] [CrossRef] [PubMed]
- Bridle, B.W.; Stephenson, K.B.; Boudreau, J.E.; Koshy, S.; Kazdhan, N.; Pullenayegum, E.; Brunellière, J.; Bramson, J.L.; Lichty, B.D.; Wan, Y. Potentiating cancer immunotherapy using an oncolytic virus. Mol. Ther. 2010, 18, 1430–1439. [Google Scholar] [CrossRef] [PubMed]
- Pol, J.G.; Zhang, L.; Bridle, B.W.; Stephenson, K.B.; Rességuier, J.; Hanson, S.; Chen, L.; Kazdhan, N.; Bramson, J.L.; Stojdl, D.F.; et al. Maraba virus as a potent oncolytic vaccine vector. Mol. Ther. 2014, 22, 420–429. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, H.L.; Taback, B.; Sherman, W.; Kim, D.W.; Shingler, W.H.; Moroziewicz, D.; DeRaffele, G.; Mitcham, J.; Carroll, M.W.; Harrop, R.; et al. Phase II trial of modified vaccinia Ankara (MVA) virus expressing 5T4 and high dose interleukin-2 (IL-2) in patients with metastatic renal cell carcinoma. J. Transl. Med. 2009, 7, 2. [Google Scholar] [CrossRef] [PubMed]
- Puzanov, I.; Milhem, M.M.; Minor, D.; Hamid, O.; Li, A.; Chen, L.; Chastain, M.; Gorski, K.S.; Anderson, A.; Chou, J.; et al. Talimogene laherparepvec in combination with ipilimumab in previously untreated, unresectable stage IIIB-IV melanoma. J. Clin. Oncol. 2016, 34, 2619–2626. [Google Scholar] [CrossRef] [PubMed]
- Zamarin, D.; Holmgaard, R.B.; Subudhi, S.K.; Park, J.S.; Mansour, M.; Palese, P.; Merghoub, T.; Wolchok, J.D.; Allison, J.P. Localized oncolytic virotherapy overcomes systemic tumor resistance to immune checkpoint blockade immunotherapy. Sci. Transl. Med. 2014, 6, 226ra32. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Sikorski, R.; Kirn, D.H.; Thorne, S.H. Synergistic anti-tumor effects between oncolytic vaccinia virus and paclitaxel are mediated by the IFN response and HMGB1. Gene Ther. 2011, 18, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J.; Peng, K.W.; Bell, J.C. Oncolytic virotherapy. Nat. Biotechnol. 2012, 30, 658–670. [Google Scholar] [CrossRef] [PubMed]
- Jha, B.K.; Dong, B.; Nguyen, C.T.; Polyakova, I.; Silverman, R.H. Suppression of antiviral innate immunity by sunitinib enhances oncolytic virotherapy. Mol. Ther. 2013, 21, 1749–1757. [Google Scholar] [CrossRef] [PubMed]
- Bossow, S.; Grossardt, C.; Temme, A.; Leber, M.F.; Sawall, S.; Rieber, E.P.; Cattaneo, R.; von Kalle, C.; Ungerechts, G. Armed and targeted measles virus for chemovirotherapy of pancreatic cancer. Cancer Gene Ther. 2011, 18, 598–608. [Google Scholar] [CrossRef] [PubMed]
- Abate-Daga, D.; Andreu, N.; Camacho-Sánchez, J.; Alemany, R.; Herance, R.; Millán, O.; Fillat, C. Oncolytic adenoviruses armed with thymidine kinase can be traced by PET imaging and show potent antitumoural effects by ganciclovir dosing. PLoS ONE 2011, 6, e26142. [Google Scholar] [CrossRef] [PubMed]
- Breitbach, C.J.; Arulanandam, R.; De Silva, N.; Thorne, S.H.; Patt, R.; Daneshmand, M.; Moon, A.; Ilkow, C.; Burke, J.; Hwang, T.H.; et al. Oncolytic vaccinia virus disrupts tumor-associated vasculature in humans. Cancer Res. 2013, 73, 1265–1275. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.C.; Hwang, T.; Park, B.H.; Bell, J.; Kirn, D.H. The targeted oncolytic poxvirus JX-594 demonstrates antitumoral, antivascular, and anti-HBV activities in patients with hepatocellular carcinoma. Mol. Ther. 2008, 16, 1637–1642. [Google Scholar] [CrossRef] [PubMed]
- Arulanandam, R.; Batenchuk, C.; Angarita, F.A.; Ottolino-Perry, K.; Cousineau, S.; Mottashed, A.; Burgess, E.; Falls, T.J.; De Silva, N.; Tsang, J.; et al. VEGF-mediated induction of PRD1-BF1/Blimp1 expression sensitizes tumor vasculature to oncolytic virus infection. Cancer Cell 2015, 28, 210–224. [Google Scholar] [CrossRef] [PubMed]
- Bose, A.; Taylor, J.L.; Alber, S.; Watkins, S.C.; Garcia, J.A.; Rini, B.I.; Ko, J.S.; Cohen, P.A.; Finke, J.H.; Storkus, W.J. Sunitinib facilitates the activation and recruitment of therapeutic anti-tumor immunity in concert with specific vaccination. Int. J. Cancer 2011, 129, 2158–2170. [Google Scholar] [CrossRef] [PubMed]
- Monod, J. The Growth of Bacterial Cultures. Ann. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.L.; Johnson, K.A.; Goody, R.S. The original Michaelis constant: Translation of the 1913 Michaelis-Menten paper. Biochemistry 2011, 50, 8264–8269. [Google Scholar] [PubMed]
- Wodarz, D.; Chan, C.N.; Trinité, B.; Komarova, N.L.; Levy, D.N. On the laws of virus spread through cell populations. J. Virol. 2014, 88, 13240–13248. [Google Scholar] [CrossRef] [PubMed]
- Komarova, N.L.; Anghelina, D.; Voznesensky, I.; Trinité, B.; Levy, D.N.; Wodarz, D. Relative contribution of free-virus and synaptic transmission to the spread of HIV-1 through target cell populations. Biol. Lett. 2013, 9, 20121049. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, K.; Pilyugin, S.S. Analysis of a mathematical model for tumor therapy with a fusogenic oncolytic virus. Math. Biosci. 2015, 270, 169–182. [Google Scholar] [CrossRef] [PubMed]
- Aref, S.; Bailey, K.; Fielding, A. Measles to the rescue: A review of oncolytic measles virus. Viruses 2016, 8, 294. [Google Scholar] [CrossRef] [PubMed]
- Atienza, J.M.; Zhu, J.; Wang, X.; Xu, X.; Abassi, Y. Dynamic monitoring of cell adhesion and spreading on microelectronic sensor arrays. J. Biomol. Screen. 2005, 10, 795–805. [Google Scholar] [CrossRef] [PubMed]
- Crivelli, J.J.; Foldes, J.; Kim, P.S.; Wares, J.R. A mathematical model for cell cycle-specific cancer virotherapy. J. Biol. Dyn. 2012, 6, 104–120. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, G.J.; Thillainadesan, G.; Yousef, A.F.; Ablack, J.N.; Mossman, K.L.; Torchia, J.; Mymryk, J.S. Adenovirus evasion of interferon-mediated innate immunity by direct antagonism of a cellular histone posttranslational modification. Cell Host Microbe 2012, 11, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Herschke, F.; Plumet, S.; Duhen, T.; Azocar, O.; Druelle, J.; Laine, D.; Wild, T.F.; Rabourdin-Combe, C.; Gerlier, D.; Valentin, H. Cell-cell fusion induced by measles virus amplifies the type I interferon response. J. Virol. 2007, 81, 12859–12871. [Google Scholar] [CrossRef] [PubMed]
- Roediger, E.K.; Kugathasan, K.; Zhang, X.; Lichty, B.D.; Xing, Z. Heterologous boosting of recombinant adenoviral prime immunization with a novel vesicular stomatitis virus-vectored tuberculosis vaccine. Mol. Ther. 2008, 16, 1161–1169. [Google Scholar] [CrossRef] [PubMed]
- Bridle, B.W.; Boudreau, J.E.; Lichty, B.D.; Brunellière, J.; Stephenson, K.; Koshy, S.; Bramson, J.L.; Wan, Y. Vesicular stomatitis virus as a novel cancer vaccine vector to prime antitumor immunity amenable to rapid boosting with adenovirus. Mol. Ther. 2009, 17, 1814–1821. [Google Scholar] [CrossRef] [PubMed]
- Reis, C.L.; Pacheco, J.M.; Ennis, M.K.; Dingli, D. In silico evolutionary dynamics of tumour virotherapy. Integr. Biol. 2010, 2, 41–45. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.T.; Byrne, H.M.; Kirn, D.H.; Wein, L.M. Modeling and analysis of a virus that replicates selectively in tumor cells. Bull. Math. Biol. 2001, 63, 731–768. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.; Tao, Y. Analysis of a model of a virus that replicates selectively in tumor cells. J. Math. Biol. 2003, 47, 391–423. [Google Scholar] [CrossRef] [PubMed]
- Bateman, A.R.; Harrington, K.J.; Kottke, T.; Ahmed, A.; Melcher, A.A.; Gough, M.J.; Linardakis, E.; Riddle, D.; Dietz, A.; Lohse, C.M.; et al. Viral fusogenic membrane glycoproteins kill solid tumor cells by nonapoptotic mechanisms that promote cross presentation of tumor antigens by dendritic cells. Cancer Res. 2002, 62, 6566–6578. [Google Scholar] [PubMed]
- Kavanová, L.; Matiašková, K.; Levá, L.; Štěpánová, H.; Nedbalcová, K.; Matiašovic, J.; Faldyna, M.; Salát, J. Concurrent infection with porcine reproductive and respiratory syndrome virus and Haemophilus parasuis in two types of porcine macrophages: Apoptosis, production of ROS and formation of multinucleated giant cells. Vet. Res. 2017, 48, 28. [Google Scholar] [CrossRef] [PubMed]
- Kozak, R.A.; Hattin, L.; Biondi, M.J.; Corredor, J.C.; Walsh, S.; Xue-Zhong, M.; Manuel, J.; McGilvray, I.D.; Morgenstern, J.; Lusty, E.; et al. Replication and oncolytic activity of an avian orthoreovirus in human hepatocellular carcinoma cells. Viruses 2017, 9, 90. [Google Scholar] [CrossRef] [PubMed]
- Soomro, M.H.; Shi, R.; She, R.; Yang, Y.; Wang, T.; Wu, Q.; Li, H.; Hao, W. Molecular and structural changes related to hepatitis E virus antigen and its expression in testis inducing apoptosis in Mongolian gerbil model. J. Viral Hepat. 2017. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Wang, L.; Wang, Y.; Shen, J.; Pan, C.; Meng, Y.; Yang, C.; Ji, H.; Dong, W. Autophagy and apoptosis induced by Chinese giant salamander (Andrias davidianus) iridovirus (CGSIV). Vet. Microbiol. 2016, 195, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Reshi, L.; Wu, H.C.; Wu, J.L.; Wang, H.V.; Hong, J.R. GSIV serine/threonine kinase can induce apoptotic cell death via p53 and pro-apoptotic gene Bax upregulation in fish cells. Apoptosis 2016, 21, 443–458. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.Y.; Wen, C.M.; Wu, J.L.; Su, Y.C.; Hong, J.R. Giant seaperch iridovirus (GSIV) induces mitochondria-mediated cell death that is suppressed by bongkrekic acid and cycloheximide in a fish cell line. Virus Res. 2016, 213, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Nardacci, R.; Perfettini, J.L.; Grieco, L.; Thieffry, D.; Kroemer, G.; Piacentini, M. Syncytial apoptosis signaling network induced by the HIV-1 envelope glycoprotein complex: An overview. Cell Death Dis. 2015, 6, e1846. [Google Scholar] [CrossRef] [PubMed]
- ClinicalTrials.gov. Available online: https://clinicaltrials.gov/ (accessed on 12 July 2017).
- Kelly, E.; Russell, S.J. History of oncolytic viruses: Genesis to genetic engineering. Mol. Ther. 2007, 15, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.L.; Robinson, M.; Han, Z.Q.; Branston, R.H.; English, C.; Reay, P.; McGrath, Y.; Thomas, S.K.; Thornton, M.; Bullock, P.; et al. ICP34.5 deleted herpes simplex virus with enhanced oncolytic, immune stimulating, and anti-tumour properties. Gene Ther. 2003, 10, 292–303. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.; Coffin, R.S.; Lilley, C.E.; Ponce, R.; Kaufman, H.L. Critical analysis of an oncolytic herpesvirus encoding granulocyte-macrophage colony stimulating factor for the treatment of malignant melanoma. Oncolytic Virother. 2014, 3, 11–20. [Google Scholar] [PubMed]
- Andtbacka, R.H.; Kaufman, H.L.; Collichio, F.; Amatruda, T.; Senzer, N.; Chesney, J.; Delman, K.A.; Spitler, L.E.; Puzanov, I.; Agarwala, S.S.; et al. Talimogene laherparepvec improves durable response rate in patients with advanced melanoma. J. Clin. Oncol. 2015, 33, 2780–2788. [Google Scholar] [CrossRef] [PubMed]
- Kohlhapp, F.J.; Kaufman, H.L. Molecular Pathways: Mechanism of Action for Talimogene Laherparepvec, a New Oncolytic Virus Immunotherapy. Clin. Cancer Res. 2016, 22, 1048–1054. [Google Scholar] [CrossRef] [PubMed]
- Kirn, B.; Starc, V. Continuous axial contraction wave in the free wall of the guinea pig left ventricle. Comput. Biol. Med. 2007, 37, 1394–1397. [Google Scholar] [CrossRef] [PubMed]
- Kirn, D.H.; Thorne, S.H. Targeted and armed oncolytic poxviruses: A novel multi-mechanistic therapeutic class for cancer. Nat. Rev. Cancer 2009, 9, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Parato, K.A.; Breitbach, C.J.; Le Boeuf, F.; Wang, J.; Storbeck, C.; Ilkow, C.; Diallo, J.S.; Falls, T.; Burns, J.; Garcia, V.; et al. The oncolytic poxvirus JX-594 selectively replicates in and destroys cancer cells driven by genetic pathways commonly activated in cancers. Mol. Ther. 2012, 20, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Heo, J.; Reid, T.; Ruo, L.; Breitbach, C.J.; Rose, S.; Bloomston, M.; Cho, M.; Lim, H.Y.; Chung, H.C.; Kim, C.W.; et al. Randomized dose-finding clinical trial of oncolytic immunotherapeutic vaccinia JX-594 in liver cancer. Nat. Med. 2013, 19, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Dispenzieri, A.; Tong, C.; LaPlant, B.; Lacy, M.Q.; Laumann, K.; Dingli, D.; Zhou, Y.; Federspiel, M.J.; Gertz, M.A.; Hayman, S.; et al. Phase I trial of systemic administration of Edmonston strain of measles virus genetically engineered to express the sodium iodide symporter in patients with recurrent or refractory multiple myeloma. Leukemia 2017. [Google Scholar] [CrossRef] [PubMed]
- Galanis, E.; Atherton, P.J.; Maurer, M.J.; Knutson, K.L.; Dowdy, S.C.; Cliby, W.A.; Haluska, P.; Long, H.J.; Oberg, A.; Aderca, I.; et al. Oncolytic measles virus expressing the sodium iodide symporter to treat drug-resistant ovarian cancer. Cancer Res. 2015, 75, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Dingli, D.; Peng, K.W.; Harvey, M.E.; Greipp, P.R.; O’Connor, M.K.; Cattaneo, R.; Morris, J.C.; Russell, S.J. Image-guided radiovirotherapy for multiple myeloma using a recombinant measles virus expressing the thyroidal sodium iodide symporter. Blood 2004, 103, 1641–1646. [Google Scholar] [CrossRef] [PubMed]
- Myers, R.M.; Greiner, S.M.; Harvey, M.E.; Griesmann, G.; Kuffel, M.J.; Buhrow, S.A.; Reid, J.M.; Federspiel, M.; Ames, M.M.; Dingli, D.; et al. Preclinical pharmacology and toxicology of intravenous MV-NIS, an oncolytic measles virus administered with or without cyclophosphamide. Clin. Pharmacol. Ther. 2007, 82, 700–710. [Google Scholar] [CrossRef] [PubMed]
- Lech, P.J.; Pappoe, R.; Nakamura, T.; Tobin, G.J.; Nara, P.L.; Russell, S.J. Antibody neutralization of retargeted measles viruses. Virology 2014, 454–455, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J.; Federspiel, M.J.; Peng, K.W.; Tong, C.; Dingli, D.; Morice, W.G.; Lowe, V.; O’Connor, M.K.; Kyle, R.A.; Leung, N.; et al. Remission of disseminated cancer after systemic oncolytic virotherapy. Mayo Clin. Proc. 2014, 89, 926–933. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J. Measles as a versatile oncolytic agent. In Proceedings of the International Meeting on Replicating Oncolytic Virus Therapeutics, Vancouver, BC, Canada, 1–4 October 2016. [Google Scholar]
- Croyle, M.A.; Callahan, S.M.; Auricchio, A.; Schumer, G.; Linse, K.D.; Wilson, J.M.; Brunner, L.J.; Kobinger, G.P. PEGylation of a vesicular stomatitis virus G pseudotyped lentivirus vector prevents inactivation in serum. J. Virol. 2004, 78, 912–921. [Google Scholar] [CrossRef] [PubMed]
- Hudacek, A.W.; Navaratnarajah, C.K.; Cattaneo, R. Development of measles virus-based shielded oncolytic vectors: Suitability of other paramyxovirus glycoproteins. Cancer Gene Ther. 2013, 20, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Miest, T.S.; Yaiw, K.C.; Frenzke, M.; Lampe, J.; Hudacek, A.W.; Springfeld, C.; von Messling, V.; Ungerechts, G.; Cattaneo, R. Envelope-chimeric entry-targeted measles virus escapes neutralization and achieves oncolysis. Mol. Ther. 2011, 19, 1813–1820. [Google Scholar] [CrossRef] [PubMed]
- Evgin, L.; Ilkow, C.S.; Bourgeois-Daigneault, M.C.; de Souza, C.T.; Stubbert, L.; Huh, M.S.; Jennings, V.A.; Marguerie, M.; Acuna, S.A.; Keller, B.A.; et al. Complement inhibition enables tumor delivery of LCMV glycoprotein pseudotyped viruses in the presence of antiviral antibodies. Mol. Ther. Oncolytics 2016, 3, 16027. [Google Scholar] [CrossRef] [PubMed]
- Lilly, C.L.; Villa, N.Y.; de Lemos Matos, A.; Ali, H.M.; Dhillon, J.S.; Hofland, T.; Rahman, M.M.; Chan, W.; Bogen, B.; Cogle, C.; McFadden, G. Ex vivo oncolytic virotherapy with myxoma virus arms multiple allogeneic bone marrow transplant leukocytes to enhance graft versus tumor. Mol. Ther. Oncolytics 2017, 4, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Ong, H.T.; Federspiel, M.J.; Guo, C.M.; Ooi, L.L.; Russell, S.J.; Peng, K.W.; Hui, K.M. Systemically delivered measles virus-infected mesenchymal stem cells can evade host immunity to inhibit liver cancer growth. J. Hepatol. 2013, 59, 999–1006. [Google Scholar] [CrossRef] [PubMed]
- Ong, H.T.; Hasegawa, K.; Dietz, A.B.; Russell, S.J.; Peng, K.W. Evaluation of T cells as carriers for systemic measles virotherapy in the presence of antiviral antibodies. Gene Ther. 2007, 14, 324–333. [Google Scholar] [CrossRef] [PubMed]
- Mader, E.K.; Maeyama, Y.; Lin, Y.; Butler, G.W.; Russell, H.M.; Galanis, E.; Russell, S.J.; Dietz, A.B.; Peng, K.W. Mesenchymal stem cell carriers protect oncolytic measles viruses from antibody neutralization in an orthotopic ovarian cancer therapy model. Clin. Cancer Res. 2009, 15, 7246–7255. [Google Scholar] [CrossRef] [PubMed]
- Brun, J.; McManus, D.; Lefebvre, C.; Hu, K.; Falls, T.; Atkins, H.; Bell, J.C.; McCart, J.A.; Mahoney, D.; Stojdl, D.F. Identification of genetically modified Maraba virus as an oncolytic rhabdovirus. Mol. Ther. 2010, 18, 1440–1449. [Google Scholar] [CrossRef] [PubMed]
- Travassos da Rosa, A.P.; Tesh, R.B.; Travassos da Rosa, J.F.; Herve, J.P.; Main, A.J., Jr. Carajas and Maraba viruses, two new vesiculoviruses isolated from phlebotomine sand flies in Brazil. Am. J. Trop. Med. Hyg. 1984, 33, 999–1006. [Google Scholar] [CrossRef] [PubMed]
- Zamarin, D.; Pesonen, S. Replication-competent viruses as cancer immunotherapeutics: Emerging clinical data. Hum. Gene Ther. 2015, 26, 538–549. [Google Scholar] [CrossRef] [PubMed]
- Geletneky, K.; Huesing, J.; Rommelaere, J.; Schlehofer, J.R.; Leuchs, B.; Dahm, M.; Krebs, O.; von Knebel Doeberitz, M.; Huber, B.; Hajda, J. Phase I/IIa study of intratumoral/intracerebral or intravenous/intracerebral administration of parvovirus H-1 (ParvOryx) in patients with progressive primary or recurrent glioblastoma multiforme: ParvOryx01 protocol. BMC Cancer 2012, 12, 99. [Google Scholar] [CrossRef] [PubMed]
- Geletneky, K.; Weiss, C.; Bernhard, H.; Capper, D.; Leuchs, B.; Marchini, A.; Rommelaere, J. Atim-29. First clinical observation of improved anti-tumor effects of viro-immunotherapy with oncolytic parvovirus H-1 in combination with PD-1 checkpoint blockade and bevacicumab in patients with recurrent glioblastoma. Neuro Oncol. 2016, 18, vi24. [Google Scholar] [CrossRef]
- Zhou, J.; Xi, Y.; Mu, X.; Zhao, R.; Chen, H.; Zhang, L.; Wu, Y.; Li, Q. Antitumor immunity induced by VE-cadherin modified DC vaccine. Oncotarget 2017. [Google Scholar] [CrossRef]
- Escribà-Garcia, L.; Alvarez-Fernández, C.; Tellez-Gabriel, M.; Sierra, J.; Briones, J. Dendritic cells combined with tumor cells and α-galactosylceramide induce a potent, therapeutic and NK-cell dependent antitumor immunity in B cell lymphoma. J. Transl. Med. 2017, 15, 115. [Google Scholar] [CrossRef] [PubMed]
- Nolan, E.; Savas, P.; Policheni, A.N.; Darcy, P.K.; Vaillant, F.; Mintoff, C.P.; Dushyanthen, S.; Mansour, M.; Pang, J.B.; Fox, S.B.; et al. Combined immune checkpoint blockade as a therapeutic strategy for BRCA1-mutated breast cancer. Sci. Transl. Med. 2017, 9, eaal4922. [Google Scholar] [CrossRef] [PubMed]
- Dammeijer, F.; Lievense, L.A.; Kaijen-Lambers, M.E.; van Nimwegen, M.; Bezemer, K.; Hegmans, J.P.; van Hall, T.; Hendriks, R.W.; Aerts, J.G. Depletion of tumor-associated macrophages with a CSF-1r kinase inhibitor enhances antitumor immunity and survival induced by DC immunotherapy. Cancer Immunol. Res. 2017, 5, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.H.; Zhang, S.N.; Choi, K.J.; Choi, I.K.; Kim, J.H.; Lee, M.G.; Lee, M.; Kim, H.; Yun, C.O. Therapeutic and tumor-specific immunity induced by combination of dendritic cells and oncolytic adenovirus expressing IL-12 and 4-1BBL. Mol. Ther. 2010, 18, 264–274. [Google Scholar] [CrossRef] [PubMed]
- Nishio, N.; Diaconu, I.; Liu, H.; Cerullo, V.; Caruana, I.; Hoyos, V.; Bouchier-Hayes, L.; Savoldo, B.; Dotti, G. Armed oncolytic virus enhances immune functions of chimeric antigen receptor-modified T cells in solid tumors. Cancer Res. 2014, 74, 5195–5205. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.; Enderling, H. From concept to clinic: Mathematically informed immunotherapy. Curr. Probl. Cancer 2016, 40, 68–83. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; DeWeese, T.; Dilley, J.; Zhang, Y.; Li, Y.; Ramesh, N.; Lee, J.; Pennathur-Das, R.; Radzyminski, J.; Wypych, J.; et al. CV706, a prostate cancer-specific adenovirus variant, in combination with radiotherapy produces synergistic antitumor efficacy without increasing toxicity. Cancer Res. 2001, 61, 5453–5460. [Google Scholar] [PubMed]
- Friedman, A.; Tian, J.P.; Fulci, G.; Chiocca, E.A.; Wang, J. Glioma virotherapy: Effects of innate immune suppression and increased viral replication capacity. Cancer Res. 2006, 66, 2314–2319. [Google Scholar] [CrossRef] [PubMed]
- Ganly, I.; Mautner, V.; Balmain, A. Productive replication of human adenoviruses in mouse epidermal cells. J. Virol. 2000, 74, 2895–2899. [Google Scholar] [CrossRef] [PubMed]
- Jogler, C.; Hoffmann, D.; Theegarten, D.; Grunwald, T.; Uberla, K.; Wildner, O. Replication properties of human adenovirus in vivo and in cultures of primary cells from different animal species. J. Virol. 2006, 80, 3549–3558. [Google Scholar] [CrossRef] [PubMed]
- Li, H.L.; Li, S.; Shao, J.Y.; Lin, X.B.; Cao, Y.; Jiang, W.Q.; Liu, R.Y.; Zhao, P.; Zhu, X.F.; Zeng, M.S.; et al. Pharmacokinetic and pharmacodynamic study of intratumoral injection of an adenovirus encoding endostatin in patients with advanced tumors. Gene Ther. 2008, 15, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, H.; Li, C.Y.; Yuan, F. Effects of rate, volume, and dose of intratumoral infusion on virus dissemination in local gene delivery. Mol. Cancer Ther. 2006, 5, 362–366. [Google Scholar] [CrossRef] [PubMed]
- De Boer, R.J.; Oprea, M.; Antia, R.; Murali-Krishna, K.; Ahmed, R.; Perelson, A.S. Recruitment times, proliferation, and apoptosis rates during the CD8+ T-cell response to lymphocytic choriomeningitis virus. J. Virol. 2001, 75, 10663–10669. [Google Scholar] [CrossRef] [PubMed]
- Del Vecchio, M.; Bajetta, E.; Canova, S.; Lotze, M.T.; Wesa, A.; Parmiani, G.; Anichini, A. Interleukin-12: Biological properties and clinical application. Clin. Cancer Res. 2007, 13, 4677–4685. [Google Scholar] [CrossRef] [PubMed]
- Van Stipdonk, M.J.; Lemmens, E.E.; Schoenberger, S.P. Naïve CTLs require a single brief period of antigenic stimulation for clonal expansion and differentiation. Nat. Immunol. 2001, 2, 423–429. [Google Scholar] [PubMed]
- Veiga-Fernandes, H.; Walter, U.; Bourgeois, C.; McLean, A.; Rocha, B. Response of naïve and memory CD8+ T cells to antigen stimulation in vivo. Nat. Immunol. 2000, 1, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.N.; Choi, I.K.; Huang, J.H.; Yoo, J.Y.; Choi, K.J.; Yun, C.O. Optimizing DC vaccination by combination with oncolytic adenovirus coexpressing IL-12 and GM-CSF. Mol. Ther. 2011, 19, 1558–1568. [Google Scholar] [CrossRef] [PubMed]
- Barish, S.; Ochs, M.F.; Sontag, E.D.; Gevertz, J.L. Evaluating optimal therapy robustness by virtual expansion of a sample population, with a case study in cancer immunotherapy. Proc. Natl. Acad. Sci. USA 2017, 114, E6277–E6286. [Google Scholar] [CrossRef] [PubMed]
- Ungerechts, G.; Bossow, S.; Leuchs, B.; Holm, P.S.; Rommelaere, J.; Coffey, M.; Coffin, R.; Bell, J.; Nettelbeck, D.M. Moving oncolytic viruses into the clinic: Clinical-grade production, purification, and characterization of diverse oncolytic viruses. Mol. Ther. Methods Clin. Dev. 2016, 3, 16018. [Google Scholar] [CrossRef] [PubMed]
- Breitbach, C.J.; Lichty, B.D.; Bell, J.C. Oncolytic viruses: Therapeutics with an identity crisis. EBioMedicine 2016, 9, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J.; Peng, K.W. Oncolytic virotherapy: A contest between apples and oranges. Mol. Ther. 2017, 25, 1107–1116. [Google Scholar] [CrossRef] [PubMed]
- McGuire, M.F.; Enderling, H.; Wallace, D.I.; Batra, J.; Jordan, M.; Kumar, S.; Panetta, J.C.; Pasquier, E. Formalizing an integrative, multidisciplinary cancer therapy discovery workflow. Cancer Res. 2013, 73, 6111–6117. [Google Scholar] [CrossRef] [PubMed]
- Friedman, G.K.; Markert, J.M.; Gillespie, G.Y. Combination strategies enhance oncolytic virotherapy. Oncotarget 2017, 8, 34020–34021. [Google Scholar] [CrossRef] [PubMed]
- Komarova, N.L.; Wodarz, D. Virus dynamics in the presence of synaptic transmission. Math. Biosci. 2013, 242, 161–171. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santiago, D.N.; Heidbuechel, J.P.W.; Kandell, W.M.; Walker, R.; Djeu, J.; Engeland, C.E.; Abate-Daga, D.; Enderling, H. Fighting Cancer with Mathematics and Viruses. Viruses 2017, 9, 239. https://doi.org/10.3390/v9090239
Santiago DN, Heidbuechel JPW, Kandell WM, Walker R, Djeu J, Engeland CE, Abate-Daga D, Enderling H. Fighting Cancer with Mathematics and Viruses. Viruses. 2017; 9(9):239. https://doi.org/10.3390/v9090239
Chicago/Turabian StyleSantiago, Daniel N., Johannes P. W. Heidbuechel, Wendy M. Kandell, Rachel Walker, Julie Djeu, Christine E. Engeland, Daniel Abate-Daga, and Heiko Enderling. 2017. "Fighting Cancer with Mathematics and Viruses" Viruses 9, no. 9: 239. https://doi.org/10.3390/v9090239
APA StyleSantiago, D. N., Heidbuechel, J. P. W., Kandell, W. M., Walker, R., Djeu, J., Engeland, C. E., Abate-Daga, D., & Enderling, H. (2017). Fighting Cancer with Mathematics and Viruses. Viruses, 9(9), 239. https://doi.org/10.3390/v9090239