Rooting and Dating Large SARS-CoV-2 Trees by Modeling Evolutionary Rate as a Function of Time
Abstract
1. Introduction
2. An Improved TRAD Method
2.1. The Rooting Step
2.2. The Dating Step
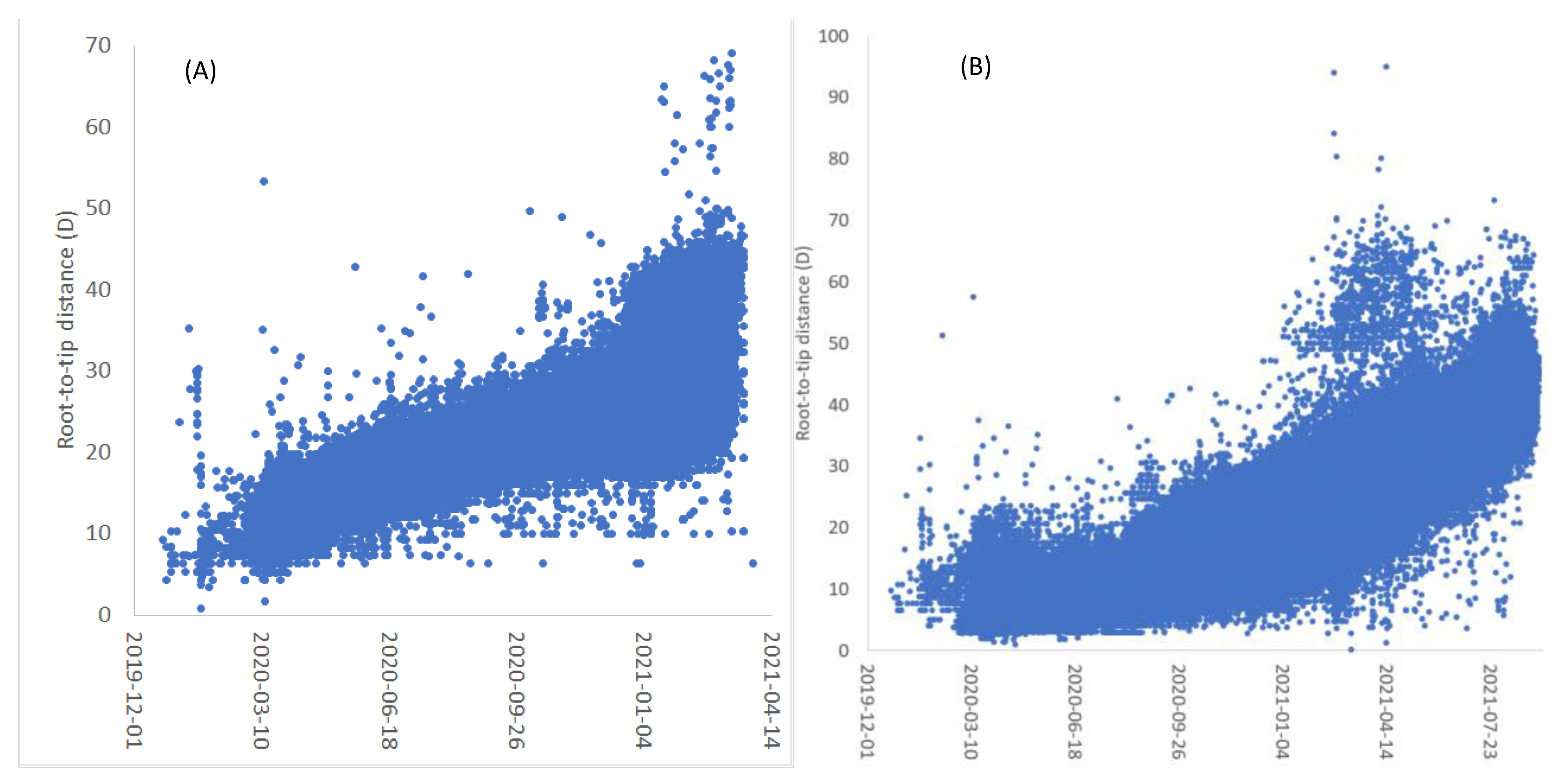
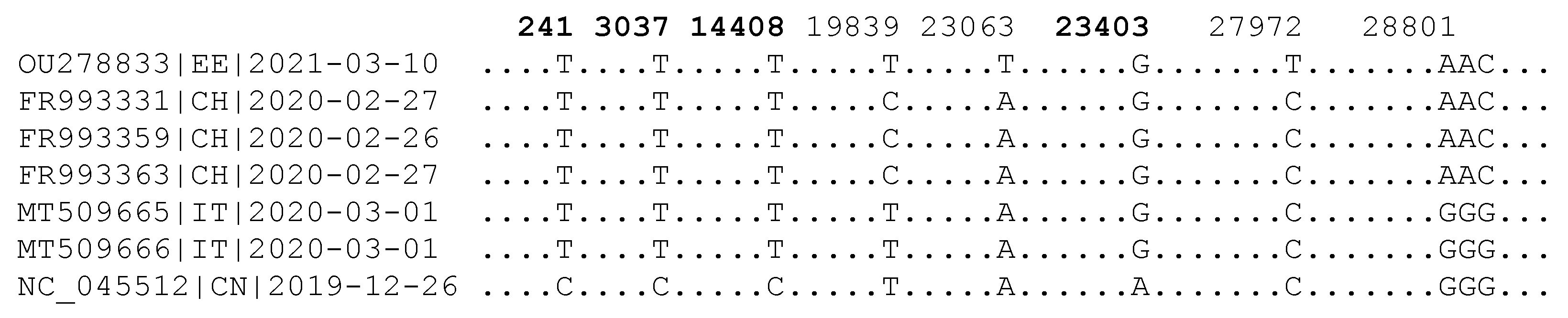
3. Results
4. Discussion
4.1. The Pros and Cons of Using Large Trees
4.2. Strict and Uncorrelated Relaxed Clock
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MacLean, O.A.; Lytras, S.; Weaver, S.; Singer, J.B.; Boni, M.F.; Lemey, P.; Kosakovsky Pond, S.L.; Robertson, D.L. Natural selection in the evolution of SARS-CoV-2 in bats created a generalist virus and highly capable human pathogen. PLoS Biol. 2021, 19, e3001115. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pipes, L.; Nielsen, R. Synonymous mutations and the molecular evolution of SARS-CoV-2 origins. Virus Evol. 2021, 7, veaa098. [Google Scholar] [CrossRef] [PubMed]
- Boni, M.F.; Lemey, P.; Jiang, X.; Lam, T.T.-Y.; Perry, B.; Castoe, T.; Rambaut, A.; Robertson, D.L. Evolutionary origins of the SARS-CoV-2 sarbecovirus lineage responsible for the COVID-19 pandemic. Nat. Microbiol. 2020, 5, 1408–1417. [Google Scholar] [CrossRef] [PubMed]
- Lytras, S.; Xia, W.; Hughes, J.; Jiang, X.; Robertson, D.L. The animal origin of SARS-CoV-2. Science 2021, 373, 968–970. [Google Scholar] [CrossRef]
- Xia, X. Dating the Common Ancestor from an NCBI Tree of 83688 High-Quality and Full-Length SARS-CoV-2 Genomes. Viruses 2021, 13, 1790. [Google Scholar] [CrossRef] [PubMed]
- Xia, X. Distance-Based Phylogenetic Methods. In Bioinformatics and the Cell: Modern Computational Approaches in Genomics, Proteomics and Transcriptomics; Springer: Cham, Switzerland, 2018; pp. 343–379. [Google Scholar]
- Xia, X. DAMBE5: A comprehensive software package for data analysis in molecular biology and evolution. Mol. Biol. Evol. 2013, 30, 1720–1728. [Google Scholar] [CrossRef]
- Rambaut, A.; Lam, T.T.; Max Carvalho, L.; Pybus, O.G. Exploring the temporal structure of heterochronous sequences using TempEst (formerly Path-O-Gen). Virus Evol. 2016, 2, vew007. [Google Scholar] [CrossRef]
- Himmelmann, L.; Metzler, D. TreeTime: An extensible C++ software package for Bayesian phylogeny reconstruction with time-calibration. Bioinformatics 2009, 25, 2440–2441. [Google Scholar] [CrossRef]
- To, T.-H.; Jung, M.; Lycett, S.; Gascuel, O. Fast Dating Using Least-Squares Criteria and Algorithms. Syst. Biol. 2016, 65, 82–97. [Google Scholar] [CrossRef]
- Volz, E.M.; Frost, S.D.W. Scalable relaxed clock phylogenetic dating. Virus Evol. 2017, 3, vex025. [Google Scholar] [CrossRef]
- Kumar, S.; Tao, Q.; Weaver, S.; Sanderford, M.; Caraballo-Ortiz, M.A.; Sharma, S.; Pond, S.L.K.; Miura, S. An Evolutionary Portrait of the Progenitor SARS-CoV-2 and Its Dominant Offshoots in COVID-19 Pandemic. Mol. Biol. Evol. 2021, 38, 3046–3059. [Google Scholar] [CrossRef] [PubMed]
- Pekar, J.; Worobey, M.; Moshiri, N.; Scheffler, K.; Wertheim, J.O. Timing the SARS-CoV-2 index case in Hubei province. Science 2021, 372, 412–417. [Google Scholar] [CrossRef]
- van Dorp, L.; Acman, M.; Richard, D.; Shaw, L.P.; Ford, C.E.; Ormond, L.; Owen, C.J.; Pang, J.; Tan, C.C.S.; Boshier, F.A.T.; et al. Emergence of genomic diversity and recurrent mutations in SARS-CoV-2. Infect. Genet. Evol. 2020, 83, 104351. [Google Scholar] [CrossRef]
- Gómez-Carballa, A.; Bello, X.; Pardo-Seco, J.; Martinón-Torres, F.; Salas, A. Mapping genome variation of SARS-CoV-2 worldwide highlights the impact of COVID-19 super-spreaders. Genome Res. 2020, 30, 1434–1448. [Google Scholar] [CrossRef]
- Rambaut, A.; Holmes, E.C.; O’Toole, Á.; Hill, V.; McCrone, J.T.; Ruis, C.; du Plessis, L.; Pybus, O.G. A dynamic nomenclature proposal for SARS-CoV-2 lineages to assist genomic epidemiology. Nat. Microbiol. 2020, 5, 1403–1407. [Google Scholar] [CrossRef] [PubMed]
- Chaw, S.-M.; Tai, J.-H.; Chen, S.-L.; Hsieh, C.-H.; Chang, S.-Y.; Yeh, S.-H.; Yang, W.-S.; Chen, P.-J.; Wang, H.-Y. The origin and underlying driving forces of the SARS-CoV-2 outbreak. J. Biomed. Sci. 2020, 27, 73. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, S.; Shi, C.-M.; Song, S.; Zhu, S.; Su, Y.; Zhao, W.; Li, M.; Bao, Y.; Xue, Y.; et al. Population Genetics of SARS-CoV-2: Disentangling Effects of Sampling Bias and Infection Clusters. Genom. Proteom. Bioinform. 2020, 18, 640–647. [Google Scholar] [CrossRef]
- Duchene, S.; Featherstone, L.; Haritopoulou-Sinanidou, M.; Rambaut, A.; Lemey, P.; Baele, G. Temporal signal and the phylodynamic threshold of SARS-CoV-2. Virus Evol. 2020, 6, veaa061. [Google Scholar] [CrossRef] [PubMed]
- Tay, J.H.; Porter, A.F.; Wirth, W.; Duchene, S. The Emergence of SARS-CoV-2 Variants of Concern Is Driven by Acceleration of the Substitution Rate. Mol. Biol. Evol. 2022, 39, msac013. [Google Scholar] [CrossRef]
- Pekar, J.E.; Magee, A.; Parker, E.; Moshiri, N.; Izhikevich, K.; Havens, J.L.; Gangavarapu, K.; Malpica Serrano, L.M.; Crits-Christoph, A.; Matteson, N.L.; et al. The molecular epidemiology of multiple zoonotic origins of SARS-CoV-2. Science 2022, 377, 960–966. [Google Scholar] [CrossRef]
- Xia, X. TRAD: Tip-Rooting and Ancestor-Dating; University of Ottawa: Ottawa, ON, Canada, 2021. [Google Scholar]
- Xia, X. DAMBE7: New and improved tools for data analysis in molecular biology and evolution. Mol. Biol. Evol. 2018, 35, 1550–1552. [Google Scholar] [CrossRef] [PubMed]
- Thorne, J.L.; Kishino, H.; Painter, I.S. Estimating the rate of evolution of the rate of molecular evolution. Mol. Biol. Evol. 1998, 15, 1647–1657. [Google Scholar] [CrossRef] [PubMed]
- Aris-Brosou, S.; Yang, Z. Effects of models of rate evolution on estimation of divergence dates with special reference to the metazoan 18S ribosomal RNA phylogeny. Syst. Biol. 2002, 51, 703–714. [Google Scholar] [CrossRef] [PubMed]
- Hatcher, E.L.; Zhdanov, S.A.; Bao, Y.; Blinkova, O.; Nawrocki, E.P.; Ostapchuck, Y.; Schäffer, A.A.; Brister, J.R. Virus Variation Resource—Improved response to emergent viral outbreaks. Nucleic Acids Res. 2017, 45, D482–D490. [Google Scholar] [CrossRef]
- Xia, X. Improved method for rooting and tip-dating a viral phylogeny. In Handbook of Computational Statistics, II; Lu, H.H.-S., Scholkopf, B., Wells, M.T., Zhao, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Worobey, M.; Levy, J.I.; Malpica Serrano, L.; Crits-Christoph, A.; Pekar, J.E.; Goldstein, S.A.; Rasmussen, A.L.; Kraemer, M.U.G.; Newman, C.; Koopmans, M.P.G.; et al. The Huanan Seafood Wholesale Market in Wuhan was the early epicenter of the COVID-19 pandemic. Science 2022, 377, 951–959. [Google Scholar] [CrossRef]
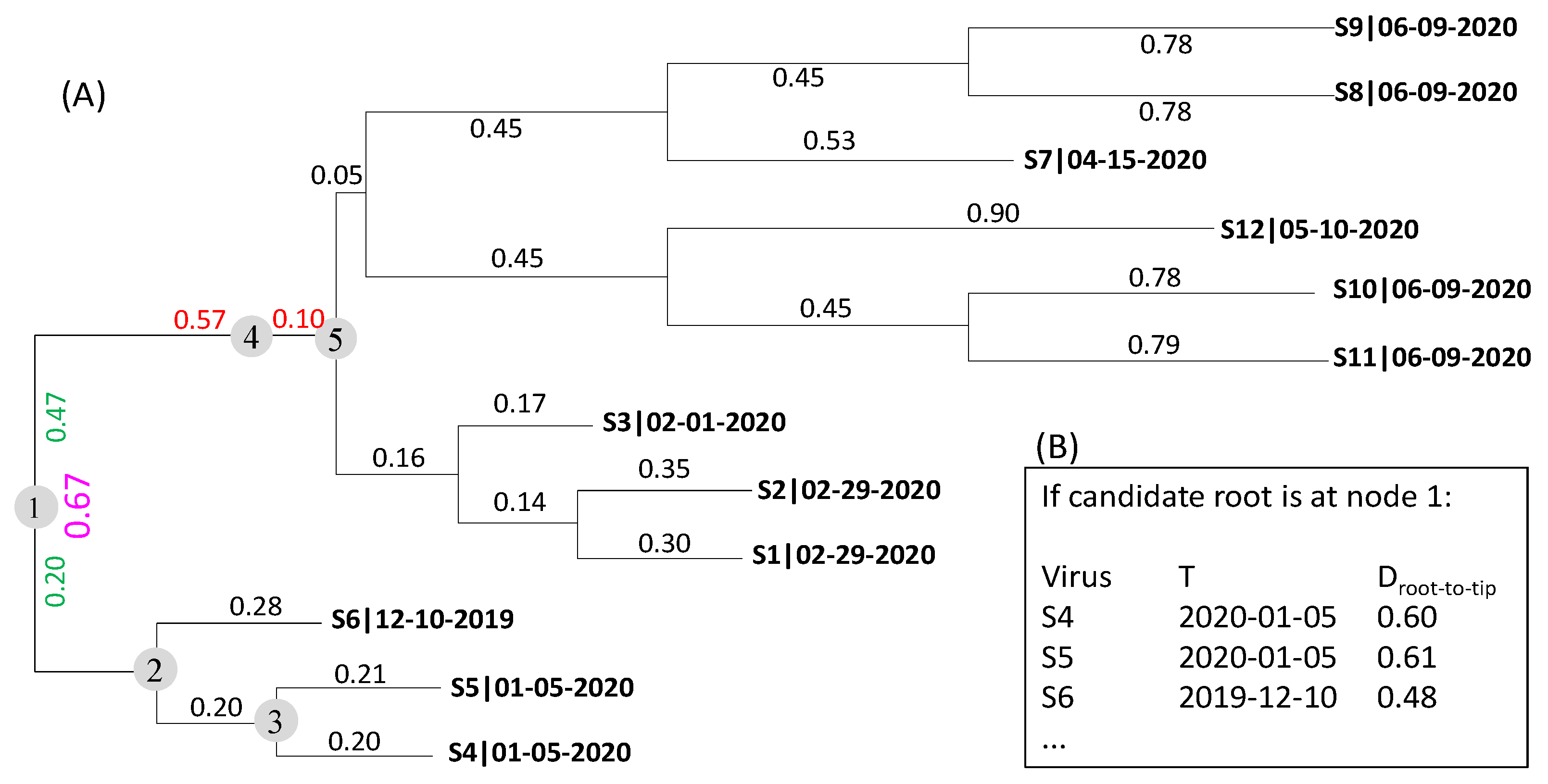
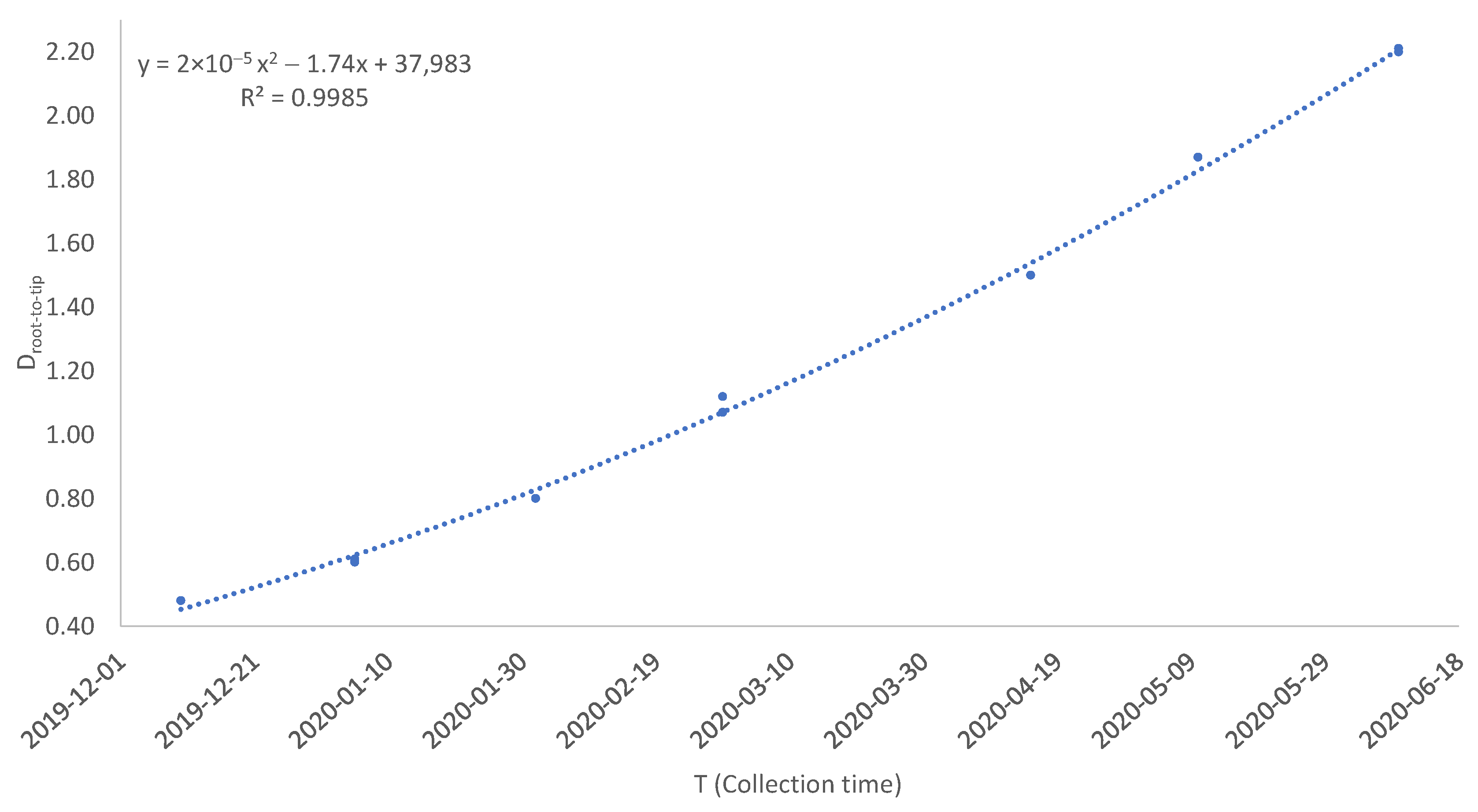
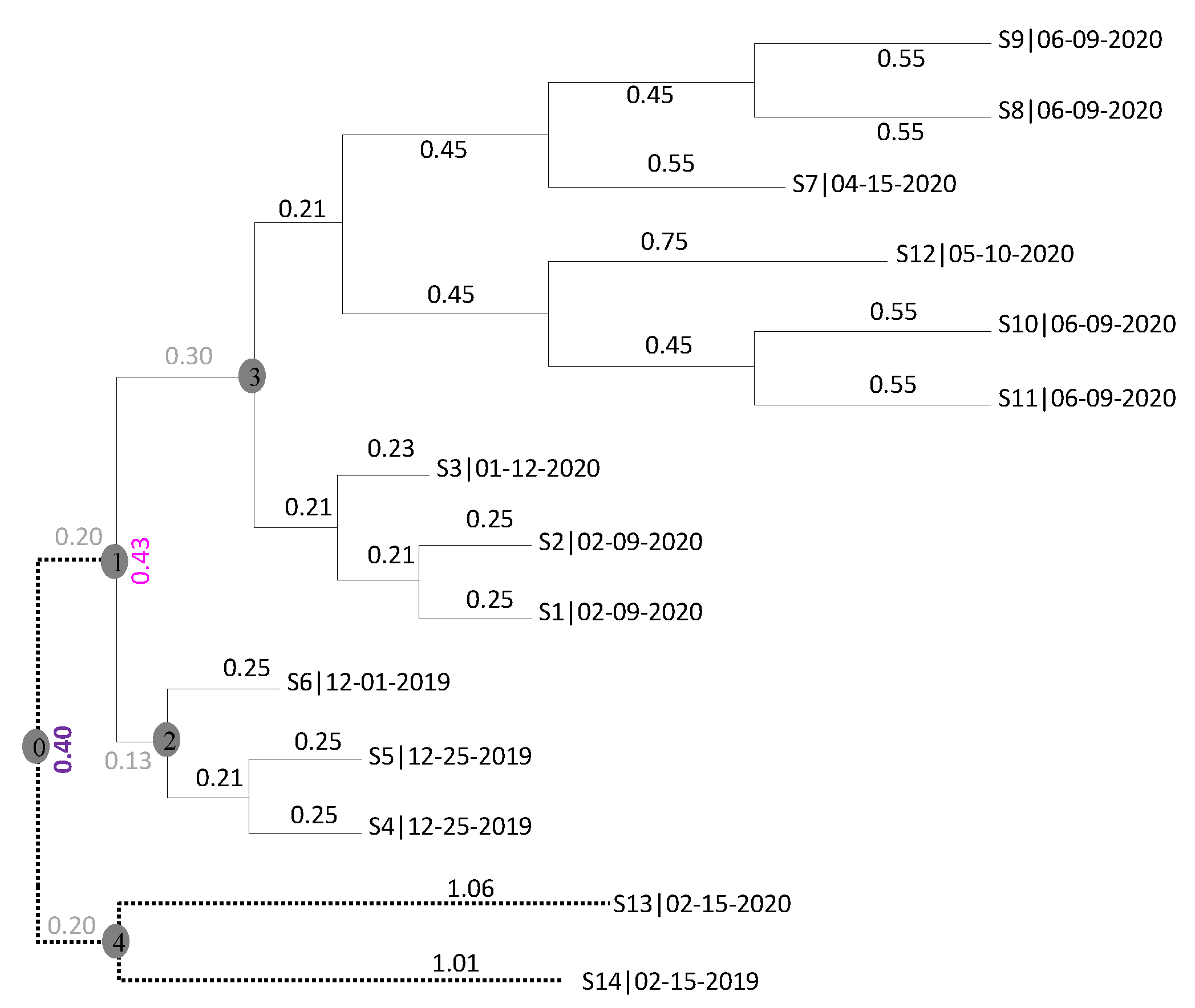
| Virus | T | D1 | D2 | D3 | D4 | Dmax.r | |
|---|---|---|---|---|---|---|---|
| S4 | 2020-01-05 | 0.60 | 0.40 | 0.20 | 0.97 | 0.51291 | 0.60664 |
| S5 | 2020-01-05 | 0.61 | 0.41 | 0.21 | 0.98 | 0.52291 | 0.61664 |
| S6 | 2019-12-10 | 0.48 | 0.28 | 0.48 | 0.85 | 0.39291 | 0.48664 |
| S1 | 2020-02-29 | 1.07 | 1.27 | 1.47 | 0.70 | 1.15709 | 1.06336 |
| S2 | 2020-02-29 | 1.12 | 1.32 | 1.52 | 0.75 | 1.20709 | 1.11336 |
| S3 | 2020-02-01 | 0.80 | 1.00 | 1.20 | 0.43 | 0.88709 | 0.79336 |
| S7 | 2020-04-15 | 1.50 | 1.70 | 1.90 | 1.13 | 1.58709 | 1.49336 |
| S8 | 2020-06-09 | 2.20 | 2.40 | 2.60 | 1.83 | 2.28709 | 2.19336 |
| S9 | 2020-06-09 | 2.20 | 2.40 | 2.60 | 1.83 | 2.28709 | 2.19336 |
| S10 | 2020-06-09 | 2.20 | 2.40 | 2.60 | 1.83 | 2.28709 | 2.19336 |
| S11 | 2020-06-09 | 2.21 | 2.41 | 2.61 | 1.84 | 2.29709 | 2.20336 |
| S12 | 2020-05-10 | 1.87 | 2.07 | 2.27 | 1.50 | 1.95709 | 1.86336 |
| r | 0.9953 | 0.9949 | 0.9749 | 0.8580 | 0.99786 | 0.99486 | |
| R2 | 0.9985 | 0.9909 | 0.9538 | 0.9362 | 0.99662 | 0.99854 |
| The Apr3_21 Tree | The May7_22 Tree | |||
|---|---|---|---|---|
| Model 1 (1) | Model 2 (2) | Model 1 (1) | Model2 (2) | |
| B0 (3) | −2415.05517 | 38,679.17639 | −3247.86320 | 122,456.46937 |
| B1 (3) | 0.05527 | −1.80887 | 0.073993 | −5.61023 |
| B2 (3) | N/A | 2.114018 × 10−5 | N/A | 6.425812 × 10−5 |
| µ (4) | 0.05527 | 0.073993 | ||
| TA (5) | 2019-08-16 | 2019-06-12 | 2020-03-04 | 2019-07-07 |
| R2 (6) | 0.74468 | 0.74550 | 0.82732 | 0.84360 |
| lnL (7) | −235,496.173 | −235,359.894 | −2,677,701.465 | −2,631,291.332 |
| AIC (7) | 470,996.346 | 470,725.788 | 5,355,408.930 | 5,262,588.663 |
| BIC (7) | 471,015.015 | 470,753.793 | 5,355,444.288 | 5,262,624.021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X. Rooting and Dating Large SARS-CoV-2 Trees by Modeling Evolutionary Rate as a Function of Time. Viruses 2023, 15, 684. https://doi.org/10.3390/v15030684
Xia X. Rooting and Dating Large SARS-CoV-2 Trees by Modeling Evolutionary Rate as a Function of Time. Viruses. 2023; 15(3):684. https://doi.org/10.3390/v15030684
Chicago/Turabian StyleXia, Xuhua. 2023. "Rooting and Dating Large SARS-CoV-2 Trees by Modeling Evolutionary Rate as a Function of Time" Viruses 15, no. 3: 684. https://doi.org/10.3390/v15030684
APA StyleXia, X. (2023). Rooting and Dating Large SARS-CoV-2 Trees by Modeling Evolutionary Rate as a Function of Time. Viruses, 15(3), 684. https://doi.org/10.3390/v15030684






