Cocktail, a Computer Program for Modelling Bacteriophage Infection Kinetics
Abstract
1. Introduction
2. Materials and Methods
2.1. Bacteria
2.2. Resources
2.3. Phages
2.4. Model Settings
2.4.1. Primary Adsorption: Standard Model
2.4.2. Secondary Adsorption: Poisson
2.4.3. Resistance Mutation
2.4.4. Refuge Cells
2.4.5. Time Step Size
3. Results
4. Technical Information
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.; Ahn, J. Evolutionary Dynamics between Phages and Bacteria as a Possible Approach for Designing Effective Phage Therapies against Antibiotic-Resistant Bacteria. Antibiotics 2022, 11, 915. [Google Scholar] [CrossRef] [PubMed]
- Kortright, K.E.; Chan, B.K.; Koff, J.L.; Turner, P.E. Phage Therapy: A Renewed Approach to Combat Antibiotic-Resistant Bacteria. Cell Host Microbe 2019, 25, 219–232. [Google Scholar] [CrossRef] [PubMed]
- Międzybrodzki, R.; Borysowski, J.; Weber-Dąbrowska, B.; Fortuna, W.; Letkiewicz, S.; Szufnarowski, K.; Pawełczyk, Z.; Rogóż, P.; Kłak, M.; Wojtasik, E.E.; et al. Clinical Aspects of Phage Therapy. Adv. Virus Res. 2012, 83, 73–121. [Google Scholar] [PubMed]
- Chanishvili, N. Phage Therapy-History from Twort and d’Herelle Through Soviet Experience to Current Approaches. Adv. Virus Res. 2012, 83, 3–40. [Google Scholar] [PubMed]
- Styles, K.M.; Brown, A.T.; Sagona, A.P. A Review of Using Mathematical Modeling to Improve Our Understanding of Bacteriophage, Bacteria, and Eukaryotic Interactions. Front. Microbiol. 2021, 12, 2752. [Google Scholar] [CrossRef]
- Bull, J.J.; Vegge, C.S.; Schmerer, M.; Chaudhry, W.N.; Levin, B.R. Phenotypic resistance and the dynamics of bacterial escape from phage control. PLoS ONE 2014, 9, e94690. [Google Scholar]
- Chaudhry, W.N.; Pleška, M.; Shah, N.N.; Weiss, H.; McCall, I.C.; Meyer, J.R.; Gupta, A.; Guet, C.C.; Levin, B.R. Leaky resistance and the conditions for the existence of lytic bacteriophage. PLoS Biol. 2018, 16, e2005971. [Google Scholar] [CrossRef]
- Krysiak-Baltyn, K.; Martin, G.J.O.; Stickland, A.D.; Scales, P.J.; Gras, S.L. Computational models of populations of bacteria and lytic phage. Crit. Rev. Microbiol. 2016, 7828, 942–968. [Google Scholar] [CrossRef]
- Bull, J.J.; Levin, B.R.; Molineux, I.J. Promises and pitfalls of in vivo evolution to improve phage therapy. Viruses 2019, 11, 1083. [Google Scholar] [CrossRef]
- Levin, B.R.; Stewart, F.M.; Chao, L. Resource-limited growth, competition, and predation: A model and experimental studies with bacteria and bacteriophage. Am. Nat. 1977, 111, 3–24. [Google Scholar] [CrossRef]
- Abedon, S. Deconstructing Chemostats Towards Greater Phage-Modeling Precision. In Contemporary Trends in Bacteriophage Research; Adams, H., Ed.; Nova Science Publishers: New York, NY, USA, 2009; pp. 249–283. ISBN 9781606921814. [Google Scholar]
- Cairns, B.J.; Timms, A.R.; Jansen, V.A.; Connerton, I.F.; Payne, R.J. Quantitative models of in vitro bacteriophage-host dynamics and their application to phage therapy. PLoS Pathog 2009, 5, e1000253. [Google Scholar] [CrossRef] [PubMed]
- Gill, J.J. Modeling of bacteriophage therapy. In Bacteriophage Ecology: Population Growth, Evolution, and Impact of Bacterial Viruses; Abedon, S.T., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 439–464. ISBN 9780511541483. [Google Scholar]
- Hodyra-Stefaniak, K.; Miernikiewicz, P.; Drapała, J.; Drab, M.; Jonczyk-Matysiak, E.; Lecion, D.; Kazmierczak, Z.; Beta, W.; Majewska, J.; Harhala, M.; et al. Mammalian Host-Versus-Phage immune response determines phage fate in vivo. Sci. Rep. 2015, 5, 14802. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.Y.J.; Weitz, J.S. Modeling the synergistic elimination of bacteria by phage and the innate immune system. J. Theor. Biol. 2017, 429, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Kyaw, E.E.; Zheng, H.; Wang, J.; Hlaing, H.K. Stability analysis and persistence of a phage therapy model. Math. Biosci. Eng. 2021, 18, 5552–5570. [Google Scholar] [CrossRef]
- Li, G.; Leung, C.Y.; Ward, Y.; Debarbieux, L.; Weitz, J.S. Optimizing the Timing and Composition of Therapeutic Phage Cocktails: A Control-Theoretic Approach. Bull. Math. Biol. 2021, 82, 75. [Google Scholar] [CrossRef]
- Nilsson, A.S. Pharmacological limitations of phage therapy. Ups. J. Med. Sci. 2019, 124, 218–227. [Google Scholar] [CrossRef] [PubMed]
- Lenski, R.E. Dynamics of interactions between bacteria and virulent bacteriophage. Adv. Microb. Ecol. 1988, 10, 1–44. [Google Scholar]
- Levin, B.R.; Bull, J.J. Population and evolutionary dynamics of phage therapy. Nat. Rev. Microbiol. 2004, 2, 166–173. [Google Scholar] [CrossRef]
- Monod, J. Recherches sur la croissance des cultures bactériennes. In Actualités Scientifiques Et Industrielles; Hermann & Cie: Paris, France, 1942. [Google Scholar]
- Senn, H.; Lendenmann, U.; Snozzi, M.; Hamer, G.; Egli, T. The growth of Escherichia coli in glucose-limited chemostat cultures: A re-examination of the kinetics. Biochim. Biophys. Acta 1994, 1201, 424–436. [Google Scholar] [CrossRef]
- Wang, P.; Robert, L.; Pelletier, J.; Dang, W.L.; Taddei, F.; Wright, A.; Jun, S. Robust growth of Escherichia coli. Curr. Biol. 2010, 20, 1099–1103. [Google Scholar] [CrossRef]
- Perkins, T.L.; Perrow, K.; Rajko-Nenow, P.; Jago, C.F.; Jones, D.L.; Malham, S.K.; McDonald, J.E. Decay rates of faecal indicator bacteria from sewage and ovine faeces in brackish and freshwater microcosms with contrasting suspended particulate matter concentrations. Sci. Total Environ. 2016, 572, 1645–1652. [Google Scholar] [CrossRef] [PubMed]
- Kasman, L.M.; Kasman, A.; Westwater, C.; Dolan, J.; Schmidt, M.G.; Norris, J.S. Overcoming the phage replication threshold: A mathematical model with implications for phage therapy. J. Virol. 2002, 76, 5557–5564. [Google Scholar] [CrossRef] [PubMed]
- Bohannan, B.J.M.; Lenski, R.E. Effect of resource enrichment on a chemostat community of bacteria and bacteriophage. Ecology 1997, 78, 2303–2315. [Google Scholar] [CrossRef]
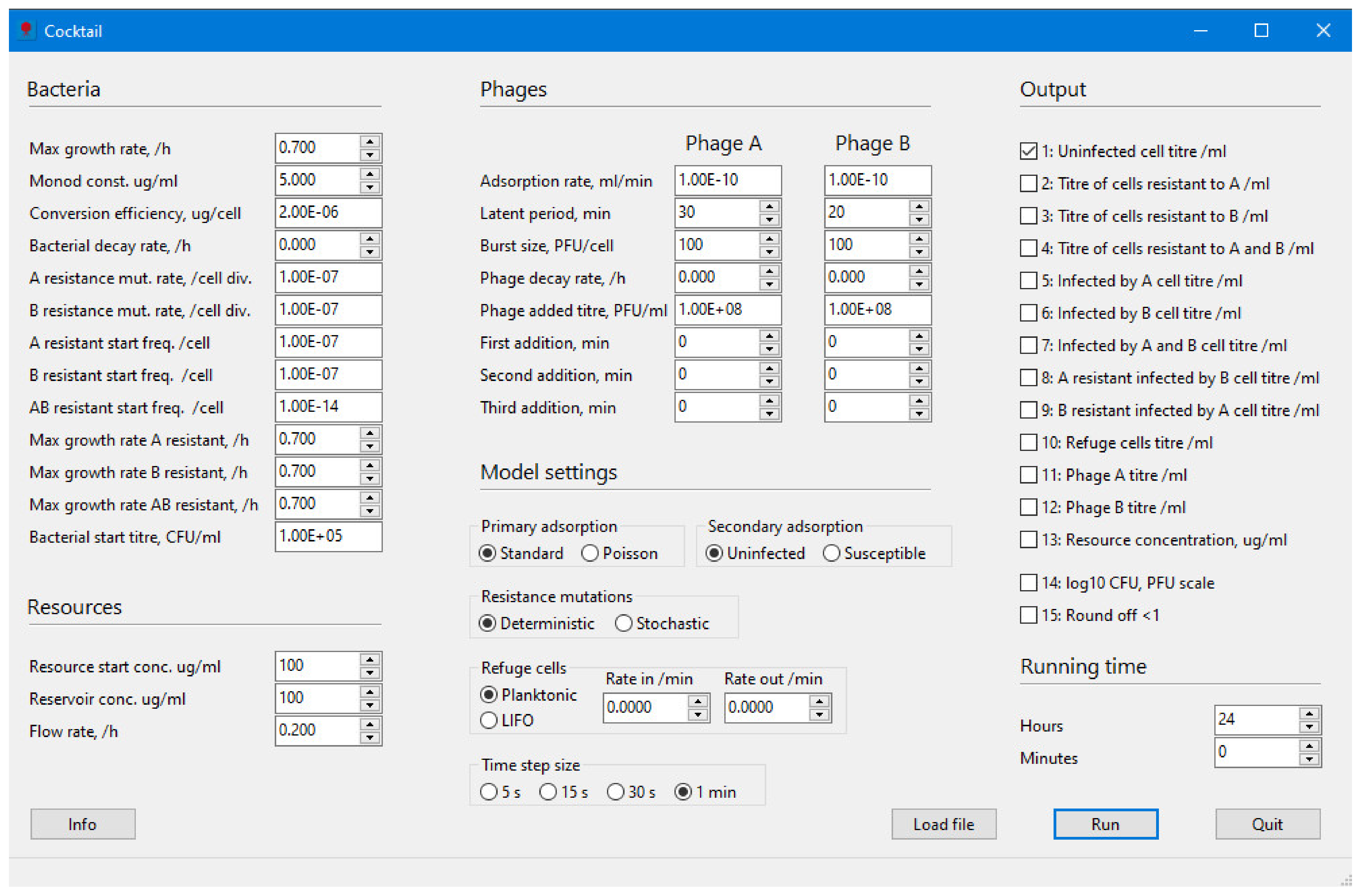

| Start Values | ||||
|---|---|---|---|---|
| Symbol | Description | Default | Allowed Range | Unit |
| Bacteria | ||||
| S | Uninfected, susceptible bacteria | 1 × 105 | 10−1 × 1012 | CFU/mL |
| IA | Bacteria infected by phage A | - | - | | |
| IB | Bacteria infected by phage B | - | - | | |
| IAB | Bacteria infected by phages A and B | - | - | | |
| RA | Bacteria resistant to phage A | 1 × 10−7 | 0–1 × 10−2 | | |
| RB | Bacteria resistant to phage B | 1 × 10−7 | 0–1 × 10−2 | | |
| RAB | Bacteria resistant to phages A and B | 1 × 10−14 | 0–1 × 10−6 | | |
| RAIB | Bacteria resistant to A infected with B | - | - | | |
| RBIA | Bacteria resistant to B infected with A | - | - | | |
| Sr | Susceptible bacteria in a refuge | 0 | - | | |
| RrA | Bacteria resistant to A in a refuge | - | - | | |
| RrB | Bacteria resistant to B in a refuge | - | - | | |
| RrAB | Bacteria resistant to AB in a refuge | - | - | CFU/mL |
| Parameters | ||||
| ψ | Growth rate of S | 0.7 | 0–1.5 | /h |
| K | Monod constant | 5.0 | 0.01–100 | µg/mL * |
| ε | Resource for division of one bacterium | 2 × 10−6 | 1 × 10−8–1 × 10−4 | µg/cell * |
| γ | Bacterial decay rate | 0 | 0–1 | /h |
| µA | Mutation rate for resistance against A | 1 × 10−7 | 0–1 × 10−2 | /cell div. |
| µB | Mutation rate for resistance against B | 1 × 10−7 | 0–1 × 10−2 | /cell div. |
| Growth rate of RA | 0.7 | 0–1.5 | /h | |
| Growth rate of RB | 0.7 | 0–1.5 | /h | |
| Growth rate of RAB | 0.7 | 0–1.5 | /h | |
| σ | Rate of bacteria into refuge | 0 | 0–0.01 | /min |
| ρ | Rate of bacteria out from refuge | 0 | 0–0.01 | /min |
| C0 | Available resources from start | 100 | 0–1000 | µg/mL * |
| C | Resources flowing in from a reservoir | 100 | 0–1000 | µg/mL * |
| ω | Flow rate | 0.2 | 0–100 | /h |
| Phages | ||||
| Parameters | ||||
| A | Titre of phage A | 1 × 108 | 0–1 × 1013 | PFU/mL |
| B | Titre of phage B | 1 × 108 | 0–1 × 1013 | PFU/mL |
| δA | Adsorption rate of A | 1 × 10−10 | 1 × 10−14–1 × 10−7 | mL/min |
| δB | Adsorption rate of B | 1 × 10−10 | 1 × 10−14–1 × 10−7 | mL/min |
| lA | Latent period of A | 30 | 1–60 | min |
| lB | Latent period of B | 20 | 1–60 | min |
| βA | Burst size of A | 100 | 0–1000 | PFU/cell |
| βB | Burst size of B | 100 | 0–1000 | PFU/cell |
| φA | Decay rate of phage A | 0 | 0–1 | /h |
| φB | Decay rate of phage B | 0 | 0–1 | /h |
| Primary Adsorption Setting | Standard | Poisson | ||
|---|---|---|---|---|
| Secondary Adsorption Setting | Uninfected | Susceptible | Uninfected | Susceptible |
| Phages adsorb one at a time to uninfected non-resistant cells | Phages adsorb one at a time to non-resistant cells | A number of phages adsorb according to a Poisson probability with lambda = MOI to uninfected non-resistant cells | A number of phages adsorb according to a Poisson probability with lambda = MOI to non-resistant cells | |
| Bacteria | Conceivably adsorbing phages | |||
| S = Susceptible | A or B | A or B | A and B | A and B |
| IA = Infected by A | B | A or B | B | A and B |
| IB = Infected by B | A | A or B | A | A and B |
| IAB = Infected by A and B | - | A or B | - | A and B |
| RA = Resistant to infections by A | B | B | B | B |
| RB = Resistant to infections by B | A | A | A | A |
| RAB = Resistant to infections by A and B | - | - | - | - |
| RAIB = Resistant to infections by A infected with B | - | B | - | B |
| RBIA = Resistant to infections by B infected with A | - | A | - | A |
| Sr = Susceptible planktonic bacteria in a refuge | - | A or B No infection | A and B No infection | A and B No infection |
| RrA = Planktonic bacteria resistant to A in a refuge | - | B No infection | B No infection | B No infection |
| RrB = Planktonic bacteria resistant to B in a refuge | - | A No infection | A No infection | A No infection |
| RrAB = Planktonic bacteria resistant to AB in a refuge | - | - | - | - |
| Sr = Susceptible bacteria in a LIFO refuge | - | - | - | - |
| RrA = Bacteria resistant to A in a LIFO refuge | - | - | - | - |
| RrB = Bacteria resistant to B in a LIFO refuge | - | - | - | - |
| RrAB = Bacteria resistant to AB in a LIFO refuge | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nilsson, A.S. Cocktail, a Computer Program for Modelling Bacteriophage Infection Kinetics. Viruses 2022, 14, 2483. https://doi.org/10.3390/v14112483
Nilsson AS. Cocktail, a Computer Program for Modelling Bacteriophage Infection Kinetics. Viruses. 2022; 14(11):2483. https://doi.org/10.3390/v14112483
Chicago/Turabian StyleNilsson, Anders S. 2022. "Cocktail, a Computer Program for Modelling Bacteriophage Infection Kinetics" Viruses 14, no. 11: 2483. https://doi.org/10.3390/v14112483
APA StyleNilsson, A. S. (2022). Cocktail, a Computer Program for Modelling Bacteriophage Infection Kinetics. Viruses, 14(11), 2483. https://doi.org/10.3390/v14112483






