Will SARS-CoV-2 Become Just Another Seasonal Coronavirus?
Abstract
1. Introduction
1.1. Small SARS-CoV-2 Doses Are Associated with Mild COVID-19 Disease
1.2. Children Develop Mild COVID-19 Infections
1.3. Partial Immunity Results in Mild Disease
1.4. Non-Pharmaceutical Interventions (NPI) Promote Mild Disease
1.5. Vaccines
2. Methods
2.1. Model with Two Infection Types
2.2. Model with Age-Structure Only
2.3. The Full Model
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| JASC | Just Another Seasonal Coronavirus |
Appendix A
Appendix A.1. Full Steady State Solution for the Model with Two Infection Types
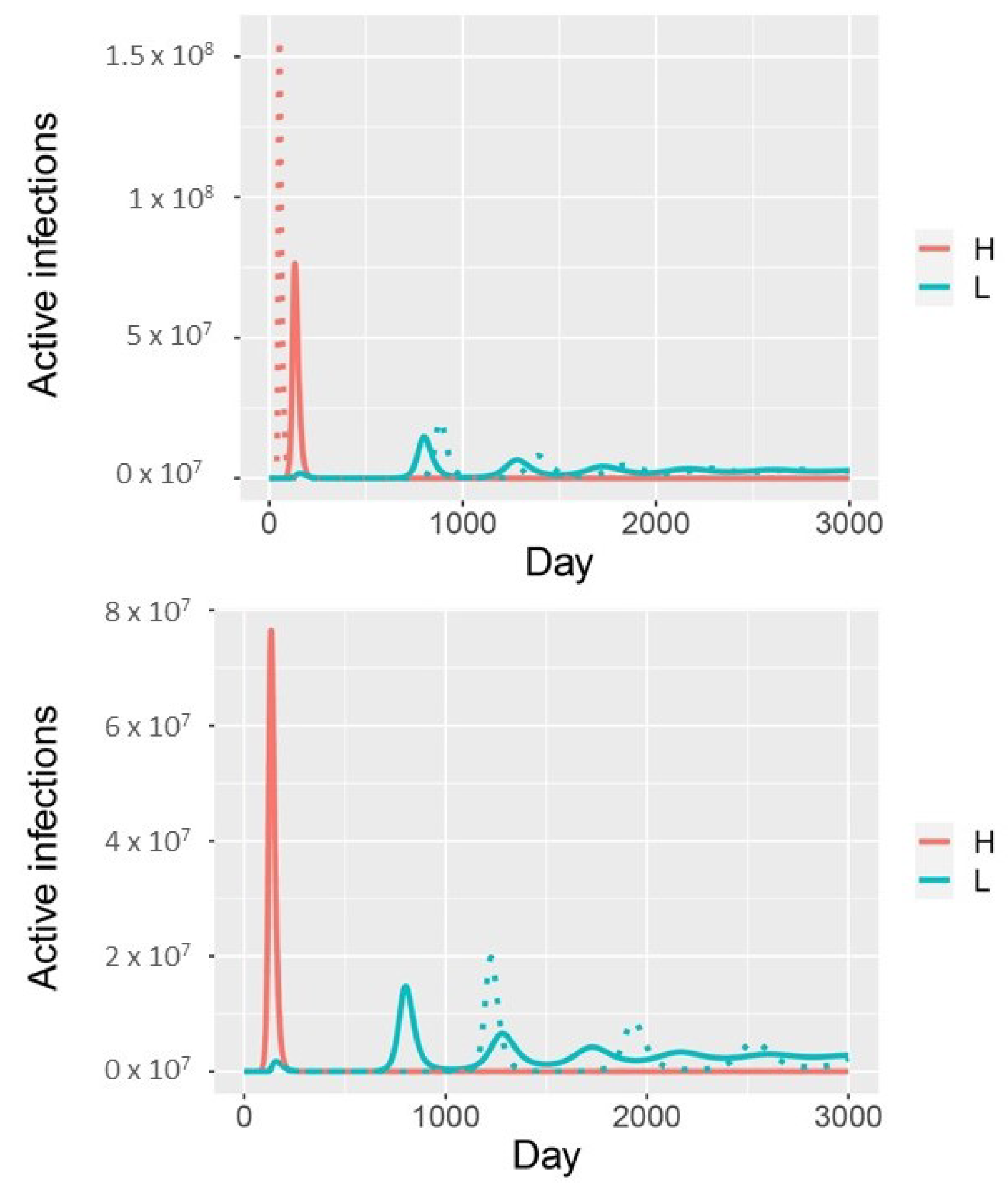
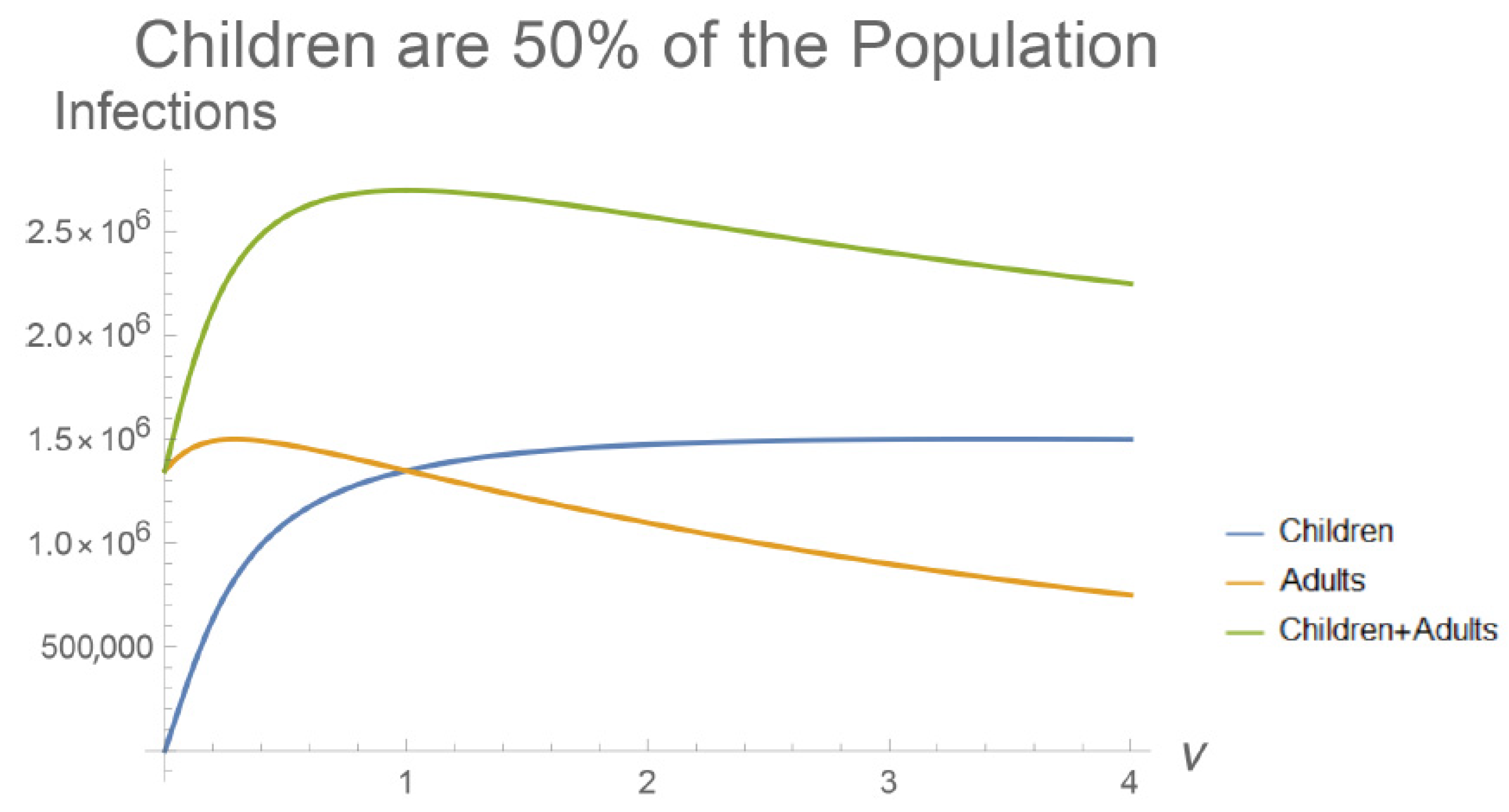
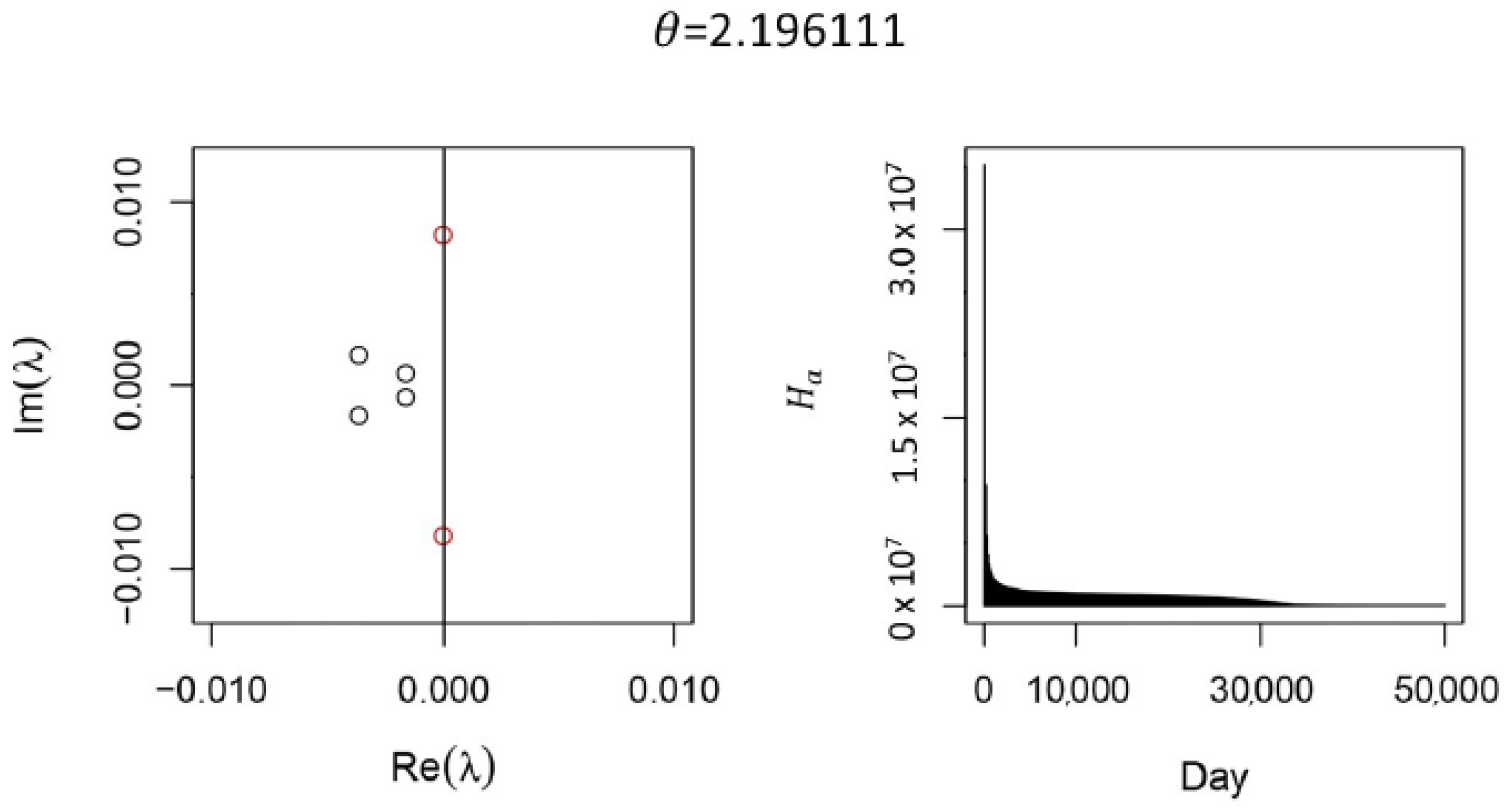
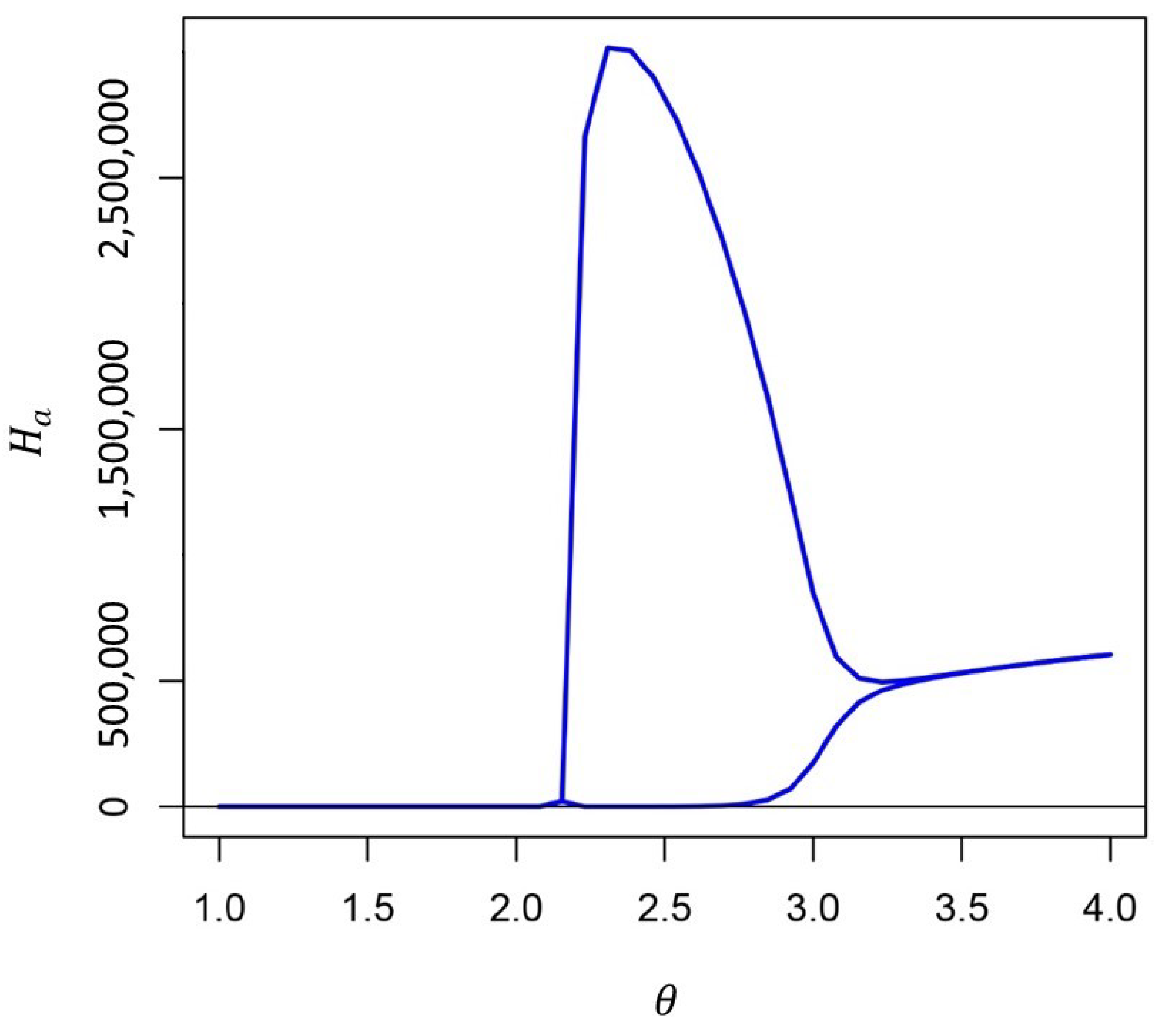
Appendix A.2. Simplifying the Full Model
References
- Paules, C.I.; Marston, H.D.; Fauci, A.S. Coronavirus infections—More than just the common cold. JAMA 2020, 323, 707–708. [Google Scholar] [CrossRef]
- Raoult, D.; Zumla, A.; Locatelli, F.; Ippolito, G.; Kroemer, G. Coronavirus infections: Epidemiological, clinical and immunological features and hypotheses. Cell Stress 2020, 4, 66. [Google Scholar] [CrossRef] [PubMed]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the post-pandemic period. MedRxiv 2020. [Google Scholar] [CrossRef]
- Vijgen, L.; Keyaerts, E.; Moës, E.; Thoelen, I.; Wollants, E.; Lemey, P.; Vandamme, A.M.; Van Ranst, M. Complete genomic sequence of human coronavirus OC43: Molecular clock analysis suggests a relatively recent zoonotic coronavirus transmission event. J. Virol. 2005, 79, 1595–1604. [Google Scholar] [CrossRef]
- Jia, H.P.; Look, D.C.; Shi, L.; Hickey, M.; Pewe, L.; Netland, J.; Farzan, M.; Wohlford-Lenane, C.; Perlman, S.; McCray, P.B. ACE2 receptor expression and severe acute respiratory syndrome coronavirus infection depend on differentiation of human airway epithelia. J. Virol. 2005, 79, 14614–14621. [Google Scholar] [CrossRef]
- Hofmann, H.; Pyrc, K.; van der Hoek, L.; Geier, M.; Berkhout, B.; Pöhlmann, S. Human coronavirus NL63 employs the severe acute respiratory syndrome coronavirus receptor for cellular entry. Proc. Natl. Acad. Sci. USA 2005, 102, 7988–7993. [Google Scholar] [CrossRef]
- Holmes, M.; Reed, S.E.; Stott, E.; Tyrrell, D. Studies of experimental rhinovirus type 2 infections in polar isolation and in England. Epidemiol. Infect. 1976, 76, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Byington, C.L.; Ampofo, K.; Stockmann, C.; Adler, F.R.; Herbener, A.; Miller, T.; Sheng, X.; Blaschke, A.J.; Crisp, R.; Pavia, A.T. Community surveillance of respiratory viruses among families in the Utah Better Identification of Germs-Longitudinal Viral Epidemiology (BIG-LoVE) study. Clin. Infect. Dis. 2015, 61, 1217–1224. [Google Scholar] [CrossRef] [PubMed]
- Zinkernagel, R.M. On immunity against infections and vaccines: Credo 2004. Scand. J. Immunol. 2004, 60, 9–13. [Google Scholar] [CrossRef]
- Van Damme, W.; Dahake, R.; van de Pas, R.; Vanham, G.; Assefa, Y. COVID-19: Does the infectious inoculum dose-response relationship contribute to understanding heterogeneity in disease severity and transmission dynamics? Med. Hypotheses 2020, 110431. [Google Scholar] [CrossRef]
- Watanabe, T.; Bartrand, T.A.; Weir, M.H.; Omura, T.; Haas, C.N. Development of a dose-response model for SARS coronavirus. Risk Anal. Int. J. 2010, 30, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.F.W.; Yuan, S.; Zhang, A.J.; Poon, V.K.M.; Chan, C.C.S.; Lee, A.C.Y.; Fan, Z.; Li, C.; Liang, R.; Cao, J.; et al. Surgical mask partition reduces the risk of non-contact transmission in a golden Syrian hamster model for Coronavirus Disease 2019 (COVID-19). Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Guallar, M.P.; Meiriño, R.; Donat-Vargas, C.; Corral, O.; Jouvé, N.; Soriano, V. Inoculum at the time of SARS-CoV-2 exposure and risk of disease severity. Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Hu, C.; Su, F.; Song, Q.; Wang, Z. Exposure to SARS-CoV-2 in a high transmission setting increases the risk of severe COVID-19 compared to exposure to a low transmission setting? J. Travel Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Pujadas, E.; Chaudhry, F.; McBride, R.; Richter, F.; Zhao, S.; Wajnberg, A.; Nadkarni, G.; Glicksberg, B.S.; Houldsworth, J.; Cordon-Cardo, C. SARS-CoV-2 Viral Load Predicts COVID-19 Mortality. MedRxiv 2020. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Sang, L.; Ye, F.; Ruan, S.; Zhong, B.; Song, T.; Alshukairi, A.N.; Chen, R.; Zhang, Z.; et al. Kinetics of viral load and antibody response in relation to COVID-19 severity. J. Clin. Investig. 2020, 130. [Google Scholar] [CrossRef]
- Sayampanathan, A.A.; Heng, C.S.; Pin, P.H.; Pang, J.; Leong, T.Y.; Lee, V.J. Infectivity of asymptomatic versus symptomatic COVID-19. Lancet 2021, 397, 93–94. [Google Scholar] [CrossRef]
- Granados, A.; Goodall, E.C.; Luinstra, K.; Smieja, M.; Mahony, J. Comparison of asymptomatic and symptomatic rhinovirus infections in university students: Incidence, species diversity, and viral load. Diagn. Microbiol. Infect. Dis. 2015, 82, 292–296. [Google Scholar] [CrossRef] [PubMed]
- Paulo, A.C.; Correia-Neves, M.; Domingos, T.; Murta, A.G.; Pedrosa, J. Influenza infectious dose may explain the high mortality of the second and third wave of 1918–1919 influenza pandemic. PLoS ONE 2010, 5, e11655. [Google Scholar] [CrossRef]
- Zimmermann, P.; Curtis, N. Coronavirus infections in children including COVID-19: An overview of the epidemiology, clinical features, diagnosis, treatment and prevention options in children. Pediatr. Infect. Dis. J. 2020, 39, 355. [Google Scholar] [CrossRef] [PubMed]
- Kelvin, A.A.; Halperin, S. COVID-19 in children: The link in the transmission chain. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Castagnoli, R.; Votto, M.; Licari, A.; Brambilla, I.; Bruno, R.; Perlini, S.; Rovida, F.; Baldanti, F.; Marseglia, G.L. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection in children and adolescents: A systematic review. JAMA Pediatr. 2020. [Google Scholar] [CrossRef] [PubMed]
- Van Bever, H.P.; Chng, S.Y.; Goh, D.Y. Childhood severe acute respiratory syndrome, coronavirus infections and asthma. Pediatr. Allergy Immunol. 2004, 15, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Kindler, E.; Thiel, V. To sense or not to sense viral RNA—Essentials of coronavirus innate immune evasion. Curr. Opin. Microbiol. 2014, 20, 69–75. [Google Scholar] [CrossRef]
- Dandekar, A.A.; Perlman, S. Immunopathogenesis of coronavirus infections: Implications for SARS. Nat. Rev. Immunol. 2005, 5, 917–927. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, F.; Liu, F.; Cuconati, A.; Chang, J.; Block, T.M.; Guo, J.T. Interferon induction of IFITM proteins promotes infection by human coronavirus OC43. Proc. Natl. Acad. Sci. USA 2014, 111, 6756–6761. [Google Scholar] [CrossRef]
- Lu, X.; Xiang, Y.; Du, H.; Wing-Kin Wong, G. SARS-CoV-2 infection in children—Understanding the immune responses and controlling the pandemic. Pediatr. Allergy Immunol. 2020. [Google Scholar] [CrossRef]
- Hua, C.Z.; Miao, Z.P.; Zheng, J.S.; Huang, Q.; Sun, Q.F.; Lu, H.P.; Su, F.F.; Wang, W.H.; Huang, L.P.; Xu, Z.W.; et al. Epidemiological features and viral shedding in children with SARS-CoV-2 infection. J. Med. Virol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Isaacs, D.; Britton, P.; Howard-Jones, A.; Kesson, A.; Khatami, A.; Marais, B.; Nayda, C.; Outhred, A. To what extent do children transmit SARS-CoV-2 virus? J. Paediatr. Child Health 2020, 56, 978. [Google Scholar] [CrossRef] [PubMed]
- Yonker, L.M.; Neilan, A.M.; Yannic, B.; Patel, A.B.; Regan, J.; Puneeta, A.; Gootkind, E.; Park, G.; Hardcastle, M.; St. John, A.; et al. Pediatric SARS-CoV-2: Clinical Presentation, Infectivity, and Immune Responses. J. Pediatr. 2020. [Google Scholar] [CrossRef]
- Hruskova, J.; Heinz, F.; Svandova, E.; Pennigerova, S. Antibodies to human coronaviruses 229E and OC43 in the population of CR. Acta Virol. 1990, 34, 346–352. [Google Scholar]
- Lehel, F.; Madar, Z.; Toth, I. Antibodies to Coronavirus OC 43 strain in the population of North-Eastern Hungary. Acta Microbiol. Hung. 1983, 30, 163. [Google Scholar] [PubMed]
- Adler, F.R.; Stockmann, C.; Ampofo, K.; Pavia, A.T.; Byington, C.L. Transmission of rhinovirus in the Utah BIG-LoVE families: Consequences of age and household structure. PLoS ONE 2018, 13, e0199388. [Google Scholar] [CrossRef]
- Tunbridge, A.; Breuer, J.; Jeffery, K. Chickenpox in adults-clinical management. J. Infect. 2008, 57, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Perry, R.T.; Halsey, N.A. The clinical significance of measles: A review. J. Infect. Dis. 2004, 189, S4–S16. [Google Scholar] [PubMed]
- Rostgaard, K.; Balfour, H.H., Jr.; Jarrett, R.; Erikstrup, C.; Pedersen, O.; Ullum, H.; Nielsen, L.P.; Voldstedlund, M.; Hjalgrim, H. Primary Epstein-Barr virus infection with and without infectious mononucleosis. PLoS ONE 2019, 14, e0226436. [Google Scholar] [CrossRef]
- Littman, A.J.; Rossing, M.A.; Madeleine, M.M.; Tang, M.T.C.; Yasui, Y. Association between late age at infectious mononucleosis, Epstein-Barr virus antibodies, and ovarian cancer risk. Scand. J. Infect. Dis. 2003, 35, 728–735. [Google Scholar] [CrossRef]
- Hall, C.B.; Weinberg, G.A.; Iwane, M.K.; Blumkin, A.K.; Edwards, K.M.; Staat, M.A.; Auinger, P.; Griffin, M.R.; Poehling, K.A.; Erdman, D.; et al. The burden of respiratory syncytial virus infection in young children. N. Engl. J. Med. 2009, 360, 588–598. [Google Scholar] [CrossRef]
- Shaman, J.; Galanti, M. Direct Measurement of Rates of Asymptomatic Infection and Clinical Care-Seeking for Seasonal Coronavirus. MedRxiv 2020. [Google Scholar] [CrossRef]
- Oran, D.P.; Topol, E.J. Prevalence of asymptomatic SARS-CoV-2 infection: A narrative review. Ann. Intern. Med. 2020. [Google Scholar] [CrossRef]
- Gorse, G.J.; Patel, G.B.; Vitale, J.N.; O’Connor, T.Z. Prevalence of antibodies to four human coronaviruses is lower in nasal secretions than in serum. Clin. Vaccine Immunol. 2010, 17, 1875–1880. [Google Scholar] [CrossRef]
- Zielecki, F.; Weber, M.; Eickmann, M.; Spiegelberg, L.; Zaki, A.M.; Matrosovich, M.; Becker, S.; Weber, F. Human cell tropism and innate immune system interactions of human respiratory coronavirus EMC compared to those of severe acute respiratory syndrome coronavirus. J. Virol. 2013, 87, 5300–5304. [Google Scholar] [CrossRef] [PubMed]
- Netea, M.G.; Giamarellos-Bourboulis, E.J.; Domínguez-Andrés, J.; Curtis, N.; van Crevel, R.; van de Veerdonk, F.L.; Bonten, M. Trained Immunity: A Tool for Reducing Susceptibility to and the Severity of SARS-CoV-2 Infection. Cell 2020. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Eubank, S.; Eckstrand, I.; Lewis, B.; Venkatramanan, S.; Marathe, M.; Barrett, C. Commentary on Ferguson, et al., Impact of Non-pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Bull. Math. Biol. 2020, 82, 1–7. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College COVID-19 Response Team: London, UK, 2020. [Google Scholar]
- Little, P.; Read, R.C.; Amlôt, R.; Chadborn, T.; Rice, C.; Bostock, J.; Yardley, L. Reducing risks from coronavirus transmission in the home—The role of viral load. BMJ 2020, 369. [Google Scholar] [CrossRef] [PubMed]
- Zeng, N.; Li, Z.; Ng, S.; Chen, D.; Zhou, H. Epidemiology reveals mask wearing by the public is crucial for COVID-19 control. Med. Microecol. 2020, 100015. [Google Scholar] [CrossRef]
- Bielecki, M.; Züst, R.; Siegrist, D.; Meyerhofer, D.; Crameri, G.A.G.; Stanga, Z.G.; Stettbacher, A.; Buehrer, T.W.; Deuel, J.W. Social distancing alters the clinical course of COVID-19 in young adults: A comparative cohort study. Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Cao, Q.; Chen, Y.C.; Chen, C.L.; Chiu, C.H. SARS-CoV-2 infection in children: Transmission dynamics and clinical characteristics. J. Formos. Med. Assoc. 2020, 119, 670. [Google Scholar] [CrossRef]
- Ludvigsson, J.F. Children are unlikely to be the main drivers of the COVID-19 pandemic—A systematic review. Acta Paediatr. 2020. [Google Scholar] [CrossRef]
- Carlsson, R.M.; Childs, L.M.; Feng, Z.; Glasser, J.W.; Heffernan, J.M.; Li, J.; Röst, G. Modeling the waning and boosting of immunity from infection or vaccination. J. Theor. Biol. 2020, 110265. [Google Scholar] [CrossRef]
- Schuette, M.C.; Hethcote, H.W. Modeling the effects of varicella vaccination programs on the incidence of chickenpox and shingles. Bull. Math. Biol. 1999, 61, 1031–1064. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- United States Census Bureau. 2019 Population Estimates by Age, Sex, Race and Hispanic Origin. 2020; Data Retrieved from United States Census Bureau. Available online: https://www.census.gov/newsroom/press-kits/2020/population-estimates-detailed.html (accessed on 18 March 2021).
- Centers for Disease Control and Prevention, COVID-19 Response. COVID-19 Case Surveillance Public Data Access, Summary, and Limitations, (Version Date: 31 March 2021). Available online: https://catalog.data.gov/dataset/united-states-covid-19-cases-and-deaths-by-state-over-time (accessed on 18 March 2021).
- Xia, W.; Shao, J.; Guo, Y.; Peng, X.; Li, Z.; Hu, D. Clinical and CT features in pediatric patients with COVID-19 infection: Different points from adults. Pediatr. Pulmonol. 2020, 11, 1–14. [Google Scholar] [CrossRef]
- Edridge, A.W.; Kaczorowska, J.; Hoste, A.C.; Bakker, M.; Klein, M.; Loens, K.; Jebbink, M.F.; Matser, A.; Kinsella, C.M.; Rueda, P.; et al. Seasonal coronavirus protective immunity is short-lasting. Nat. Med. 2020, 26, 1691–1693. [Google Scholar] [CrossRef]
- Chia, W.N.; Zhu, F.; Ong, S.W.X.; Young, B.E.; Fong, S.W.; Le Bert, N.; Tan, C.W.; Tiu, C.; Zhang, J.; Tan, S.Y.; et al. Dynamics of SARS-CoV-2 neutralising antibody responses and duration of immunity: A longitudinal study. Lancet Microbe 2021. [Google Scholar] [CrossRef]
- Mo, H.; Zeng, G.; Ren, X.; Li, H.; Ke, C.; Tan, Y.; Cai, C.; Lai, K.; Chen, R.; Chan-Yeung, M.; et al. Longitudinal profile of antibodies against SARS-coronavirus in SARS patients and their clinical significance. Respirology 2006, 11, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Papachristodoulou, E.; Kakoullis, L.; Parperis, K.; Panos, G. Long-term and herd immunity against SARS-CoV-2: Implications from current and past knowledge. Pathog. Dis. 2020, 78, ftaa025. [Google Scholar] [CrossRef]
- Sanche, S.; Lin, Y.T.; Xu, C.; Romero-Severson, E.; Hengartner, N.; Ke, R. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2. Emerg. Infect. Dis. 2020, 26, 1470–1477. [Google Scholar] [CrossRef]
- Walsh, K.A.; Spillane, S.; Comber, L.; Cardwell, K.; Harrington, P.; Connell, J.; Teljeur, C.; Broderick, N.; de Gascun, C.F.; Smith, S.M.; et al. The duration of infectiousness of individuals infected with SARS-CoV-2. J. Infect. 2020. [Google Scholar] [CrossRef] [PubMed]
- Cevik, M.; Tate, M.; Lloyd, O.; Maraolo, A.E.; Schafers, J.; Ho, A. SARS-CoV-2, SARS-CoV, and MERS-CoV viral load dynamics, duration of viral shedding, and infectiousness: A systematic review and meta-analysis. Lancet Microbe 2020. [Google Scholar] [CrossRef]
- Lavine, J.S.; Bjornstad, O.N.; Antia, R. Immunological characteristics govern the changing severity of COVID-19 during the transition to endemicity. MedRxiv 2020. [Google Scholar] [CrossRef]
- Hufsky, F.; Lamkiewicz, K.; Almeida, A.; Aouacheria, A.; Arighi, C.; Bateman, A.; Baumbach, J.; Beerenwinkel, N.; Brandt, C.; Cacciabue, M.; et al. Computational strategies to combat COVID-19: Useful tools to accelerate SARS-CoV-2 and coronavirus research. Briefings Bioinform. 2021, 22, 642–663. [Google Scholar] [CrossRef] [PubMed]
- Ewald, J.; Sieber, P.; Garde, R.; Lang, S.N.; Schuster, S.; Ibrahim, B. Trends in mathematical modeling of host–pathogen interactions. Cell. Mol. Life Sci. 2020, 77, 467–480. [Google Scholar] [CrossRef] [PubMed]
- Mackinnon, M.J.; Read, A.F. Immunity promotes virulence evolution in a malaria model. PLoS Biol. 2004, 2, e230. [Google Scholar] [CrossRef]
- Kerr, P.J.; Cattadori, I.M.; Liu, J.; Sim, D.G.; Dodds, J.W.; Brooks, J.W.; Kennett, M.J.; Holmes, E.C.; Read, A.F. Next step in the ongoing arms race between myxoma virus and wild rabbits in Australia is a novel disease phenotype. Proc. Natl. Acad. Sci. USA 2017, 114, 9397–9402. [Google Scholar] [CrossRef] [PubMed]

| Variable | Description | Initial Condition |
|---|---|---|
| Susceptible adults and children | 271,833,136 and 56,406,387 [55] | |
| Partially resistant adults, children | 0 | |
| Low-shedding infected adults, children | 0 | |
| High-shedding infected adults, children | 1, 0 | |
| Resistant adults/children | 0 | |
| after low-shedding/high-shedding infection |
| Parameter | Description | Value |
|---|---|---|
| Loss rate of partial immunity | per year [58,59,60,61] | |
| Loss rate of sterilizing immunity | per year [58,59,60,61] | |
| Contact rate between adults and children | Calibrated to | |
| daily incidence data | ||
| or [56,62] | ||
| Contact rate between adults | Calibrated to | |
| daily incidence data | ||
| or [56,62] | ||
| Contact rate between children | Calibrated to | |
| daily incidence data | ||
| or [56,62] | ||
| Infectiousness of high-shedding cases | ||
| relative to low-shedding cases | [1, 5] | |
| Maturation rate | per year [55] | |
| Death rate | per year [55] | |
| Recovery rate from infection | per day [63,64] | |
| Susceptibility, S child | [0, 5] | |
| Susceptibility, P adult | ||
| Susceptibility, P child | ||
| Probability an individual in develops | [0, 1] | |
| low-shedding infection upon contact with | ||
| an infection of type y | ||
| Probability an individual in develops | [,1] | |
| low-shedding infection upon contact with | ||
| an infection of type y | ||
| Daily vaccination rate | [, ] | |
| from days 360–460 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beams, A.B.; Bateman, R.; Adler, F.R. Will SARS-CoV-2 Become Just Another Seasonal Coronavirus? Viruses 2021, 13, 854. https://doi.org/10.3390/v13050854
Beams AB, Bateman R, Adler FR. Will SARS-CoV-2 Become Just Another Seasonal Coronavirus? Viruses. 2021; 13(5):854. https://doi.org/10.3390/v13050854
Chicago/Turabian StyleBeams, Alexander B., Rebecca Bateman, and Frederick R. Adler. 2021. "Will SARS-CoV-2 Become Just Another Seasonal Coronavirus?" Viruses 13, no. 5: 854. https://doi.org/10.3390/v13050854
APA StyleBeams, A. B., Bateman, R., & Adler, F. R. (2021). Will SARS-CoV-2 Become Just Another Seasonal Coronavirus? Viruses, 13(5), 854. https://doi.org/10.3390/v13050854






