The Epidemiological Signature of Pathogen Populations That Vary in the Relationship between Free-Living Parasite Survival and Virulence
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Motivation and Application
2.2. Model Description
2.3. Simulations of Outbreaks
2.4. Population Definitions and Parameter Values
2.5. Virulence Definition
2.6. Survival Definition
2.7. Basic Reproductive Ratio
3. Results
3.1. Model Sensitivity Analysis
3.2. Illustrative Dynamics of Model System
3.3. The Epidemic Consequences of Varying Virulence and Survival
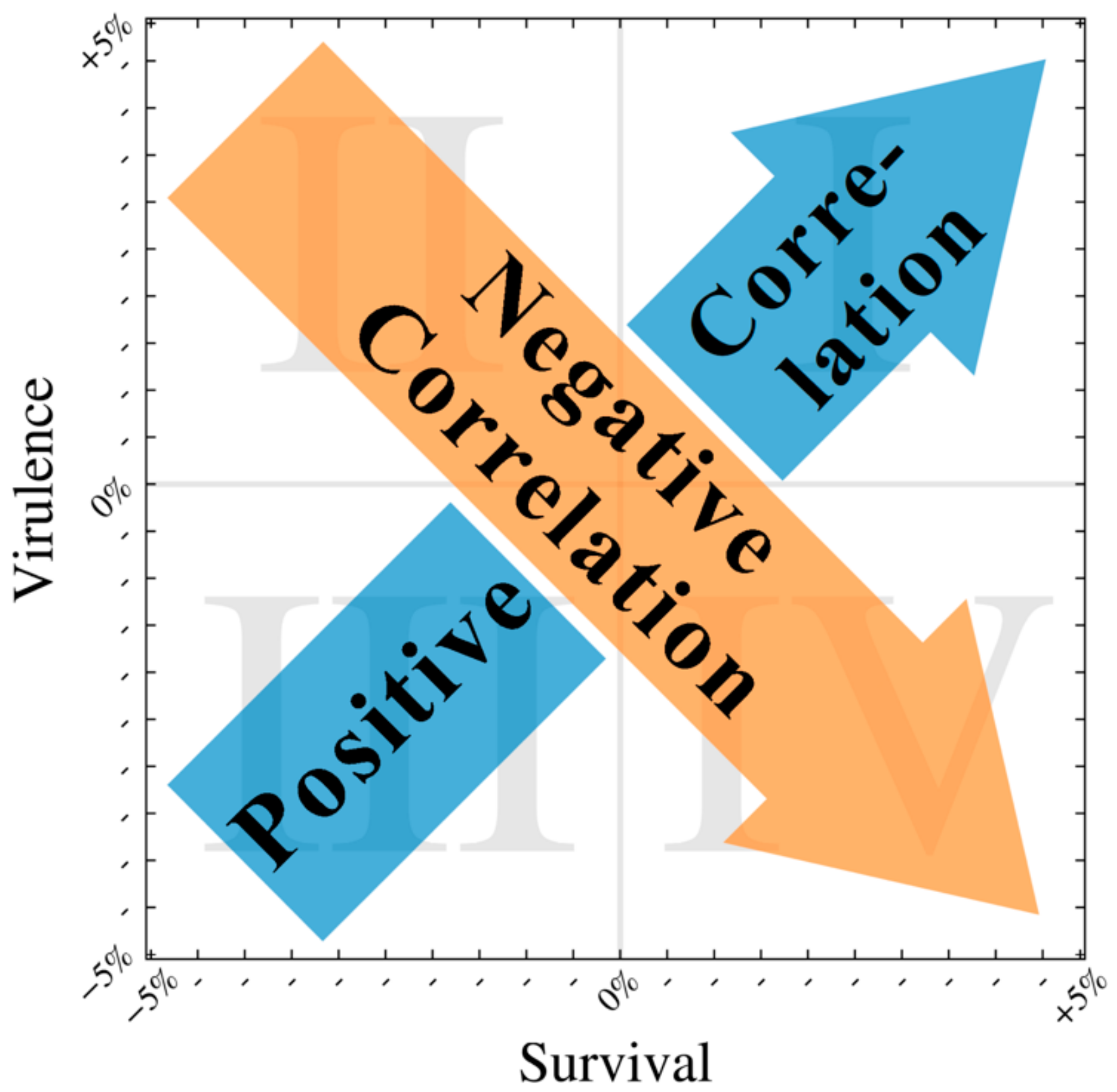
3.4. Implications of Virulence–Survival Relationships at Their Relative Extremes
3.5. Positive Correlation Between Survival and Virulence
3.6. Negative Correlation Between Survival and Virulence
3.7. Dynamics of Epidemics at Extreme Values for Virus Free-Living Survival
4. Discussion
Practical Implications for the Understanding of Outbreaks Caused by Emerging Viruses
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ewald, P.W. Host-parasite relations, vectors, and the evolution of disease severity. Annu. Rev. Ecol. Syst. 1983, 14, 465–485. [Google Scholar] [CrossRef]
- Goldhill, D.; Turner, P.E. The evolution of life history trade-offs in viruses. Curr. Opin. Virol. 2014, 8, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.; Roy, M.; Robert, R.M. Trends and perspectives: Coevolution of hosts and parasites. Parasitology 1982, 85, 411–426. [Google Scholar] [CrossRef] [PubMed]
- Bonhoeffer, S.; Lenski, R.; Ebert, D. The curse of the pharaoh: The evolution of virulence in pathogens with long living propagules. Proc. R. Soc. B Biol. Sci. 1996, 263, 715–721. [Google Scholar] [CrossRef]
- Gandon, S. The curse of the pharoah hypothesis. Proc. R. Soc. B Biol. Sci. 1998, 265, 1545–1552. [Google Scholar] [CrossRef] [PubMed]
- Alizon, S.; Hurford, A.; Mideo, N.; van Baalen, M. Virulence evolution and the trade-off hypothesis: History, current state of affairs and the future. J. Evol. Biol. 2008, 22, 245–259. [Google Scholar] [CrossRef]
- Cressler, C.E.; McLeod, D.V.; Rozins, C.; Hoogen, J.V.D.; Day, T. The adaptive evolution of virulence: A review of theoretical predictions and empirical tests. Parasitology 2015, 143, 915–930. [Google Scholar] [CrossRef]
- Rafaluk-Mohr, C. The relationship between parasite virulence and environmental persistence: A meta-analysis. Parasitology 2019, 146, 897–902. [Google Scholar] [CrossRef]
- Ogbunugafor, C.B.; Alto, B.W.; Overton, T.M.; Bhushan, A.; Morales, N.M.; Turner, P.E. Evolution of increased survival in RNA viruses specialized on cancer-derived cells. Am. Nat. 2013, 181, 585–595. [Google Scholar] [CrossRef]
- Rafaluk, C.; Jansen, G.; Schulenburg, H.; Joop, G. When experimental selection for virulence leads to loss of virulence. Trends Parasitol. 2015, 31, 426–434. [Google Scholar] [CrossRef]
- Corelli, M. The Curse of Osiris; Daily News: London, UK, 1923; p. 1. [Google Scholar]
- Roche, B.; Drake, J.M.; Rohani, P. The curse of the Pharaoh revisited: Evolutionary bi-stability in environmentally transmitted pathogens. Ecol. Lett. 2011, 14, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Walther, B.A.; Ewald, P.W. Pathogen survival in the external environment and the evolution of virulence. Biol. Rev. 2004, 79, 849–869. [Google Scholar] [CrossRef] [PubMed]
- Frank, S.A. Models of parasite virulence. Q. Rev. Biol. 1996, 71, 37–78. [Google Scholar] [CrossRef] [PubMed]
- De Paepe, M.; Taddei, F. Viruses’ life history: Towards a mechanistic basis of a trade-off between survival and reproduction among phages. PLoS Biol. 2006, 4, 1248–1256. [Google Scholar] [CrossRef] [PubMed]
- Stearns, S.C. Trade-offs in life-history evolution. Funct. Ecol. 1989, 3, 259. [Google Scholar] [CrossRef]
- Kamo, M.; Boots, M. The curse of the pharaoh in space: Free-living infectious stages and the evolution of virulence in spatially explicit populations. J. Theor. Biol. 2004, 231, 435–441. [Google Scholar] [CrossRef]
- Day, T. Virulence evolution via host exploitation and toxin production in spore-producing pathogens. Ecol. Lett. 2002, 5, 471–476. [Google Scholar] [CrossRef]
- Caraco, T.; Wang, I.-N. Free-living pathogens: Life-history constraints and strain competition. J. Theor. Biol. 2008, 250, 569–579. [Google Scholar] [CrossRef][Green Version]
- Barker, J.; Stevens, D.; Bloomfield, S. Spread and prevention of some common viral infections in community facilities and domestic homes. J. Appl. Microbiol. 2001, 91, 7–21. [Google Scholar] [CrossRef]
- Boone, S.A.; Gerba, C.P. Significance of fomites in the spread of respiratory and enteric viral disease. Appl. Environ. Microbiol. 2007, 73, 1687–1696. [Google Scholar] [CrossRef]
- Ogbunugafor, C.B.; Miller-Dickson, M.; Meszaros, V.A.; Gomez, L.M.; Murillo, A.L.; Scarpino, S.V. The intensity of COVID-19 outbreaks is modulated by SARS-CoV-2 free-living survival and environmental transmission. medRxiv 2020. [Google Scholar] [CrossRef]
- Miller-Dickson, M.D.; Meszaros, V.A.; Almagro-Moreno, S.; Ogbunugafor, C.B. Hepatitis C virus modelled as an indirectly transmitted infection highlights the centrality of injection drug equipment in disease dynamics. J. R. Soc. Interface 2019, 16, 20190334. [Google Scholar] [CrossRef] [PubMed]
- Meszaros, V.A.; Miller-Dickson, M.D.; Baffour-Awuah, F.; Almagro-Moreno, S.; Ogbunugafor, C.B. Direct transmission via households informs models of disease and intervention dynamics in cholera. PLoS ONE 2020, 15, e0229837. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.-Y.; Chen, L.; Wang, M. Presumed asymptomatic carrier transmission of COVID-19. JAMA 2020, 323, 1406. [Google Scholar] [CrossRef] [PubMed]
- Park, S.W.; Cornforth, D.M.; Dushoff, J.; Weitz, J.S. The time scale of asymptomatic transmission affects estimates of epidemic potential in the COVID-19 outbreak. Epidemics 2020, 31, 100392. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Cheng, P.; Chen, W.; Wan, P.; Chen, Y.; Yuan, G.; Chen, J.; Huo, D.; Guan, G.; Sun, D.; et al. High incidence of asymptomatic SARS-CoV-2 infection, Chongqing, China. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Santarpia, J.L.; Rivera, D.N.; Herrera, V.L.; Morwitzer, M.J.; Creager, H.M.; Santarpia, G.W.; Crown, K.K.; Brett-Major, D.M.; Schnaubelt, E.R.; Broadhurst, M.J.; et al. Aerosol and surface contamination of SARS-CoV-2 observed in quarantine and isolation care. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef]
- Eisenberg, M.C.; Robertson, S.; Tien, J.H. Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J. Theor. Biol. 2013, 324, 84–102. [Google Scholar] [CrossRef]
- Cortez, M.H.; Weitz, J.S. Distinguishing between indirect and direct modes of transmission using epidemiological time series. Am. Nat. 2013, 181, E43–E52. [Google Scholar] [CrossRef]
- Roosa, K.; Chowell, G. Assessing parameter identifiability in compartmental dynamic models using a computational approach: Application to infectious disease transmission models. Theor. Biol. Med Model. 2019, 16, 1. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovsk, E.; Petersom, P.; Wekesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Duffy, S.; Turner, P.E.; Burch, C.L. Pleiotropic costs of niche expansion in the RNA bacteriophage Φ 6. Genetics 2005, 172, 751–757. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.H. Notes on R0. Calif. Dep. Anthropol. Sci. 2007, 323, 1–19. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2009, 7, 873–885. [Google Scholar] [CrossRef]
- Scarpino, S.V.; Petri, G. On the predictability of infectious disease outbreaks. Nat. Commun. 2019, 10, 898. [Google Scholar] [CrossRef]
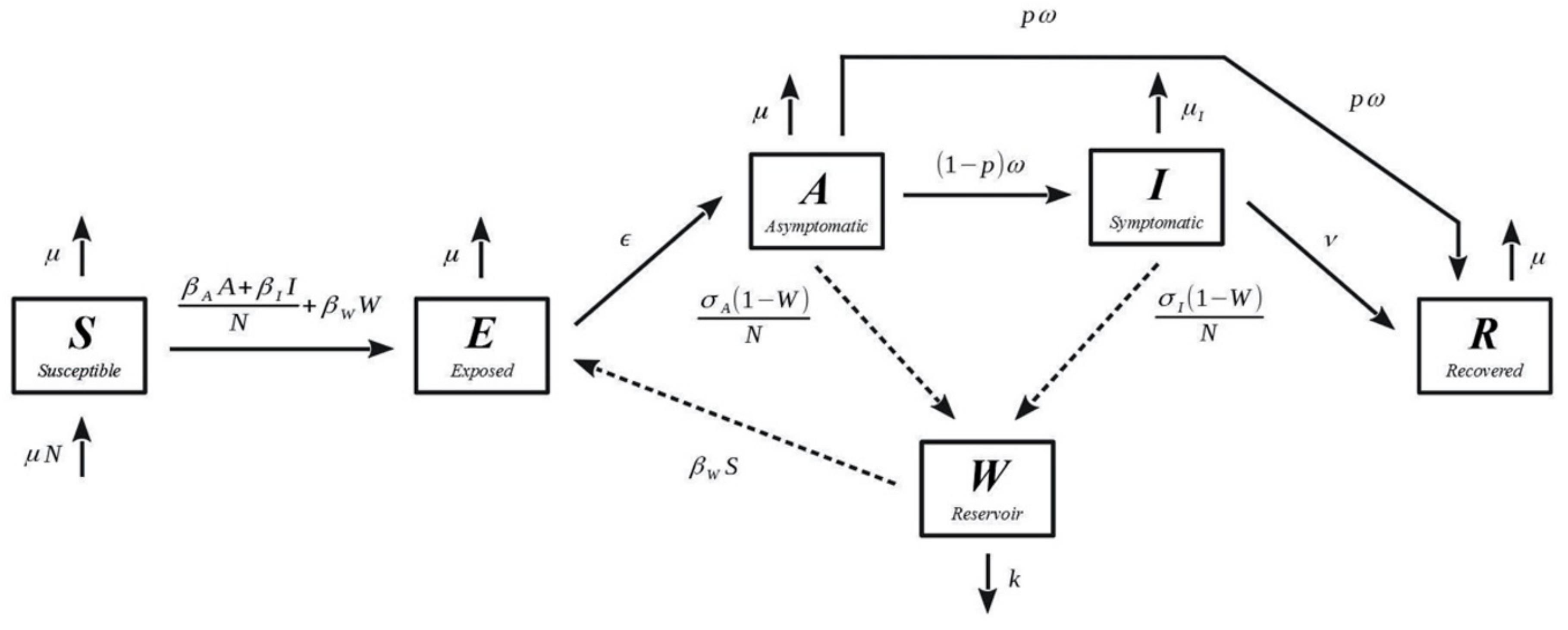
| Symbols | Value | Units | Definitions |
|---|---|---|---|
| S0 | 57.05 × 106 | people | Susceptible individuals |
| E0 | 66.50 | people | Exposed individuals |
| A0 | 13.30 | people | Asymptomatic individuals |
| I0 | 13.30 | people | Symptomatic individuals |
| Rec0 | 0 | people | Recovered individuals |
| W0 | 1% | unitless | % of viral pathogen in environment |
| Symbols | Values | Units | Definitions |
|---|---|---|---|
| 𝜇 | 1/(80.3 × 365) | 1/day | Natural death rate (reciprocal of the upper bound of average human lifespan) |
| 𝜇I | 0.00159 | 1/day | Infected death rate (natural death rate + disease-induced death rate) |
| 𝜂 = (⍵ − ε−1) | 5.5 | days | SARS-CoV-2 incubation period |
| 1/⍵ | 𝜂 − ε−1 | days | Expected time in the asymptomatic state |
| ν | 0.0305 | 1/day | Recovery rate (average of 3 to 6 weeks) |
| p | 95.6% | percent | Percent that moves along the “mild” recovery track |
| k | 0.649 | 1/day | Waning virus rate in the environment (using the average of all material values, wood, steal, cardboard, and plastic) |
| βa | 0.550 | 1/day | Contact rate of people with people × transmission probability of people to people by A-person |
| βI | 0.491 | 1/day | Contact rate of people with people × transmission probability of people to people by I-person |
| βW | 0.031 | 1/day | Contact rate of person with environment × transmission probability of environment to people |
| 𝜎a | 3.404 | 1/day | Contact rate of person with environment × probability of shedding by A-people to environment |
| 𝜎I | 13.492 | 1/day | Contact rate of person with environment) × probability of shedding by I-people to environment |
| 1/ε | 2.478 | days | Average number of days before infectiousness |
| Symbols | Definition | Virulence Increased | Virulence Decreased |
|---|---|---|---|
| 𝜇I | Infected death rate (natural death rate + disease induced death rate) | ↑ | ↓ |
| 𝜂 = (⍵ − ε−1) | SARS-CoV-2 incubation period | ↓ | ↑ |
| 1/⍵ | Expected time in the asymptomatic state | ↑ | ↓ |
| ν | Recovery rate (average of 3 to 6 weeks) | ↓ | ↑ |
| p | Percent that moves along the “mild” recovery track | ↓ | ↑ |
| βA | Contact rate of people with people × transmission probability of people to people by A-person | ↑ | ↓ |
| βI | Contact rate of people with people × transmission probability of people to people by I-person | ↑ | ↓ |
| 𝜎A | Contact rate of person with environment) × (probability of shedding by A-people to environment | ↑ | ↓ |
| 𝜎I | Contact rate of person with environment × probability of shedding by I-people to environment | ↑ | ↓ |
| 1/ε | Average number of days before infectious | ↓ | ↑ |
| Symbols | Definition | Survival Increased | Survival Decreased |
|---|---|---|---|
| k | Waning virus rate in environment (using the average of all material values, wood, steal, cardboard, and plastic) | ↓ | ↑ |
| βW | Contact rate of person with environment × transmission probability of environment to people | ↑ | ↓ |
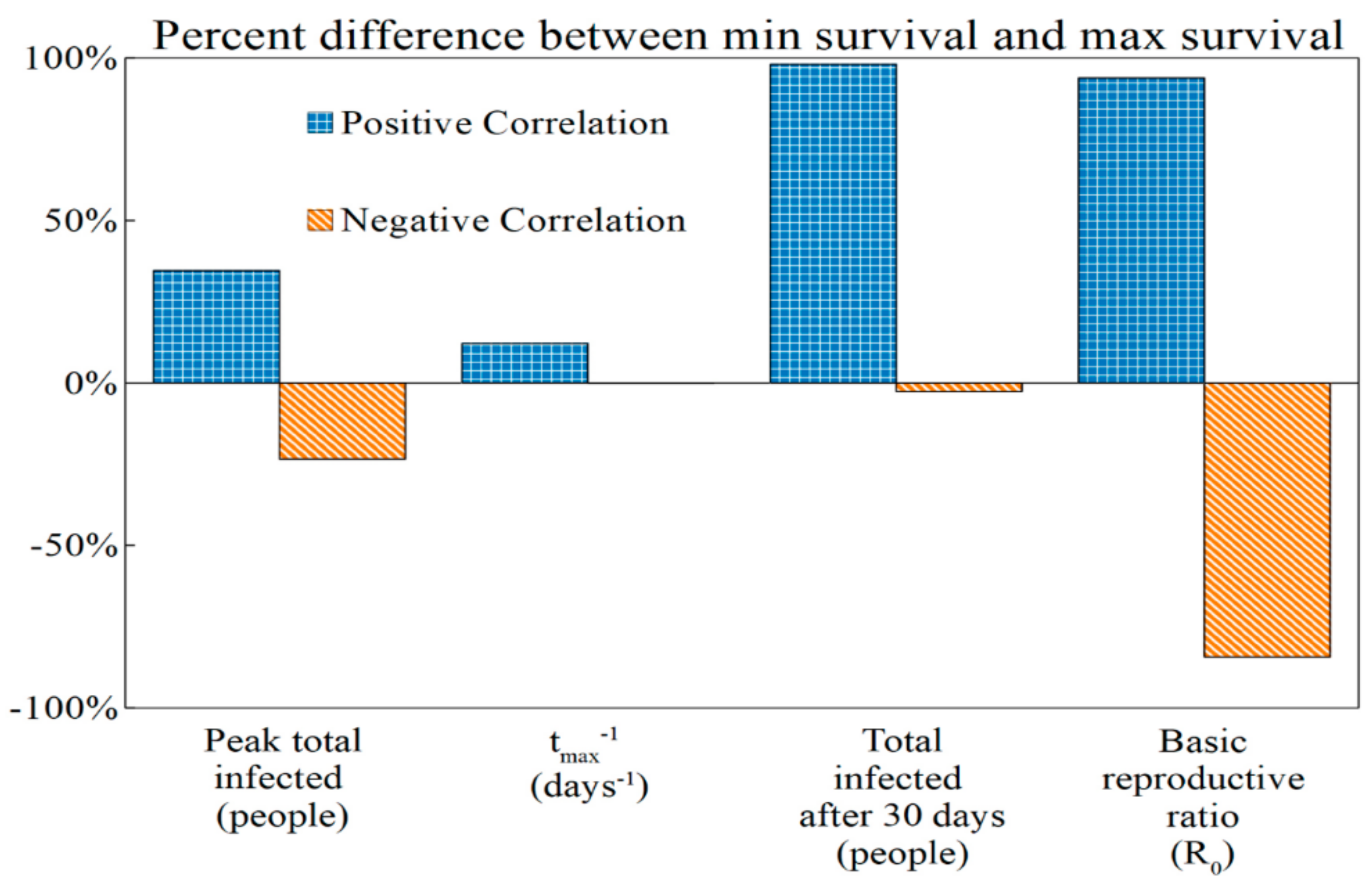
| Epidemic Metric | min Virulence, min Survival | max Virulence, max Survival | % Difference between min Survival and max Survival |
|---|---|---|---|
| Peak total infected (people) | 5.68 × 106 | 7.64 × 106 | +34.51% |
| tmax−1 (days−1) | 1.99 × 10−2 | 2.23 × 10−2 | +12.06% |
| Total after 30 days (people) | 8.18 × 107 | 1.62 × 108 | +98.04% |
| Basic reproductive ratio (R0) | 1.95 | 3.78 | +93.84% |
| Epidemic Metric | max Virulence, min Survival | min Virulence, max Survival | % Difference between min Survival and max Survival |
|---|---|---|---|
| Peak total infected (people) | 7.39 × 106 | 5.99 × 106 | −23.47% |
| tmax−1 (days−1) | 2.10 × 10−2 | 2.23 × 10−2 | −0.15% |
| Total infected after 30 days (people) | 1.16 × 108 | 1.13 × 108 | −2.68% |
| Basic reproductive ratio (R0) | 3.67 | 1.99 | −84.39% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, L.M.; Meszaros, V.A.; Turner, W.C.; Ogbunugafor, C.B. The Epidemiological Signature of Pathogen Populations That Vary in the Relationship between Free-Living Parasite Survival and Virulence. Viruses 2020, 12, 1055. https://doi.org/10.3390/v12091055
Gomez LM, Meszaros VA, Turner WC, Ogbunugafor CB. The Epidemiological Signature of Pathogen Populations That Vary in the Relationship between Free-Living Parasite Survival and Virulence. Viruses. 2020; 12(9):1055. https://doi.org/10.3390/v12091055
Chicago/Turabian StyleGomez, Lourdes M., Victor A. Meszaros, Wendy C. Turner, and C. Brandon Ogbunugafor. 2020. "The Epidemiological Signature of Pathogen Populations That Vary in the Relationship between Free-Living Parasite Survival and Virulence" Viruses 12, no. 9: 1055. https://doi.org/10.3390/v12091055
APA StyleGomez, L. M., Meszaros, V. A., Turner, W. C., & Ogbunugafor, C. B. (2020). The Epidemiological Signature of Pathogen Populations That Vary in the Relationship between Free-Living Parasite Survival and Virulence. Viruses, 12(9), 1055. https://doi.org/10.3390/v12091055





