Understanding the Evolutionary Ecology of host–pathogen Interactions Provides Insights into the Outcomes of Insect Pest Biocontrol
Abstract
1. Introduction
2. Heterogeneity in Pathogen Transmission
2.1. Modeling Heterogeneity in Transmission in Insect–Pathogen Systems
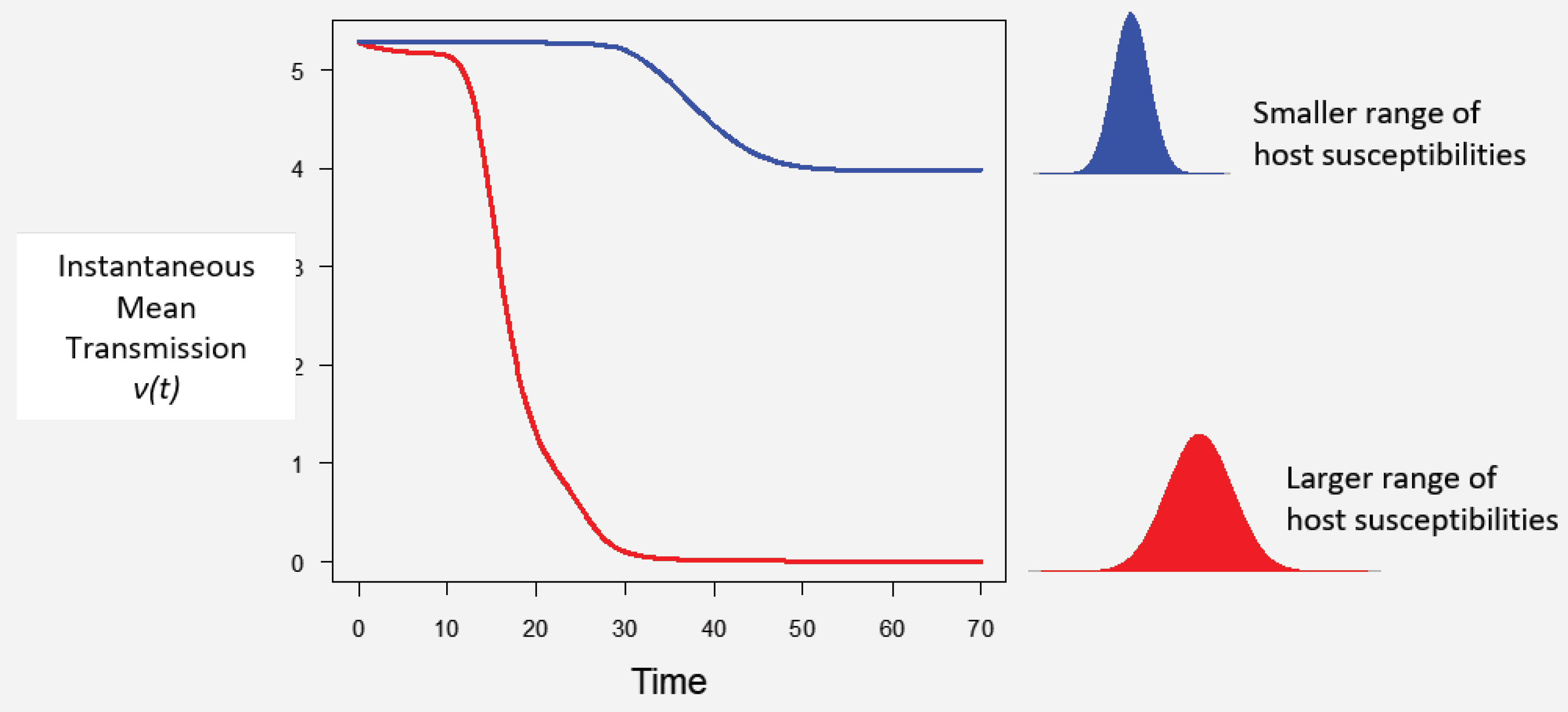
- The models presented here incorporate heterogeneity as a continuous Gamma distribution described by the mean transmission and the squared coefficient of variation of transmission (which is unitless). We term this heterogeneity in transmission rather than host heterogeneity to recognize that it is a trait of both pathogen and host and can arise from various sources, including within-host stochastic processes [28], host behavior [53], environmental factors [80], as well as both host and pathogen genetics and G × G interactions [15,16,17,63,79]. When heterogeneity equals 0, all individuals are identical in their susceptibility to disease and the infection process will be completely driven by the mean transmission rate. When heterogeneity is greater than 0 (), then there are differences between individuals in susceptibility, with some individuals being more susceptible to infection than others (Figure 1).

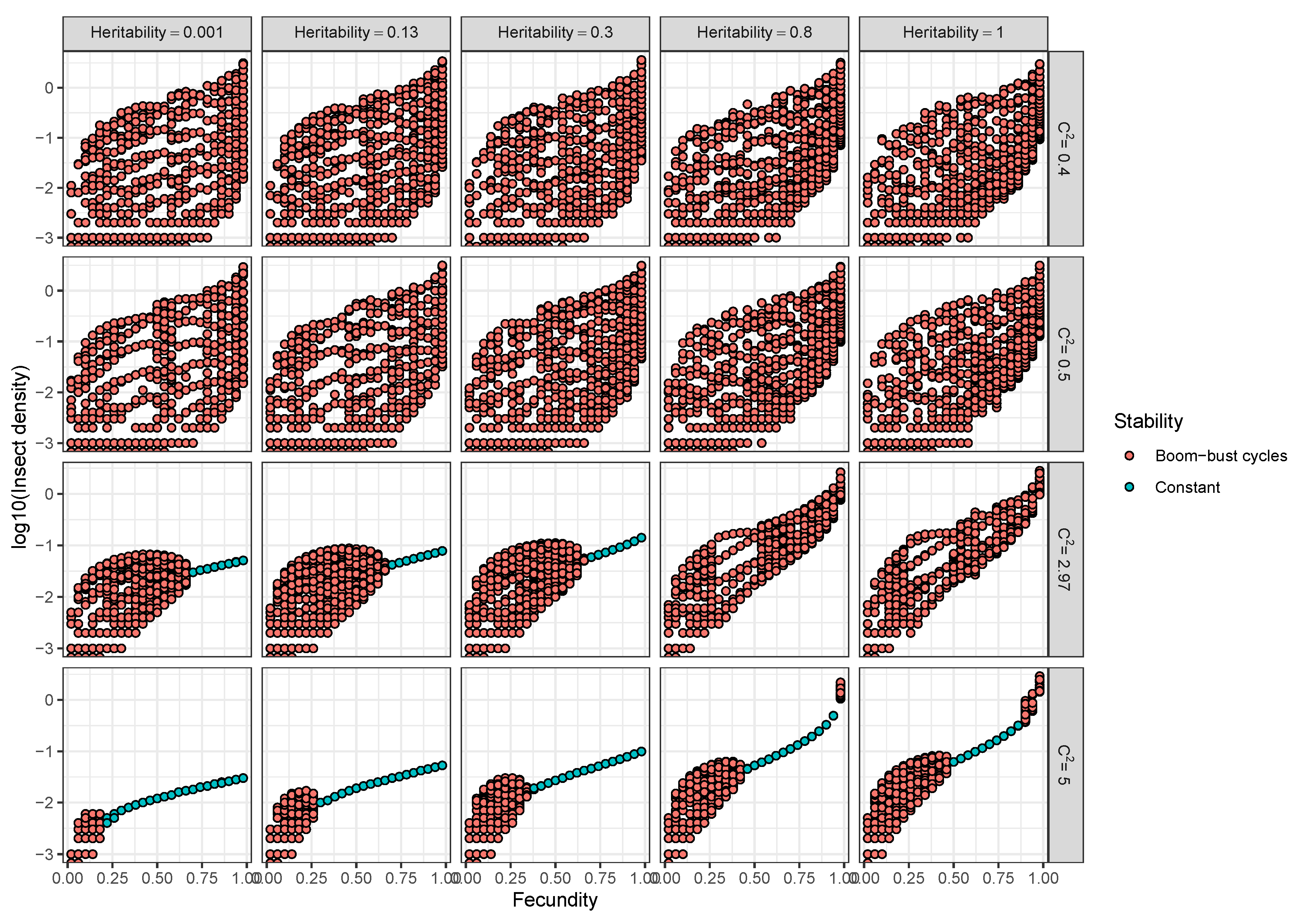
- Assuming a continuous distribution of host susceptibilities, as the epidemic progresses, the most susceptible hosts are removed first, and thus the individuals left in the population are those of lower than average susceptibility (Figure 1). The transmission rate thus drops as it becomes more and more difficult for the pathogen to infect the remaining hosts (Figure 2). Comparing two host populations with different levels of heterogeneity, the range of host susceptibilities is narrower in the population with a lower heterogeneity of transmission . Thus, the individuals that were removed are more similar to the individuals remaining uninfected, and the transmission rate does not drop as dramatically. This process is essentially strong selection for low host susceptibility and has a strong effect on host density (Figure 3). In a model incorporating host evolution (Table 1, Model 3), the distribution of insect susceptibilities is characterized by genetic variation and so transmission is allowed to evolve from host generation to host generation. Evolution of towards infinitely small values is however constrained by tradeoffs between transmission and insect fecundity (see Box 2). By contrast to the evolution model, in the other models (Table 1, Models 1-2,4) the mean transmission value starts at the same value of at the beginning of the next epizootic. Thus the evolution model adds realism by allowing the hosts to evolve.Note that heterogeneity is also a trait of the infecting pathogen. Two pathogen strains might result in two different distributions of susceptibilities in the same host population, if the hosts are more variable in their susceptibilities to one strain than the other. Thus, the two examples in Figure 2 could also be produced by two different pathogen strains in the same host population. In the two-strain model, heterogeneity is attributed to pathogen strain as the strains share a single host population (Table 1, Model 4). Host evolution is excluded from this model for simplicity, and the mean transmission rate is assumed to reset at the same value at the beginning of each outbreak.

2.2. Consequences of Heterogeneity in Transmission for Biocontrol
3. Ecological and Evolutionary Tradeoffs
3.1. Modeling Tradeoffs with Transmission in insect–pathogen Systems
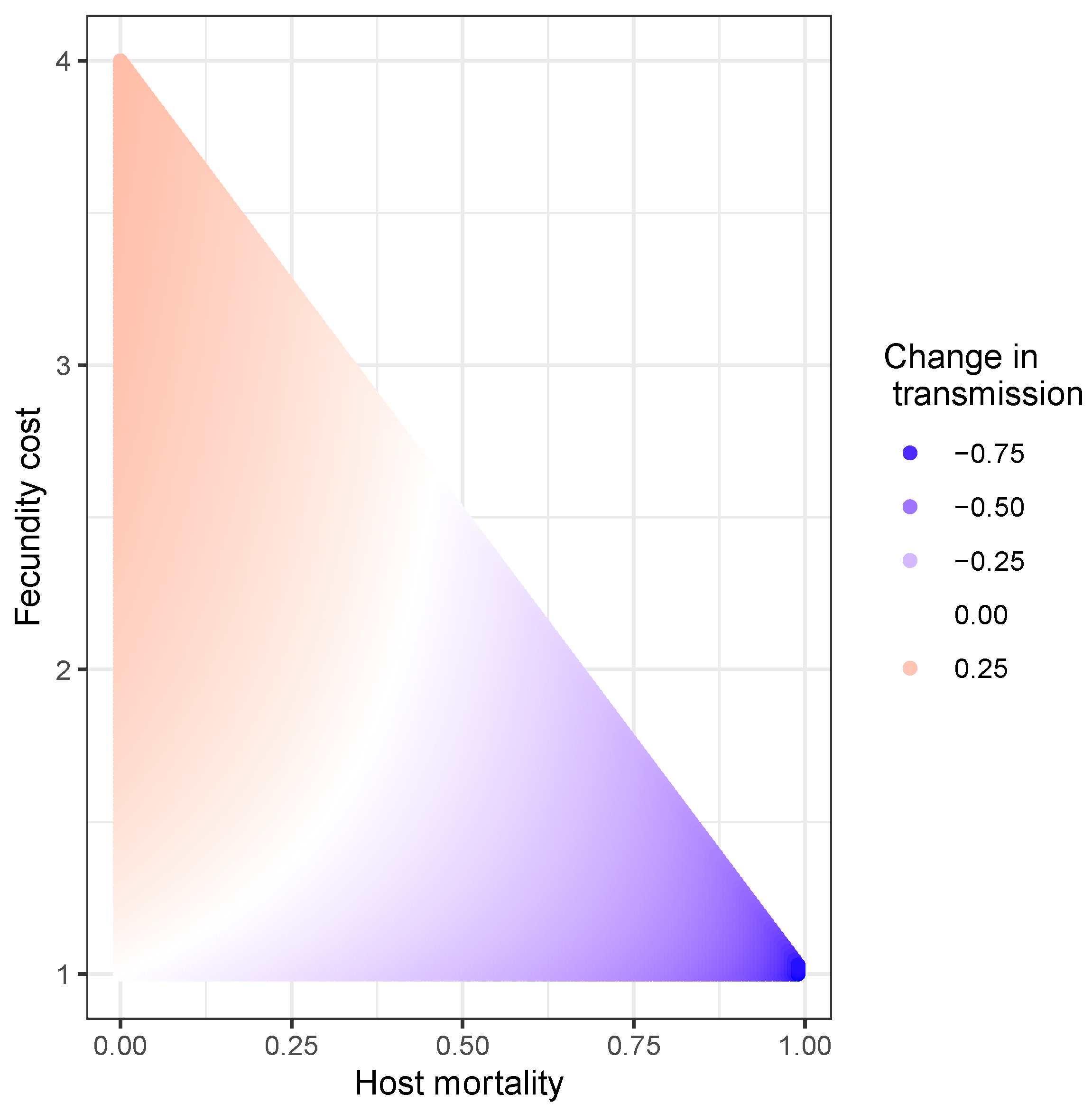
- Life history tradeoffs occur when an evolutionarily advantageous trait comes at the cost of lower fitness in another trait. In a plot of two traits that both influence fitness, the presence of a correlation between traits may indicate presence of a tradeoff constraining fitness. This correlation may be positive or negative depending on whether higher or lower trait values are associated with higher fitness (Figure 9). For example, in the classic evolution of virulence tradeoff [94,95], both host mortality and between-host transmission tend to increase with higher rates of pathogen replication within the host (but see, [102,103]). Higher transmission is associated with higher pathogen fitness, but higher host mortality is associated with lower pathogen fitness. Thus, the presence of a positive correlation in a plot of pathogen transmission against host mortality (virulence) is consistent with a tradeoff. In the absence of tradeoffs, optimal pathogen fitness would occur at the highest possible values for transmission but the lowest values of mortality. However, the positive correlation between these two traits constrains their evolution such that high-transmission (higher fitness) strains also induce high host mortality (lower fitness). Thus, this correlation indicates the presence of a tradeoff.
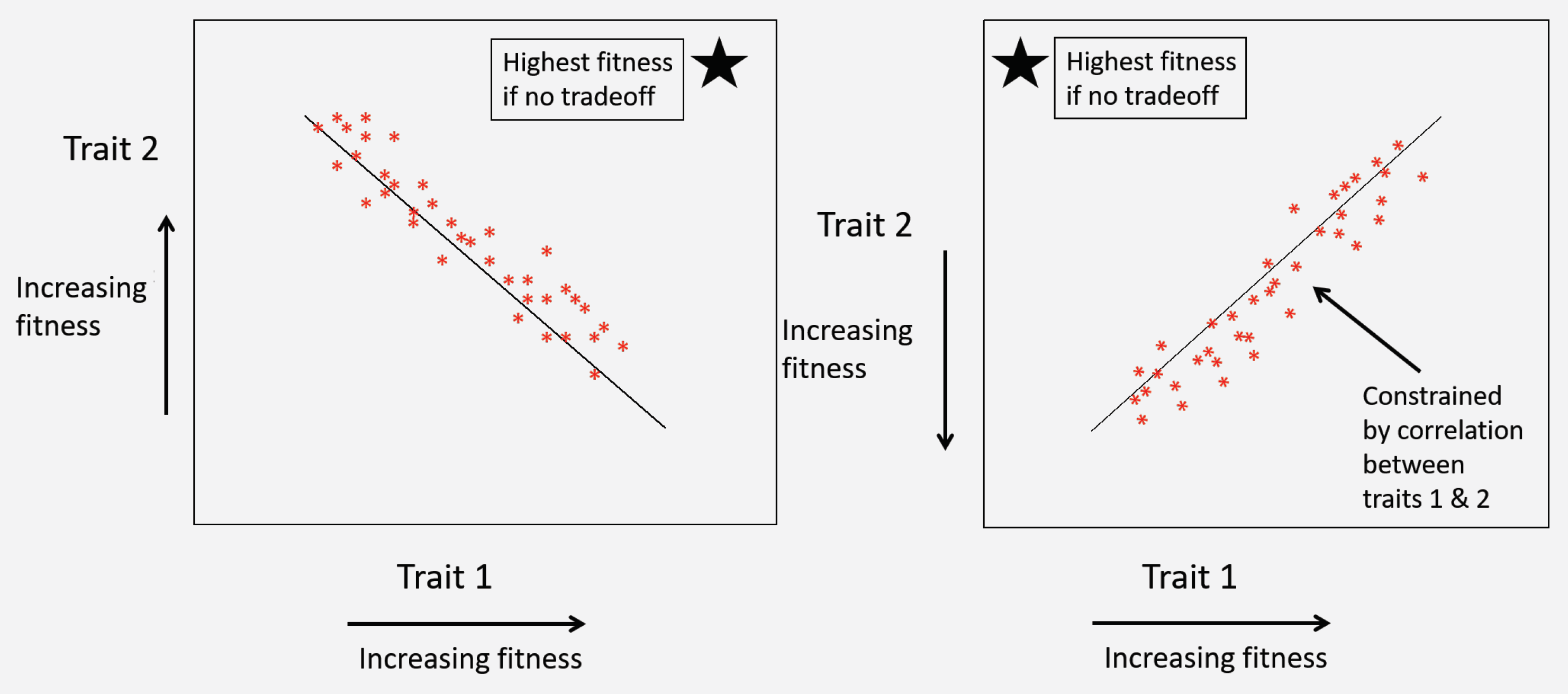
- The key pathogen life history tradeoff we discuss in this paper is one we term the transmission-heterogeneity tradeoff. Heterogeneity of transmission is described by the coefficient of variation (seeBox 1), and its positive correlation with the mean transmission rate indicates a pathogen life-history tradeoff (Figure 10). This tradeoff has been observed empirically in the baculovirus that infects gypsy moths, using different field-collected strains [79], and likely arises in part due to interactions with host genotype; high transmission rate in some hosts comes at a cost of reduced ability to infect others [17] (see also Box 1). Intriguingly, a similar tradeoff between mean transmission and heterogeneity arises via a different mechanism in the host evolution model (Model 3 in Table 1), as an effect of the host life-history tradeoff between fecundity and disease resistance. This is because higher heterogeneity in that model is in part attributed to host genetic variation, so that at high heterogeneity, hosts evolve more rapidly to high transmission values, because the associated high fecundity is so advantageous [15].

3.2. Consequences of Tradeoffs for Biocontrol
4. Conclusions
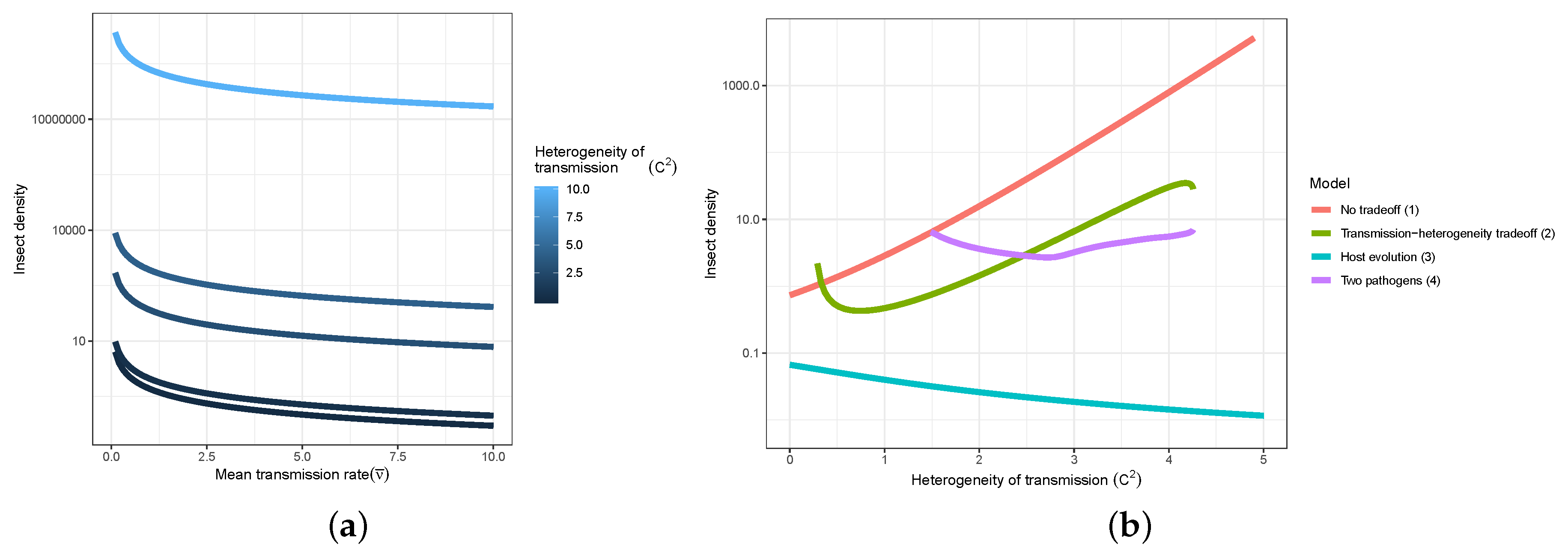
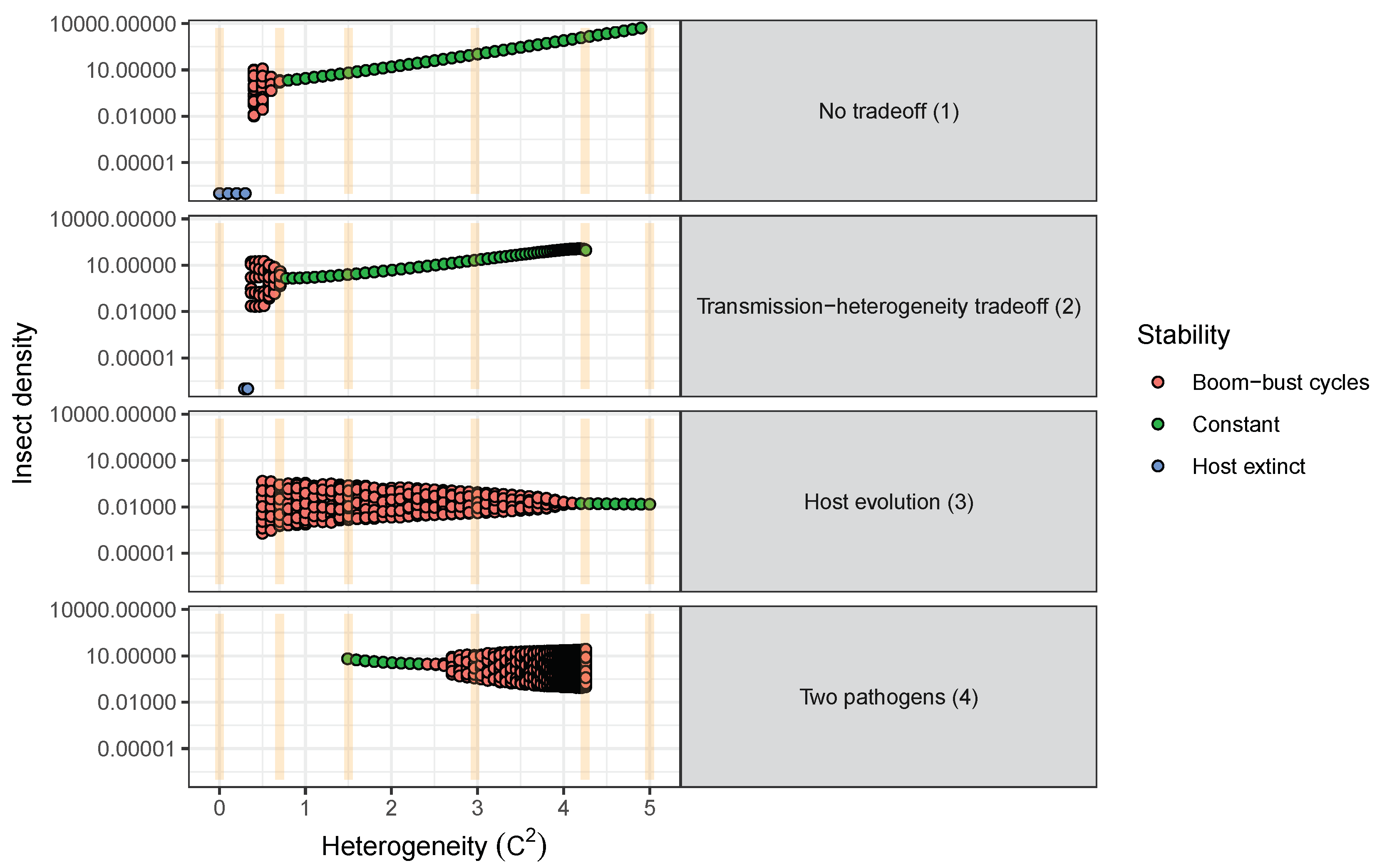
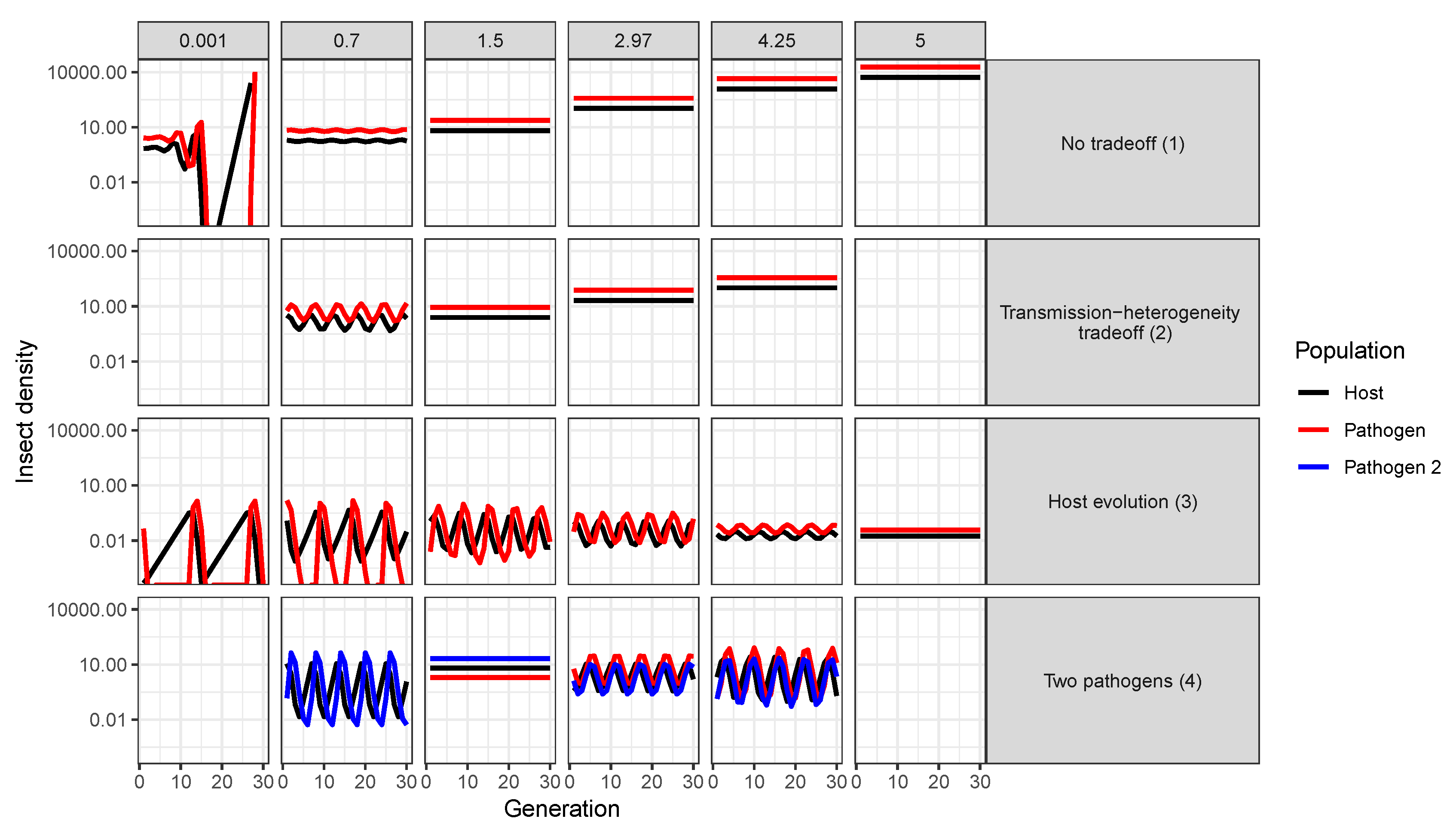
- Models used to predict viral biocontrol outcomes should incorporate heterogeneity of transmission. For single-strain non-evolutionary models, increasing heterogeneity of transmission led to higher insect population densities if it was not constrained by the mean transmission rate (i.e., there was no tradeoff; Figure 4a). Across all of the single strain models studied here, the population dynamics also became more stable as the heterogeneity increased. Although the mechanisms generating heterogeneity of transmission are likely to vary across insect–pathogen systems, the models used here [15,44,72,79] are general so that the effects of heterogeneity on population dynamics may be examined even when the sources of heterogeneity are not entirely understood.
- Use wild-collected insects from local populations to test potential control agents. Heterogeneity in transmission depends in part on host genetic variation, so experiments using a lab strain of insects is likely to misrepresent heterogeneity as well as mean transmission. In addition, the amount of variation in insect susceptibility that is explained by host genetic versus environmental effects can result in different long-term outcomes as genetic variation affects the potential for evolution of host susceptibility (and thus transmission) by natural selection. In contrast to non-evolutionary single-strain models, when evolution of host susceptibility was included, higher heterogeneity led to lower average insect densities (Figure 4b), due to the tradeoff between average transmission and insect fecundity. However, cycles are more frequent over a wider range of heterogeneity values for the evolutionary model, compared to the non-evolutionary models. Thus, it is important to consider evolutionary processes, which in turn requires considering the existing genetic variation in the targeted populations.
- When possible, selection of particular virus strains for biocontrol should consider empirical measurements of heterogeneity of transmission and not just mean transmission rate. Specifically, we recommend avoiding laboratory dose response experiments in selecting or developing a particular pathogen strain for use as a control agent. While these dose response experiments might be a good proxy for the average pathogen transmission rate, they do not contain information on heterogeneity of transmission, which surprisingly has even stronger implications for a strain’s success as a control agent (Figure 4a). Even when it is not possible to directly estimate heterogeneity of transmission using controlled epidemic experiments [44], the observed tradeoff between mean transmission and heterogeneity in transmission implies that low-mean-transmission, low-heterogeneity strains might be more effective for biocontrol than the ‘stronger’ high-mean-transmission, high-heterogeneity strains that would typically have a low lethal dose (LD50) in laboratory dose response experiments. Thus, a range of low and high LD50 strains should be field-tested before selecting a control agent, but future studies should focus on characterizing the relationship between mean transmission and heterogeneity in transmission [73].
- Using multiple pathogen strains simultaneously might be better or worse than a single strain for controlling insect populations. In our model simulations, average insect density was depressed only when the second viral strain was quite phenotypically different from the first, with a heterogeneity of transmission at least three times greater than the first strain. In other words, biocontrol using multiple pathogen strains is less effective than using a single strain if the pathogen strains have similar transmission rates and heterogeneities of transmission. This is because strains that are similar in their transmission characteristics effectively compete for the same hosts. Moreover, even in cases where two strains caused a decreased average insect population, lower mean population density was also associated with more extreme population cycles. These results thus suggest that the viral strains used in biocontrol programs should be selected based on differences in transmission characteristics, while keeping in mind the ecological risks of altering long-term characteristics of population dynamics.
Limitations and Need for Future Studies
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hajek, A.E. Natural Enemies: An Introduction to Biological Control; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kenis, M.; Hurley, B.P.; Hajek, A.E.; Cock, M.J.W. Classical biological control of insect pests of trees: Facts and figures. Biol. Invasions 2017, 19, 3401–3417. [Google Scholar] [CrossRef]
- Cock, M.J.; Murphy, S.T.; Kairo, M.T.; Thompson, E.; Murphy, R.J.; Francis, A.W. Trends in the classical biological control of insect pests by insects: An update of the BIOCAT database. BioControl 2016, 61, 349–363. [Google Scholar] [CrossRef]
- Greathead, D.; Greathead, A. Biological control of insect pests by insect parasitoids and predators: The BIOCAT. Biocontrol 1992, 13, 61N–68N. [Google Scholar]
- Simberloff, D.; Stiling, P. Risks of species introduced for biological control. Biol. Conserv. 1996, 78, 185–192. [Google Scholar] [CrossRef]
- Brodeur, J. Host specificity in biological control: Insights from opportunistic pathogens. Evol. Appl. 2012, 5, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Nylin, S. Life history perspectives on pest insects: What’s the use? Austral Ecol. 2001, 26, 507–517. [Google Scholar] [CrossRef]
- Hufbauer, R.A.; Roderick, G.K. Microevolution in biological control: Mechanisms, patterns, and processes. Biol. Control 2005, 35, 227–239. [Google Scholar] [CrossRef]
- Kenis, M.; Hurley, B.; Colombari, F.; Lawson, S.; Sun, J.; Wilcken, C.; Weeks, R.; Sathyapala, S. Guide to the Classical Biological Control of Insect Pests in Planted and Natural Forests; Food and Agriculture Organization of the United Nations: Rome, Italy, 2009. [Google Scholar]
- Hochberg, M.; Hawkins, B. The Implications of Population Dynamics Theory to Parasitoid Diversity and Biological Control. In Parasitoid Community Ecology; Oxford University Press: Oxford, UK, 1994; pp. 451–471. [Google Scholar]
- Schmid-Hempel, P. Evolutionary Parasitology: The Integrated Study of Infections, Immunology, Ecology, and Genetics; Number 574.5249 S2; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Hairston, N.G.; Ellner, S.P.; Geber, M.A.; Yoshida, T.; Fox, J.A. Rapid evolution and the convergence of ecological and evolutionary time. Ecol. Lett. 2005, 8, 1114–1127. [Google Scholar] [CrossRef]
- Cory, J.S.; Franklin, M.T. Evolution and the microbial control of insects. Evol. Appl. 2012, 5, 455–469. [Google Scholar] [CrossRef]
- Carrière, Y.; Crowder, D.W.; Tabashnik, B.E. Evolutionary ecology of insect adaptation to Bt crops. Evol. Appl. 2010, 3, 561–573. [Google Scholar] [CrossRef]
- Páez, D.J.; Dukic, V.; Dushoff, J.; Fleming-Davies, A.; Dwyer, G. Eco-evolutionary theory and insect outbreaks. Am. Nat. 2017, 189, 616–629. [Google Scholar] [CrossRef]
- Páez, D.J.; Fleming-Davies, A.E.; Dwyer, G. Effects of pathogen exposure on life-history variation in the gypsy moth (Lymantria dispar). J. Evol. Biol. 2015, 28, 1828–1839. [Google Scholar] [CrossRef] [PubMed]
- Hudson, A.; Fleming-Davies, A.; Páez, D.; Dwyer, G. Genotype-by-genotype interactions between an insect and its pathogen. J. Evol. Biol. 2016, 29, 2480–2490. [Google Scholar] [CrossRef] [PubMed]
- Cotter, S.C.; Wilson, K. Heritability of immune function in the caterpillar Spodoptera littoralis. Heredity 2002, 88, 229. [Google Scholar] [CrossRef] [PubMed]
- Cotter, S.C.; Kruuk, L.E.B.; Wilson, K. Costs of resistance: Genetic correlations and potential trade-offs in an insect immune system. J. Evol. Biol. 2004, 17, 421–429. [Google Scholar] [CrossRef] [PubMed]
- Cory, J.S.; Myers, J.H. Adaptation in an insect host–plant pathogen interaction. Ecol. Lett. 2004, 7, 632–639. [Google Scholar] [CrossRef]
- Schwarzenbach, G.; Hosken, D.; Ward, P. Sex and immunity in the yellow dung fly Scathophaga stercoraria. J. Evol. Biol. 2005, 18, 455–463. [Google Scholar] [CrossRef]
- Kraaijeveld, A.; Godfray, H. Trade-off between parasitoid resistance and larval competitive ability in Drosophila melanogaster. Nature 1997, 389, 278. [Google Scholar] [CrossRef]
- Duffy, M.A.; Sivars-Becker, L. Rapid evolution and ecological host–parasite dynamics. Ecol. Lett. 2007, 10, 44–53. [Google Scholar] [CrossRef]
- Viljakainen, L.; Evans, J.D.; Hasselmann, M.; Rueppell, O.; Tingek, S.; Pamilo, P. Rapid evolution of immune proteins in social insects. Mol. Biol. Evol. 2009, 26, 1791–1801. [Google Scholar] [CrossRef]
- Yoshida, T.; Ellner, S.P.; Jones, L.E.; Bohannan, B.J.; Lenski, R.E.; Hairston, N.G., Jr. Cryptic population dynamics: Rapid evolution masks trophic interactions. PLoS Biol. 2007, 5, e235. [Google Scholar] [CrossRef] [PubMed]
- Roderick, G.K.; Hufbauer, R.; Navajas, M. Evolution and biological control. Evol. Appl. 2012, 5, 419. [Google Scholar] [CrossRef] [PubMed]
- Holt, R.D.; Hochberg, M.E. When is biological control evolutionarily stable (or is it)? Ecology 1997, 78, 1673–1683. [Google Scholar] [CrossRef]
- Kennedy, D.; Dwyer, G. Effects of multiple sources of genetic drift on pathogen variation within hosts. PLoS Biol. 2018, 16, e2004444. [Google Scholar] [CrossRef]
- Lacey, L.A.; Frutos, R.; Kaya, H.; Vail, P. Insect pathogens as biological control agents: Do they have a future? Biol. Control 2001, 21, 230–248. [Google Scholar] [CrossRef]
- Lacey, L.; Grzywacz, D.; Shapiro-Ilan, D.; Frutos, R.; Brownbridge, M.; Goettel, M. Insect pathogens as biological control agents: Back to the future. J. Invertebr. Pathol. 2015, 132, 1–41. [Google Scholar] [CrossRef]
- Myers, J.H.; Cory, J.S. Ecology and evolution of pathogens in natural populations of Lepidoptera. Evol. Appl. 2016, 9, 231–247. [Google Scholar] [CrossRef]
- Herniou, E.A.; Olszewski, J.A.; O’reilly, D.R.; Cory, J.S. Ancient coevolution of baculoviruses and their insect hosts. J. Virol. 2004, 78, 3244–3251. [Google Scholar] [CrossRef]
- Cory, J.S.; Myers, J.H. The ecology and evolution of insect baculoviruses. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 239–272. [Google Scholar] [CrossRef]
- Grove, M.J.; Hoover, K. Intrastadial developmental resistance of third instar gypsy moths (Lymantria dispar L.) to L. dispar nucleopolyhedrovirus. Biol. Control 2007, 40, 355–361. [Google Scholar] [CrossRef]
- Turchin, P.; Taylor, A.D. Complex dynamics in ecological time series. Ecology 1992, 73, 289–305. [Google Scholar] [CrossRef]
- Fleming-Davies, A.E.; Dwyer, G. Phenotypic variation in overwinter environmental transmission of a baculovirus and the cost of virulence. Am. Nat. 2015, 186, 797–806. [Google Scholar] [CrossRef]
- Elderd, B.D.; Rehill, B.J.; Haynes, K.J.; Dwyer, G. Induced plant defenses, host–pathogen interactions, and forest insect outbreaks. Proc. Natl. Acad. Sci. USA 2013, 110, 14978–14983. [Google Scholar] [CrossRef]
- Dwyer, G.; Dushoff, J.; Yee, S.H. The combined effects of pathogens and predators on insect outbreaks. Nature 2004, 430, 341. [Google Scholar] [CrossRef]
- Kennedy, D.A.; Dukic, V.; Dwyer, G. Pathogen growth in insect hosts: Inferring the importance of different mechanisms using stochastic models and response-time data. Am. Nat. 2014, 184, 407–423. [Google Scholar] [CrossRef]
- Wikramaratna, P.S.; Kucharski, A.; Gupta, S.; Andreasen, V.; McLean, A.R.; Gog, J.R. Five challenges in modelling interacting strain dynamics. Epidemics 2015, 10, 31–34. [Google Scholar] [CrossRef]
- Gog, J.R.; Pellis, L.; Wood, J.L.; McLean, A.R.; Arinaminpathy, N.; Lloyd-Smith, J.O. Seven challenges in modeling pathogen dynamics within-host and across scales. Epidemics 2015, 10, 45–48. [Google Scholar] [CrossRef]
- Lively, C.M.; de Roode, J.C.; Duffy, M.A.; Graham, A.L.; Koskella, B. Interesting open questions in disease ecology and evolution. Am. Nat. 2014, 184, S1–S8. [Google Scholar] [CrossRef]
- Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the effect of individual variation on disease emergence. Nature 2005, 438, 355. [Google Scholar] [CrossRef]
- Dwyer, G.; Elkinton, J.S.; Buonaccorsi, J.P. Host heterogeneity in susceptibility and disease dynamics: Tests of a mathematical model. Am. Nat. 1997, 150, 685–707. [Google Scholar] [CrossRef]
- Hess, G. Disease in metapopulation models: Implications for conservation. Ecology 1996, 77, 1617–1632. [Google Scholar] [CrossRef]
- Dwyer, G. The roles of density, stage, and patchiness in the transmission of an insect virus. Ecology 1991, 72, 559–574. [Google Scholar] [CrossRef]
- Hassell, M.P.; Comins, H.N.; Mayt, R.M. Spatial structure and chaos in insect population dynamics. Nature 1991, 353, 255. [Google Scholar] [CrossRef]
- Buckee, C.O.; Koelle, K.; Mustard, M.J.; Gupta, S. The effects of host contact network structure on pathogen diversity and strain structure. Proc. Natl. Acad. Sci. USA 2004, 101, 10839–10844. [Google Scholar] [CrossRef] [PubMed]
- Leventhal, G.E.; Hill, A.L.; Nowak, M.A.; Bonhoeffer, S. Evolution and emergence of infectious diseases in theoretical and real-world networks. Nat. Commun. 2015, 6, 6101. [Google Scholar] [CrossRef] [PubMed]
- Dobelmann, J.; Loope, K.J.; Wilson-Rankin, E.; Quinn, O.; Baty, J.W.; Gruber, M.A.; Lester, P.J. Fitness in invasive social wasps: The role of variation in viral load, immune response and paternity in predicting nest size and reproductive output. Oikos 2017, 126, 1208–1218. [Google Scholar] [CrossRef]
- González-Santoyo, I.; Córdoba-Aguilar, A. Phenoloxidase: A key component of the insect immune system. Entomol. Exp. Appl. 2012, 142, 1–16. [Google Scholar] [CrossRef]
- Bolzoni, L.; Real, L.; De Leo, G. Transmission heterogeneity and control strategies for infectious disease emergence. PLoS ONE 2007, 2, e747. [Google Scholar] [CrossRef]
- Eakin, L.; Wang, M.; Dwyer, G. The effects of the avoidance of infectious hosts on infection risk in an insect–pathogen interaction. Am. Nat. 2014, 185, 100–112. [Google Scholar] [CrossRef]
- de Roode, J.C.; Lefèvre, T. Behavioral immunity in insects. Insects 2012, 3, 789–820. [Google Scholar] [CrossRef]
- Schneider, D.S.; Chambers, M.C. Rogue insect immunity. Science 2008, 322, 1199–1200. [Google Scholar] [CrossRef]
- Shirasu-Hiza, M.M.; Schneider, D.S. Confronting physiology: How do infected flies die? Cell. Microbiol. 2007, 9, 2775–2783. [Google Scholar] [CrossRef] [PubMed]
- Parker, B.J.; Elderd, B.D.; Dwyer, G. Host behaviour and exposure risk in an insect–pathogen interaction. J. Anim. Ecol. 2010, 79, 863–870. [Google Scholar] [CrossRef] [PubMed]
- Khush, R.S.; Lemaitre, B. Genes that fight infection: What the Drosophila genome says about animal immunity. Trends Genet. 2000, 16, 442–449. [Google Scholar] [CrossRef]
- Boots, M.; Roberts, K.E. Maternal effects in disease resistance: Poor maternal environment increases offspring resistance to an insect virus. Proc. R. Soc. B Biol. Sci. 2012, 279, 4009–4014. [Google Scholar] [CrossRef]
- Tidbury, H.J.; Pedersen, A.B.; Boots, M. Within and transgenerational immune priming in an insect to a DNA virus. Proc. R. Soc. B Biol. Sci. 2010, 278, 871–876. [Google Scholar] [CrossRef]
- Sadd, B.M.; Kleinlogel, Y.; Schmid-Hempel, R.; Schmid-Hempel, P. Trans-generational immune priming in a social insect. Biol. Lett. 2005, 1, 386–388. [Google Scholar] [CrossRef]
- Reber, A.; Chapuisat, M. No evidence for immune priming in ants exposed to a fungal pathogen. PLoS ONE 2012, 7, e35372. [Google Scholar] [CrossRef]
- Elderd, B.D.; Dushoff, J.; Dwyer, G. host–pathogen interactions, insect outbreaks, and natural selection for disease resistance. Am. Nat. 2008, 172, 829–842. [Google Scholar] [CrossRef]
- Tate, A.; Rudolf, V. Impact of life stage specific immune priming on invertebrate disease dynamics. Oikos 2012, 121, 1083–1092. [Google Scholar] [CrossRef]
- Pedrini, N.; Ortiz-Urquiza, A.; Huarte-Bonnet, C.; Fan, Y.; Juárez, M.P.; Keyhani, N.O. Tenebrionid secretions and a fungal benzoquinone oxidoreductase form competing components of an arms race between a host and pathogen. Proc. Natl. Acad. Sci. USA 2015, 112, E3651–E3660. [Google Scholar] [CrossRef]
- Unckless, R.L.; Lazzaro, B.P. The potential for adaptive maintenance of diversity in insect antimicrobial peptides. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150291. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361. [Google Scholar] [CrossRef] [PubMed]
- McCallum, H.; Barlow, N.; Hone, J. How should pathogen transmission be modelled? Trends Ecol. Evol. 2001, 16, 295–300. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Begon, M.; Bennett, M.; Bowers, R.G.; French, N.P.; Hazel, S.; Turner, J. A clarification of transmission terms in host-microparasite models: Numbers, densities and areas. Epidemiol. Infect. 2002, 129, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Fenton, A.; Fairbairn, J.P.; Norman, R.; Hudson, P.J. Parasite transmission: Reconciling theory and reality. J. Anim. Ecol. 2002, 71, 893–905. [Google Scholar] [CrossRef]
- Dwyer, G.; Dushoff, J.; Elkinton, J.S.; Levin, S.A. Pathogen-driven outbreaks in forest defoliators revisited: Building models from experimental data. Am. Nat. 2000, 156, 105–120. [Google Scholar] [CrossRef]
- Vazquez-Prokopec, G.M.; Perkins, T.A.; Waller, L.A.; Lloyd, A.L.; Reiner, R.C., Jr.; Scott, T.W.; Kitron, U. Coupled Heterogeneities and Their Impact on Parasite Transmission and Control; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Farrington, C.P.; Whitaker, H.J.; Unkel, S.; Pebody, R. Correlated infections: Quantifying individual heterogeneity in the spread of infectious diseases. Am. J Epidemiol. 2013, 177, 474–486. [Google Scholar] [CrossRef]
- Nagelkerke, N.J.; de Vlas, S.J.; Jha, P.; Luo, M.; Plummer, F.A.; Kaul, R. Heterogeneity in host HIV susceptibility as a potential contributor to recent HIV prevalence declines in Africa. AIDS 2009, 23, 125. [Google Scholar] [CrossRef]
- Fleming-Davies, A.E.; Williams, P.D.; Dhondt, A.A.; Dobson, A.P.; Hochachka, W.M.; Leon, A.E.; Ley, D.H.; Osnas, E.E.; Hawley, D.M. Incomplete host immunity favors the evolution of virulence in an emergent pathogen. Science 2018, 359, 1030–1033. [Google Scholar] [CrossRef]
- Langwig, K.E.; Wargo, A.R.; Jones, D.R.; Viss, J.R.; Rutan, B.J.; Egan, N.A.; Sá-Guimarães, P.; Kim, M.S.; Kurath, G.; Gomes, M.G.M.; et al. Vaccine Effects on Heterogeneity in Susceptibility and Implications for Population Health Management. mBio 2017, 8, e00796-17. [Google Scholar] [CrossRef] [PubMed]
- Dushoff, J. Host heterogeneity and disease endemicity: A moment-based approach. Theor. Popul. Biol. 1999, 56, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Fleming-Davies, A.E.; Dukic, V.; Andreasen, V.; Dwyer, G. Effects of host heterogeneity on pathogen diversity and evolution. Ecol. Lett. 2015, 18, 1252–1261. [Google Scholar] [CrossRef]
- Kyle, C.H.; Liu, J.; Gallagher, M.E.; Dukic, V.; Dwyer, G. Stochasticity and infectious-disease dynamics: Density and weather effects on a fungal insect pathogen. Am. Nat. 2019. [Google Scholar] [CrossRef]
- Liebhold, A.M.; Tobin, P.C. Exploiting the Achilles heels of pest invasions: Allee effects, stratified dispersal and management of forest insect establishment and spread. N. Z. J. For. Sci. 2010, 40, S25–S33. [Google Scholar]
- Rolff, J.; Siva-Jothy, M. Invertebrate ecological immunology. Science 2003, 301, 472–475. [Google Scholar] [CrossRef]
- Hawley, D.M.; Altizer, S.M. Disease ecology meets ecological immunology: Understanding the links between organismal immunity and infection dynamics in natural populations. Funct. Ecol. 2011, 25, 48–60. [Google Scholar] [CrossRef]
- Sadd, B.M.; Siva-Jothy, M.T. Self-harm caused by an insect’s innate immunity. Proc. R. Soc. B Biol. Sci. 2006, 273, 2571–2574. [Google Scholar] [CrossRef]
- Simmons, L.W.; Roberts, B. Bacterial immunity traded for sperm viability in male crickets. Science 2005, 309, 2031. [Google Scholar] [CrossRef]
- Kerr, A.M.; Gershman, S.N.; Sakaluk, S.K. Experimentally induced spermatophore production and immune responses reveal a trade-off in crickets. Behav. Ecol. 2010, 21, 647–654. [Google Scholar] [CrossRef]
- Brunner, F.S.; Schmid-Hempel, P.; Barribeau, S.M. Protein-poor diet reduces host-specific immune gene expression in Bombus terrestris. Proc. R. Soc. B Biol. Sci. 2014, 281, 20140128. [Google Scholar] [CrossRef] [PubMed]
- Vogelweith, F.; Thiery, D.; Moret, Y.; Moreau, J. Immunocompetence increases with larval body size in a phytophagous moth. Physiol. Entomol. 2013, 38, 219–225. [Google Scholar] [CrossRef]
- Meaden, S.; Paszkiewicz, K.; Koskella, B. The cost of phage resistance in a plant pathogenic bacterium is context-dependent. Evolution 2015, 69, 1321–1328. [Google Scholar] [CrossRef] [PubMed]
- Sugumaran, M.; Nellaiappan, K.; Valivittan, K. A new mechanism for the control of phenoloxidase activity: Inhibition and complex formation with quinone isomerase. Arch. Biochem. Biophys. 2000, 379, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Hosken, D.J. Sex and death: Microevolutionary trade-offs between reproductive and immune investment in dung flies. Curr. Biol. 2001, 11, R379–R380. [Google Scholar] [CrossRef]
- De Roode, J.C.; Yates, A.J.; Altizer, S. Virulence-transmission trade-offs and population divergence in virulence in a naturally occurring butterfly parasite. Proc. Natl. Acad. Sci. USA 2008, 105, 7489–7494. [Google Scholar] [CrossRef]
- Thrall, P.H.; Burdon, J.J. Evolution of virulence in a plant host–pathogen metapopulation. Science 2003, 299, 1735–1737. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Coevolution of hosts and parasites. Parasitology 1982, 85, 411–426. [Google Scholar] [CrossRef]
- Levin, S.; Pimentel, D. Selection of intermediate rates of increase in parasite-host systems. Am. Nat. 1981, 117, 308–315. [Google Scholar] [CrossRef]
- Boots, M.; Haraguchi, Y. The evolution of costly resistance in host–parasite systems. Am. Nat. 1999, 153, 359–370. [Google Scholar] [CrossRef]
- Boots, M.; Begon, M. Trade-offs with resistance to a granulosis virus in the Indian meal moth, examined by a laboratory evolution experiment. Funct. Ecol. 1993, 528–534. [Google Scholar] [CrossRef]
- Sasaki, A.; Godfray, H. A model for the coevolution of resistance and virulence in coupled host–parasitoid interactions. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1999, 266, 455–463. [Google Scholar] [CrossRef]
- May, R.M.; Anderson, R.M. Epidemiology and genetics in the coevolution of parasites and hosts. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1983, 219, 281–313. [Google Scholar]
- Frank, S.A. Coevolutionary genetics of plants and pathogens. Evol. Ecol. 1993, 7, 45–75. [Google Scholar] [CrossRef]
- Bergelson, J.; Dwyer, G.; Emerson, J. Models and data on plant-enemy coevolution. Annu. Revi. Genet. 2001, 35, 469–499. [Google Scholar] [CrossRef]
- Acevedo, M.A.; Dillemuth, F.P.; Flick, A.J.; Faldyn, M.J.; Elderd, B.D. Virulence-driven trade-offs in disease transmission: A meta-analysis. Evolution 2018, 73, 636–647. [Google Scholar] [CrossRef]
- Alizon, S.; Michalakis, Y. Adaptive virulence evolution: The good old fitness-based approach. Trends Ecol. Evol. 2015, 30, 248–254. [Google Scholar] [CrossRef]
- Restif, O.; Hayman, D.T.; Pulliam, J.R.; Plowright, R.K.; George, D.B.; Luis, A.D.; Cunningham, A.A.; Bowen, R.A.; Fooks, A.R.; O’Shea, T.J.; et al. Model-guided fieldwork: Practical guidelines for multidisciplinary research on wildlife ecological and epidemiological dynamics. Ecol. Lett. 2012, 15, 1083–1094. [Google Scholar] [CrossRef]
- Dwyer, G. On the spatial spread of insect pathogens: Theory and experiment. Ecology 1992, 73, 479–494. [Google Scholar] [CrossRef]
- Fuller, E.; Elderd, B.D.; Dwyer, G. Pathogen persistence in the environment and insect-baculovirus interactions: Disease-density thresholds, epidemic burnout, and insect outbreaks. Am. Nat. 2012, 179, E70–E96. [Google Scholar] [CrossRef]
- Ezenwa, V.O.; Jolles, A.E. From Host Immunity to Pathogen Invasion: The Effects of Helminth Coinfection on the Dynamics of Microparasites; Oxford Academic Press: Oxford, UK, 2011. [Google Scholar]
- Shaw, R.G.; Shaw, F. Quantitative genetic study of the adaptive process. Heredity 2014, 112, 13. [Google Scholar] [CrossRef] [PubMed]
- King, A.A.; Nguyen, D.; Ionides, E.L. Statistical inference for partially observed Markov processes via the R package pomp. arXiv preprint 2015, arXiv:1509.00503. [Google Scholar]
- Hall, S.R.; Becker, C.R.; Duffy, M.A.; Cáceres, C.E. Variation in resource acquisition and use among host clones creates key epidemiological trade-offs. Am. Nat. 2010, 176, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Fellowes, M.D.; Travis, J.M. Linking the coevolutionary and population dynamics of host–parasitoid interactions. Popul. Ecol. 2000, 42, 195–203. [Google Scholar] [CrossRef]
- Kraaijeveld, A.R.; Godfray, H.C.J. Geographic patterns in the evolution of resistance and virulence in Drosophila and its parasitoids. Am. Nat. 1999, 153, S61–S74. [Google Scholar] [CrossRef]
| Model Description | Force of Infection | Heterogeneity | Tradeoffs | Reference |
|---|---|---|---|---|
| (0) One pathogen strain, homogeneous host, no evolution | None (linear transmission described by ) | None | [44] | |
| (1) One pathogen strain, Gamma distribution of host susceptibility, no evolution, no tradeoffs | Host susceptibility, described by CV of transmission (C) | None | [44,72] | |
| (2) One pathogen strain, same as (1) above but with evolutionary tradeoff between pathogen mean transmission and heterogeneity of transmission described by function | Host susceptibility, described by CV of transmission (C) | Evolutionary tradeoff between pathogen mean transmission and heterogeneity of transmission described by function | [72,79] | |
| (3) One pathogen strain, Gamma distribution of host susceptibility, host evolution | Host susceptibility described by the average transmission in generation n and genetic and environmental variation in susceptibility | Selection on imposed through host mortality and a tradeoff between host reproduction and susceptibility, described by | [15] | |
| (4) Two pathogen strains, Gamma distribution of host susceptibility, no evolution | Host susceptibility and pathogen genotype, described by mean , CV of transmission , and interstrain transmission correlation | Evolutionary tradeoff between pathogen mean transmission and heterogeneity of transmission described by function | [79] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Páez, D.J.; Fleming-Davies, A.E. Understanding the Evolutionary Ecology of host–pathogen Interactions Provides Insights into the Outcomes of Insect Pest Biocontrol. Viruses 2020, 12, 141. https://doi.org/10.3390/v12020141
Páez DJ, Fleming-Davies AE. Understanding the Evolutionary Ecology of host–pathogen Interactions Provides Insights into the Outcomes of Insect Pest Biocontrol. Viruses. 2020; 12(2):141. https://doi.org/10.3390/v12020141
Chicago/Turabian StylePáez, David J., and Arietta E. Fleming-Davies. 2020. "Understanding the Evolutionary Ecology of host–pathogen Interactions Provides Insights into the Outcomes of Insect Pest Biocontrol" Viruses 12, no. 2: 141. https://doi.org/10.3390/v12020141
APA StylePáez, D. J., & Fleming-Davies, A. E. (2020). Understanding the Evolutionary Ecology of host–pathogen Interactions Provides Insights into the Outcomes of Insect Pest Biocontrol. Viruses, 12(2), 141. https://doi.org/10.3390/v12020141





