Mutation and Epistasis in Influenza Virus Evolution
Abstract
1. Introduction
2. Effects of Single Mutations
2.1. Genome-Wide Distribution of Mutational Fitness Effects
2.2. Deep Mutational Scanning of Influenza Proteins
3. Epistasis
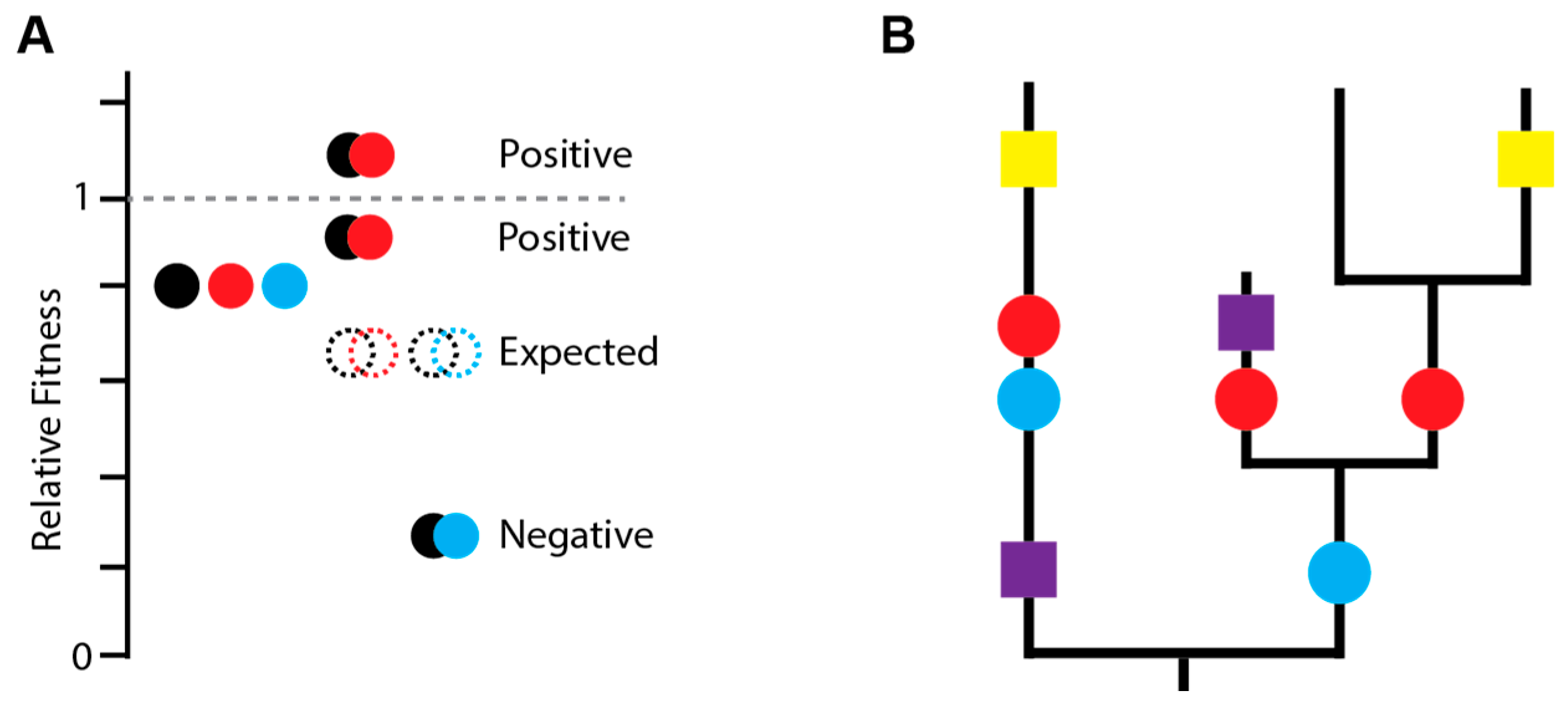
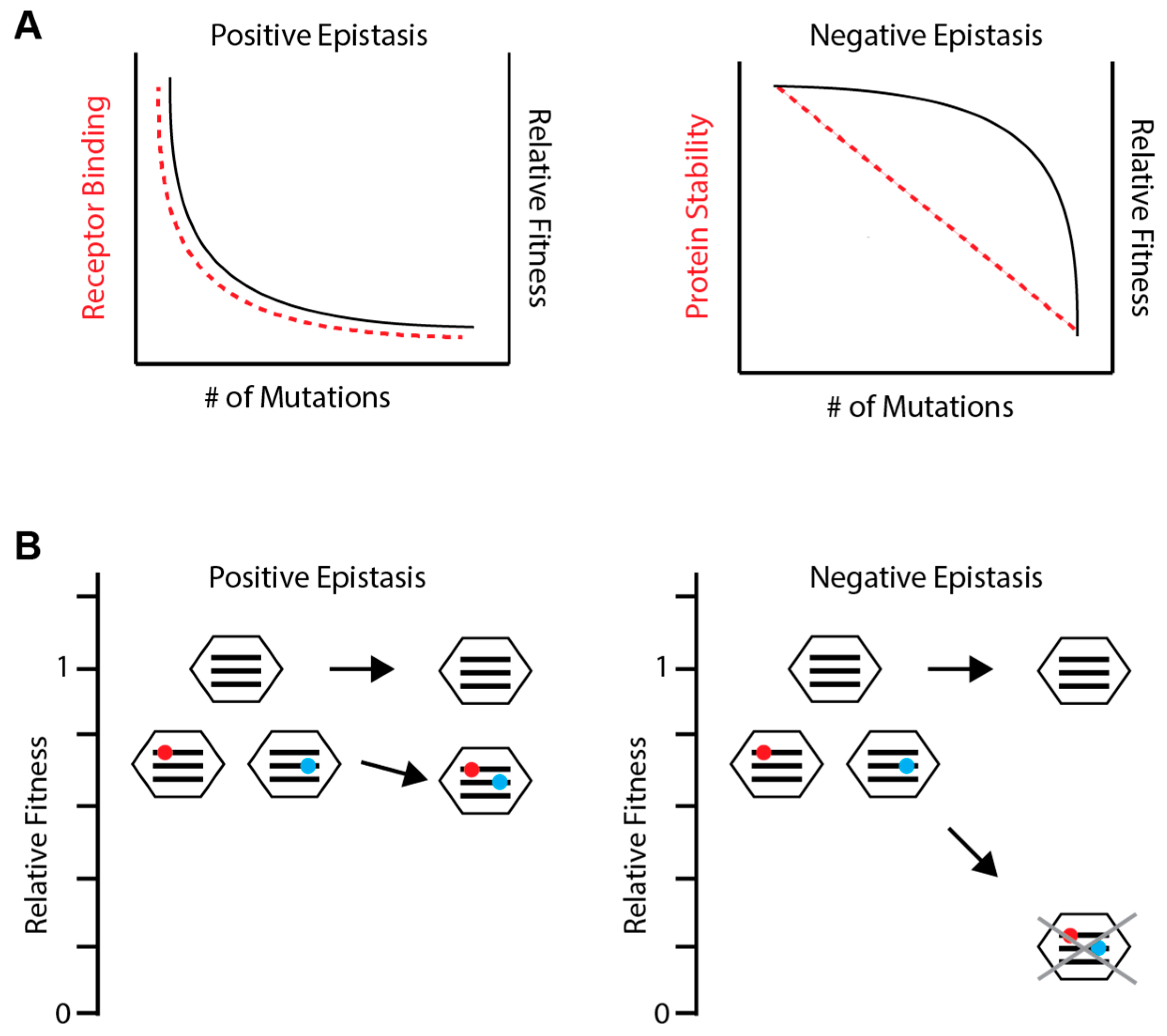
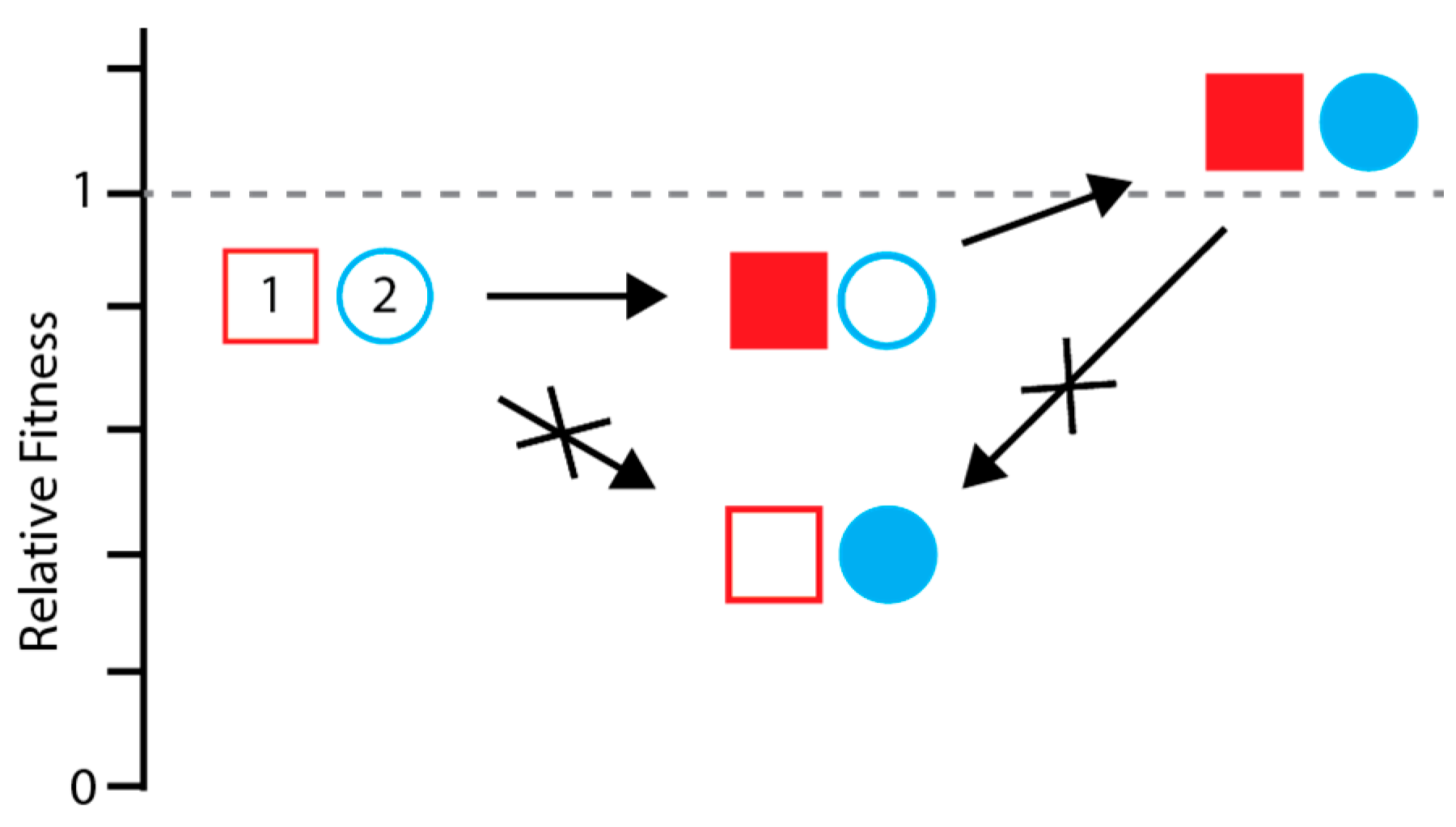
3.1. Detecting and Measuring Epistasis
3.2. General Epistatic Patterns in Influenza Viruses
3.3. Epistasis in the Adaptive Evolution of Influenza Virus
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Sanjuán, R. Mutational fitness effects in RNA and single-stranded DNA viruses: Common patterns revealed by site-directed mutagenesis studies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 1975–1982. [Google Scholar] [CrossRef] [PubMed]
- Visher, E.; Whitefield, S.E.; McCrone, J.T.; Fitzsimmons, W.; Lauring, A.S. The Mutational Robustness of Influenza A Virus. PLoS Pathog. 2016, 12, e1005856. [Google Scholar] [CrossRef] [PubMed]
- Fowler, D.M.; Fields, S. Deep mutational scanning: A new style of protein science. Nat. Meth. 2014, 11, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Olson, C.A.; Du, Y.; Le, S.; Tran, K.; Remenyi, R.; Gong, D.; Al-Mawsawi, L.Q.; Qi, H.; Wu, T.T.; et al. Functional Constraint Profiling of a Viral Protein Reveals Discordance of Evolutionary Conservation and Functionality. PLoS Genet. 2015, 11, e1005310. [Google Scholar] [CrossRef] [PubMed]
- McCrone, J.T.; Woods, R.J.; Martin, E.T.; Malosh, R.E.; Monto, A.S.; Lauring, A.S. Stochastic processes constrain the within and between host evolution of influenza virus. eLife 2018, 7, e35962. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, R.; Yang, Z. Estimating the Distribution of Selection Coefficients from Phylogenetic Data with Applications to Mitochondrial and Viral DNA. Mol. Biol. Evol. 2003, 20, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
- Poon, L.L.M.; Song, T.; Rosenfeld, R.; Lin, X.; Rogers, M.B.; Zhou, B.; Sebra, R.; Halpin, R.A.; Guan, Y.; Twaddle, A.; et al. Quantifying influenza virus diversity and transmission in humans. Nat. Genet. 2016, 48, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Tamuri, A.U.; dos Reis, M.; Goldstein, R.A. Estimating the Distribution of Selection Coefficients from Phylogenetic Data Using Sitewise Mutation-Selection Models. Genetics 2012, 190, 1101–1115. [Google Scholar] [CrossRef] [PubMed]
- Dawson, W.K.; Lazniewski, M.; Plewczynski, D. RNA structure interactions and ribonucleoprotein processes of the influenza A virus. Brief. Funct. Genomics 2017. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Watanabe, S.; Noda, T.; Fujii, Y.; Kawaoka, Y. Exploitation of nucleic acid packaging signals to generate a novel influenza virus-based vector stably expressing two foreign genes. J. Virol. 2003, 77, 10575–10583. [Google Scholar] [CrossRef] [PubMed]
- Carrasco, P.; de la Iglesia, F.; Elena, S.F. Distribution of fitness and virulence effects caused by single-nucleotide substitutions in Tobacco Etch virus. J. Virol. 2007, 81, 12979–12984. [Google Scholar] [CrossRef] [PubMed]
- Domingo-Calap, P.; Cuevas, J.M.; Sanjuá, R. The fitness effects of random mutations in single-stranded DNA and RNA bacteriophages. PLoS Genet. 2009, 5, e1000742. [Google Scholar] [CrossRef] [PubMed]
- Peris, J.B.; Davis, P.; Cuevas, J.M.; Nebot, M.R.; Sanjuán, R. Distribution of fitness effects caused by single-nucleotide substitutions in bacteriophage f1. Genetics 2010, 185, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Sanjuán, R.; Moya, A.; Elena, S.F. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA 2004, 101, 8396–8401. [Google Scholar] [CrossRef] [PubMed]
- Eyre-Walker, A.; Keightley, P.D. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 2007, 8, 610–618. [Google Scholar] [CrossRef] [PubMed]
- Sanjuán, R.; Elena, S.F. Epistasis correlates to genomic complexity. Proc. Natl. Acad. Sci. USA 2006, 103, 14402–14405. [Google Scholar] [CrossRef] [PubMed]
- Plotkin, J.B.; Dushoff, J. Codon bias and frequency-dependent selection on the hemagglutinin epitopes of influenza A virus. Proc. Natl. Acad. Sci. USA 2003, 100, 7152–7157. [Google Scholar] [CrossRef] [PubMed]
- Heaton, N.S.; Sachs, D.; Chen, C.-J.; Hai, R.; Palese, P. Genome-wide mutagenesis of influenza virus reveals unique plasticity of the hemagglutinin and NS1 proteins. Proc. Natl. Acad. Sci. USA 2013, 110, 20248–20253. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M.; Huddleston, J.; Doud, M.B.; Hooper, K.A.; Wu, N.C.; Bedford, T.; Bloom, J.D. Deep mutational scanning of hemagglutinin helps predict evolutionary fates of human H3N2 influenza variants. bioRxiv 2018, 298364. [Google Scholar] [CrossRef]
- Thyagarajan, B.; Bloom, J.D. The inherent mutational tolerance and antigenic evolvability of influenza hemagglutinin. eLife 2014, 3, e03300. [Google Scholar] [CrossRef] [PubMed]
- Fulton, B.O.; Sachs, D.; Beaty, S.M.; Won, S.T.; Lee, B.; Palese, P.; Heaton, N.S. Mutational Analysis of Measles Virus Suggests Constraints on Antigenic Variation of the Glycoproteins. Cell Rep. 2015, 11, 1331–1338. [Google Scholar] [CrossRef] [PubMed]
- Bloom, J.D. An experimentally determined evolutionary model dramatically improves phylogenetic fit. Mol. Biol. Evol. 2014, 31, 1956–1978. [Google Scholar] [CrossRef] [PubMed]
- Erbelding, E.J.; Post, D.J.; Stemmy, E.J.; Roberts, P.C.; Augustine, A.D.; Ferguson, S.; Paules, C.I.; Graham, B.S.; Fauci, A.S. A Universal Influenza Vaccine: The Strategic Plan for the National Institute of Allergy and Infectious Diseases. J. Infect. Dis. 2018, 218, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Pauly, M.D.; Procario, M.C.; Lauring, A.S. A novel twelve class fluctuation test reveals higher than expected mutation rates for influenza A viruses. eLife 2017, 6, e26437. [Google Scholar] [CrossRef] [PubMed]
- Debbink, K.; McCrone, J.T.; Petrie, J.G.; Truscon, R.; Johnson, E.; Mantlo, E.K.; Monto, A.S.; Lauring, A.S. Vaccination has minimal impact on the intrahost diversity of H3N2 influenza viruses. PLoS Pathog. 2017, 13, e1006194. [Google Scholar] [CrossRef] [PubMed]
- Dinis, J.M.; Florek, N.W.; Fatola, O.O.; Moncla, L.H.; Mutschler, J.P.; Charlier, O.K.; Meece, J.K.; Belongia, E.A.; Friedrich, T.C. Deep sequencing reveals potential antigenic variants at low frequency in influenza A-infected humans. J. Virol. 2016, 90, 3355–3365. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Xiao, H.; Baillie, G.; Warry, A.; Essen, S.C.; Londt, B.; Brookes, S.M.; Brown, I.H.; McCauley, J.W. Within-host variation of avian influenza viruses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2009, 364, 2739–2747. [Google Scholar] [CrossRef] [PubMed]
- Leonard, A.S.; McClain, M.T.; Smith, G.J.D.; Wentworth, D.E.; Halpin, R.A.; Lin, X.; Ransier, A.; Stockwell, T.B.; Das, S.R.; Gilbert, A.S.; et al. The effective rate of influenza reassortment is limited during human infection. PLoS Pathog. 2017, 13, e1006203. [Google Scholar] [CrossRef]
- Murcia, P.R.; Baillie, G.J.; Daly, J.; Elton, D.; Jervis, C.; Mumford, J.A.; Newton, R.; Parrish, C.R.; Hoelzer, K.; Dougan, G.; et al. Intra- and interhost evolutionary dynamics of equine influenza virus. J. Virol. 2010, 84, 6943–6954. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.S.; Stevens-Ayers, T.; Campbell, A.P.; Englund, J.A.; Pergam, S.A.; Boeckh, M.; Bloom, J.D. Parallel evolution of influenza across multiple spatiotemporal scales. eLife 2017, 6, e26875. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.S.; Bloom, J.D. Reconciling disparate estimates of viral genetic diversity during human influenza infections. bioRxiv 2018, 364430. [Google Scholar] [CrossRef]
- Pybus, O.G.; Rambaut, A.; Belshaw, R.; Freckleton, R.P.; Drummond, A.J.; Holmes, E.C. Phylogenetic evidence for deleterious mutation load in RNA viruses and its contribution to viral evolution. Mol. Biol. Evol. 2007, 24, 845–852. [Google Scholar] [CrossRef] [PubMed]
- Koelle, K.; Rasmussen, D.A. The effects of a deleterious mutation load on patterns of influenza A/H3N2’s antigenic evolution in humans. eLife 2015, 4, e07361. [Google Scholar] [CrossRef] [PubMed]
- Raghwani, J.; Thompson, R.N.; Koelle, K. Selection on non-antigenic gene segments of seasonal influenza A virus and its impact on adaptive evolution. Virus Evol. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Lyons, D.M.; Lauring, A.S. Evidence for the Selective Basis of Transition-to-Transversion Substitution Bias in Two RNA Viruses. Mol. Biol. Evol. 2017, 34, 3205–3215. [Google Scholar] [CrossRef] [PubMed]
- Doud, M.B.; Bloom, J.D. Accurate Measurement of the Effects of All Amino-Acid Mutations on Influenza Hemagglutinin. Viruses 2016, 8, 155. [Google Scholar] [CrossRef] [PubMed]
- Doud, M.B.; Ashenberg, O.; Bloom, J.D. Site-Specific Amino Acid Preferences Are Mostly Conserved in Two Closely Related Protein Homologs. Mol. Biol. Evol. 2015, 32, 2944–2960. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Wu, N.C.; Jiang, L.; Zhang, T.; Gong, D.; Shu, S.; Wu, T.T.; Sun, R. Annotating Protein Functional Residues by Coupling High-Throughput Fitness Profile and Homologous-Structure Analysis. MBio 2016, 7, e01801-16. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Xin, L.; Shi, Y.; Zhang, T.H.; Wu, N.C.; Dai, L.; Gong, D.; Brar, G.; Shu, S.; Luo, J.; et al. Genome-wide identification of interferon-sensitive mutations enables influenza vaccine design. Science 2018, 359, 290–296. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Young, A.P.; Dandekar, S.; Wijersuriya, H.; Al-Mawsawi, L.Q.; Wu, T.T.; Sun, R. Systematic identification of H274Y compensatory mutations in influenza A virus neuraminidase by high-throughput screening. J. Virol. 2013, 87, 1193–1199. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Young, A.P.; Al-Mawsawi, L.Q.; Olson, C.A.; Feng, J.; Qi, H.; Luan, H.H.; Li, X.; Wu, T.-T.; Sun, R. High-throughput identification of loss-of-function mutations for anti-interferon activity in the influenza A virus NS segment. J. Virol. 2014, 88, 10157–10164. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Young, A.P.; Al-Mawsawi, L.Q.; Olson, C.A.; Feng, J.; Qi, H.; Chen, S.H.; Lu, I.H.; Lin, C.Y.; Chin, R.G.; et al. High-throughput profiling of influenza A virus hemagglutinin gene at single-nucleotide resolution. Sci. Rep. 2014, 4, 4942. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Du, Y.; Le, S.; Young, A.P.; Zhang, T.H.; Wang, Y.; Zhou, J.; Yoshizawa, J.M.; Dong, L.; Li, X.; et al. Coupling high-throughput genetics with phylogenetic information reveals an epistatic interaction on the influenza A virus M segment. BMC Genomics 2016, 17, 46. [Google Scholar] [CrossRef] [PubMed]
- Duchêne, S.; Ho, S.Y.; Holmes, E.C. Declining transition/transversion ratios through time reveal limitations to the accuracy of nucleotide substitution models. BMC Evol. Biol. 2015, 15, 36. [Google Scholar] [CrossRef] [PubMed]
- Hilton, S.K.; Bloom, J.D. Modeling site-specific amino-acid preferences deepens phylogenetic estimates of viral divergence. bioRxiv 2018, 302703. [Google Scholar] [CrossRef]
- Bloom, J.D. Identification of positive selection in genes is greatly improved by using experimentally informed site-specific models. Biol. Direct 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Hilton, S.K.; Doud, M.B.; Bloom, J.D. phydms: Software for phylogenetic analyses informed by deep mutational scanning. PeerJ 2017, 5, e3657. [Google Scholar] [CrossRef] [PubMed]
- Doud, M.B.; Lee, J.M.; Bloom, J.D. How single mutations affect viral escape from broad and narrow antibodies to H1 influenza hemagglutinin. Nat. Commun. 2018, 9, 1386. [Google Scholar] [CrossRef] [PubMed]
- Doud, M.B.; Hensley, S.E.; Bloom, J.D. Complete mapping of viral escape from neutralizing antibodies. PLoS Pathog. 2017, 13, e1006271. [Google Scholar] [CrossRef] [PubMed]
- Phillips, P.C. Epistasis—The essential role of gene interactions in the structure and evolution of genetic systems. Nat. Rev. Genet. 2008, 9, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Elena, S.F.; Solé, R.V.; Sardanyés, J. Simple genomes, complex interactions: Epistasis in RNA virus. Chaos 2010, 20, 026106. [Google Scholar] [CrossRef] [PubMed]
- Mani, R.; St. Onge, R.P.; Hartman, J.L.; Giaever, G.; Roth, F.P. Defining genetic interaction. Proc. Natl. Acad. Sci. USA 2008, 105, 3461–3466. [Google Scholar] [CrossRef] [PubMed]
- Bloom, J.D.; Gong, L.I.; Baltimore, D. Permissive Secondary Mutations Enable the Evolution of Influenza Oseltamivir Resistance. Science 2010, 328, 1272–1275. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.I.; Suchard, M.A.; Bloom, J.D. Stability-mediated epistasis constrains the evolution of an influenza protein. eLife 2013, 2, e00631. [Google Scholar] [CrossRef] [PubMed]
- Pauly, M.D.; Lyons, D.M.; Fitzsimmons, W.J.; Lauring, A.S. Epistatic Interactions within the Influenza A Virus Polymerase Complex Mediate Mutagen Resistance and Replication Fidelity. mSphere 2017, 2, e00323-17. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Xie, J.; Zheng, T.; Nycholat, C.M.; Grande, G.; Paulson, J.C.; Lerner, R.A.; Wilson, I.A. Diversity of Functionally Permissive Sequences in the Receptor-Binding Site of Influenza Hemagglutinin. Cell Host Microbe 2017, 21, 742–753. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.C.; Thompson, A.J.; Xie, J.; Lin, C.-W.; Nycholat, C.M.; Zhu, X.; Lerner, R.A.; Paulson, J.C.; Wilson, I.A. A complex epistatic network limits the mutational reversibility in the influenza hemagglutinin receptor-binding site. Nat. Commun. 2018, 9, 1264. [Google Scholar] [CrossRef] [PubMed]
- Das, S.R.; Hensley, S.E.; Ince, W.L.; Brooke, C.B.; Subba, A.; Delboy, M.G.; Russ, G.; Gibbs, J.S.; Bennink, J.R.; Yewdell, J.W. Defining influenza A virus hemagglutinin antigenic drift by sequential monoclonal antibody selection. Cell Host Microbe 2013, 13, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, B.; Rambaut, A.; Pybus, O.G.; Holmes, E.C. A phylogenetic method for detecting positive epistasis in gene sequences and its application to RNA virus evolution. Mol. Biol. Evol. 2006, 23, 1724–1730. [Google Scholar] [CrossRef] [PubMed]
- Akand, E.H.; Downard, K.M. Identification of epistatic mutations and insights into the evolution of the influenza virus using a mass-based protein phylogenetic approach. Mol. Phylogenet. Evol. 2018, 121, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Kryazhimskiy, S.; Dushoff, J.; Bazykin, G.A.; Plotkin, J.B. Prevalence of epistasis in the evolution of influenza A surface proteins. PLoS Genet. 2011, 7, e1001301. [Google Scholar] [CrossRef] [PubMed]
- Neverov, A.D.; Kryazhimskiy, S.; Plotkin, J.B.; Bazykin, G.A. Coordinated Evolution of Influenza A Surface Proteins. PLoS Genet. 2015, 11, e1005404. [Google Scholar] [CrossRef] [PubMed]
- Rambaut, A.; Pybus, O.G.; Nelson, M.I.; Viboud, C.; Taubenberger, J.K.; Holmes, E.C. The genomic and epidemiological dynamics of human influenza A virus. Nature 2008, 453, 615–619. [Google Scholar] [CrossRef] [PubMed]
- Neverov, A.D.; Lezhnina, K.V.; Kondrashov, A.S.; Bazykin, G.A. Intrasubtype reassortments cause adaptive amino acid replacements in H3N2 influenza genes. PLoS Genet. 2014, 10, e1004037. [Google Scholar] [CrossRef] [PubMed]
- Nshogozabahizi, J.C.; Dench, J.; Aris-Brosou, S. Widespread Historical Contingency in Influenza Viruses. Genetics 2017, 205, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Bershtein, S.; Segal, M.; Bekerman, R.; Tokuriki, N.; Tawfik, D.S. Robustness-epistasis link shapes the fitness landscape of a randomly drifting protein. Nature 2006, 444, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Qian, W.; Maclean, C.J.; Zhang, J. The fitness landscape of a tRNA gene. Science 2016, 352, 837–840. [Google Scholar] [CrossRef] [PubMed]
- Sarkisyan, K.S.; Bolotin, D.A.; Meer, M.V.; Usmanova, D.R.; Mishin, A.S.; Sharonov, G.V.; Ivankov, D.N.; Bozhanova, N.G.; Baranov, M.S.; Soylemez, O.; et al. Local fitness landscape of the green fluorescent protein. Nature 2016, 533, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Puchta, O.; Cseke, B.; Czaja, H.; Tollervey, D.; Sanguinetti, G.; Kudla, G. Network of epistatic interactions within a yeast snoRNA. Science 2016, 352, 840–844. [Google Scholar] [CrossRef] [PubMed]
- Lehner, B. Molecular mechanisms of epistasis within and between genes. Trends Genet. 2011, 27, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Sanjuán, R.; Nebot, M.R. A network model for the correlation between epistasis and genomic complexity. PLoS ONE 2008, 3, e2663. [Google Scholar] [CrossRef] [PubMed]
- Gros, P.A.; Nagard, H.L.; Tenaillon, O. The evolution of epistasis and its links with genetic robustness, complexity and drift in a phenotypic model of adaptation. Genetics 2009, 182, 277–293. [Google Scholar] [CrossRef] [PubMed]
- Wilke, C.O.; Christoph, A. Interaction between directional epistasis and average mutational effects. Proc. Biol. Sci. 2001, 268, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Wilke, C.O.; Lenski, R.E.; Adami, C. Compensatory mutations cause excess of antagonistic epistasis in RNA secondary structure folding. BMC Evol. Biol. 2003, 3, 3. [Google Scholar] [CrossRef]
- Chao, L. Evolution of sex in RNA viruses. J. Theor. Biol. 1988, 133, 99–112. [Google Scholar] [CrossRef]
- Kondrashov, A.S. Deleterious mutations and the evolution of sexual reproduction. Nature 1988, 336, 435–440. [Google Scholar] [CrossRef] [PubMed]
- Kouyos, R.D.; Silander, O.K.; Bonhoeffer, S. Epistasis between deleterious mutations and the evolution of recombination. Trends Ecol. Evol. 2007, 22, 308–315. [Google Scholar] [CrossRef] [PubMed]
- Campbell, P.J.; Danzy, S.; Kyriakis, C.S.; Deymier, M.J.; Lowen, A.C.; Steel, J. The M segment of the 2009 pandemic influenza virus confers increased neuraminidase activity, filamentous morphology, and efficient contact transmissibility to A/Puerto Rico/8/1934-based reassortant viruses. J. Virol. 2014, 88, 3802–3814. [Google Scholar] [CrossRef] [PubMed]
- Danzy, S.; Studdard, L.R.; Manicassamy, B.; Solorzano, A.; Marshall, N.; García-Sastre, A.; Steel, J.; Lowen, A.C. Mutations to PB2 and NP proteins of an avian influenza virus combine to confer efficient growth in primary human respiratory cells. J. Virol. 2014, 88, 13436–13446. [Google Scholar] [CrossRef] [PubMed]
- Morens, D.M.; Taubenberger, J.K.; Fauci, A.S. The Persistent Legacy of the 1918 Influenza Virus. N. Engl. J. Med. 2009, 361, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Zeldovich, K.B.; Liu, P.; Renzette, N.; Foll, M.; Pham, S.T.; Venev, S.V.; Gallagher, G.R.; Bolon, D.N.; Kurt-Jones, E.A.; Jensen, J.D.; et al. Positive Selection Drives Preferred Segment Combinations during Influenza Virus Reassortment. Mol. Biol. Evol. 2015, 32, 1519–1532. [Google Scholar] [CrossRef] [PubMed]
- Villa, M.; Lässig, M. Fitness cost of reassortment in human influenza. PLoS Pathog. 2017, 13, e1006685. [Google Scholar] [CrossRef] [PubMed]
- Ward, M.J.; Lycett, S.J.; Avila, D.; Bollback, J.P.; Leigh Brown, A.J. Evolutionary interactions between haemagglutinin and neuraminidase in avian influenza. BMC Evol. Biol. 2013, 13, 222. [Google Scholar] [CrossRef] [PubMed]
- Koelle, K.; Cobey, S.; Grenfell, B.; Pascual, M. Epochal Evolution Shapes the Phylodynamics of Interpandemic Influenza A (H3N2) in Humans. Science 2006, 314, 1898–1903. [Google Scholar] [CrossRef] [PubMed]
- Taggi, L.; Colaiori, F.; Loreto, V.; Tria, F. Dynamical correlations in the escape strategy of Influenza A virus. EPL 2013, 101, 68003. [Google Scholar] [CrossRef]
- Tria, F.; Pompei, S.; Loreto, V. Dynamically correlated mutations drive human Influenza A evolution. Sci. Rep. 2013, 3, 2705. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K.; Nobusawa, E.; Nagy, A.; Nakajima, S. Accumulation of amino acid substitutions promotes irreversible structural changes in the hemagglutinin of human influenza AH3 virus during evolution. J. Virol. 2005, 79, 6472–6477. [Google Scholar] [CrossRef] [PubMed]
- Das, S.R.; Hensley, S.E.; David, A.; Schmidt, L.; Gibbs, J.S.; Puigbò, P.; Ince, W.L.; Bennink, J.R.; Yewdell, J.W. Fitness costs limit influenza A virus hemagglutinin glycosylation as an immune evasion strategy. Proc. Natl. Acad. Sci. USA 2011, 108, E1417–E1422. [Google Scholar] [CrossRef] [PubMed]
- Mitnaul, L.J.; Matrosovich, M.N.; Castrucci, M.R.; Tuzikov, A.B.; Bovin, N.V.; Kobasa, D.; Kawaoka, Y. Balanced hemagglutinin and neuraminidase activities are critical for efficient replication of influenza A virus. J. Virol. 2000, 74, 6015–6020. [Google Scholar] [CrossRef] [PubMed]
- Myers, J.L.; Wetzel, K.S.; Linderman, S.L.; Li, Y.; Sullivan, C.B.; Hensley, S.E. Compensatory hemagglutinin mutations alter antigenic properties of influenza viruses. J. Virol. 2013, 87, 11168–11172. [Google Scholar] [CrossRef] [PubMed]
- Underwood, P.A.; Skehel, J.J.; Wiley, D.C. Receptor-binding characteristics of monoclonal antibody-selected antigenic variants of influenza virus. J. Virol. 1987, 61, 206–208. [Google Scholar] [PubMed]
- Kosik, I.; Ince, W.L.; Gentles, L.E.; Oler, A.J.; Kosikova, M.; Angel, M.; Magadán, J.G.; Xie, H.; Brooke, C.B.; Yewdell, J.W. Influenza A virus hemagglutinin glycosylation compensates for antibody escape fitness costs. PLoS Pathog. 2018, 14, e1006796. [Google Scholar] [CrossRef]
- Hensley, S.E.; Das, S.R.; Gibbs, J.S.; Bailey, A.L.; Schmidt, L.M.; Bennink, J.R.; Yewdell, J.W. Influenza A virus hemagglutinin antibody escape promotes neuraminidase antigenic variation and drug resistance. PLoS ONE 2011, 6, e15190. [Google Scholar] [CrossRef] [PubMed]
- Weinreich, D.M.; Watson, R.A.; Chao, L.; Harrison, R. Perspective: Sign epistasis and genetic constraint on evolutionary trajectories. Evolution 2005, 59, 1165–1174. [Google Scholar] [CrossRef] [PubMed]
- Abed, Y.; Pizzorno, A.; Bouhy, X.; Boivin, G. Role of permissive neuraminidase mutations in influenza A/Brisbane/59/2007-like (H1N1) viruses. PLoS Pathog. 2011, 7, e1002431. [Google Scholar] [CrossRef] [PubMed]
- Duan, S.; Govorkova, E.A.; Bahl, J.; Zaraket, H.; Baranovich, T.; Seiler, P.; Prevost, K.; Webster, R.G.; Webby, R.J. Epistatic interactions between neuraminidase mutations facilitated the emergence of the oseltamivir-resistant H1N1 influenza viruses. Nat. Commun. 2014, 5, 5029. [Google Scholar] [CrossRef] [PubMed]
- Ginting, T.E.; Shinya, K.; Kyan, Y.; Makino, A.; Matsumoto, N.; Kaneda, S.; Kawaoka, Y. Amino acid changes in hemagglutinin contribute to the replication of oseltamivir-resistant H1N1 influenza viruses. J. Virol. 2012, 86, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Dong, G.; Peng, C.; Luo, J.; Wang, C.; Han, L.; Wu, B.; Ji, G.; He, H. Adamantane-resistant influenza A viruses in the world (1902-2013): Frequency and distribution of M2 gene mutations. PLoS ONE 2015, 10, e0119115. [Google Scholar] [CrossRef] [PubMed]
- Abed, Y.; Goyette, N.; Boivin, G. Generation and characterization of recombinant influenza A (H1N1) viruses harboring amantadine resistance mutations. Antimicrob. Agents Chemother. 2005, 49, 556–559. [Google Scholar] [CrossRef] [PubMed]
- Durrant, M.G.; Eggett, D.L.; Busath, D.D. Investigation of a recent rise of dual amantadine-resistance mutations in the influenza A M2 sequence. BMC Genet. 2015, 16, S3. [Google Scholar] [CrossRef] [PubMed]
- Łuksza, M.; Lässig, M. A predictive fitness model for influenza. Nature 2014, 507, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Morris, D.H.; Gostic, K.M.; Pompei, S.; Bedford, T.; Łuksza, M.; Neher, R.A.; Grenfell, B.T.; Lässig, M.; McCauley, J.W. Predictive Modeling of Influenza Shows the Promise of Applied Evolutionary Biology. Trends Microbiol. 2018, 26, 102–118. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyons, D.M.; Lauring, A.S. Mutation and Epistasis in Influenza Virus Evolution. Viruses 2018, 10, 407. https://doi.org/10.3390/v10080407
Lyons DM, Lauring AS. Mutation and Epistasis in Influenza Virus Evolution. Viruses. 2018; 10(8):407. https://doi.org/10.3390/v10080407
Chicago/Turabian StyleLyons, Daniel M., and Adam S. Lauring. 2018. "Mutation and Epistasis in Influenza Virus Evolution" Viruses 10, no. 8: 407. https://doi.org/10.3390/v10080407
APA StyleLyons, D. M., & Lauring, A. S. (2018). Mutation and Epistasis in Influenza Virus Evolution. Viruses, 10(8), 407. https://doi.org/10.3390/v10080407





