A New Model for the Dynamics of Hepatitis C Infection: Derivation, Analysis and Implications
Abstract
1. Introduction
- Globally, an estimated 71 million people were living with chronic HCV infection;
- An estimated 1.75 million new HCV infections occurred worldwide, while 399,000 people died from end-stage HCV infection and 843,000 were cured;
- 20% of HCV-infected persons (14 million) have been diagnosed, and of these, 7.4% (1.1 million) had started treatment;
- HCV infection affects all regions with the highest reported prevalence in the Eastern Mediterranean and European Regions.
2. A Review of Existing Models of HCV Infection
2.1. The Neumann Model
2.2. The First Dahari Model
2.3. The Second Dahari Model
2.4. Other Models
3. A New Model of HCV Infection
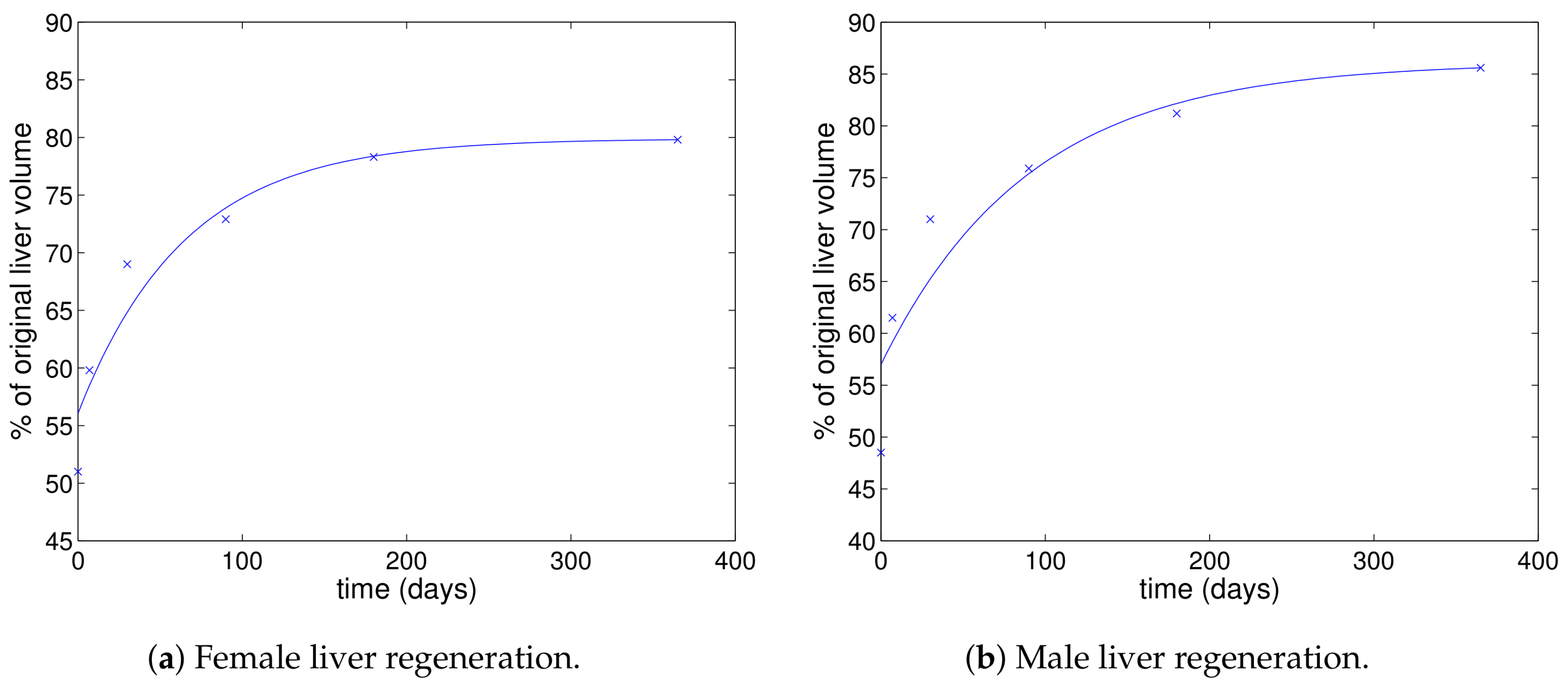
3.1. Cell Regeneration
3.2. Stem Cells
3.3. Infection
3.4. The Revised Model
3.5. Spontaneous Clearance
3.6. Non-Dimensionalisation
4. Validation of the New HCV Model
5. Analysis of the New HCV Model
5.1. Assumptions
5.2. Steady States ()
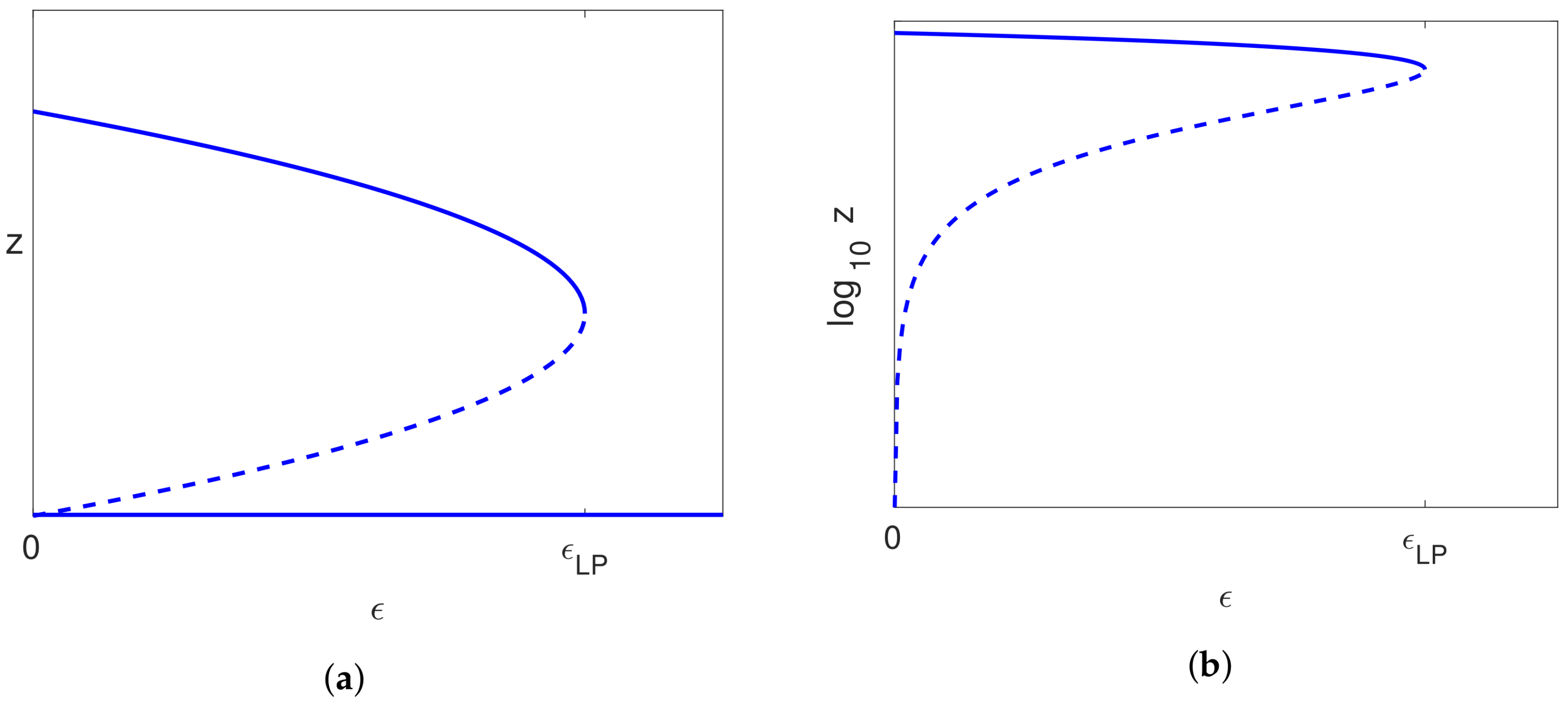
5.3. Bifurcations
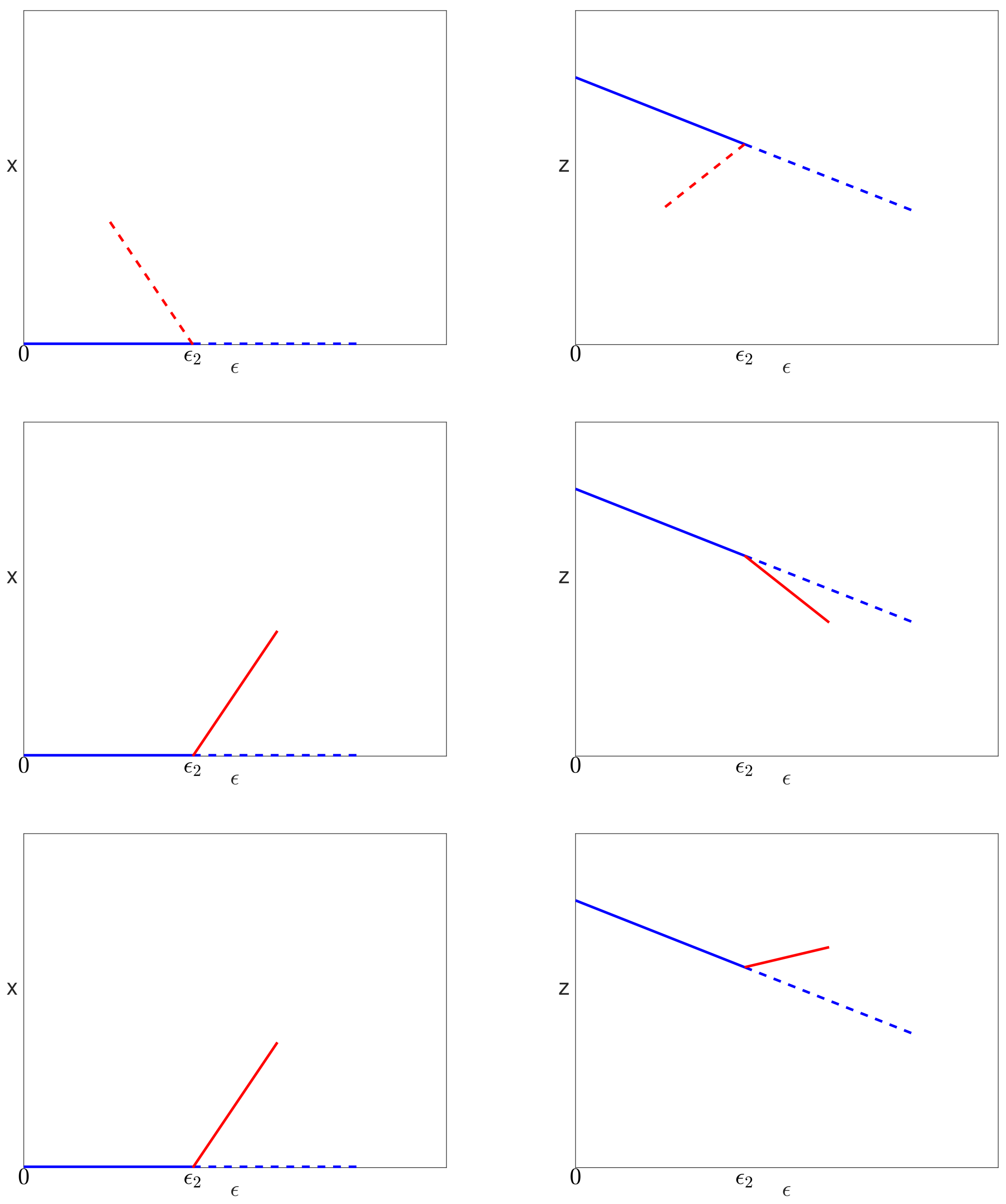
5.3.1. Bifurcation on the Uninfected Branch
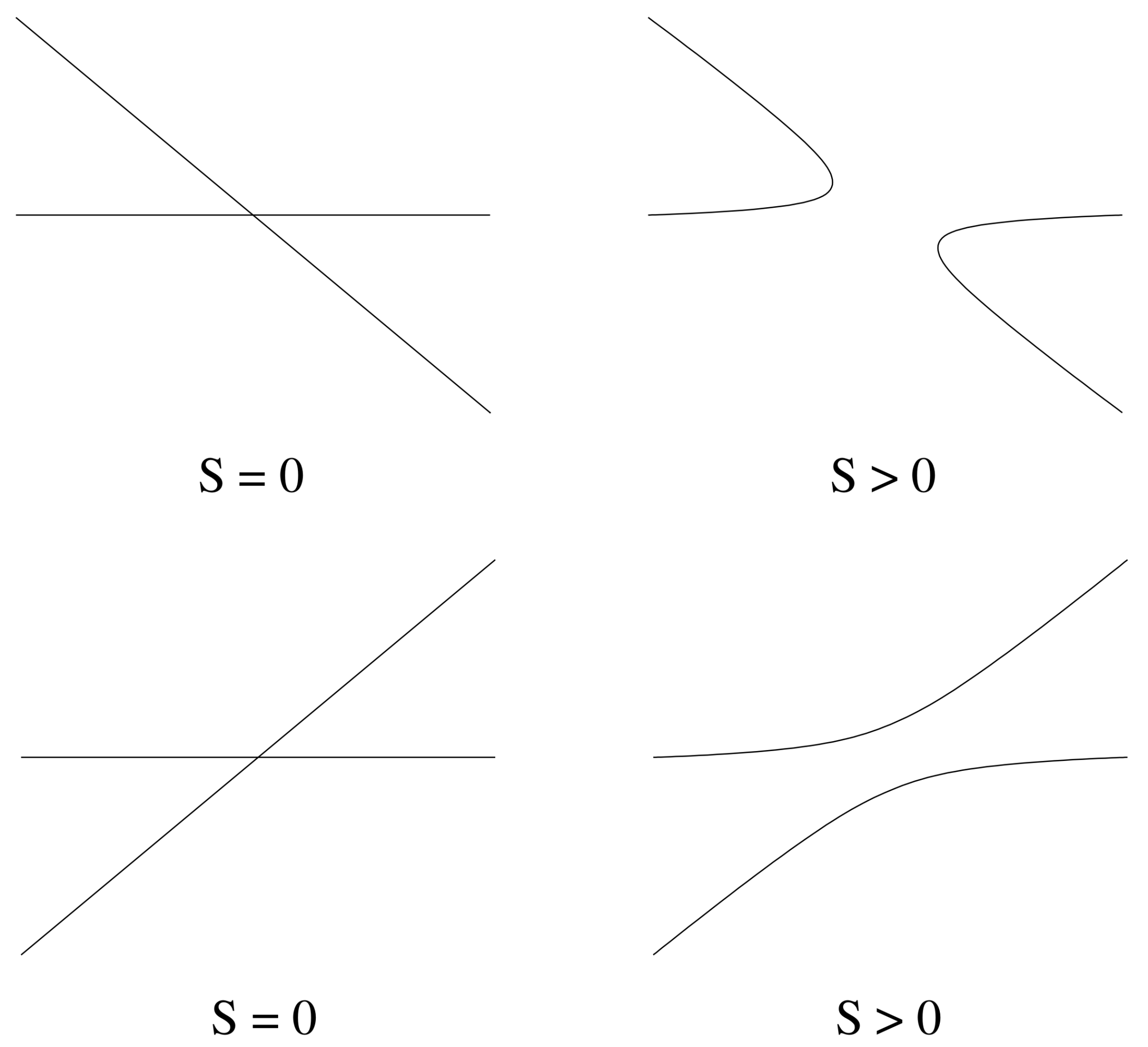
5.3.2. Bifurcation on the Pure Infection Branch
- if , then has a positive slope, and valid solutions exist locally only for ;
- if , then has a negative slope, and valid solutions exist locally only for .
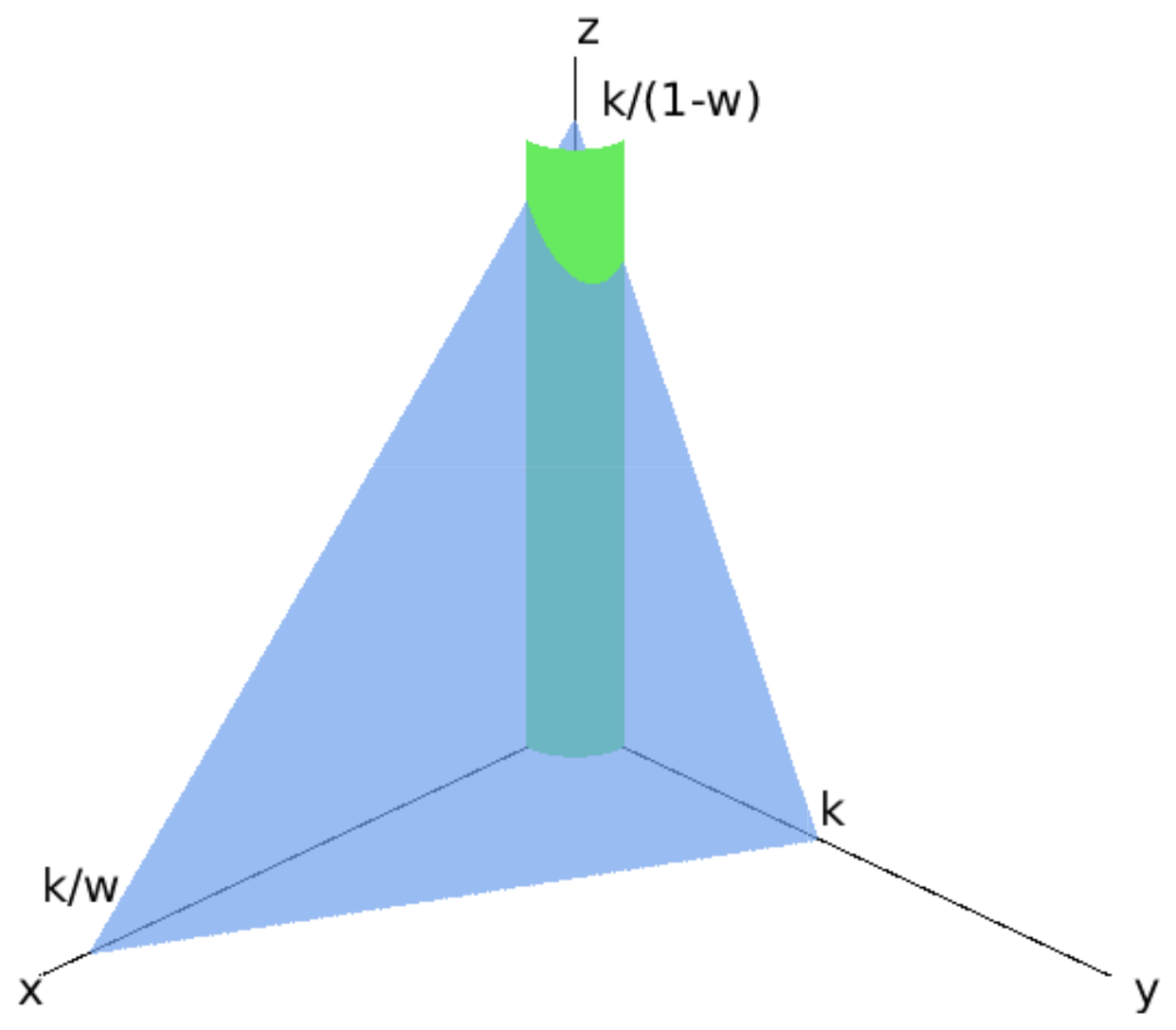
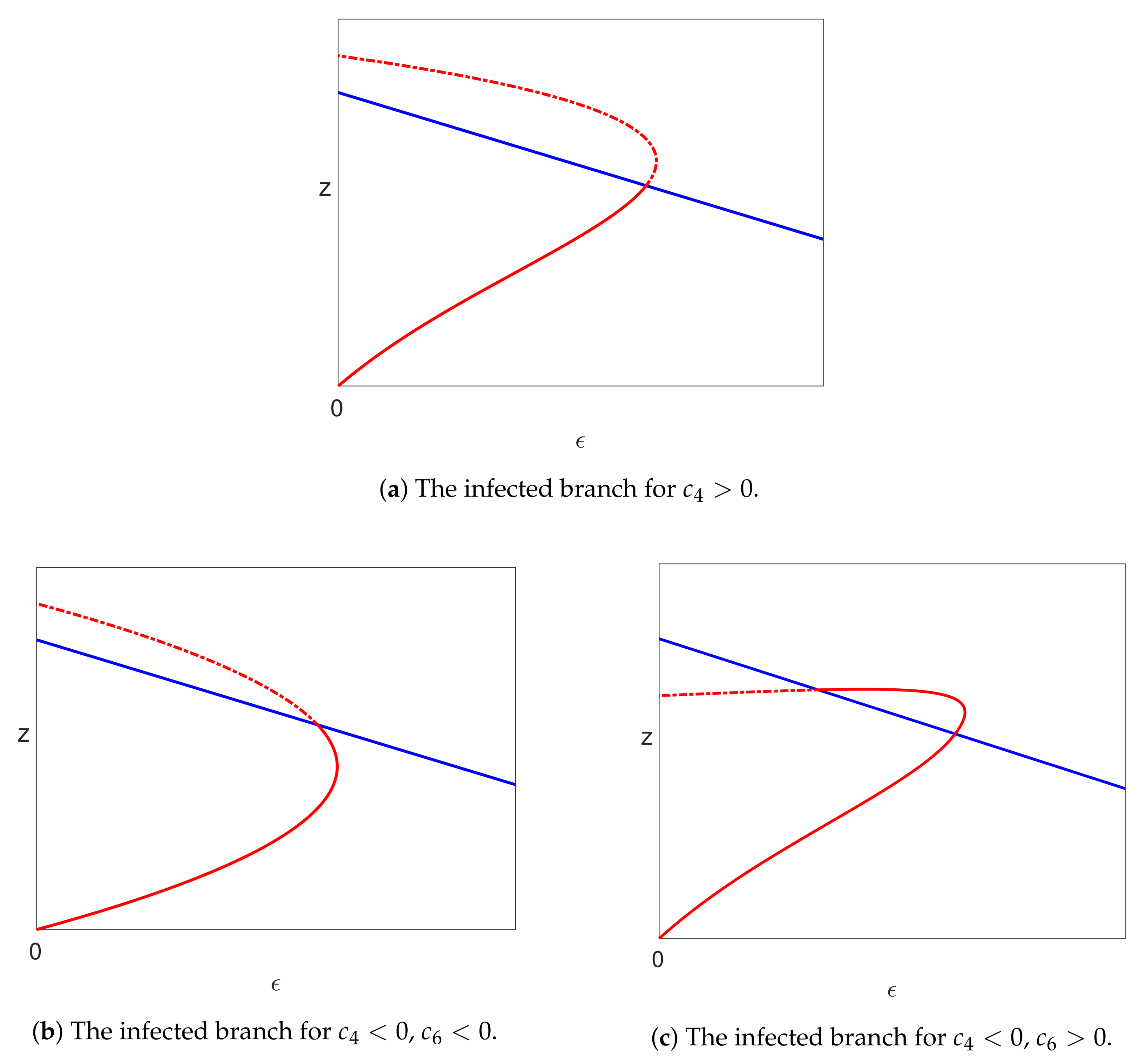
5.3.3. The Infected Steady State Branch ()
5.4. Steady States ()
5.4.1. Bifurcation on the Uninfected Branch
5.4.2. Bifurcation on the Pure Infection Branch
- if , then no limit points exist;
- if , then there are two limit points at .
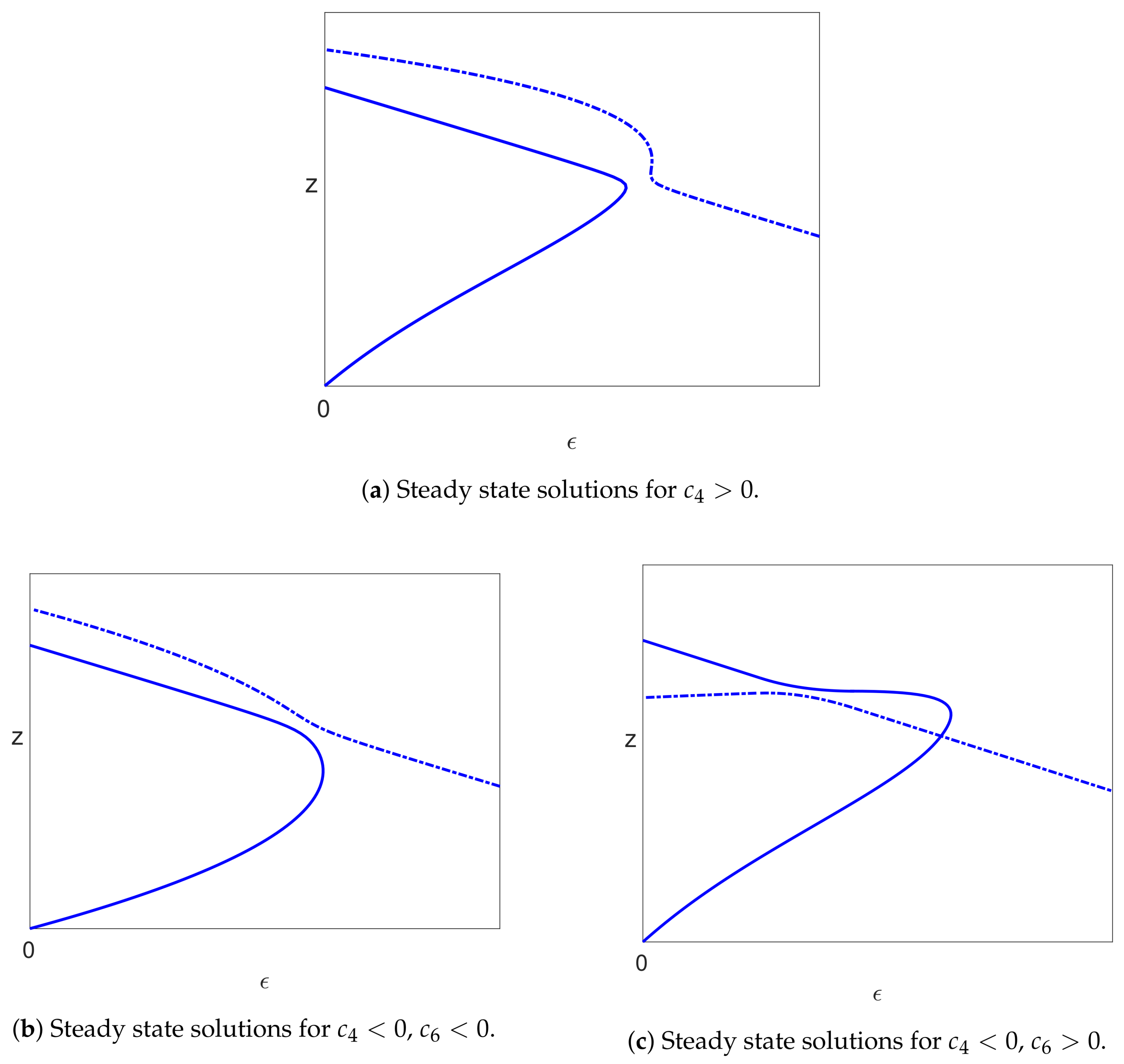
5.4.3. Infected Branch of Solutions
5.4.4. The Case of
6. Stability
7. Comparison with the Neumann/Dahari Models
- For the Neumann/Dahari models, treatment will only be effective once the treatment factor exceeds a critical value determined by the bifurcation point, regardless of the viral load when treatment commences. For our model, if the viral load is close to the infected steady state before treatment starts, then similarly, the treatment factor must exceed the critical value determined by the limit point for the treatment to be effective. However, if the infection is caught and treated in the early stages, while the viral load is still relatively low, then our model predicts that a lower drug dose, with a corresponding smaller value of the treatment parameter , will be effective.
- As mentioned previously, once treatment is stopped, the prediction of the Neumann/Dahari models is that the infection will take hold again unless the infected hepatocytes and virus have been completed eliminated during treatment. The prediction from our model, if the bifurcation point on the uninfected solution branch occurs at a negative value of (), is that the body will be able to eliminate a small amount of infected hepatocytes and virus cells without further treatment once their levels have been reduced sufficiently. On the other hand, if the bifurcation point on the uninfected branch occurs at a positive value of (), then our model predicts in this case that the infection will take hold again on cessation of treatment unless the infected hepatocytes and virus cells have been completely eliminated during treatment. However, our model also predicts that continuing with a low level of drug treatment, corresponding to a small value of , will stop the infection recurring in this case.
- The Neumann/Dahari models suggest that treatment will only be effective if the treatment parameter is greater than the critical value during the whole period of treatment, which is the way that patients are generally treated in practice. Our model suggests that the drug dose could be reduced as treatment progresses and that this will still be effective, provided that it is not reduced too far too quickly. If this is indeed the case, it could save some of the costs of treatment, and a lower drug dosage may also mean a reduction in side effects, which would benefit the patient.
8. Description of Observed Viral Load Profiles
8.1. Sustained Virologic Response
8.2. Relapse
8.3. Partial Virologic Response
8.4. Breakthrough
8.5. Null Response
8.6. Biphasic and Triphasic Decline
8.7. Initial Increase in Viral Load
8.8. Direct Acting Antiviral Agents
- (i)
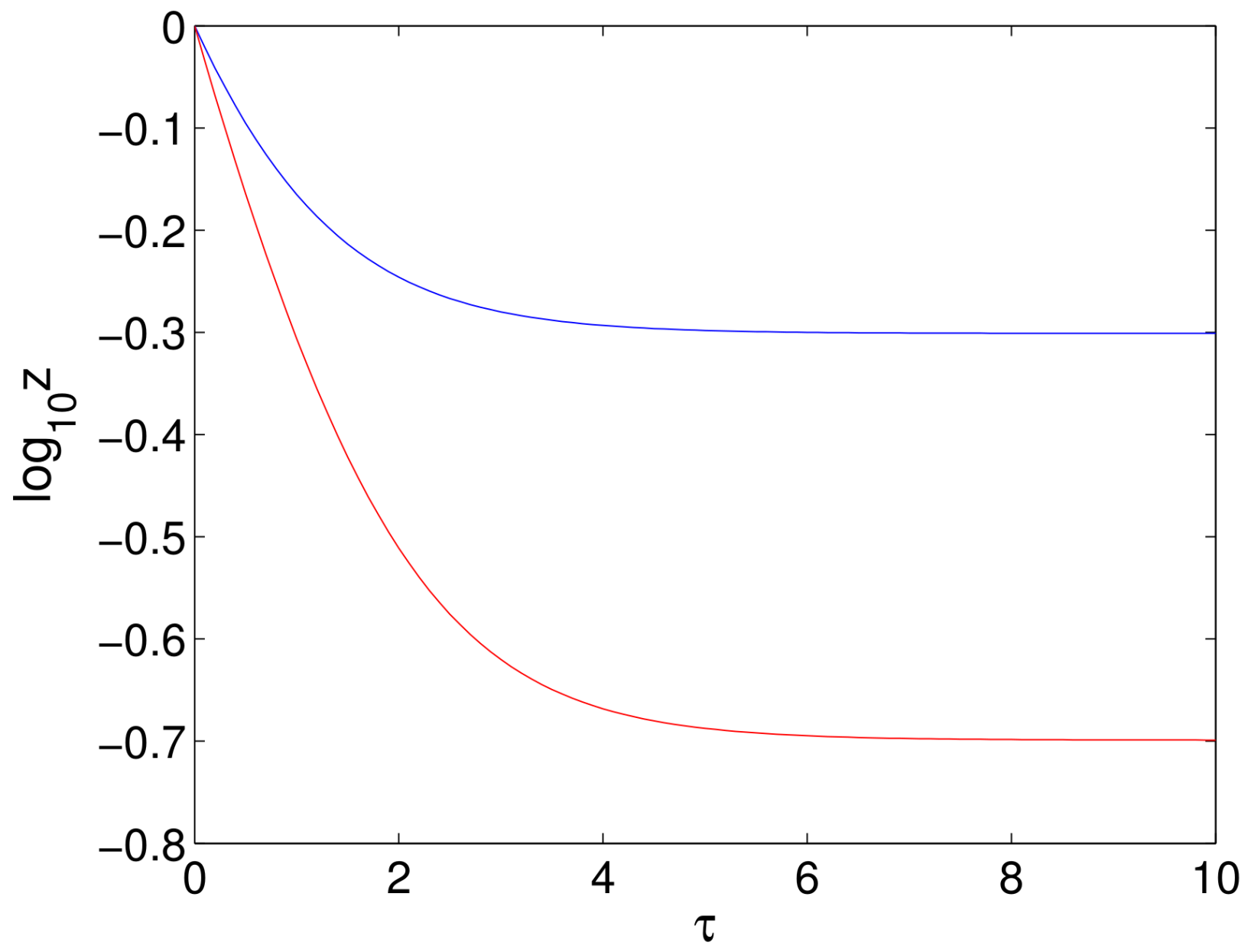
- It has been noted that the first phase decline when treating with DAAs is both longer and faster than when using IFN and RBV. Since the rate of the first phase decline is essentially given by the parameter C (or c for the original equations), it has been suggested that both and c should be increased in the models for treatment with DAAs [25]. However, we claim that an increase in alone is sufficient to produce a longer and faster first phase. To see this, we consider the decline in viral load during the first phase that is given in (77). For this solution, we find that the initial rate of decline is:since , and so, the initial slope increases as the treatment factor increases, with maximum slope only being achieved when (which corresponds to . Clearly, the steady state is also reduced as is increased. These two effects result in an increase in the length of the decline in the viral load together with a more rapid decline. This is illustrated in Figure 11.
- (ii)
- The second observation made for DAAs is that the second phase is also faster than that for treatment with IFN and RBV. We have seen in Section 8.6 that for our model, the rate of decay in the second phase is proportional to where is the solution of the characteristic equation (78) that is closest to zero. With our assumption that is constant, (78) becomes:Differentiating this equation with respect to and solving for gives:and evaluating at gives:for . The sign of the denominator is not clear. However, substituting into given by (81) gives:using (38) and the assumption that . The quadratic coefficient of in (81) is positive, and so, is only negative between the two roots and , which implies that:It follows from this that the denominator of (82) is positive, and so, . Hence, if is increased from , then the eigenvalue will decrease to first order, thereby increasing the rate of the second phase decline.
9. Data Fitting
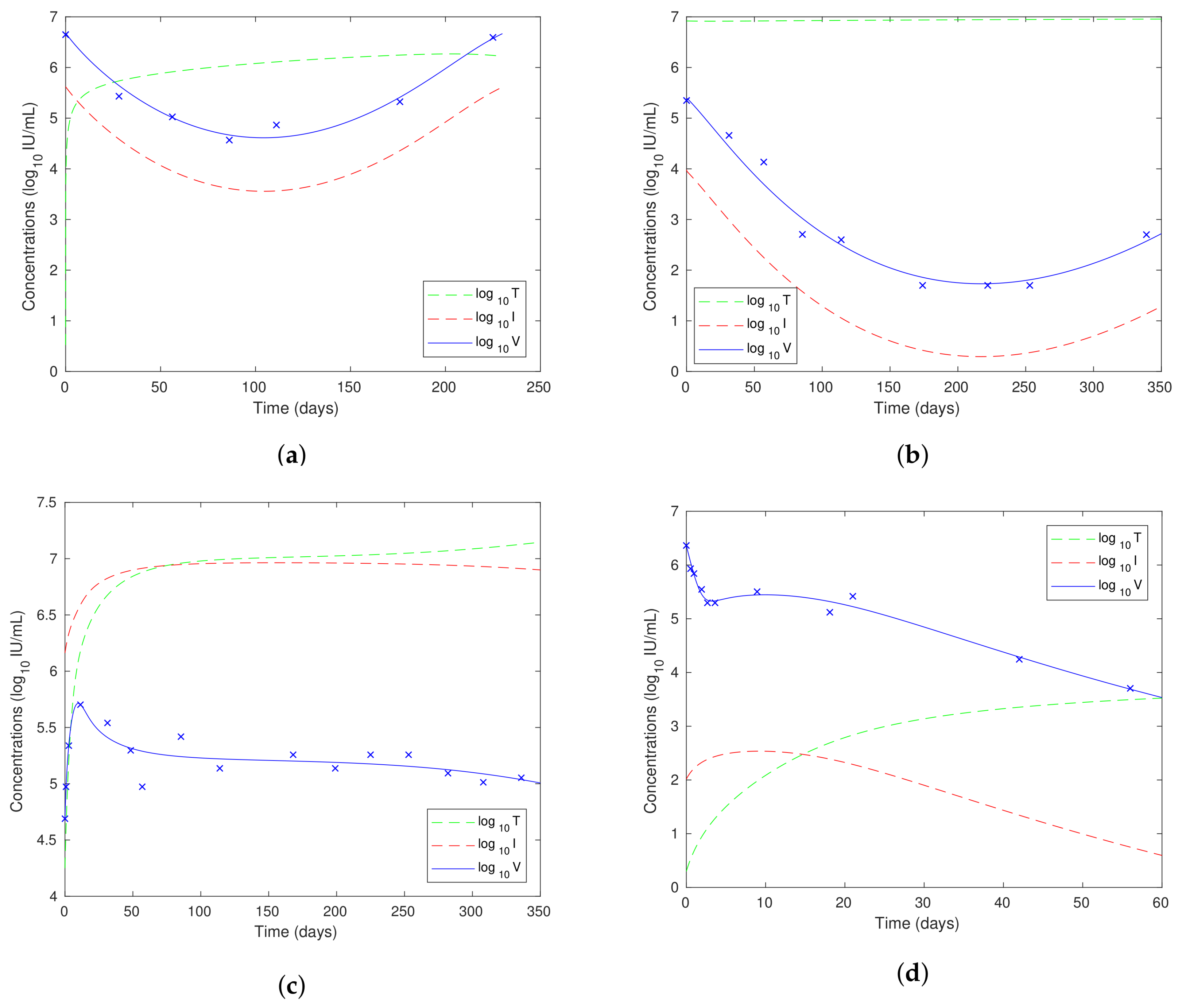
- In the PVR, breakthrough and triphasic cases, we have for all t, but in the null response case, is significantly higher than .
- The initial viral load is highest in the PVR case, and we predicted in Section 8.3 that PVR would be associated with a high initial viral load.
- In the null response case, it is interesting to observe that the fitted viral load V and infected hepatocyte concentration I both reduce towards zero, but very slowly. The start of the decline in these variables can be observed from around 300 days in Figure 12c. At 1000 days after the start of treatment, the predicted values are and .
- In Section 8.6, we stated that triphasic decline might be expected when the patient has been infected for a long time before treatment, which means that the viral load will be high while the healthy hepatocyte concentration will be very low. This is precisely the situation observed in Figure 12d.
- In Section 8.7, we showed that an initial increase in viral load at the start of treatment is possible, and we see this in the null response case.
- We saw in Section 3.1 that the regeneration rate for a healthy liver is day for females and day for males. This is effectively the parameter in our new model. The value of this parameter when fitted to data is a little lower than this for the PVR and breakthrough cases and is slightly higher in the null response and triphasic cases.
- The condition (33) for the solution to be bounded for all in terms of the parameters we are using here is given by:The term on the LHS for each of the fits to the data is given by: PVR: ; breakthrough: ; null response: ; triphasic: . All of these values are negative, which ensures that each of the solutions exists and is bounded for all time by Theorem 3.
10. Conclusions
- If the infection is caught and treated in the early stages, then our model predicts that a lower drug dose may be effective in eliminating the infection.
- If the viral load relapses on cessation of treatment, then continuing with a low level of drug treatment may keep the viral load low.
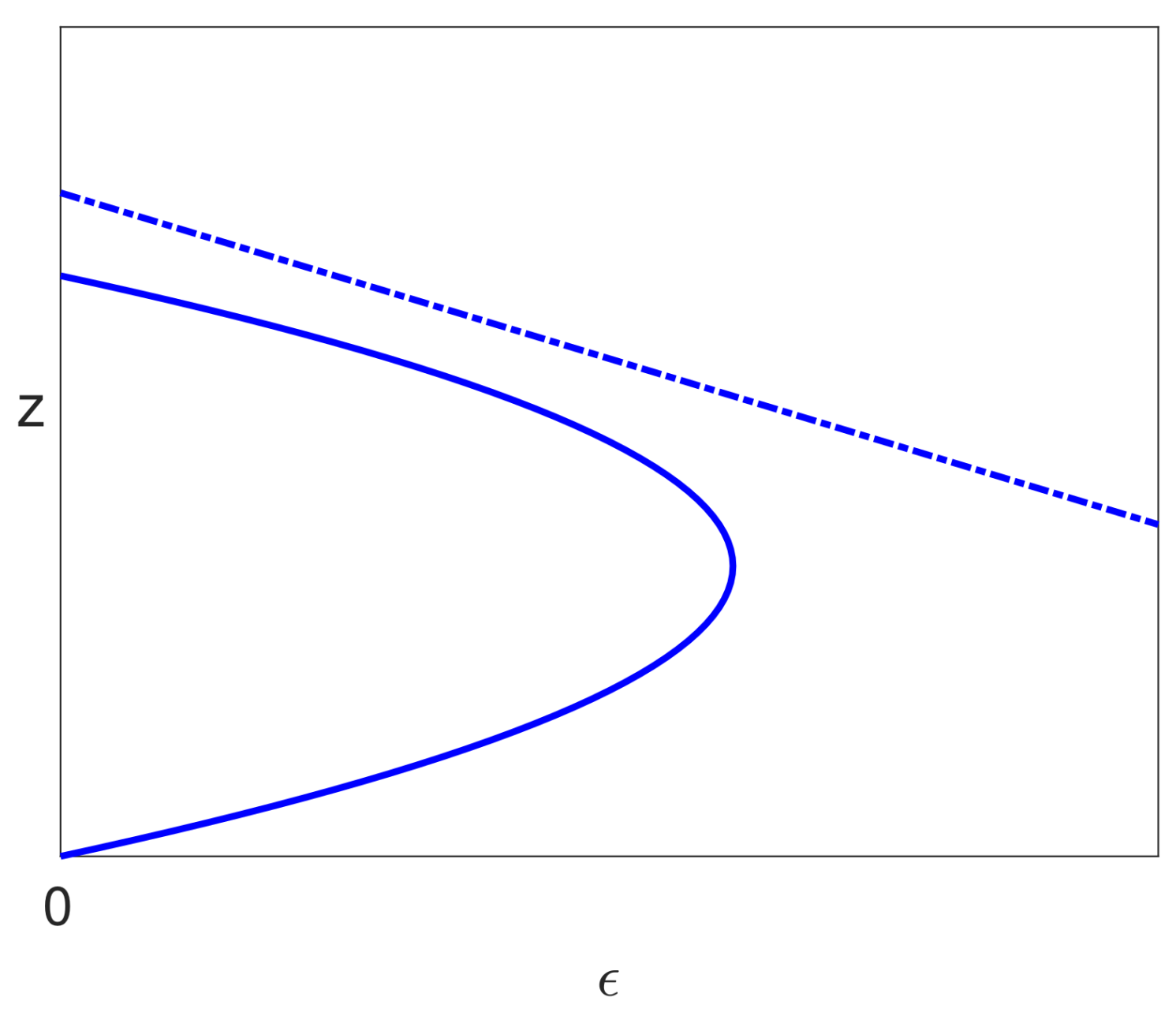
- The infected branch from the bifurcation on the uninfected branch to the limit point has a positive slope, and this suggests that the drug dose could be reduced as treatment progresses, which could save some of the costs of treatment and give a reduction in side effects for the patient.
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Global Hepatitis Report 2017; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Neumann, A.U.; Lam, N.P.; Dahari, H.; Gretch, D.R.; Wiley, T.E.; Layden, T.J.; Perelson, A.S. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-α therapy. Science 1998, 282, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Lo, A.; Ribeiro, R.M.; Perelson, A.S. Modelling hepatitis C virus dynamics: Liver regeneration and critical drug efficacy. J. Theor. Biol. 2007, 247, 371–381. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Ribeiro, R.M.; Perelson, A.S. Triphasic decline of hepatitis C virus RNA during antiviral therapy. Hepatology 2007, 46, 16–21. [Google Scholar] [CrossRef] [PubMed]
- Snoeck, E.; Chanu, P.; Lavielle, M.; Jacqmin, P.; Jonsson, E.N.; Jorga, K.; Goggin, T.; Grippo, J.; Jumbe, N.L.; Frey, N. A comprehensive hepatitis C viral kinetic model explaining cure. Clin. Pharm. Therapeut. 2010, 87, 706–713. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, E.; Lee, J.H.; Marinos, G.; Modi, M.; Zeuzem, S. Effect of ribavirin on hepatitis C viral kinetics in patients treated with pegylated interferon. Hepatology 2003, 37, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Neumann, A.U. Global stability and periodic solution of the viral dynamics. J. Math. Anal. Appl. 2007, 329, 281–297. [Google Scholar] [CrossRef]
- Dahari, H.; Major, M.; Zhang, X.; Mihalik, K.; Rice, C.M.; Perelson, A.S.; Feinstone, S.M.; Neumann, A.U. Mathematical modeling of primary hepatitis C infection: Noncytolytic clearance and early blockage of virion production. Gastroenterology 2005, 128, 1056–1066. [Google Scholar] [CrossRef] [PubMed]
- Reluga, T.C.; Dahari, H.; Perelson, A.S. Analysis of hepatitis C virus infection models with hepatocyte homeostasis. SIAM J. Appl. Math. 2009, 69, 999–1023. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Itoh, T.; Tanimizu, N.; Miyajima, A. Liver stem/progenitor cells: Their characteristics and regulatory mechanisms. J. Biochem. 2011, 149, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Marshall, A.; Rushbrook, S.; Davies, S.E.; Morris, L.S.; Scott, I.S.; Vowler, S.L.; Coleman, N.; Alexander, G. Relation between hepatocyte G1 arrest, impaired hepatic regeneration, and fibrosis in chronic hepatitis C virus infection. Gastroenterology 2005, 128, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Pomfret, E.A.; Pomposelli, J.J.; Gordon, F.D.; Erbay, N.; Price, L.L.; Lewis, W.D.; Jenkins, R.L. Liver regeneration and surgical outcome in donors of right lobe liver grafts. Transplantation 2003, 76, 5–10. [Google Scholar] [CrossRef] [PubMed]
- Darwiche, H.; Petersen, B.E. Biology of the adult hepatic progenitor cell: “Ghosts in the machine”. Prog. Mol. Biol. Transl. Sci. 2010, 97, 229–249. [Google Scholar] [PubMed]
- Katoonizadeh, A.; Nevens, F.; Verslype, C.; Pirenne, J.; Roskams, T. Liver regeneration in acute severe liver impairment: A clinicopathological correlation study. Liver Int. 2006, 26, 1225–1233. [Google Scholar] [CrossRef] [PubMed]
- DebRoy, S.; Bolkerzand, B.M.; Martcheva, M. Bistability and long-term cure in a within-host model of hepatitis C. J. Biol. Sys. 2011, 19, 533–550. [Google Scholar] [CrossRef]
- Turner, R.; Lozoya, O.; Wang, Y.; Cardinale, V.; Gaudio, E.; Alpini, G.; Mendel, G.; Wauthier, E.; Barbier, C.; Alvaro, D.; et al. Human hepatic stem cell and maturational liver lineage biology. Hepatology 2011, 53, 1035–1045. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.M.; Banks, H.T.; Davidian, M.; Kwon, H.D.; Tran, H.T.; Wynne, S.N.; Rosenberg, E.S. HIV dynamics: Modeling, data analysis, and optimal treatment protocols. J. Comp. Appl. Math. 2005, 184, 10–49. [Google Scholar] [CrossRef]
- Hepatitis C Fact Sheet. World Health Organization, 2017. Available online: http://www.who.int/mediacentre/factsheets/fs164/en/ (accessed on 11 April 2018).
- Rong, L.; Perelson, A.S. Treatment of hepatitis C virus infection with interferon and small molecule direct antivirals: Viral kinetics and modeling. Crit. Rev. Immunol. 2010, 30, 131–148. [Google Scholar] [CrossRef] [PubMed]
- Grimshaw, R. Nonlinear Ordinary Differential Equations; Blackwell: Oxford, UK, 1990. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Hsu, C.S.; Hsu, S.J.; Chen, H.C.; Tseng, T.C.; Liu, C.H.; Niu, W.F.; Jeng, J.; Liu, C.J.; Lai, M.Y.; Chen, P.J.; et al. Associate of IL28B gene variations with mathematical modeling of viral kinetics in chronic hepatitis C patients with IFN plus ribavirin therapy. Proc. Natl. Acad. Sci. USA 2011, 108, 3719–3724. [Google Scholar] [CrossRef] [PubMed]
- Guedj, J.; Dahari, H.; Perelson, A.S. Understanding the nature of early HCV RNA blips and the use of mathematical modeling of viral kinetics during IFN-based therapy. Proc. Natl. Acad. Sci. USA 2011, 108, E302. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Perelson, A.S. Mathematical analysis of multiscale models for hepatitis C virus dynamics under therapy with direct-acting antiviral agents. Math. Biosci. 2013, 245, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Guedj, J.; Perelson, A.S.; Layden, T.J. Hepatitis C viral kinetics in the era of direct acting antiviral agents and IL28B. Curr. Hepat. Rep. 2011, 10, 214–227. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Guedj, J.; Dahari, H.; Coffield, D.J., Jr.; Levi, M.; Smith, P.; Perelson, A.S. Analysis of hepatitis C virus decline during treatment with the protease inhibitor danoprevir using a multiscale model. PLOS Comp. Biol. 2013, 9, e1002959. [Google Scholar] [CrossRef] [PubMed]
- TenCate, V.; Sainz, B., Jr.; Cotler, S.J.; Uprichard, S.L. Potential treatment options and future research to increase hepatitis C virus treatment response rate. Hepat. Med. 2010, 2, 125–145. [Google Scholar]
- Arthur, J.G.; Tran, H.T.; Aston, P.J. Feasibility of parameter estimation in hepatitis C viral dynamics models. J. Inverse Ill-Posed Probl. 2017, 25, 69–80. [Google Scholar] [CrossRef]

| PVR | Breakthrough | Null Response | Triphasic | |
|---|---|---|---|---|
| s (day) | ||||
| (IU/ml/day) | ||||
| (day) | ||||
| R | ||||
| D | ||||
| (ml/IU/day) | ||||
| (day) | ||||
| c (day) | ||||
| (IU/ml) | ||||
| (IU/ml) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aston, P.J. A New Model for the Dynamics of Hepatitis C Infection: Derivation, Analysis and Implications. Viruses 2018, 10, 195. https://doi.org/10.3390/v10040195
Aston PJ. A New Model for the Dynamics of Hepatitis C Infection: Derivation, Analysis and Implications. Viruses. 2018; 10(4):195. https://doi.org/10.3390/v10040195
Chicago/Turabian StyleAston, Philip J. 2018. "A New Model for the Dynamics of Hepatitis C Infection: Derivation, Analysis and Implications" Viruses 10, no. 4: 195. https://doi.org/10.3390/v10040195
APA StyleAston, P. J. (2018). A New Model for the Dynamics of Hepatitis C Infection: Derivation, Analysis and Implications. Viruses, 10(4), 195. https://doi.org/10.3390/v10040195




