Quantitative Analysis of Hepatitis C NS5A Viral Protein Dynamics on the ER Surface
Abstract
1. Introduction
2. Materials and Methods
- Geometric setup: We use previously published confocal microscopic microscopy z-stack data [5] of cells labeled with ER markers which allow for reconstructions of realistic ER surfaces. These fine level data provide the geometric constraints for NS5A movement.
- A model and corresponding simulations: Our previous model of NS5A dynamics [35] has not been adapted to biological data so far. In this study, we perform simulations using an extended version of the model and fit the simulation parameters in order to match the experimental data.
2.1. FRAP Experiments—Basics
2.2. Expermimental Data and Cell types
2.3. NS5A Movement Properties
2.4. Modeling FRAP Experiments
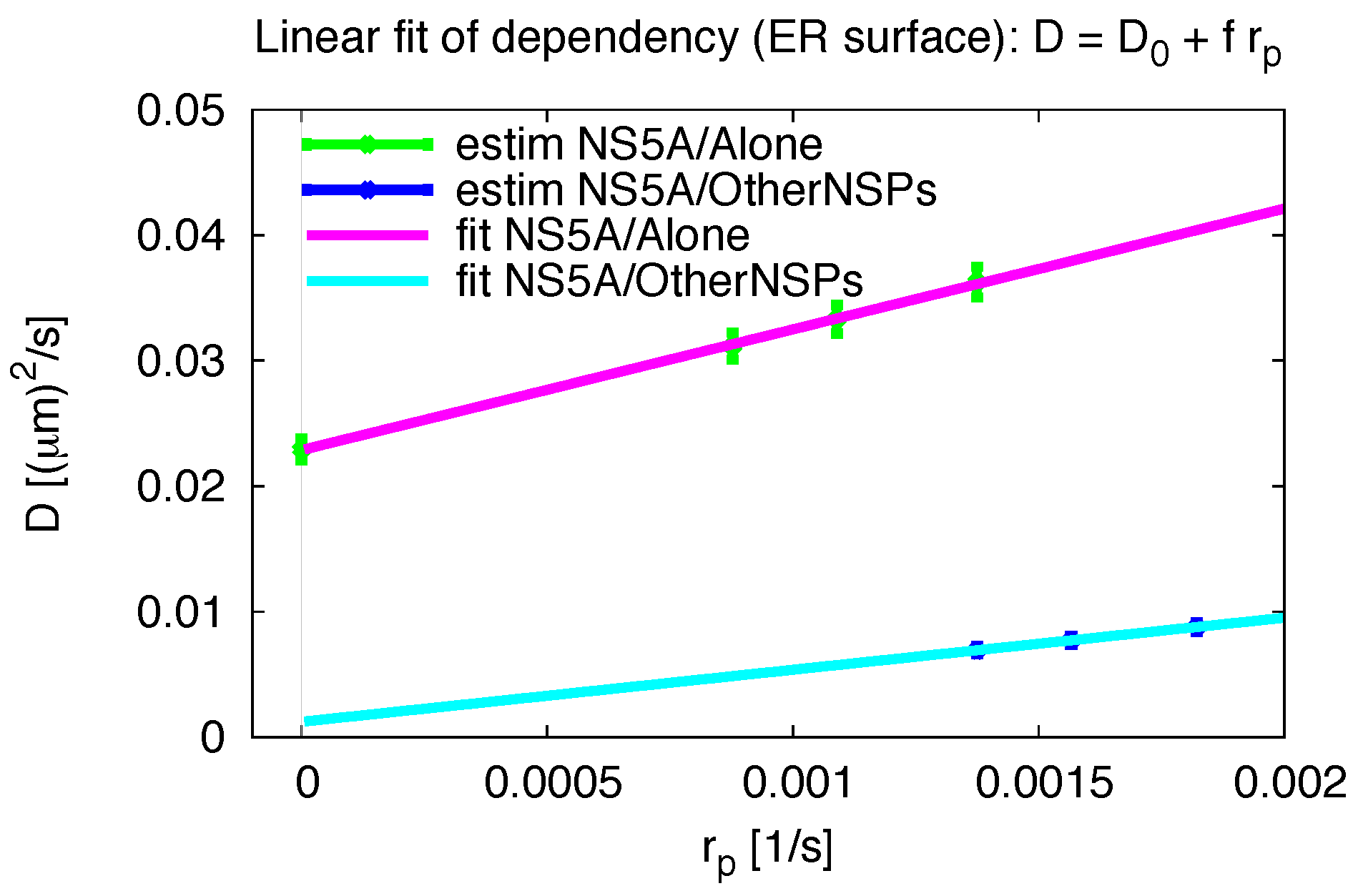
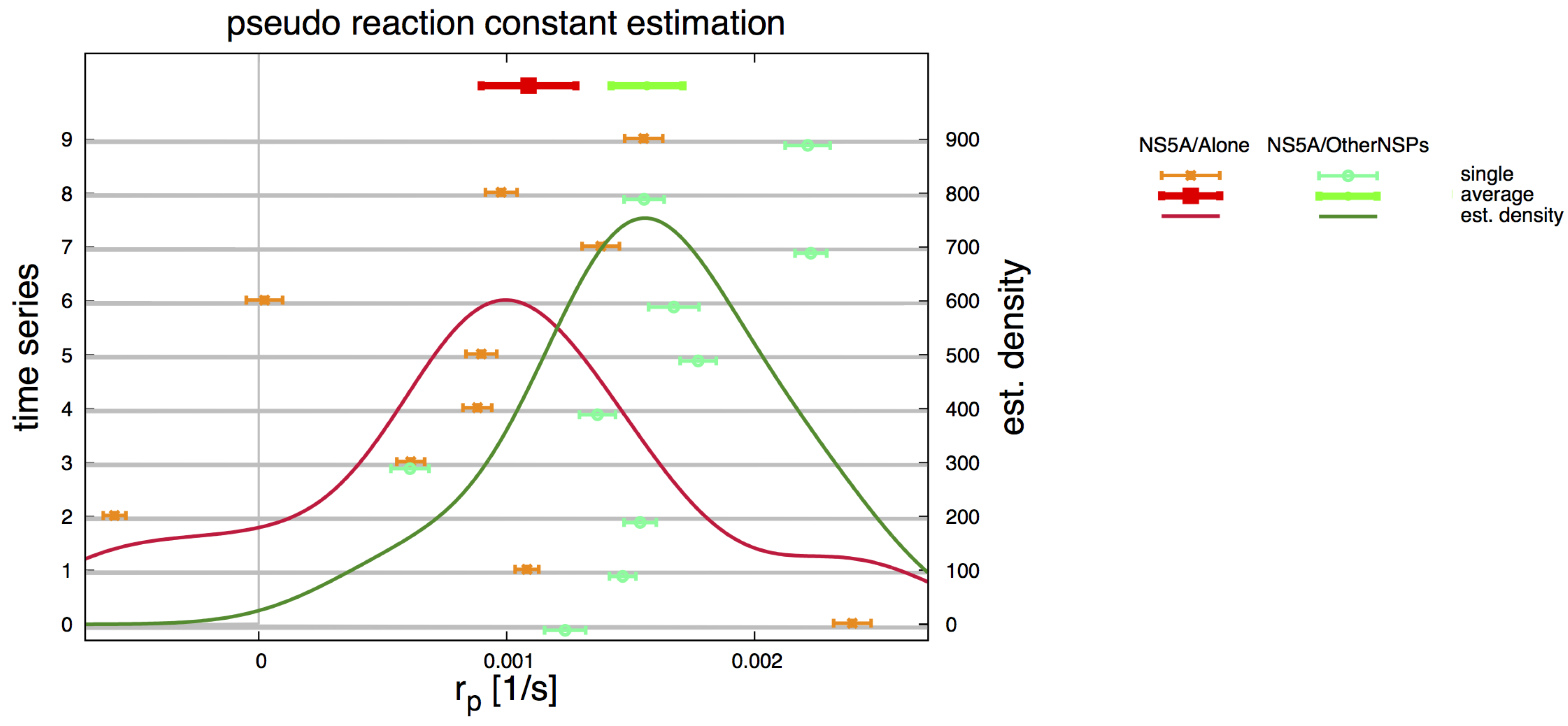
2.5. Pseudo Reaction Constant Fit
2.6. ER Geometry Reconstruction
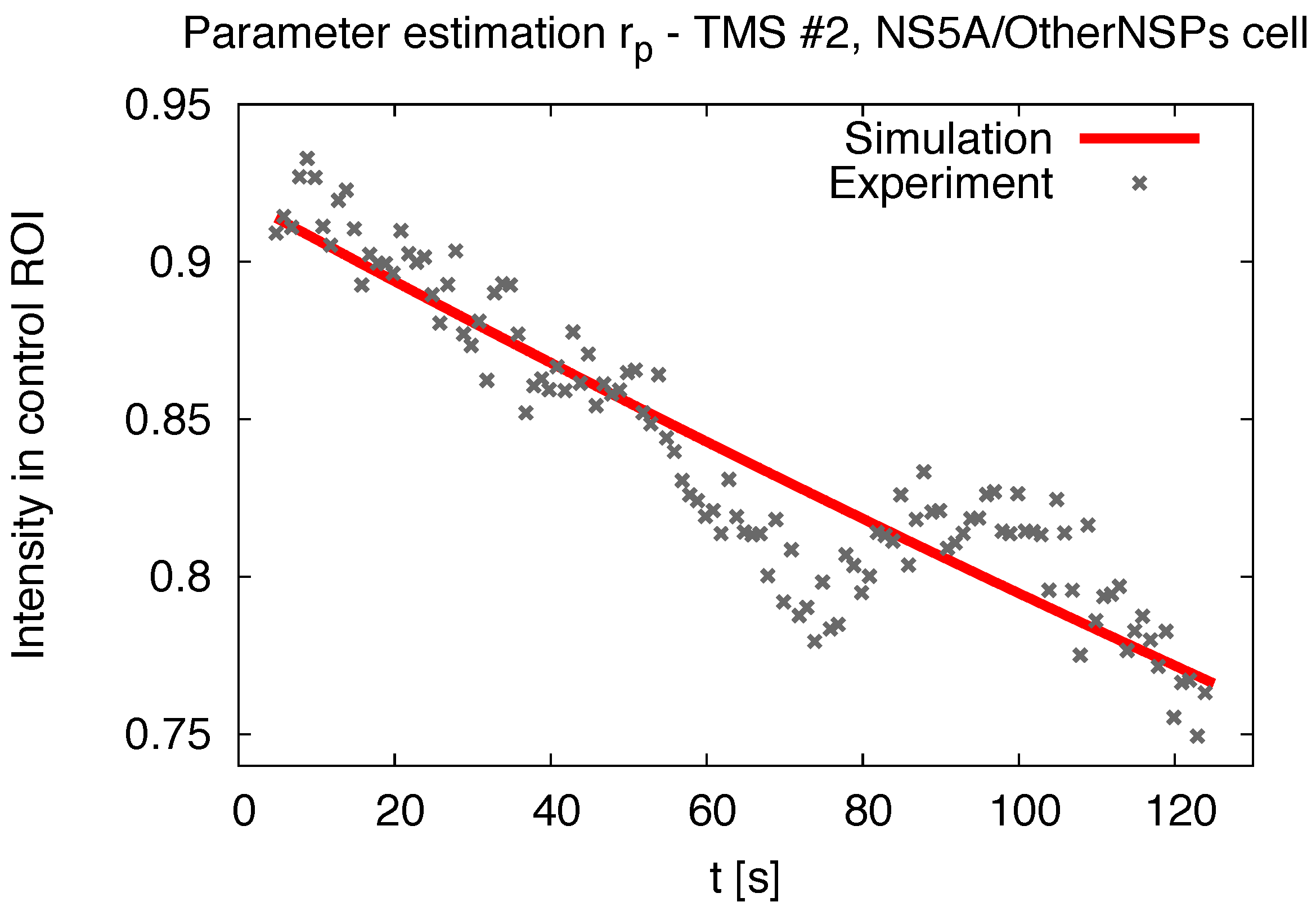
2.7. Comparing Experiment and Simulation
3. Results
3.1. Realistic Simulation of FRAP Experiments
3.2. Estimation of the NS5A Diffusion Constant
3.3. Influence of Geometry and Time Series
3.4. Refinement Stability
3.5. Influence of the Measurement Process
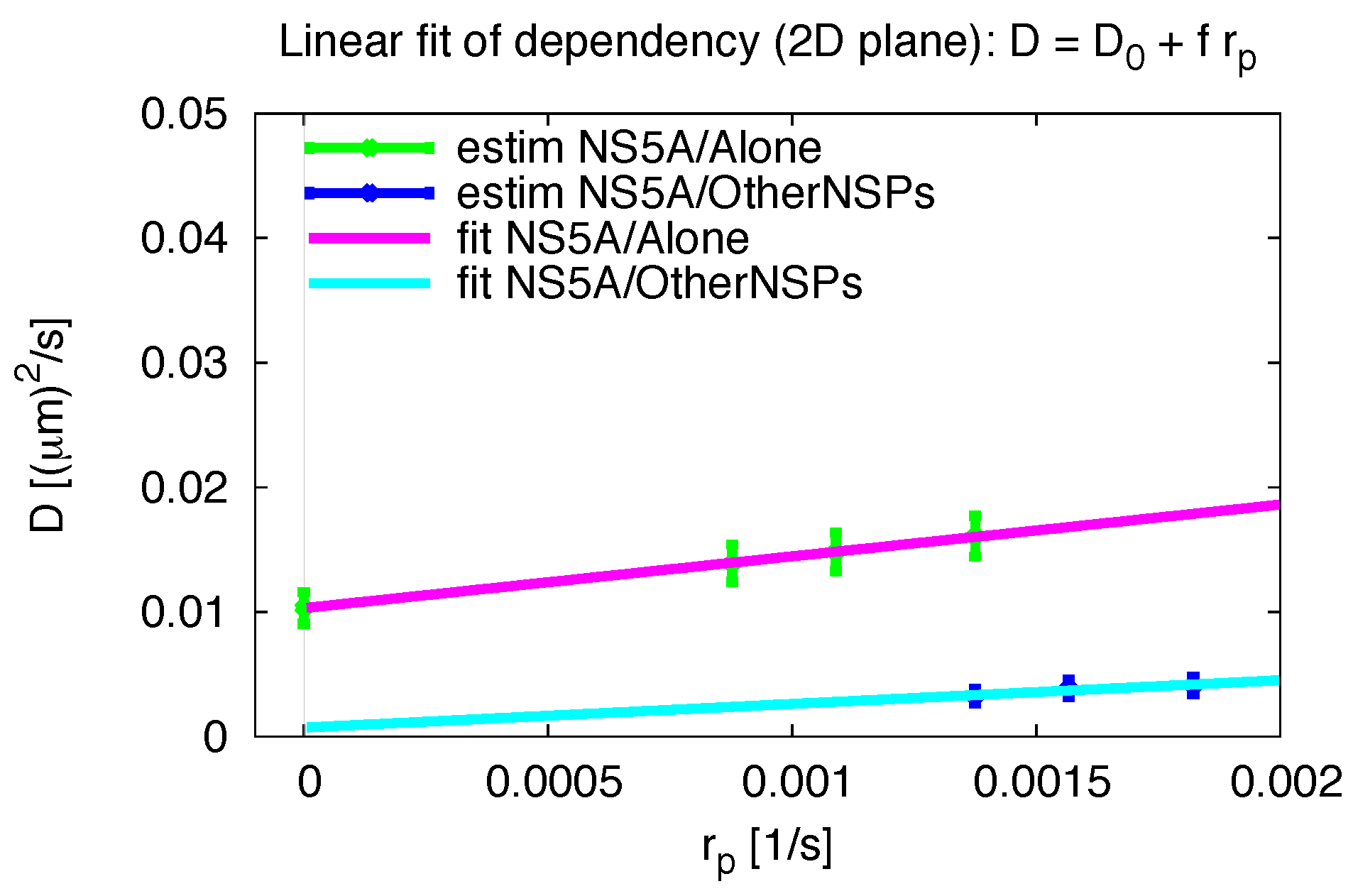
3.6. Comparative 2D Simulations
3.7. Final Averaged Results
4. Discussion
4.1. Interpretation of the Diffusion Constant Values
4.2. The Context of Spatial HCV Models
4.3. Related Work
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FRAP | Fluorescence recovery after photobleaching |
| FLIP | Fluorescence loss in photobleaching |
| ROI | region of interest |
| HCV | Hepatitis C virus |
| vRNA | viral RNA |
| NSP | non structural viral protein |
| NS5A | HCV non structural protein number 5 |
| SP | structural protein |
| DMV | Double membrane vesicle |
| TMS | time series |
| ER | Endoplasmatic Reticulum |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| sPDE | surface Partial Differential Equation |
| FV | Finite Volumes |
| MG | Multi Grid |
| GMG | Geometric Multi Grid |
| UG4 | Unstructured Grids version 4 [50,51] |
| NeuRA2 | Neuron reconstruction algorithm, version 2.3 [35,68] |
| geo(m) | geometry |
| psr | pseudo reaction |
Appendix A. Supplemental Movies, Short Description
Appendix A.1. S1 Video: Movie of FRAP Simulation at ER Geometry I
Appendix A.2. S2 Video: Movie of FRAP Simulation at ER Geometry IV
Appendix A.3. S3 Video: Movie of Classical FRAP Simulation at 2D Continuum Plane
Appendix B. Realistic Reconstructed ER Geometries—Further Details
Appendix C. Simple Planar 2D Geometry and Simulations—Details
Appendix D. Neglecting the Measurement Process Induced Intensity Reduction
| Geo | L | DoF | DoF | DoF | Faces |
|---|---|---|---|---|---|
| 0 | 815,111 | 794,128 | 20,983 | 1,636,803 | |
| 1 | 3,270,924 | 3,187,566 | 83,358 | 6,547,212 | |
| 2 | 13,092,959 | 12,761,035 | 331,924 | 26,188,848 | |
| 0 | 1,212,622 | 1,174,204 | 38,418 | 2,430,181 | |
| 1 | 4,861,079 | 4,708,431 | 152,648 | 9,720,724 | |
| 2 | 19,448,536 | 18,840,730 | 607,806 | 38,882,896 | |
| 0 | 170,209 | 140,022 | 30,187 | 340,108 | |
| 1 | 680,786 | 560,740 | 120,046 | 1,360,432 | |
| 2 | 2,722,264 | 2,243,664 | 478,600 | 5,441,728 | |
| 0 | 601,706 | 591,336 | 10,370 | 1,208,661 | |
| 1 | 2,414,802 | 2,373,711 | 41,091 | 4,834,644 | |
| 2 | 9,666,977 | 9,503,511 | 163,466 | 19,338,576 | |
| 0 | 728,636 | 699,338 | 29,298 | 1,463,597 | |
| 1 | 2,924,907 | 2,808,345 | 116,562 | 5,854,388 | |
| 2 | 11,708,240 | 11,243,894 | 464,346 | 23,417,552 |
| L | DoF | DoF | DoF | faces |
|---|---|---|---|---|
| 0 | 37 | 24 | 13 | 36 |
| 1 | 133 | 96 | 37 | 144 |
| 2 | 505 | 384 | 121 | 576 |
| 3 | 1,969 | 1,536 | 433 | 2,304 |
| 4 | 7,777 | 6,144 | 1,633 | 9,216 |
| 5 | 30,913 | 24,576 | 6,337 | 36,864 |
| 6 | 123,265 | 98,304 | 24,961 | 147,456 |
| 7 | 492,289 | 393,216 | 99,073 | 589,824 |
| 8 | 1,967,617 | 1,572,864 | 394,753 | 2,359,296 |
Appendix E. Refinement Stability
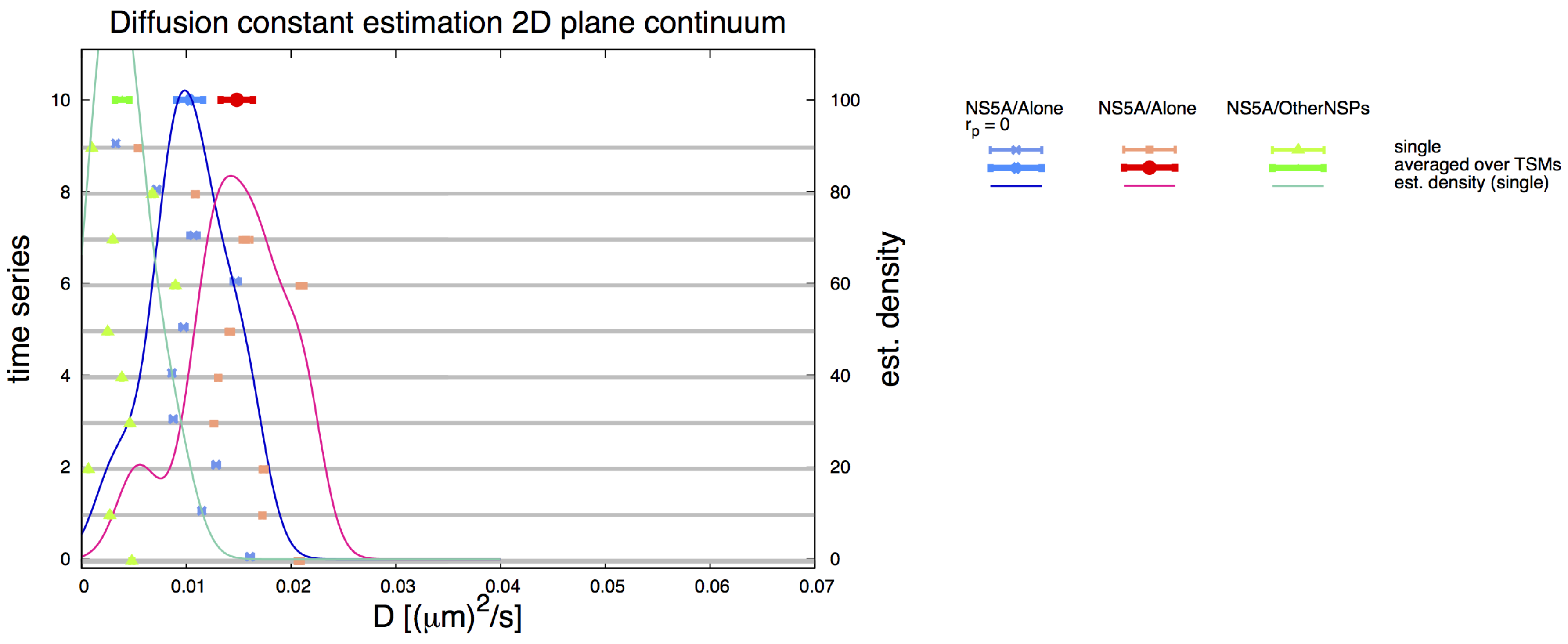
| Geoms | ||
|---|---|---|
| , NS5A/Alone cells | ||
| plane 2D | 0.010328 | 0.001274 |
| ER surface | 0.022915 | 0.000887 |
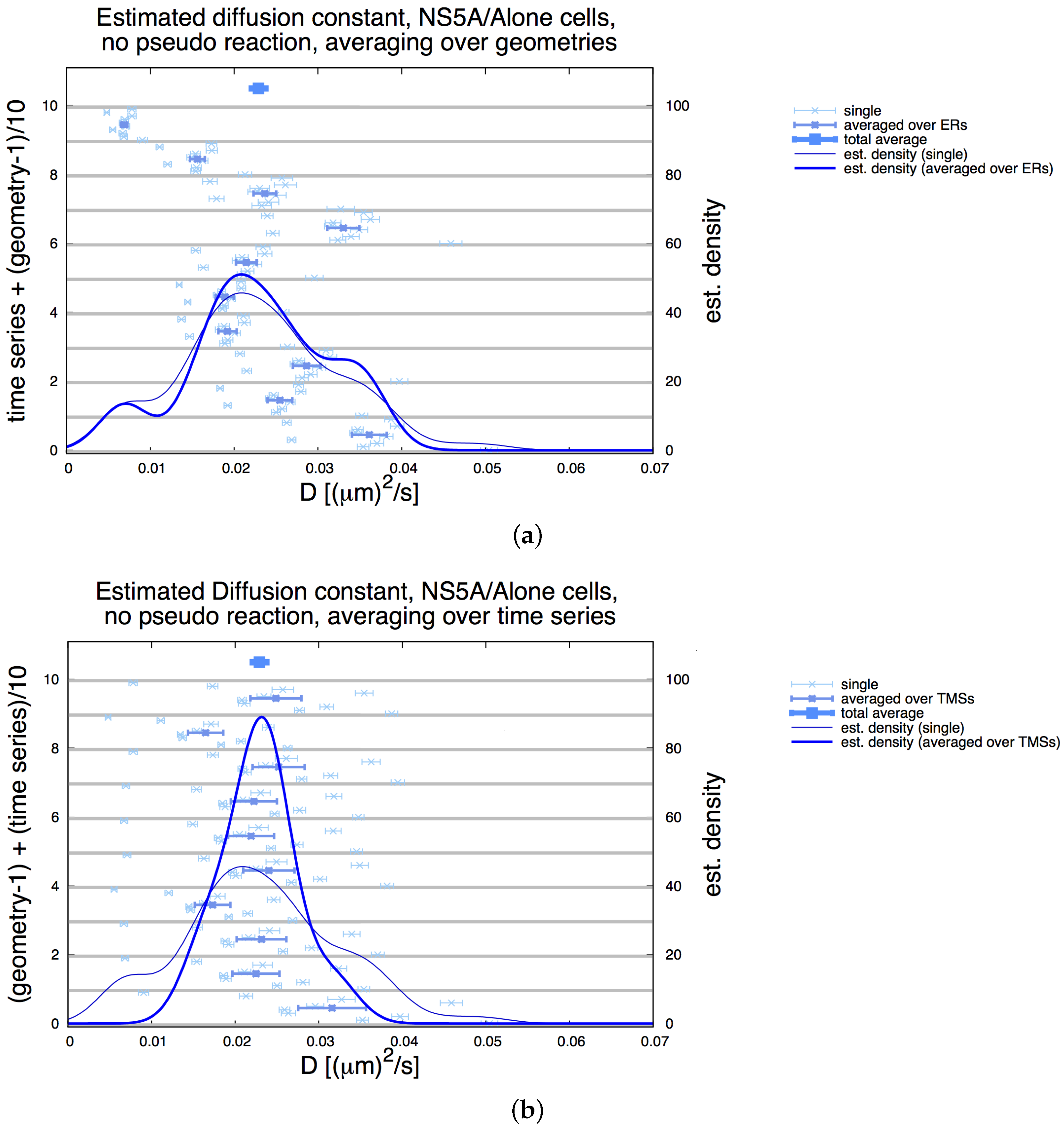
| Geometries | R | C | ||
|---|---|---|---|---|
| NS5A/Alone Cells, | ||||
| 2D planar | 5 | 0.012133 | 0.001415 | — |
| 6 | 0.011093 | 0.001334 | 9.378 | |
| 7 | 0.010582 | 0.001294 | 4.832 | |
| 8 | 0.010328 | 0.001274 | 2.452 | |
| 5 ERs | 1 | 0.023701 | 0.001309 | — |
| 2 | 0.023239 | 0.001288 | 1.989 | |
| NS5A/OtherNSPs Cells, | ||||
| 5 ERs | 1 | 0.007837 | 0.000513 | — |
| 2 | 0.007602 | 0.000493 | 2.996 | |
Appendix F. Variation of Pseudo Reaction
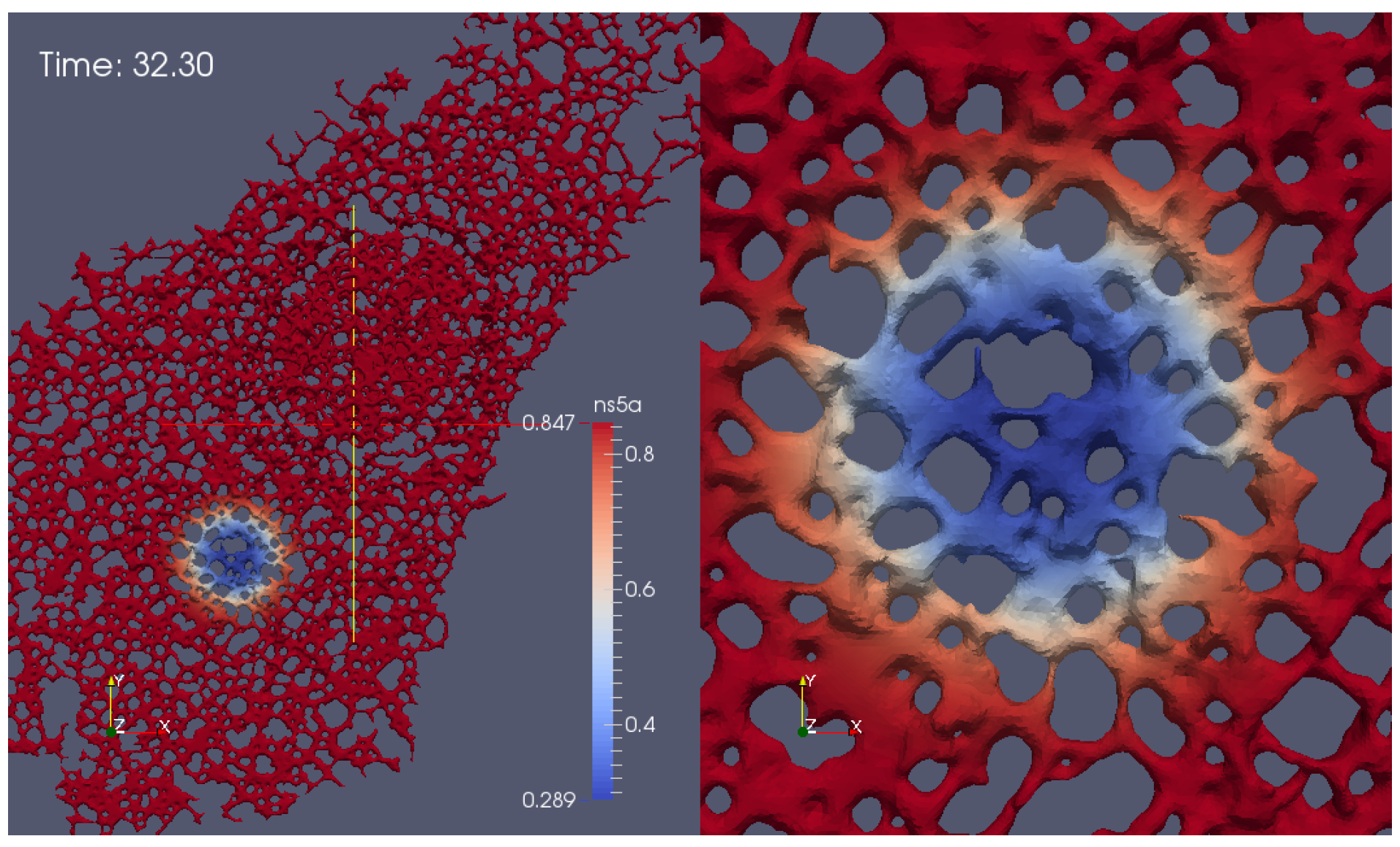
Appendix G. Additional Simulation Screenshot
| Cells | ||
|---|---|---|
| NS5A/Alone | 0.0228726 | 9.62539 |
| NS5A/OtherNSPs | 0.0012175 | 4.14657 |
| Cells | ||
|---|---|---|
| NS5A/Alone | 0.0103104 | 4.15337 |
| NS5A/OtherNSPs | 0.0007236 | 1.89964 |
References
- Moradpour, D.; Penin, F.; Rice, C.M. Replication of hepatitis C virus. Nat. Rev. Microbiol. 2007, 5, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Paul, D.; Bartenschlager, R. Architecture and biogenesis of plus- strand RNA virus replication factories. World. J. Virol. 2013, 2, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Chatel-Chaix, L.; Bartenschlager, R. Dengue virus and Hepatitis C virus-induced replication and assembly compartments: The enemy inside—Caught in the web. J. Virol. 2014, 88, 5907–5911. [Google Scholar] [CrossRef] [PubMed]
- Welsch, S.; Miller, S.; Romero-Brey, I.; Merz, A.; Bleck, C.; Walther, P.; Fuller, S.; Antony, C.; Krijnse-Locker, J.; Bartenschlager, R. Composition and three-dimensional architecture of the dengue virus replication and assembly sites. Cell Host Microb. 2009, 5, 365–375. [Google Scholar] [CrossRef] [PubMed]
- Targett-Adams, P.; Boulant, S.; McLauchlan, J. Visualization of double-stranded RNA in cells supporting hepatitis C virus RNA replication. J. Virol. 2008, 82, 2182–2195. [Google Scholar] [CrossRef] [PubMed]
- Romero-Brey, I.; Merz, A.; Chiramel, A.; Lee, J.; Chlanda, P.; Haselman, U.; Santarella-Mellwig, R.; Habermann, A.; Hoppe, S.; Kallis, S.; et al. Three-dimensional architecture and biogenesis of membrane structures associated with hepatitis C virus replication. PLoS Pathog. 2012, 8, e1003056. [Google Scholar] [CrossRef] [PubMed]
- Targett-Adams, P.; Graham, E.; Middleton, J.; Palmer, A.; Shaw, S.; Lavender, H.; Brain, P.; Tran, T.; Jones, L.; Wakenhut, F.; et al. Small molecules targeting hepatitis C virus-encoded NS5A cause subcellular redistribution of their target: Insights into compound modes of action. J. Virol. 2011, 85, 6353–6368. [Google Scholar] [CrossRef] [PubMed]
- Chukkapalli, V.; Berger, K.L.; Kelly, S.M.; Thomas, M.; Deiters, A.; Randall, G. Daclatasvir inhibits hepatitis C virus NS5A motility and hyper-accumulation of phosphoinositides. Virology 2015, 476, 168–179. [Google Scholar] [CrossRef] [PubMed]
- Wölk, B.; Büchele, B.; Moradpour, D.; Rice, C. A dynamic view of hepatitis C virus replication complexes. J. Virol. 2008, 82, 10519–10531. [Google Scholar] [CrossRef] [PubMed]
- Eyre, N.; Fiches, G.; Aloia, A.; Helbig, K.; McCartney, E.; McErlean, C.; Li, K.; Aggarwal, A.; Turville, S.G.; Bearda, M. Dynamic imaging of the hepatitis C virus NS5A protein during a productive infection. J. Virol. 2014, 88, 3636–3652. [Google Scholar] [CrossRef] [PubMed]
- Hoenen, T.; Biedenkopf, N.; Zielecki, F.; Jung, S.; Groseth, A.; Feldmann, H.; Becker, S. Oligomerization of Ebola Virus VP40 Is Essential for Particle Morphogenesis and Regulation of Viral Transcription. J. Virol. 2010, 84, 7053–7063. [Google Scholar] [CrossRef] [PubMed]
- Hoenen, T.; Shabman, R.; Groseth, A.; Herwig, A.; Weber, M.; Schudt, G.; Dolnik, O.; Basler, C.; Becker, S.; Feldmann, H. Inclusion Bodies Are a Site of Ebolavirus Replication. J. Virol. 2012, 86, 11779–11788. [Google Scholar] [CrossRef] [PubMed]
- Noda, T.; Ebihara, H.; Muramoto, Y.; Fujii, K.; Takada, A.; Sagara, H.; Kawaoka, Y. Assembly and budding of Ebolavirus. PLoS Pathog. 2006, 2, e99. [Google Scholar] [CrossRef] [PubMed]
- Stahelin, R. Membrane binding and bending in Ebola VP40 assembly and egress. Front. Microbiol. 2014, 5, 300. [Google Scholar] [PubMed]
- Bhattacharyya, S.; Hope, T. Full-length Ebola glycoprotein accumulates in the endoplasmic reticulum. J. Virol. 2011, 8, 11. [Google Scholar] [CrossRef] [PubMed]
- Bharat, T.; Noda, T.; Riches, J.; Kraehling, V.; Kolesnikovac, L.; Becker, S.; Kawaok, Y.; Briggs, J. Structural dissection of Ebola virus and its assembly determinants using cryo-electron tomography. Proc. Natl. Acad. Sci. USA 2012, 109, 4275–4280. [Google Scholar] [CrossRef] [PubMed]
- Frieman, M.; Yount, B.; Heise, M.; Kopecky-Bromberg, S.; Palese, P.; Baric, R. Severe Acute Respiratory Syndrome Coronavirus ORF6 Antagonizes STAT1 Function by Sequestering Nuclear Import Factors on the Rough Endoplasmic Reticulum/Golgi Membrane. J. Virol. 2007, 81, 9812–9824. [Google Scholar] [CrossRef] [PubMed]
- Olejnik, J.; Ryabchikova, E.; Corley, R.; Mühlberger, E. Intracellular Events and Cell Fate in Filovirus Infection. Viruses 2011, 3, 1501–1531. [Google Scholar] [CrossRef] [PubMed]
- Pegoraro, G.; Bavari, S.; Panchal, R. Shedding Light on Filovirus Infection with High-Content Imaging. Viruses 2012, 4, 1354–1371. [Google Scholar] [CrossRef] [PubMed]
- Schudt, G.; Kolesnikova, L.; Dolnik, O.; Sodeik, B.; Becker, S. Live-cell imaging of Marburg virus-infected cells uncovers actin-dependent transport of nucleocapsids over long distances. Proc. Natl. Acad. Sci. USA 2013, 110, 14402–14407. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Voeltz, G. The ER in 3D: A multifunctional dynamic membrane network. Trends Cell Biol. 2011, 21, 709–717. [Google Scholar] [CrossRef] [PubMed]
- Guedj, J.; Rong, L.; Dahari, H.; Perelson, A. A perspective on modelling hepatitis C virus infection. J. Viral Hepat. 2010, 17, 825–833. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Ribeiro, R.; Rice, C.; Perelson, A. Mathematical Modeling of Subgenomic Hepatitis C Virus Replication in Huh-7 Cells. J. Virol. 2007, 81, 750–760. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Sainz, B.; Sainz, J.; Perelson, A.; Uprichard, S. Modeling Subgenomic Hepatitis C Virus RNA Kinetics during Treatment with Alpha Interferon. J. Virol. 2009, 83, 6383–6390. [Google Scholar] [CrossRef] [PubMed]
- Adiwijaya, B.S.; Herrmann, E.; Hare, B.; Kieffer, T.; Lin, C.; Kwong, A.D.; Garg, V.; Randle, J.C.R.; Sarrazin, C.; Zeuzem, S.; et al. A Multi-Variant, Viral Dynamic Model of Genotype 1 HCV to Assess the in vivo Evolution of Protease-Inhibitor Resistant Variants. PLoS Comp. Biol. 2010, 6, e1000745. [Google Scholar] [CrossRef] [PubMed]
- Binder, M.; Sulaimanov, N.; Clausznitzer, D.; Schulze, M.; Hüber, C.; Lenz, S.; Schlöder, J.; Trippler, M.; Bartenschlager, R.; Lohmann, V.; et al. Replication vesicles are load- and choke-points in the hepatitis C virus lifecycle. PLoS Pathog. 2013, 9, e1003561. [Google Scholar] [CrossRef] [PubMed]
- Knodel, M.M.; Reiter, S.; Vogel, A.; Targett-Adams, P.; Grillo, A.; Herrmann, E.; Wittum, G. 3D spatially resolved models of the intracellular dynamics of the Hepatitis C genome replication cycle. Viruses 2017, 9, 282. [Google Scholar] [CrossRef] [PubMed]
- Belda, O.; Targett-Adams, P. Small molecule inhibitors of the hepatitis C virus-encoded NS5A protein. Virus Res. 2012, 170, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Appel, N.; Zayas, M.; Miller, S.; Krijnse-Locker, J.; Schaller, T.; Friebe, P.; Kallis, S.; Engel, U.; Bartenschlager, R. Essential Role of Domain III of Nonstructural Protein 5A for Hepatitis C Virus Infectious Particle Assembly. PLoS Pathog. 2010, 4, e1000035. [Google Scholar] [CrossRef] [PubMed]
- Wilby, K.; Partovi, N.; Ford, J.; Greanya, E.; Yoshida, E. Review of boceprevir and telaprevir for the treatment of chronic hepatitis C. Can. J. Gastroenterol. 2012, 26, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Nevo-Yassaf, I.; Yaffe, Y.; Asher, M.; Ravid, O.; Eizenberg, S.; Henis, Y.; Nahmias, Y.; Hirschberg, K.; Sklan, E. Role for TBC1D20 and Rab1 in Hepatitis C Virus Replication via Interaction with Lipid Droplet-Bound Nonstructural Protein 5A. J. Virol. 2012, 86, 6491–6502. [Google Scholar] [CrossRef] [PubMed]
- Reits, E.; Neefjes, J. From fixed to FRAP: Measuring protein mobility and activity in living cells. Nat. Cell Biol. 2001, 3, E145–E147. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa-Ankerhold, H.; Ankerhold, R.; Drummen, G. Advanced Fluorescence Microscopy Techniques—FRAP, FLIP, FLAP, FRET and FLIM. Molecules 2012, 17, 4047–4132. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.; Gretton, S.; McLauchlan, J.; Targett-Adams, P. Mobility analysis of an NS5A-GFP fusion protein in cells actively replicating hepatitis C virus subgenomic RNA. J. Gener. Virol. 2007, 88, 470–475. [Google Scholar] [CrossRef] [PubMed]
- Knodel, M.M.; Nägel, A.; Reiter, S.; Rupp, M.; Vogel, A.; Targett-Adams, P.; Herrmann, E.; Wittum, G. Multigrid analysis of spatially resolved hepatitis C virus protein simulations. Comput. Visualization Sci. 2015, 17, 235–253. [Google Scholar] [CrossRef]
- Krieger, N.; Lohmann, V.; Bartenschlager, R. Enhancement of hepatitis C virus RNA replication by cell culture-adaptive mutations. J. Virol. 2001, 75, 4614–4624. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, V.; Korner, F.; Dobierzewska, A.; Bartenschlager, R. Mutations in hepatitis C virus RNAs conferring cell culture adaptation. J. Virol. 2001, 75, 1437–1449. [Google Scholar] [CrossRef] [PubMed]
- Fiches, G.N.; Eyre, N.S.; Aloia, A.L.; Van Der Hoek, K.; Betz-Stablein, B.; Luciani, F.; Chopra, A.; Beard, M.R. HCV RNA traffic and association with NS5A in living cells. Virology 2016, 493, 60–74. [Google Scholar] [CrossRef] [PubMed]
- Vallotton, P.; van Oijen, A.; Whitchurch, C.; Gelfand, V.; Yeo, L.; Tsiavaliaris, G.; Heinrich, S.; Dultz, E.; Weis, K.; Grünwald, D. Diatrack particle tracking software: Review of applications and performance evaluation. Traffic 2017, 18, 840–852. [Google Scholar] [CrossRef] [PubMed]
- Soumpasis, D. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 1983, 41, 95–97. [Google Scholar] [CrossRef]
- Axelrod, D.; Koppel, D.; Schlessinger, J.; Elson, E.; Webb, W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976, 16, 1055–1069. [Google Scholar] [CrossRef]
- Phair, R.; Misteli, T. Kinetic modelling approaches to in vivo imaging. Nat. Rev. Mol. Cell Biol. 2001, 2, 898–907. [Google Scholar] [CrossRef] [PubMed]
- Sprague, B.L.; McNally, J.G. FRAP analysis of binding: Proper and fitting. Trends Cell Biol. 2005, 15, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Sprague, B.L.; Pego, R.L.; Stavreva, D.A.; McNally, J.G. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 2004, 86, 3473–3495. [Google Scholar] [CrossRef] [PubMed]
- Houtsmuller, A. Fluorescence recovery after photobleaching: Application to nuclear proteins. In Advances in Biochemical Engineering/Biotechnology; Springer: Berlin/Heidelberg, Germany, 2005; Volume 95, pp. 177–199. [Google Scholar]
- Zadeh, K.S.; Montas, H.J.; Shirmohammadi, A. Identification of biomolecule mass transport and binding rate parameters in living cells by inverse modeling. Theor. Biol. Med. Model. 2006, 3, 36. [Google Scholar] [CrossRef] [PubMed]
- Hansen, C.V.; . Schroll, H.J.; Wüstner, D. Computational modeling of fluorescence loss in photobleaching. In Computing and Visualization in Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 17, pp. 151–166. [Google Scholar]
- Kühnel, W. Differential Geometry: Curves—Surfaces–Manifolds; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Heppner, I.; Lampe, M.; Nägel, A.; Reiter, S.; Rupp, M.; Vogel, A.; Wittum, G. Software Framework ug4: Parallel Multigrid on the Hermit Supercomputer. In High Performance Computing in Science and Engineering; Wolfgang, E., Nagel, D.H., Kröner, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Reiter, S.; Vogel, A.; Heppner, I.; Rupp, M.; Wittum, G. A massively parallel geometric multigrid solver on hierarchically distributed grids. Comput. Vis. Sci. 2013, 16, 151–164. [Google Scholar] [CrossRef]
- Vogel, A.; Reiter, S.; Rupp, M.; Nägel, A.; Wittum, G. UG 4: A novel flexible software system for simulating PDE based models on high performance computers. Comput. Vis. Sci. 2013, 16, 165–179. [Google Scholar] [CrossRef]
- Hackbusch, W. Elliptic Differential Equations: Theory and Numerical Treatment; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Bey, J. Finite-Volumen- Und Mehrgitter-Verfahren Für Elliptische Randwertprobleme; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Vogel, A.; Xu, J.; Wittum, G. A generalization of the vertex-centered finite volume scheme to arbitrary high order. Comput. Vis. Sci. 2010, 13, 221–228. [Google Scholar] [CrossRef]
- Hackbusch, W. Multi-Grid Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Hackbusch, W. Iterative Solution of Large Sparse Systems of Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Reiter, S.; Logashenko, D.; Stichel, S.; Wittum, G.; Grillo, A. Models and simulations of variable-density flow in fractured porous media. Int. J. Comput. Sci. Eng. 2014, 9, 416–432. [Google Scholar] [CrossRef]
- Grillo, A.; Lampe, M.; Logashenko, D.; Stichel, S.; Wittum, G. Simulation of salinity-and thermohaline-driven flow in fractured porous media. J. Porc. Med. 2012, 15, 439–458. [Google Scholar] [CrossRef]
- Wittmann, M.; Queisser, G.; Eder, A.; Wiegert, J.; Bengton, C.; Hellwig, A.; Wittum, G.; Bading, H. Synaptic Activity Induces Dramatic Changes in the Geometry of the Cell Nucleus: Interplay Between Nuclear Structure, Histone H3 Phosphorylation, and Nuclear Calcium Signaling. J. Neurosci. 2009, 29, 14687–14700. [Google Scholar] [CrossRef] [PubMed]
- Knodel, M.; Geiger, R.; Ge, L.; Bucher, D.; Grillo, A.; Wittum, G.; Schuster, C.; Queisser, G. Synaptic bouton properties are tuned to best fit the prevailing firing pattern. Front. Comput. Neurosci. 2014, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Xylouris, K.; Queisser, G.; Wittum, G. A Three-Dimensional Mathematical Model of Active Signal Processing in Axons. Comput. Vis. Sci. 2011, 13, 409–418. [Google Scholar] [CrossRef]
- Grein, S.; Stepniewski, M.; Reiter, S.; Knodel, M.; Queisser, G. 1D-3D Hybrid Modelling—From Multi-Compartment Models to Full Resolution Models in Space and Time. Front. Neuroinform. 2014, 8, 68. [Google Scholar] [CrossRef] [PubMed]
- Nägel, A.; Hansen, S.; Neumann, D.; Lehr, C.; Schaefer, U.; Wittum, G.; Heisig, M. In-silico model of skin penetration based on experimentally determined input parameters. Part II: Mathematical modelling of in-vitro diffusion experiments. Identification of critical input parameters. Eur. J. Pharm. Biopharm. 2008, 68, 368–379. [Google Scholar] [CrossRef] [PubMed]
- Nägel, A.; Heisig, M.; Wittum, G. A comparison of two-and three-dimensional models for the simulation of the permeability of human stratum corneum. Eur. J. Pharm. Biopharm. 2009, 72, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Borenstein, M.; Hedges, L.; Higgins, J.; Rothstein, H. Introduction to Meta-Analysis; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hothorn, T.; Everitt, B.S. A Handbook of Statistical Analyses Using R, 3rd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Broser, P.; Schulte, R.; Roth, A.; Helmchen, F.; Waters, J.; Lang, S.; Sakmann, B.; Wittum, G. Nonlinear anisotropic diffusion filtering of three-dimensional image data from 2-photon microscopy. J. Biomed. Opt. 2004, 9, 1253–1264. [Google Scholar] [CrossRef] [PubMed]
- Jungblut, D.; Queisser, G.; Wittum, G. Inertia Based Filtering of High Resolution Images Using a GPU Cluster. Comput. Vis. Sci. 2011, 14, 181–186. [Google Scholar] [CrossRef]
- Hilversum, N. Scientific Volume Imaging B.V., Huygens Comute Engine, Software. 2014. Available online: http://www.svi.nl/HuygensSoftware (accessed on 6 January 2018).
- Björck, A. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Müller, F.; Mazza, D.; Stasevich, T.; McNally, J. FRAP and kinetic modeling in the analysis of nuclear protein dynamics: What do we really know? Curr. Opin. Cell Biol. 2010, 22, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Ross-Thriepland, D.; Mankouri, J.; Harris, M. Serine phosphorylation of the hepatitis C virus NS5A protein controls the establishment of replication complexes. J. Virol. 2015, 89, 3123–3135. [Google Scholar] [CrossRef] [PubMed]
- Sbalzarini, I.; Mezzacasa, A.; Helenius, A.; Koumoutsakos, P. Effects of Organelle Shape on Fluorescence Recovery after Photobleaching. Biophys. J. 2005, 89, 1482–1492. [Google Scholar] [CrossRef] [PubMed]
- Sbalzarini, I.; Hayer, A.; Helenius, A.; Koumoutsakos, P. Simulations of (An)Isotropic Diffusion on Curved Biological Surfaces. Biophys. J. 2006, 90, 878–885. [Google Scholar] [CrossRef] [PubMed]
- Dukhovny, A.; Papadopulos, A.; Hirschberg, K. Quantitative live-cell analysis of microtubule-uncoupled cargo-protein sorting in the ER. J. Cell. Sci. 2008, 121, 865–876. [Google Scholar] [CrossRef] [PubMed]
- Nehls, S.; Snapp, E.L.; Cole, N.B.; Zaal, K.J.; Kenworthy, A.K.; Roberts, T.H.; Ellenberg, J.; Presley, J.F.; Siggia, E.; Lippincott-Schwartz, J. Dynamics and retention of misfolded proteins in native ER membranes. Nat. Cell Biol. 2000, 2, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Henis, Y.; Rotblat, B.; Kloog, Y. FRAP beam-size analysis to measure palmitoylation-dependent membrane association dynamics and microdomain partitioning of Ras proteins. Method 2006, 40, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Kühn, T.; Ihalainen, T.O.; Hyvaluoma, J.; Dross, N.; Willman, S.F.; Langowski, J.; Vihinen-Ranta, M.; Timonen, J. Protein Diffusion in Mammalian Cell Cytoplasm. PLoS ONE 2011, 6, e22962. [Google Scholar] [CrossRef] [PubMed]
- Beaudouin, J.; Mora-Bermudez, F.; Klee, T.; Daigle, N.; Ellenberg, J. Dissecting the Contribution of Diffusion and Interactions to the Mobility of Nuclear Proteins. Biophys. J. 2006, 90, 1878–1894. [Google Scholar] [CrossRef] [PubMed]
- Bronstein, I.; Israel, Y.; Kepten, E.; Mai, S.; Shav-Tal, Y.; Barkai, E.; Garini, Y. Transient Anomalous Diffusion of Telomeres in the Nucleus of Mammalian Cells. Phys. Rev. Lett. 2009, 103, 018102. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.; Tejedor, V.; Burov, S.; Barkai, E.; Selhuber-Unkel, C.; Berg-Sorensen, K.; Oddershede, L.; Metzler, R. In Vivo Anomalous Diffusion andWeak Ergodicity Breaking of Lipid Granules. Phys. Rev. Lett. 2011, 106, 048103. [Google Scholar] [CrossRef] [PubMed]
- Shav-Tal, Y.; Darzacq, X.; Shenoy, S.M.; Fusco, D.; Janicki, S.M.; Spector, D.L.; Singer, R. H. Dynamics of Single mRNPs in Nuclei of Living Cells. Science 2004, 304, 1797. [Google Scholar] [CrossRef] [PubMed]
- Görisch, S.; Wachsmuth, M.; Ittrich, C.; Bacher, C.; Rippe, K.; Lichter, P. Nuclear body movement is determined by chromatin accessibility and dynamics. Proc. Natl. Acad. Sci. USA 2004, 101, 13221–13226. [Google Scholar] [CrossRef] [PubMed]
- Carmo-Fonseca, M.; Platani, M.; Swedlow, R. Macromolecular mobility inside the cell nucleus. Trends Cell Biol. 2002, 12, 491–495. [Google Scholar] [CrossRef]
- Platani, M.; Goldberg, I.; Lamond, A.; Swedlow, J. Cajal Body dynamics and association with chromatin are ATP-dependent. Nat. Cell Biol. 2002, 4, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.; Cherstvy, A.; Metzler, R. Sensing Viruses by Mechanical Tension of DNA in Responsive Hydrogels. Phys. Rev. X 2014, 4, 021002. [Google Scholar] [CrossRef]
- Zareh, S.; DeSantis, M.; Kessler, J.; Li, J.; Y, W. Single-Image Diffusion Coefficient Measurements of Proteins in Free Solution. Biophys. J. 2012, 102, 1685–1691. [Google Scholar] [CrossRef] [PubMed]
- Means, S.; Smith, A.; Shepherd, J.; Shadid, J.; Fowler, J.; Wojcikiewicz, R.H.; Mazel, T.; Smith, G.D.; Wilson, B.S. Reaction diffusion modeling of calcium dynamics with realistic ER geometry. Biophys. J. 2006, 91, 537–557. [Google Scholar] [CrossRef] [PubMed]
- Hannemann, H.; Sung, P.Y.; Chiu, H.C.; Yousuf, A.; Bird, J.; Lim, S.; Davidson, A. Serotype Specfic Differences in Dengue Virus Non-Structural Protein 5 Nuclear Localization. J. Biol. Chem. 2013, 288, 22621–22635. [Google Scholar] [CrossRef] [PubMed]
- Knodel, M.M.; Nägel, A.; Reiter, S.; Rupp, M.; Vogel, A.; Lampe, M.; Targett-Adams, P.; Herrmann, E.; Wittum, G. On Estimation of a Viral Protein Diffusion Constant on the Curved Intracellular ER Surface. In High Performance Computing in Science and Engineering 15: Transactions of the High Performance Computing Center, Stuttgart (HLRS); Nagel, E.W., Kröner, H.D., Resch, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 641–657. [Google Scholar]


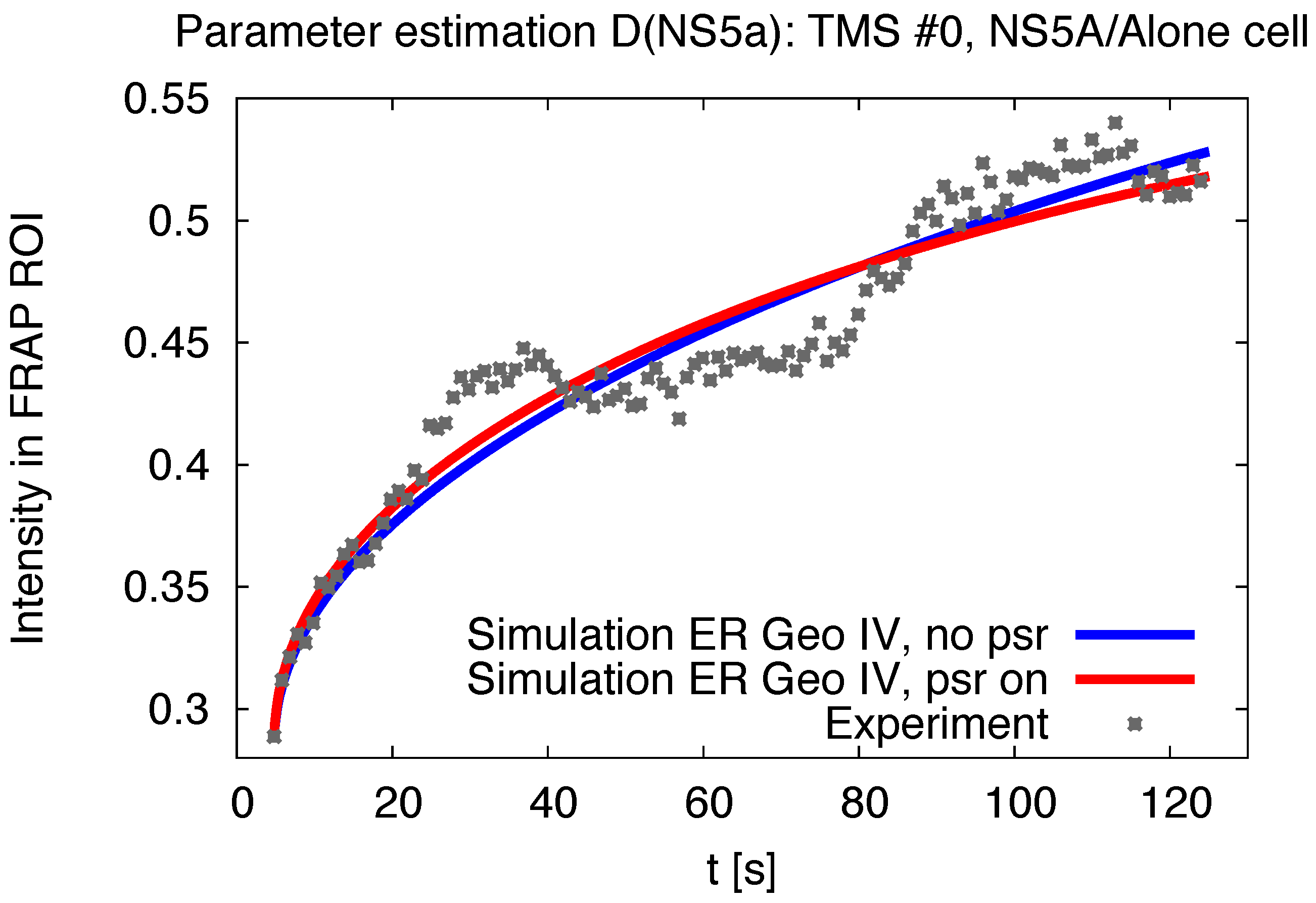
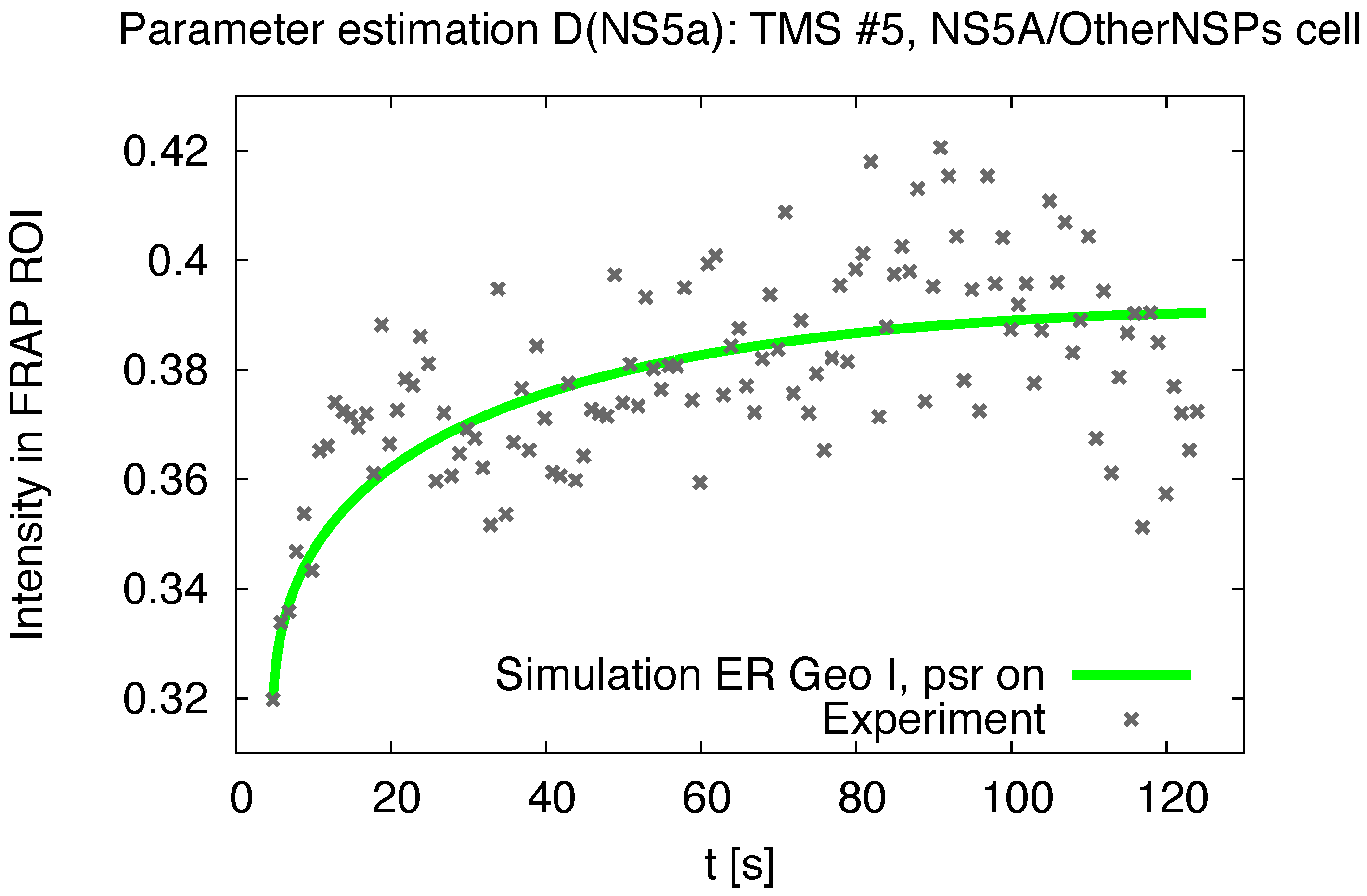
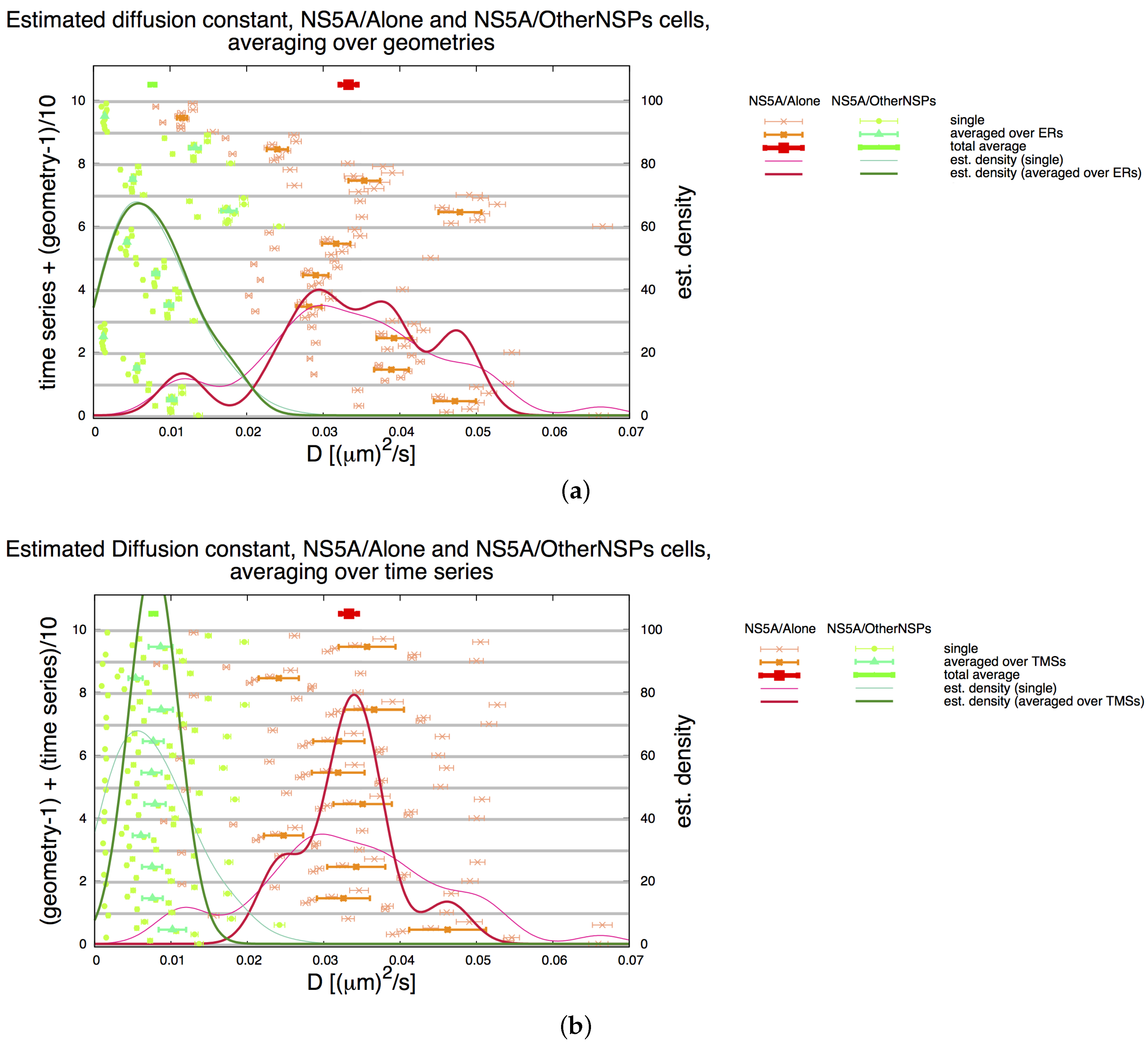
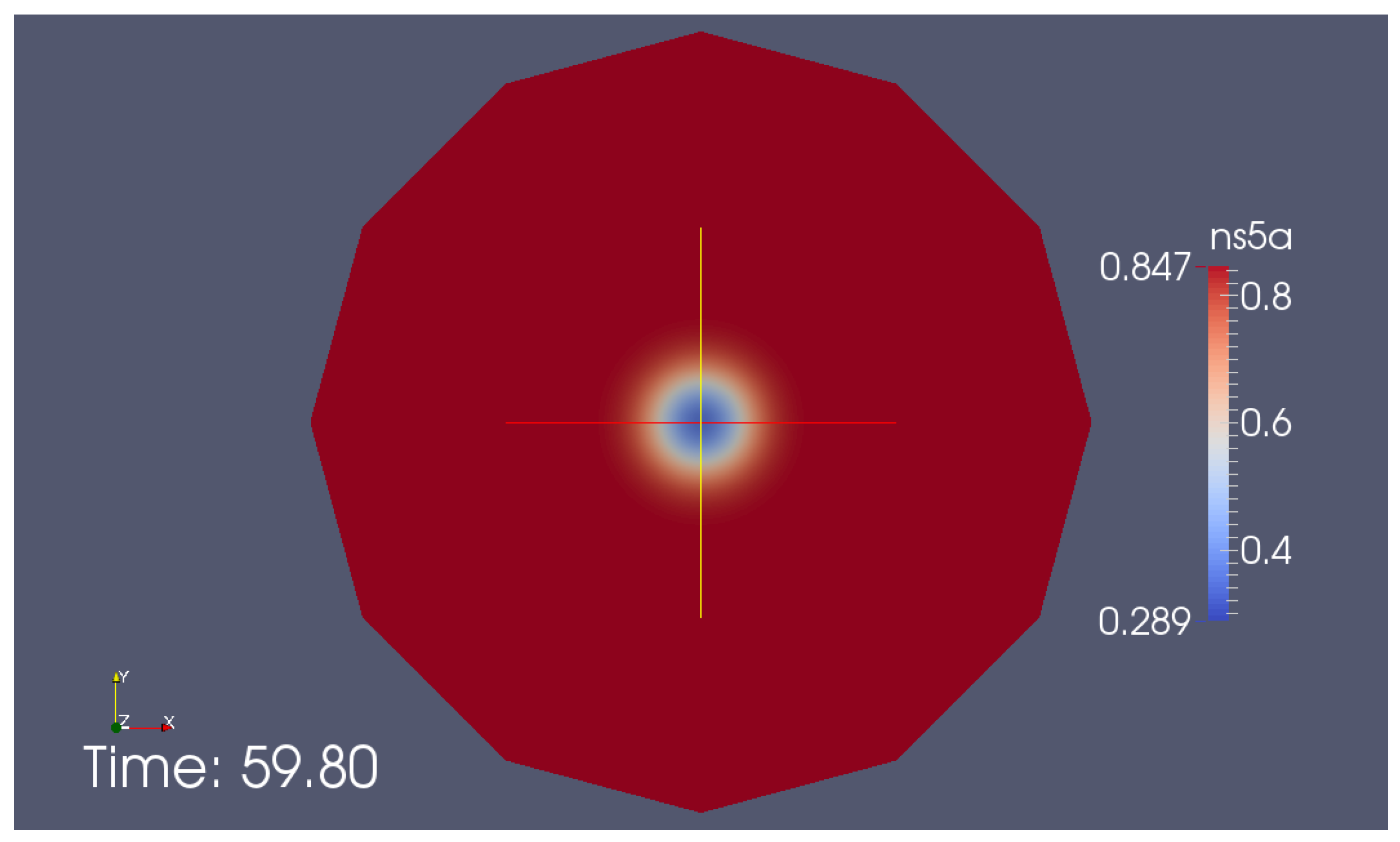
| Geoms | ||
|---|---|---|
| NS5A/Alone cell type | ||
| plane 2D | 0.014815 | 0.001546 |
| ER surface | 0.033307 | 0.001142 |
| NS5A/OtherNSPs cell type | ||
| plane 2D | 0.003873 | 0.000695 |
| ER surface | 0.007696 | 0.000353 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knodel, M.M.; Nägel, A.; Reiter, S.; Vogel, A.; Targett-Adams, P.; McLauchlan, J.; Herrmann, E.; Wittum, G. Quantitative Analysis of Hepatitis C NS5A Viral Protein Dynamics on the ER Surface. Viruses 2018, 10, 28. https://doi.org/10.3390/v10010028
Knodel MM, Nägel A, Reiter S, Vogel A, Targett-Adams P, McLauchlan J, Herrmann E, Wittum G. Quantitative Analysis of Hepatitis C NS5A Viral Protein Dynamics on the ER Surface. Viruses. 2018; 10(1):28. https://doi.org/10.3390/v10010028
Chicago/Turabian StyleKnodel, Markus M., Arne Nägel, Sebastian Reiter, Andreas Vogel, Paul Targett-Adams, John McLauchlan, Eva Herrmann, and Gabriel Wittum. 2018. "Quantitative Analysis of Hepatitis C NS5A Viral Protein Dynamics on the ER Surface" Viruses 10, no. 1: 28. https://doi.org/10.3390/v10010028
APA StyleKnodel, M. M., Nägel, A., Reiter, S., Vogel, A., Targett-Adams, P., McLauchlan, J., Herrmann, E., & Wittum, G. (2018). Quantitative Analysis of Hepatitis C NS5A Viral Protein Dynamics on the ER Surface. Viruses, 10(1), 28. https://doi.org/10.3390/v10010028






