Effect of Rotation Age and Thinning Regime on Visual and Structural Lumber Grades of Douglas-Fir Logs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Tree, Log, and Lumber Measurements
2.3. Data Analysis
3. Results
3.1. Initial Data Summary
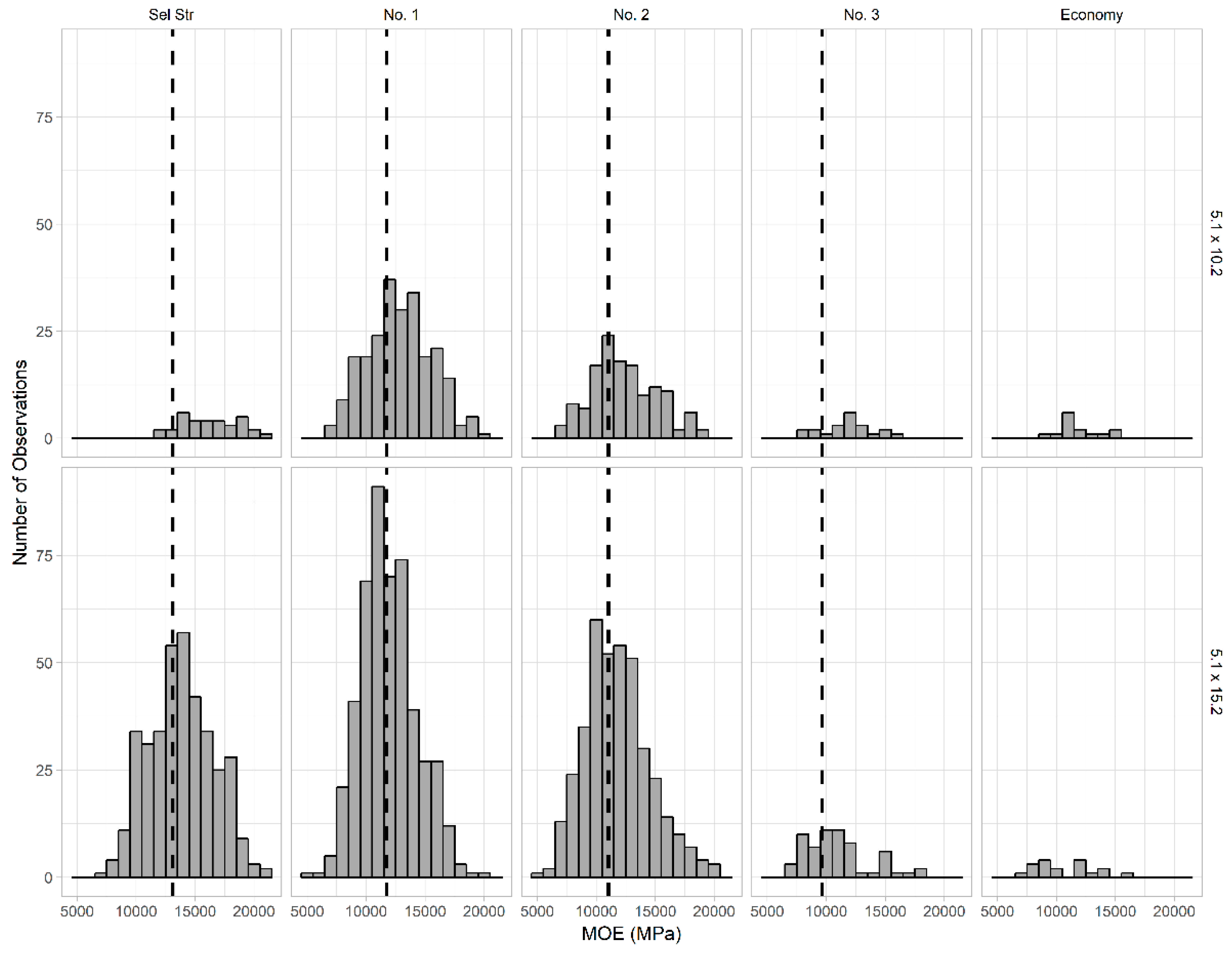
3.1.1. Branch Index
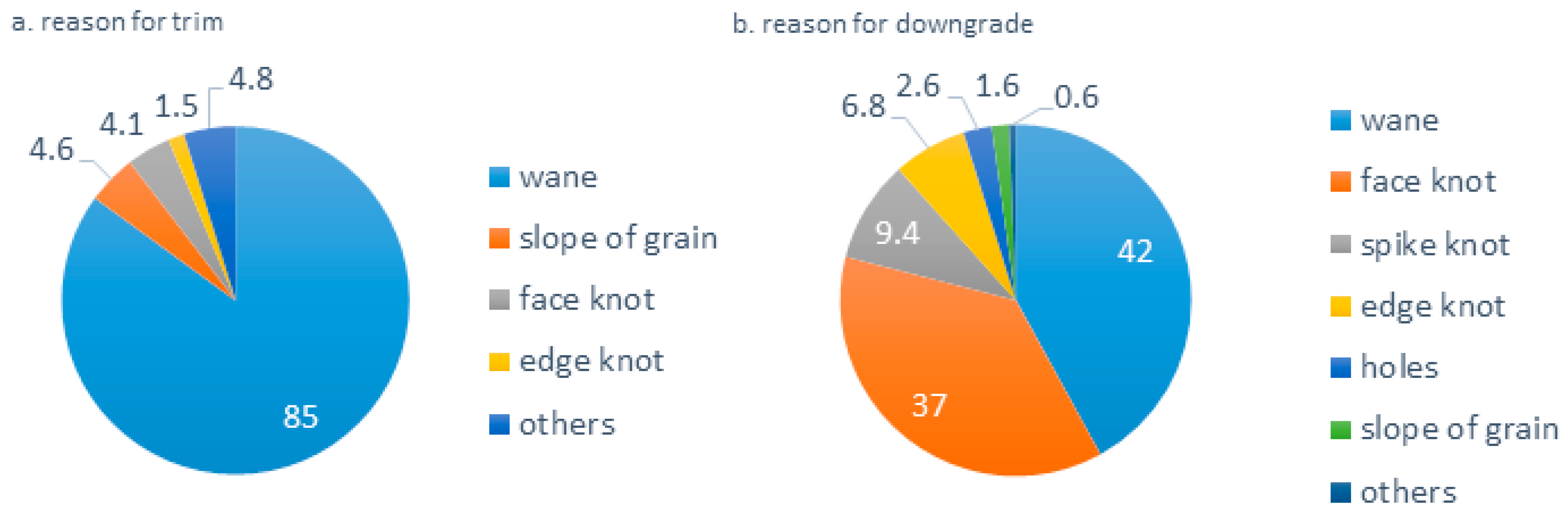
3.1.2. Grade-Limiting Defect
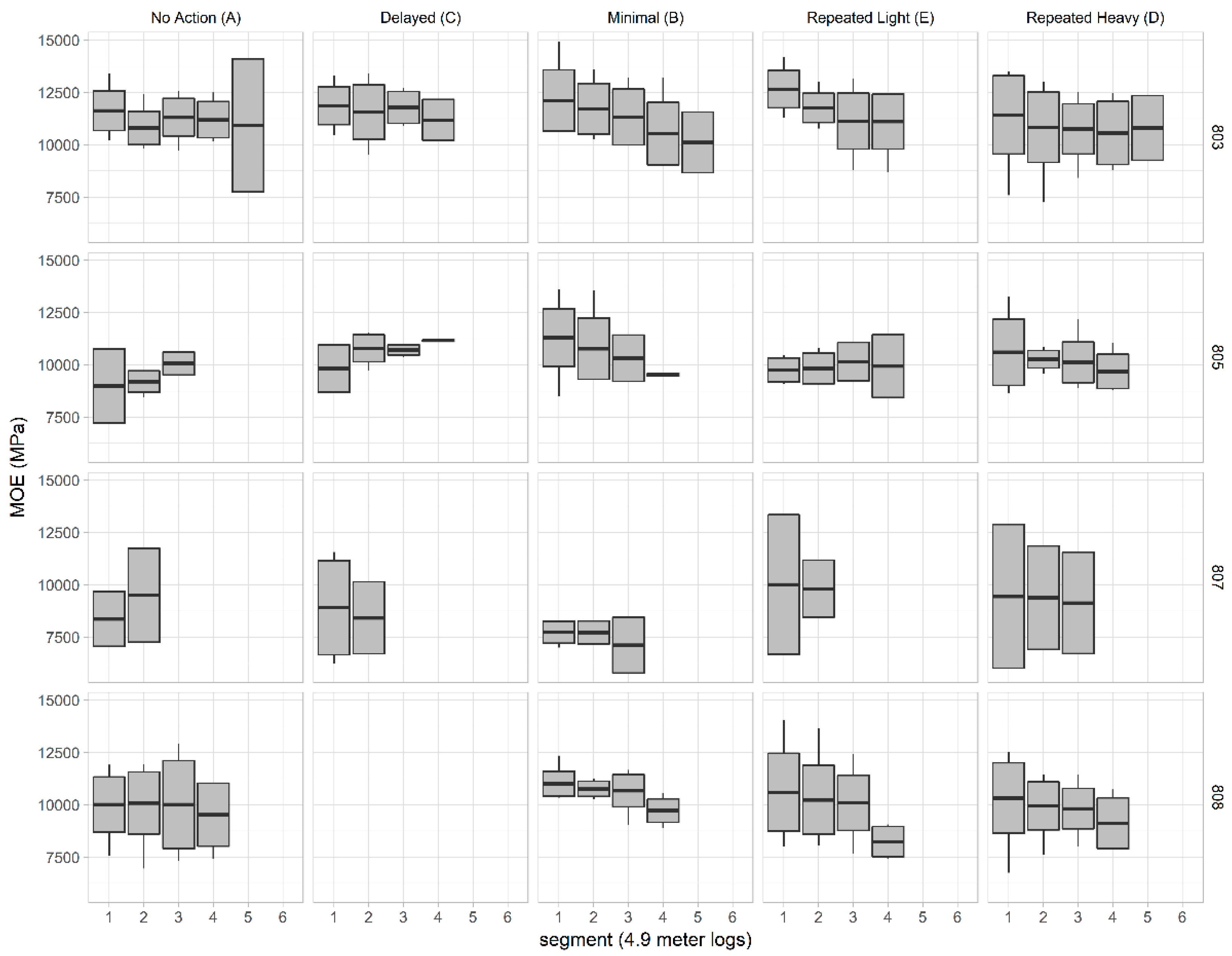
3.1.3. Lumber Stiffness
3.2. Modeling Summary
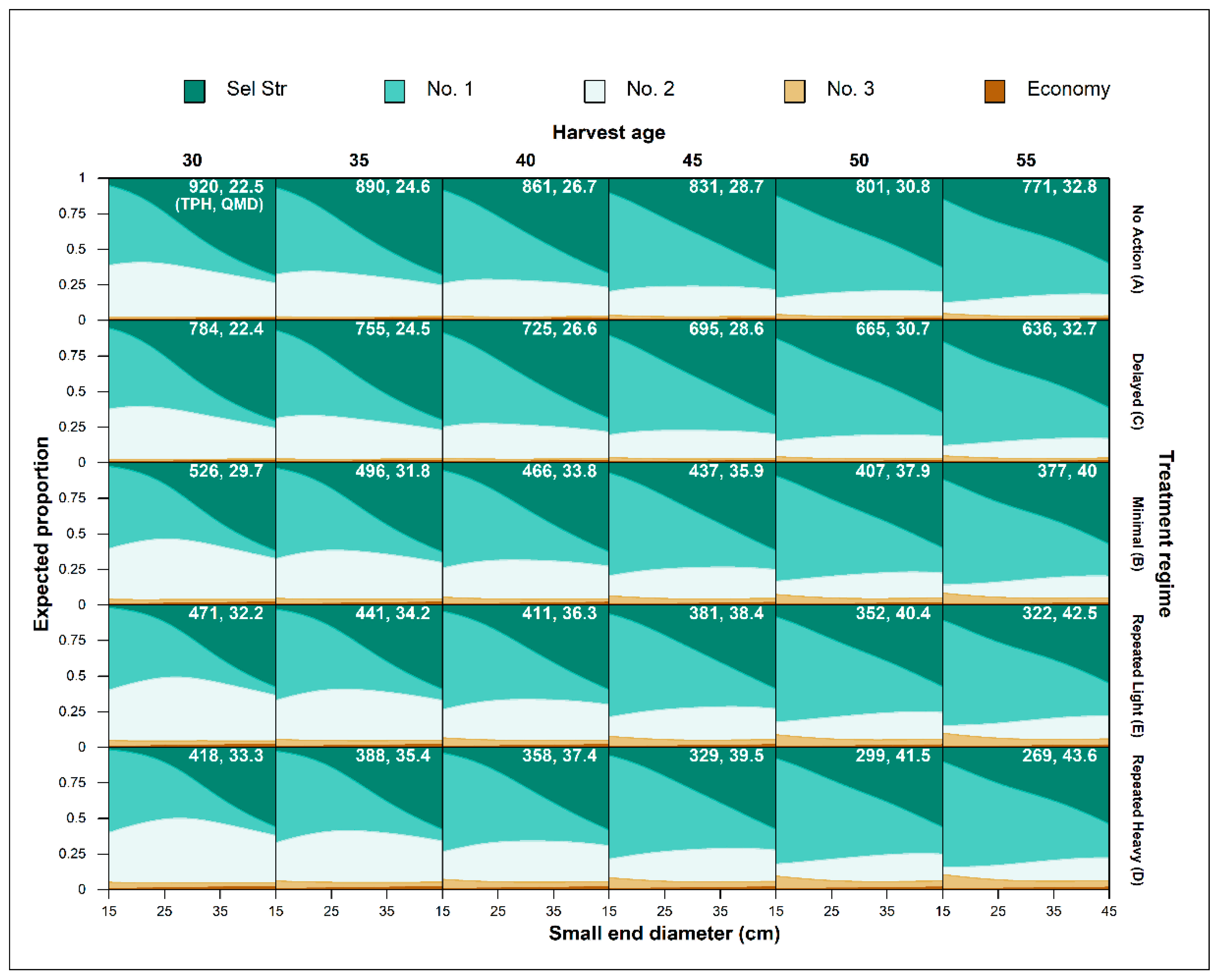
3.2.1. Lumber Grade Distribution
3.2.2. Lumber Structural Grade
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barbour, R.J.; Kellogg, R.M. Forest management and end-product quality: A Canadian perspective. Can. J. For. Res. 1990, 20, 405–414. [Google Scholar] [CrossRef]
- Vance, E.D.; Maguire, D.A.; Zalesney, R.S., Jr. Research Strategies for Increasing Productivity of Intensively Managed Forest Plantations. J. For. 2010, 108, 183–192. [Google Scholar]
- Cherry, M.; Vikas, V.; Briggs, D.; Cress, D.W.; Howe, G.T. Genetic variation in direct and indirect measures of wood stiffness in coastal Douglas-fir. Can. J. For. Res. 2008, 38, 2476–2486. [Google Scholar] [CrossRef]
- Vikram, V.; Cherry, M.L.; Briggs, D.; Cress, D.W.; Evans, R.; Howe, G.T. Stiffness of Douglas-fir lumber: Effects of wood properties and genetics. Can. J. For. Res. 2011, 41, 1160–1173. [Google Scholar] [CrossRef]
- Jozsa, L.A.; Middleton, G.R. A Discussion of Wood Quality Attributes and Their Practical Implications, SP-34; Forintek Canada Corp.: Vancouver, BC, Canada, 1994. [Google Scholar]
- Kennedy, R.W. Coniferous wood quality in the future: Concerns and strategies. Wood Sci. Technol. 1995, 29, 321–338. [Google Scholar] [CrossRef]
- Gartner, B.L. Assessing wood characteristics and wood quality in intensively managed plantations. J. For. 2005, 103, 75–77. [Google Scholar]
- Megraw, R. Douglas-fir Wood Properties. In Douglas-Fir: Stand Management for the Future; Oliver, C.D., Hanley, D.P., Johnson, J.A., Eds.; College of Forest Resources, University of Washington: Seattle, WA, USA, 1986; pp. 81–96. [Google Scholar]
- Abdel-Gadir, A.Y.; Krahmer, R.L. Estimating the age of demarcation of juvenile and mature wood in Douglas-fir. Wood Fiber Sci. 2007, 25, 242–249. [Google Scholar]
- Aubry, C.A.; Adams, W.T.; Fahey, T.D. Determination of relative economic weights for multitrait selection in coastal Douglas-fir. Can. J. For. Res. 1998, 28, 1164–1170. [Google Scholar] [CrossRef]
- Kellogg, R.M. Second Growth Douglas-Fir: Its Management and Conversion for Value, SP-32; Forintek Canada Corp.: Vancouver, BC, Canada, 1989. [Google Scholar]
- Barratt, J.D.; Kellogg, R.M. Lumber Quality from second growth managed forests. In A Technical Workshop: Juvenile Wood–What Does It Mean to Forest Management and Forest Products? Forest Products Research Society: Madison, WI, USA, 1986; pp. 57–71. [Google Scholar]
- Barrett, J.D.; Kellogg, R.M. Strength and Stiffness of Dimension Lumber. In Second Growth Douglas-Fir; Its Management and Conversion for Value, Special Publ. SP-32; Kellogg, R.M., Ed.; Forintek Canada Corp.: Vancouver, BC, Canada, 1989; pp. 50–58. [Google Scholar]
- Fahey, T.D.; Cahill, J.M.; Snellgrove, T.A.; Heath, L.S. Lumber and Veneer Recovery from Intensively Managed Young-Growth Douglas-Fir; US Department of Agriculture, Forest Service: Portland, OR, USA, 1991.
- Bendtsen, B.A.; Plantinga, P.L.; Snellgrove, T.A. The influence of juvenile wood on the mechanical properties of 2 by 4’s cut from Douglas-fir plantations. In Proceedings of the International Conference on Timber Engineering, Pullman, WA, USA, 19–22 September 1988; Washington State Univ.: Pullman, WA, USA, 1988; pp. 226–240. [Google Scholar]
- Lowell, E.C.; Maguire, D.A.; Briggs, D.G.; Turnblom, E.C.; Jayawickrama, K.J.; Bryce, J. Effects of silviculture and genetics on branch/knot attributes of coastal Pacific Northwest Douglas-fir and implications for wood quality—A Synthesis. Forests 2014, 5, 1717–1736. [Google Scholar] [CrossRef]
- Curtis, R.O.; Reukema, D.L. Crown development and site estimates in a Douglas-fir plantation spacing test. For. Sci. 1970, 16, 287–301. [Google Scholar]
- Grah, R.F. Relationship between tree spacing, knot size, and log quality in young Douglas-fir stands. J. For. 1961, 59, 270–272. [Google Scholar]
- Weiskittel, A.R.; Maguire, D.A.; Monserud, R.A.; Rose, R.; Turnblom, E.C. Intensive management influence on Douglas fir stem form, branch characteristics, and simulated product recovery. N. Z. J. For. Sci. 2006, 36, 293–312. [Google Scholar]
- Brix, H. Effects of thinning and nitrogen fertilization on branch and foliage production in Douglas-fir. Can. J. For. Res. 1981, 11, 502–511. [Google Scholar] [CrossRef]
- Maguire, D.A.; Kershaw, J.A., Jr.; Hann, D.W. Predicting the effects of silvicultural regime on branch size and crown wood core in Douglas-fir. For. Sci. 1991, 37, 1409–1428. [Google Scholar]
- Maguire, D.A.; Johnston, S.R.; Cahill, J. Predicting branch diameters on second-growth Douglas-fir from tree-level descriptors. Can. J. For. Res. 1999, 29, 1829–1840. [Google Scholar] [CrossRef]
- Briggs, D.G.; Kantavichai, R.; Turnblom, E.C. Predicting the diameter of the largest breast-height region branch of Douglas-fir trees in thinned and fertilized plantations. For. Prod. J. 2010, 60, 322–330. [Google Scholar] [CrossRef]
- Reukema, D.L. Crown expansion and stem radial growth of Douglas-fir as influenced by release. For. Sci. 1964, 10, 192–199. [Google Scholar]
- Barbour, R.J.; Parry, D.L. Log and Lumber Grades as Indicators of Wood Quality in 20- to 100-Year Old Douglas-Fir Trees from Thinned and Unthinned Stands; US Department of Agriculture, Forest Service: Portland, OR, USA, 2001.
- Western Wood Products Association (WWPA). Western Lumber Grading Rules; Western Wood Products Association: Portland, OR, USA, 2017. [Google Scholar]
- Middleton, G.R.; Munro, B.D. Log and Lumber Yields. In Second Growth Douglas-Fir: Its Management and Conversion for Value; Kellogg, R.M., Ed.; Forintek Canada Corp.: Vancouver, BC, Canada, 1989; Chapter 7; pp. 66–74. [Google Scholar]
- Briggs, D.G.; Ingaramo, L.; Turnblom, E.C. Number and Diameter of Breast-height Region Branches in a Douglas-fir Spacing Trial and Linkage to Log Quality. For. Prod. J. 2007, 57, 28–34. [Google Scholar]
- Ross, R.J.; McDonald, K.A.; Green, D.W.; Schad, K. Relationship between log and lumber modulus of elasticity. For. Prod. J. 1997, 47, 89–92. [Google Scholar]
- Ross, R.J.; Willits, S.A.; VonSegen, W.; Black, T.; Brashaw, B.K.; Pellerin, R.F. A stress wave based approach to NDE of logs for assessing potential veneer quality. Part I. Small diameter ponderosa pine. For. Prod. J. 1999, 49, 60–62. [Google Scholar]
- Ridoutt, B.G.; Wealleans, K.R.; Booker, R.E.; McConchie, D.L.; Ball, R.D. Comparison of log segregation methods for structural lumber yield improvement. For. Prod. J. 1999, 49, 63–66. [Google Scholar]
- Carter, P.; Briggs, D.; Ross, R.J.; Wang, X. Acoustic testing to enhance western forest values and meet customer wood quality needs. In Productivity of Western Forests: A Forest Products Focus; Harrington, C.A., Schoenholz, S.H., Eds.; US Department of Agriculture Forest Service: Portland, OR, USA, 2005; pp. 121–129. [Google Scholar]
- Wang, X.; Ross, R.J.; McClellan, M.; Barbour, R.J.; Erickson, J.R.; Forsman, J.W.; McGinnis, G.D. Nondestructive evaluation of standing trees with a stress wave method. Wood Fiber Sci. 2001, 33, 522–533. [Google Scholar]
- Wang, X.; Carter, P.; Ross, R.J.; Brashaw, B.K. Acoustic assessment of wood quality of raw forest materials—A path to increased profitability. For. Prod. J. 2007, 57, 6–14. [Google Scholar]
- Wang, X.; Ross, R.J.; Carter, P. Acoustic evaluation of wood in standing trees. Part I. Acoustic wave behavior. Wood Fiber Sci. 2007, 39, 28–38. [Google Scholar]
- Amishev, D.; Murphy, G.E. In-forest assessment of veneer grade Douglas-fir logs based on acoustic measurement of wood stiffness. For. Prod. J. 2008, 58, 42–47. [Google Scholar]
- Briggs, D.G.; Thienel, G.; Turnblom, E.C.; Lowell, E.; Dykstra, D.; Ross, R.J.; Wang, X.; Carter, P. Influence of thinning on acoustic velocity of Douglas-fir trees in western Washington and western Oregon. In Proceedings of the 15th International Symposium on Nondestructive Testing of Wood, Duluth, MN, USA, 10–12 September 2007; pp. 113–123. [Google Scholar]
- Maguire, D.A.; Bennett, W.S.; Kershaw, J.A., Jr.; Gonyea, R.; Chappell, H.N. Establishment Report Stand Management Cooperative Project Field Installations, Institute of Forest Resources Contrib. 72; College of Forest Resources, University of Washington: Seattle, WA, USA, 1991. [Google Scholar]
- Curtis, R.O. A simple index of stand density for Douglas-fir. For. Sci. 1982, 28, 92–94. [Google Scholar]
- Evans, J.W.; Kretschmann, D.E.; Herian, V.L.; Green, D.W. Procedures for Developing Allowable Properties for a Single Species Under ASTM1900 and Computer Programs Useful for the Calculation; US Department of Agriculture, Forest Service: Madison, WI, USA, 2001.
- Ramalho, E.A.; Ramalho, J.J.; Murteira, J.M. Alternative estimating and testing empirical strategies for fractional regression models. J. Econ. Surv. 2011, 25, 19–68. [Google Scholar] [CrossRef]
- American Forest and Paper Association/American Wood Council (AF & PA/AWC). Wood Structural Design Data; American Forest and Paper Association: Washington, DC, USA, 2004. [Google Scholar]
- Zhao, D.; Borders, B.; Wang, M. Survival model for fusiform rust infected loblolly pine plantations with and without mid-rotation understory vegetation control. For. Ecol. Manag. 2006, 235, 232–239. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S.; Christensen, R.H.B.; Singmann, H.; Dai, B.; Scheipl, F.; Grothendieck, G.; Green, P. Linear Mixed-Effects Models Using ‘Eigen’ and S4: Package ‘lme4’. 2018. Available online: https://cran.r-project.org/web/packages/lme4/lme4.pdf (accessed on 19 February 2018).
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics; Update Edition; Wiley: New York, NY, USA, 1996; 520p. [Google Scholar]
- Northwest Log Rules Advisory Group. Official Rules for the Following Log Scaling and Grading Bureaus: Columbia River, Grays Harbor, Northern California, Puget Sound, Southern Oregon, Yamhill; Northwest Log Rules Advisory Group: Eugene, OR, USA, 1998; 48p. [Google Scholar]
- Hoibo, O.A.; Turnblom, E.C. Models of knot characteristics in young coastal U.S. Douglas-fir: Are the effects of tree and site data visibly rendered in the annual ring width pattern at breast height? For. Prod. J. 2017, 67, 29–38. [Google Scholar]
- Todoroki, C.L.; Lowell, E.C.; Kantavichai, R. Growth and mortality in response to climatic extremes and competition in thinning trials of Douglas-fir. manuscript in preparation.
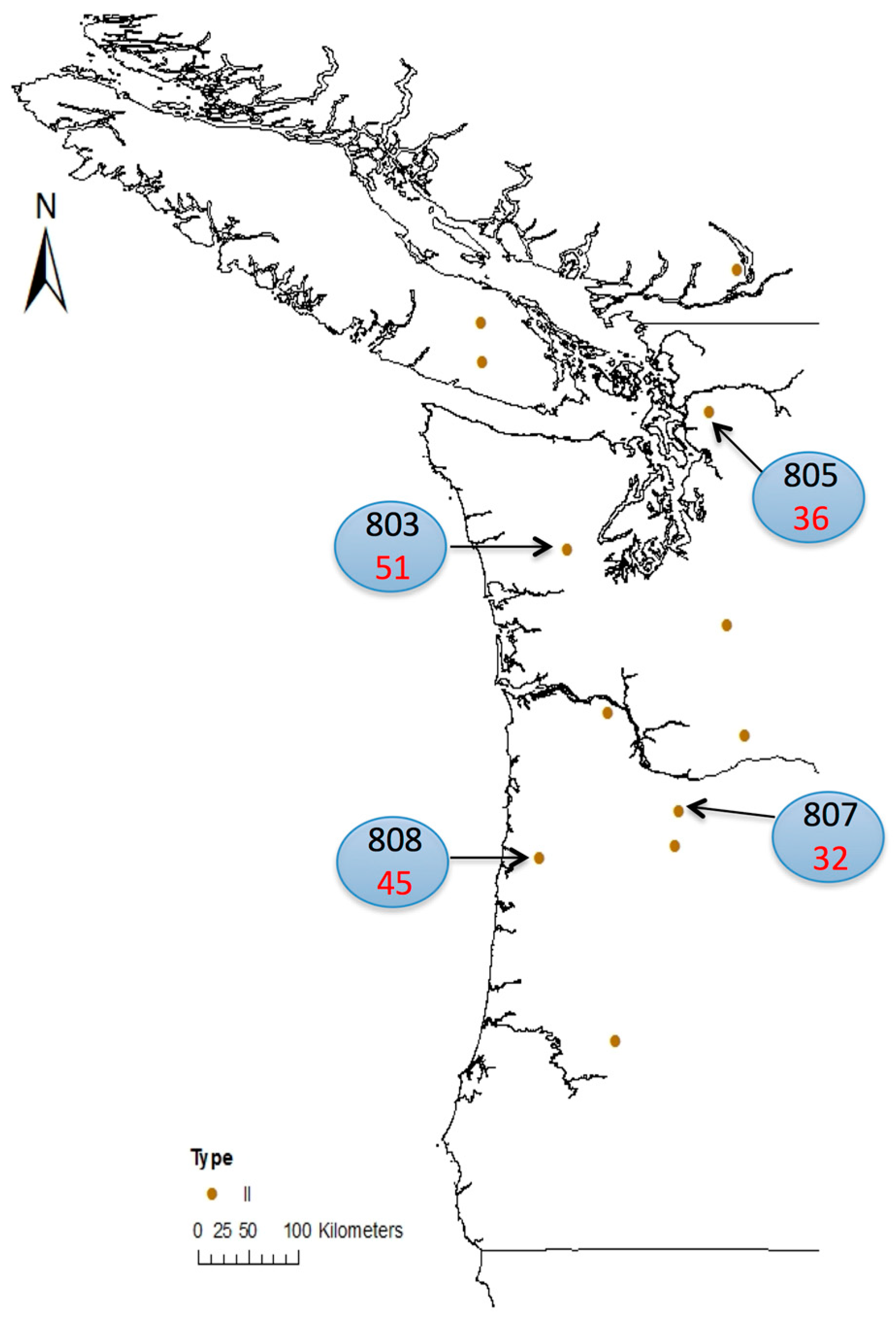
| Treatment Code | Thinning Regime | RD a Trigger Sequence | Installation Thinning Dates (Age at Thinning) | |||
|---|---|---|---|---|---|---|
| 803 | 805 | 807 | 808 | |||
| A | No thinning (Control) | none | none | none | none | |
| B | Thin heavy once | RD55-RD30; | 1987 | 1990 | 1989 | 1991 |
| no further thinning | (33) | (21) | (15) | (31) | ||
| C | Delayed thinning | RD65-RD35; no further thinning | none | none | 1993 (19) | 1993 (33) |
| D | Repeated, heavy thinning | RD55-RD30; subsequent thinnings RD50-RD30 | 1987 (33) | 1990 (21) 2004 (34) | 1989 (15) 2001 (30) | 1993 (33) |
| E | Repeated, | RD55-RD35; | 1987(33) | 1996(27) | 1989(15) | 1991(31) |
| light thinning | RD55-RD40; subsequent thinnings RD60-RD40 | |||||
| Rotation age | (Final harvest age) | 51 | 36 | 45 | 32 | |
| Inst. (elev, m) | Plot | SI a | Density | BA b | QMD c | Ht | Avg Stem Taper | LCR d | LLAD Butt Log e |
|---|---|---|---|---|---|---|---|---|---|
| (slope, %) | m@50y | trees/ha | m2/ha | cm | m | cm/m | % | cm | |
| 803 | A | 36 | 791 | 56 | 30.0 | 36.6 | 1.05 | 30 | 2.54 |
| (585) | B | 37 | 306 | 45 | 43.4 | 39.0 | 1.12 | 37 | 2.54 |
| (1) | C | 35 | 899 | 52 | 26.9 | 35.1 | 0.97 | 29 | 1.78 |
| D | 35 | 336 | 45 | 41.4 | 35.4 | 1.17 | 33 | 3.30 | |
| E | 34 | 459 | 47 | 36.1 | 33.8 | 1.05 | 30 | 1.78 | |
| 805 | A | 38 | 860 | 52 | 27.7 | 30.8 | 0.94 | 36 | 4.57 |
| (168) | B | 40 | 454 | 40 | 33.5 | 31.4 | 1.03 | 37 | 3.05 |
| (15) | C | 39 | 366 | 33 | 34.0 | 32.3 | 1.00 | 41 | 4.32 |
| D | 41 | 420 | 42 | 35.6 | 32.0 | 1.24 | 39 | 2.79 | |
| E | 39 | 405 | 36 | 33.8 | 32.3 | 1.12 | 39 | 5.33 | |
| 807 | A | 33 | 1398 | 49 | 21.1 | 24.1 | 1.13 | 27 | 1.27 |
| (152) | B | 33 | 741 | 39 | 25.9 | 24.7 | 1.12 | 34 | 2.03 |
| (1) | C | 30 | 825 | 36 | 23.4 | 23.2 | 1.12 | 37 | 2.54 |
| D | 35 | 395 | 27 | 29.2 | 25.9 | 1.17 | 43 | 3.05 | |
| E | 37 | 929 | 40 | 23.4 | 27.1 | 1.05 | 33 | 0.76 | |
| 808 | A | 34 | 731 | 62 | 32.8 | 31.1 | 1.28 | 37 | 2.03 |
| (762) | B | 33 | 296 | 44 | 43.4 | 30.9 | 1.42 | 47 | 2.79 |
| (5) | C | - | - | - | - | - | - | - | - |
| D | 31 | 247 | 42 | 46.7 | 28.7 | 1.57 | 51 | 2.29 | |
| E | 33 | 351 | 50 | 42.4 | 30.8 | 1.46 | 39 | 3.05 |
| Inst. | Age | Tree | DBH | Height | Logs Processed | Lumber Pieces | Lumber Grade | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| yr | n | cm | m | n | n | pct | |||||
| Sel Str a | No. 1 | No. 2 | No. 3 | Econ b | |||||||
| 803 | 51 | 29 | 39.11 | 35.97 | 119 | 718 | 29 | 40 | 26 | 4 | 1 |
| 805 | 36 | 27 | 35.05 | 31.70 | 77 | 368 | 23 | 44 | 29 | 3 | 2 |
| 807 | 32 | 17 | 28.70 | 24.69 | 33 | 119 | 7 | 35 | 49 | 6 | 3 |
| 808 | 45 | 24 | 43.43 | 30.18 | 88 | 553 | 23 | 37 | 31 | 7 | 2 |
| Total | 97 | 317 | 1758 | ||||||||
| Site | Density | MOE | Sel Str (13,100) | No. 1 (11,721) | No. 2 (11,032) | No. 3 (9653) | Econ |
|---|---|---|---|---|---|---|---|
| (kg/m3) | MPa | ||||||
| 803 | 569 | 13,334 | 14,162 ^ | 12,473 * | 12,638 * | 12,555 ** | 12,052 |
| 805 | 551 | 11,625 | 12,114 | 11,438 | 11,052 ^ | 10,587 ** | 11,101 |
| 807 | 521 | 10,004 | 11,749 | 9694 | 9894 | 11,018 * | 10,949 |
| 808 | 580 | 11,521 | 13,017 | 11,321 | 10,839 | 9218 | 10,018 |
| Variable | Sel Str | No. 1 | No. 2 | No. 3 | Econ |
|---|---|---|---|---|---|
| Intercept | −3.4227 ** | 0.1283 | 1.4725 | −4.6907 *** | −5.9568 *** |
| Plot QMD | 0.0926 * | −0.0539 * | |||
| Tree DBH | 0.0943 *** | ||||
| Tree height | −0.1158 ** | ||||
| Tree taper | −4.3120 *** | ||||
| Log SED | 0.2006 *** | 0.0707 * | 0.1554 *** | 0.1007 ** | |
| Log LLAD | 0.1194 ** | ||||
| Log position | −1.6142 * | ||||
| 0.4847 | 0.0789 | 0.0097 | 0.0958 | 0.9674 |
| Variable | Sel Str | No. 1 | No. 2 | No. 3 | Econ |
|---|---|---|---|---|---|
| Intercept | 5.7471 ** | 1.9021 | −1.1781 + | −0.1635 | 1.620 |
| Installation slope | 0.0985 + | ||||
| Plot TPA | 0.0009 * | ||||
| Plot QMD | 0.0491 + | ||||
| Plot site index | −0.1135 * | −0.1440 ** | |||
| Tree DBH | −0.0481 * | ||||
| Tree height | 0.0994 *** | ||||
| Tree taper | −1.6227 + | 1.3858 ** | |||
| Tree velocity | 7.7888 * | ||||
| Log SED | −0.1264 *** | −0.0593 *** | −0.0384 * | −0.2373 + | |
| Log LLAD | 0.0773 * | ||||
| 0.0661 | 0.0097 | 0.0132 | 0.0058 | NA | |
| 1.4872 | 1.6036 | 1.3930 | 0.4116 | 1.8578 |
| Statistic | Value |
|---|---|
| Adjusted R-squared | 0.4279 |
| Root Mean Squared Error | 0.2015 |
| Mean Absolute Deviation | 0.1409 |
| Mean Bias | 2.4939 × 10−18 |
| Mean Percent Error | 0.7045 |
| Variable | Sel Str | No. 1 | No. 2 | No. 3 |
|---|---|---|---|---|
| Intercept | −10.2863 ** | −3.5808 *** | −4.1380 ** | −29.5200 * |
| Harvest age | 0.0997 ** | 0.0642 ** | ||
| Tree height | 0.2028 *** | |||
| Tree velocity | 21.5060 * | 83.0200 * | ||
| Log position | −3.0699 ** | −2.1948 ** | ||
| Log SED | 0.0642 ** | |||
| 0.0629 | 0.0770 | 0.1012 | 3.5360 |
| Variable | Sel Str | No. 1 | No. 2 | No. 3 |
|---|---|---|---|---|
| Intercept | −6.4760 + | −4.9053 + | 7.7580 *** | 9.495 *** |
| Tree velocity | 22.7280 ** | 16.6633 * | ||
| Tree taper | −3.6568 *** | −4.2934 *** | ||
| Log LLAD | −0.1663 * | |||
| 0.2970 | 9.142 × 10−16 | 4.113 × 10−16 | NA | |
| 4.4090 | 4.7690 | 4.3180 | 1.9061 |
| Statistic | Sel Str | No. 1 | No. 2 | No. 3 |
|---|---|---|---|---|
| Adjusted R-squared | 0.1533 | 0.0407 | 0.1405 | 0.3649 |
| Root Mean Squared Error | 0.3714 | 0.3804 | 0.3821 | 0.3092 |
| Mean Absolute Deviation | 0.3269 | 0.3320 | 0.3403 | 0.2153 |
| Mean Bias | −1.601 × 10−17 | 2.0497 × 10−17 | −5.7301 × 10−19 | −4.8720 × 10−18 |
| Mean Percent Error | 0.4631 | 0.5559 | 0.4952 | 0.2539 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowell, E.C.; Turnblom, E.C.; Comnick, J.M.; Huang, C. Effect of Rotation Age and Thinning Regime on Visual and Structural Lumber Grades of Douglas-Fir Logs. Forests 2018, 9, 576. https://doi.org/10.3390/f9090576
Lowell EC, Turnblom EC, Comnick JM, Huang C. Effect of Rotation Age and Thinning Regime on Visual and Structural Lumber Grades of Douglas-Fir Logs. Forests. 2018; 9(9):576. https://doi.org/10.3390/f9090576
Chicago/Turabian StyleLowell, Eini C., Eric C. Turnblom, Jeff M. Comnick, and CL Huang. 2018. "Effect of Rotation Age and Thinning Regime on Visual and Structural Lumber Grades of Douglas-Fir Logs" Forests 9, no. 9: 576. https://doi.org/10.3390/f9090576
APA StyleLowell, E. C., Turnblom, E. C., Comnick, J. M., & Huang, C. (2018). Effect of Rotation Age and Thinning Regime on Visual and Structural Lumber Grades of Douglas-Fir Logs. Forests, 9(9), 576. https://doi.org/10.3390/f9090576




