Next Article in Journal
Eddy Covariance vs. Biometric Based Estimates of Net Primary Productivity of Pedunculate Oak (Quercus robur L.) Forest in Croatia during Ten Years
Next Article in Special Issue
Variation in Climate Signals in Teak Tree-Ring Chronologies in Two Different Growth Areas
Previous Article in Journal
Investigation of Bamboo Grid Packing Properties Used in Cooling Tower
Previous Article in Special Issue
Recovery of Functional Diversity Following Shifting Cultivation in Tropical Monsoon Forests
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 9
Issue 12
10.3390/f9120763
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

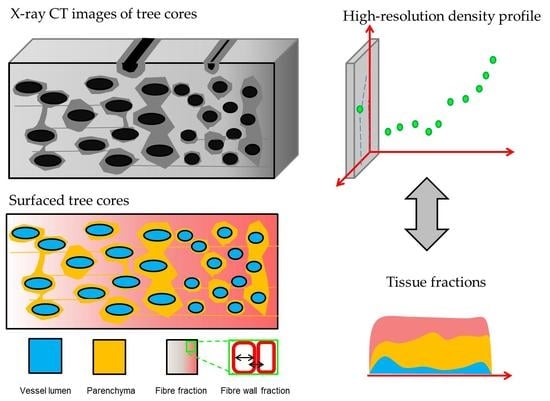
Wood Density Profiles and Their Corresponding Tissue Fractions in Tropical Angiosperm Trees

by
Tom De Mil
1,2,*,
Yegor Tarelkin
1,2,3,
Stephan Hahn
4,
Wannes Hubau
1,2,
Victor Deklerck
2,
Olivier Debeir
4,
Joris Van Acker
2,
Charles De Cannière
3,
Hans Beeckman
1 and
Jan Van den Bulcke
2
1
Royal Museum for Central Africa, Wood Biology Service, Leuvensesteenweg 13, B-3080 Tervuren, Belgium
2
UGCT-UGent-Woodlab, Laboratory of Wood Technology, Department of Environment, Ghent University, Coupure Links 653, B-9000 Gent, Belgium
3
Landscape Ecology and Plant Production Systems Unit, Université Libre de Bruxelles, CP 264/2, B-1050 Bruxelles, Belgium
4
Laboratory of Image, Signal processing and Acoustics—Brussels School of Engineering, Université libre de Bruxelles (ULB), B-1050 Brussels, Belgium
*
Author to whom correspondence should be addressed.
Forests 2018, 9(12), 763; https://doi.org/10.3390/f9120763
Submission received: 12 October 2018 / Revised: 22 November 2018 / Accepted: 27 November 2018 / Published: 7 December 2018
(This article belongs to the Special Issue Wood Science and Tropical Forest Ecology)
Browse Figures
Versions Notes

Abstract

:
Wood density profiles reveal a tree’s life strategy and growth. Density profiles are, however, rarely defined in terms of tissue fractions for wood of tropical angiosperm trees. Here, we aim at linking these fractions to corresponding density profiles of tropical trees from the Congo Basin. Cores of 8 tree species were scanned with X-ray Computed Tomography to calculate density profiles. Then, cores were sanded and the outermost 3 cm were used to semi-automatically measure vessel lumen, parenchyma and fibre fractions using the Weka segmentation tool in ImageJ. Fibre wall and lumen widths were measured using a newly developed semi-automated method. An assessment of density variation in function of growth ring boundary detection is done. A mixed regression model estimated the relative contribution of each trait to the density, with a species effect on slope and intercept of the regression. Position-dependent correlations were made between the fractions and the corresponding wood density profile. On average, density profile variation mostly reflects variations in fibre lumen and wall fractions, but these are species- and position-dependent: on some positions, parenchyma and vessels have a more pronounced effect on density. The model linking density to traits explains 92% of the variation, with 65% of the density profile variation attributed to the three measured traits. The remaining 27% is explained by species as a random effect. There is a clear variation between trees and within trees that have implications for interpreting density profiles in angiosperm trees: the exact driving anatomical fraction behind every density value will depend on the position within the core. The underlying function of density will thus vary accordingly.

Graphical Abstract

1. Introduction

Wood specific gravity or wood density is an integrating variable [1] and a property defined by chemical and anatomical traits [2]. In general, wood density is measured in the framework of ecology and carbon dynamics within and across species, taxa, and across a continent [3]. Wood density varies considerably from pith to bark, especially in tropical trees [4,5]. A large portion of the variation, especially in softwood, occurs between ring boundaries due to seasonal dynamics of wood formation [6], which is of particular importance in climate reconstructions and studies on impact of climate change on trees.
To study these inter and intra-annual patterns of density variation, high-resolution density profiles are needed. High-resolution densitometry can be obtained with blue intensity [7] or X-ray densitometry [8] systems that combine densitometry with anatomical observations [9,10], and many other devices exist as well [11]. X-ray Computed Tomography (CT) microdensitometry is a technique that allows obtaining 3D density volumes, that can be converted to large datasets of density profiles [12,13], with resolution ranging from submicron level [14] to coarser resolutions to perform tree-ring analysis [15,16]. Maximum latewood density of conifers is next to tree-ring width one of the parameters used to, for instance, reconstruct summer temperature [17], and earlywood is being explored as well [18]. The relation between density and cell fractions is straightforward for coniferous species: tracheid size lumina and the cell wall width of tracheids determine the density variation in a ring [18]. As such, a growth ring boundary is marked at the position where latewood to earlywood transition is associated with a sharp decrease. Densitometry is a promising technique to assist in tree ring analysis of some tropical tree species [19], but knowledge of underlying anatomical patterns that determine ring boundaries is necessary for its application.
Density profiles were constructed for tropical tree species shortly after the establishment of X-ray densitometry [8] for fast growing species such as Aucoumea klaineana Pierre [20] and Terminalia ivorensis A. Chev. [21], and more recently in semi-arid regions [22] in order to delineate ring boundaries or to assess wood quality. However, these profiles never related wood density to the underlying wood anatomical fractions. Density profiles for angiosperms are indeed less clearly defined compared to softwoods, as the underlying anatomical signal is more variable due to a combination of vessels, axial and ray parenchyma and fibres that vary within the growth ring. Attempts to disentangle density profiles locally into vessels, parenchyma and fibres have been reported for angiosperm temperate species such as Quercus petraea (Matt.) Liebl. [23] and in some tropical ones [24], but a plethora of angiosperm tropical species with a wide range of wood anatomical patterns [25] remains largely understudied. In the tropics, there is also a high level of unclear and less distinct ring borders and intra- and inter-ring variability of anatomical patterns due to weak seasonality. Moreover, density is regarded as a functional trait [1], but many uncertainties exist in what the underlying components cause density variations, which for angiosperms is a combination of wood anatomical variables [26] and other chemical components.
In this study, we define wood density profiles in terms of (i) ring boundaries and (ii) the underlying wood anatomical fractions. To do so, we compare high-resolution X-ray CT profiles with vessel, parenchyma and fibre wall fractions of eight common tropical species at high detail (110 µm). We investigate which anatomical feature influences wood density the most and explore the effect of species. Finally, we assess local radial variations that help in interpreting the density profile. We hypothesize that due to high anatomical variability, this relation will be different from species to species and depends on the radial position.

2. Materials and Methods

2.1. Study Site and Samples

To assess the general variability between density and tissue fractions, tree increment cores (ø 5.15 mm) were taken at breast height from eight species, one core per species (Table 1) from the Luki Biosphere reserve (Kongo Central province; 5.39° S 13.4° E), the Bolobo forests of Malebo (Mai-Ndombe province; 2.49° S, 16.50° E) and the Yoko reserve (Tshopo province; 0.33° N, 25.31° E), all in the Democratic Republic of the Congo. Those species were selected in order to represent a wide range of wood densities, life strategies and leaf shedding habits. All samples received a unique Tervuren Wood identification number of the Xylarium (Tw) and are stored at the Africamuseum Tervuren Xylarium (http://www.africamuseum.be/en/research/collections_libraries/biology/collections/xylarium). These samples were also verified via reference samples where microsections show detailed anatomy of the selected species (Figure 1).

2.2. X-Ray CT Densitometry

Wood cores were inserted in paper straws and oven dried for 24 hours before being scanned at 110 µm using the NanoWood CT facility [28], developed in collaboration with XRE (X-ray Engineering, www.XRE.be). The scanned images were reconstructed (GPU GeForce GPX 770 4 GB) with the Octopus reconstruction software package ([29,30], X-ray Engineering, www.XRE.be) and further processed (extraction of volumes, tilt correction, tangential correction) through a tailored toolchain [13]. X-ray CT wood density profiles result from correcting structure direction of fibre and ring deviations, calibrating with a reference material, and averaging in tangential and axial direction [15], based on 30–40 voxels at a given radial plane. The obtained wood density measurements are defined as ovendry wood weight, divided by ovendry volume, after calibrating with a reference material of known density [31].

2.3. Wood Anatomical Measurements

Cores were then glued in a wooden sample holder and their transversal surface was sanded with increasingly finer sandpaper (grit 80–1200). The last three cm of the outer wood (until the cambial zone) was imaged (StreamMotion, Olympus, Japan) on a scanning stage (SCAN 100 × 100, Märzhäuser Wetzlar, Germany) with a camera (3.2 MP, 2048 × 1536 pixels; UC30, Olympus (Tokyo, Japan)) mounted on a reflected light microscope (BX60, Olympus, magnification ×10). The final images consisted of overlapping images stitched together with the Multiple Image Alignment algorithm (Olympus). These images were then used to measure the fractions of different anatomical fractions (vessel lumina, axial and ray parenchyma, fibres). For the fibre fraction, the local fibre wall fractions (the ratio fibre wall/total cell size) were measured as well.

2.3.1. Parenchyma and Vessels

Delineating vessel lumina (VL) and parenchyma fractions (PRM) is a time-consuming process, and therefore these fractions were segmented using the trainable Weka plugin [32] in ImageJ [33]. The Weka plugin combines a set of machine learning algorithms, to perform pixel-based segmentations of images. In a graphical user interface, a sub-region was selected as training set and all vessels, parenchyma and fibres were manually labelled in that sub-region. The trained model was then applied on the entire image. A block processing approach was implemented for handling the rather large images and reducing processing speed on a desktop computer (Intel®Core™i5-4570 CPU @ 3.20 GHz 3.20 GHz, 16 GB RAM). The image was therefore subdivided using a user-defined grid, each grid cell was classified separately and all grid cells were stitched after processing resulting in a classification of the entire image. The results are displayed as a single probability map per feature, and each probability map has the same size as the original image and every pixel has a value between 0 and 1, indicating the probability of that feature. These probability maps were visually converted to binary maps via thresholding, for the final delineation of the anatomical fractions. Vessels filled with sawdust, not recognized by the algorithm, were indicated manually in ImageJ (Figure 2).
Binary maps of vessels and parenchyma were converted to profiles by tangential averaging in ImageJ. The images were also used as masks on the original images prior to measuring the lumen diameters and fibre wall thicknesses (Figure 2a). Fibres were delineated as subtract of total fraction (i.e., 1) minus the sum of parenchyma fraction and vessel lumen fraction at a given radial position.

2.3.2. Fibres

Fibre fraction (F) is then subdivided in fibre walls and fibre lumina. Fibre lumina diameter and wall thickness were measured using pattern recognition based on self-developed software. First, the original images were binarized in order to clearly separate fibre walls from lumina for further steps (Figure 3b): light-coloured pixels (corresponding to lumina) were selected with the colour thresholding tool in ImageJ. Adjacent selected pixels formed different shapes that were filtered based on their circularity and size to ensure that the retained shapes correspond to the fibre lumina.
For the detection of individual fibre lumina and wall thickness, we followed a protocol [34] consisting of a segmentation, tracking and measurement sequence. Segmentation detects and labels individual cells based on criteria such as the size, the shape and the surrounding pixel intensity variation ([35,36]; Figure 3c). Tracking allows connecting different fibre’s centroids to form the longest chains in the radial direction by using a nearest neighbours (KNN) algorithm: from the nth centroid, the nth + 1 was searched within a specified distance and with a maximum allowed angle of deviation from the radial direction (Figure 3d). Pixel intensity was then measured along numerous paths created by the tracking, with fibres lumina/walls showing pixels with high/low values. The width of fibres lumina and fibre walls was then measured by counting the number of adjacent pixels with high/low intensity values respectively. A user interface was developed to inspect the results at each process step and to adapt the segmentation parameters if required. Implementation of this user interface was based on the Scikit image [37] and Scikit learn [38] libraries in Python. The code is on an available repository (https://github.com/stephahn/WoodSection).
All measurements of the anatomical variables were interpolated to the coarser X-ray CT resolution of 110 µm so that each wood density at a given position corresponds to a value of fibre, vessel lumen and parenchyma fraction, as well as to the ratio of fibre wall/total fibre diameter (further referred to as fibre wall fraction (FW)). Fibre fraction is inversely related to the sum of the vessel lumen and parenchyma fraction and is thus a linear combination. Therefore, it was not taken in account for further analysis and model construction.

2.4. Model and Local Correlation

For the overall relationship between wood density and anatomy, we used a Gaussian linear mixed framework with random intercepts and slopes to investigate the potential of predicting wood density using the vessel lumina, parenchyma and fibre wall fraction as fixed effects and species as random effects. This model assesses the importance of a species effect in the relationship between wood density and wood anatomy, and was performed in R software (version 3.4.1, R Foundation for Statistical Computing, Vienna, Austria).
W D i , j = β 0 , k + β 1 , k x i , j , k + α 0 , j , k + α 1 , j , k ε i , j , k + ε i , j
where WD(i,j) are i-th measure of wood density of species j, β(0,k) is the intercept and β(1,k) is the slope for the k-th variable regardless of species, α(0,j,k) is the deviation from the global intercept and α(1,j,k) is the deviation from the global slope for the k-th variable of species j.
To analyze the spatially explicit local relationship between wood density and wood anatomy, we subdivided the density and anatomical measurements profiles into sections of 30 data points and constructed a linear model with parenchyma, vessel lumen and fibre wall fractions as explaining variables. All anatomical data was standardized per species (subtracted the values with the mean and divided by the standard deviation) in order to assess the relative importance of the three variables. Furthermore, we calculated Pearson correlation between wood density, parenchyma, vessel lumen fraction, total fibre fraction and fibre wall fraction, with a moving window of 30 points (trade-off between sufficient datapoints and the 110 µm resolution), which was performed in Matlab R2016b (Mathworks, Natick, MA, USA).

3. Results

3.1. General Wood Density—Anatomical Fractions Relationship

Average wood density values range from 510 kg·m−3 to 794 kg·m−3. On average, fibres form the highest fraction, followed by parenchyma and vessel lumen fractions. The fibre wall fraction of the total fibre fraction part varied between 0.22 and 0.49 (Table 2).
Overall, fibre wall fraction is positively correlated with wood density while vessel lumina and parenchyma slightly decrease density (Table 3). Fibre wall fraction impacts density the most, followed respectively by vessel and parenchyma fractions. The model also shows the importance of the species effect on the relationship between wood density and wood anatomy: more than 25% of wood density variability is influenced by species.
For all species, the fibre wall fraction appears to be the most important driver of wood density variability, as higher fibre wall fractions increase wood density (Figure 4a). The relation of vessel lumen fraction with wood density is, in most cases, the lowest of all anatomical fractions.
While the slopes of the regression lines between wood density and the fibre wall fraction are variable between species but remain positive (Figure 4a), the effects of parenchyma or vessels can vary strongly between species (Figure 4b,c). Parenchyma has a general positive effect on profiles (e.g., P. suaveolens and A. mannii). For three samples (E. angolense, T. didymostemon, P. angolensis), the vessel fraction does negatively influence the density profile (Figure 4b). While the influence of fibres remains positive throughout the profile, the influence of parenchyma and vessels can vary substantially from one sub-section of the core to the other: parenchyma can be both positively and negatively correlated to wood density within one individual and vessels, although not significant overall, can play an important role locally.

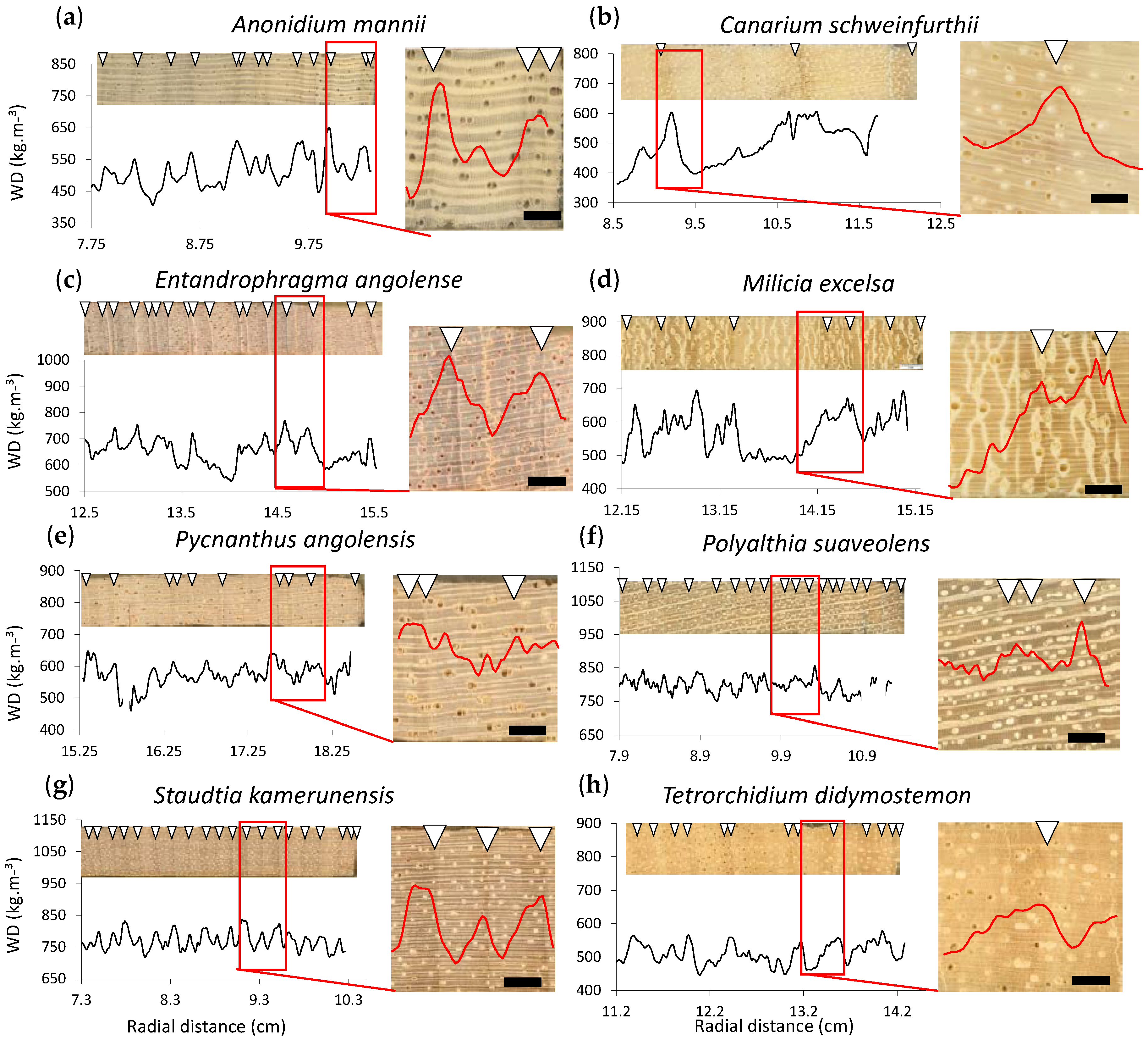
3.2. Local Definition of the Density Profile: Growth Ring Boundary Criterion

All species have varying radial patterns of wood density. Some species, such as P. suaveolens and S. kamerunensis, show small, high-frequency density variations along the profile (Figure 4f,g), while other species show large, low-frequency variations, seen as narrow and wide growth rings respectively.
Anonidium mannii boundaries are characterized by alternating fibre and parenchyma bands that narrow down towards the growth ring boundary (Figure 1a). This causes a density increase, seen in the profile (Figure 4a). Canarium schweinfurthii has a clear variation in fibre lumen and wall size, causing a density increase (Figure 4b). Entandrophragma angolense has a fibre lumen and wall size variation combined with terminal parenchyma, but also with clear density increases. In Milicia excelsa, there is a fibre variation and in some cases a terminal parenchyma band (Figure 1d). The density profiles show clear variations in density, but these are, in some cases, masked by parenchyma bands (Figure 4d). Ring boundaries of Pyncanthus angolensis are difficult to detect, despite the variation in density, as the ring boundary is indistinct: fibre lumen decrease is gradual (Figure 1e and Figure 4e). Alternating fibre and parenchyma bands determine the growth ring boundary in Polyalthia suaveolens, as well as distended rays (Figure 1f), but on the density profile these subtle anatomical changes are harder to detect (Figure 4f). Staudtia kamerunensis shows flattened fibres towards the end of the growth ring, only in some cases accompanied with a terminal parenchyma band (Figure 1g), and this is clearly seen in the density profile as peaks (Figure 4g). Tetrorchidium didymostemon is characterised by flattened fibres as well (Figure 4h but not seen in Figure 1h), but this is subtle, and although clear variation is seen, the ring limit is not so sharp and difficult to observe in the density profile.

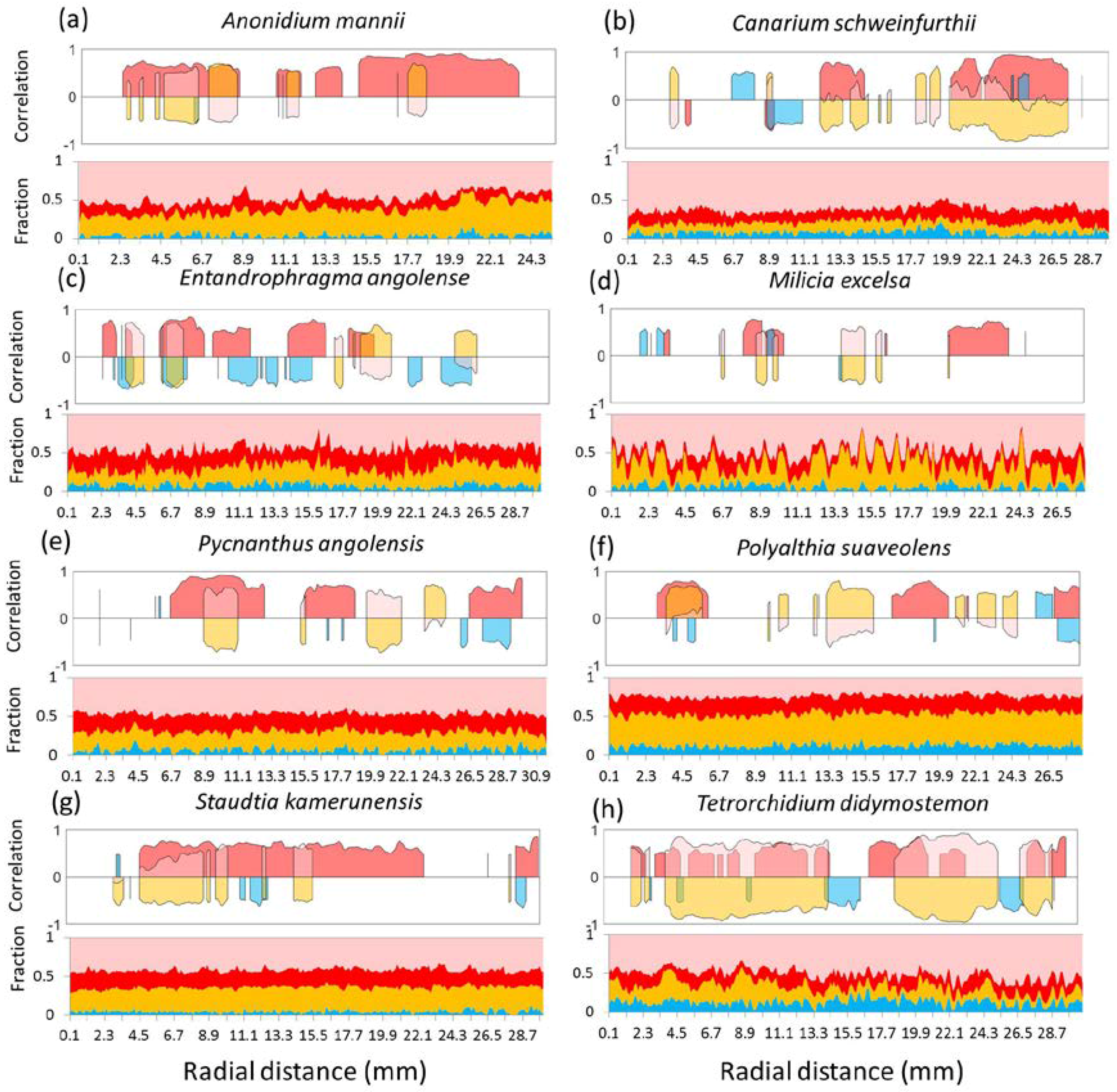
3.3. Local Radial Variation in the Relation between Wood Density and Wood Anatomical Fractions

When assessing the exact local correlation between each of the variables and the wood density values at a given position, these values change considerably. The moving correlations (Figure 5) show that each of the components can prevail at a certain radial position. On species such as Entandrophragma angolense (Figure 5c), the vessel lumina fraction does influence the density profile locally at most, especially between growth ring boundaries. For Tetrorchidium didymostemon (Figure 5h) and Canarium schweinfurthii (Figure 5b), parenchyma and total fibre fraction act inversely to a high extent in certain regions negatively and positively in certain regions. For Polyalthia suaveolens (Figure 5f), parenchyma positively influences the density profile. In species such as Staudtia kamerunensis (Figure 5g) and Anonidium manii, the fibre wall fractions determine wood density variations the most (Figure 5a), which can also be seen due to the growth ring structure of flattened fibres (Figure 1a,g). Milicia excelsa shows high correlation with fibre wall fraction at the growth ring boundaries (Figure 1d), whereas in between, parenchyma bands determine the density pattern (Figure 5d). For Pycnanthus angolensis, the variation between prevailing fractions is large (Figure 5e).

4. Discussion

A general positive influence of fibre wall fraction on wood density was described by previous studies [24,39,40]. Fibre fractions and fibre wall fraction within this fibre fraction determine the area occupied by walls and by lumina which affects wood density the most (Table 3). Differences in average wood density between species are thus driven by the fractions of their anatomy.
Although several tropical species show ring boundaries defined by density fluctuations due to fibre wall thickness variations [31,41], we show that other types of tissue also influence wood density and that other density variations are due to fractions other than fibres. So far, it appears difficult to detect rings delimited by parenchyma bands or vessels, whereas for flattened fibres, this appears evident, as seen in Figure 1 and Figure 4. This additional variability of the density profile makes fibre-driven density variations difficult to detect among all the others [42]. Density profiles can show tropical tree-ring boundaries in some cases, and we showed that wood density is only closely related to species with clear fibre wall variation. The visibility of macroscopically visible growth ring boundaries on the density profile depends on the four anatomical types of growth ring boundaries [43,44,45].
Species-specific interactions between parenchyma and other xylem fractions can also occur: parenchyma bands can be associated with vessels (i.e., confluent parenchyma Milicia excelsa, Figure 1d and Figure 4d), which potentially mixes the effects of both fractions and makes it difficult to measure the influence on wood density of parenchyma alone.
The link between wood density and vessel lumen fraction is also variable. Although vessel lumina represent “void volume” [2] and can locally significantly impact wood density, they have only a limited influence overall in the density profile variation (Table 3). Moreover, its negative effect on wood density can be counteracted by other anatomical factors, such as associated parenchyma or fibres of reduced lumen size.
Our results stress the importance of studying the species-specific wood anatomy–wood density relationship. Different anatomical fractions vary within different ranges and their effect on wood density varies in function of the studied species and the position within the growth ring, as shown in Figure 5.
Density variability at different radial positions is difficult to capture if studying only averaged values of anatomical measurements over large sections of wood (e.g., determined via water immersion method) so that several local trends (e.g., the vessel–wood density relationship, Figure 5c) might be missed. Given the definition of wood density as a property [2], depending on the position within the stem, this wood density could be a property of stability (fibre and fibre wall fractions), protection (parenchyma), and hydraulics (vessel lumina) and these properties vary from one radial position to another.
In this study, parenchyma was simplistically considered as a tissue with uniform properties and influence on wood density, it is a complex tissue with different cell types and dimensions: rays and axial parenchyma have different biological functions that influence their size, chemical composition and density [46,47]. The observed variability of the parenchyma effect on wood density may thus be driven by differences in size of parenchyma cells between species. In some positions, parenchyma positively influenced wood density (Figure 5a,f): no distinction is made between axial and ray parenchyma here, while it has been proven that axial parenchyma decreases density, whereas ray parenchyma increases wood density [48]. The effect of this latter relation will also depend on the fraction (i.e., width) of the rays, which will vary between species.
Given the above, we observe that different tissue fractions determine wood density at some positions. Thus, discussing wood density as a functional trait is problematic [49]. Despite the general trend of fibre wall fraction determining wood density, in some positions, other tissues such as parenchyma and vessels drive wood density variations. When low variation of fibre wall fraction concurs with a constant fraction of vessels and parenchyma, the density variation will be minimal as well (seen as blank areas with no correlation in Figure 5) and no relation can be established between wood density variation and the variation of the tissue fractions. This highlights the complexity of the relationship of wood density with its fractions: it can significantly vary between species but also along the radial direction.

5. Conclusions

In this study, we present the link between wood density and tissue fractions at the submillimetre level. We first assessed the anatomy and ring boundaries on flatbed images to find whether these are also visible on the density profile. Then, the density profile in terms of wood anatomical fractions was defined by using a combination of existing software and newly developed tools for quantification of fibre wall fraction. It was shown that the growth ring boundary is in some cases visible in the density profile, especially when flattened fibres are anatomically observed on the growth ring boundaries. Other types of ring boundaries, such as marginal parenchyma, are difficult to observe in a one-dimensional density profile alone. When comparing wood density to the wood anatomical traits in general, fibre wall fraction has the largest effect on wood density, whereas vessels and parenchyma affect wood density more locally and in a more varying way. The variation shown here encourages future work disentangling the local differences in the wood density–wood anatomical fraction relationship, especially in tropical species with a high diversity in wood anatomical patterns.

Author Contributions

T.D.M., Y.T., S.H., W.H., O.D., J.V.A., C.D.C, H.B., and J.V.d.B. conceptualized the study; methodology was developed by T.D.M, Y.T., V.D., W.H., and S.H.; software on fibre lumen and fibre width was developed by Y.T. and S.H.; software on densitometry by J.V.d.B and T.D.M; validation was done by V.D. and W.H.; formal analysis was done by T.D.M. and Y.T. Original draft was prepared by T.D.M. and Y.T.; review and editing was done by all authors; visualization, optimized by V.D. and W.H.; supervision done by O.D., J.V.A., C.D.C, H.B., and J.V.d.B.

Funding

T.D.M. and V.D. were funded by the HERBAXYLAREDD BELSPO Brain program (Federaal Wetenschapsbeleid) of the Belgian Federal Government (BR/143/A3/HERBAXYLAREDD). The PhD project of T.D.M and the tenure track of J.V.d.B. were supported by Ghent University Special Research Fund (BOF) (grant no. for T.D.M.: BOF.DOC.2014.0037.01). W.H. was funded by the BELSPO Brain program (Federaal Wetenschapsbeleid) of the Belgian Federal Government (BR/132/A1/AFRIFORD). Y.T. is funded by FRIA (FC 1371), as well as Jaumotte Demoulin Foundation and Van Buren Fund. Field missions were partly covered by the Leopold III fund for Nature Conservation. The PhD of S.H. was funded by the BRIDGE programme of Innoviris (2013-PFS-EH-7).

Acknowledgments

Sample preparation was assisted by Kévin Lievens, Stijn Willen, and Jean-Claude Serre. Logistics in the field were also made possible by WWF RDC (Laurent Nsenga). Logistics were also provided by INERA-RDC. We also want to thank three reviewers for their valuable comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Lachenbruch, B.; Mcculloh, K.A. Traits, properties, and performance: How woody plants combine hydraulic and mechanical functions in a cell, tissue, or whole plant. New Phytol. 2014, 204, 747–764. [Google Scholar] [CrossRef] [PubMed]
  3. Baker, T.R.; Phillips, O.L.; Malhi, Y.; Almeida, S.; Arroyo, L.; Di Fiore, A.; Erwin, T.; Killeen, T.J.; Laurance, S.G.; Laurance, W.F.; et al. Variation in wood density determines spatial patterns in Amazonian forest biomass. Glob. Chang. Biol. 2004, 10, 545–562. [Google Scholar] [CrossRef]
  4. Hietz, P.; Valencia, R.; Joseph Wright, S. Strong radial variation in wood density follows a uniform pattern in two neotropical rain forests. Funct. Ecol. 2013, 27, 684–692. [Google Scholar] [CrossRef] [Green Version]
  5. Bastin, J.F.; Fayolle, A.; Tarelkin, Y.; Van Den Bulcke, J.; De Haulleville, T.; Mortier, F.; Beeckman, H.; Van Acker, J.; Serckx, A.; Bogaert, J.; et al. Wood specific gravity variations and biomass of central African tree species: The simple choice of the outer wood. PLoS ONE 2015, 10, e0142146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Bouriaud, O.; Leban, J.-M.; Bert, D.; Deleuze, C. Intra-annual variations in climate influence growth and wood density of Norway spruce. Tree Physiol. 2005, 25, 651–660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Björklund, J.A.; Gunnarson, B.E.; Seftigen, K.; Esper, J.; Linderholm, H.W. Blue intensity and density from northern Fennoscandian tree rings, exploring the potential to improve summer temperature reconstructions with earlywood information. Clim. Past 2014, 10, 877–885. [Google Scholar] [CrossRef]
  8. Polge, H. Établissement des courbes de variation de la densité du bois par exploration densitométrique de radiographies d’échantillons prélevés à la tarière sur des arbres vivants. Applications dans les domaines Technologique et Physiologique. Ann. Sci. For. 1966, 23, 215. [Google Scholar] [CrossRef]
  9. Evans, R. Rapid measurement of the transverse Dimensions of Tracheids in radial wood sections from Pinus radiata. Holzforschung 1994, 48, 168–172. [Google Scholar] [CrossRef]
  10. Chen, F.F.; Evans, R. Automated measurement of vessel properties in birch and poplar wood. Holzforschung 2010, 64, 369–374. [Google Scholar] [CrossRef]
  11. Jacquin, P.; Longuetaud, F.; Leban, J.M.; Mothe, F. X-ray microdensitometry of wood: A review of existing principles and devices. Dendrochronologia 2017, 42, 42–50. [Google Scholar] [CrossRef]
  12. Bergsten, U.; Lindeberg, J.; Rindby, A.; Evans, R. Batch measurements of wood density on intact or prepared drill cores using x-ray microdensitometry. Wood Sci. Technol. 2001, 35, 435–452. [Google Scholar] [CrossRef]
  13. De Mil, T.; Vannoppen, A.; Beeckman, H.; Van Acker, J.; Van den Bulcke, J. A field-to-desktop toolchain for X-ray CT densitometry enables tree ring analysis. Ann. Bot. 2016, 117, 1187–1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Van den Bulcke, J.; Boone, M.N.; Van Acker, J.; Stevens, M.; Van Hoorebeke, L. X-ray tomography as a tool for detailed anatomical analysis. Ann. For. Sci. 2009, 66, 1–12. [Google Scholar] [CrossRef]
  15. Van den Bulcke, J.; Wernersson, E.L.G.; Dierick, M.; Van Loo, D.; Masschaele, B.; Brabant, L.; Boone, M.N.; Van Hoorebeke, L.; Haneca, K.; Brun, A.; et al. 3D tree-ring analysis using helical X-ray tomography. Dendrochronologia 2014, 32, 39–46. [Google Scholar] [CrossRef]
  16. Steffenrem, A.; Kvaalen, H.; Dalen, K.S.; Høibø, O.A. A high-throughput X-ray-based method for measurements of relative wood density from unprepared increment cores from Picea abies. Scand. J. For. Res. 2014, 29, 506–514. [Google Scholar] [CrossRef]
  17. Briffa, K.R. Trees tell of past climates: But are they speaking less clearly today? Philos. Trans. R. Soc. Lond. B Biol. Sci. 1998, 353, 65–73. [Google Scholar] [CrossRef]
  18. Björklund, J.; Seftigen, K.; Schweingruber, F.; Fonti, P.; von Arx, G.; Bryukhanova, M.V.; Cuny, H.E.; Carrer, M.; Castagneri, D.; Frank, D.C. Cell size and wall dimensions drive distinct variability of earlywood and latewood density in Northern Hemisphere conifers. New Phytol. 2017, 216, 728–740. [Google Scholar] [CrossRef] [PubMed]
  19. Goldstein, G.; Santiago, S.L. Tropical Tree Physiology; Springer: Berlin, Germany, 2016; p. 467. ISBN 9783319274201. [Google Scholar]
  20. Mariaux, A. Les cernes dans les bois tropicaux africains, nature et périodicité: Peuvent-ils révéler l’âge des arbres? Bois For. Trop. 1967, 113, 3–14. [Google Scholar]
  21. Nepveu, G. Croissance et qualité du bois de framiré. Evolution de la largeur de cerne et des composantes densitométriques en fonction de l’âge. Bois For. Trop. 1976, 165, 39–58. [Google Scholar]
  22. Pagotto, M.A.; DeSoto, L.; Carvalho, A.; Nabais, C.; Filho, M.T.; Ribeiro, A.; Lisi, C.S. Evaluation of X-ray densitometry to identify tree-ring boundaries of two deciduous species from semi-arid forests in Brazil. Dendrochronologia 2017, 42, 94–103. [Google Scholar] [CrossRef]
  23. Guilley, E.; Mothe, F.; Nepveu, G. A procedure based on conditional probabilities to estimate proportions and densities of tissues from X-ray images of Quercus petraea samples. IAWA J. 2002, 23, 235–252. [Google Scholar] [CrossRef]
  24. Roque, R.M.; Tomazelo-Filho, M. Relationships between anatomical features and intra-ring wood density profiles in Gmelina arborea applying X-ray densitometry. Cerne 2007, 13, 384–392. [Google Scholar]
  25. Fichtler, E.; Worbes, M. Wood anatomical variables in tropical trees and their relation to site conditions and individual tree morphology. IAWA J. 2012, 33, 119–140. [Google Scholar] [CrossRef]
  26. Leclercq, A. Influence of beechwood anatomical features upon its physico-mechanical properties. Mitt. Bundesforsch. Forst-Holzw. Hamburg Reinbek 1980, 131, 33–47. [Google Scholar]
  27. Benedet, F.; Doucet, J.; Fayolle, A.; Gourlet-Fleury, S.; Vincke, D. Cofortraits, African Plant Traits Information Database. Version 1.0. Available online: http://coforchange.cirad.fr/african_plant_trait (accessed on 12 October 2018).
  28. Dierick, M.; Van Loo, D.; Masschaele, B.; Van den Bulcke, J.; Van Acker, J.; Cnudde, V.; Van Hoorebeke, L. Recent micro-CT scanner developments at UGCT. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2014, 324, 35–40. [Google Scholar] [CrossRef] [Green Version]
  29. Dierick, M.; Masschaele, B.; Van Hoorebeke, L. Octopus, a fast and user-friendly tomographic reconstruction package developed in LabView®. Meas. Sci. Technol. 2004, 15, 1366–1370. [Google Scholar] [CrossRef]
  30. Vlassenbroeck, J.; Dierick, M.; Masschaele, B.; Cnudde, V.; Van Hoorebeke, L.; Jacobs, P. Software tools for quantification of X-ray microtomography at the UGCT. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 580, 442–445. [Google Scholar] [CrossRef]
  31. De Ridder, M.; Van den Bulcke, J.; Vansteenkiste, D.; Van Loo, D.; Dierick, M.; Masschaele, B.; De Witte, Y.; Mannes, D.; Lehmann, E.; Beeckman, H.; et al. High-resolution proxies for wood density variations in Terminalia superba. Ann. Bot. 2011, 107, 293–302. [Google Scholar] [CrossRef]
  32. Arganda-Carreras, I.; Kaynig, V.; Rueden, C.; Eliceiri, K.W.; Schindelin, J.; Cardona, A.; Seung, H.S. Trainable Weka Segmentation: A machine learning tool for microscopy pixel classification. Bioinformatics 2017, 33, 2424–2426. [Google Scholar] [CrossRef]
  33. Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Kennel, P.; Subsol, G.; Guéroult, M.; Borianne, P. Automatic identification of cell files in light microscopic images of conifer wood. In Proceedings of the 2010 2nd International Conference on Image Processing Theory, Tools and Applications, Paris, France, 7–10 July 2010; pp. 98–103. [Google Scholar] [CrossRef]
  35. Wu, K.; Otoo, E.; Shoshani, A. Optimizing connected component labeling algorithms. In Proceedings of the Medical Imaging 2005: Image Processing, San Diego, CA, USA, 12–17 February 2005. [Google Scholar] [CrossRef]
  36. Fiorio, C.; Gustedt, J. Two linear time Union-Find strategies for image processing. Theor. Comput. Sci. 1996, 154, 165–181. [Google Scholar] [CrossRef]
  37. Van Der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
  38. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
  39. Ziemińska, K.; Butler, D.W.; Gleason, S.M.; Wright, I.J.; Westoby, M. Fibre wall and lumen fractions drive wood density variation across 24 Australian angiosperms. AoB Plants 2013, 5. [Google Scholar] [CrossRef] [Green Version]
  40. Dadzie, P.K.; Amoah, M.; Frimpong-Mensah, K.; Shi, S.Q. Comparison of density and selected microscopic characteristics of stem and branch wood of two commercial trees in Ghana. Wood Sci. Technol. 2016, 50, 91–104. [Google Scholar] [CrossRef]
  41. Worbes, M. One hundred years of tree-ring research in the tropics-a brief history and an outlook to future challenges. Dendrochronologia 2002, 20, 217–231. [Google Scholar] [CrossRef]
  42. Worbes, M. How to Measure Growth Dynamics in Tropical Trees. IAWA J. 1995, 16, 337–351. [Google Scholar] [CrossRef]
  43. Worbes, M. Structural and other adaptations to long-term flooding by trees in Central Amazonia. Amazoniana 1985, 9, 459–484. [Google Scholar]
  44. Coster, C. Zur anatomie und physiologie der zuwachszonen-und jahresringbildung in den tropen. Ann. Jard. Bot. Buitenzorg 1927, 37, 49–161. [Google Scholar]
  45. Tarelkin, Y.; Delvaux, C.; De Ridder, M.; El Berkani, T.; De Cannière, C.; Beeckman, H. Growth-ring distinctness and boundary anatomy variability in tropical trees. IAWA J. 2016, 37, S1–S7. [Google Scholar] [CrossRef]
  46. Spicer, R. Symplasmic networks in secondary vascular tissues: Parenchyma distribution and activity supporting long-distance transport. J. Exp. Bot. 2014, 65, 1829–1848. [Google Scholar] [CrossRef] [PubMed]
  47. Morris, H.; Plavcová, L.; Cvecko, P.; Fichtler, E.; Gillingham, M.A.F.; Martínez-Cabrera, H.I.; Mcglinn, D.J.; Wheeler, E.; Zheng, J.; Ziemiska, K.; et al. A global analysis of parenchyma tissue fractions in secondary xylem of seed plants. New Phytol. 2016, 209, 1553–1565. [Google Scholar] [CrossRef] [PubMed]
  48. Zheng, J.; Martínez-Cabrera, H.I. Wood anatomical correlates with theoretical conductivity and wood density across China: Evolutionary evidence of the functional differentiation of axial and radial parenchyma. Ann. Bot. 2013, 112, 927–935. [Google Scholar] [CrossRef] [PubMed]
  49. Beeckman, H. Wood anatomy and trait-based ecology. IAWA J. 2016, 37, 127–151. [Google Scholar] [CrossRef]
Forests 09 00763 g001a 550Forests 09 00763 g001b 550
Figure 1. Microscopic sections of Tervuren Wood references samples of the corresponding species, showing wood anatomy, and, when available, the growth ring boundaries (white triangles). The species are mostly diffuse porous, with vessels solitary or slightly grouped. (a) Anonidium mannii, Tw72, (b) Canarium schweinfurthii, Tw61151, (c) Entandrophragma angolense Tw1432, (d) Milicia escelsa Tw943, (e) Pycnanthus angolensis Tw1513, (f) Polyaltia suaveolens Engl. & Diels. Tw32618, (g) Staudtia kamerunensis Tw62707, and (h) Tetrorchidium didymostemon Tw2049. Scale bar: 200 µm.
Figure 1. Microscopic sections of Tervuren Wood references samples of the corresponding species, showing wood anatomy, and, when available, the growth ring boundaries (white triangles). The species are mostly diffuse porous, with vessels solitary or slightly grouped. (a) Anonidium mannii, Tw72, (b) Canarium schweinfurthii, Tw61151, (c) Entandrophragma angolense Tw1432, (d) Milicia escelsa Tw943, (e) Pycnanthus angolensis Tw1513, (f) Polyaltia suaveolens Engl. & Diels. Tw32618, (g) Staudtia kamerunensis Tw62707, and (h) Tetrorchidium didymostemon Tw2049. Scale bar: 200 µm.
Forests 09 00763 g001aForests 09 00763 g001b
Forests 09 00763 g002 550
Figure 2. Flowchart for delineating vessels and parenchyma on a segment of a sanded surface of Polyalthia suaveolens with the trainable Weka plugin. The plugin assesses the probability for different portions of the image to be classified as vessel or parenchyma before being manually corrected. (a) Original sanded surface is imaged, (b) probability map for parenchyma with mismatches for vessel lumina, (c) correction through manual indication of vessels to become binary images of (d) vessel lumina and (e) parenchyma fractions. (f) Fibre fraction, as the subtract of the total image with vessel and parenchyma fraction. Scale 500 µm.
Figure 2. Flowchart for delineating vessels and parenchyma on a segment of a sanded surface of Polyalthia suaveolens with the trainable Weka plugin. The plugin assesses the probability for different portions of the image to be classified as vessel or parenchyma before being manually corrected. (a) Original sanded surface is imaged, (b) probability map for parenchyma with mismatches for vessel lumina, (c) correction through manual indication of vessels to become binary images of (d) vessel lumina and (e) parenchyma fractions. (f) Fibre fraction, as the subtract of the total image with vessel and parenchyma fraction. Scale 500 µm.
Forests 09 00763 g002
Forests 09 00763 g003 550
Figure 3. Flowchart of the preparation of a segment of a sanded surface on Pycnanthus angolensis for measurement of fibre wall thickness and lumina diameter. (a) Original sanded and scanned image, where parenchyma and vessel lumina were masked (obtained with Weka segmentation plugin in imageJ). (b) Binarization of the image in order to separate fibre lumina and walls. (c) Recognition and labelling of individual cells and (d) tracking and linking of individual cells. Pixel intensity is then analysed along the numerous created paths and the widths of lumina and fibre walls extracted. Scale 100 µm.
Figure 3. Flowchart of the preparation of a segment of a sanded surface on Pycnanthus angolensis for measurement of fibre wall thickness and lumina diameter. (a) Original sanded and scanned image, where parenchyma and vessel lumina were masked (obtained with Weka segmentation plugin in imageJ). (b) Binarization of the image in order to separate fibre lumina and walls. (c) Recognition and labelling of individual cells and (d) tracking and linking of individual cells. Pixel intensity is then analysed along the numerous created paths and the widths of lumina and fibre walls extracted. Scale 100 µm.
Forests 09 00763 g003
Forests 09 00763 g004 550
Figure 4. Visual interpretation of the density profile. Sanded wood core sections in upper panel, where ring widths were indicated. The outermost section of density profiles of 8 selected species from the Congo Basin, with a zoom showing to what extent the ring boundaries visually indicated with white triangles on the wood surface, concur with the density profile at the ring boundary. Wood density is defined as the ovendry wood density (kg·m−3). Species shown are (a) Anonidium mannii, (b) Canarium schweinfurthii, (c) Entandrophragma angolense, (d) Milicia excelsa, (e) Pycnanthus angolensis, (f) Polyalthia suaveolens, (g) Staudtia kamerunensis, and (h) Tetrorchidium didymostemom. Scalebar 500 µm.
Figure 4. Visual interpretation of the density profile. Sanded wood core sections in upper panel, where ring widths were indicated. The outermost section of density profiles of 8 selected species from the Congo Basin, with a zoom showing to what extent the ring boundaries visually indicated with white triangles on the wood surface, concur with the density profile at the ring boundary. Wood density is defined as the ovendry wood density (kg·m−3). Species shown are (a) Anonidium mannii, (b) Canarium schweinfurthii, (c) Entandrophragma angolense, (d) Milicia excelsa, (e) Pycnanthus angolensis, (f) Polyalthia suaveolens, (g) Staudtia kamerunensis, and (h) Tetrorchidium didymostemom. Scalebar 500 µm.
Forests 09 00763 g004
Forests 09 00763 g005 550
Figure 5. Moving significant (p < 0.05) Pearson correlation plots (window width = 30 density values) in upper panel with fibre wall fraction (red), fibre lumina (pink), parenchyma (orange), and vessels (blue). Bottom panel shows fractions with fibre walls (red), fibre lumina (pink), parenchyma (orange), and vessels (blue). Species shown are (a) Anonidium mannii, (b) Canarium schweinfurthii, (c) Entandrophragma angolense, (d) Milicia excelsa, (e) Pycnanthus angolensis, (f) Polyalthia suaveolens, (g) Staudtia kamerunensis, and (h) Tetrorchidium didymostemon.
Figure 5. Moving significant (p < 0.05) Pearson correlation plots (window width = 30 density values) in upper panel with fibre wall fraction (red), fibre lumina (pink), parenchyma (orange), and vessels (blue). Bottom panel shows fractions with fibre walls (red), fibre lumina (pink), parenchyma (orange), and vessels (blue). Species shown are (a) Anonidium mannii, (b) Canarium schweinfurthii, (c) Entandrophragma angolense, (d) Milicia excelsa, (e) Pycnanthus angolensis, (f) Polyalthia suaveolens, (g) Staudtia kamerunensis, and (h) Tetrorchidium didymostemon.
Forests 09 00763 g005
Table
Table 1. Summary of the collected species that were used to link wood density to the tissue fractions. Diameter at breast height (DBH) of the sampled tree and Tervuren Wood identification number at the xylarium (Tw) is given as well. Life strategy and leaf phenology was extracted from [27].
Table 1. Summary of the collected species that were used to link wood density to the tissue fractions. Diameter at breast height (DBH) of the sampled tree and Tervuren Wood identification number at the xylarium (Tw) is given as well. Life strategy and leaf phenology was extracted from [27].
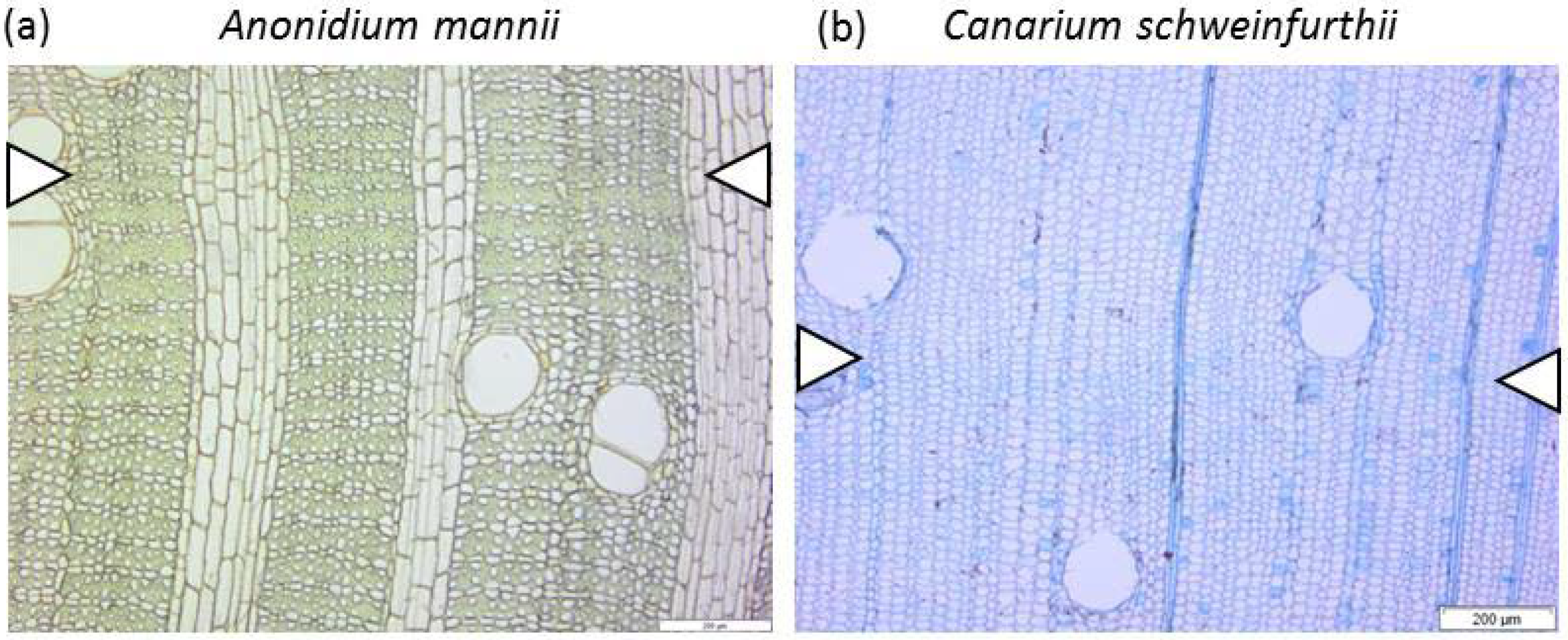
Test SpeciesTw LabelFamilyDBH (cm)SiteLife StrategyPhenology
Anonidium mannii (Oliv.) Engl. & DielsTw64366Annonaceae26.7MaleboShade bearerEvergreen
Canarium schweinfurthii Engl.Tw78659Burseraceae31.7LukiLight demandingDeciduous
Entandrophragma angolense (Welw.) C.DC.Tw78727Meliaceae37.2MaleboLight demandingDeciduous
Milicia excelsa (Welw.) C.C. BergTw78904Moraceae32LukiLight demandingDeciduous
Pycnanthus angolensis (Welw.) Warb.Tw78728Myristicaceae44MaleboLight demandingEvergreen
Polyalthia suaveolens Engl. & DielsTw68771Annonaceae27.5YokoShade bearerEvergreen
Staudtia kamerunensis Warb.Tw68713Myristicaceae23.8LukiShade bearerEvergreen
Tetrorchidium didymostemon (Baill.) Pax & K.Hoffm.Tw78828Myristicaceae33.4LukiLight demandingEvergreen
Table
Table 2. Measured values of the 8 tested samples. Wood density (WD, kg/m³), parenchyma fraction (PRM), vessel lumina fraction (VL), as well as fibre (F) and fibre wall fraction (FW, defined as the fibre wall width divided by the sum of fibre wall and lumen diameter). Standard deviation is given between brackets.
Table 2. Measured values of the 8 tested samples. Wood density (WD, kg/m³), parenchyma fraction (PRM), vessel lumina fraction (VL), as well as fibre (F) and fibre wall fraction (FW, defined as the fibre wall width divided by the sum of fibre wall and lumen diameter). Standard deviation is given between brackets.
SpeciesWD (kg·m−3)PRM (-)VL (-)F (-)FW (-)
A. mannii513.15 (48.77)0.34 (0.07)0.04 (0.03)0.62 (0.09)0.23 (0.06)
C. schweinfurthii500.91 (60.75)0.13 (0.03)0.09 (0.04)0.78 (0.04)0.22 (0.04)
E. angolense651.89 (47.61)0.23 (0.07)0.08 (0.04)0.69 (0.08)0.35 (0.06)
M. excelsa571.17 (57.71)0.28 (0.14)0.06 (0.04)0.66 (0.16)0.25 (0.06)
P. angolensis570.79 (36.30)0.23 (0.03)0.07 (0.04)0.7 (0.04)0.33 (0.03)
P. suaveolens794.36 (25.82)0.42 (0.03)0.12 (0.04)0.46 (0.04)0.49 (0.06)
S. kamerunensis768.67 (26.51)0.31 (0.03)0.05 (0.02)0.64 (0.03)0.35 (0.05)
T. didymostemon510.30 (30.72)0.19 (0.08)0.13 (0.05)0.67 (0.09)0.25 (0.05)
Table
Table 3. Coefficients from a Gaussian linear mixed model (random intercept + slope) predicting wood density from the anatomical variables for 8 tropical species investigated. Coefficient estimates are provided for the fixed effects (at 95% of confidence interval).
Table 3. Coefficients from a Gaussian linear mixed model (random intercept + slope) predicting wood density from the anatomical variables for 8 tropical species investigated. Coefficient estimates are provided for the fixed effects (at 95% of confidence interval).
Fixed effects
Intercept490.92
Parenchyma fraction−24.39
Vessel lumina fraction−94.22
Fibre wall fraction453.67
% of variance65%
Random effectsContribution to total variance (%)
Species4
Species|parenchyma4
Species|vessels6
Species|fibre walls13
Residuals8

Share and Cite

MDPI and ACS Style

De Mil, T.; Tarelkin, Y.; Hahn, S.; Hubau, W.; Deklerck, V.; Debeir, O.; Van Acker, J.; De Cannière, C.; Beeckman, H.; Van den Bulcke, J. Wood Density Profiles and Their Corresponding Tissue Fractions in Tropical Angiosperm Trees. Forests 2018, 9, 763. https://doi.org/10.3390/f9120763

AMA Style

De Mil T, Tarelkin Y, Hahn S, Hubau W, Deklerck V, Debeir O, Van Acker J, De Cannière C, Beeckman H, Van den Bulcke J. Wood Density Profiles and Their Corresponding Tissue Fractions in Tropical Angiosperm Trees. Forests. 2018; 9(12):763. https://doi.org/10.3390/f9120763

Chicago/Turabian Style

De Mil, Tom, Yegor Tarelkin, Stephan Hahn, Wannes Hubau, Victor Deklerck, Olivier Debeir, Joris Van Acker, Charles De Cannière, Hans Beeckman, and Jan Van den Bulcke. 2018. "Wood Density Profiles and Their Corresponding Tissue Fractions in Tropical Angiosperm Trees" Forests 9, no. 12: 763. https://doi.org/10.3390/f9120763

APA Style

De Mil, T., Tarelkin, Y., Hahn, S., Hubau, W., Deklerck, V., Debeir, O., Van Acker, J., De Cannière, C., Beeckman, H., & Van den Bulcke, J. (2018). Wood Density Profiles and Their Corresponding Tissue Fractions in Tropical Angiosperm Trees. Forests, 9(12), 763. https://doi.org/10.3390/f9120763

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop