A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation
Abstract
1. Introduction
2. Materials and Methods
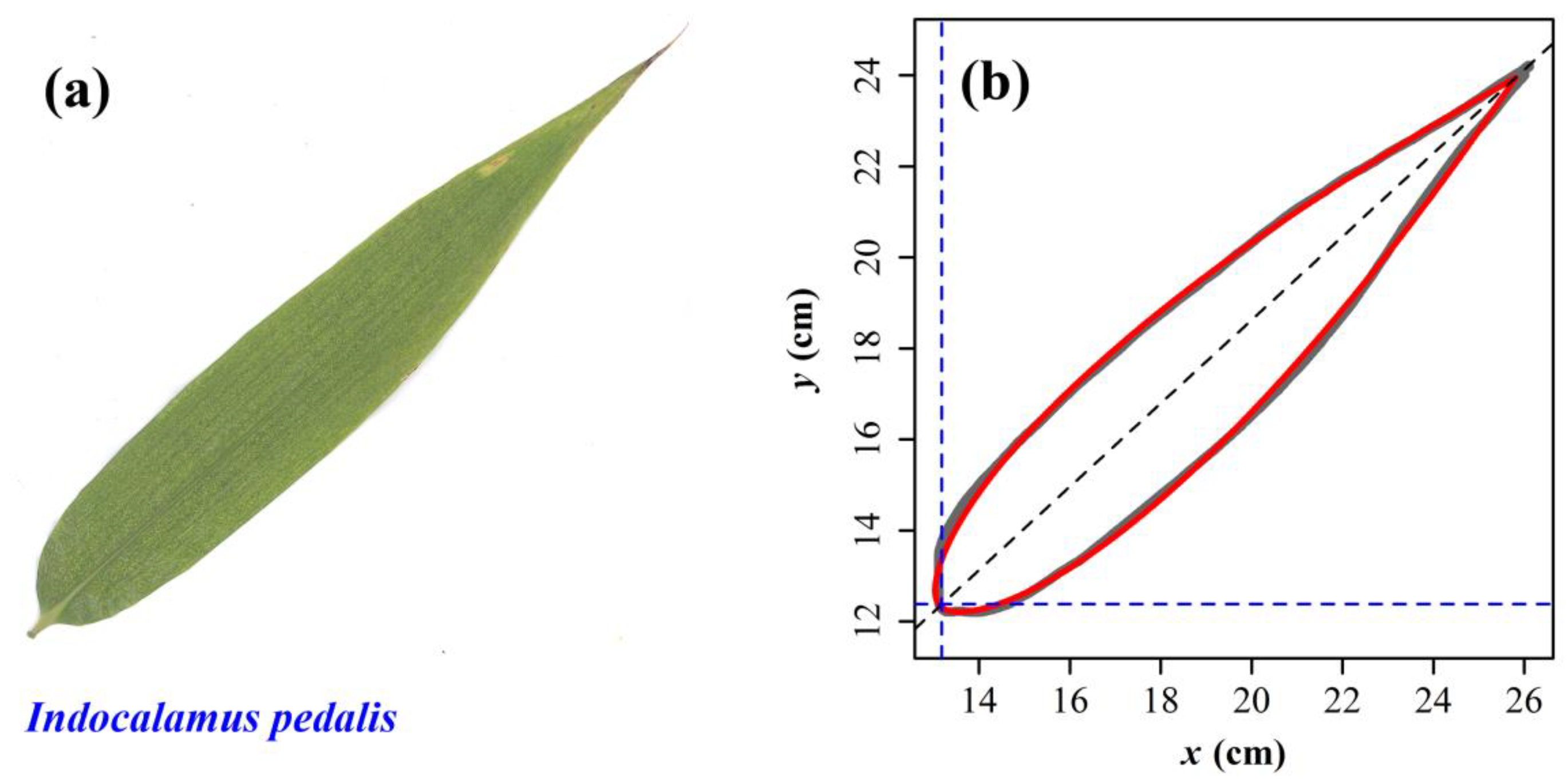
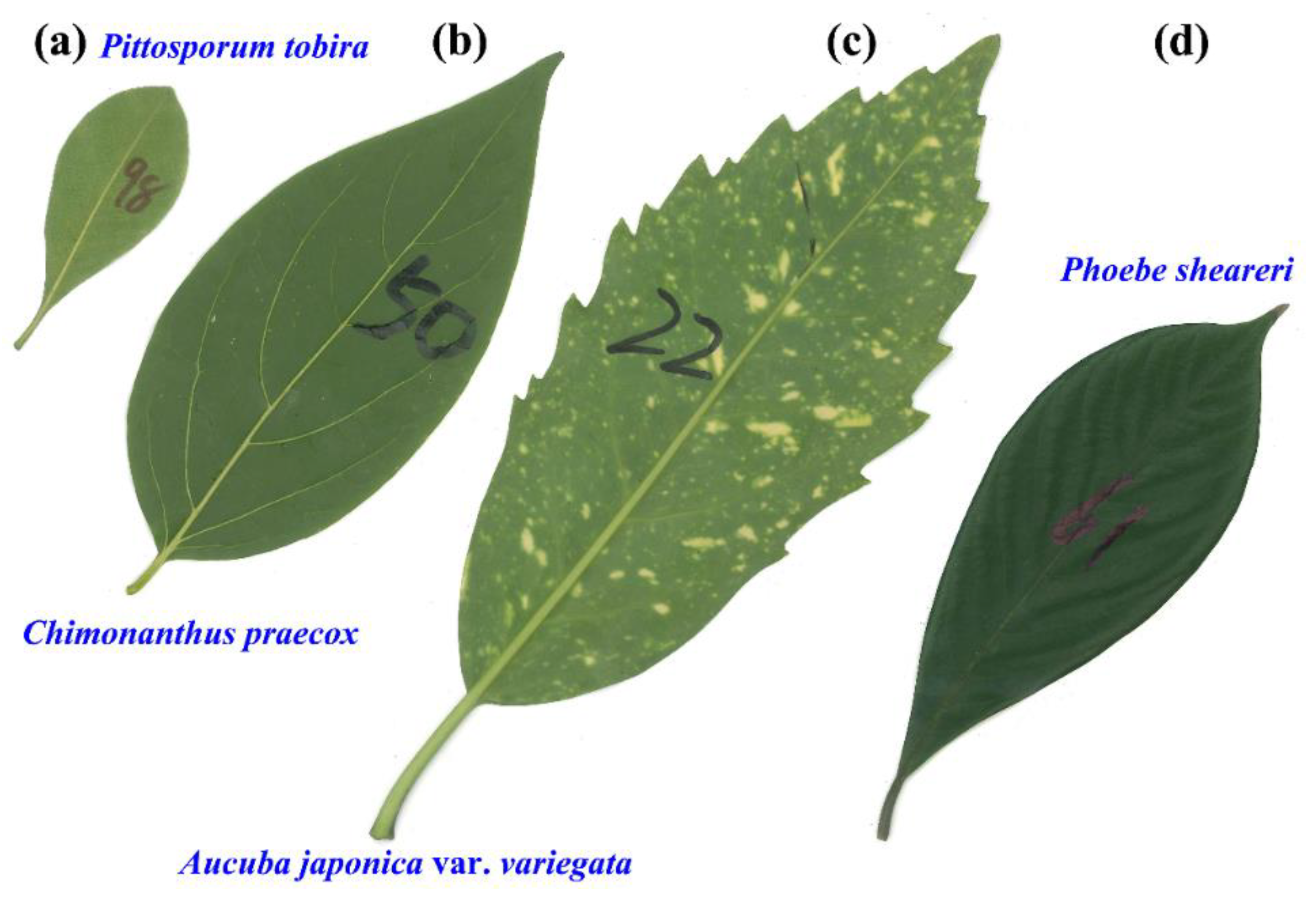
2.1. Materials
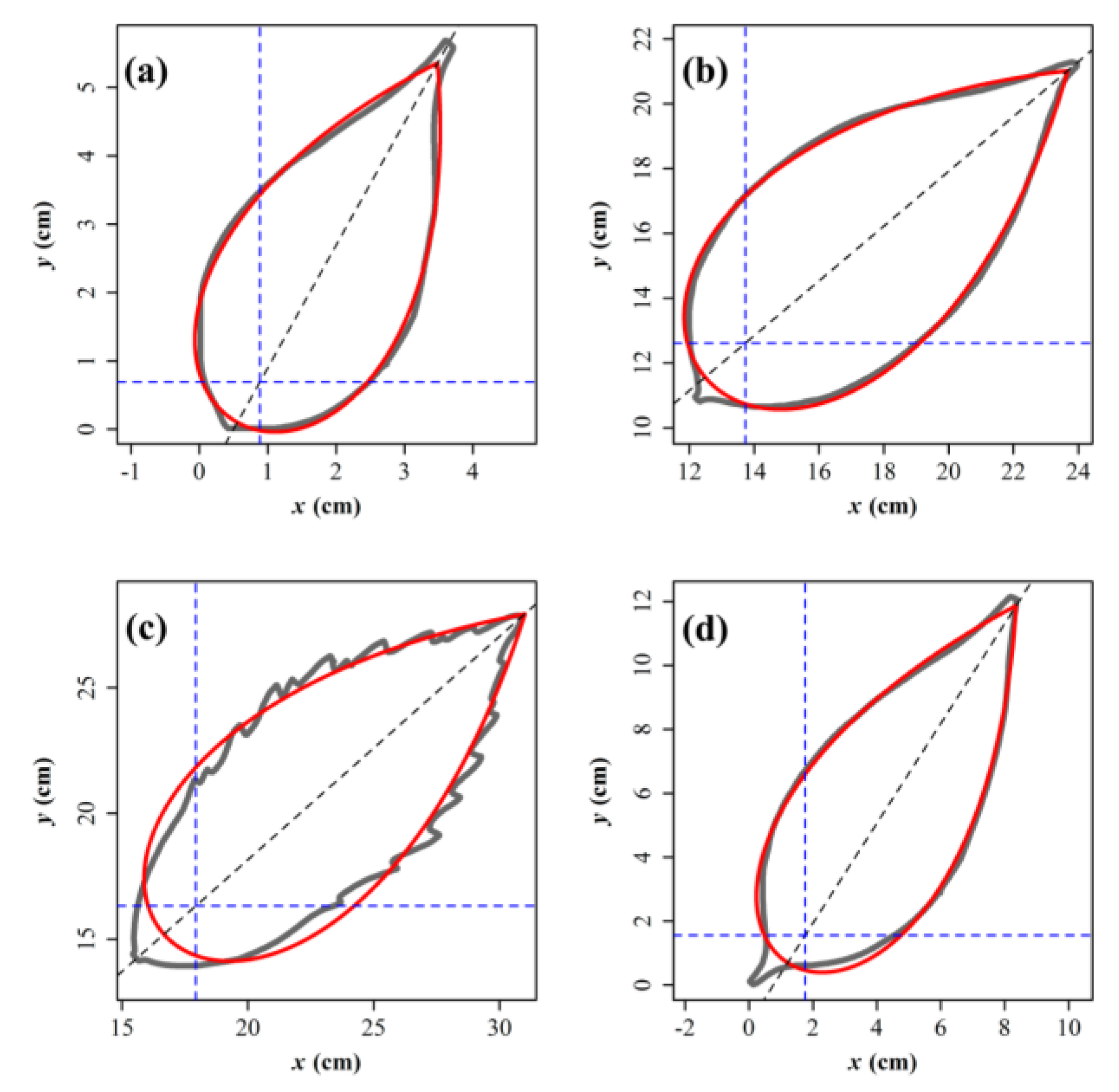
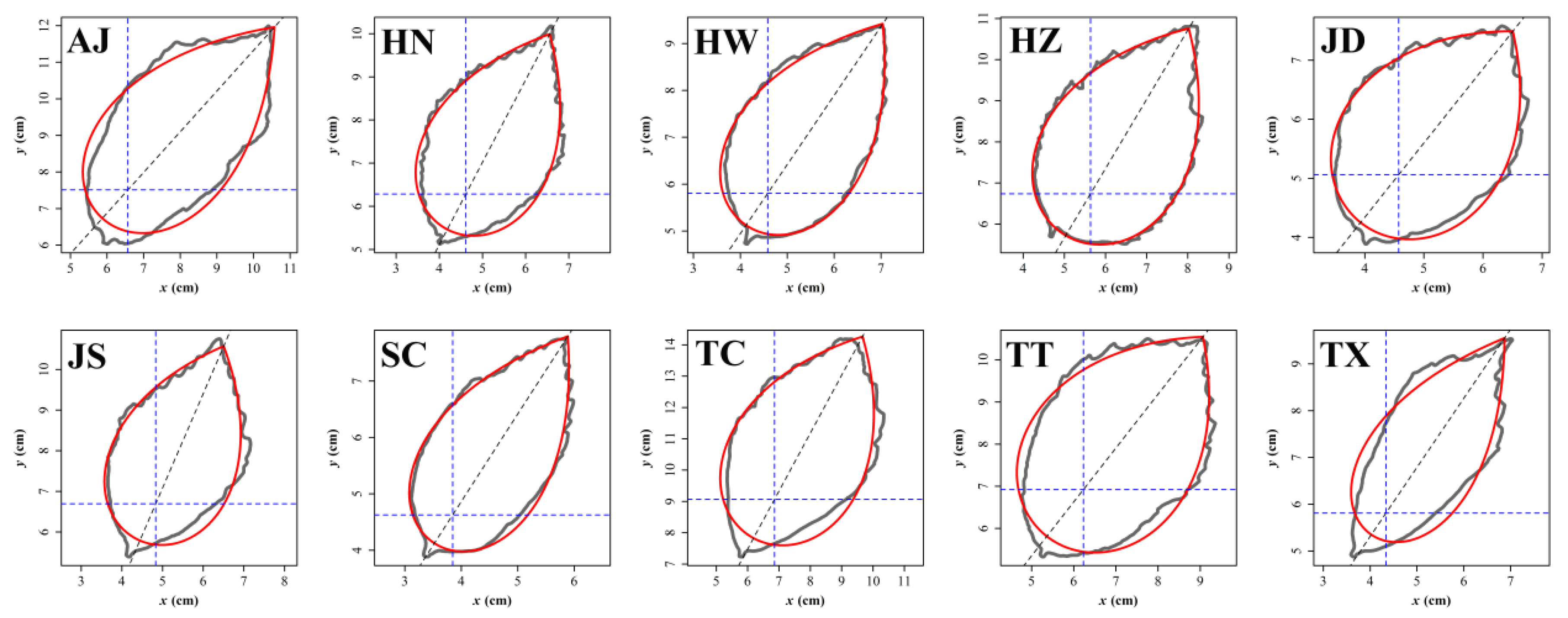
2.2. Models
2.3. Statistical Analyses
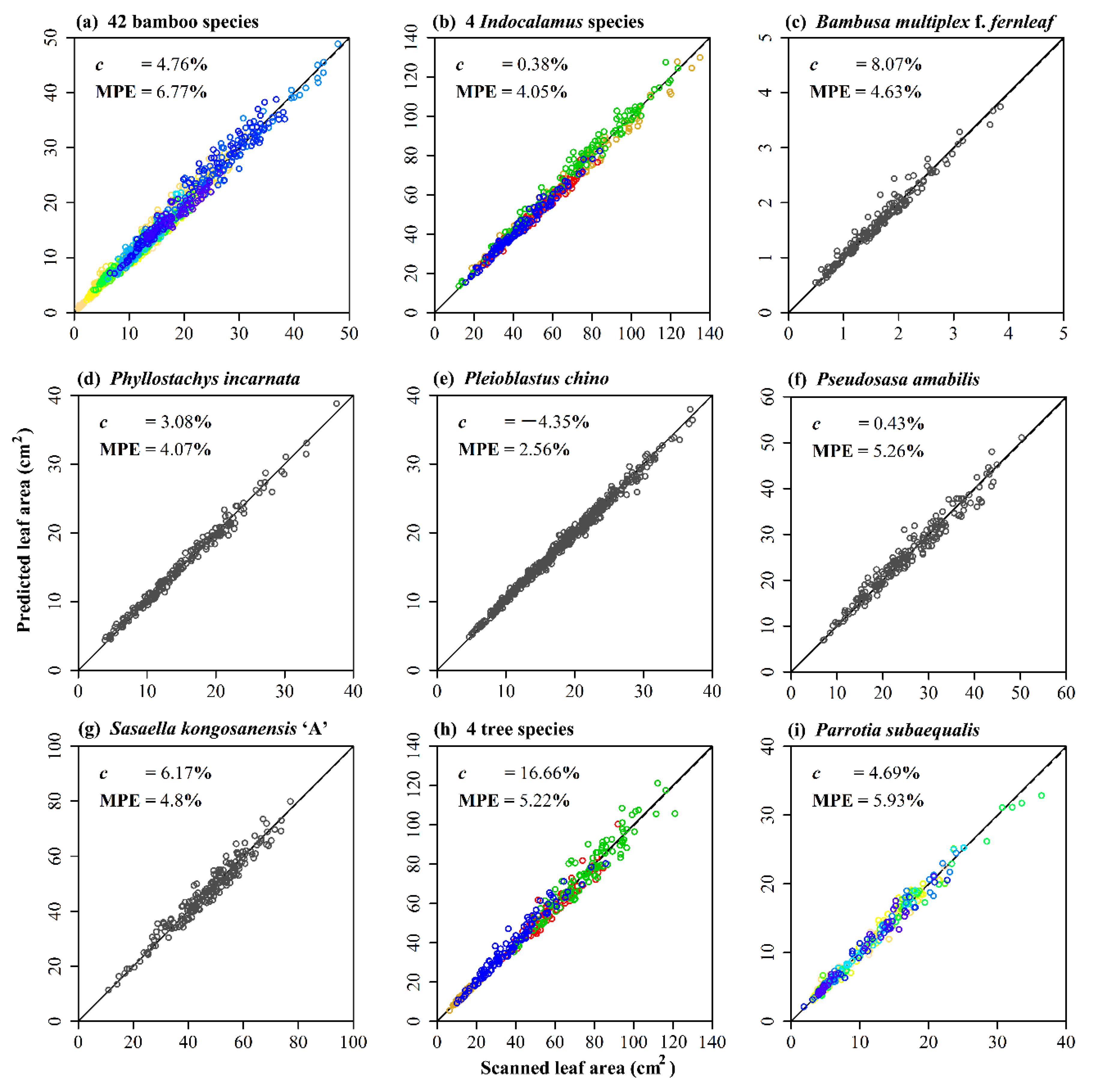
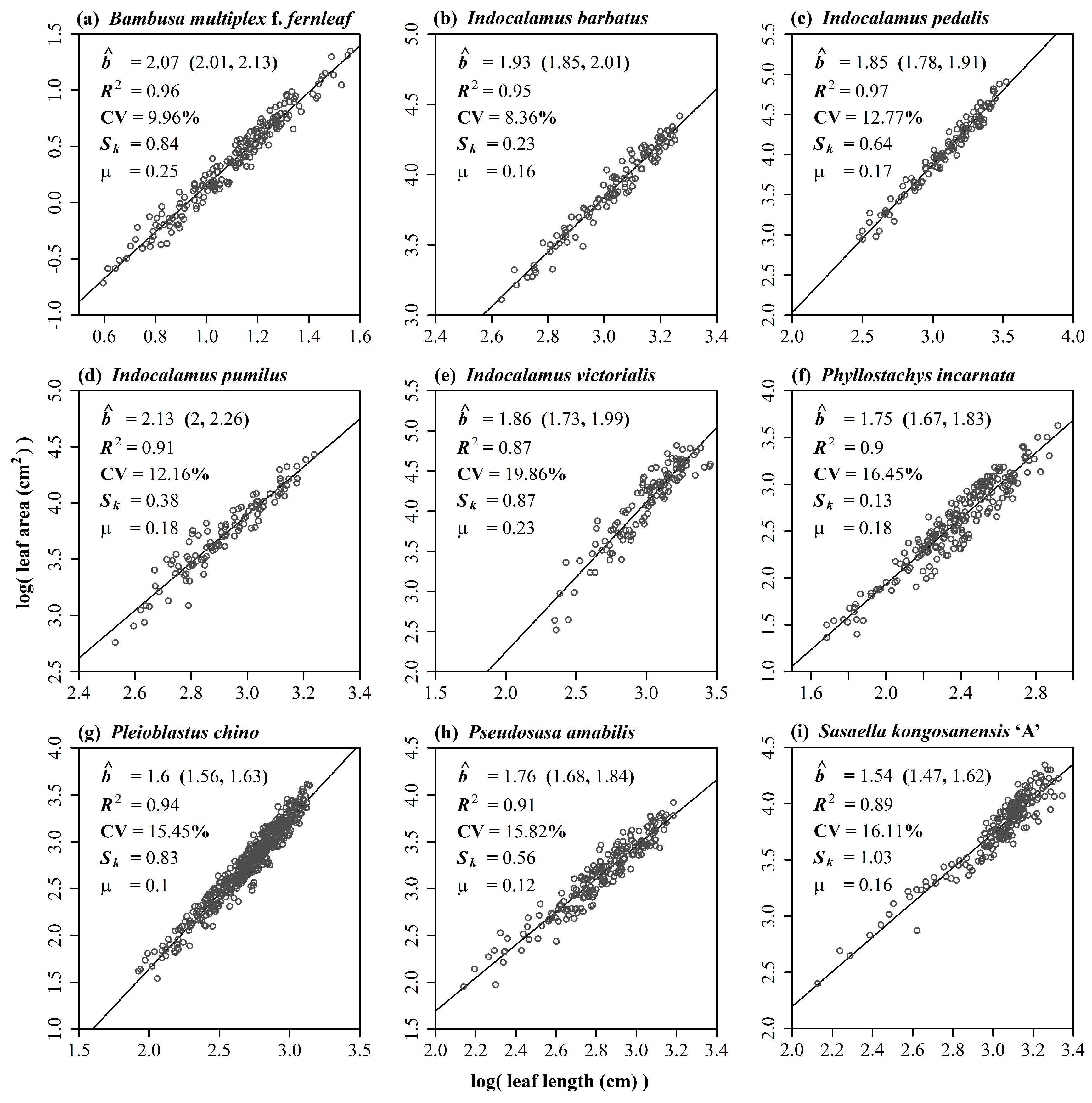
3. Results
4. Discussion
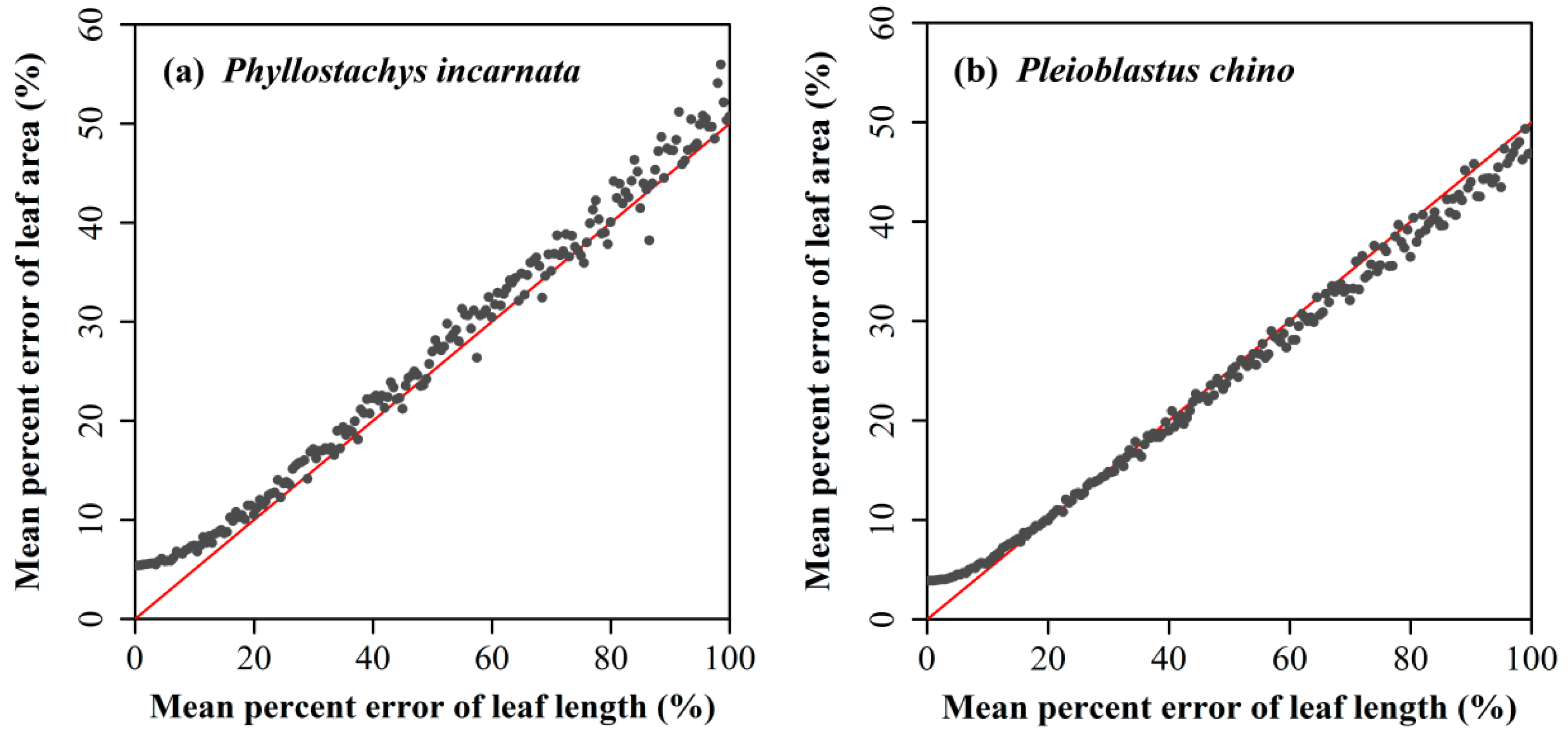
4.1. Influence of the Prediction Error in Leaf Length on Computing the Leaf Area
4.2. Beyond the Power Law between Leaf Length and Leaf Area
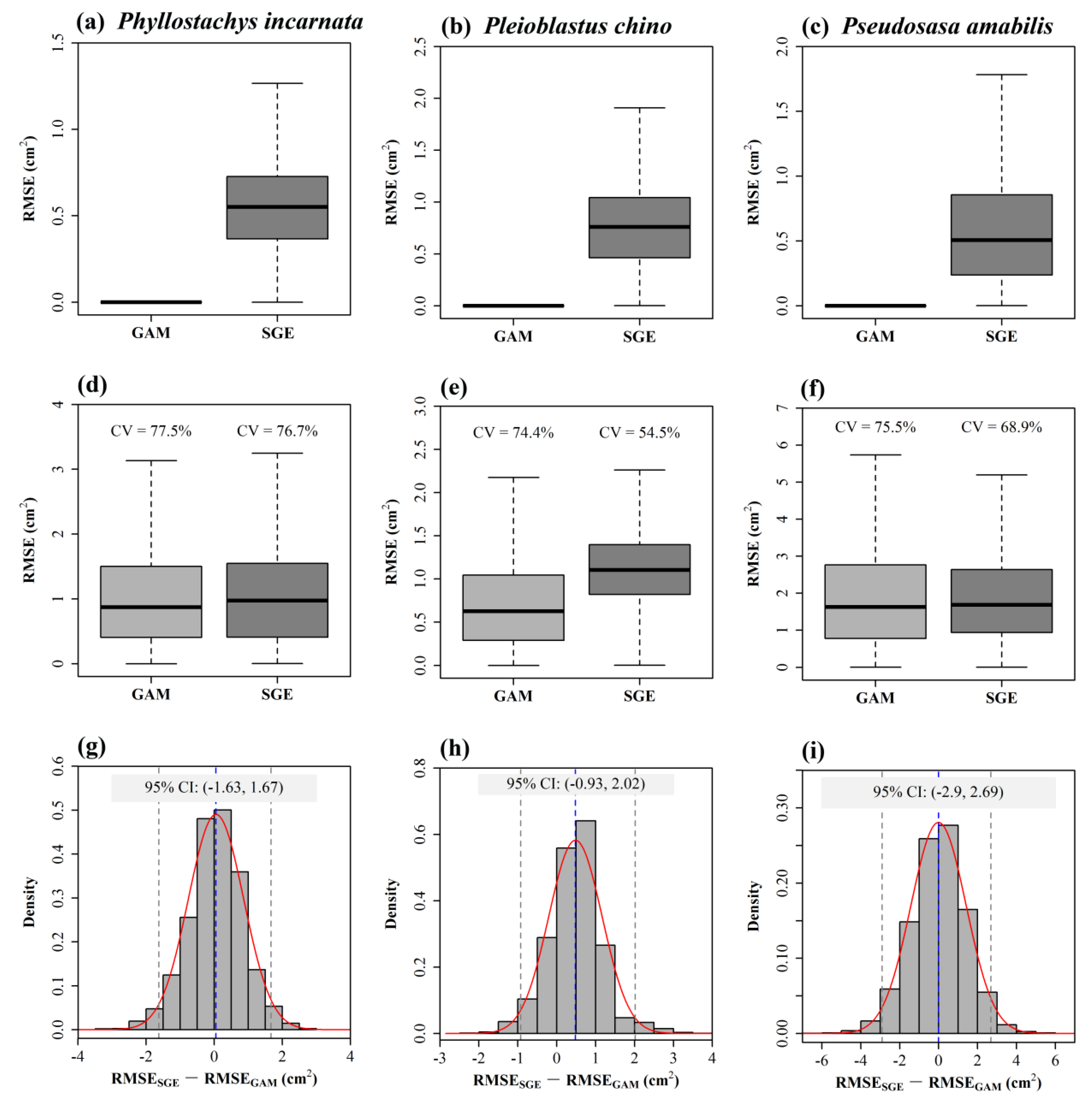
4.3. Comparison between a Non-Parametric Model and the Gielis Equation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jurik, T.W. Temporal and spatial patterns of specific leaf weight in successional northern hardwood trees species. Am. J. Bot. 1986, 73, 1083–1092. [Google Scholar] [CrossRef]
- Milla, R.; Reich, P.B. The scaling of leaf area and mass: The cost of light interception increases with leaf size. Proc. R. Soc. Biol. Sci. 2007, 274, 2109–2114. [Google Scholar] [CrossRef] [PubMed]
- Schrader, J.; Pillar, G. Leaf-IT: An Android application form measuring leaf area. Ecol. Evol. 2017, 7, 9731–9738. [Google Scholar] [CrossRef] [PubMed]
- Dornbusch, T.; Watt, J.; Baccar, R.; Fournier, C.; Andrieu, B. A comparative analysis of leaf shape of wheat, barley and maize using an empirical shape model. Ann. Bot. 2011, 107, 865–873. [Google Scholar] [CrossRef] [PubMed]
- Gielis, J. Inventing the Circle: The Geometry of Nature; Geniaal Press: Antwerpen, Belgium, 2003. [Google Scholar]
- Gielis, J. The Geometrical Beauty of Plants; Atlantis Press: Paris, France, 2007. [Google Scholar]
- Shi, P.; Xu, Q.; Sandhu, H.S.; Gielis, J.; Ding, Y.; Li, H.; Dong, X. Comparison of dwarf bamboos (Indocalamus sp.) leaf parameters to determine relationship between spatial density of plants and total leaf area per plant. Ecol. Evol. 2015, 5, 4578–4589. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Zhang, L.; Reddy, G.V.P.; Hui, C.; Gielis, J.; Ding, Y.; Shi, P. A geometrical model for testing bilateral symmetry of bamboo leaf with a simplified Gielis equation. Ecol. Evol. 2016, 6, 6798–6806. [Google Scholar] [CrossRef] [PubMed]
- Nicotra, A.B.; Leigh, A.; Boyce, C.K.; Jones, C.S.; Niklas, K.J.; Royer, D.L.; Tsukaya, H. The evolution and functional significance of leaf shape in the angiosperms. Funct. Plant Biol. 2011, 38, 535–552. [Google Scholar] [CrossRef]
- Jones, C.S.; Bakker, F.T.; Schlichting, C.D.; Nicotra, A.B. Leaf shape evolution in the South African genus Pelargonium L’ Hér. (Geraniaceae). Evolution 2008, 63, 479–497. [Google Scholar] [CrossRef] [PubMed]
- Runions, A.; Fuhrer, M.; Lane, B.; Federl, P.; Rolland-Lagan, A.-G.; Prusinkiewicz, P. Modeling and visualization of leaf venation patterns. ACM Trans. Gr. 2005, 24, 702–711. [Google Scholar] [CrossRef]
- Runions, A.; Tsiantis, M.; Prusinkiewicz, P. A common developmental program can produce diverse leaf shapes. New Phytol. 2017, 216, 401–418. [Google Scholar] [CrossRef] [PubMed]
- Brodribb, T.J.; Feild, T.S.; Jordan, G.J. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiol. 2007, 144, 1890–1898. [Google Scholar] [CrossRef] [PubMed]
- Price, C.A.; Symonova, O.; Mileyko, Y.; Hilley, T.; Weitz, J.S. Leaf extraction and analysis framework graphical user interface: Segmenting and analyzing the structure of leaf veins and areoles. Plant Physiol. 2011, 155, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Shi, P.; Zheng, X.; Ratkowsky, D.A.; Li, Y.; Wang, P.; Cheng, L. A simple method for measuring the bilateral symmetry of leaves. Symmetry 2018, 10, 118. [Google Scholar] [CrossRef]
- Lin, S.; Shao, L.; Hui, C.; Song, Y.; Reddy, G.V.P.; Gielis, J.; Li, F.; Ding, Y.; Wei, Q.; Shi, P. Why does not the leaf weight-area allometry of bamboos follow the 3/2-power law? Front. Plant Sci. 2018, 9, 583. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Huang, J.; Hui, C.; Grissino-Mayer, H.D.; Tardif, J.; Zhai, L.; Li, B. Capturing spiral radial growth of conifers using the super ellipse to model tree-ring geometric shape. Front. Plant Sci. 2015, 6, 856. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.W. On Growth and Form; Cambridge University Press: London, UK, 1917. [Google Scholar]
- O’Shea, B.; Mordue-Luntz, A.J.; Fryer, R.J.; Pert, C.C.; Bricknell, I.R. Determination of the surface area of a fish. J. Fish. Dis. 2006, 29, 437–440. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Ishikawa, T.; Sandhu, H.S.; Hui, C.; Chakraborty, A.; Jin, X.; Tachihara, K.; Li, B. On the 3/4-exponent von Bertalanffy equation for ontogenetic growth. Ecol. Model. 2014, 276, 23–28. [Google Scholar] [CrossRef]
- Firman, D.M.; Allen, E.J. Estimating individual leaf area of potato from leaf length. J. Agric. Sci. 1989, 112, 425–426. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Shi, P.; Chen, Z.; Reddy, G.V.P.; Hui, C.; Huang, J.; Xiao, M. Timing of cherry tree blooming: Contrasting effects of rising winter low temperatures and early spring temperatures. Agric. For. Meteorol. 2017, 240–241, 78–89. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1993. [Google Scholar]
- Sandhu, H.S.; Shi, P.; Kuang, X.; Xue, F.; Ge, F. Applications of the bootstrap to insect physiology. Fla. Entomol. 2011, 94, 1036–1041. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Ratkowsky, D.A.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation. Forests 2018, 9, 714. https://doi.org/10.3390/f9110714
Shi P, Ratkowsky DA, Li Y, Zhang L, Lin S, Gielis J. A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation. Forests. 2018; 9(11):714. https://doi.org/10.3390/f9110714
Chicago/Turabian StyleShi, Peijian, David A. Ratkowsky, Yang Li, Lifang Zhang, Shuyan Lin, and Johan Gielis. 2018. "A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation" Forests 9, no. 11: 714. https://doi.org/10.3390/f9110714
APA StyleShi, P., Ratkowsky, D. A., Li, Y., Zhang, L., Lin, S., & Gielis, J. (2018). A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation. Forests, 9(11), 714. https://doi.org/10.3390/f9110714






