Short Rotations in Forest Plantations Accelerate Virulence Evolution in Root-Rot Pathogenic Fungi
Abstract
:1. Introduction
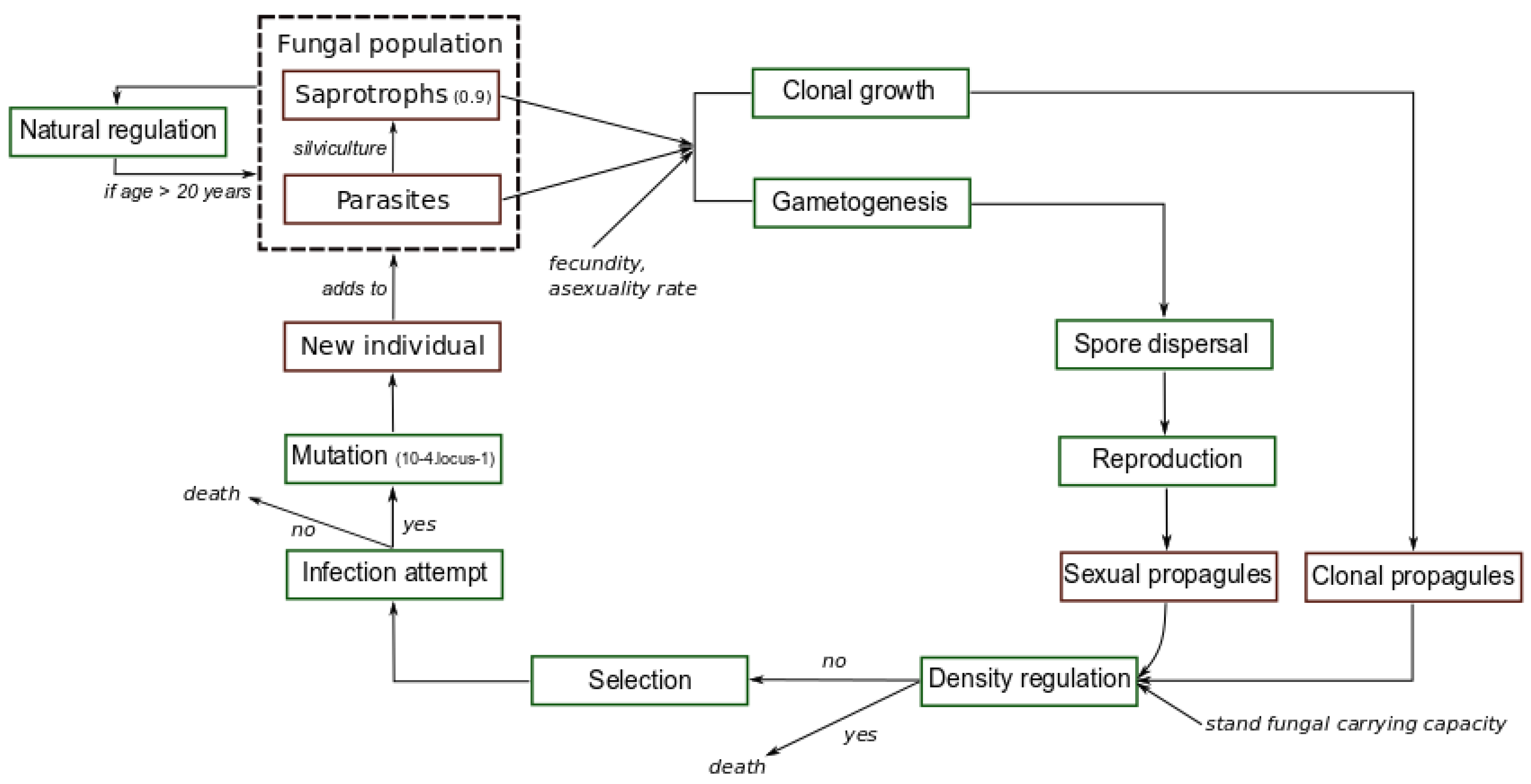
2. Materials and Methods
2.1. Fungal Pathogen
2.2. Forest Plantation and Silvicultural Operations
2.3. Simulated Scenarios
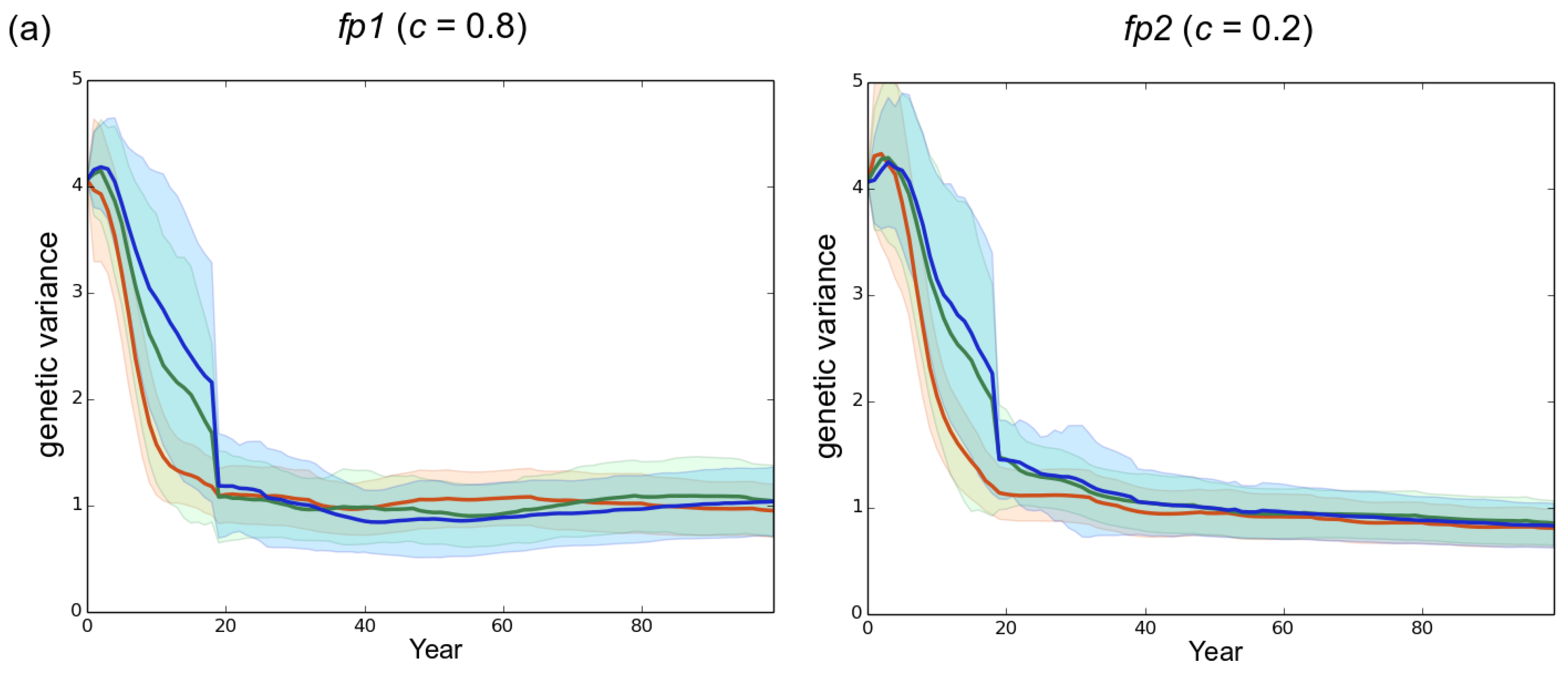
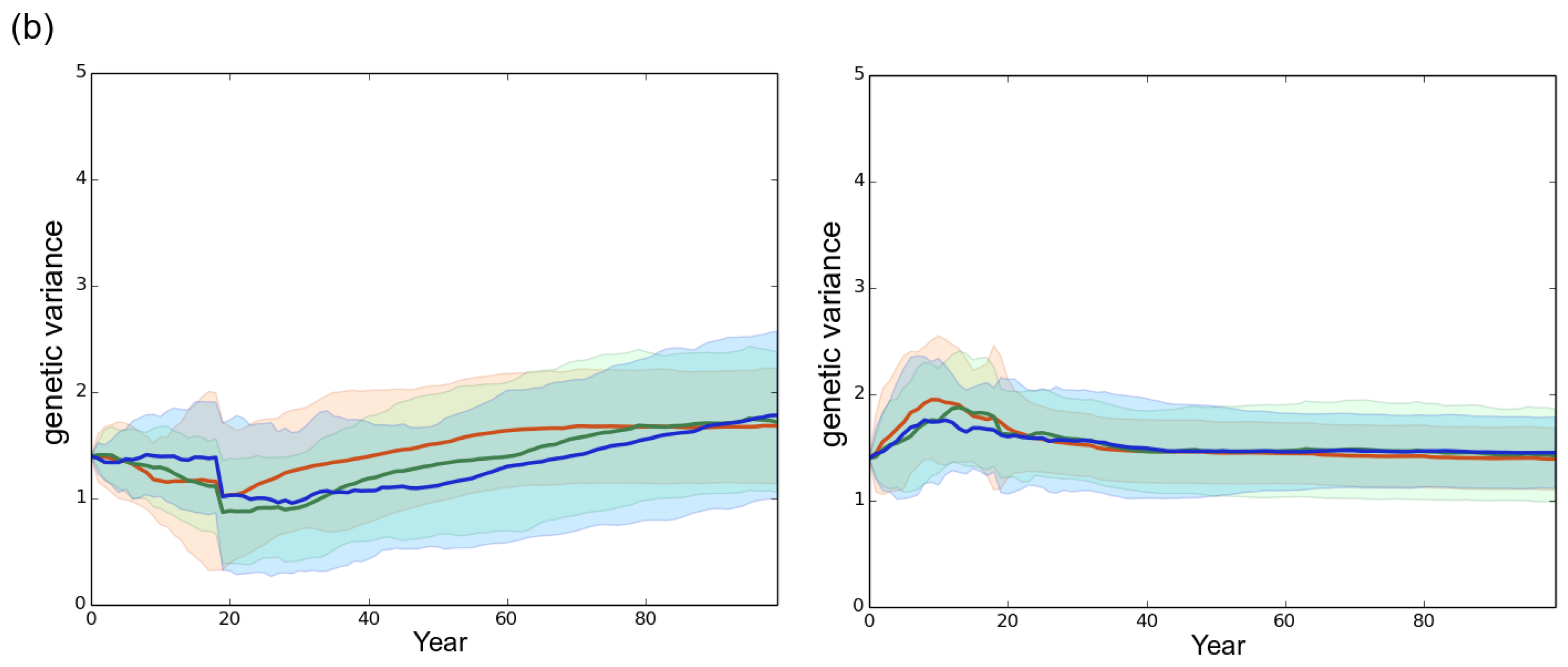
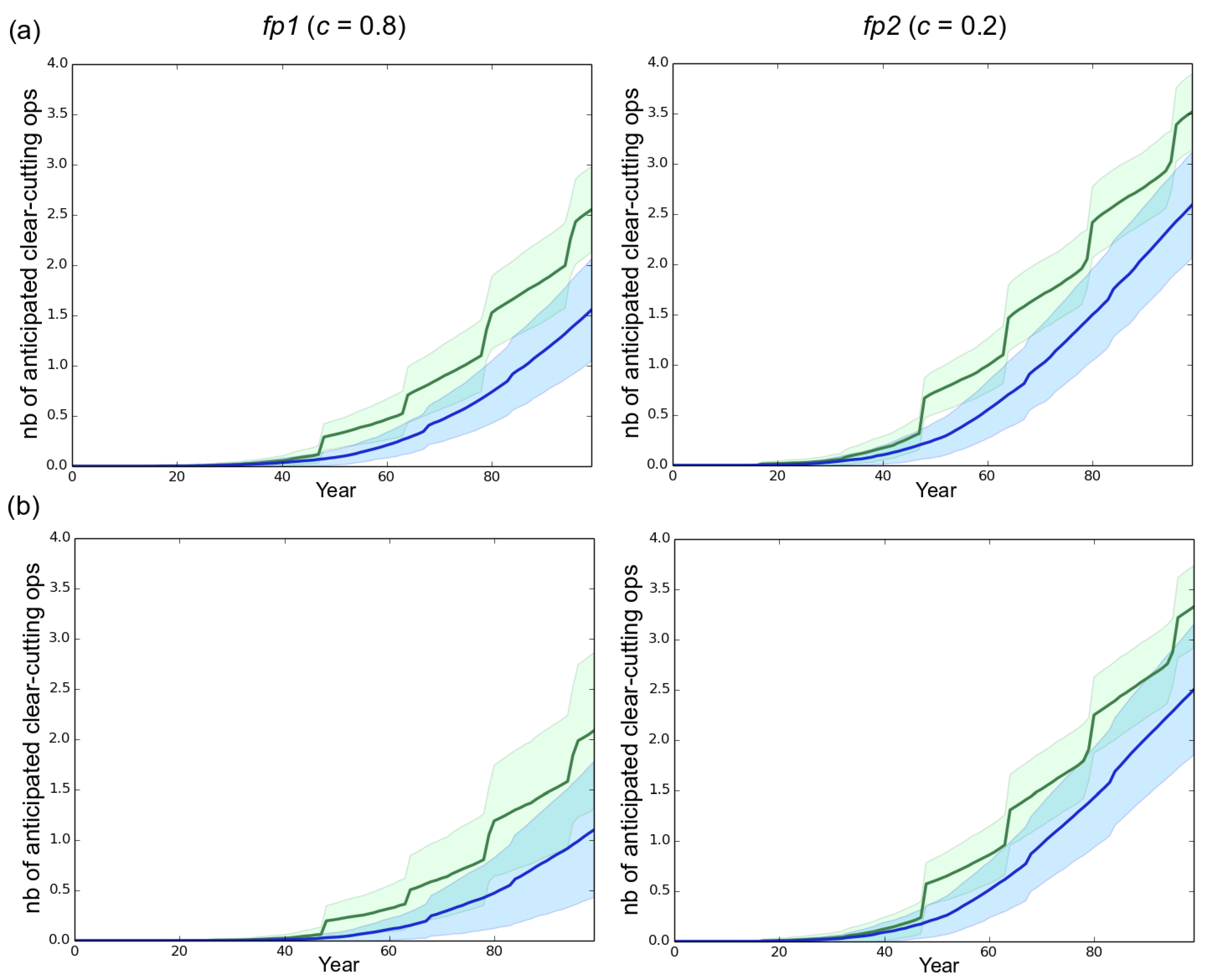
3. Results
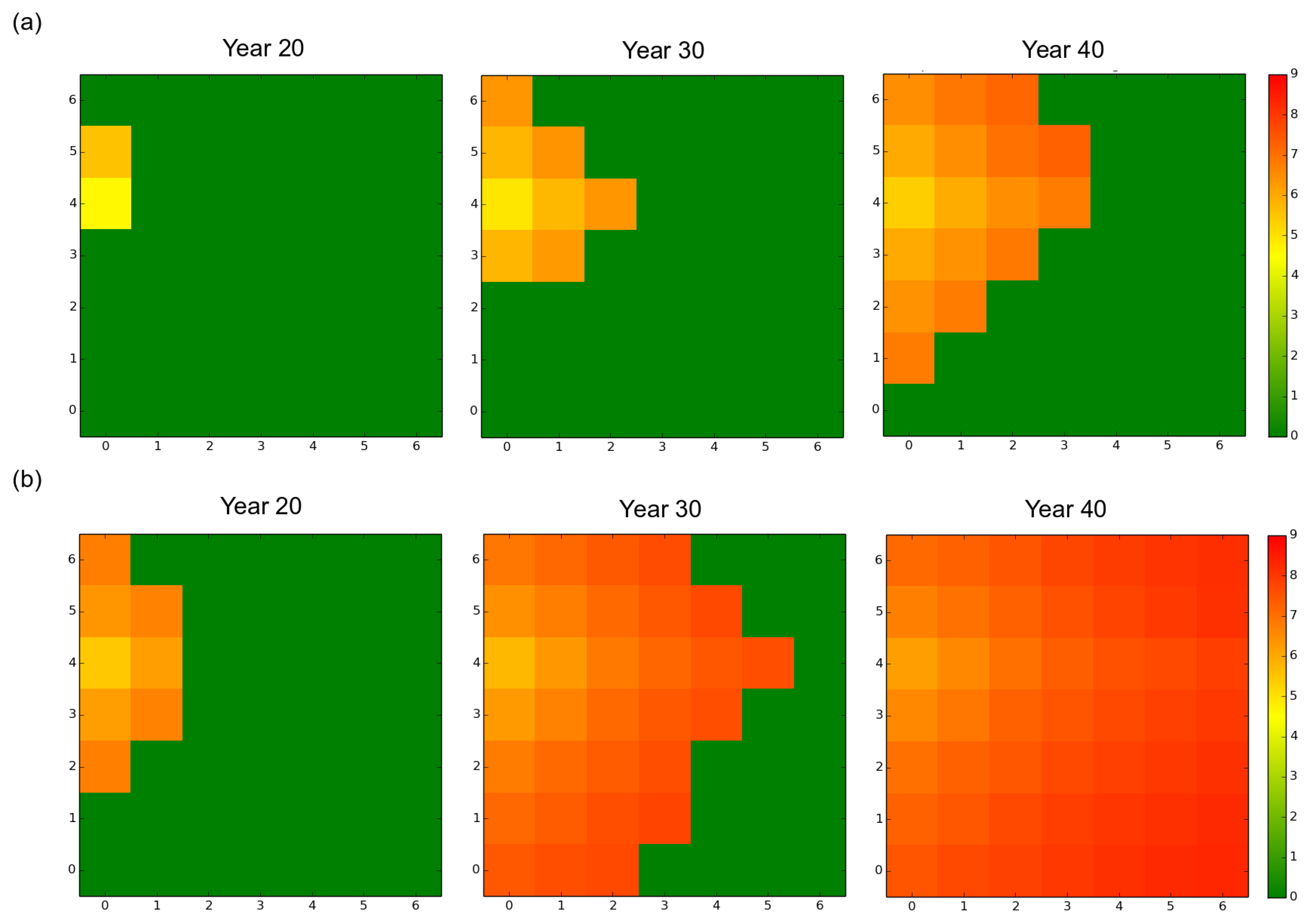
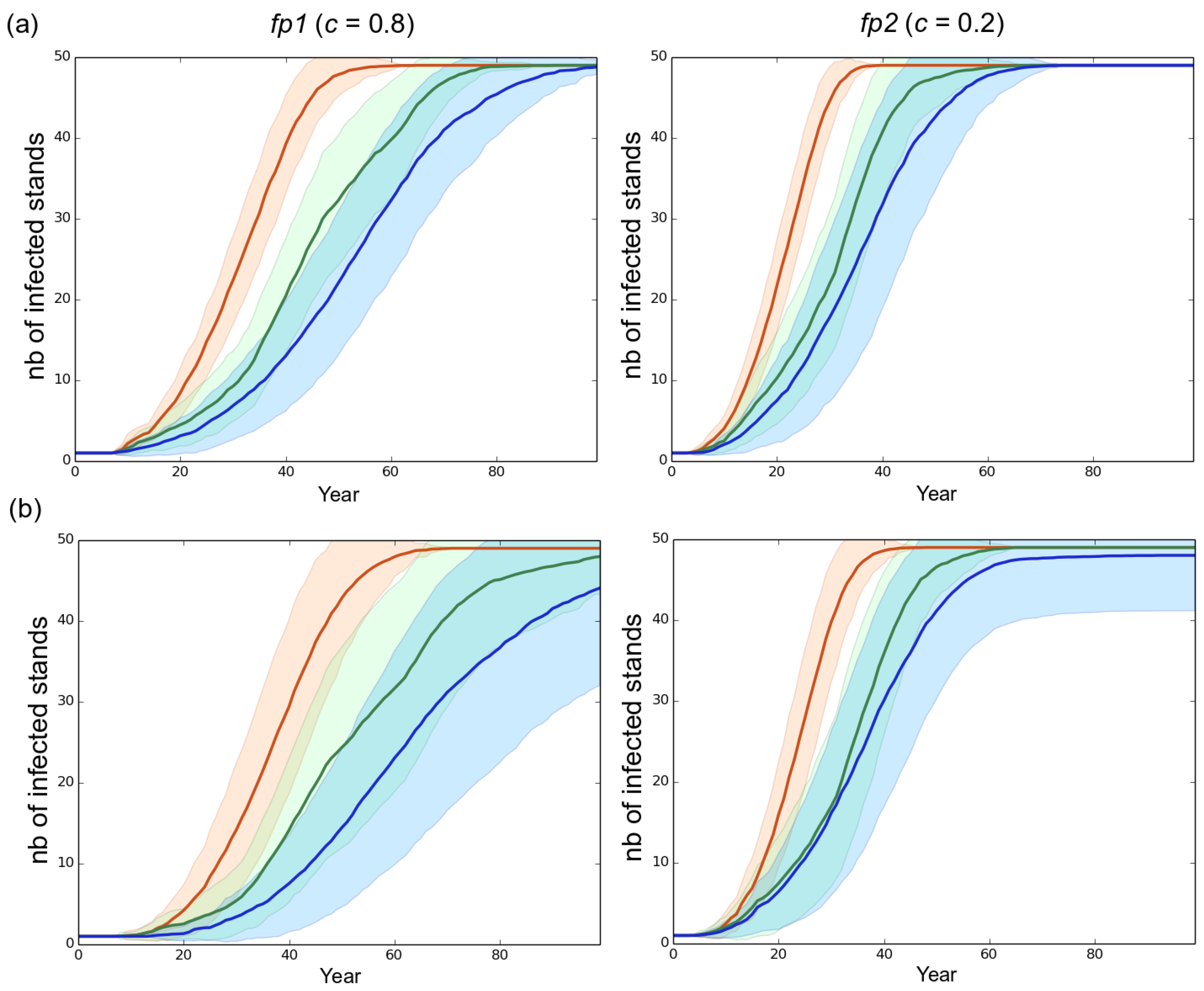
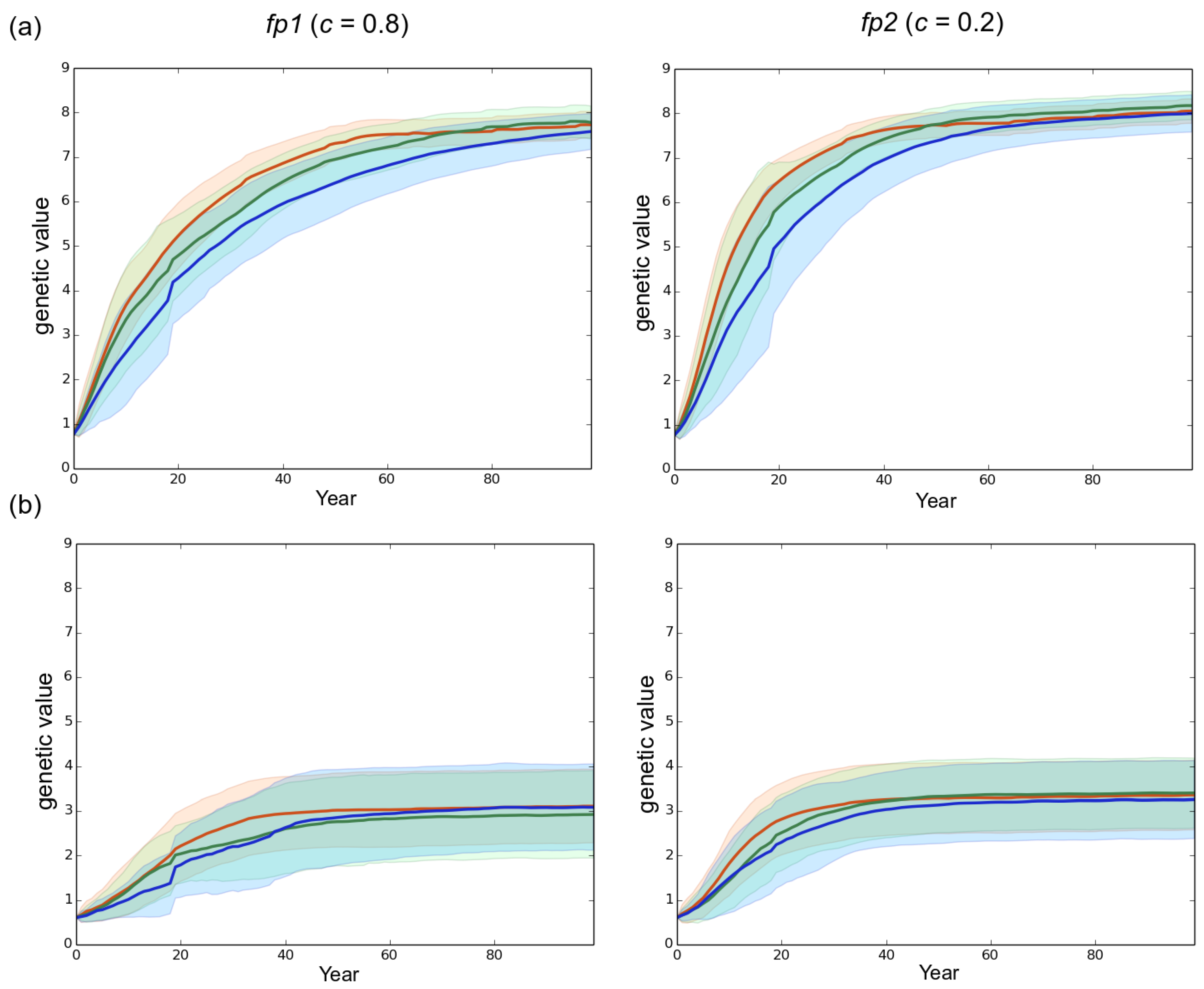
3.1. Observed Epidemiological and Evolutionary Dynamics
3.2. Effect of the Rotation Length on Pathogen Propagation and Virulence Evolution
4. Discussion
4.1. The Effect of Silvicultural Operations on a Necrotroph Fungal Pathogen Alternating Parasitic and Saprotrophic Stages
4.2. The Importance of Initial Genetic Variation
4.3. The Importance of the Reproduction System
4.4. Generalization and Future Directions
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- FAO. Planted forests are a vital resource for future green economies. In Planted Forests Increasing in Importance Worldwide, Proceedings of the Third International Congress on Planted Forests, Estoril, Portugal, 15–21 May 2013; FAO: Roma, Italy, 2013; p. 6. [Google Scholar]
- WWF (World Wildlife Fund). WWF’s Living Forest Report: Chapter 4—Forests and Wood Products; World Wildlife Fund: Washington, DC, USA, 2013. [Google Scholar]
- Santini, A.; Ghelardini, L.; Pace, C.D.; Desprez-Loustau, M.L.; Capretti, P.; Chandelier, A.; Hantula, J. Biogeographical patterns and determinants of invasion by forest pathogens in Europe. New Phytol. 2013, 197, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Ennos, R.A. Resilience of forests to pathogens: An evolutionary ecology perspective. Forestry 2015, 88, 41–52. [Google Scholar] [CrossRef]
- Wingfield, M.J.; Brockerhoff, E.G.; Wingfield, B.D.; Slippers, B. Planted forest health: The need for a global strategy. Science 2015, 349, 832–836. [Google Scholar] [CrossRef] [PubMed]
- Desprez-Loustau, M.L.; Aguayo, J.; Dutech, C.; Hayden, K.J.; Husson, C.; Jakushkin, B.; Vacher, C. An evolutionary ecology perspective to address forest pathology challenges of today and tomorrow. Ann. For. Sci. 2016, 73, 45–67. [Google Scholar] [CrossRef]
- Perkins, T.A. Evolutionarily labile species interactions and spatial spread of invasive species. Am. Nat. 2012, 179, E37–E54. [Google Scholar] [CrossRef] [PubMed]
- Sapoukhina, N.; Durel, C.E.; Le Cam, B. Spatial deployment of gene-for-gene resistance governs evolution and spread of pathogen populations. Theor. Ecol. 2009, 2, 229–238. [Google Scholar] [CrossRef]
- Perkins, T.A.; Phillips, B.L.; Baskett, M.L.; Hastings, A. Evolution of dispersal and life history interact to drive accelerating spread of an invasive species. Ecol. Lett. 2013, 16, 1079–1087. [Google Scholar] [CrossRef] [PubMed]
- Burdon, J.J.; Thrall, P.H. Pathogen evolution across the agro-ecological interface: Implications for disease management. Evolut. Appl. 2008, 1, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Berngruber, T.W.; Froissart, R.; Choisy, M.; Gandon, S. Evolution of virulence in emerging epidemics. PLoS Pathog. 2013, 9, e1003209. [Google Scholar] [CrossRef] [PubMed]
- Cressler, C.E.; McLEOD, D.V.; Rozins, C.; Van Den Hoogen, J.; Day, T. The adaptive evolution of virulence: A review of theoretical predictions and empirical tests. Parasitology 2016, 143, 915–930. [Google Scholar] [CrossRef] [PubMed]
- Lannou, C. Variation and selection of quantitative traits in plant pathogens. Annu. Rev. Phytopathol. 2012, 50, 319–338. [Google Scholar] [CrossRef] [PubMed]
- Alizon, S.; Michalakis, Y. Adaptative virulence evolution: The good old fitness-based approach. Trends Ecol. Evol. 2015, 30, 248–254. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, U. Adaptive Dynamics of Pathogen-Host Interactions; IIASA Interim Report; IIASA: Laxenburg, Austria, 2002. [Google Scholar]
- Griette, Q.; Raoul, G.; Gandon, S. Virulence evolution at the front line of spreading epidemics. Evolution 2015, 69, 2810–2819. [Google Scholar] [CrossRef] [PubMed]
- Day, T.; Proulx, S.R. A general theory for the evolutionary dynamics of virulence. Am. Nat. 2004, 163, E40–E63. [Google Scholar] [CrossRef] [PubMed]
- Day, T.; Gandon, S. Applying population-genetic models in theoretical evolutionary epidemiology. Ecol. Lett. 2007, 10, 876–888. [Google Scholar] [CrossRef] [PubMed]
- Bolker, B.M.; Nanda, A.; Shah, D. Transient virulence of emerging pathogens. J. R. Soc. Interface 2010, 7, 811–822. [Google Scholar] [CrossRef] [PubMed]
- Bazin, É.; Mathé-Hubert, H.; Facon, B.; Carlier, J.; Ravigné, V. The effect of mating system on invasiveness: Some genetic load may be advantageous when invading new environments. Biol. Invasions 2014, 16, 875–886. [Google Scholar] [CrossRef]
- Papaïx, J.; David, O.; Lannou, C.; Monod, H. Dynamics of adaptation in spatially heterogeneous metapopulations. PLoS ONE 2013, 8, e54697. [Google Scholar] [CrossRef] [PubMed]
- Fabre, F.; Rousseau, E.; Mailleret, L.; Moury, B. Epidemiological and evolutionary management of plant resistance: Optimizing the deployment of cultivar mixtures in time and space in agricultural landscapes. Evol. Appl. 2015, 8, 919–932. [Google Scholar] [CrossRef] [PubMed]
- Bourget, R.; Chaumont, L.; Sapoukhina, N. Timing of pathogen adaptation to a multicomponent treatment. PLoS ONE 2013, 8, e71926. [Google Scholar] [CrossRef] [PubMed]
- Chevin, L.M.; Lande, R.; Mace, G.M. Adaptation, plasticity, and extinction in a changing environment: Towards a predictive theory. PLoS Biol. 2010, 8, e1000357. [Google Scholar] [CrossRef] [PubMed]
- Segelbacher, G.; Cushman, S.A.; Epperson, B.K.; Fortin, M.J.; Francois, O.; Hardy, O.J.; Manel, S. Applications of landscape genetics in conservation biology: Concepts and challenges. Conserv. Genet. 2010, 11, 375–385. [Google Scholar] [CrossRef]
- Lion, S.; Gandon, S. Evolution of spatially structured host–parasite interactions. J. Evolut. Biol. 2015, 28, 10–28. [Google Scholar] [CrossRef] [PubMed]
- Borshchev, A.; Filippov, A. From system dynamics and discrete event to practical agent based modeling: Reasons, techniques, tools. In Proceedings of the 22nd International Conference of the System Dynamics Society, Oxford, UK, 25–29 July 2004; Volume 22. [Google Scholar]
- Evans, M.R.; Grimm, V.; Johst, K.; Knuuttila, T.; De Langhe, R.; Lessells, C.; Merz, M.; Wilkinson, D.J. Do simple models lead to generality in ecology? Trends Ecol. Evol. 2013, 28, 578–583. [Google Scholar] [CrossRef] [PubMed]
- Stillman, R.A.; Railsback, S.F.; Giske, J.; Berger, U.; Grimm, V. Making predictions in a changing world: The benefits of individual-based ecology. BioScience 2015, 65, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Le Corre, V.; Machon, N.; Petit, R.J.; Kremer, A. Colonization with long-distance seed dispersal and genetic structure of maternally inherited genes in forest trees: A simulation study. Genet. Res. 1997, 69, 117–125. [Google Scholar] [CrossRef]
- Austerlitz, F.; Mariette, S.; Machon, N.; Gouyon, P.H.; Godelle, B. Effects of colonization processes on genetic diversity: Differences between annual plants and tree species. Genetics 2000, 154, 1309–1321. [Google Scholar] [PubMed]
- Yeaman, S.; Guillaume, F. Predicting adaptation under migration load: The role of genetic skew. Evolution 2009, 63, 2926–2938. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S.M.; Barfield, M.; Holt, R.D. The genetics of phenotypic plasticity. XI. Joint evolution of plasticity and dispersal rate. Ecol. Evolut. 2012, 2, 2027–2039. [Google Scholar] [CrossRef] [PubMed]
- Soularue, J.P.; Kremer, A. Assortative mating and gene flow generate clinal phenological variation in trees. BMC Evolut. Biol. 2012, 12, 79. [Google Scholar] [CrossRef] [PubMed]
- Soularue, J.P.; Kremer, A. Evolutionary responses of tree phenology to the combined effects of assortative mating, gene flow and divergent selection. Heredity 2014, 113, 485–494. [Google Scholar] [CrossRef] [PubMed]
- Schiffers, K.; Bourne, E.C.; Lavergne, S.; Thuiller, W.; Travis, J.M. Limited evolutionary rescue of locally adapted populations facing climate change. Philos. Trans. R. Soc. B 2013, 368, 20120083. [Google Scholar] [CrossRef] [PubMed]
- Bourne, E.C.; Bocedi, G.; Travis, J.M.; Pakeman, R.J.; Brooker, R.W.; Schiffers, K. Between migration load and evolutionary rescue: Dispersal, adaptation and the response of spatially structured populations to environmental change. Proc. R. Soc. Lond. B Biol. Sci. 2014, 281, 20132795. [Google Scholar] [CrossRef] [PubMed]
- Guillaumin, J.J.; Mohammed, C.; Anselmi, N.; Courtecuisse, R.; Gregory, S.C.; Holdenrieder, O.; Rishbeth, J. Geographical distribution and ecology of the Armillaria species in western Europe. For. Pathol. 1993, 23, 321–341. [Google Scholar] [CrossRef]
- Morrison, D.; Mallett, K. Silvicultural management of armillaria root disease in western Canadian forests. Can. J. Plant Pathol. 1996, 18, 194–199. [Google Scholar] [CrossRef]
- Garbelotto, M.; Gonthier, P. Biology, epidemiology, and control of Heterobasidion species worldwide. Annu. Rev. Phytopathol. 2013, 51, 39–59. [Google Scholar] [CrossRef] [PubMed]
- Barrett, L.G.; Thrall, P.H.; Burdon, J.J.; Linde, C.C. Life history determines genetic structure and evolutionary potential of host–parasite interactions. Trends Ecol. Evolut. 2008, 23, 678–685. [Google Scholar] [CrossRef] [PubMed]
- Redfern, D.B.; Filip, G.M. Inoculum and infection. Agric. Handb. USA 1991, 691, 48–61. [Google Scholar]
- Labbé, F.; Lung-Escarmant, B.; Fievet, V.; Soularue, J.P.; Laurent, C.; Robin, C.; Dutech, C. Variation in traits associated with parasitism and saprotrophism in a fungal root-rot pathogen invading intensive pine plantations. Fungal Ecol. 2017, 26, 99–108. [Google Scholar] [CrossRef]
- Lung-Escarmant, B.; Guyon, D. Temporal and spatial dynamics of primary and secondary infection by Armillaria ostoyae in a Pinus pinaster plantation. Phytopathology 2004, 94, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Labbé, F.; Marcais, B.; Dupouey, J.L.; Bélouard, T.; Capdevielle, X.; Piou, D.; Dutech, C. Pre-existing forests as sources of pathogens? The emergence of Armillaria ostoyae in a recently planted pine forest. For. Ecol. Manag. 2015, 357, 248–258. [Google Scholar] [CrossRef]
- Bürger, R.; Lynch, M. Adaptation and extinction in changing environments. In Environmental Stress, Adaptation and Evolution; Birkhäuser: Basel, Switzerland, 1997; pp. 209–239. [Google Scholar]
- Holt, R.D.; Gomulkiewicz, R.; Barfield, M. The phenomenology of niche evolution via quantitative traits in a ‘black-hole’ sink. Proc. R. Soc. Lond. B Biol. Sci. 2008, 270, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Python Software Fundation (US). Available online: https://www.python.org/ (accessed on 8 June 2017).
- Walt, S.V.D.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Hunter, J. D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Legrand, P.; Ghahari, S.; Guillaumin, J.J. Occurrence of genets of Armillaria spp. in four mountain forests in Central France: The colonization strategy of Armillaria ostoyae. New Phytol. 1996, 133, 321–332. [Google Scholar] [CrossRef]
- Prospero, S.; Lung-Escarmant, B.; Dutech, C. Genetic structure of an expanding Armillaria root rot fungus (Armillaria ostoyae) population in a managed pine forest in southwestern France. Mol. Ecol. 2008, 17, 3366–3378. [Google Scholar] [CrossRef] [PubMed]
- Dutech, C.; Labbé, F.; Capdevielle, X.; Lung-Escarmant, B. Genetic analysis reveals efficient sexual spore dispersal at a fine spatial scale in Armillaria ostoyae, the causal agent of root-rot disease in conifers. Fungal Biol. 2017. [Google Scholar] [CrossRef]
- Bendel, M.; Kienast, F.; Rigling, D. Genetic population structure of three Armillaria species at the landscape scale: A case study from Swiss Pinus mugo forests. Mycol. Res. 2006, 110, 705–712. [Google Scholar] [CrossRef] [PubMed]
- Prospero, S.; Holdenrieder, O.; Rigling, D. Primary resource capture in two sympatric Armillaria species in managed Norway spruce forests. Mycol. Res. 2003, 107, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, B.A.; Dreisbach, T.A.; Parks, C.G.; Filip, G.M.; Schmitt, C.L. Coarse-scale population structure of pathogenic Armillaria species in a mixed-conifer forest in the Blue Mountains of northeast Oregon. Can. J. For. Res. 2003, 33, 612–623. [Google Scholar] [CrossRef]
- Kimura, M.; Weiss, G.H. The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 1964, 49, 561. [Google Scholar] [PubMed]
- Lynch, M.; Walsh, B. Genetics and Analysis of Quantitative Traits; Sinauer: Sunderland, MA, USA, 1998; Volume 1, p. 4. [Google Scholar]
- Orr, H.A. Fitness and its role in evolutionary genetics. Nat. Rev. Genet. 2009, 10, 531–539. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Kimmel, M.; Amos, C.I. Forward-Time Population Genetics Simulations: Methods, Implementation, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rishbeth, J. Armillaria in an ancient broadleaved woodland. For. Pathol. 1991, 21, 239–249. [Google Scholar] [CrossRef]
- Hanrahan, J.P.; Eisen, E.J.; Legates, J.E. Effects of population size and selection intensity on short-term response to selection for postweaning gain in mice. Genetics 1973, 73, 513–530. [Google Scholar] [PubMed]
- Hiscox, J.; Savoury, M.; Müller, C.T.; Lindahl, B.D.; Rogers, H.J.; Boddy, L. Priority effects during fungal community establishment in beech wood. ISME J. 2015, 9, 2246–2260. [Google Scholar] [CrossRef] [PubMed]
- Lande, R.; Shannon, S. The role of genetic variation in adaptation and population persistence in a changing environment. Evolution 1994, 50, 434–437. [Google Scholar] [CrossRef] [PubMed]
- Barrett, R.D.; Schluter, D. Adaptation from standing genetic variation. Trends Ecol. Evolut. 2008, 23, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Prentis, P.J.; Wilson, J.R.; Dormontt, E.E.; Richardson, D.M.; Lowe, A.J. Adaptive evolution in invasive species. Trends Plant Sci. 2008, 13, 288–294. [Google Scholar] [CrossRef] [PubMed]
- Otto, S.P.; Lenormand, T. Resolving the paradox of sex and recombination. Nat. Rev. Genet. 2002, 3, 252–261. [Google Scholar] [CrossRef] [PubMed]
- Austerlitz, F.; Garnier-Géré, P.H. Modelling the impact of colonisation on genetic diversity and differentiation of forest trees: Interaction of life cycle, pollen flow and seed long-distance dispersal. Heredity 2003, 90, 282–290. [Google Scholar] [CrossRef] [PubMed]
- Pukkala, T.; Möykkynen, T.; Thor, M.; Rönnberg, J.; Stenlid, J. Modeling infection and spread of Heterobasidion annosum in even-aged Fennoscandian conifer stands. Can. J. For. Res. 2005, 35, 74–84. [Google Scholar] [CrossRef]
- Noël, E.; Jarne, P.; Glémin, S.; MacKenzie, A.; Segard, A.; Sarda, V.; David, P. Experimental evidence for the negative effects of selffertilization on the adaptive potential of populations. Curr. Biol. 2017, 27, 237–242. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value |
|---|---|
| Initial genetic variance | 1.63, 4.06 |
| Mean initial genetic value | 0.33, 0.77 |
| Asexuality rate c | 0.2, 0.8 |
| Rotation length in years | 15, 30, 50 |
| Parameter | Value |
|---|---|
| Number of stands | 49 |
| Tree age classes in years () | |
| Carrying capacities K of stands () | |
| Mean resistance levels R of stands | |
| Initial proportions in J, A and M stands | |
| Threshold before anticipated clear-cut | 150 |
| Size n of the initial fungal population | 10 |
| Optimal phenotype | 10 |
| Number of loci | 10 |
| Intensity of stabilizing selection | 20 |
| Mutation rate | |
| Mutational variance | |
| Recombination rate | 0.5 |
| Fecundity f | 5 |
| Ploidy p | 2 |
| Proportion of spores dispersed among stands | 5% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soularue, J.-P.; Robin, C.; Desprez-Loustau, M.-L.; Dutech, C. Short Rotations in Forest Plantations Accelerate Virulence Evolution in Root-Rot Pathogenic Fungi. Forests 2017, 8, 205. https://doi.org/10.3390/f8060205
Soularue J-P, Robin C, Desprez-Loustau M-L, Dutech C. Short Rotations in Forest Plantations Accelerate Virulence Evolution in Root-Rot Pathogenic Fungi. Forests. 2017; 8(6):205. https://doi.org/10.3390/f8060205
Chicago/Turabian StyleSoularue, Jean-Paul, Cécile Robin, Marie-Laure Desprez-Loustau, and Cyril Dutech. 2017. "Short Rotations in Forest Plantations Accelerate Virulence Evolution in Root-Rot Pathogenic Fungi" Forests 8, no. 6: 205. https://doi.org/10.3390/f8060205
APA StyleSoularue, J.-P., Robin, C., Desprez-Loustau, M.-L., & Dutech, C. (2017). Short Rotations in Forest Plantations Accelerate Virulence Evolution in Root-Rot Pathogenic Fungi. Forests, 8(6), 205. https://doi.org/10.3390/f8060205






