Assessing Climate Change Impacts on Wildfire Risk in the United States
Abstract
:1. Introduction
2. Methods
2.1. Statistical Model Specification and Estimation
- = the correlation parameter;
- D = the diagonal matrix; = the variance of marginal mean ;
- = the working correlation matrix.
- i = 1, 2, …, N for individual state in the US;
- t = 1, 2, …, T for year;
- FORISK = the wildfire risk (ratio of area burned to total forested area in 1000 ha);
- POP = human population density (person/km2);
- BIOM = total tree biomass density (Mg/ha);
- HARV = annual tree removals (m3/ha);
- MORT = annual tree mortality (m3/ha);
- WNT = winter average monthly temperature (K: Kelvin);
- SPT = spring average monthly temperature (K);
- SMT = summer average monthly temperature (K);
- FLT = fall average monthly temperature (K);
- WNP = monthly total winter precipitation (mm);
- SPP = monthly total spring precipitation (mm);
- SMP = monthly total summer precipitation (mm);
- FLP = monthly total fall precipitation (mm);
- Φ = standard normal cumulative distribution function;
- ci = unobserved effect.
2.2. Projections of Wildfire Risk under Climate Change
| t-Test Result | Mean | Standard Error | p-Value | ||
|---|---|---|---|---|---|
| GCMs | Historical Observation | GCMs | Historical Observation | ||
| Average spring monthly temperature, F | 51.49 | 50.93 | 0.438 | 0.448 | 0.37 |
| Average summer monthly temperature, F | 71.75 | 71.35 | 0.320 | 0.307 | 0.38 |
| Average fall monthly temperature, F | 53.65 | 52.95 | 0.405 | 0.410 | 0.23 |
| Average winter monthly temperature, F | 31.77 | 32.68 | 0.574 | 0.608 | 0.28 |
| Monthly total spring precipitation, mm | 248.65 | 251.00 | 4.913 | 6.450 | 0.77 |
| Monthly total summer precipitation, mm | 257.29 | 267.46 | 5.793 | 7.068 | 0.27 |
| Monthly total fall precipitation, mm | 225.62 | 231.06 | 4.967 | 5.967 | 0.48 |
| Monthly total winter precipitation, mm | 223.84 | 212.93 | 7.078 | 7.065 | 0.28 |
2.3. Data
3. Results and Discussion
3.1. Factors Attributable to Wildfire Risk
| Independent Variable | Marginal Effect | Standard ERR | p-Value |
|---|---|---|---|
| Pop (Population density, persons/km2) | 0.0110 | 0.0065 | 0.093 |
| BIOM (Tree biomass density, Mg/ha) | −0.0140 | 0.0045 | 0.004 |
| HARV(Annual timber removal, m3/ha) | 0.0010 | 0.0017 | 0.466 |
| MORT(Annual tree mortality, m3/ha) | −0.0020 | 0.0041 | 0.640 |
| SPT (Average spring monthly temperature, K) | 0.1500 | 0.0613 | 0.014 |
| SMT (Average summer monthly temperature, K) | 0.4540 | 0.0800 | 0.000 |
| FLT (Average fall monthly temperature, K) | 0.0540 | 0.0800 | 0.499 |
| WNT (Average winter monthly temperature, K) | 0.1200 | 0.0500 | 0.015 |
| SPP (monthly total spring precipitation, mm) | −0.0003 | 0.0007 | 0.632 |
| SMP (monthly total summer precipitation, mm) | −0.0030 | 0.0009 | 0.005 |
| FLP (monthly total fall precipitation mm) | −0.0004 | 0.0006 | 0.519 |
| WNP (monthly total winter precipitation, mm) | −0.0003 | 0.0012 | 0.818 |
3.2. Climate Change Impact on Wildfire Risk
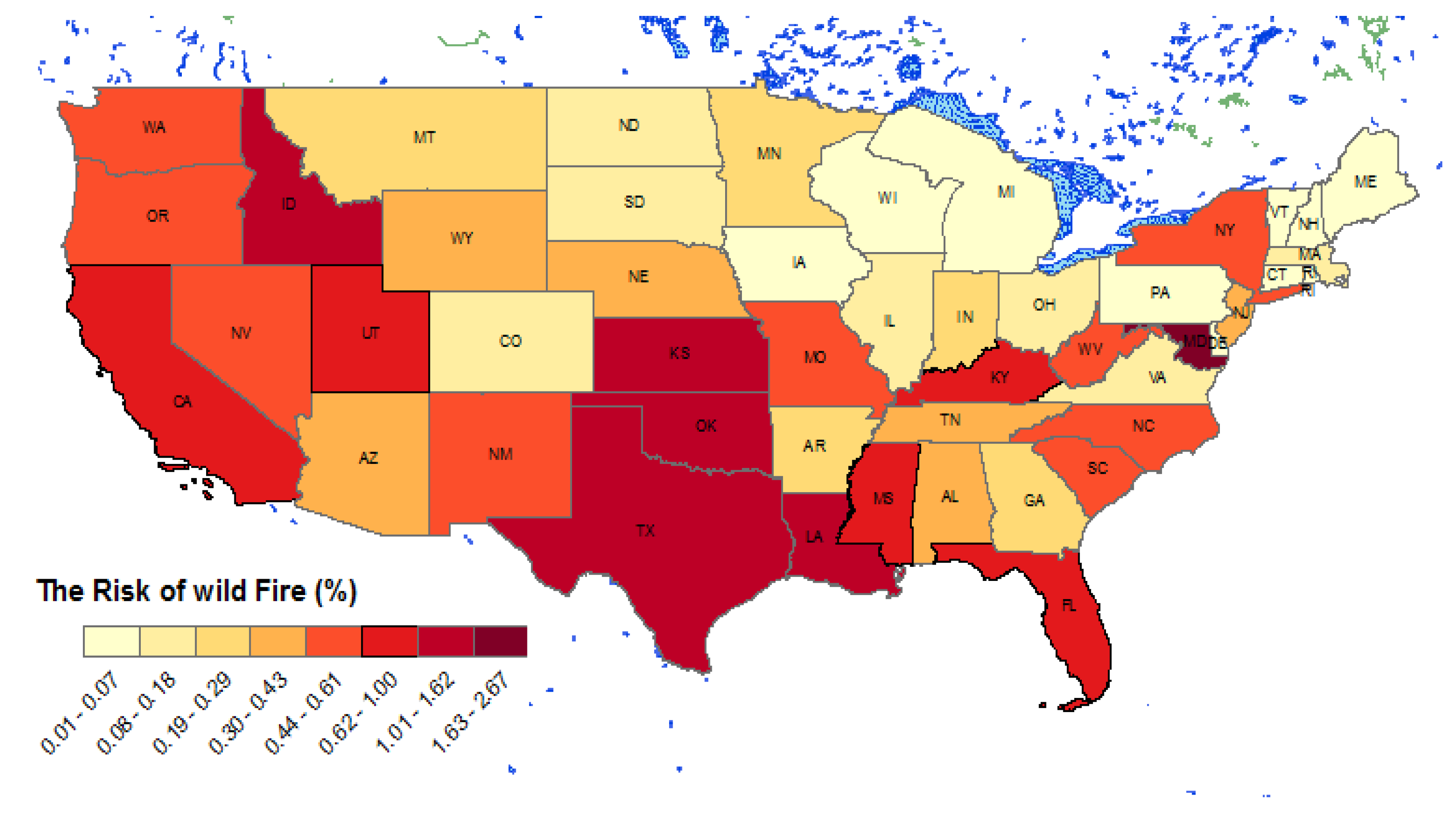

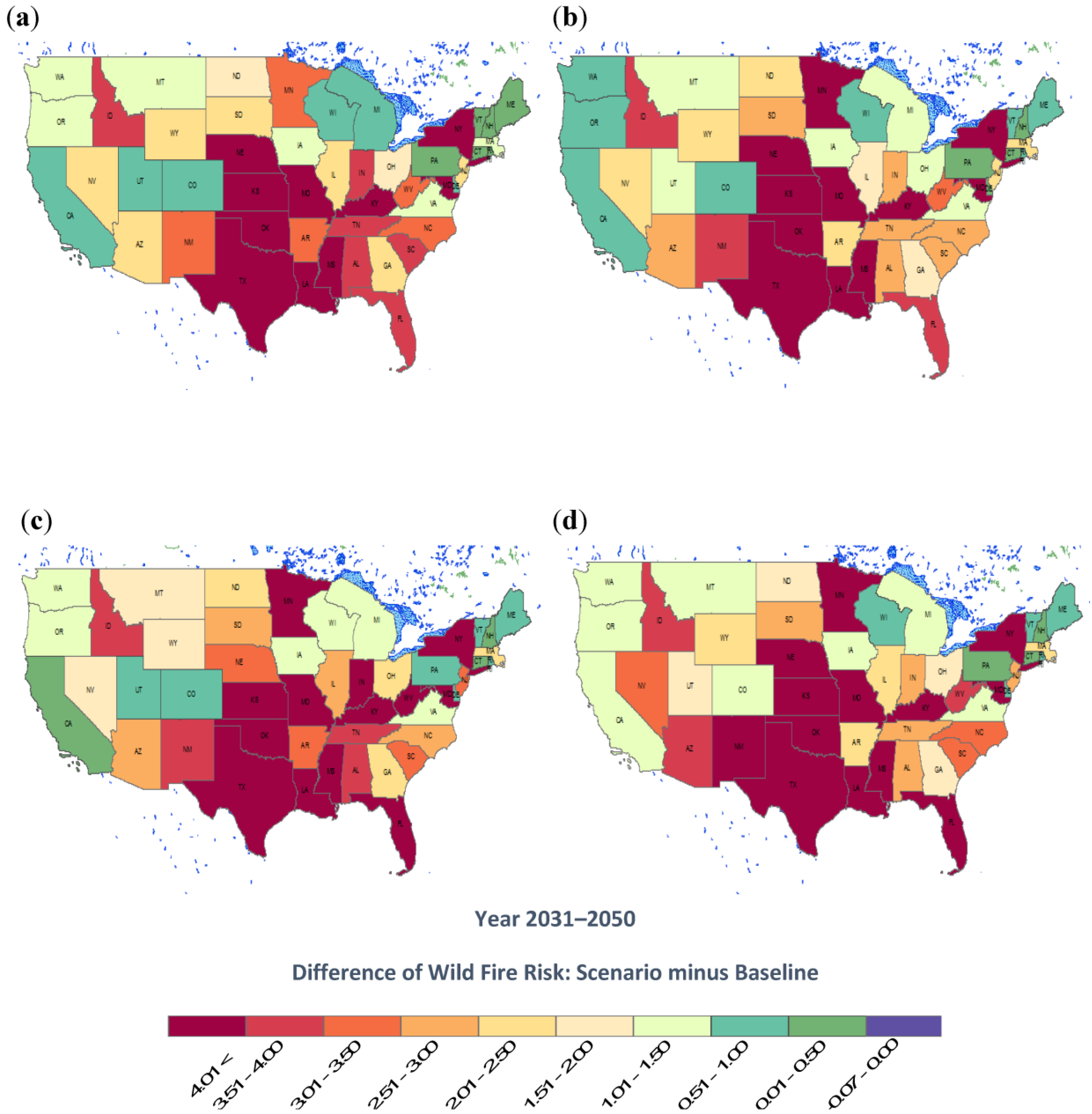
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC Working Group. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and earlier spring increase western U.S. forest wildfire activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Stanturf, J.; Goodrick, S. Trends in global wildfire potential in a changing climate. For. Ecol. Manag. 2010, 259, 685–697. [Google Scholar] [CrossRef]
- Jeremy, S.; Littell, D.M. Climate and wildfire area burned in western U.S. ecoprovinces, 1916–2003. Ecol. Appl. Publ. Ecol. Soc. Am. 2009, 19, 1003–1021. [Google Scholar]
- Moritz, M.A.; Parisien, M.-A.; Batllori, E.; Krawchuk, M.A.; van Dorn, J.; Ganz, D.J.; Hayhoe, K. Climate change and disruptions to global fire activity. Ecosphere 2012, 3. art49. [Google Scholar] [CrossRef]
- Dennison, P.E.; Brewer, S.C.; Arnold, J.D.; Moritz, M.A. Large wildfire trends in the western United States, 1984–2011. Geophys. Res. Lett. 2014, 41. [Google Scholar] [CrossRef]
- Preisler, H.; Westerling, A.L.; Gebert, K.M.; Munoz-Arriola, F.; Holmes, T.P. Spatially explicit forecasts of large wildland fire probability and suppression costs for California. Int. J. Wildland Fire 2011, 20, 508–517. [Google Scholar] [CrossRef]
- Hardin, J.W. Generalized Estimating Equations (GEE). In Encyclopedia of Statistics in Behavioral Science; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zeileis, A. Econometric Computing with HC and HAC Covariance Matrix Estimators. Available online: http://epub.wu.ac.at/520/ (accessed on 18 June 2015).
- Baltagi, B.H. Econometric Analysis of Panel Data, 4th ed.; Wiley: Chichester, UK; Hoboken, NJ, USA, 2008. [Google Scholar]
- Hsiao, C. Analysis of Panel Data; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Gan, J. New Research on Forest Ecosystems; Nova Publishers: Hauppauge, NY, USA, 2005. [Google Scholar]
- Papke, L.E.; Wooldridge, J.M. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. J. Appl. Econ. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Westerling, A.L.; Bryant, B.P. Climate change and wildfire in California. Clim. Chang. 2008, 87, S231–S249. [Google Scholar] [CrossRef]
- Hardin, J.W.; Hilbe, J.M. Generalized Estimating Equations, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Cushman, S.A.; Chase, M.; Griffin, C. Elephants in Space and Time. Oikos 2005, 109, 331–341. [Google Scholar] [CrossRef]
- Brillinger, D.R.; Preisler, H.K.; Benoit, J.W. Probabilistic risk assessment for wildfires. Environmetrics 2006, 17, 623–633. [Google Scholar] [CrossRef]
- Gibbons, R.D.; Hedeker, D.; DuToit, S. Advances in analysis of longitudinal data. Annu. Rev. Clin. Psychol. 2010, 6, 79–107. [Google Scholar] [CrossRef] [PubMed]
- IPCC Data Distribution Center. Available online: http://www.ipcc-data.org/guidelines/pages/gcm_guide.html (accessed on 25 August 2014).
- Dietrich-Egensteiner, W. A Beginner’s Guide to the IPCC Climate Change Reports. Available online: http://www.popularmechanics.com/science/environment/climate-change/a-beginners-guide-to-the-ipcc-climate-change-reports-15991849 (accessed on 23 July 2015).
- Fitzmaurice, G.M.; Laird, N.M.; Ware, J.H. Applied Longitudinal Analysis, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Anderson, H.E. Aids to Determining Fuel Models for Estimating Fire Behavior; U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1981. [Google Scholar]
- Rothermel, R.C.; Philpot, C.W. Predicting changes in chaparral flammability. Available online: http://texasamcolstattx.library.ingentaconnect.com/content/saf/jof/1973/00000071/00000010/art00013 (accessed on 23 July 2015).
- United States Department of Agriculture, Forest Service. 1991–1997 Wildland Fire Statistics; USDA Forest Service, Fire and Aviation Management: Washington, DC, USA, 1998. [Google Scholar]
- Westerling, A.L.; Swetnam, T.W. Interannual to decadal drought and wildfire in the western United States. Eos Trans. Am. Geophys. Union 2003, 84, 545–555. [Google Scholar] [CrossRef]
- Whitlock, C.; Shafer, S.L.; Marlon, J. The role of climate and vegetation change in shaping past and future fire regimes in the northwestern US and the implications for ecosystem management. For. Ecol. Manag. 2003, 178, 5–21. [Google Scholar] [CrossRef]
- Climate at a Glance. Available online: http://www.ncdc.noaa.gov/cag/ (accessed on 1 February 2015).
- Smith, W.B. Forest Resources of the United States, 1997. [Microform]; General Technical Report NC: 219; North Central Research Station, Forest Service—U.S. Depatment of Agriculture: St. Paul, MN, USA, 2001. [Google Scholar]
- Brekke, L.; Thrasher, B.L.; Maurer, E.P.; Pruitt, T. Downscaled CMIP3 and CMIP5 Climate Projections: Release of Downscaled CMIP5 Climate Projections, Comparison with Preceding Information, and Summary of User Needs; U.S. Department of the Interior, Bureau of Reclamation, Technical Service Center: Denver, CO, USA. Available online: http://gdodcp.ucllnl.org/downscaled_cmip_projections (accessed on 13 July 2014).
- Pan, W. Akaike’s Information criterion in generalized estimating equations. Biometrics 2001, 57, 120–125. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.H. Climate Change Science and Policy; Island Press: Washington, DC, USA, 2009. [Google Scholar]
- Yue, X.; Mickley, L.J.; Logan, J.A.; Kaplan, J.O. Ensemble projections of wildfire activity and carbonaceous aerosol concentrations over the western United States in the mid-21st century. Atmos. Environ. 2013, 77, 767–780. [Google Scholar] [CrossRef] [PubMed]
- Abatzoglou, J.T.; Brown, T.J. A comparison of statistical downscaling methods suited for wildfire applications. Int. J. Climatol. 2012, 32, 772–780. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, H.; Gan, J.; Cho, S.J. Assessing Climate Change Impacts on Wildfire Risk in the United States. Forests 2015, 6, 3197-3211. https://doi.org/10.3390/f6093197
An H, Gan J, Cho SJ. Assessing Climate Change Impacts on Wildfire Risk in the United States. Forests. 2015; 6(9):3197-3211. https://doi.org/10.3390/f6093197
Chicago/Turabian StyleAn, Hyunjin, Jianbang Gan, and Sung Ju Cho. 2015. "Assessing Climate Change Impacts on Wildfire Risk in the United States" Forests 6, no. 9: 3197-3211. https://doi.org/10.3390/f6093197
APA StyleAn, H., Gan, J., & Cho, S. J. (2015). Assessing Climate Change Impacts on Wildfire Risk in the United States. Forests, 6(9), 3197-3211. https://doi.org/10.3390/f6093197





