1. Introduction
Airborne lidar has been used extensively to characterize the structure of forest canopies [
1,
2,
3], and to a lesser extent to identify tree species (e.g., [
4,
5,
6,
7,
8]). In both cases, two alternative methods were tested: the now classical area-based approach (ABA, e.g., [
9]) and the individual tree crown (ITC) methods (see [
10], and [
11] for reviews). For structural attribute quantification, both ABA and ITC can now achieve results of relatively high accuracy. However, for more species-specific attributes estimations in mixed forests, it can be argued that ABA reaches limitations and ITC methods can theoretically produce more detailed information [
12,
13] because the point cloud characteristics of individual trees can be linked to species-specific features, such as crown shape, porosity or reflectance [
7,
14]. ABA on the other hand can only describe overall point cloud features on a plot or stand basis, leading to substantial ambiguity when multiple species are present. ITC also offers the advantage of enabling object-based reconstruction of tree size distributions in forests having a complex structure, such as old growth natural forests. It also has the capacity to characterize species-specific tree size distribution characterization when species can be well identified. For these reasons, and because of the great importance of species data in forest inventories, ecological studies, or carbon stock assessment, we here focus our attention on ITC implementations of species identification based on 3D representations of forest canopies.
ITC has hitherto been applied either to monoscopic high resolution images [
15,
16,
17,
18] (see [
19] for a review) or to lidar point clouds or canopy height models ([
20,
21,
22,
23,
24]; see [
25] for a review of different algorithms over diverse types of forest). Species identification of individual trees using only the 3D data of lidar has been demonstrated [
6] using alpha shapes and height distribution, intensity and textural features derived from canopy height models (CHMs). For example, Holmgren and Persson [
4] achieved 95% identification accuracy in separating scots pine and Norway spruce. Brandtberg [
5] obtained a 64% accuracy for three deciduous species (oaks, red maple and yellow poplar) in leaf-off conditions, while Ørka
et al. [
7] reached 88% in the case of dominant trees and 64% for non-dominants when classifying spruce and birch. Moreover, Korpela
et al. [
8] obtained 88%–90% accuracy when discriminating between pine, spruce and birch. However, reaching high accuracy classification results using only lidar data may not be always possible [
26]. This has led researchers to combine lidar data with spectral information extracted from optical multispectral sensor images to improve species classification. Among them, Persson
et al. [
27] achieved overall accuracies of 90% and Holmgren
et al. [
28] achieved up to 96% accuracy when classifying scots pine, Norway spruce and deciduous trees. Similar results were obtained by Ørka
et al. [
29], whereas some studies involving combining lidar and hyperspectral images also achieved good success [
30,
31].
A largely uninvestigated alternative to using lidar alone or in conjunction with imagery consists of using photogrammetric point clouds (PPC). We here define a PPC as a 3D point cloud extracted by image matching and carrying the multispectral brightness information of the matched images. By subtracting the ground elevations obtained from a high accuracy digital terrain model (DTM) from the elevation component (Z) of a PPC, one obtains a set of XYH colored points where H represents the height of the canopy surface at location XY (planimetric position). These point clouds have been shown to be very similar to those created using lidar, especially when based on high overlap photos acquired from unmanned aerial vehicles [
32]. However, photogrammetric results generally appear smoother than corresponding point clouds [
33], may not describe the full 3D scene because of occlusions effects, and may contain artefacts caused by mismatch [
34].
Due to the recent improvement of image matching algorithms that has brought PPCs to new levels of density and accuracy [
35,
36], ITC implementations based on PPCs are possibly within reach. While several researchers have reported on the accuracy and practical advantages of PPCs when exploited through the ABA [
37,
38,
39,
40,
41,
42,
43], only recently has the possibility of applying ITC approaches to PPCs started to emerge [
44,
45]; see also [
46] for a precursor hybrid approach. Although some non-forest centric studies have documented the accuracy of PPCs with the most advanced image matching algorithms on different surfaces [
47,
48,
49], it is still unclear if the current generation of PPCs provide 3D data sufficient to ensure proper tree delineation, if they are precise enough to reflect the height distribution of single trees, and if they contain reliable 3D and reflectance features for identifying tree species. In these regards, PPC-based ITC results have not been compared to corresponding lidar-based results.
The general objective of the present study was to assess the individual tree information contents of PPCs of a mixed boreal forest by comparing them to a corresponding lidar dataset. More specifically, we analysed the effect of aerial photo viewing geometry and forest structure on the accuracy of the 3D point reconstruction and end results. The latter was comprised of lidar-based and PPC-based ITC delineations, comparisons of tree height and crown area distributions, and assessment of the respective percentages of correct species classification based on both types of data.
4. Results
The aerial photos were registered to the lidar DTM based on ground control points with resulting RMSEs varying between 0.26 m and 0.53 m in planimetric accuracy, and between 0.94 m and 1.51 m in altimetric accuracy. The image matching process produced a point density three to five times higher than the lidar first return density (
Table 5). The highest densities were obtained for the dense conifer sites, while oblique views always led to somewhat lower densities for a given forest structure.
Table 5.
Density of points (points/m2) for lidar first returns and PPCs for each site.
Table 5.
Density of points (points/m2) for lidar first returns and PPCs for each site.
| | DCv | DCo | OCv | OCo | DMv | DMo |
|---|
| Lidar | 6.1 | 6.4 | 5.8 | 6.5 | 7.0 | 7.4 |
| PPC | 29.6 | 26.1 | 24.4 | 21.9 | 23.4 | 22.7 |
Figure 1 and
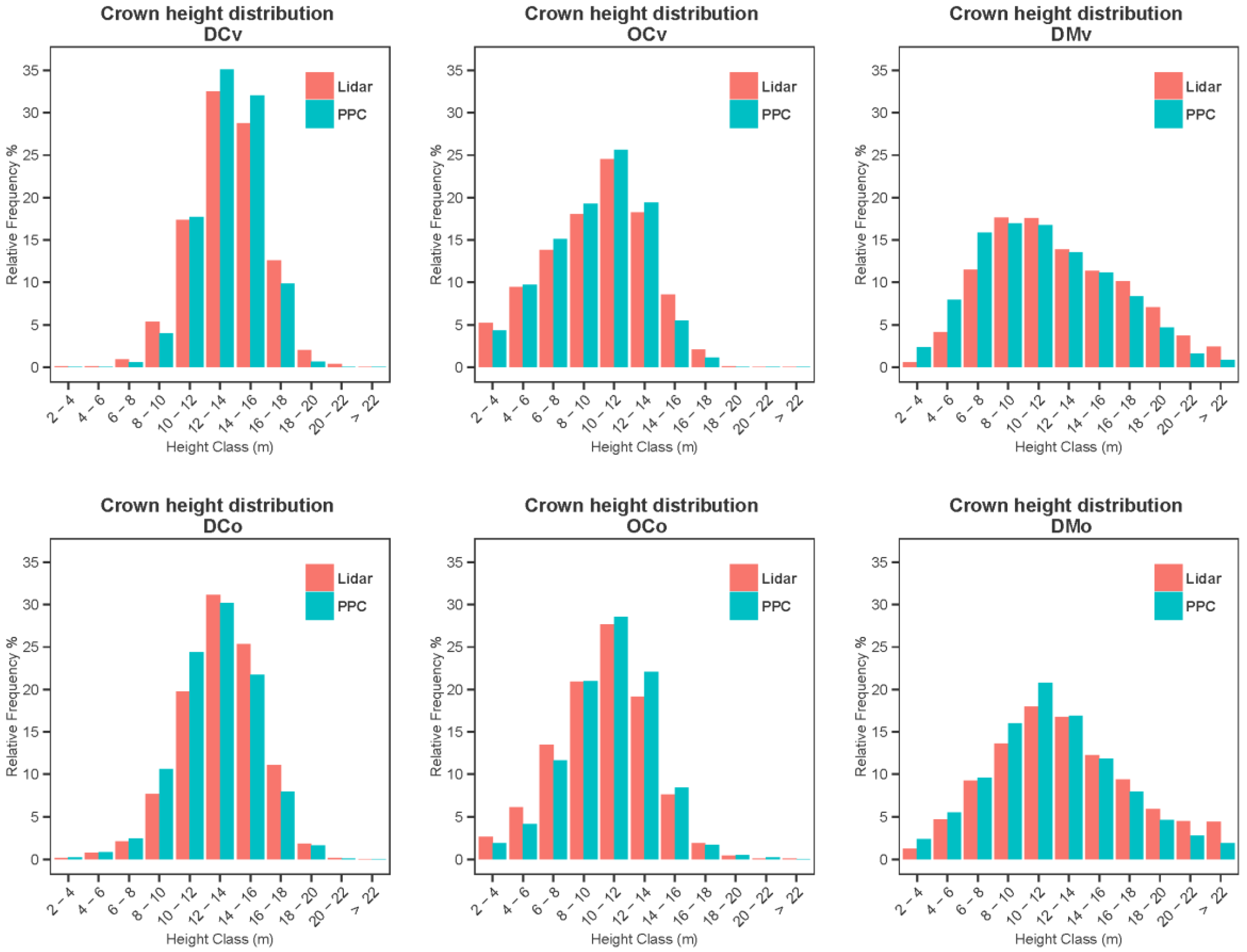
Figure 2 show different renderings of the lidar and PPC data. In the first figure the lidar and photogrammetric points are presented from a virtual oblique view direction, revealing the content and structure of the point clouds for the dense conifer site viewed at a near vertical angle. We see that the point density of the PPC is higher than that of the lidar, but that the photogrammetric points sometimes occurred in dense clusters, leaving small gaps. The characteristic elongated and conical shape of the firs can be well perceived in the PPC, as well as in the lidar data, although with a lesser point density. The second figure shows the lidar and PPC-based canopy height models of the six sites. In each of these, the corresponding CHMs are visually strikingly similar. Individual tree crowns are easily visible as bright blobs in the PPC-based CHM also. However, they appear less well resolved in the DCo site in the PPC-based CHM, compared to the DCv site.
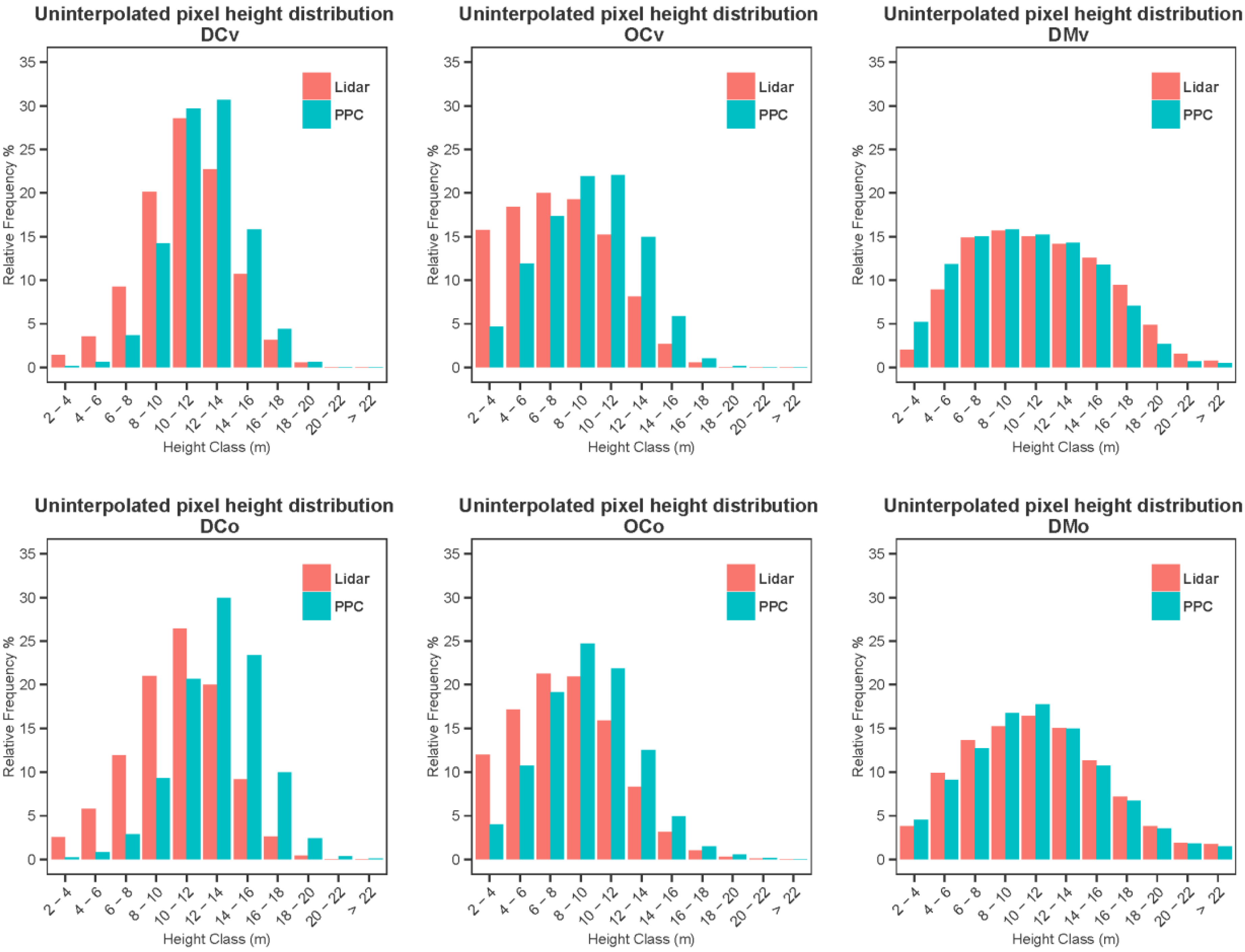
The corresponding relative histograms of lidar and photogrammetric point height at corresponding pixel locations are presented for the uninterpolated CHM (
Figure 3) and interpolated CHM (
Figure 4). As could be expected, the relative lidar frequencies of smaller point heights were greater in the more open sites as smaller trees and shrubs were visible between higher trees, and the dense even-age conifer sites having trees of similar sizes presented a more leptokurtic distribution. Disparities between the lidar and PPC distributions varied from very small in the case of dense mixed sites (viewed vertically or obliquely), to moderate, in the case of the dense conifer stands. In this latter case, low height relative frequencies were markedly underestimated, leading to an overestimation of the frequency of greater heights. This underestimation was stronger in the oblique view. Frequency differences were not as great in open conifer stands and the effect of obliquity was less pronounced in that case.
Figure 1.
From left to right, virtual views of photogrammetric point clouds (dark colored points), lidar (red points) and both of a balsam fir stand (horizontal view in the first row, vertical view in the bottom row).
Figure 1.
From left to right, virtual views of photogrammetric point clouds (dark colored points), lidar (red points) and both of a balsam fir stand (horizontal view in the first row, vertical view in the bottom row).
Figure 2.
Lidar (left) and photogrammetric (PPC)-based (middle) canopy height models 250 m × 250 m excerpts (brightness proportional to height) with corresponding orthophoto (right) of the six sites. DC: dense conifers; OC: open conifers; DM: dense mixed woods; v: vertical; o: oblique.
Figure 2.
Lidar (left) and photogrammetric (PPC)-based (middle) canopy height models 250 m × 250 m excerpts (brightness proportional to height) with corresponding orthophoto (right) of the six sites. DC: dense conifers; OC: open conifers; DM: dense mixed woods; v: vertical; o: oblique.
Figure 3.
Relative point height distributions of lidar and photogrammetric points for corresponding locations of the uninterpolated canopy height models (CHMs).
Figure 3.
Relative point height distributions of lidar and photogrammetric points for corresponding locations of the uninterpolated canopy height models (CHMs).
The points used to calculate the histograms of
Figure 3 are those for which both a lidar and a photogrammetric point existed at a given pixel location. The spatial distribution of the photogrammetric points was much less uniform than that of the lidar points. In PPCs, we could often observe (e.g.,
Figure 1) dense clusters on visible sides of crowns, surrounded by voids (absence of points). Interpolating the lidar and photogrammetric points has evened the spatial distributions and filled the voids with predicted values, with the effect of diminishing the discrepancies between the lidar and PPC relative point height distributions (
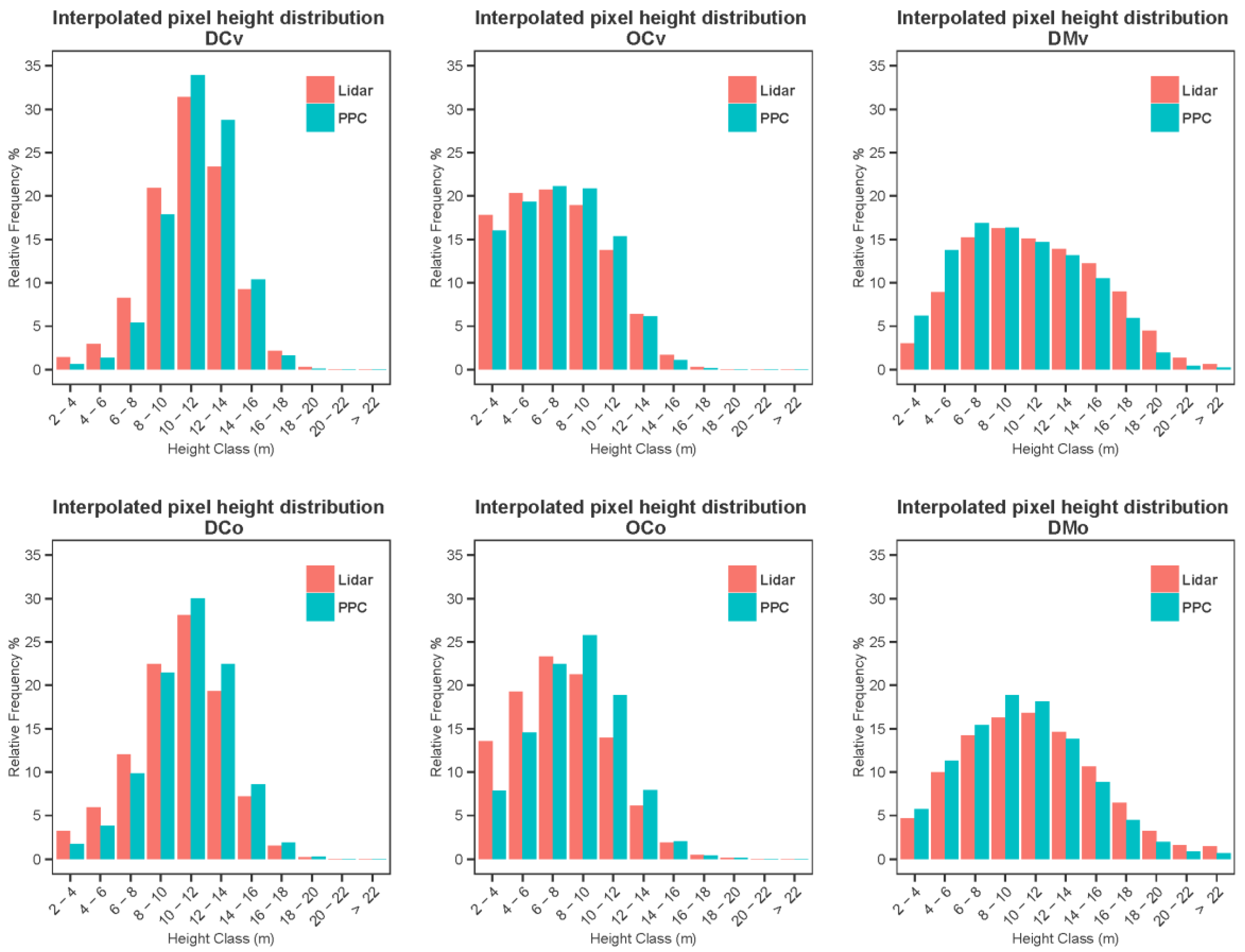
Figure 4). The most notable improvement brought about by interpolation is for dense conifers viewed obliquely. Moreover, the difference between the lidar and PPC distributions in the case of dense mixed sites was not sensibly improved by interpolation.
Figure 4.
Relative point height distributions of lidar and photogrammetric points for corresponding locations of the interpolated CHMs.
Figure 4.
Relative point height distributions of lidar and photogrammetric points for corresponding locations of the interpolated CHMs.
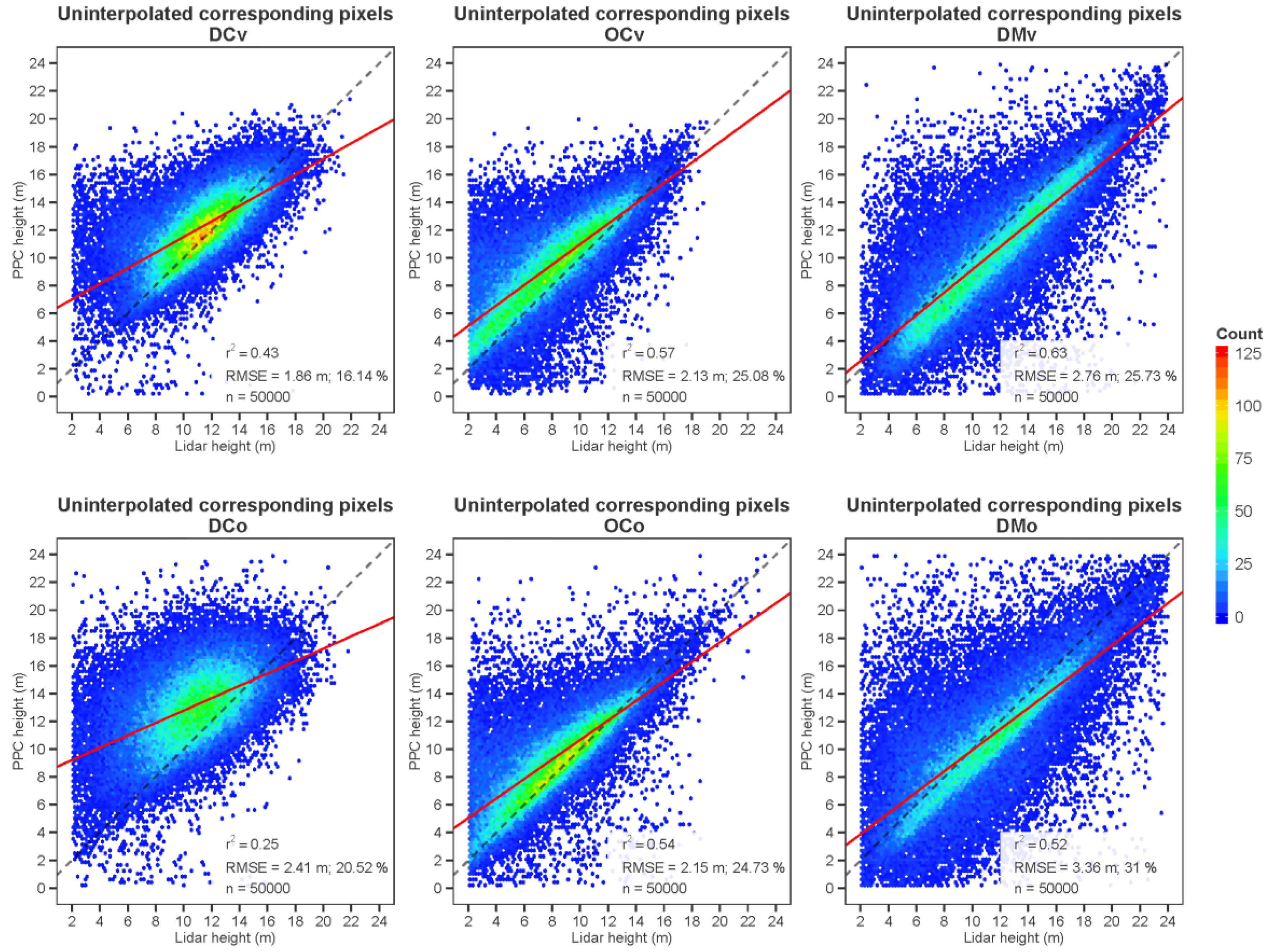
Figure 5 and
Figure 6 present scatter plots of the relationships between lidar and photogrammetric heights based on the corresponding pixels of the uninterpolated and interpolated CHMs respectively, as well as the slope, coefficient of determination and RMSEs of these relationships. The worst correspondence was that of dense conifers viewed obliquely (
r2 of 0.25; RMSE = 2.41 m; a strong departure from the 1:1 slope). The best relationship was seen for dense mixed woods viewed vertically. The slope was in this case much closer to the 1:1 line, and the
r2 much higher at 0.63. The absolute RMSE was somewhat high, but this was likely due to the presence of a greater range in height (up to 24 m). Oblique viewing worsens the correspondence in all case, but obliquity has less of an effect in the case of open conifers.
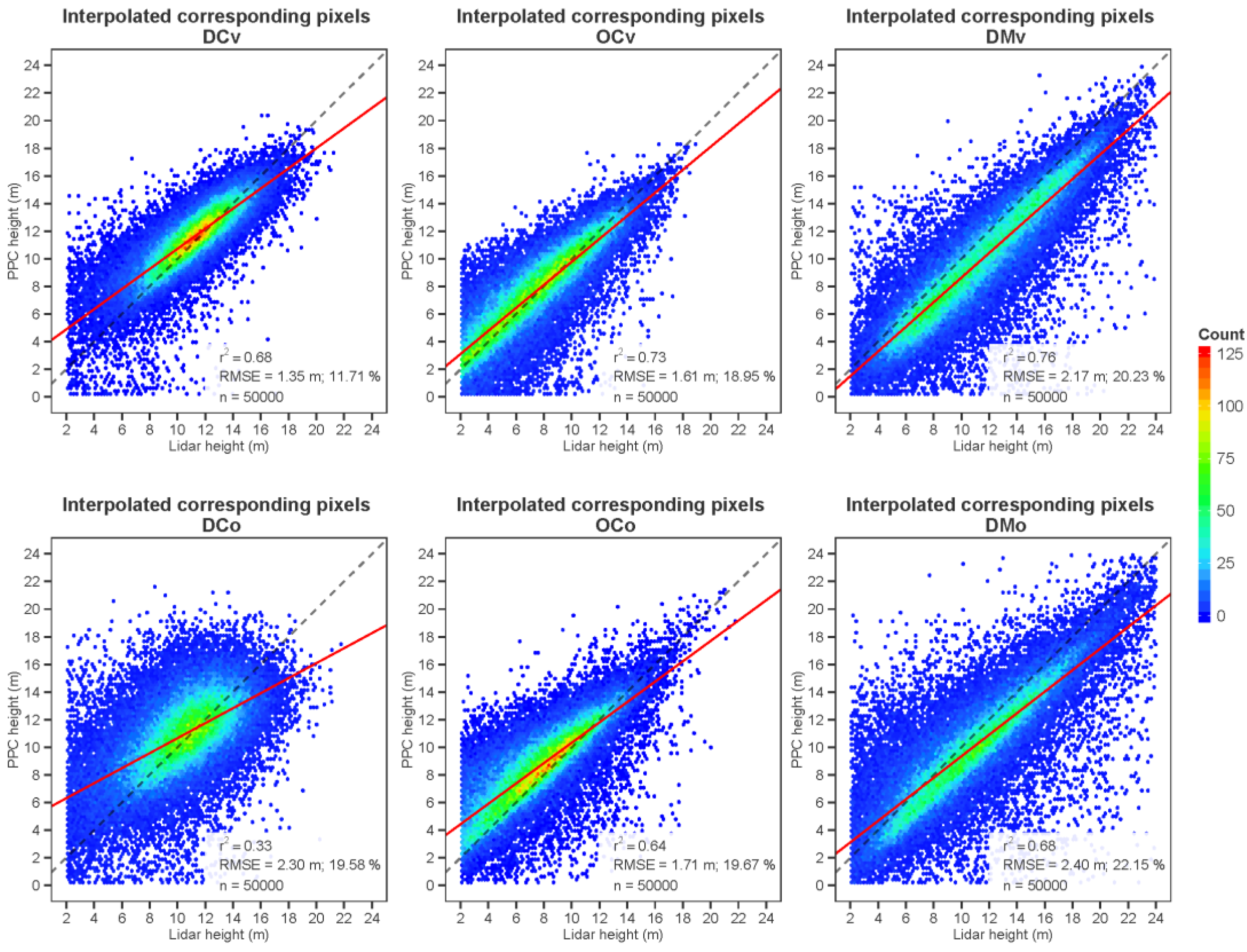
As evidenced by
Figure 6, interpolation markedly improved the correspondence between lidar and photogrammetric heights. The improvement is important for all sites except the dense conifer site viewed obliquely where the
r2 remains low, at 0.33.
Figure 5.
Scatterplots of the height correspondence between lidar and photogrammetric uninterpolated CHMs (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Figure 5.
Scatterplots of the height correspondence between lidar and photogrammetric uninterpolated CHMs (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
The individual crowns automatically extracted from the lidar and PPC-based CHMs respectively are presented in
Figure 7. Single tree extraction was possible on the photogrammetric CHMs, but did not perform as well as in the lidar case. In several cases, for example, single tree crowns extracted from the lidar were merged in the photogrammetric delineations, as evidenced in
Table 6. The number of detected crowns in the PPC-based CHMs were somewhat lower (11.7%–19.9% less) than what was found in their lidar counterpart, except in the case of the DCo site where 1.3% more crowns were found in the PPC. The underestimation was always less in the case of the oblique views.
Table 6.
Number of delineated trees based respectively on the lidar and PPC-based CHMs, and relative difference (PPC minus lidar) in %.
Table 6.
Number of delineated trees based respectively on the lidar and PPC-based CHMs, and relative difference (PPC minus lidar) in %.
| | DCv | DCo | OCv | OCo | DMv | DMo |
|---|
| Lidar | 4773 | 4769 | 2893 | 3021 | 8803 | 8776 |
| PPC | 3974 | 4829 | 2316 | 2486 | 7055 | 7751 |
| Difference (%) | −16.7 | 1.3 | −19.9 | −17.7 | −19.9 | −11.7 |
Figure 6.
Scatterplots of the height correspondence between lidar and photogrammetric interpolated CHMs (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Figure 6.
Scatterplots of the height correspondence between lidar and photogrammetric interpolated CHMs (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Figure 7.
Crown delineation results for lidar (green outlines) and PPC-based CHMs (blue outlines). All image excerpts are 65 m × 65 m (DC: dense conifers, OC: open conifers, DM: dense mixed woods, v: vertical, o: oblique).
Figure 7.
Crown delineation results for lidar (green outlines) and PPC-based CHMs (blue outlines). All image excerpts are 65 m × 65 m (DC: dense conifers, OC: open conifers, DM: dense mixed woods, v: vertical, o: oblique).
Before proceeding to the comparison of the lidar and PPC-based crown heights, we assessed the accuracy of the former, considered as the reference, by comparing them to heights measured in the field. A general average
r2 of 0.93 and RMSE of 1.29 m with a bias of −0.98 m were obtained over the 431 control trees (all species). These values were respectively 0.93, 1.31 m and −1.12 m for balsam firs, 0.93, 1.10 m and 1.62 m for spruces, and 0.98, 0.32 m and −0.26 m for deciduous trees. Moreover, the discrepancies between lidar and PPC-based relative tree height frequencies (
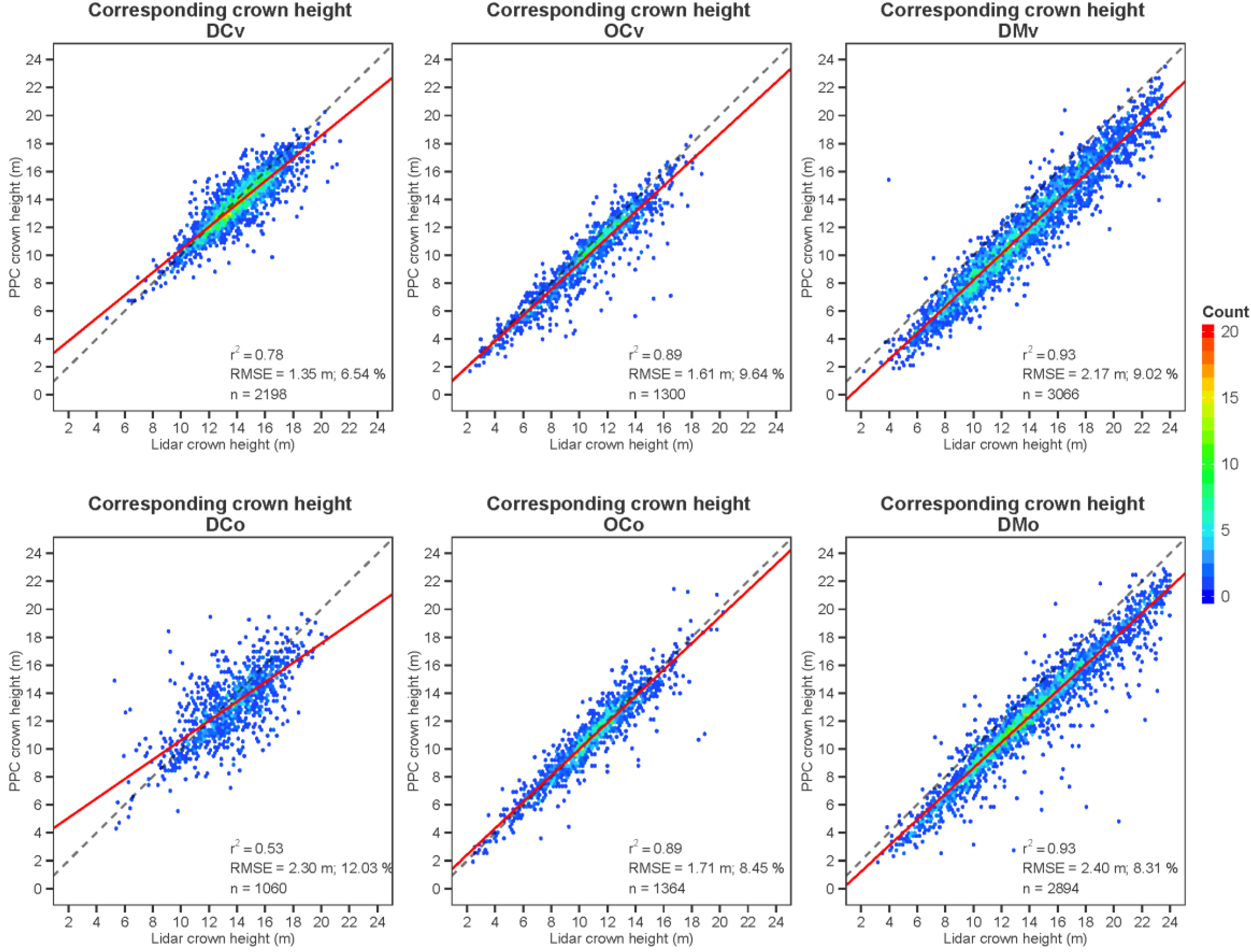
Figure 8) were similar to those observed at point level in the interpolated CHMs, but modest improvements appeared for open conifers viewed obliquely (OCo). However, the height correspondence between lidar and PPC crowns was much greater at tree level (
Figure 9), than for individual points of the CHMs (
Figure 5 and
Figure 6), with
r2 ranging from 0.53 to 0.93, and RMSEs as low as 1.35 m. In the case of open conifers and dense mixed forests, obliquity did not significantly modify the performance of height retrieval. The dense mixed site imaged obliquely presented the greatest level of error, with a RMSE of 2.40 m.
Figure 8.
Relative tree height distributions derived respectively from lidar and PPCs.
Figure 8.
Relative tree height distributions derived respectively from lidar and PPCs.
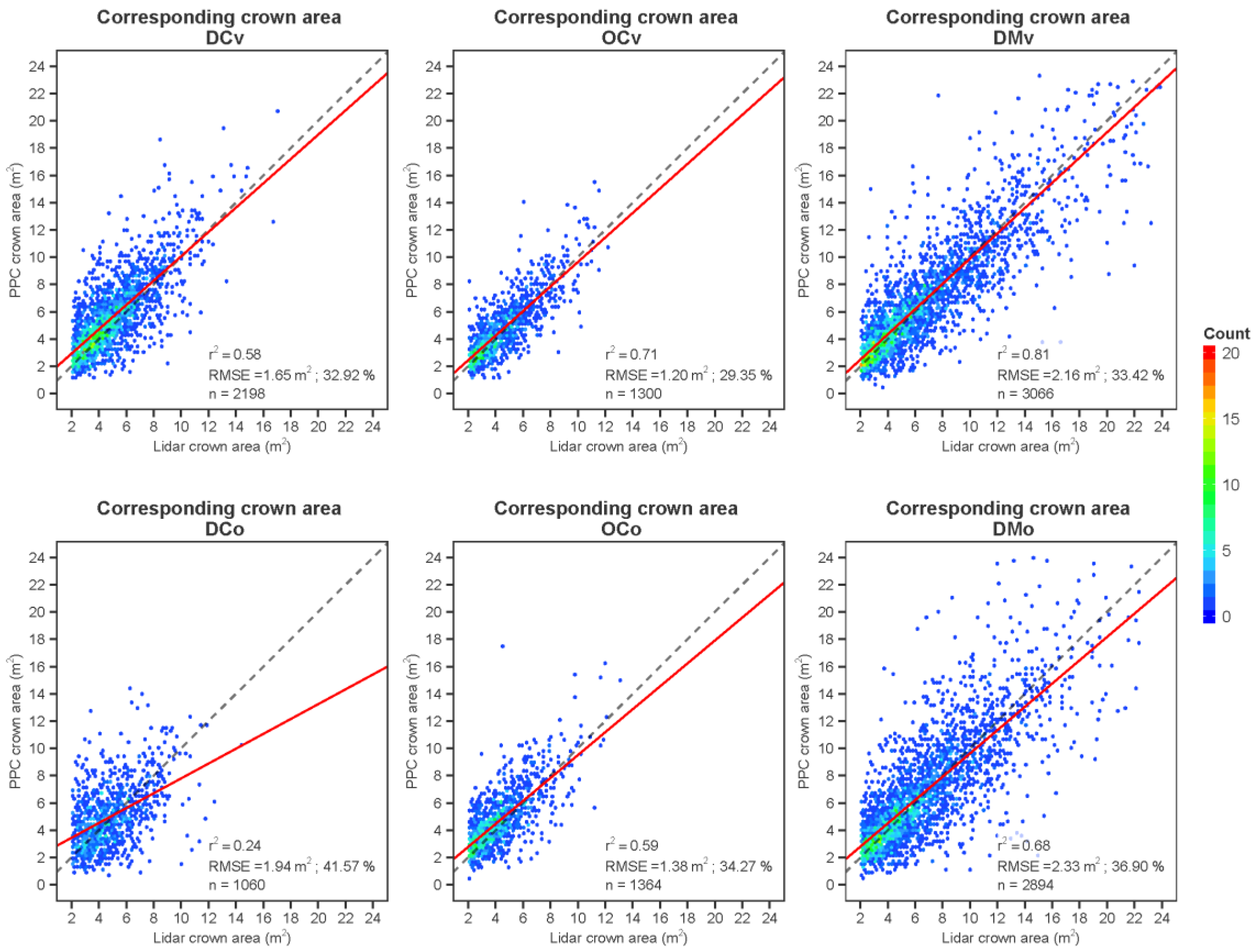
The correspondence of the delineated areas of crowns was much less than for height (
Figure 10). The best relationship based on the coefficient of determination was obtained for the dense mixed woods viewed vertically (
r2 of 0.81 and a RMSE of 2.16 m
2). The slope of the relationships was quite close to 1, except for tree height in the case of the DCo site.
Figure 9.
Scatterplots of the lidar and PPC-based tree heights (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Figure 9.
Scatterplots of the lidar and PPC-based tree heights (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
The random forest classification results for deciduous, fir and spruce trees are presented in
Table 7. In this table, OOB designates the out of bag error of the random forest classification from training dataset. The overall accuracy, producer’s and user’s accuracy and kappa coefficient results were calculated by classifying the validation dataset. Overall classification accuracies varied from 79.0% to 89.0%. The PPC-based classifications involving both 3D and intensity metrics were systematically the best, but were just marginally superior to those obtained from lidar. The lidar 3D metrics were superior to their photogrammetric counterpart, but the addition of the intensity metrics provided a strong increase of accuracy in the case of the photo-based results, while not causing any sensible improvement for lidar. In general, producer’s and user’s classification accuracies were lower for the spruce class. Obliquity did not have a strong effect on the species identification results. Training and applying the random forest classifier on the crowns of the two sites taken as a whole did not affect the results despite the variations that may exist in the 3D point clouds or photographic intensity characteristics.
The usefulness of the different metrics evaluated through the mean decrease in accuracy, and mean decrease of the Gini index they bring about, is presented in
Table 8. It shows that the curve-based metrics, indicative of the crown 3D shape, and the area over height ratio (proportion), came out first for both lidar (with or without intensity) and 3D-only PPCs. However, when the full PPC data was used,
i.e., including multispectral image brightness, the two most useful variables were intensity based (R_std and NIR_mean), outperforming the curved-based variables.
Figure 10.
Scatterplots of the lidar and PPC-based tree crown areas (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Figure 10.
Scatterplots of the lidar and PPC-based tree crown areas (red line represents the slope of the relationships and dashed line represents the 1:1 relationship).
Table 7.
Species classification results from lidar and PPC data.
Table 7.
Species classification results from lidar and PPC data.
| Variables Set | OOB | Overall Accuracy | Kappa | Producer’s/User’s Accuracy | n Variables |
|---|
| Deciduous | Fir | Spruce |
|---|
| DMv |
| Lidar 3D | 19 | 83 | 62 | 79/76 | 91/85 | 37/88 | 23 |
| Lidar 3D + intensity | 18 | 86 | 68 | 84/86 | 95/86 | 32/86 | 29 |
| PPC 3D | 19 | 79 | 55 | 61/71 | 89/80 | 54/81 | 15 |
| PPC 3D + spectral | 9 | 89 | 78 | 88/92 | 95/89 | 63/83 | 21 |
| DMo |
| Lidar 3D | 17 | 85 | 65 | 77/84 | 95/85 | 21/75 | 24 |
| Lidar 3D + intensity | 15 | 86 | 67 | 79/84 | 95/86 | 29/80 | 30 |
| PPC 3D | 18 | 79 | 54 | 60/86 | 94/79 | 29/56 | 14 |
| PPC 3D + spectral | 12 | 87 | 72 | 82./91 | 96/86 | 35/67 | 21 |
| DMv + DMo |
| Lidar 3D | 17 | 86 | 67 | 77/82 | 94.64/87 | 36/86 | 24 |
| Lidar 3D + intensity | 17 | 86 | 68 | 82/83 | 93.87/88 | 36/80 | 30 |
| PPC 3D | 18 | 79 | 55 | 65/74 | 90.00/82 | 41/65 | 14 |
| PPC 3D + spectral | 11 | 89 | 76 | 87/90 | 94.80/90 | 54/73 | 21 |
Table 8.
Mean decrease in accuracy, and mean decrease of the Gini index associated to the metrics for each of the classifications.
Table 8.
Mean decrease in accuracy, and mean decrease of the Gini index associated to the metrics for each of the classifications.
| | Mean Decrease Accuracy | Mean Decrease Gini | | Mean Decrease Accuracy | Mean Decrease Gini |
|---|
| Lidar 3D | PPC 3D |
| Curve_75 | 24.49 | 36.56 | Curve_75 | 23.17 | 32.39 |
| Curve_50 | 16.05 | 23.24 | Curve_50 | 21.52 | 29.58 |
| Curve_all | 13.52 | 23.22 | Area/H | 17.78 | 28.08 |
| Area/H | 12.08 | 26.46 | Hull_50 | 16.97 | 26.86 |
| Md1_max1 | 11.86 | 26.44 | Hull_75 | 16.22 | 23.47 |
| Hull_75 | 10.83 | 20.34 | Rcurve_50 | 14.83 | 25.07 |
| Hull_50 | 10.61 | 24.28 | Rcurve_all | 14.50 | 25.60 |
| Rcurve_50 | 8.33 | 14.32 | Pt_75-100 | 13.62 | 24.49 |
| Hull_all | 8.06 | 18.59 | Pt_50-75 | 12.94 | 22.74 |
| Pt_50–75 | 7.94 | 17.93 | Rcurve_75 | 11.45 | 15.07 |
| Lidar 3D + intensity | PPC 3D + spectral |
| Curve_75 | 16.60 | 27.98 | Std_r | 29.58 | 35.24 |
| Curve_50 | 12.26 | 20.03 | Mean_nir | 26.89 | 39.49 |
| Curve_all | 12.25 | 21.69 | Curve_75 | 15.00 | 24.37 |
| Area/H | 9.77 | 22.26 | Ndvi | 14.27 | 30.32 |
| Md1_max1 | 9.75 | 20.86 | Curve_50 | 12.22 | 25.58 |
| Hull_75 | 9.38 | 20.29 | Cv_ir | 10.89 | 22.95 |
| Hull_50 | 8.81 | 19.75 | Rcurve_all | 9.74 | 24.36 |
| Mn1_max1 | 7.36 | 19.13 | Area/H | 8.35 | 20.49 |
| Hull_all | 6.97 | 15.62 | Rcurve_50 | 8.32 | 21.69 |
| Mn1_maxA | 6.95 | 16.05 | Hull_all | 5.42 | 18.71 |
5. Discussion
While previous studies on the characterization of forest structure or composition have compared only the end results obtained from airborne lidar and photogrammetric data [
39,
42,
43], we have studied the difference between these two types of data over the full analysis workflow, from raw point cloud characteristics to classification results. This allowed a more complete understanding of the discrepancies and gave us the capacity to understand the effects of discrepancies at each processing level. We here outline the main differences between lidar and PPC-based results, at these different levels, and provide contextualized explanations.
Airborne lidar and aerial photos differ in their acquisition geometry. The maximum scan angle of lidar is commonly set to about 15 degrees from nadir. This can be contrasted with the much wider maximum lateral view angle of airborne photography (48 degrees in the case of the UltraCam). Although the maximum azimuthal view angle (along the flight axis) is less, and view angle problems can be alleviated in this direction by increasing the forward overlap of photographs at no cost, reducing these problems in the lateral direction is only possible by decreasing the distance between the flight lines, at relatively high cost. What is more, a photogrammetric point is generated for a given XYZ location only when this location is visible from at least two viewpoints. For this reason, the overall visibility of the trees is much less in the photogrammetric case than it is in the lidar case. This effect is more pronounced for trees having an elongated shape (e.g., boreal conifer trees) than for those with a more spherical crown, such as boreal deciduous trees, because seeing within the deep troughs between close-by trees is difficult in the case of conifers. Thus, view obliquity has lesser effects in dense mixed woods (and in theory also in pure deciduous forests). This effect appears clearly in
Figure 3 where the histograms of the uninterpolated pixel values are quite similar between lidar and PPCs for the DMv and DMo sites. Other researchers noted similar effects [
10,
36]. Openness of the canopy decreases the effect of obliquity (
Figure 3) because inter-tree occlusions are less frequent. Interpolation improves the correspondence between the two types of data, and decreases the effect of obliquity, because it fills data voids according to the immediate 3D context with values that often seem to concord between lidar and PPCs. However, a full explanation of this improvement would necessitate a deeper investigation, which is outside the scope of the present study.
The correspondence between individual tree heights (
Figure 8 and
Figure 9) is markedly higher than the in the pixel-based comparison, a result that is not surprising considering that the tree apices are viewed much more easily than their low sides in the photogrammetric case. The overall number of detected trees is lower in the case of the photogrammetric results because some crowns are not resolved in the PPC-based CHM. One of the main causes of this is that occlusion of the low sides or far sides of trees sometimes leaves data gaps between visible apices that are then bridged by the interpolation. Also, because matching is performed using, among other things, small matching windows (e.g., having a size of 7 × 7 pixels), the resulting photogrammetric point cloud is expected to be somewhat smoother than corresponding lidar point clouds. The tree delineation algorithm, sensing no significant inter-tree valley in this case, will merge neighboring crowns. Nevertheless, the relative frequencies per height class were very similar (
Figure 8), making the characterization of the height distribution quite accurate. The PPC height of single trees was also very accurate, being highly correlated to that of lidar, which itself was demonstrated to be close to the ground truth values. However, the loss of 3D resolution in the PPC-based CHM caused by the smoothing effect and the loss of points due to occlusions created much higher discrepancies in the case of crown area. Not being always able to reconstruct the full 3D shape of the trees in the PPC case resulted in much less reliable crown outline boundaries, with a logical impact on the crown area estimation.
Notwithstanding the abovementioned limitations of the PPCs, the tree species classification results for deciduous, fir and spruce trees were superior for this data type when using all the available 3D and intensity metrics. As could be expected, the 3D metrics of lidar outperformed those of PPCs, albeit not markedly, for reasons related to the previously highlighted shortcomings of the photogrammetric data. However, the rich multispectral contents of the PPCs did compensate for its lower 3D information contents. Lidar intensity did not improve the classification results by much, probably because the lidar 3D information itself was very rich, making the single wavelength intensity information content largely redundant. Although the vertical and oblique sites (DMv and DMo) were extracted from respectively close areas, far away from the aerial image centers, and although they fell on different images, it appears that the photo intensity response was nevertheless quite similar. This was demonstrated by the DMv + DMo classification in
Table 7 where classification accuracy did not clearly decrease even though the sun-target-sensor geometry was quite different between the sites. Radiometric normalization however remains recommendable when using image intensity metrics, particularly if the photos were acquired over different days.
We recognize that the present study has certain limitations. First, the 3D coregistration between the lidar and photogrammetric models was not highly accurate. In these dense forests, the ground is often invisible, leaving few areas where accurate ground control points extracted from the lidar DTM can be associated to photo pixels. This logically affects the CHM-based correspondences more than the ITC based results. Using more accurate coregistration techniques, such as point cloud registration [
58], we suspect that the lidar-PPC discrepancies of
Figure 3 and
Figure 4 would somewhat diminish, and the regression lines of the pixel and crown height relationships would move closer to the 1:1 lines.
Secondly, the results on crown height concern corresponding lidar-PPC crowns that were automatically selected, and the results on species were obtained from crowns selected by the photo-interpreter with a possible involuntary subjective bias occurring during the selection process. This likely leaves out many erroneously delineated PPC crowns from which incorrect 3D and intensity metrics values would be extracted and introduced into the classification, leading to lower identification accuracies. A full assessment of the comparative performances of lidar and photogrammetry in this regard would require comparisons with ground truthed crown delineations, a very labor intensive and costly endeavor. Furthermore, a wider set of lidar and PPC-based metrics should be tested, and a larger number of lidar and aerial images reflecting various conditions of forest structure, composition (with a greater number of species), topography and acquisition geometries should be investigated. However, the six study sites in our experiments covered areas ranging from 3 to 12 ha. In particular, classification tests were conducted on two 12 ha sites, which is likely to confer robustness to the results. We therefore think that the results presented in this study are highly indicative of the potential of forest structure and composition characterization based on photogrammetric point clouds analyzed with an individual tree crown approach.
6. Conclusions
The results of this study lead us to conclude that the characterization of the tree height distribution and general species composition of boreal forests based on ITC analysis of photogrammetric point clouds can be achieved with an accuracy similar to that obtained from airborne lidar data. Despite occlusion effects in the PPCs that are apparent at the level of points or pixels, crown-based results do not differ markedly. However, the estimation of crown areas showed much higher discrepancies between lidar and PPC-based results. We also found that the quality of the ITC-based results, in terms of height estimation or species identification, was rather uniform across the image space, i.e., not strongly affected by photographic viewing geometry. Finally, the PPC 3D classification metrics provided important species identification data which, when combined to multispectral image intensities, led to higher classification accuracies than the lidar 3D and intensity metrics.
Aerial photo acquisition remains significantly less expensive than that of airborne lidar due to higher flying altitudes, wider view angles and greater flight speeds. For this reason, provided that an accurate DTM is available, from lidar or other sources, the general characterization of the height structure and species composition based on photogrammetric point clouds becomes possible. PPC-based results could be further improved by reducing the effects of occlusions in the stereo models, either by using a more intelligent approach for height interpolation to fill the PPC data gaps, or by increasing the lateral overlap of aerial images. This latter solution would entail higher acquisition costs due to the greater number of required flight lines, but could be configured to be still less costly than lidar. Furthermore, the operational deployment of such technology over large territories creates the obligation to tackle the issue of variable sun elevations or atmospheric conditions which affect image intensities in a complex way, thus requiring the implementation of intensity normalization strategies. Notwithstanding these processing complications, forest managers and scientist will certainly benefit from the data gathering capacities offered by individual tree crown analysis of photogrammetric point clouds.