Abstract
Stem characteristics of plants are of great importance to both ecology study and forest management. Terrestrial laser scanning (TLS) may provide an effective way to characterize the fine-scale structures of vegetation. However, clumping plants, dense foliage and thin structure could intensify the shadowing effect and pose a series of problems in identifying stems, distinguishing neighboring stems, and merging disconnected stem parts in point clouds. This paper presents a new method to automatically detect stems in dense and homogeneous forest using single-scan TLS data. Stem points are first identified with a two-scale classification method. Then a clustering approach is used to group the candidate stem points. Finally, a direction-growing algorithm based on a simple stem curve model is applied to merge stem points. Field experiments were carried out in two different bamboo plots with a stem density of about 7500 stems/ha. Overall accuracy of the stem detection is 88% and the quality of detected stems is mainly affected by the shadowing effect. Results indicate that the proposed method is feasible and effective in detection of bamboo stems using TLS data, and can be applied to other species of single-stem plants in dense forests.
1. Introduction
A stem or culm refers to the main structural axis of a plant above ground. It transports fluids, supports the whole plant and stores the energy. Stems are of vital importance to ecology study and forest management. Diameter at the breast height (DBH) and plant density are key parameters for estimating biomass productivity and carbon storage [1,2,3]. In forestry, stem mapping and stem curve measurement are necessary for monitoring forest growth and managing forest harvest [4,5]. However, the traditional survey of vegetation characteristics (e.g., DBH, plant density) is usually done by on-site manual measurement, which is time consuming, labor intensive, and often subject toerrors associated with manual works [5,6,7]. Moreover, it is usually difficult to gather some stem properties (e.g., diameters at different heights, stem curvature) using the manual survey, unless destructive methods are employed. Some automatic, accurate, and efficient approaches to obtain the properties of stems are needed. In recent years, terrestrial LiDAR (Light Detection And Ranging), also known as Terrestrial Laser Scanning (TLS) has been widely used in constructing forest inventory, because it can record high density three dimensional (3-D) point clouds and thus obtain high resolution structural information from forests [8,9,10].
Detecting stems from point clouds has been discussed in many previous studies [4,8,11,12,13,14,15,16]. Maas et al. [14] first extracted horizontal point slices above ground, then a clustering and circle fitting procedure was conducted to determine the existence of stem points. The stem detection rate was about 97% in the test plots with a stem density less than 600 stem/ha. Similarly, a cylinder/circle fitting method has been used to identify the stem positions in some other studies (e.g., [13,15,16]). These methods usually require the terrain surface information that is often difficult to obtain, especially in heterogeneous forest with rough terrain and low vegetation cover. Liang et al. [8] proposed a two-step procedure for stem mapping in a denser forest (plot density ≈1500 stem/ha). They first identified the points with flatten or vertical shapes as the candidate trunk returns, then used a robust cylinder fitting and trunk following algorithm to verify the location of stems. The correction rate of stem mapping using the single-scan TLS was 73%. This method was then applied in stem detection in a forest plot (plot density <500 stem/ha) using mobile laser scanning (MLS) and 87.5% of all the reference stems were mapped correctly [11]. Range imagery [17] and full-waveform [9] data were also utilized in stem detection, but these data need special instruments that are not widely used nowadays and more pre-processes are always needed.
MLS has also been applied to stem detection in urban area. Hetti Arachchige [18] extracted the candidate stem subsets based on the shape indices and geometric features. Roadside stems were detected and connected using an orientation-based layer wise searching algorithm. About 90% of reference trees were correctly detected. Lehtomäki et al. [19] proposed an algorithm to detect the pole-like objects from mobile laser scanning point clouds. Their algorithm has four steps: segmentation, clustering, merging and classification, and was able to identify 77.7% of 148 poles (e.g., lamp, tree trunk and traffic sign pole), but no identification of stems between stems and other pole-like objects was carried out [19]. The spacing between roadside trees in urban areas is usually regular and neighboring trees are not close together. In addition, relatively flat ground in urban areas makes stem detection quite different from that in forestry regions.
In summary, most of previous studies of stem detection focused on forests with some typical tree densities (usually less than 1500 stem/ha) and trees in the studied plots (e.g., pine, spruce, birch, and 2 Douglas-fir forest) usually had a mean DBH value >10 cm. However, in a forest with a high stem density, e.g., more than 5000 stem/ha, the shadowing effect could become more significant. A single stem may be disconnected or partly missed in the point clouds. Consequently, the cylinder (or circle) fitting and trunk following processes will be affected directly. Moreover, clumping plants, thin and bended structures can pose new challenges to separate stems from neighboring stems, which seldom happen in low-density forests. Therefore, a study of the effective stem detection in high-dense forests using TLS data is deserved.
In this paper, we present a novel and feasible algorithm to detect stems in high-dense forests using TLS point clouds. To avoid the time-consuming registration process of point clouds as well as to improve the feasibility of field scanning, we use single-scan measurements. The method is tested in a dense bamboo area (about 7500 stem/ha). Unlike some previous studies, our method does not require information about the terrain surface and no circle or cylinder fitting is needed. Furthermore, the algorithm contains a new and simple method to separate stems from neighboring stems, and this problem has not been addressed in previous studies. The arrangement of this paper is as follows. Section 2 describes study area and data. Section 3 introduces the method. Section 4 presents experiments and results. Discussion is in Section 5. Section 6 is a summary.
2. Study Area and Data
The study area is a mature bamboo forest located in Sichuan Giant Panda Sanctuaries (30.06° N, 103.01° E), China. Bamboo belongs to the grass family Poaceae and grows on all continents, except Antarctica and usually has a high population density in both wildwoods and plantations [20,21,22]. The bamboo stem density of the study area is approximately 7500 stem/ha. Young bamboos (height below 3 m), weeds and fallen bamboos were also found on the ground. The single-scan LiDAR dataset was collected in November of 2013 using a Leica ScanStationC10 (Leica Geosystems Ltd., Heerbrugg, Switzerland). The instrument transmits a wave of 532 nm (green light) and accuracy of the distance measurement at a distance of 50 m from the target is about 4 mm. The beam divergence is 0.24 mrad and the spot size is 4.5 mm at 50 m distance. A high point density is required to record the structure information. Rough point spacing was about 3 mm at a 10 m distance.
The scanner was mounted on a tripod. Because the clear space for TLS placement was limited by the dense canopy, we found it was quite safe and convenient to setup the scanner adjacent to the plots instead of within them. The original measurement range was wide and the data were collected near the road, there were some no-vegetation objects in the original point clouds, such as cars, power towers and buildings. Two approximate rectangle plots (Plot A and Plot B) were carefully selected and clipped from the original data using the Cyclone™ SCAN software (Leica Ltd., Heerbrugg, Switzerland ). As this study mainly focuses on stem detection, DBH or tree height is not requisite in both detection and validation. Therefore, we only measured the DBH and height of some representative bamboos in the field. Actually, only five sampled bamboos are located in two plots. According to the field measurements, the heights of the sampled species varied from 6 m to 13 m and their DBHs ranged from 3 cm to 8 cm.
Figure 1 shows the diagram of two plots. Plot A is about 100 m2 and the distance between the nearest bamboo and the scanner was about 4.0 m. Plot B covers a ground area of about 120 m2 and the distance between the front side and the LiDAR was about 5.0 m. The terrain surfaces in both plots are uneven and common in natural forests. There were 82 reference stems in Plot A and 84 in Plot B. The number of reference plants and relative stem map was recorded manually using Terrascan™ software (Terrasolid Ltd., Helsinki, Finland). To avoid false statistics in 3-D point clouds, we divided the plots into small sections; then the number and relative positions were recorded successively. In terms of the undergrowth, stem density and topographic relief, Plot A and Plot B are quite typical. Although the areas of two plots are smaller than those in previous studies, the number of reference stems is sufficient compared to relevant studies [5,8,14,18].
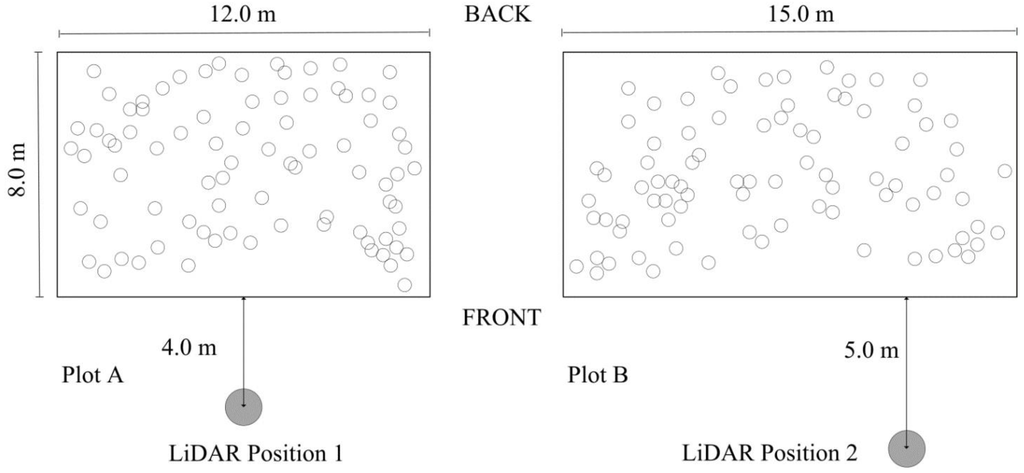
Figure 1.
Diagram of two plots. The side near the LiDAR position is defined as front and its opposite is defined as back. Circles indicate relative stem locations.
3. Methods
The proposed method contains three phases (Figure 2). First, candidate stem points are identified from original point clouds through classifying the points at two scales (dashed boxes in Figure 2). Then, the stem points are grouped using a clustering algorithm. These clusters are recognized as stem sections. Finally, a simple single-stem model is used to merge the clusters and separate stems from their neighboring stems.

Figure 2.
Phases of stem detection algorithm.
3.1. Two-Scale Classification
Taking advantage of points’ geometric features, we proposed a two-scale classification method for stem detection in this section. In the following, we first analyzed multi-scale geometric features in vegetation point clouds and discussed the optimal radius selection subsequently. Finally, we introduced a stem recognition method using two-scale features.
3.1.1. Multi-Scale Features of Vegetation Point Clouds
Generally, geometric features can be identified through analyzing the spatial distribution of local points. Points in the spherical neighborhood centered at a laser point form a local point set. Principal component analysis (PCA) is performed on each set to obtain three eigenvalues (λ1, λ2, λ3) (λ1 ≥ λ2 ≥ λ3) and three associated eigenvectors (e1, e2, e3) representing three orthotropic axes of the spatial distribution of local points [23]. The axial lengths are (i = 1,2,3). Three geometric features are defined to represent the shape of local point set distribution (Equation (1)). Each point is classified as linear (a1D), planar (a2D) or volumetric (a3D) according to the maximum value among a1D, a2D, and a3D [24].
The radius of neighborhood area defines the feature scale. The spatial distribution of local points set varies with scales even for the same object. To illustrate the multi-scale performance, we manually extracted some point samples from original data in Section 2. Table 1 shows classification results of sampled stem points as the radius increased from 1 cm to 12 cm. These red/blue/green colors are corresponding to linear/planar/volumetric classification results of each point. This sample contains 3080 points and the estimated radius is about 4 cm. The salience feature of these points changed from linear (r = 1 cm, 52.24%) to planar (r = 4 cm, 96.43%) and became linear (r = 12 cm, 100%) again. Similarly, salience features of other objects (e.g., branch, foliage, grass, and ground) in forest scenes also change with scales. Table 2 summarizes the classification results of other samples when the radiuses are set as 4 and 12 cm and associated image widths and heights. Compared with stem samples listed in Table 1, these objects show different properties. Branch points always exhibit “linear” due to the thin structures. The volumetric distribution is the salience feature of foliage samples at both scales. The grass sample shows linear or volumetric distribution at a small-scale r (e.g., r = 4 cm) and becomes more volumetric at a bigger scale (e.g., r = 12 cm). As for the ground points, they are mainly classified as planar at both scales.
In a nutshell, different objects have variable percentages of class types (i.e., linear, planar, and volumetric), which change differently with scales. These multi-scale features are useful for recognizing objects, which had been studied in some applications [24,25]. However, since vegetation objects (e.g., stem, branch, grass, and shrub) are quite irregular and usually clumping, multi-scale features were seldom used in processing vegetation point clouds, especially in natural forest.

Table 1.
Percentages of classified features in sampled stem data.
| Point clouds of stem (Height ≈ 80 cm, Radius ≈ 4 cm) |  |  |  |  |  |  |  |  |  |  |  |  |
| radius (cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| linear (%) | 52.24 | 6.62 | 4.06 | 2.82 | 16.23 | 88.44 | 91.13 | 93.47 | 95.91 | 98.41 | 99.94 | 100 |
| planar (%) | 47.11 | 75.32 | 95.55 | 96.43 | 82.24 | 11.23 | 8.86 | 6.54 | 4.09 | 1.59 | 0.06 | 0 |
| Volumetric (%) | 0.65 | 18.06 | 0.39 | 0.75 | 1.43 | 0.33 | 0.01 | 0 | 0 | 0 | 0 | 0 |

Table 2.
Percentages of classified features in other samples.
| Branch | Foliage | Grass | Ground | |||||
|---|---|---|---|---|---|---|---|---|
| point number | 119 | 67,537 | 5996 | 7287 | ||||
| classified points | 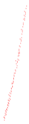 | 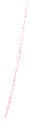 | 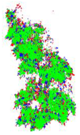 |  |  |  |  |  |
| dimensions (m) | 0.1/0.5 | 1.5/2.3 | 0.8/1.8 | 0.6/1.2 | ||||
| radius (cm) | 4 | 12 | 4 | 12 | 4 | 12 | 4 | 12 |
| linear (%) | 100 | 100 | 10.50 | 7.69 | 49.87 | 14.28 | 6.24 | 2.83 |
| planar (%) | 0 | 0 | 11.49 | 13.27 | 16.84 | 5.85 | 84.29 | 97.17 |
| volumetric (%) | 0 | 0 | 78.01 | 79.04 | 33.29 | 79.87 | 9.47 | 0 |
3.1.2. Optimal Radius Selection
In many applications, features of points were usually calculated within a sphere with a fixed radius [8,11,15,23]. However, suitable neighborhood for each point varies. For instance, different stems may have diverse DBHs, and the radius of a single stem usually decreases with height. Therefore, an adaptive optimal radius selection method is necessary in the two-scale classification.
Demantké et al. [26] developed a radius selection criteria to identify the optimal radius of each point. In this method, an entropy function E is defined as
A radius interval [r1, ru] that contains candidate optimal radius is predefined. E values with radiuses in the given interval for each point are computed. Finally, for each point, the radius with minimal E is selected as the optimal radius. The pseudo code of the scale determination is presented in Algorithm 1. According to Equation (2), a smaller E value indicates that one of the feature values (i.e., a1D, a2D, a3D) is much greater than the other two [26], which can be used as an index to distinguish geometric feature.
| Algorithm 1. Scale selection | ||
| Input: Point clouds P; Given interval Output: radius set R | ||
| for every point Pi ∈ P do | ||
| for every radius rj ∈ [r1, ru] do | ||
| Find the neighboring points set sj of pi with . Calculate geometric features according to Equation (1). Calculate and record the entropy function Ej according to Equation (2). | ||
| end for | ||
| The radius rmin with minimal Emin is selected as the optimal radius for . Add rmin to R. | ||
| end for | ||
3.1.3. Candidate Stem Points Recognition
As illustrated in Section 3.1.1, stem points can be labeled as “planar” at a small scale (e.g., 4 cm) and show a linear distribution at a big scale (e.g., 12 cm). However, other types of objects (e.g., branch, foliage, grass, and ground) in forest scenes show different multi-scale properties. Therefore, combining features at different scales can be helpful in stem recognition.
In this study, a two-scale classification method is proposed to recognize candidate stem points from raw point clouds. Two intervals, [r1, r2] and [r3, r4] (r1 < r2 ≤ r3 < r4), corresponding to two scales, are introduced to find optimal radiuses for each point at different scales. A small increment of radius will improve the precision, but also increase the calculation load. It was set to 0.5 cm in both intervals to keep a balance between precision and computing time according to tests. By using the Algorithm 1, the optimal radiuses for each point at each scale are acquired. Then points will be classified into linear, planar or volumetric according to Equation (1) at both scales. Finally, stem points can be recognized by combining two-scale features. The main steps of classification are listed in Algorithm 2. The ranges of two intervals can be set according to the radius of trees. In our method, the lower bound (r1) of the first interval should be larger than the point spacing while its upper bound (r2) should be smaller than the max stem radius in the scene. As for the second interval, its lower bound (r3) should be no less than r2. Because a wider range of interval will increase the unnecessary computation, it is suitable to set the upper bound (r4) around double the value of r3 according to trials
Unlike the previous methods in which multi-scale features are computed using all original points, we compute second scale features using only a subset of original points. As in Algorithm 2, only the “planar” points remain after the first scale classification. Feature calculation at second scale is performed on this subset only. Specifically, to keep the geometry significance, if the number of neighboring points is less than a threshold (e.g., 5 in this study), the given radius will not be selected as the optimal radius. If there is no optimal radius in the intervals, then the point will be classified as “volumetric”.
| Algorithm 2. Two-scale classification | |
| Input: Point clouds P; Given intervals [r1, r2] and [r3, r4] Output: Candidate stem point set Pstem | |
| (1) Run Algorithm 1 with interval [r1, r2], get optimal radiuses for all points. | |
| (2) Classify each point into linear, planar or volumetric according to Equation (1). | |
| (3) Only “planar” points remain | |
| (4) Run Algorithm 1 with interval [r3, r4], get optimal radiuses for remaining points. | |
| (5) Classify these points into linear, planar or volumetric according to Equation (1). | |
| (6) These “linear” points are recognized as candidate stem points Pstem | |
3.2. Clustering
Stem points will remain after the two-scale classification while most of points from foliage, grass, ground and branch are excluded. Due to the ambiguity of eigenvalue-based spatial distribution analysis and noise, there are still a few non-stem points (mainly foliage points) left. Nevertheless, after the two-scale classifications the density of residual non-stem points is much less than stem points, and groups of non-stem points are disconnected and dispersed. These facts are useful for verifying the detected stem points.
The Euclidean clustering algorithm is introduced to exclude non-stem points and create stem groups. Any two points with their spacing less than de will be considered as subordinates to the same cluster, otherwise they belong to two different clusters. Update the clusters until all points are assigned to a certain cluster. The number of points in each cluster is used to name cluster size, which is determined by the point spacing. Generally, stem clusters are much bigger than the residual non-stem clusters. Therefore, clusters with their size less than Nc are excluded from the candidate stem clusters. Nc can be specified according to the original point density. de is the only parameter needed to be set in clustering and has a major influence on the cluster size. The aim of clustering is to group the “planar” points and therefore de should be selected according to “planar” points’ density. Generally speaking, neighbors within the optimal radius of one point are considered to have similar properties. Therefore, in this method, the mean optimal radius of “planar” points at the first scale classification is used as de adaptively.
The distance-growing method, i.e., Euclidean clustering algorithm, takes advantage of the point density change of no-stem objects after two-scale classification. If other methods are applied to segment stem sections, for example, RANSAC (RANdom SAmple Consensus) for cylindrical model detection, we have to take the stem diameter variation into account, because the bamboo stem is thin and long, and a cylindrical model may not represent the real stem very well due to the curved structure of bamboo stem. In addition, it is difficult to determine the end conditions for cylinder extraction methods, as the number of stem sections in point clouds is unknown and points from other objects may also be detected as stem if a big distance threshold (i.e., point distance to model) of RANSAC is used. By way of contrast, the distance-growing method is simple but feasible and need less computation time. For the record, if there exits many noise points in original point clouds, the distance-growing method may fail in section detection. However, due to the high accuracy of TLS, this situation rarely happens.
3.3. Merging Stem Clusters
After the clustering step, stem points are grouped. The next step is to group the stem points that come from the same plant. In fact, stem points are usually divided into several clusters due to the shadowing effect caused by dense foliage, crowded stems, and the limitation of the single scan method. Separating stems from neighboring stems in a high density forest is a difficult task that has not been studied in previous studies [27]. Merging clusters simply by analyzing the overlapping and orientation of neighboring clusters might not be effective to handle bended stems [19]. In this study, a direction-growing method to merge detached stem clusters is proposed and only one distance threshold is needed in this method.
First, we assume that a stem can be approximately represented by a quadratic curve in a three-dimensional coordinate given in Equation (3).
In Equation (3), x and y coordinates of the stem are functions of height z, and z is the plant height to be determined. Figure 3a shows a typical stem curve in a rectangular coordinate system. ouz is the local 2D coordinate system and u points the direction of stem curve projection (line ef). u can be in any direction in the oxy plane. Equation (4) shows the expression fef (a, b, c are parameters) of line ef, which is the projection of a stem on ouz plane, and it also can be expressed as a function of x and y (Equation (5)) while the relationship between x and y is linear (Equation (6)). If we eliminate y in Equation (6) by substituting Equation (5), line ef can be expressed as Equation (7). Then, the left hand side term of Equation (4) is substituted by the right hand side term of Equation (7). Finally, the relationship between x and z can be expressed as Equation (8). Furthermore, fy(z) can be expressed in the same way like .
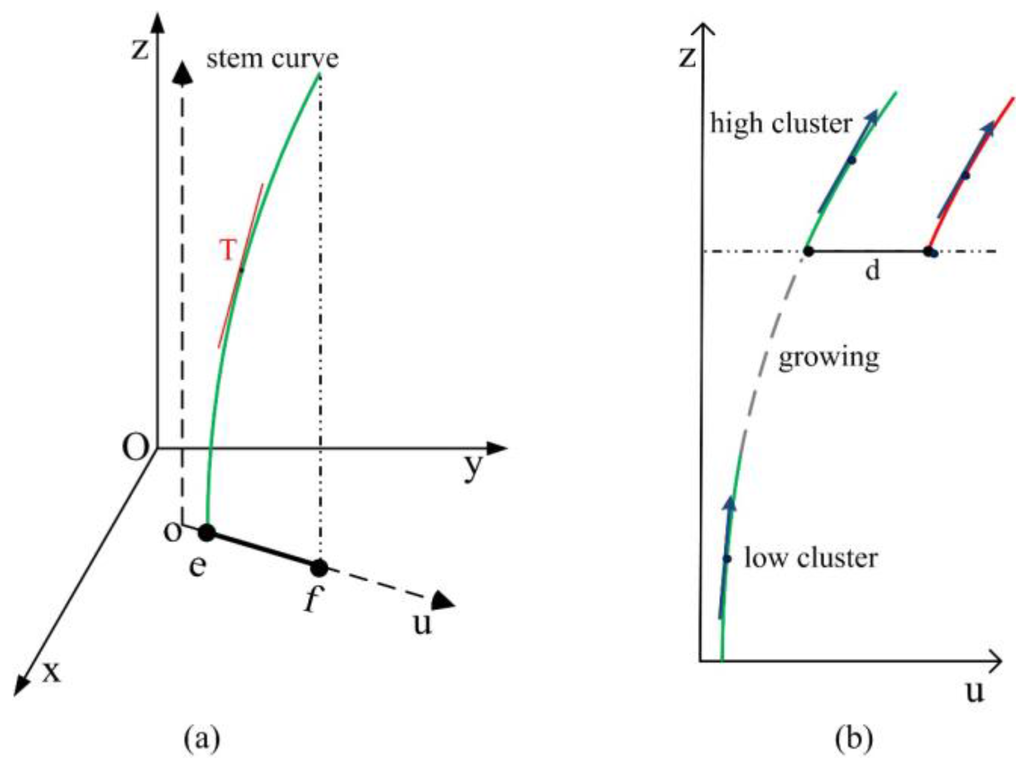
Figure 3.
(a) Simplified stem model; and (b) direction-growing example.
Note that Equation (6) is usually in the form of y = kx + m, in which k is slope and m is intercept. However, when a stem cluster is under calculating, we transform the horizontal coordinate to the origin by subtracting the minimal x and y (e.g., x and y of point e in Figure 3a), then change back later by an inverse transform. Thus, m is very close to zero after coordinate transformation and can be dropped from Equation (6).
The direction vector T(Tx, Ty, Tz) of stem (e.g., red line in Figure 3a) can be expressed as the derivative of Equation (3). It forms a simple stem model as shown in Equation (9). Ai and Bi are direction parameters.
The main idea of the direction–growing algorithm is that if the position of one cluster can be predicted by another cluster, these two clusters are from the same plant. In calculating the directions, for a pair of stem clusters, parameters in Equation (9) can be solved using their orientation vectors and cluster’s mean height z. The direction vector of a cluster can be estimated by PCA using all its points approximately. The eigenvector corresponding to the maximum eigenvalue is considered as orientation of the cluster. Then in the “growing” phase, the highest point in lower cluster is selected as the seed point. With the height increasing, update the coordinate of the seed point according to Equation (10) until the height is no less than the bottom of the higher cluster. A small height increment will improve the accuracy and 1 cm for the growing process is accurately. Only if the distance between the seed and bottom points of the higher cluster is smaller than threshold dstem, two clusters are considered from the same stem. Figure 3b shows an example of the direction–growing algorithm. Two higher stem clusters have the same direction vector and height, but after the lower cluster grows up, the left cluster will be merged with the lower one according to the distance comparison. This merging process is summarized in Algorithm 3.
| Algorithm 3. Merging of stem clusters | |||
| Input: points clusters C Output: stems list Cs | |||
| Initialize an empty list of Cs | |||
| for every cluster ci ∈ C do | |||
| for every stem csj ∈ Cs do | |||
| find the cluster ck ∈ csj which is nearest to ci calculate the direction vectors of ck and ci | |||
| solve parameters of linear models in Equation (9) using two direction vectors | |||
| growing of the seed point according to Equation (10) until it meets the higher cluster | |||
| if distance (ck, ci) < dstem then | |||
| add ci to csj; break; | |||
| end if | |||
| end for | |||
| if ci is not added to any csj ∈ Cs then | |||
| create a new stem and add it to Cs | |||
| end if | |||
| end for | |||
4. Experiments and Results
Four parameters were defined for both plots. Two intervals in centimeter units were set as [1,4] and [9,17] corresponding to two scales in classification. Nc, a parameter used in clustering, was set as 50, which means only a cluster’s bigger than 50 will be considered as a stem cluster. Nc = 50 was determined based on tests in the plots and density of the raw points. The last parameter dstem depends on the minimum distance between neighboring stems and was set to 8 cm in two plots. Additionally, fallen bamboos on the ground can also be detected in two plots. Thus, any merged stem with its height, i.e., maximum height minus minimum height in the group, less than 30 cm will be excluded.
During the experiment, the number of points decreased during different phases. Table 3 lists the total number of points after different phases. As the table shows, the downward trend of points in two plots is similar. In both plots, nearly 75% of original points were removed as no-stem points after two-scale classification. The number of stem points after stem merging account for less than 10% of the original points cloud.

Table 3.
Points counts after different phases.
| Original | First Scale Classified | Second Scale Classified | Clustering | Merging | |
|---|---|---|---|---|---|
| Plot A | 3,384,528 | 1,095,781 | 551,077 | 340,133 | 329,417 |
| Plot B | 3,050,403 | 995,032 | 494,154 | 283,083 | 280,335 |
All the algorithms in the experiment were implemented in C++. The experiment runs on a computer with 4-GB RAM and an Intel Core i7-2600 CPU at 3.4 GHZ. In Plot A, it takes about 5.8 min to classify points in the first scale and another 4.9 min to finish the second scale classification. Similarly, it takes approximately 8.7 min to complete the two-scale classification phases in Plot B. The time used in clustering and merging phases in Plot A is about 7.6 s and 3.8 s, respectively. In addition, in Plot B, it takes about 5.3 s and 3.2 s to finish the last two steps. It follows that most of the computing time is spent on feature calculation. However, the optimal radius search for each point at the same scale is parallelizable and hence the algorithms can be implemented using parallelization framework to reduce the computation time.
To assess the accuracy, the completeness is defined as follow:
True stem (T) indicates the number of correctly detected stems. Reference stem (R) is the number of stems manually counted in the original data (in Section 2). The results overlapping in the second column of Figure 4 made the validation process easier. There are two types of error. Type I error relates to omission and is the number of stems that are not recognized. Type II error, or commission, means stems are falsely merged. For example, two neighboring stems were recognized as one or a stem contains some clusters from others. Table 4 lists the accuracy assessments for both plots. Among 157 detected targets, 11 of them belong to Type II error. Among 11 falsely detected stems, six stems contained some clusters from others, four consisted of two stems, and one contained three neighboring stems. Finally, the completeness is 88%.
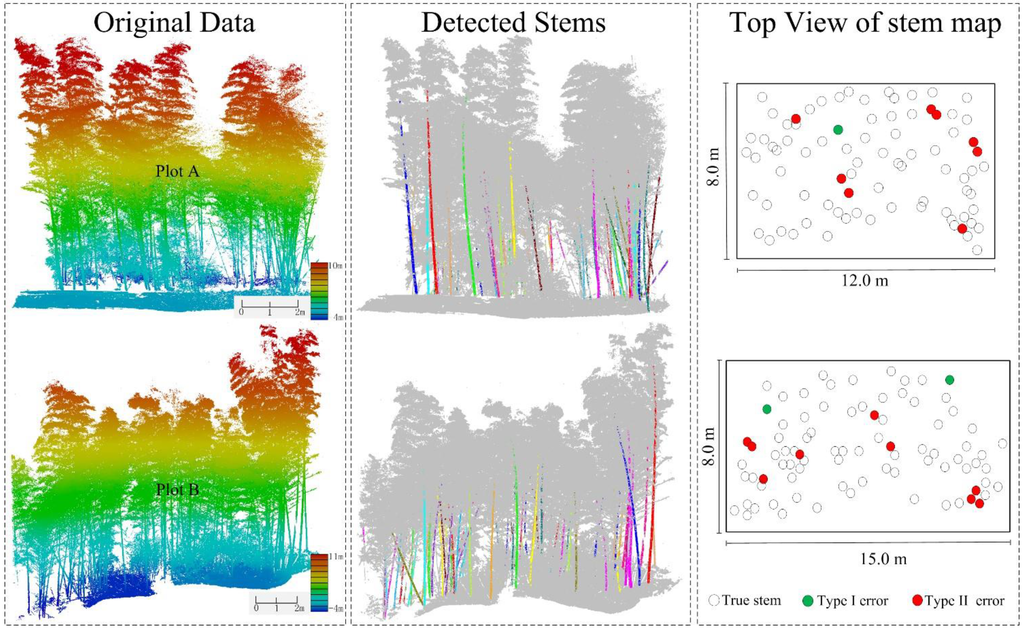
Figure 4.
Original point clouds, detected stems and top view of stem detection results.

Table 4.
Results and assessments of stem detection.
| Reference Bamboos | Detected Culms | Type I Error | Type II Error | True Culms | Completeness | |
|---|---|---|---|---|---|---|
| A | 82 | 78 | 1 | 5 | 73 | 89% |
| B | 84 | 79 | 2 | 6 | 73 | 86.9% |
| Total | 166 | 157 | 3 | 11 | 146 | 88.0% |
Figure 4 shows the original point clouds and stem detection results in both plots. Images in the first row and second row of Figure 4 are very similar in size. Colors of detected stems are selected randomly to distinguish different ones and the original data (in grey) are overlain by detected results. The column of Figure 4 shows the detected stems and errors in the x–y plane in both plots. According to Figure 4, it is evident that most of the stems are well detected.
5. Discussion
5.1. Stem Points Identification and Type I Error
In this paper, the stem point clouds are first recognized using two scale features. Unlike previous scale-based classification methods, the number of points that are involved in feature calculation decreases with scales. Only a subset of original point clouds will be reserved for the next scale classification (Section 3.1.2). Benefits of this method are clear: (i) Points from branches will be excluded after the first scale classification, and will improve the robustness of feature classification at the second scale. (ii) The density of non-stem points drops quickly which increases the difference between stem and no-stem points. (iii) The two-scale classification algorithm can reduce data volume as well as improve the computation efficiency. Figure 5 presents an example of the two-scale classification. A bamboo with DBH about 8 cm was selected manually from original data. At the first scale, most of the points of stem and ground are labeled as “planar”. Branches connected with stems are classified as “linear” and were deleted after the first scale analysis. Significantly, the “linear” points on the ground in Figure 5 are from fallen bamboos.
In theory, the two-scale stem classification can be applied to stems with varies diameters. As it seems that two-scale properties have little relationship to stem diameters, i.e., stem points can usually be labeled as “planar” at certain scale and “linear” at a larger one. However, stems with very small diameter (e.g., 2 cm in this study) will show little “planar” distribution due to lack of enough points at small scale. Furthermore, for stems with large diameters (e.g., bigger than 20 cm), the radius-based point feature calculation and optimal radius search will take massive computation if the second interval ([r3, r4]) becomes much bigger. In fact, if stem diameters are much bigger, the stem density in forests as well as the shadowing effect may reduce. Therefore, classical cylinder fitting methods [8,13,15,16] may be feasible and fast for stem detection in these circumstances.
Besides the point number reduction in the scale calculation, an automatic radius selection method is used to specify the optimal radius for each point at each scale. This entropy function-based method has been tested on various data sets with different stem densities and performed well. Details of this method can be found in many studies (e.g., [26,28,29]).
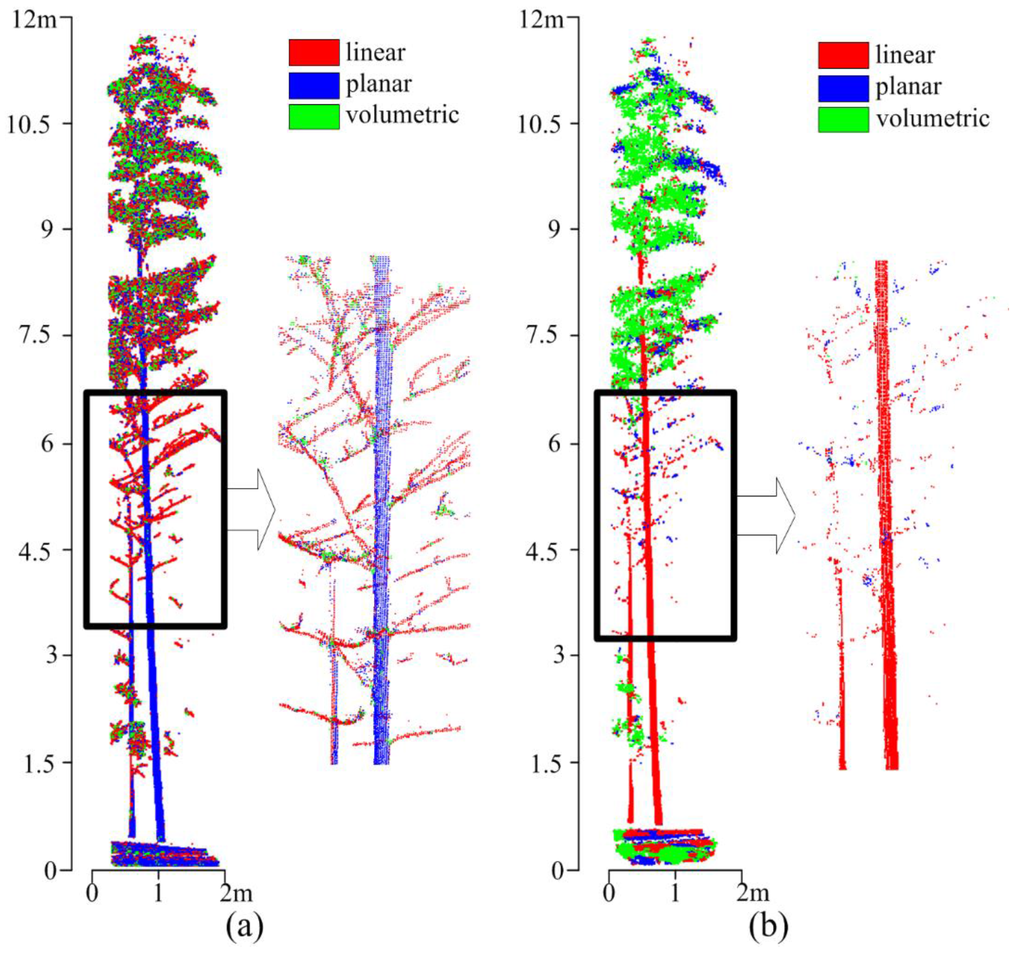
Figure 5.
An example of two-scale classification: (a) classification results at the first scale; and (b) classification results at the second scale.
Type I error is the number of stems that can be found in original data, but totally missed in the stem detection results. It happens during the two-scale classification and clustering. This is mainly caused by two reasons. First, the missed bamboos are all found near the back of plots where the shadowing effect caused by foreground objects (e.g., stem, branch and dense foliage) is most prominent, and therefore stem points from these bamboos are tend to be separated into small pieces. Second, the point density decreases with the distance from the scanner. So point numbers in clusters from rear stems are usually smaller than those from front stems. Consequently, small pieces of stems may be identified as non-stem classes and removed at the classification or clustering phases. However, only three bamboos are totally missed in the tests (Figure 4). This indicates that the proposed stem identification method is feasible and effective.
5.2. Clusters Merging and Type II Error
In the final phase, we proposed a clusters merging algorithm based on the geometric properties of stem.
Compared to other curve or cylinder fitting methods which handle point clouds, such as RANSAC, this direction-growing method saves computation time because its processing unit is cluster rather than single point. Moreover, in those point-based methods, if two clusters belong to the same stem but differ greatly in size, an un-weighted fitting method may overlook the smaller cluster and cause errors. In addition, curve or cylinder fitting methods should take the stem diameter variation into account, which could increase the computation complexity. Finally, our merging method needs only one threshold that is intuitively clear.
Using this direction-growing algorithm, stem clusters from the same bamboo are merged. Although many bamboos in the test plots grew aslant and large gaps existed between clusters, the proposed method could still merge the clusters correctly. Figure 6 shows details of merged stems in both plots. Colors of stems were randomly selected to distinguish each other.
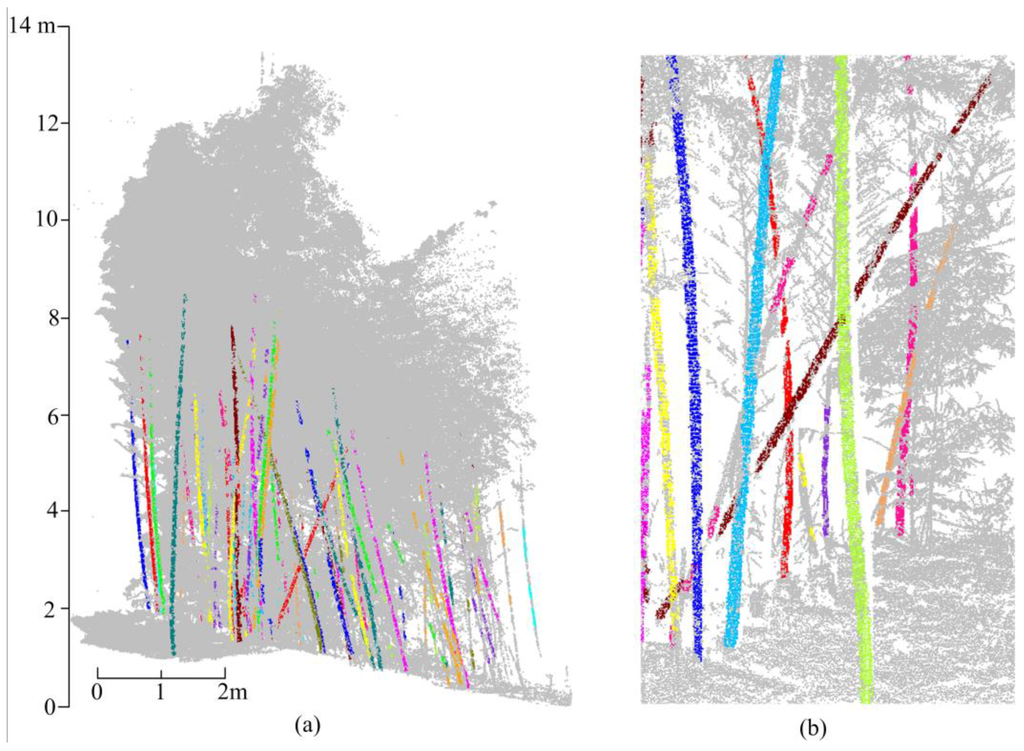
Figure 6.
(a) Side view of Plot A: Bamboo on the hillside is inclined and stem clusters are fragmentized. (b) Details of Plot B: Stems are clumped and some are seriously inclined.
However, there are still 11 falsely connected stems that belong to Type II error. Figure 4 shows that the main cause of Type II error is related to the spatial distribution between neighboring stems, not the distance to the scanner. Possible errors are illustrated in Figure 7. Figure 7a shows neighboring bamboos that are very close to each other or even cling together. If the distance between bamboos is shorter than the threshold dstem in the direction–growing process, they will be merged as one stem and thus cause errors in counting. In addition, if parts of stems cling together, the points from different stems will be grouped together in the clustering and lead to Type II errors directly. However, this kind of situation rarely happens.
Most of errors happen in the situations as shown in Figure 7b–e. If stems are close to each other and their curves are approximately in the same plane, different clusters may be connected incorrectly after the seed growing. Some false stems may contain parts of others (Figure 7c,d). Although these cases will make no difference in number counting, but in the validation process, they will be labeled as wrong stems. Some detected stem may consist of neighboring stems (Figure 7e) and thus reduce the number of mapped stems. In this study, 10 out of 11 stems of Type II error belong to these situations as shown in Figure 7b–e.
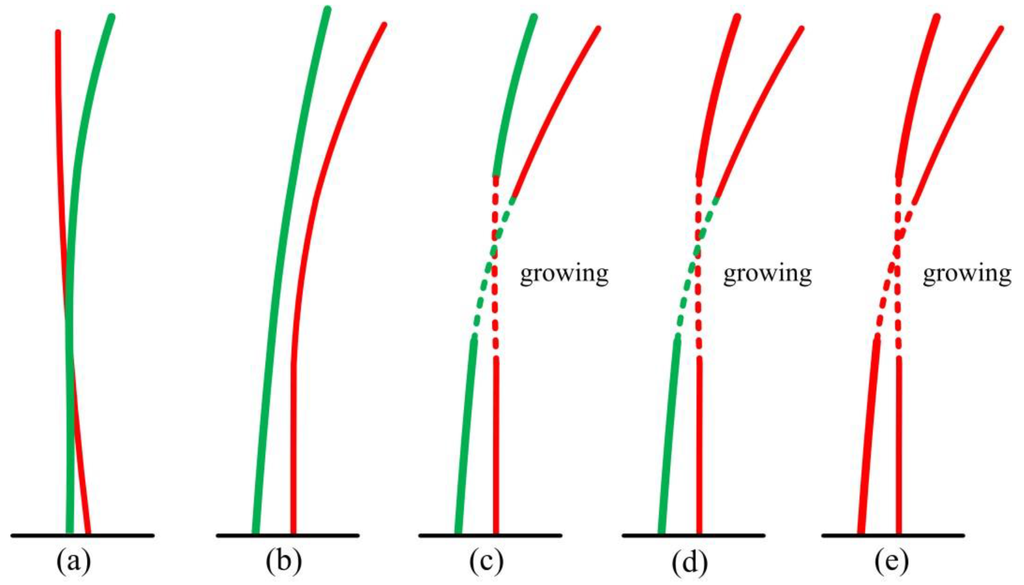
Figure 7.
Error types: (a) Bamboos are too close to each other; (b) two independent stems; (c) mutual containment of two stems after growing; (d) one stem (in red) contains part from the other one; and (e) two stems are totally merged as one.
Although errors that occur during the direction-growing process seem unavoidable, there are still two possible ways to reduce errors during the clusters merging. Firstly, a smaller threshold dstem is helpful in reducing the Type II error. For instance, three neighboring stems were recognized as one (magenta) in Figure 8a. In Figure 8b, by setting dstem = 5cm, one (red) of the three stems can be separated. The second method is to adopt a bigger Nc to delete small stem clusters, because the directions of small clusters are often incorrect and affect the results. In Figure 8c, by setting Nc = 80, three stems are separated correctly. However, changing parameters for eliminating some errors may affect the results of other stems. It is better to extract false stems first and then set specific parameters to achieve better results.
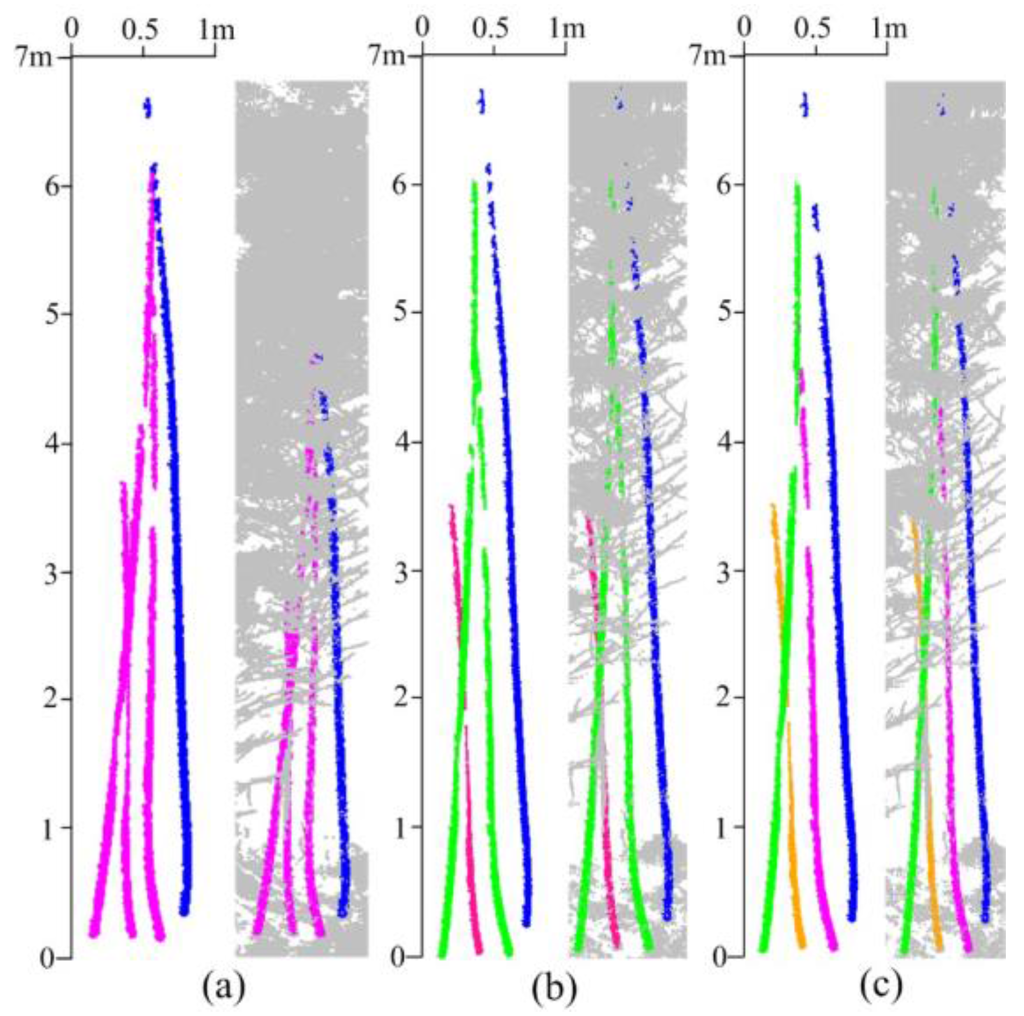
Figure 8.
Error correction: (a) Error connected results; (b) results by setting dstem = 5cm; and (c) merged results by setting Nc = 80.
5.3. Measuring Range and Quality Assessment
Since the high density of the plants has a strong influence on data collections, areas of both plots are smaller compared with previous studies in sparse forest. To reduce the shadowing effect, the scanner was put adjacent to plots instead of inside of the plot during the field experiments. However, the canopy density and the distance to the scanner still have a strong influence on integrity of stem points. In brief, the visibility is limited and few laser returns can be recorded at a slightly long distance, for example, 8 m in tested plots. Therefore, a suitable measuring range in very dense forest is worth discussing.
To give a general idea of original points cloud in dense forest, a slice with distance ranges from 0 to 16 m was extracted and presented in Figure 9. It shows that the point density dropped significantly as the distance increases. In fact, when the distance is further than a certain value (e.g., 8 m) in this slice, the appearance of bamboo could hardly be recognized in points cloud. These sparse points are less valuable in forest investigation and hence the measuring range should be smaller than a threshold. However, it is difficult to give an exactly measuring range threshold in dense forest, because various factors contribute to the threshold determination. First, stem density and distribution in different forests are quite different, for example, trees in man-planted forest are usually spaced at regular intervals while the same species in natural environment may be clumped, and this will pose different influences on the shadowing effect. Second, the measuring range threshold should also take the original point density and the quality of data, e.g., noise level as well as accuracy into account. This can be done through browsing the original data directly and then selecting a suitable range according to the experimental objective and experience. Last, as for the stem mapping method in this paper, although we chose 8 m as the measuring range threshold, further discussion about the stem detection quality along with its relationship with the shadowing effect is needed.

Figure 9.
A slice of original point clouds. Left side is near to the scanner.
To make quantitative analysis about detected results, we proposed an indicator named effective height (He). The indictor is defined in Equation (12) where n is the number of contained clusters in each stem. Di(Pi,h, Pi,1) is the distance between Pi,h and Pi,1 corresponding to the highest and lowest points of each cluster, respectively.
Effective height is, essentially, the total length of a detected stem. A large He indicates a good stem quality. Table 5 summarizes the statistical results of He in both plots. Only the correctly detected stems are analyzed. There are about 52% of all the stems with their heights higher than 4.0 m and 17 detected stems are more than 6.0 m high. However, 17.1% of detected stems are lower than 2.0 m, which indicates that only a small fraction (less than 20%) of a whole stem is detected. In general, the mean effective height is about 4.0 m.

Table 5.
Statistics on effective height (He) of detected stems.
| He (m) | <2.0 | 2.0–3.0 | 3.0–4.0 | 4.0–5.0 | 5.0–6.0 | 6.0–7.0 | >7.0 | Sum |
|---|---|---|---|---|---|---|---|---|
| Plot A | 15 | 13 | 7 | 19 | 12 | 3 | 4 | 73 |
| Plot B | 10 | 14 | 11 | 18 | 10 | 6 | 4 | 73 |
| Total | 25 | 27 | 18 | 37 | 22 | 9 | 8 | 146 |
| Percentage | 17.1% | 18.5% | 12.3% | 25.3% | 15.1% | 6.2% | 5.5% |
Several factors affect the total length of detected stems. As discussed in Section 5.1, clusters in small size may be ignored during classification and clustering processes. However, these clusters are small in height (e.g., less than 0.1 m) and have little influence on the final results. Furthermore, the defect in identifying the upper parts of stems may lead an under-estimation of stem length. As the diameter of stems decreases with height, if a stem’s diameter is small enough (e.g., 2 cm in this study), its two-scale properties will be similar to the branch, thus upper parts can be easily missed after classification. However, this error is not just caused by classification method, in fact, upper parts of stems are usually surrounded by dense foliage, which makes their visibility quite low, and few points from upper stems can be recorded. This will increase the ambiguity in eigenvalue-based geometric calculation and make points more likely to be classified as “volumetric” which will been discarded soon afterwards.
The shadowing effect and distance to scanner are strongly coupled. For clarity, effective height (He), the grid density (i.e., number of points in every 0.5 m along the distance) and the measuring range of Plot A are plotted in Figure 10. It can be found that the grid density dropped rapidly after the first row of bamboo stands. However, if there are no objects (e.g., foliage) shading the lasers, the point spacing within a small measuring range (e.g., 8 m in this paper) will change little, so the reason for a sharp decline in point number is shadowing. The bamboo in the front blocks much of the emitted lasers. In addition, the effective height (He) tends to decrease as the measuring range increases in Figure 10. According to the trend line in Figure 10, when the distance is greater than 5.5 m, He is more likely to be less than 3.0 m. However, if only the stems within 3.5 m along measuring range are evaluated, the mean effective height is 5.1 m (27 detected stems in total).
In summary, the fragmentary clusters, the missing upper stems and the drastic reduction in returns are all directly related to the shadowing effect, which is the primary cause of stem height underestimation. Therefore, the effective measuring range is largely decided by the shadowing effect, which varies in species, stem density and the spatial distribution of the plant distribution.
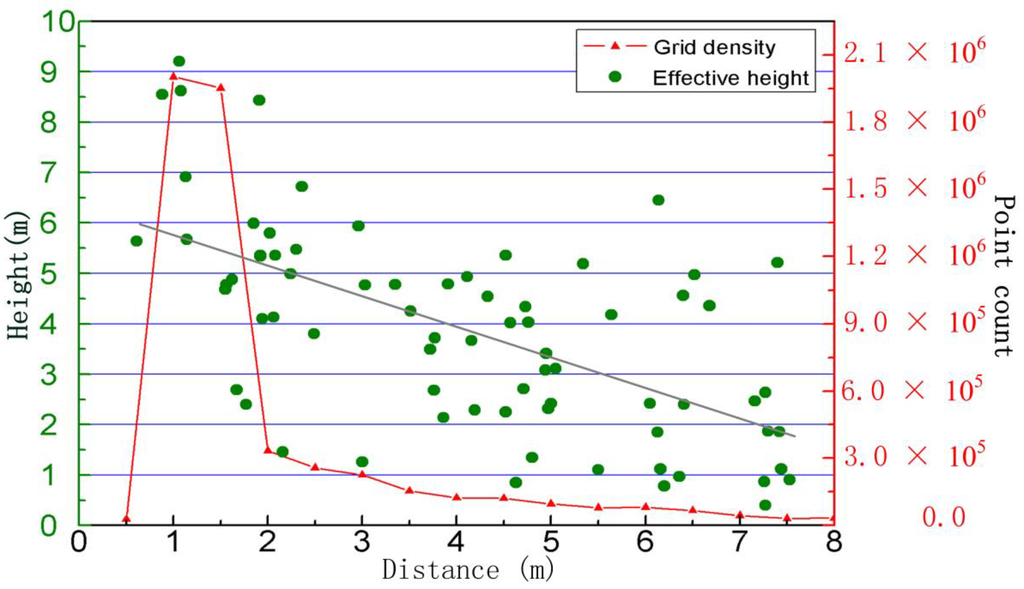
Figure 10.
Point counts and He change with distance in Plot A. The correlation coefficient between trend line and height data is 0.37.
There are two ways for selecting a suitable measuring range. First, stem points are assumed to be classified as “planar” at first scale in classification. Significantly, the upper bound (r2) of the first interval is usually smaller than the stem radius (e.g., 4 cm in this paper), and thus to keep the geometry significance, sufficient points within the upper bound of a point are needed. In addition, a large point spacing of stem points will lead the stem cluster to be fragmentary and ignored during clustering process. Thus, the minimum point spacing of stem points is recommended to be a fifth of the stem radius empirically. The measuring range can be determined according to this criterion. Besides, a direct way is to run the detection algorithm on original point clouds first and we can get a relationship between distance and effective height, e.g., the trend line in Figure 10. Then the effective measuring range can be determined according to requirements, for example, if the detected stem height is expected to be no less than 3.0 m, the measuring range in Figure 10 should be less than 5.5 m.
Besides selecting a suitable effective measuring range, there are still several ways to get better results. For example, to improve the detected length of stems, it is possible to model the stem curve using the detected sections first, and then search candidate stem points along the stem curve in the original point clouds. However, the stem diameters vary at different height while the DBH and tree height are usually required to model precise stem curve. Liang et al. [5] modeled the stem curve automatically from point clouds, but their study was done in a sparse forest (600 stems/ha) using multi-scan point clouds and validated with many field measurements. Therefore, the potential improvement of mapping stem length remained unclear at this stage and further research is needed.
Selecting the scanner position carefully to reduce blocking or combining points from multi-scans may also improve the detection accuracy. However, the shadowing effect is inevitable and unpredictable in different scenes, and increasing the point density may offer little help to reduce the occlusion [5,30], especially to the upper parts of stem. However, maybe we can map stems using single-scan data and then combine detection results from multi-scans to improve the integrity of stem structure as well as the detection rate. To be more exact, stem points in each scan are detected and connected independently, and then results from all the scans are registered according to their coordinates.
This combination method will be useful in large areas. Generally, it always needs many scans to cover a large forest area, for example, Seidel et al. [31] applied the single-scan TLS to an oak forest and they took 15 scans to cover the plot (290 m2). In this paper, if we use 5.5 m as an effective measuring range in each scan, it would probably need 105 scans to cover a whole hectare, while the distance between adjacent scanners may be approximate to twice the effective measuring range, e.g., 11 m. However, if a longer measuring range in each scan is set, e.g., 8 m, and the spacing between adjacent scanners is longer than 11 m but smaller than 16 m, e.g., 14 m, we may get better stem detection results with less scans (approximately 65) in one hectare by combining multi-scan detection results. However, further experiments are needed to explore the feasibility and potential problems in practice.
Although combining multi-scan results is a potential way to reduce the number of scans, field experiments are still lab intensive and time consuming in large areas. A smaller Laser scanner or a moveable Laser scan system [32] can be applied to collect multi-scan data in forests efficiently and also the occlusion can be reduce to some extent.
6. Conclusions
Stem detection or mapping is usually studied in low-density forests (e.g., less than 1500 stem/ha) and stems with big DBH (e.g., larger than 10 cm). However, the shadowing effect is more significant in dense forests and causes new problems. For example, close-spaced plants, thin and bended stems bring new difficulty in distinguishing the neighboring stems and merging the disconnected sections. This paper presented a new method for detecting stems from the single-scan point clouds in dense and homogeneous forests. The method needs neither circle or cylinder fitting nor terrain information to determine the stem locations. A two-scale classification algorithm is designed to find candidate stem points, and then group the stem points using the Euclidean clustering. Finally, a simple stem curve model is introduced to resolve the merging problem.
The proposed method is tested in a typical bamboo forest (plant density is about 7500 stem/ha) and 144 of 166 reference stems are detected correctly. The completeness of the stem detection is 88%, which is close to that of the state-of-the-art methods. The measuring range of this method is largely decided by the shadowing effect and limited within 8 m in the experimental plots. According to the results and quality analyses, it is feasible to apply the single-scan TLS in dense forest investigation, especially for stem mapping. We also believe that vegetation point clouds classification may benefit from multi-scale features and the proposed stem-merging algorithm can be applied to other species of single-stem plants with high stem densities. Further studies on the parallel multi-scale feature computation, combination of several single-scan detection results and mapping stems in large areas are needed.
Acknowledgments
This work was supported by the Bureau of International Cooperation, Chinese Academy of Sciences (241311KYSB20130001); the International Science & Technology Cooperation Program of China (2013DFG21640); and the National Natural Science Foundation of China (91152003).
Author Contributions
Shaobo Xia was the lead author of the article and performed the experiments with Cheng Wang and Feifei Pan. Xiaohuan Xi and Hongcheng Zeng contributed expertise in data collection and pre-process. He Liu provided expertise in bamboo forest structure and management. The article was improved by the contributions of all of the co-authors at various stages of the analysis and writing process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, X.; Zhang, X.; Zhang, Y.; Booth, T.; He, X. Changes of carbon stocks in bamboo stands in china during 100 years. For. Ecol. Manag. 2009, 258, 1489–1496. [Google Scholar] [CrossRef]
- Yen, T.-M.; Ji, Y.-J.; Lee, J.-S. Estimating biomass production and carbon storage for a fast-growing makino bamboo (Phyllostachys makinoi) plant based on the diameter distribution model. For. Ecol. Manag. 2010, 260, 339–344. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Gao, S.; Huang, N.; Chen, H. Correlating the horizontal and vertical distribution of lidar point clouds with components of biomass in a picea crassifolia forest. Forests 2014, 5, 1910–1930. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Yu, X.; Hyyppa, J.; Holopainen, M. Automated stem curve measurement using terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1739–1748. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Li, G.; Xi, X. Retrieving leaf area index using ICESat/GLAS full-waveform data. Remote Sens. Lett. 2013, 4, 745–753. [Google Scholar] [CrossRef]
- Wang, C.; Glenn, N.F. A linear regression method for tree canopy height estimation using airborne lidar data. Can. J. Remote Sens. 2008, 34 (sup2), S217–S227. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Yang, X.; Strahler, A.H.; Schaaf, C.B.; Jupp, D.L.; Yao, T.; Zhao, F.; Wang, Z.; Culvenor, D.S.; Newnham, G.J.; Lovell, J.L. Three-dimensional forest reconstruction and structural parameter retrievals using a terrestrial full-waveform lidar instrument (echidna®). Remote Sens. Environ. 2013, 135, 36–51. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M.; Kim, S.-H. Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 777–786. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The use of a mobile laser scanning system for mapping large forest plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- Astrup, R.; Ducey, M.J.; Granhus, A.; Ritter, T.; von Lüpke, N. Approaches for estimating stand-level volume using terrestrial laser scanning in a single-scan mode. Can. J. For. Res. 2014, 44, 666–676. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the ransac algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- McDaniel, M.W.; Nishihata, T.; Brooks, C.A.; Salesses, P.; Iagnemma, K. Terrain classification and identification of tree stems using ground-based lidar. J. Field Robot. 2012, 29, 891–910. [Google Scholar] [CrossRef]
- Pfeifer, N.; Gorte, B.; Winterhalder, D. Automatic reconstruction of single trees from terrestrial laser scanner data. In Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, 12 July, 2004; pp. 114–119.
- Bienert, A.; Schneider, D. Range image segmentation for tree detection in forest scans. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Antalya, Turkey, 2013; Volume 5, pp. 49–54. [Google Scholar]
- Hetti Arachchige, N. Automatic tree stem detection—A geometric feature based approach for mls point clouds. In ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Antalya, Turkey, 2013; Volume 1, pp. 109–114. [Google Scholar]
- Lehtomäki, M.; Jaakkola, A.; Hyyppä, J.; Kukko, A.; Kaartinen, H. Detection of vertical pole-like objects in a road environment using vehicle-based laser scanning data. Remote Sens. 2010, 2, 641–664. [Google Scholar] [CrossRef]
- D’Oliveira, M.V.; Guarino, E.D.S.; Oliveira, L.C.; Ribas, L.A.; Acuña, M.H. Can forest management be sustainable in a bamboo dominated forest? A 12-year study of forest dynamics in western amazon. For. Ecol. Manag. 2013, 310, 672–679. [Google Scholar] [CrossRef]
- Scurlock, J.; Dayton, D.; Hames, B. Bamboo: An overlooked biomass resource? Biomass Bioenergy 2000, 19, 229–244. [Google Scholar] [CrossRef]
- Song, J.; Wang, X.; Liao, Y.; Zhen, J.; Ishwaran, N.; Guo, H.; Yang, R.; Liu, C.; Chang, C.; Zong, X. An improved neural network for regional giant panda habitat suitability mapping: A case study in Ya’An prefecture. Sustainability 2014, 6, 4059–4076. [Google Scholar] [CrossRef]
- Lalonde, J.F.; Vandapel, N.; Huber, D.F.; Hebert, M. Natural terrain classification using three-dimensional ladar data for ground robot mobility. J. Field Robot. 2006, 23, 839–861. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Bremer, M.; Wichmann, V.; Rutzinger, M. Eigenvalue and graph-based object extraction from mobile laser scanning point clouds. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbHPublisher: AntalyaCity, Turkey, 2013; Volume 5, pp. 55–60. [Google Scholar]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3D lidar point clouds. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbHPublisher: Calgary, Canada, 2011; pp. 97–102. [Google Scholar]
- Van Leeuwen, M.; Coops, N.C.; Hilker, T.; Wulder, M.A.; Newnham, G.J.; Culvenor, D.S. Automated reconstruction of tree and canopy structure for modeling the internal canopy radiation regime. Remote Sens. Environ. 2013, 136, 286–300. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z. A shape-based segmentation method for mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 81, 19–30. [Google Scholar] [CrossRef]
- Gressin, A.; Mallet, C.; Demantké, J.; David, N. Towards 3D lidar point cloud registration improvement using optimal neighborhood knowledge. ISPRS J. Photogramm. Remote Sens. 2013, 79, 240–251. [Google Scholar] [CrossRef]
- Seidel, D.; Ammer, C. Efficient measurements of basal area in short rotation forests based on terrestrial laser scanning under special consideration of shadowing. iForest Biogeosci. For. 2014, 7, 227–232. [Google Scholar] [CrossRef]
- Seidel, D.; Albert, K.; Ammer, C.; Fehrmann, L.; Kleinn, C. Using terrestrial laser scanning to support biomass estimation in densely stocked young tree plantations. Int. J. Remote Sens. 2013, 34, 8699–8709. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppa, J.; Honkavaara, E.; Jingbin, L. Forest Data Collection Using Terrestrial Image-Based Point Clouds From a Handheld Camera Compared to Terrestrial and Personal Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5132–5117. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).