Next Article in Journal
Properties of Oak Veneer Dyed with Supercritical CO2 and Vacuum-Pressurized Assisted Natural Dyes
Previous Article in Journal
Optimizing Season-Specific MET for Thermal Comfort Under Open and Closed Urban Forest Canopies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 9
10.3390/f16091427
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Forest Carbon Storage and Economic Valuation in Qilian Mountain National Park: Integrating Multi-Source Data and GARCH-M(1,1)-Driven Dynamic Carbon Pricing

by
Weibao Sun
1,
Yafang Gao
1,2,3,*,
Xuemei Yang
2,3,4 and
Yalong Zhang
5
1
College of Tourism, Northwest Normal University, Lanzhou 730070, China
2
College of Tourism, Lanzhou University of Arts and Science, Lanzhou 730030, China
3
Gansu Cultural and Tourism Industry Research Institute, Lanzhou 730030, China
4
Observation Station of Subalpine Ecology Systems in the Middle Qilian Mountains, Xining 810000, China
5
College of Geographic Sciences, Qinghai Normal University, Xining 810000, China
*
Author to whom correspondence should be addressed.
Forests 2025, 16(9), 1427; https://doi.org/10.3390/f16091427
Submission received: 28 July 2025 / Revised: 22 August 2025 / Accepted: 4 September 2025 / Published: 6 September 2025
(This article belongs to the Section Forest Ecology and Management)
Browse Figures
Versions Notes

Abstract

Qilian Mountain National Park, an important forest ecosystem in northwest China, plays a crucial role in achieving the national “dual carbon” goals and advancing sustainable forest management. This study focuses on the systematic assessment of forest carbon storage and its market economic value, employing multi-source data fusion and the GARCH-M(1,1) model to integrate forest carbon storage data from 2000 to 2020 with historical trading records from the EU and Chinese carbon markets (2017–2025). The study utilizes three dynamic carbon pricing scenarios—low, medium, and high—to assess the carbon storage capacity and economic value of the park’s forest ecosystems. Results show that forest carbon storage increased by approximately 4.0 × 107 tons, with an average annual growth rate of 0.27%. Under the high carbon pricing scenario in 2025, the forest carbon sink value in the EU market reaches CNY 518.2 billion, approximately 12.5 times that of the Chinese market, highlighting the differences in market maturity and volatility persistence. Through Monte Carlo simulations and dynamic pricing analysis, this research reveals the substantial market potential of Qilian Mountain’s forest carbon sinks, providing data-driven support for regional carbon trading optimization, ecological compensation mechanisms, and sustainable forest management, while contributing to the global carbon trading system and international cooperation in forest-based climate mitigation.

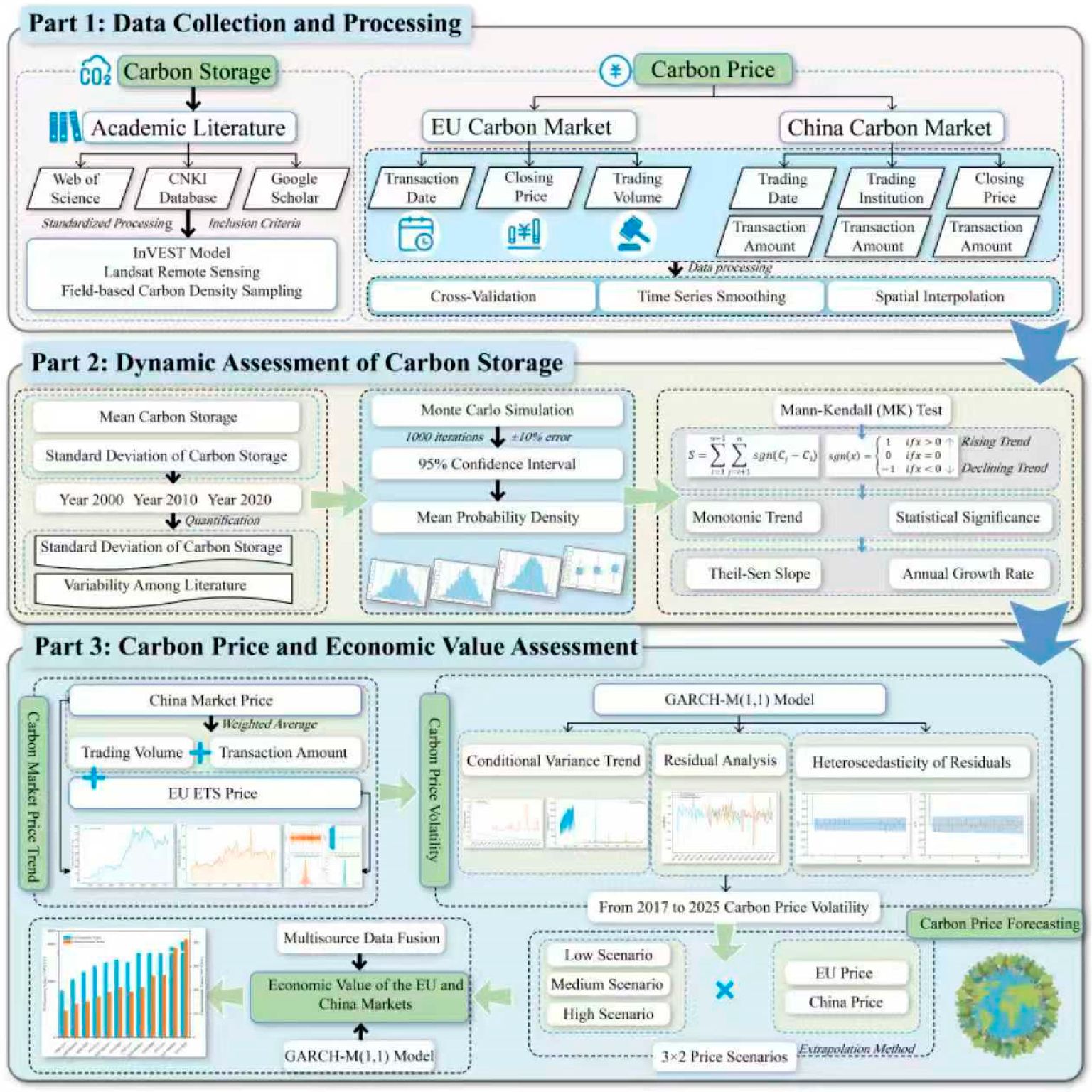
1. Introduction

Global climate change has become one of the most urgent environmental issues of the 21st century [1]. The excessive emission of greenhouse gases has led to global temperature rise, glacier retreat, and the frequent occurrence of extreme weather events, all of which pose severe threats to ecosystems, agricultural production, and human society [2]. According to the 2021 report of the Intergovernmental Panel on Climate Change (IPCC), the situation regarding global carbon reduction is becoming increasingly severe. The report states that greenhouse gases now contribute 98% to global warming. Without effective measures to significantly reduce carbon emissions, global temperatures may exceed the 1.5 °C or 2 °C rise limits, thus making it impossible to achieve the intended goals of curbing global warming [3]. To mitigate the potential negative impacts and risks of climate change, countries around the world have officially adopted, announced, or are considering net-zero targets corresponding to the Paris Agreement [4]. As the world’s largest emitter of carbon, China has pledged to peak carbon emissions by 2030 and achieve carbon neutrality by 2060. Ecological carbon sinks are one of the key pathways to achieving this goal [5]. National parks, as core protected areas of terrestrial ecosystems, play an important role in global carbon cycling and climate governance due to their high biodiversity and carbon storage potential [6]. Despite extensive research on the spatial and temporal characteristics of carbon sinks in national parks [7], scenario modeling [8], and carbon emission management [9], systematic studies on the carbon sink value of national parks and the trade and compensation for their ecological value are still insufficient. Therefore, scientifically assessing the carbon sink capacity and carbon sink value of national park ecosystems and exploring economic value trading and ecological compensation paths are of great significance for promoting the restoration of natural ecosystems, enhancing carbon sink capacity, and achieving the “carbon neutrality” goal [10].
International frameworks like the SDGs, UNFCCC, and IPCC advocate incorporating natural capital into financial systems to drive positive change [11]. Natural capital accounting monetizes processes like carbon capture and sequestration while costing emissions, enabling cross-regional resource valuation and improved management [12,13,14,15,16]. Carbon markets are essential for net-zero goals, allowing emission-exceeding entities to buy credits and under-quota ones to sell surpluses, with offsetting programs generating economic benefits and addressing biodiversity and climate crises [17,18,19].
Qilian Mountain National Park, a critical ecological barrier in northwest China and one of the first pilot national parks, holds significant carbon sink potential through its diverse ecosystems, including forests, grasslands, and wetlands. This potential supports the achievement of the “dual carbon” objectives and contributes to green development. However, challenges remain in accurately quantifying carbon sink volumes, analyzing market price volatility, and realizing the marketization of carbon sink value due to limitations in data accuracy and the underdeveloped state of trading mechanisms.
To address these challenges, this study introduces a methodological innovation by combining multi-source data fusion with the GARCH-M(1,1) model for dynamic pricing. Pioneering works such as Engle [20] (1982), which introduced the ARCH model to capture heteroscedasticity, and Bollerslev [21] (1986), who extended it to the GARCH model for modeling persistent volatility, provide the methodological foundation for this study. The study focuses on three key research questions: (1) How can the park’s carbon sink value be precisely quantified through dynamic assessment and multi-source data fusion? (2) How can price trends in the EU and China carbon markets be analyzed to support carbon sink valuation and compensation? (3) How can the incremental value of carbon sinks be measured and sustainable monetization achieved through a multi-scenario analysis?
By integrating remote sensing data (2000–2020) and carbon market trading records (2017–2025), this study quantifies carbon sink capacity and economic values under low, medium, and high pricing scenarios. A graphical summary of the analysis is presented in Figure 1. The findings propose strategies for the marketization and compensation of carbon sinks, enhancing the transparency and competitiveness of carbon credits. This research contributes to the advancement of ecological economics by optimizing park compensation mechanisms, promoting carbon sink marketization, and informing regional policies and international carbon trading cooperation.

2. Materials and Methods

2.1. Study Area Overview

Qilian Mountain National Park (94°49′18″–102°59′08″ E, 36°46′45″–39°47′05″ N) is located in the northwest of China, as shown in Figure 2. It lies at the junction of Gansu and Qinghai provinces, covering an area of approximately 5.02 × 104 km2 [22]. The park spans the Qilian Mountains and encompasses a variety of ecosystems, including coniferous forests, alpine meadows, grasslands, and glaciers. It features a typical plateau continental climate, with an average annual temperature of about 4 °C and annual precipitation of about 400 mm. This region fosters rich biodiversity and carbon storage potential. Located at the junction of the Qinghai–Tibet, Mongolian-Xinjiang, and Loess Plateaus [7], the park marks the boundary of the 200 mm annual precipitation line, the division between internal and external drainage areas, the transition from arid to semi-arid regions, and the demarcation of grassland and desert landscapes. It also represents the transitional zone between temperate continental, monsoon, and plateau climates. Qilian Mountain National Park serves as a vital ecological barrier and water conservation area in the northwest region, playing a key role in regulating the regional carbon cycle.

2.2. Data Sources

This study systematically integrates multi-source data to construct a dynamic assessment framework for ecological carbon sinks in Qilian Mountain National Park from 2000 to 2020, covering carbon storage and carbon prices. The carbon storage data were obtained by searching academic literature on carbon storage for Qilian Mountain National Park from 2000 to 2020 through Web of Science, Google Scholar, and CNKI. Carbon storage data for the years 2000, 2010, and 2020 were selected (unit: tons). The selection criteria included: (1) the study area covering the entire park or core area; (2) the use of the InVEST (3.14.2) model (Anaconda Inc.: Austin, TX, USA), Landsat remote sensing analysis, or field-based carbon density sampling methods. To ensure reliability, priority was given to literature based on the China Land Cover Dataset (CLCD) or field-verified data. Standardization was applied to eliminate systematic biases across different research methods, specifically by incorporating ±10% literature error perturbations via Monte Carlo simulation to generate confidence intervals, thereby adjusting and evaluating biases for robust estimation.
Carbon price data were sourced from daily trading records of the EU and China carbon markets from 2017 to 2025, obtained from the Greenhouse Gas Voluntary Emission Reduction Trading Platform (https://ets.sceex.com.cn/ accessed on 21 August 2025). The EU carbon market data include transaction dates, trading varieties, closing prices (EUR/ton, converted to CNY/ton based on the 27 June 2025 exchange rate of 1 EUR = 8.40 CNY), and transaction volumes (tons), reflecting the price trends of the EU Emission Trading System (EU ETS). The Chinese carbon market data cover eight major carbon trading markets and include transaction dates, trading institutions, trading varieties, closing prices (CNY/ton), transaction volumes (tons), and transaction amounts (CNY). The weighted average transaction price was used as the primary analytical indicator.
To ensure data consistency and analytical accuracy, all data were preprocessed and standardized in a Python 3.11 environment. Carbon storage and carbon price data were integrated using methods such as cross-validation, time series smoothing, and spatial interpolation to improve the reliability and comparability of the assessment results.

2.3. Research Methods

This study employs a comprehensive methodological framework to assess dynamic carbon storage and pricing. Detailed formulae for all calculations are provided in Appendix A.

2.3.1. Dynamic Carbon Storage Assessment

The average carbon storage value for year t is calculated using the mean to reflect the overall level from literature data, while the standard deviation quantifies data dispersion and consistency. A Monte Carlo simulation (1000 iterations) generates the 95% confidence interval for mean carbon storage values across the three years, incorporating literature errors (±10%) or standard deviation to evaluate the robustness and reliability of data integration.
The Mann–Kendall (MK) test was applied to detect monotonic trends and assess the statistical significance in the carbon storage time series for the years 2000, 2010, and 2020, thereby identifying long-term change patterns. To quantify the annual growth rate of carbon storage, the Theil-Sen slope estimator was employed, providing a robust estimate of the trend slope over the study period.

2.3.2. Dynamic Carbon Price Assessment

To evaluate the dynamic economic value of ecological carbon sinks in Qilian Mountain National Park, the GARCH-M(1,1) model was applied to analyze price volatility in the EU and China carbon markets. This captured heteroscedasticity and risk premiums, enabling stable price forecasts for scenario analysis. Building on GARCH-M-derived volatility for carbon prices from 2017 to 2025, three scenarios were constructed to represent lower, mean, and upper price bounds, reflecting potential market fluctuations in the EU and Chinese contexts. The 5th and 95th percentiles were selected to encompass a 90% confidence interval around the empirical price distribution, capturing tail risks and uncertainty in carbon pricing as standard in regulatory impact analyses (e.g., EPA’s Social Cost of Carbon framework, where the 95th percentile accounts for high-damage extremes), while the mean provided a central estimate for average.
  • Low scenario: Based on the 5th percentile of historical prices, reflecting undervaluation conditions.
  • Medium scenario: Based on the mean of historical prices, reflecting average market levels.
  • High scenario: Based on the 95th percentile of historical prices, reflecting high market conditions.
Annual economic values were then computed by multiplying mean carbon storage by scenario prices, generating six values per year (3 scenarios × 2 markets) for comparative analysis of differences and trends between the China and EU markets. This approach overcomes static pricing limitations through dynamic forecasting and scenario analysis, providing a robust basis for carbon sink marketization.
To assess the economic value of the ecological carbon sink in Qilian Mountain National Park between 2000 and 2020, this study gathered 8934 historical data points from eight major carbon trading markets in China. A weighted average of transaction volume and transaction amount was used to generate 1382 data points of a single carbon market price series for China. At the same time, 8453 historical data points were collected from the European Energy Exchange. The EU carbon market data prices were converted into RMB using the exchange rate of 1 EUR = 8.40 CNY as of 27 June 2025.

3. Results

3.1. Dynamic Carbon Storage Assessment of Qilian Mountain National Park from 2000 to 2020

To assess the dynamic trend of the ecological carbon sink in Qilian Mountain National Park from 2000 to 2020, this study used carbon storage data from three high-quality sources, as shown in Table 1. The literature selection focused on studies covering the entire Qilian Mountain National Park, using the InVEST model or remote sensing methods to ensure data reliability and consistency.
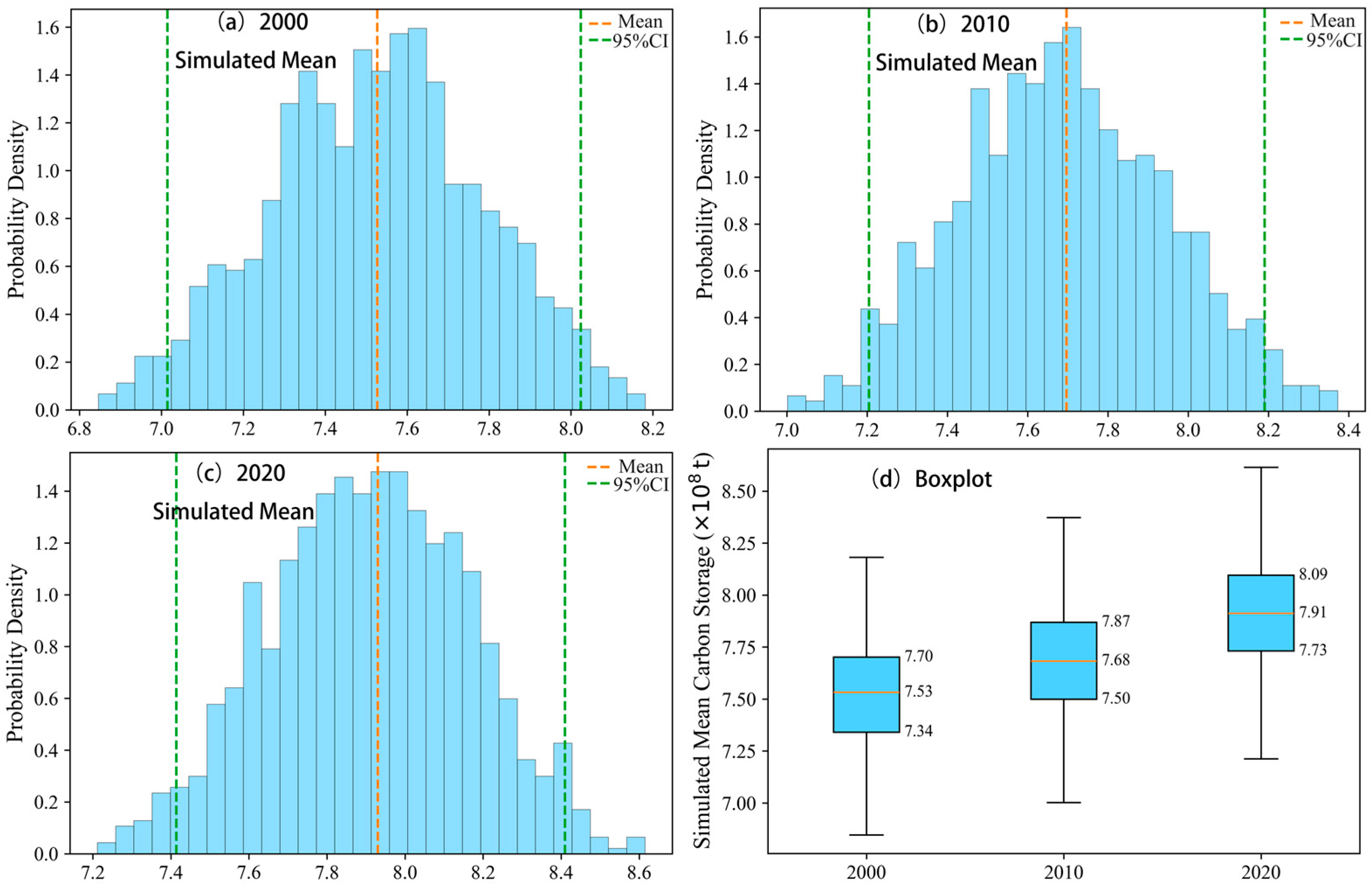
Using the data in Table 1, this study calculates the mean and standard deviation to quantify carbon storage levels for the years 2000, 2010, and 2020, as well as the variability across literature sources. A Monte Carlo simulation (1000 iterations, ±10% error) was conducted to generate a 95% confidence interval to assess the reliability of the mean estimates. The results are shown in Table 2.
The mean carbon storage in Qilian Mountain National Park increased from 7.53 × 108 tons in 2000 to 7.70 × 108 tons in 2010 and 7.93 × 108 tons in 2020, with a cumulative increase of 0.40 × 108 tons over the 20 years. The average annual increase is 0.020 × 108 tons, corresponding to an annual growth rate of 0.27%, calculated based on the mean values in Table 2. The standard deviation ranges from 1.59 to 1.68 × 108 tons, approximately 20% of the mean, reflecting the variability due to differences in the InVEST model parameters or remote sensing data across the literature. The Monte Carlo simulation, with 1000 iterations and ±10% error, generated a 95% confidence interval: for 2000, the range is 7.01 to 8.02 × 108 tons; for 2010, it is 7.20 to 8.19 × 108 tons; and for 2020, it is 7.41 to 8.41 × 108 tons, indicating the reliability of the mean estimates. Figure 3 shows the carbon storage distribution characteristics: Subplots a, b, and c represent the probability density of the mean values from the Monte Carlo simulation for 2000, 2010, and 2020, with the mean indicated by an orange dashed line and the 95% confidence interval indicated by a green dashed line; Subplot d is a boxplot from 2000 to 2020, showing the median, quartiles, and whiskers.
The Mann–Kendall trend test showed that the mean carbon storage in Qilian Mountain National Park from 2000 to 2020 exhibited a monotonic increasing trend, with a Kendall’s Tau value of 1.000. However, the p-value was 0.333 (p > 0.05), indicating that the trend is not statistically significant. The boxplot in Figure 3d further revealed that the median and interquartile range of carbon storage for 2000, 2010, and 2020 slightly increased over time, with variability remaining stable, and the standard deviation ranged from 1.59 to 1.68 × 108 tons. The 95% confidence interval (Table 2) was generated through the Monte Carlo simulation (1000 iterations, ±10% error), and the range is narrow (e.g., for 2000, it was 7.01–8.02 × 108 tons), indicating that the mean carbon storage estimate was highly reliable and provided a robust data foundation for the subsequent economic value assessment. The non-significant trend might have been due to the small number of data points (only three years) or differences in methods across the literature (such as InVEST models or remote sensing data), and further multi-year data collection was needed to verify the long-term dynamics.

3.2. Economic Value Assessment of Carbon Prices and Carbon Sinks in Qilian Mountain National Park from 2000 to 2020

3.2.1. Analysis of Price Trends in the EU and China Carbon Markets

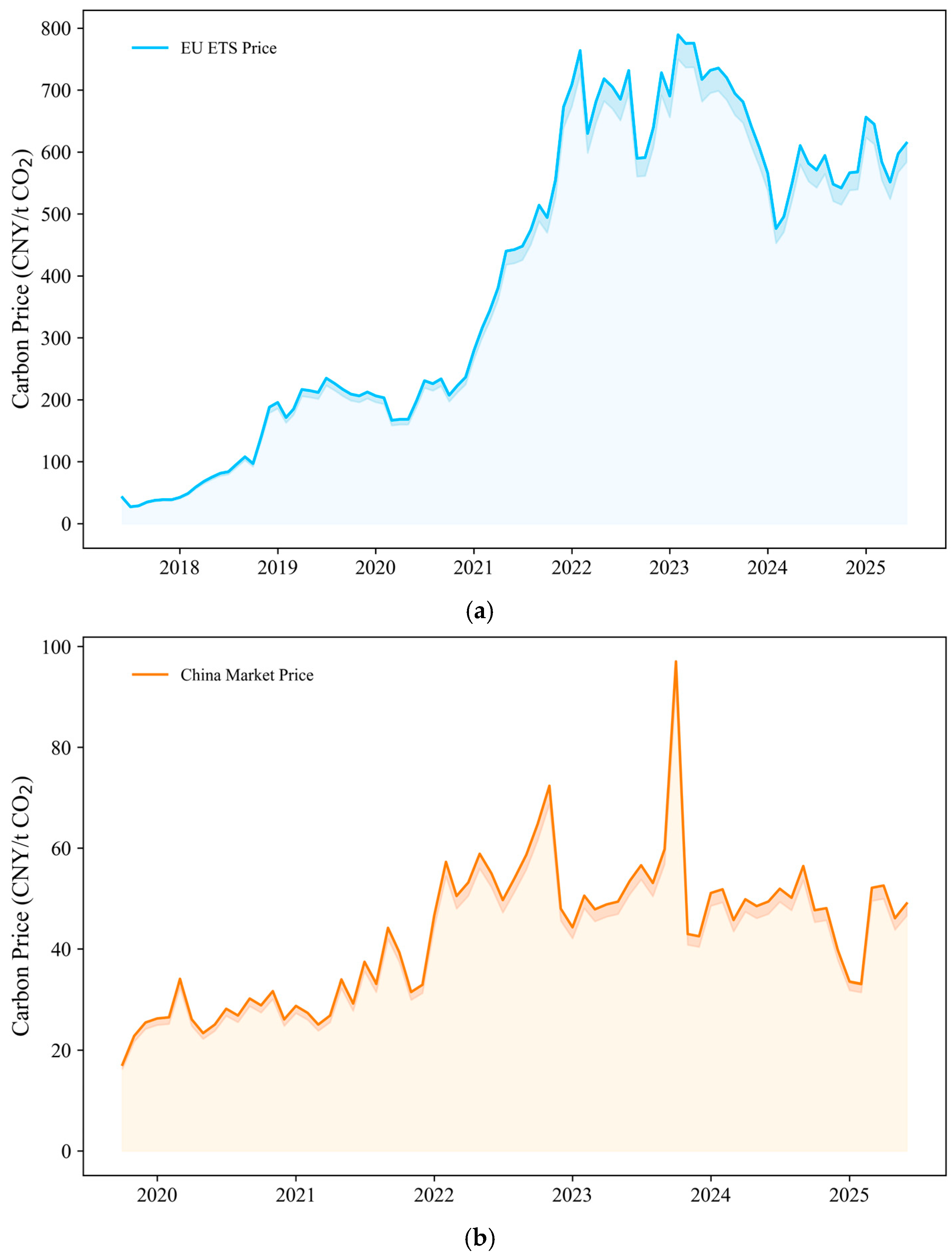
Figure 4a shows the price trend of the EU carbon market from 2017 to 2025; Figure 4b shows the price trend of the China carbon market from 2019 to 2025. The EU carbon price exhibits a significant upward trend, increasing from approximately 40 CNY/t CO2 in 2017 to about 600 CNY/t CO2 in 2025, with high volatility. This reflects the impact of policy adjustments in the EU Emission Trading System (EU ETS), industrial emission reduction targets, and energy structure transformation. During the early stages of the COVID-19 pandemic in 2020–2021, the price temporarily dropped due to reduced demand, but it gradually rebounded following economic recovery and the market stability reserve (MSR) mechanism. Since the launch of regional pilot carbon markets in 2013, China’s carbon price has steadily increased to approximately 60 CNY/t CO2 by 2025 after the national carbon emission trading market started on 16 July 2021. The volatility is relatively low, but due to the market’s immaturity, irregular trading mechanisms, and ample carbon quota supply, the price has remained at a low level for an extended period.
The price trends are based on data from 2017 to 2025. The volatility of the EU market was significantly affected by the energy crisis, leading to a phase of correction in 2023, while China’s prices have increased steadily but lacked significant breakthroughs, influenced by the transition from regional pilot markets to the national market. The analysis shows that the high volatility of the EU prices provides the dynamic feature foundation for the GARCH-M(1,1) model, while the relative stability and low-price characteristics of China’s prices offer a reference for long-term forecasting. Together, they provide data support for the subsequent price scenario analysis from 2000 to 2020 and the ecological carbon sink value assessment for Qilian Mountain National Park. The substantial valuation gap between EU and Chinese markets underscores the urgency for policy reforms in China to accelerate market maturation, potentially through international collaborations that transfer best practices for higher sink valuations.

3.2.2. Descriptive Statistics and Preliminary Tests

To ensure the data suitability for volatility modeling and to validate the appropriateness of the GARCH-M(1,1) model, this study first conducts descriptive statistics and preliminary tests on the logarithmic returns of carbon prices for the EU and China markets. Table 3 presents the descriptive statistical results of the returns.
Table 3 shows that the mean is close to zero, indicating no significant trend in the returns. The variance suggests greater volatility in the EU market. The skewness is close to zero, but the non-zero values indicate mild asymmetry. The kurtosis values exceed 3 (8.13 for China and 5.28 for the EU), indicating leptokurtic distributions. This suggests the presence of volatility clustering and heteroscedasticity in the data, which supports the application of volatility models such as GARCH.
The preliminary test results are shown in Table 4.
The ADF test results show that the original price series is stationary in China (p < 0.05) but non-stationary in the EU (p > 0.05). The return series for both markets are stationary (p = 0.0000), confirming the necessity of logarithmic differencing. The ARCH-LM test with p = 0.0000 indicates the presence of ARCH effects, supporting the use of a GARCH process. The White test reveals no significant heteroscedasticity in China (p = 0.2714), while heteroscedasticity is present in the EU (p = 0.0000), overall confirming the robustness of the data.
Figure 5 presents the time series and distribution of the returns. The time series exhibits clear volatility clustering (e.g., periods of high volatility are concentrated), supporting the use of ARCH/GARCH processes. The distribution histogram (with KDE) shows a deviation from normality (leptokurtic), further justifying the application of volatility models.

3.2.3. Construction and Parameter Estimation of the GARCH-M(1,1) Model

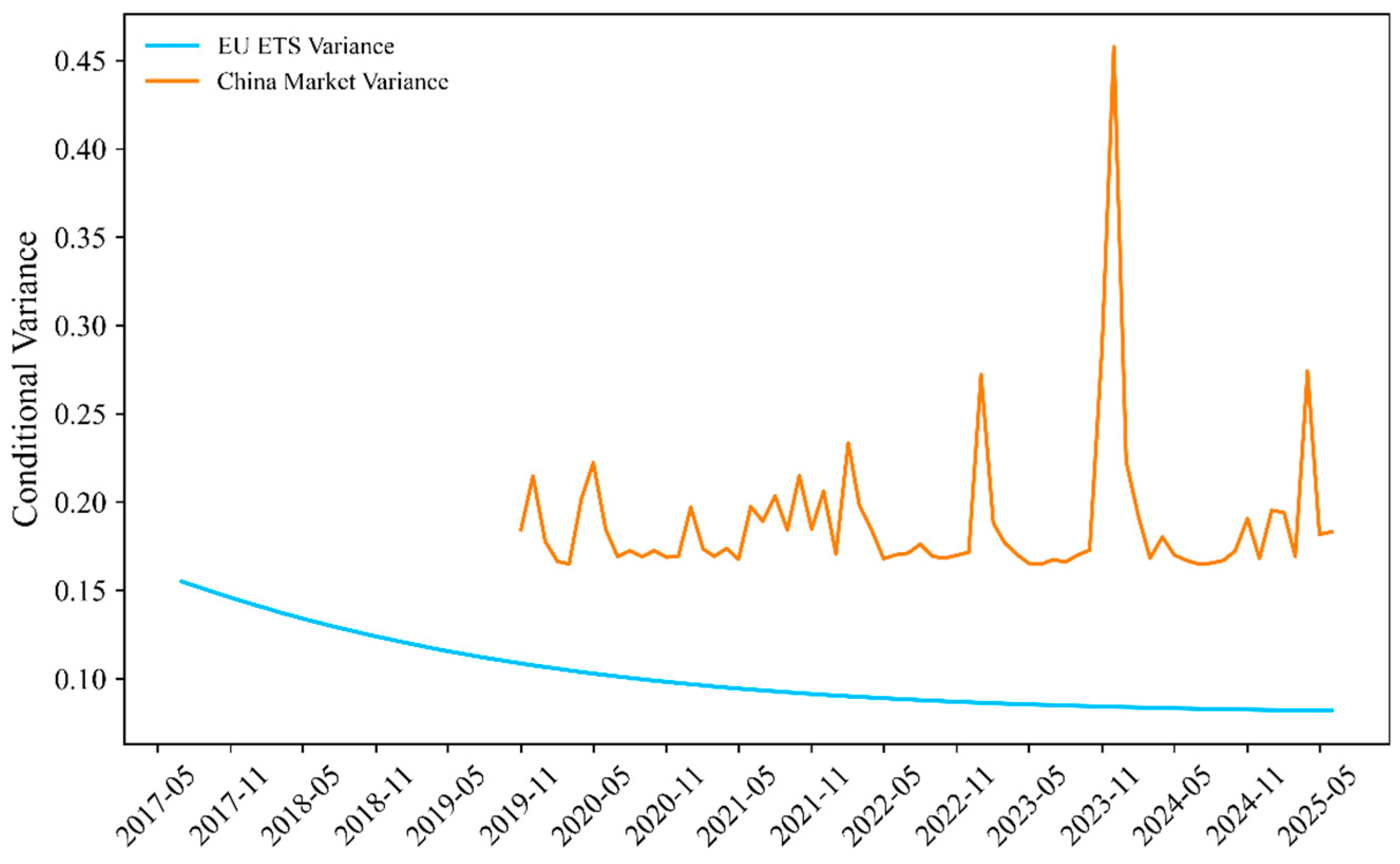
The conditional variance trends of the EU and China carbon markets from 2017 to 2025 are shown in Figure 6, based on the estimated results from the GARCH-M(1,1) model.
To further explore the dynamics of variance and ensure robustness against potential convergence issues in dynamic forecasting, we additionally employ a static forecasting method in the GARCH-M(1,1) model, as shown in Figure 7. This approach generates a more fluctuating conditional variance process, allowing for better capture of short-term volatility. The variance of the EU shows early peaks between 2018 and 2019, reflecting the EU ETS reforms, such as the Market Stability Reserve mechanism reducing surplus allowances. This is followed by stability post-2020, reflecting market maturity and policy effects, including post-COVID recovery and the push towards net-zero emission targets. The variance of China remains lower, with occasional spikes, consistent with the characteristics of its emerging market.
The model uses a t-distribution to fit 1382 data points from China and 8453 data points from the EU, reflecting market volatility characteristics. The EU parameters show a risk premium λ = 0.0237, α_0 = 0.000263, α_1 = 2.776 e−09, β_1 = 0.9587, and a degree of freedom v = 8.26, indicating that long-term volatility dominates, consistent with its mature market characteristics. The China parameters show λ = 0.0190, α_0 = 0.0238, α_1 = 0.2526, β_1 = 0.1227, and ν=3.87, reflecting that short-term volatility dominates, aligning with its emerging market characteristics. Figure 6 and Figure 8 further verify that the residuals are white noise, with Ljung–Box test p-values of 0.503 and 0.198, supporting the validity of the model and providing the parameter foundation for price forecasting from 2000 to 2020 and the ecological carbon sink value assessment for Qilian Mountain National Park.
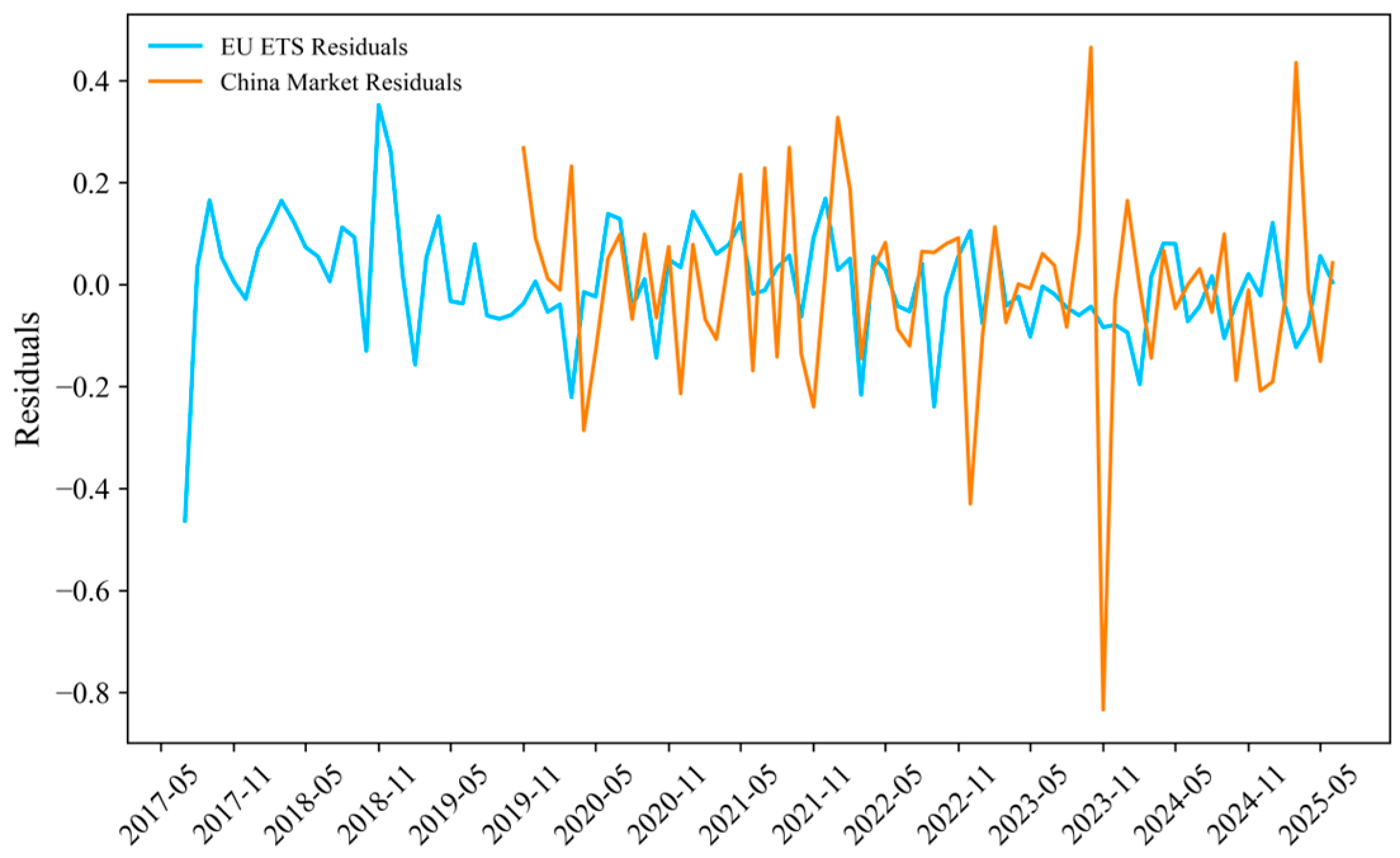
The residual analysis of the EU and China carbon markets from 2017 to 2025 based on the GARCH-M(1,1) model is shown in Figure 8. The residuals are distributed around the zero axis, and the Ljung–Box test results (EU p = 0.503, China p = 0.198 > 0.05) indicate no significant autocorrelation, confirming the residuals are white noise and validating the model’s goodness of fit. The EU residuals exhibit lower variance, consistent with the model’s parameter estimates showing dominant long-term persistence (β_1 = 0.9587). In contrast, the Chinese residuals have higher variance, aligning with parameters indicating stronger short-term effects (α_1 = 0.2526). These diagnostics enhance the model’s credibility for subsequent forecasting.
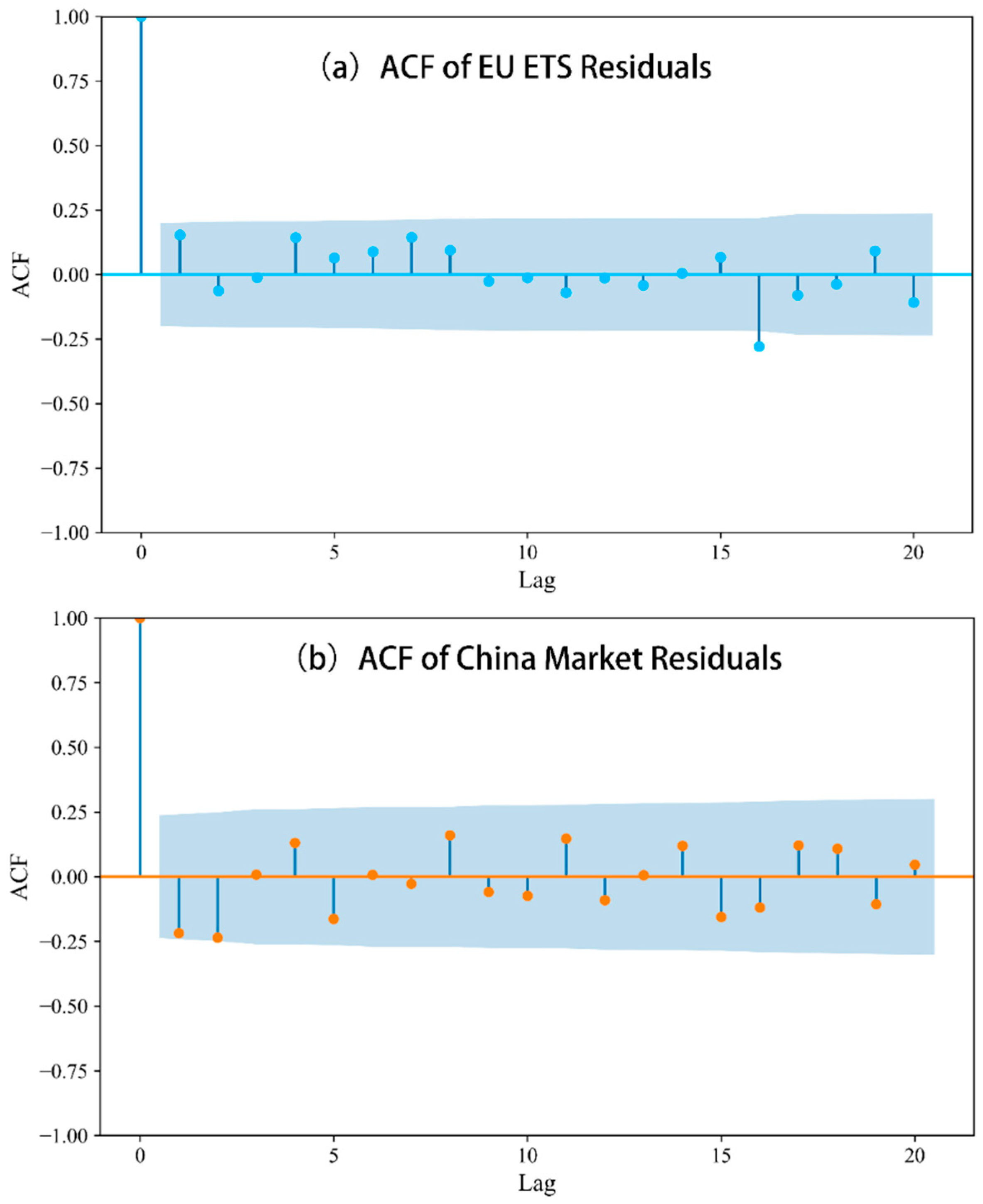
The autocorrelation function (ACF) of the residuals for the EU and China carbon markets from 2017 to 2025, using the GARCH-M(1,1) model, is presented in Figure 9. The ACF coefficients for lags up to 20 remain mostly within the confidence interval, with no significant spikes, confirming the absence of unmodeled autocorrelation. This finding is further supported by the Ljung–Box test results (EU p = 0.503, China p = 0.198, both >0.05). The residuals for both markets exhibit randomness consistent with the t-distribution assumption (degrees of freedom: EU 8.26, China 3.87), capturing the heavy tails, thus ensuring reliable parameter estimates. This provides a solid foundation for price forecasting from 2017 to 2025.

3.2.4. 3 × 2 Price Scenarios Based on the GARCH-M(1,1) Model

Based on the GARCH-M(1,1) model parameters, the carbon market prices for the EU and China from 2000 to 2025 were quantified using the extrapolation method to generate 3 × 2 price scenarios (low, medium, high × EU, China) to capture the dynamic volatility characteristics of prices. The model uses 8453 data points from the EU and 1382 data points from China from 2017 to 2025, simulating the residual distribution with a t-distribution and incorporating risk premium effects to construct a robust dynamic price series. The initial conditions are based on the historical mean and variance from 2017, and the scenarios are assumed by adjusting the volatility and trend parameters, fully considering the impacts of market policy changes and economic conditions, providing a data foundation for subsequent analysis.
The 3 × 2 price scenarios for the EU and China carbon markets from 2000 to 2025 are shown in Table 5, covering the mean and standard deviation of the low, medium, and high scenarios. The prices for 2020 and 2025 are based on actual monthly data, reflecting the low (5th percentile), medium (50th percentile), and high (95th percentile) levels for both the EU and China. For 2000 and 2010, due to GARCH recursion limitations, trend extrapolation was used to preliminarily construct the low scenario price, and linear interpolation was used to estimate the medium and high scenarios. The results show that the average EU price trend increased from 137.5 CNY/t CO2 (medium scenario) in 2000 to 605.9 CNY/t CO2 (medium scenario) in 2025. The price range expanded from 110.4 CNY/t CO2 (low scenario in 2000) to 653.5 CNY/t CO2 (high scenario in 2025), reflecting long-term volatility characteristics. The average price trend for China increased from 18.6 CNY/t CO2 (medium scenario in 2000) to 47.6 CNY/t CO2 (medium scenario in 2025), with the price range expanding from 15.0 CNY/t CO2 (low scenario in 2000) to 52.5 CNY/t CO2 (high scenario in 2025). The growth was steady, highlighting the dominance of short-term shocks, reflecting the different stages of market development in the two countries.
The EU market is driven by long-term volatility, with prices rising significantly over time. The magnitude of volatility is influenced by macroeconomic policies and energy structure adjustments. The Chinese market is dominated by short-term shocks, with relatively moderate growth, reflecting frequent policy adjustments and market immaturity. The actual data for 2020 and 2025 verified the robustness of the model, and its diversified price distribution provides a reliable quantitative basis for the subsequent ecological carbon sink value assessment.

3.2.5. Quantification of the Economic Value of Ecological Carbon Sinks in Qilian Mountain National Park

Building on the dynamic assessment of carbon prices from 2000 to 2025 and carbon storage estimates for Qilian Mountain National Park, the economic value of its ecological carbon sink is evaluated. The economic value is calculated by multiplying the corresponding scenario price by the carbon storage for each year, with the unit in hundred million CNY, reflecting the low, medium, and high scenarios at the 5th, 50th, and 95th percentiles. The carbon storage for 2025 is assumed to be the same as that for 2020 (7.93 × 108 tons). Price data comes from the extrapolation of the GARCH-M(1,1) model and historical transaction data analysis, aiming to quantify the potential revenue of carbon sinks under different market conditions.
The economic value assessment is based on multi-source data fusion and the GARCH model, using a 3 × 2 scenario (high, medium, low) analysis for the carbon sink value in Qilian Mountain National Park from 2000 to 2025, as shown in Table 6. In 2000, the EU market value ranged from 831.312 × 108 CNY (low scenario) to 1164.138 × 108 CNY (high scenario), while the China market (without a mature market, based on model-extrapolated prices) ranged from 112.950 × 108 CNY to 152.106 × 108 CNY. In 2010, the EU value increased to 1267.420 × 108 CNY (low scenario) to 1384.460 × 108 CNY (high scenario), while the China value ranged from 170.940 × 108 CNY to 210.980 × 108 CNY. From 2020 to 2025, the growth was significant, with the EU value reaching 4438.421 × 108 CNY (2025 low scenario) to 5182.255 × 108 CNY (high scenario), and the China value ranged from 263.276 × 108 CNY to 416.325 × 108 CNY. The extrapolated data for 2000–2010 and the actual data for 2020–2025 validate the model’s reliability, reflecting the continuous increase in carbon sink value with ecological restoration and market development, laying the foundation for subsequent market differentiation analysis.
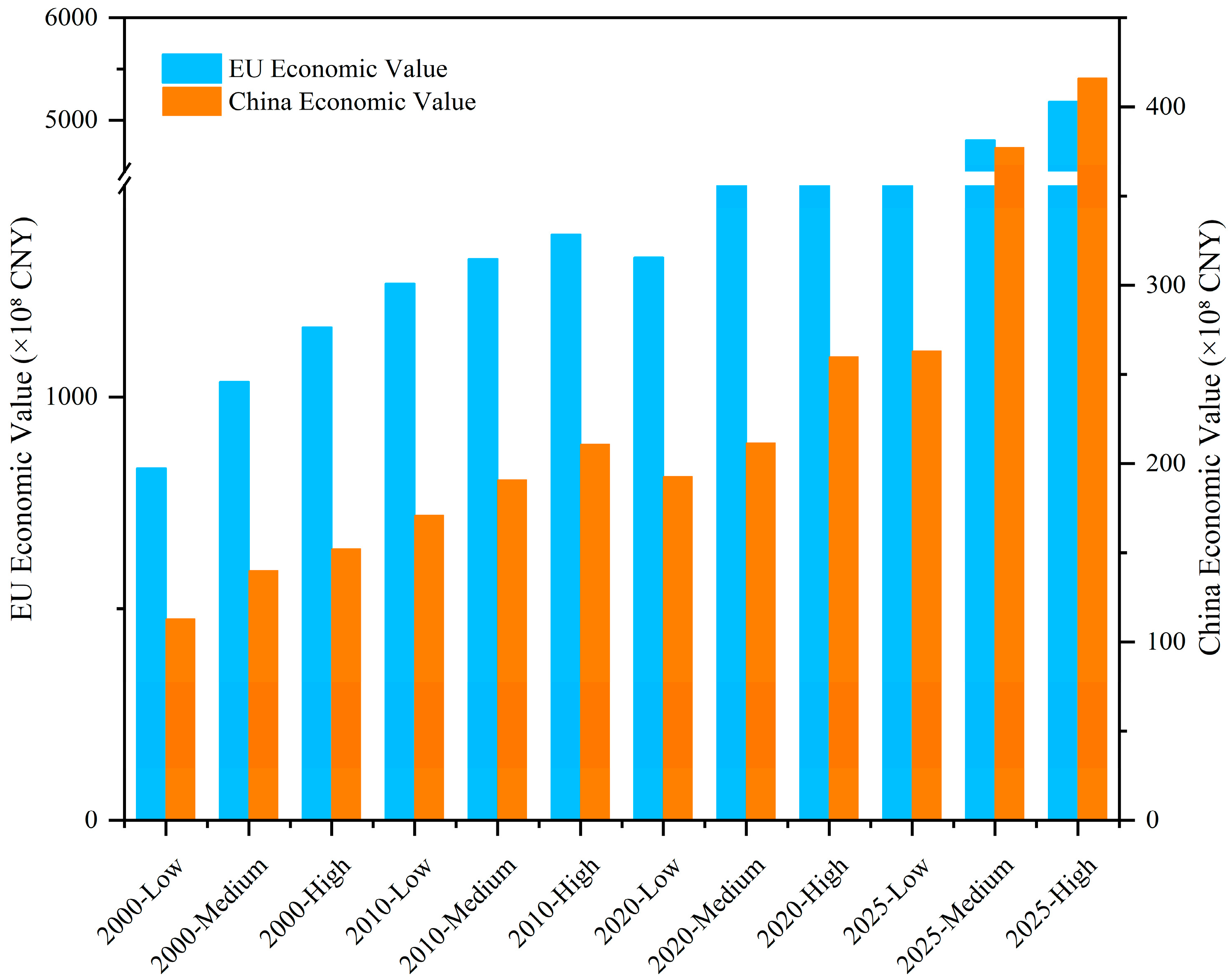
The economic value assessment outcomes are illustrated in Figure 10. The carbon sink value in Qilian Mountain National Park within the EU carbon market significantly exceeds that in China’s national carbon market. In 2025, under the high, medium, and low scenarios, the EU market values are 518.2255 billion CNY, 480.4787 billion CNY, and 443.8421 billion CNY, respectively, while the values for the China market are 41.6325 billion CNY, 37.7468 billion CNY, and 26.3276 billion CNY, making the EU market value 12.45 to 16.85 times that of the China market. The extrapolated data for 2000 and 2010 provide a reference for historical trend analysis, while the actual data for 2020 and 2025 verify the reliability of the model. The value difference stems from the EU carbon market, which has operated under the European Emission Trading System (EU-ETS) since 2005. As the world’s first carbon market, after four phases of quota allocation optimization, the EU market has a mature trading mechanism, high and stable carbon prices, and strong market demand. China’s carbon market, starting from the regional pilot markets in 2013, is still in the early stages of nationwide market construction, with limited regional trading scale, inconsistent certification standards, and low carbon price volatility, leading to an undervaluation of carbon sink value. These results highlight the decisive impact of market maturity and mechanism refinement on carbon sink economic benefits, providing data support for subsequent carbon sink value research.

4. Discussion

4.1. Methodological Innovation: Multi-Source Data Fusion and Dynamic Carbon Price Model

This study demonstrates the broader applicability of integrating multi-source data from recent high-quality literature to analyze carbon storage trends over extended periods, such as from 2000 to 2020. By employing the mean and standard deviation for validation, the approach establishes a reliable foundation for ecological carbon sink value assessments across diverse ecosystems. The observed increase in carbon storage, with standard deviations maintained within a narrow range, underscores the general reduction in uncertainty that is achievable through data fusion, which is relevant to various regions confronting data variability challenges. In contrast to reliance on a single source, this method enhances the consistency and reliability of time series data in ecosystems worldwide, aligning with the findings of Zeng et al. [26], who documented an approximately 18% improvement in accuracy through multi-source integration in plateau environments, and Khan et al. [27], who enhanced estimation precision in complex terrains by fusing optical data, SAR data, and machine learning techniques. This integration provides comprehensive dynamic perspectives on carbon storage, incorporating influences such as land use changes, and offers a scalable basis for dynamic pricing models in forest ecosystems, consistent with the methods reported by Sun et al. [28].
The primary advantage of multi-source data integration lies in its capacity to amalgamate complementary information from diverse sources, such as remote sensing for extensive spatial coverage and ground monitoring for precise local validation. As illustrated in Pan et al.’s global forest carbon sink investigation [29], this strategy can substantially mitigate estimation uncertainties on an international scale. Nonetheless, challenges such as data heterogeneity and computational complexities, as elaborated by Himeur et al. [30], require substantial resources for large-scale implementations. Extending this framework to volatility assessment, the GARCH-M(1,1) model effectively captures carbon price fluctuations, elucidating how market-driven variations influence sink values universally. This aligns with the work of Byun and Cho [31], who demonstrated the GARCH model’s superiority in volatility modeling, and Wei et al. [32] (2024), whose Transformer-LSTM-GARCH hybrid model suggests opportunities for improved forecasting accuracy in broader contexts. Lyu et al. [33], in their analysis of China’s carbon market volatility, further emphasize the critical role of carbon trading in emission reduction and the significant impact of price instability on the stability of ecological compensation funds, indicating that integrating dynamic pricing with ecosystem service assessments can support market-based valuations and compensation allocations at national and global levels.

4.2. Current Status and Potential of Carbon Sink Market Trading

As an emerging sector, carbon trading markets facilitate the reduction in emission costs through institutional innovations and trading mechanisms [34]. In 2005, the European Union established the world’s first carbon market, the EU Emissions Trading System (EU ETS) [35]. As a representative of emerging economies, China initiated carbon market pilot programs in 2013 [36] and established a national carbon market by the end of 2017 [37]. Presently, China’s carbon market constitutes the largest globally [38], thereby contributing to the advancement of carbon markets in developing countries. Nevertheless, emerging markets such as China’s remain immature, characterized by unstable trading volumes, elevated price volatility, and substantial risks.
Price fluctuations and valuation disparities between mature markets like the EU ETS and emerging ones such as China’s arise from varying degrees of market maturity. The EU ETS demonstrates low volatility attributable to stable policies, high liquidity, and stringent quota allocation mechanisms, which yield predictable pricing. Conversely, emerging markets exhibit high volatility due to fragmented regional initiatives, policy uncertainties, and quota oversupply, resulting in price instability, undervaluation, and diminished investor confidence. These dynamics underscore the pivotal role of regulatory maturity in advancing the monetization of carbon sinks on a global scale, with mature frameworks offering transferable insights for enhancing resilience in developing markets.
Carbon market trading represents an efficacious instrument for cost-effective climate change mitigation and emission reduction, serving as a fundamental pathway for the monetization of ecological carbon sink values worldwide. Analyses grounded in carbon storage estimates and GARCH(1,1) modeling of price fluctuations reveal the feasibility and potential of regional carbon sink trading, furnishing theoretical underpinnings for market-oriented pricing and establishing empirical foundations for ecological compensation and global carbon market evolution. This approach aligns with the frameworks for ecological carbon sink compensation mechanisms in protected areas, as delineated by Gao et al. [39], and facilitates the integration of carbon sinks into national and international trading systems.
Although empirical support exists for carbon market trading and ecological compensation, persistent challenges include insufficient liquidity in regional markets, which may constrain trading scales; PwC [40] posits that augmenting market participants could ameliorate liquidity. The enduring sustainability of ecological compensation hinges on robust fiscal and policy frameworks, wherein fiscal constraints at subnational levels may impede efficacy [41]. Maximizing carbon sink values necessitates seamless coordination between policy formulation and data-driven analysis. The EU ETS has established a global benchmark through standardized evaluations and market mechanisms [42]. The World Bank asserts that ecological compensation mechanisms in emerging contexts require reliance on uniform assessment methodologies and diversified funding channels [43]. Jiang et al. [44] advocate enhancing the adaptability of compensation mechanisms via policy experimentation. Integrating dependable carbon storage data with cross-market volatility analyses provides a basis for policy innovation and bolsters sustainable management practices. Future investigations should refine carbon storage estimation methodologies to underpin market integration, examine inter-regional linkage mechanisms to augment liquidity, and devise economically viable monitoring systems to optimize compensation frameworks. The incorporation of predictive models, such as machine learning algorithms, could further augment the precision of carbon price analyses and thereby elevate the efficacy of market-based valuation and compensation structures.

4.3. Limitations and Future Directions

The methodological assumptions underlying this study encompass conditional heteroscedasticity and volatility persistence in the GARCH-M(1,1) model, with data subjected to log-differencing to attain stationarity, a t-distribution employed to accommodate heavy-tailed distributions, and carbon price data utilized at a daily frequency (2017–2025). These assumptions rest on preliminary tests such as the ADF and ARCH-LM procedures (see Section 3.2.2), yet they may disregard volatility asymmetry, as extensions like EGARCH were not incorporated.
This study introduces innovative methodologies for ecological carbon sink value assessment, leveraging multi-source data integration and dynamic carbon pricing models. However, inherent constraints persist. The temporal span and resolution of remote sensing and ecological monitoring data constrain the capacity to comprehensively capture extreme climate events and localized ecological shifts. Furthermore, the incomplete incorporation of international carbon market pricing mechanisms and ecosystem service impacts may compromise the overall comprehensiveness of carbon sink evaluations. In addition, climate policy fluctuations and legal impediments, such as restrictions on carbon trading in protected zones, present formidable obstacles to the efficacious functioning of carbon markets globally.
Future investigations should prioritize the integration of high-resolution remote sensing data, the extension of temporal datasets, the refinement of carbon credit premium mechanisms, and the development of real-time carbon sink assessment systems. Incorporating climate change scenario analyses would enable the evaluation of long-term ecological protection impacts on carbon sinks and ecosystem services, thereby furnishing robust scientific evidence for ecological carbon trading, regional compensation strategies, and global carbon neutrality objectives. Moreover, forthcoming research ought to accord particular emphasis to uncertainties arising from climate policy variability and integrate these into carbon sink value assessments to enhance methodological robustness.

5. Conclusions

This study conducted a comprehensive evaluation of the market value of ecological carbon sinks in Qilian Mountain National Park through multi-source data integration and the GARCH-M(1,1) model, revealing the spatiotemporal patterns of carbon storage variations, trends in carbon market pricing, and their economic implications. This framework theoretically expands the application of dynamic pricing in ecological assessments and provides actionable insights for achieving the “dual carbon” goals. The key findings are summarized as follows:
1.
Continuous Growth of Carbon Sink
The carbon sink in Qilian Mountain National Park increased from 7.53 × 108 tons in 2000 to 7.93 × 108 tons in 2020, with a cumulative increase of 0.40 × 108 tons over 20 years, corresponding to an average annual growth rate of 0.27%. These results indicate that ecological restoration efforts have significantly enhanced the stability of carbon storage, addressing the quantification of carbon storage changes in the study and suggesting that extending policies to other parks could enhance biodiversity conservation and regional ecological resilience, thereby supporting China’s “dual carbon” goals.
2.
Divergent Trends in Carbon Market Prices
The price in the EU carbon market rose from approximately 40 CNY/ton CO2 in 2017 to about 600 CNY/ton CO2 in 2025, showing high volatility, reflecting the impact of policy adjustments and emission reduction targets on the EU ETS. The price in China’s market increased from 10 CNY/ton CO2 to 60 CNY/ton CO2, with lower volatility, constrained by the early stage of market development, regional differences, and inconsistent certification standards. These findings highlight the influence of market maturity on carbon market valuation, addressing the issue of price volatility, and emphasizing the need for China to strengthen regulatory actions to reduce uncertainty, promote international cooperation, and integrate ecological carbon storage into the global carbon exchange system.
3.
Significant Economic Value Differences
Under high, medium, and low scenarios for 2025, the value of carbon storage in Qilian Mountain National Park in the EU market is 51.82255 billion CNY, 48.04787 billion CNY, and 44.38421 billion CNY, respectively, while in China’s market, it is 4.16325 billion CNY, 3.77468 billion CNY, and 2.63276 billion CNY, making the EU market value 12.45 to 16.85 times higher than that of the Chinese market. This disparity arises from the mature market mechanism, high carbon prices, and strong demand for high-quality carbon credits in the EU carbon market. In contrast, China’s carbon market, which began in 2013, is still in its early stages, with limited trading scale and lower price levels. This suggests that Qilian Mountain National Park’s carbon storage has enormous market potential, but further exploration of market development pathways is needed, such as achieving sustainable financial support through dynamic pricing and ecological compensation designs to promote regional green development.
These findings not only deepen the understanding of the market value of ecological carbon storage but also provide actionable recommendations for policy, particularly to accelerate the maturation of China’s carbon market, bridge the valuation gap, and support the achievement of the “dual carbon” goals. For other national parks, this framework can be applied to enhance biodiversity conservation. Future research should incorporate higher-resolution temporal data and test market linkage scenarios to refine carbon storage valuations and guide the consistency of global climate policies.

Author Contributions

Conceptualization, Y.G.; Methodology, X.Y.; Validation, Y.Z.; Formal analysis, X.Y.; Data curation, W.S.; Writing—original draft, W.S.; Writing—review & editing, W.S.; Visualization, Y.Z.; Supervision, Y.Z.; Funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by: (1) Open Fund for the Field Scientific Observation and Research Station of the Sub-alpine Ecosystem in Central Qilian Mountains, Ministry of Natural Resources of China, QLSKFJJ—(2024) D0006; (2) Innovation Project for University Teachers, Gansu Provincial Department of Education (2025B-254); (3) Teaching Reform Project, Lanzhou University of Arts and Sciences (2024-ZL-jxgg-04); (4) Industry-University Cooperation and Collaborative Education Project, Ministry of Education of China (2409120553).

Data Availability Statement

The data presented in this study are openly available in Carbon Emission Trading repository at https://ets.sceex.com.cn/, accessed on 3 September 2025.

Acknowledgments

We would like to express our gratitude to the staff and the Voluntary GHG Emission Reduction Trading Platform for providing open data to support this research. We also appreciate the programming environment and tools offered by Python 3.11, which were instrumental in our data analysis and model development.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

To enhance the readability and flow of the text, the derivation formulae and model parameters have been placed in this section. This arrangement ensures that the main text remains concise and clear, with detailed content provided in the following sections.
The specific calculations are shown in Formulae (A1) and (A2):
C ¯ t = 1 n ∑ i = 1 n C i , t
In the formula: C ¯ t represents the mean carbon storage value for year t (unit: tons); C i , t represents the carbon storage value for year t in the i-th piece of literature (unit: tons); n is the number of literature sources; ∑ i = 1 n denotes the summation from i   = 1 to n .
σ t = 1 n ∑ i = 1 n ( C i , t − C ¯ t ) 2
In the formula: σ t represents the standard deviation of carbon storage for year t (unit: tons), with other variables consistent with those in Formula (A1).
The specific calculations are shown in Formulae (A3) and (A4):
S = ∑ i = 1 n = 1 ∑ j = i + 1 n s g n ( C j − C i )
s g n x = 1 i f x > 0 0 i f x = 0 − 1 i f x < 0
In the formula: S is the test statistic, representing the accumulated trend direction (positive values indicate an upward trend, negative values indicate a downward trend); C i , C j are the mean carbon storage values for years i and j (unit: tons); n is the length of the time series (in this study, n = 3 ); s g n is the sign function; ∑ i = 1 n = 1 ∑ j = i + 1 n denotes the summation over all data pairs where i < j . A significance level of p < 0.05 indicates a significant trend.
β = m e d i a n C j − C i j − i , i < j
In the formula: β is the annual growth rate (unit: tons/year); m e d i a n refers to the median calculation.
The formula for the GARCH-M(1,1) model is shown in Formula (A6):
r t = μ + λ σ t + ϵ t , σ t 2 = α 0 + α 1 ϵ t − 1 2 + β 1 σ t − 1 2
In the formula: r t is the daily logarithmic return of the carbon price at time t (%), defined as r t = l n ( P t / P t − 1 ) , based on the EU closing price or China’s average transaction price; μ is the constant term of the return, representing the average return; λ is the risk premium coefficient, measuring the impact of volatility on the return; σ t is the conditional standard deviation at time t, reflecting the price volatility risk; ϵ t is the random error term, which follows a normal distribution or t - distribution; σ t 2 is the conditional variance at time t , representing the volatility intensity; α 0 is the constant term of the variance; α 1 is the coefficient representing the impact of the previous period’s error ϵ t − 1 2 on the current variance; β 1 is the coefficient representing the persistence of the previous period’s variance σ t − 1 2 on the current variance.
The model parameters ( μ , λ , α 0 , α 1 , β 1 ) are fitted using Maximum Likelihood Estimation (MLE), and the residual heteroscedasticity is verified using the ARCH-LM test (with p > 0.05).
V s , m , t = C ¯ t × P s , m , t
In the formula: V s , m , t is the economic value for year t (2000, 2010, 2020), scenario s (low, medium, high), and market m (China, EU) (unit: CNY); C ¯ t is the mean carbon storage for year t (unit: tons); P s , m , t is the carbon price for year t , scenario s , and market m (unit: CNY/ton).

References

  1. Lin, B.; Ge, J. Carbon sinks and output of China’s forestry sector: An ecological economic development perspective. Sci. Total Environ. 2019, 655, 1169–1180. [Google Scholar] [CrossRef]
  2. Mora, C.; Spirandelli, D.; Franklin, E.C.; Lynham, J.; Kantar, M.B.; Miles, W.; Smith, C.Z.; Freel, K.; Moy, J.; Louis, L.V.; et al. Broad threat to humanity from cumulative climate hazards intensified by greenhouse gas emissions. Nat. Clim. Change 2018, 8, 1062–1071. [Google Scholar] [CrossRef]
  3. Ma, W.; Hou, S.; Su, W.; Mao, T.; Wang, X.; Liang, T. Estimation of carbon stock and economic value of Sanjiangyuan National Park, China. Ecol. Indic. 2024, 169, 112856. [Google Scholar] [CrossRef]
  4. Huang, M.-T.; Zhai, P.-M. Achieving Paris Agreement temperature goals requires carbon neutrality by middle century with far-reaching transitions in the whole society. Adv. Clim. Change Res. 2021, 12, 281–286. [Google Scholar] [CrossRef]
  5. Liu, Z.; Deng, Z.; He, G.; Wang, H.; Zhang, X.; Lin, J.; Qi, Y.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Rev. Earth Environ. 2022, 3, 141–155. [Google Scholar] [CrossRef]
  6. Hu, Q.; Zhang, J.; Xue, H.; Wang, J.; Li, A. Spatiotemporal Variations in Carbon Sources and Sinks in National Park Ecosystem and the Impact of Tourism. Sustainability 2024, 16, 7895. [Google Scholar] [CrossRef]
  7. Peng, Q.; Wang, R.; Jiang, Y.; Li, C. Contributions of climate change and human activities to vegetation dynamics in Qilian Mountain National Park, northwest China. Glob. Ecol. Conserv. 2021, 32, e01947. [Google Scholar] [CrossRef]
  8. Dimobe, K.; Kuyah, S.; Dabré, Z.; Ouédraogo, A.; Thiombiano, A. Diversity-carbon stock relationship across vegetation types in W National park in Burkina Faso. For. Ecol. Manag. 2019, 438, 243–254. [Google Scholar] [CrossRef]
  9. Grossi, G.; Vitali, A.; Bernabucci, U.; Lacetera, N.; Nardone, A. Greenhouse Gas Emissions and Carbon Sinks of an Italian Natural Park. Front. Environ. Sci. 2021, 9, 706880. [Google Scholar] [CrossRef]
  10. Zhao, N.; Wang, K.; Yuan, Y. Toward the carbon neutrality: Forest carbon sinks and its spatial spillover effect in China. Ecol. Econ. 2023, 209, 107837. [Google Scholar] [CrossRef]
  11. Ben Jabeur, S. Natural capital accounting for sustainability: Bibliometric analysis and explainable artificial intelligence modeling for citation counts. J. Clean. Prod. 2024, 451, 142138. [Google Scholar] [CrossRef]
  12. Asghar, M.; Ben Cheikh, N.; Hunjra, A.I.; Khan, A. Assessing the impact of natural capital and innovation on sustainable development in developing countries. J. Clean. Prod. 2024, 460, 142576. [Google Scholar] [CrossRef]
  13. Bagstad, K.J.; Ingram, J.C.; Shapiro, C.D.; La Notte, A.; Maes, J.; Vallecillo, S.; Casey, C.F.; Glynn, P.D.; Heris, M.P.; Johnson, J.A.; et al. Lessons learned from development of natural capital accounts in the United States and European Union. Ecosyst. Serv. 2021, 52, 101359. [Google Scholar] [CrossRef]
  14. Ingram, J.C.; Bagstad, K.J.; Vardon, M.; Rhodes, C.R.; Posner, S.; Casey, C.F.; Glynn, P.D.; Shapiro, C.D. Opportunities for businesses to use and support development of SEEA-aligned natural capital accounts. Ecosyst. Serv. 2022, 55, 101434. [Google Scholar] [CrossRef]
  15. Kurrahman, T.; Tsai, F.M.; Sethanan, K.; Lim, M.K.; Tseng, M.-L. Data-driven natural capital accounting model in Indonesia: Impacts of environmentally related economic activities on ecological processes and services. J. Clean. Prod. 2024, 469, 143213. [Google Scholar] [CrossRef]
  16. Qu, Z.; Thrush, S.; Blain, C.; Lewis, N. Assessing the carbon storage value of kelp forest restoration in the Hauraki Gulf Marine Park, New Zealand: Lessons from no-take Marine Protected Areas. Mar. Policy 2023, 154, 105682. [Google Scholar] [CrossRef]
  17. Van Tam, N.; Toan, N.Q.; Ngoc, P.H. Key strategies for achieving net-zero carbon buildings and promoting carbon credits in construction markets: A case of an emerging economy. Energy Sustain. Dev. 2024, 81, 101488. [Google Scholar] [CrossRef]
  18. Shi, B.; Li, N.; Gao, Q.; Li, G. Market incentives, carbon quota allocation and carbon emission reduction: Evidence from China’s carbon trading pilot policy. J. Environ. Manag. 2022, 319, 115650. [Google Scholar] [CrossRef]
  19. Lovell, H.C. Governing the carbon offset market. WIREs Clim. Change 2010, 1, 353–362. [Google Scholar] [CrossRef]
  20. Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
  21. Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
  22. Zhang, B.; Feng, Q.; Lu, Z.; Li, Z.; Zhang, B.; Cheng, W. Ecosystem service value and ecological compensation in Qilian Mountain National Park: Implications for ecological conservation strategies. Ecol. Indic. 2024, 167, 112661. [Google Scholar] [CrossRef]
  23. Liu, X.; Hao, Y.; Meng, Z.; He, S.; An, C.; Chen, Q.; Chu, B.; Hua, M. Spatiotemporal variation of carbon storage and its driving factors in Qilian Mountain National Park from 1990 to 2022. Acta Ecol. Sin. 2025, 45, 5263–5276. [Google Scholar]
  24. Su, D.; Zhao, J.; Li, X. Analysis and Prediction of Carbon Storage Evolution in Qilian Mountain National Park Based on the InVEST-FLUS Model. Environ. Eng. 2024, 42, 190–199. [Google Scholar]
  25. Deng, Z.; Ding, g.; Pu, t.; Lv, J.; Wang, L. Spatial-temporal Distribution of Carbon Storage in Qilian Mountain National Park Based on InVEST Model. Bullet Soil Water Conserv. 2022, 324–334, 396. [Google Scholar]
  26. Zeng, J.; Zhou, T.; Xu, Y.; Lin, Q.; Tan, E.; Zhang, Y.; Wu, X.; Zhang, J.; Liu, X. The fusion of multiple scale data indicates that the carbon sink function of the Qinghai-Tibet Plateau is substantial. Carbon Balance Manag. 2023, 18, 19. [Google Scholar] [CrossRef]
  27. Khan, K.; Khan, S.N.; Ali, A.; Khokhar, M.F.; Khan, J.A. Estimating Aboveground Biomass and Carbon Sequestration in Afforestation Areas Using Optical/SAR Data Fusion and Machine Learning. Remote Sens. 2025, 17, 934. [Google Scholar] [CrossRef]
  28. Sun, W.; Liu, X. Review on carbon storage estimation of forest ecosystem and applications in China. For. Ecosyst. 2019, 7, 4. [Google Scholar] [CrossRef]
  29. Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
  30. Himeur, Y.; Rimal, B.; Tiwary, A.; Amira, A. Using artificial intelligence and data fusion for environmental monitoring: A review and future perspectives. Inf. Fusion 2022, 86–87, 44–75. [Google Scholar] [CrossRef]
  31. Byun, S.J.; Cho, H. Forecasting carbon futures volatility using GARCH models with energy volatilities. Energy Econ. 2013, 40, 207–221. [Google Scholar] [CrossRef]
  32. Wei, B.; Liu, C.; Liu, J. Prediction of Carbon Futures Volatility Based on the Transformer-LSTM-GARCH Hybrid Model. In Proceedings of the 2024 4th International Conference on Internet of Things and Machine Learning, Nanchang, China, 9–11 August 2024; pp. 65–71. [Google Scholar]
  33. Lyu, J.; Cao, M.; Wu, K.; Li, H.; Mohi-ud-din, G. Price volatility in the carbon market in China. J. Clean. Prod. 2020, 255, 120171. [Google Scholar] [CrossRef]
  34. Dong, F.; Li, Z.; Cui, J.; Zhang, Y.; Lu, B.; Fan, K.; Xu, K.; Li, J.; Sun, J. Analysis of market risk volatility and warning in carbon trading market. J. Clean. Prod. 2024, 452, 142014. [Google Scholar] [CrossRef]
  35. Wang, M.; Kuusi, T. Trade flows, carbon leakage, and the EU Emissions Trading System. Energy Econ. 2024, 134, 107556. [Google Scholar] [CrossRef]
  36. Guo, J.; Ou, X.; Li, Y.; Liu, K. Can the Carbon Emissions Trading Pilot Policy Improve the Ecological Well-Being Performance of Cities in China? Sustainability 2024, 16, 841. [Google Scholar] [CrossRef]
  37. Tang, C.; Wu, Y.; Liu, X. Does China’s national carbon market play a role? Evidence from corporate ESG performance. Econ. Anal. Policy 2025, 85, 1053–1064. [Google Scholar] [CrossRef]
  38. Dong, Q.; Zhao, Y.; Ma, X.; Zhou, Y. Risk spillover between carbon markets and stock markets from a progressive perspective: Measurements, spillover networks, and driving factors. Energy Econ. 2024, 129, 107228. [Google Scholar] [CrossRef]
  39. Gao, Y.; Ling, W.; Sheng, C.-l.; Yi, D.; Li, X.-m. Design of ecological carbon sink compensation mechanism for national parks based on carbon trading. J. Nat. Resour. 2024, 39, 10. [Google Scholar] [CrossRef]
  40. PricewaterhouseCoopers. (n.d.). Carbon Markets—The Regional Market Solution. PwC. Retrieved 10 July 2025. Available online: https://www.pwc.com/gx/en/services/sustainability/publications/what-next-for-carbon-markets.html (accessed on 3 September 2025).
  41. Wang, Q.; Zhou, C. How does government environmental investment promote green development: Evidence from China. PLoS ONE 2023, 18, e0292223. [Google Scholar] [CrossRef] [PubMed]
  42. Kotzampasakis, M.; Woerdman, E. The Legal Objectives of the EU Emissions Trading System: An Evaluation Framework. Transnatl. Environ. Law 2024, 13, 312–336. [Google Scholar] [CrossRef]
  43. Shang, W.; Gong, Y.; Wang, Z.; Stewardson, M.J. Eco-compensation in China: Theory, practices and suggestions for the future. J. Environ. Manag. 2018, 210, 162–170. [Google Scholar] [CrossRef] [PubMed]
  44. Liu, J.; Dou, S. Eco-compensation in China: Achievement, experience, and improvement. Environ. Sci. Pollut. Res. Int. 2022, 29, 60867–60884. [Google Scholar]
Forests 16 01427 g001
Figure 1. Workflow of Dynamic Carbon Sink Valuation and Multi-Source Data Fusion.
Figure 1. Workflow of Dynamic Carbon Sink Valuation and Multi-Source Data Fusion.
Forests 16 01427 g001
Forests 16 01427 g002
Figure 2. Study Area Overview Map.
Figure 2. Study Area Overview Map.
Forests 16 01427 g002
Forests 16 01427 g003
Figure 3. Dynamic Distribution of Carbon Storage in Qilian Mountain National Park from 2000 to 2020.
Figure 3. Dynamic Distribution of Carbon Storage in Qilian Mountain National Park from 2000 to 2020.
Forests 16 01427 g003
Forests 16 01427 g004
Figure 4. (a) Dynamic Price Trends of the EU Emission Trading System from 2017 to 2025. (b) Dynamic Price Trends of China’s Carbon Market Emission Trading System from 2019 to 2025.
Figure 4. (a) Dynamic Price Trends of the EU Emission Trading System from 2017 to 2025. (b) Dynamic Price Trends of China’s Carbon Market Emission Trading System from 2019 to 2025.
Forests 16 01427 g004
Forests 16 01427 g005
Figure 5. Time Series and Distributions of Carbon Price Returns for China and EU Markets.
Figure 5. Time Series and Distributions of Carbon Price Returns for China and EU Markets.
Forests 16 01427 g005
Forests 16 01427 g006
Figure 6. Conditional Variance Trends of the EU and China Carbon Markets from 2017 to 2025 Using the GARCH-M(1,1) Model.
Figure 6. Conditional Variance Trends of the EU and China Carbon Markets from 2017 to 2025 Using the GARCH-M(1,1) Model.
Forests 16 01427 g006
Forests 16 01427 g007
Figure 7. Conditional Variance Trends of the EU and China Carbon Markets from 2017 to 2025 Using Static Forecast in the GARCH-M(1,1) Model.
Figure 7. Conditional Variance Trends of the EU and China Carbon Markets from 2017 to 2025 Using Static Forecast in the GARCH-M(1,1) Model.
Forests 16 01427 g007
Forests 16 01427 g008
Figure 8. Residual Analysis of the EU and China Carbon Markets from 2017 to 2025 Based on the GARCH-M(1,1) Model.
Figure 8. Residual Analysis of the EU and China Carbon Markets from 2017 to 2025 Based on the GARCH-M(1,1) Model.
Forests 16 01427 g008
Forests 16 01427 g009
Figure 9. Autocorrelation Function of Residuals for the EU and China Carbon Markets from 2017 to 2025 Using the GARCH-M(1,1) Model.
Figure 9. Autocorrelation Function of Residuals for the EU and China Carbon Markets from 2017 to 2025 Using the GARCH-M(1,1) Model.
Forests 16 01427 g009
Forests 16 01427 g010
Figure 10. Economic Value of Ecological Carbon Sinks in Qilian Mountain National Park from 2000 to 2025 in the EU and China Markets.
Figure 10. Economic Value of Ecological Carbon Sinks in Qilian Mountain National Park from 2000 to 2025 in the EU and China Markets.
Forests 16 01427 g010
Table 1. Original Carbon Storage Data for Qilian Mountain National Park from 2000 to 2020.
Table 1. Original Carbon Storage Data for Qilian Mountain National Park from 2000 to 2020.
YearCarbon Storage (×108 t)Source Reference
20005.85Liu et al. [23]
7.66Su et al. [24]
9.07Deng et al. [25]
20106.01Liu et al. [23]
7.92Su et al. [24]
9.16Deng et al. [25]
20206.02Liu et al. [23]
8.59Su et al. [24]
9.18Deng et al. [25]
Table 2. Statistical Analysis of Carbon Storage for Qilian Mountain National Park from 2000 to 2020.
Table 2. Statistical Analysis of Carbon Storage for Qilian Mountain National Park from 2000 to 2020.
YearMean Carbon Storage
( × 108 t)		Standard Deviation
( × 108 t)		95% Confidence Interval
( × 108 t)
20007.531.617.01–8.02
20107.701.597.20–8.19
20207.931.687.41–8.41
Table 3. Descriptive Statistics of Carbon Price Returns for China and EU Markets (2017–2025).
Table 3. Descriptive Statistics of Carbon Price Returns for China and EU Markets (2017–2025).
StatisticChina ReturnsEU Returns
Mean0.0011700.000362
Variance0.1210401.929812
Skewness0.0268670.001629
Kurtosis8.1294365.276023
Observations13817449
Table 4. Preliminary Tests for Carbon Price Returns.
Table 4. Preliminary Tests for Carbon Price Returns.
Test TypeStatistic (China)p-Value (China)Statistic (EU)p-Value (EU)
ADF on Original Prices−3.93600.0018−1.34590.6079
ADF on Returns−14.46190−23.27110
ARCH-LM376.808603433.32110
White Heteroskedasticity2.60830.27142472.65210
Table 5. Price Scenarios of the EU and China Carbon Markets from 2000 to 2025 Using the GARCH-M(1,1) Model.
Table 5. Price Scenarios of the EU and China Carbon Markets from 2000 to 2025 Using the GARCH-M(1,1) Model.
YearScenarioEU Price
(Mean ± Standard
Deviation)		China Price
(Mean ± Standard Deviation)
2000Low110.4 ± 0.115.0 ± 0.2
2000Medium137.5 ± 0.118.6 ± 0.2
2000High154.6 ± 0.120.2 ± 0.2
2010Low164.6 ± 0.122.2 ± 0.2
2010Medium172.2 ± 0.124.8 ± 0.2
2010High179.8 ± 0.127.4 ± 0.2
2020Low167.7 ± 0.024.3 ± 0.0
2020Medium206.9 ± 0.026.7 ± 0.0
2020High235.0 ± 0.032.8 ± 0.0
2025Low559.7 ± 0.033.2 ± 0.0
2025Medium605.9 ± 0.047.6 ± 0.0
2025High653.5 ± 0.052.5 ± 0.0
Table 6. Economic Value Assessment of Ecological Carbon Sinks in Qilian Mountain National Park from 2000 to 2025 in the EU and China Markets.
Table 6. Economic Value Assessment of Ecological Carbon Sinks in Qilian Mountain National Park from 2000 to 2025 in the EU and China Markets.
YearScenarioEU Economic Value
(×108 CNY)		China Economic Value
(×108 CNY)
2000Low831.312112.950
2000Medium1035.375140.058
2000High1164.138152.106
2010Low1267.420170.940
2010Medium1325.940190.960
2010High1384.460210.980
2020Low1329.861192.699
2020Medium1640.717211.731
2020High1863.550260.104
2025Low4438.421263.276
2025Medium4804.787377.468
2025High5182.255416.325
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sun, W.; Gao, Y.; Yang, X.; Zhang, Y. Forest Carbon Storage and Economic Valuation in Qilian Mountain National Park: Integrating Multi-Source Data and GARCH-M(1,1)-Driven Dynamic Carbon Pricing. Forests 2025, 16, 1427. https://doi.org/10.3390/f16091427

AMA Style

Sun W, Gao Y, Yang X, Zhang Y. Forest Carbon Storage and Economic Valuation in Qilian Mountain National Park: Integrating Multi-Source Data and GARCH-M(1,1)-Driven Dynamic Carbon Pricing. Forests. 2025; 16(9):1427. https://doi.org/10.3390/f16091427

Chicago/Turabian Style

Sun, Weibao, Yafang Gao, Xuemei Yang, and Yalong Zhang. 2025. "Forest Carbon Storage and Economic Valuation in Qilian Mountain National Park: Integrating Multi-Source Data and GARCH-M(1,1)-Driven Dynamic Carbon Pricing" Forests 16, no. 9: 1427. https://doi.org/10.3390/f16091427

APA Style

Sun, W., Gao, Y., Yang, X., & Zhang, Y. (2025). Forest Carbon Storage and Economic Valuation in Qilian Mountain National Park: Integrating Multi-Source Data and GARCH-M(1,1)-Driven Dynamic Carbon Pricing. Forests, 16(9), 1427. https://doi.org/10.3390/f16091427

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop