A Novel Approach for Inverting Forest Fuel Moisture Content Utilizing Multi-Source Remote Sensing and Deep Learning
Abstract
1. Introduction
2. Materials
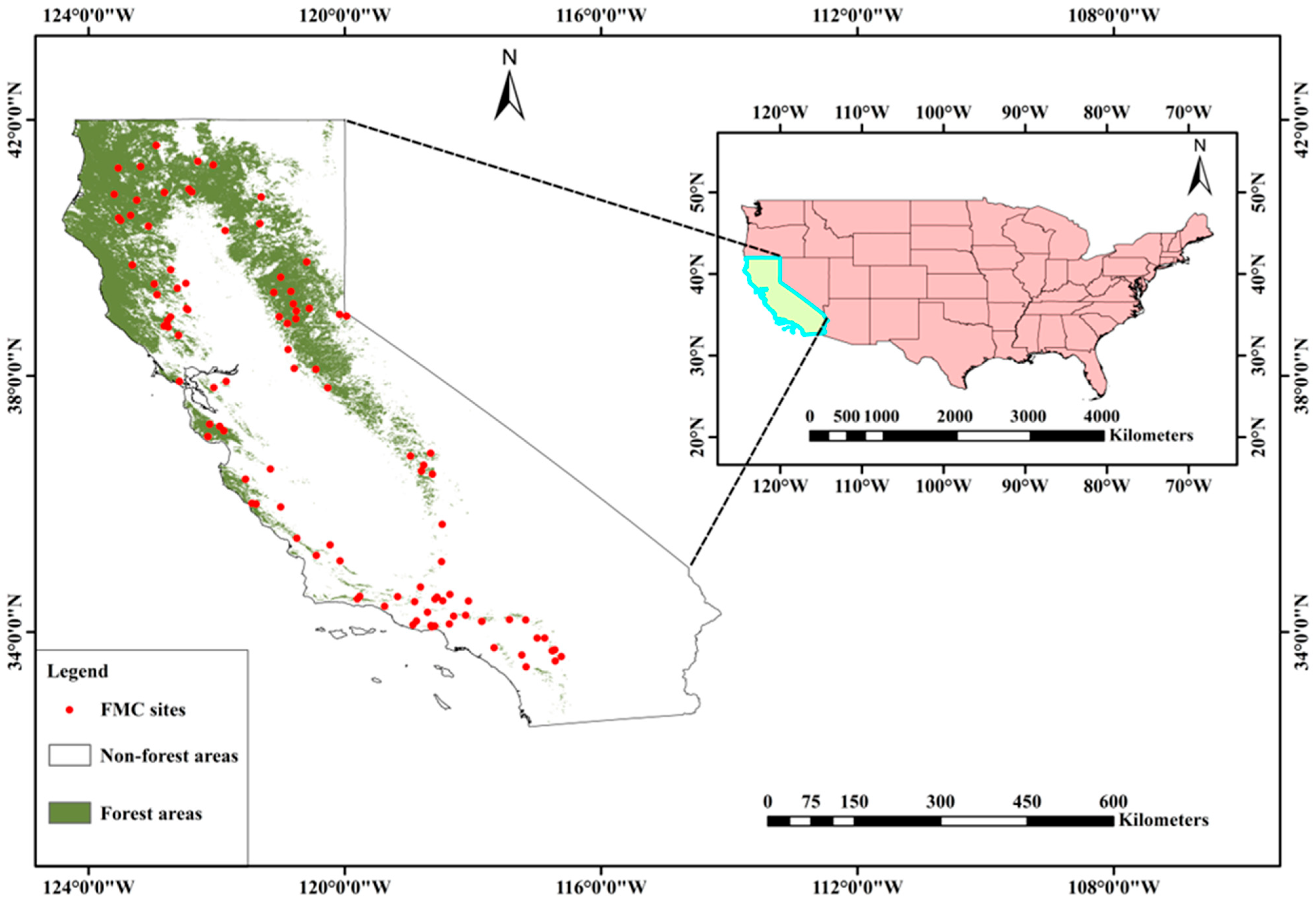
2.1. Test Site
2.2. Research Data
2.2.1. Sentinel-1 Remote Sensing Data
2.2.2. Sentinel-2 Remote Sensing Data
2.2.3. MODIS Remote Sensing Data
2.2.4. FMC Site Data
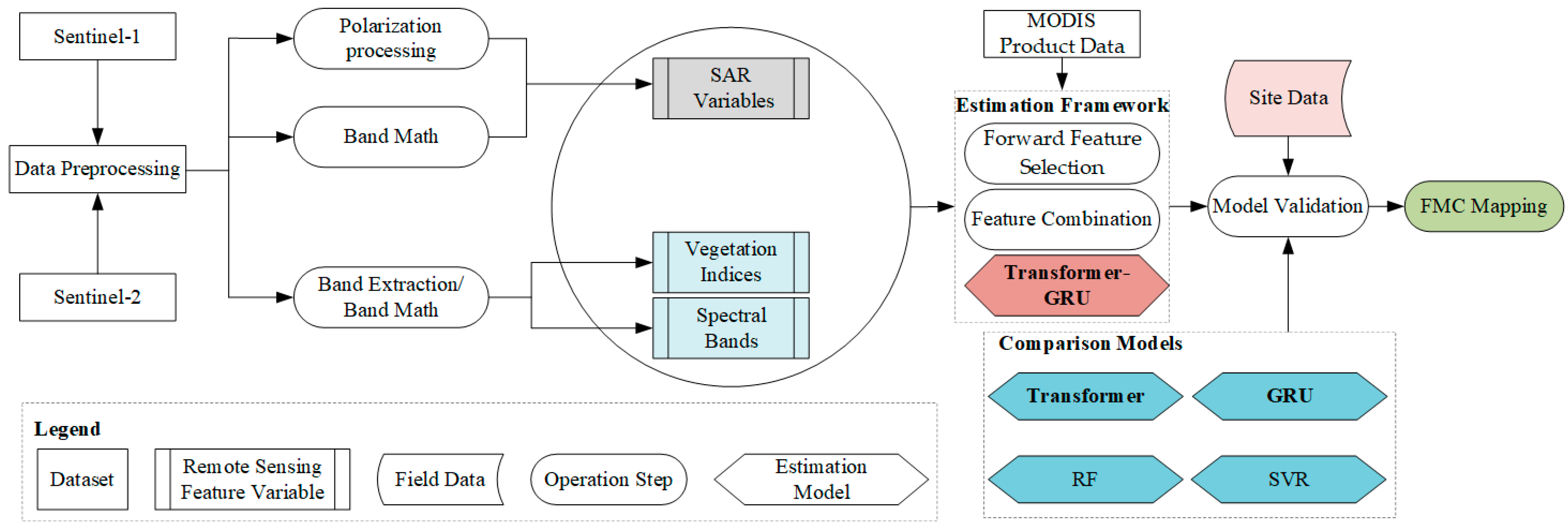
2.3. Remote Sensing Data Preprocessing
3. Methodology
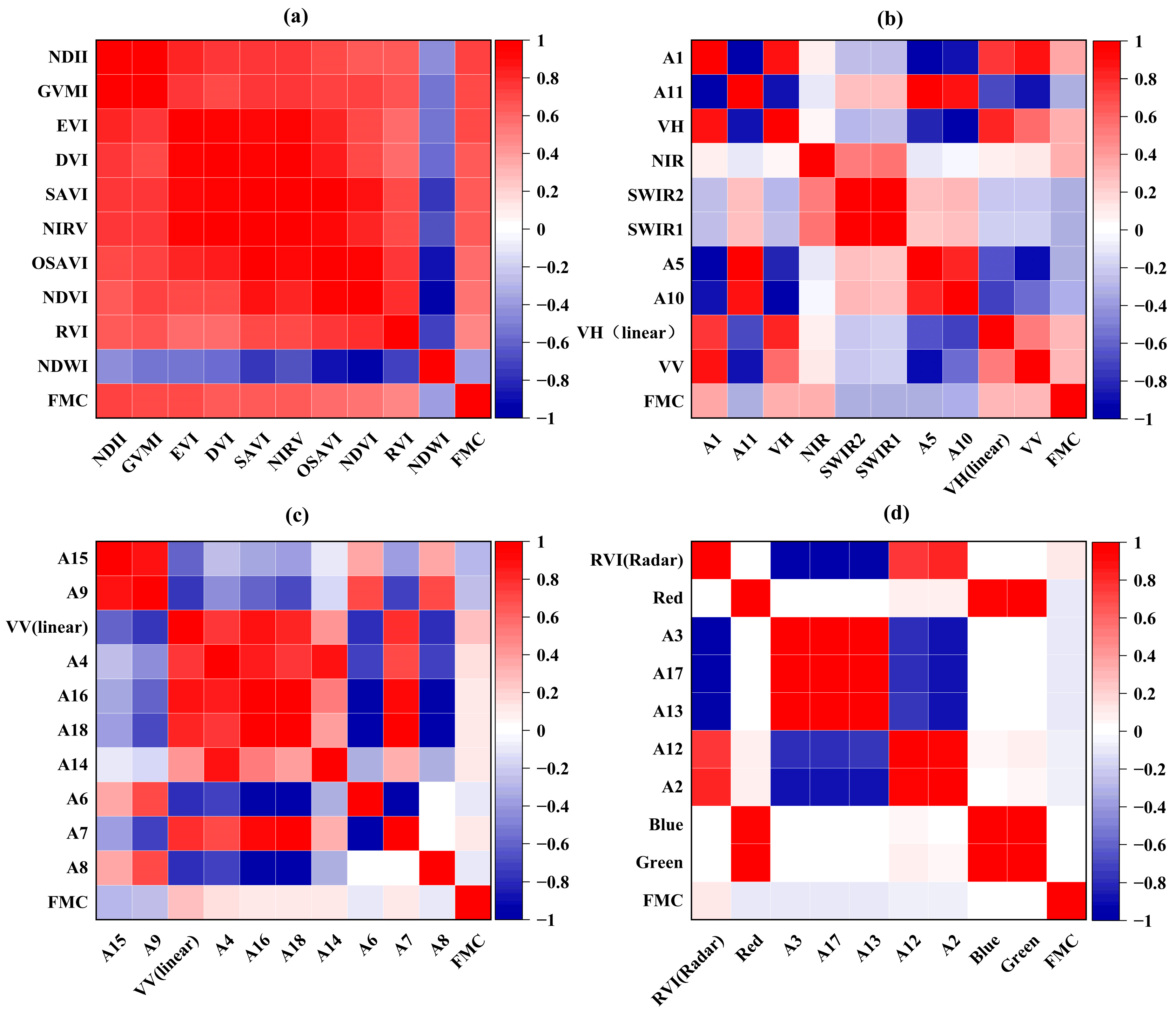
3.1. Correlation Analysis of Features Extracted from Optical and SAR Images
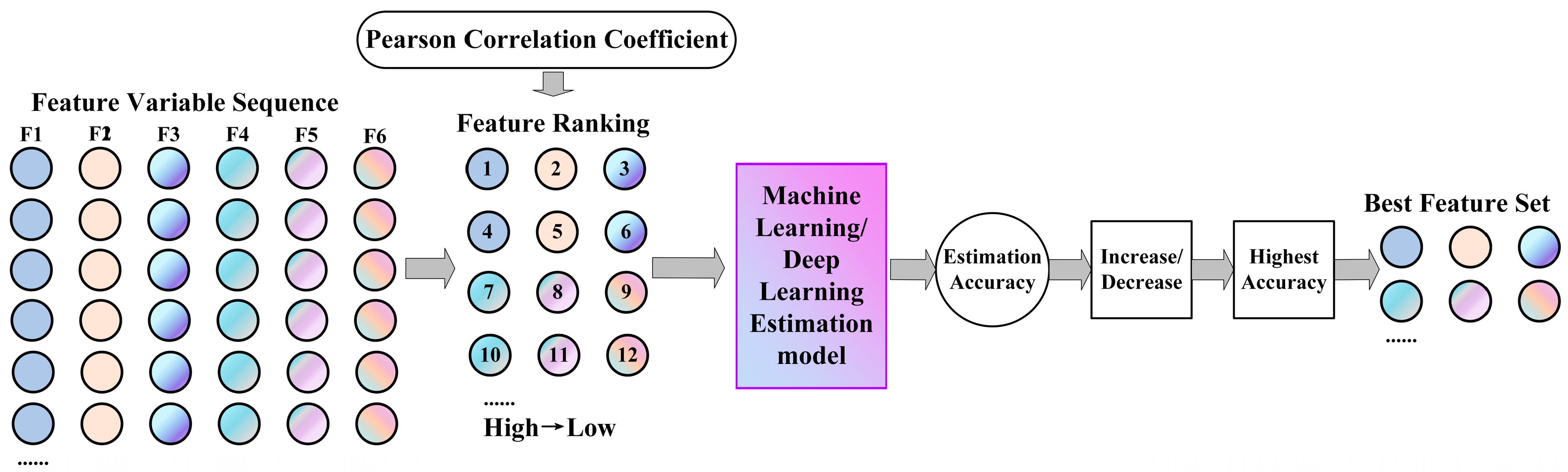
3.2. Construction of Feature Set
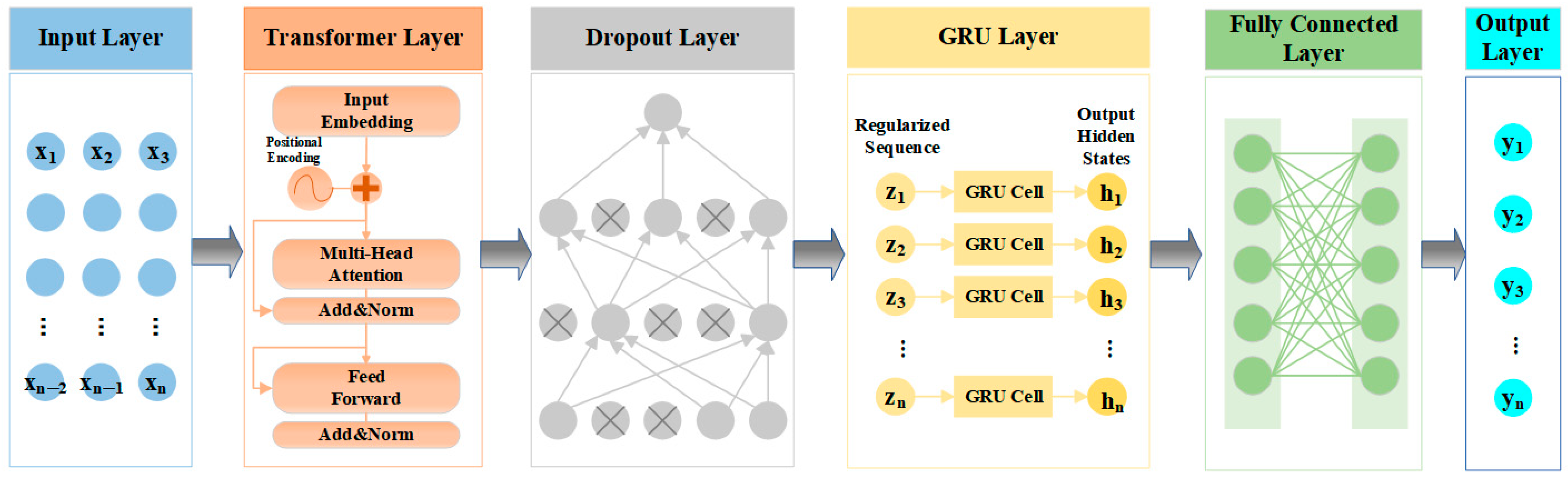
3.3. Development of Forest FMC Model
3.4. FMC Model Validation
4. Results
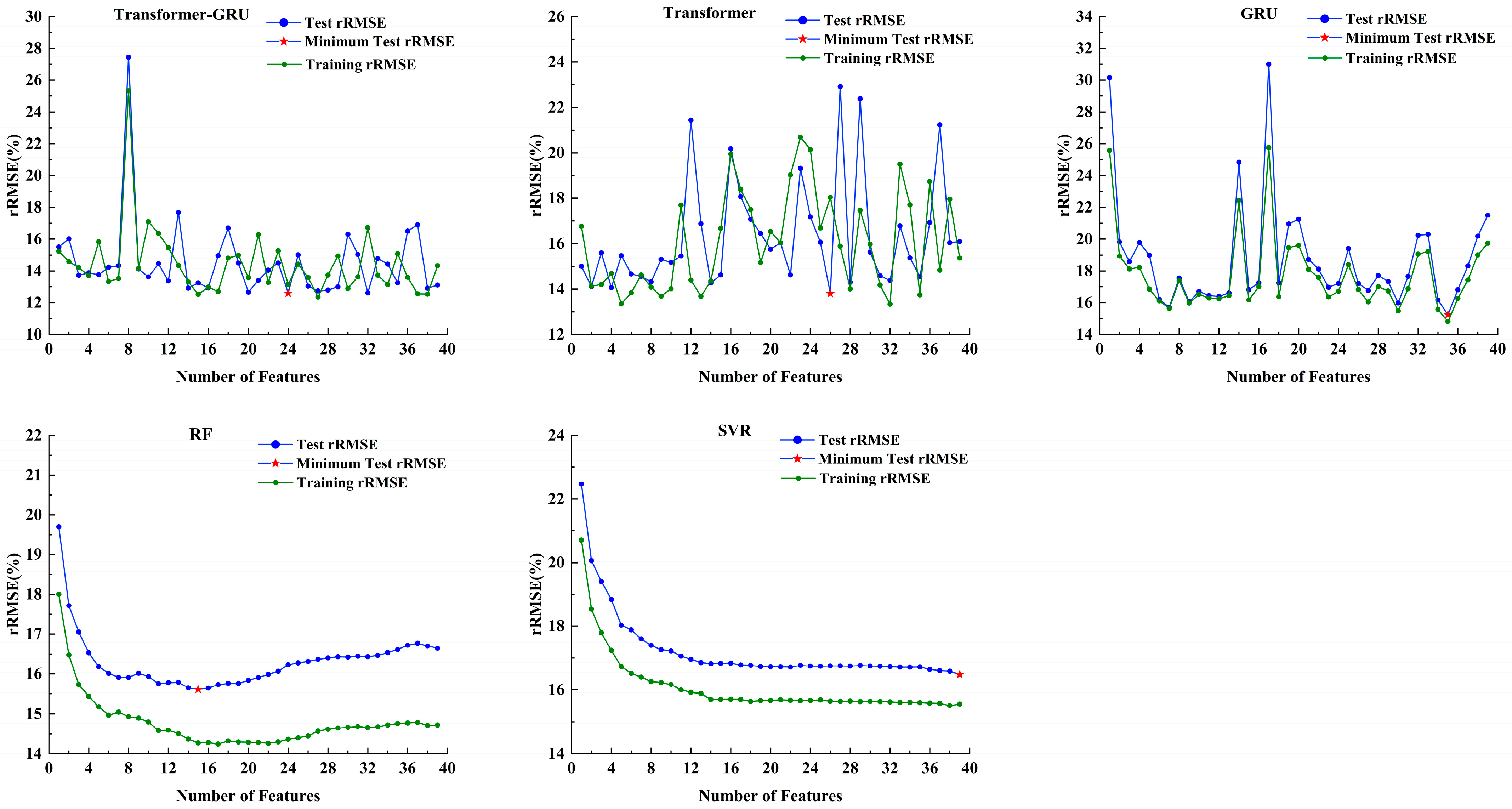
4.1. Model Performance Using Different Feature Groups in FMC Prediction
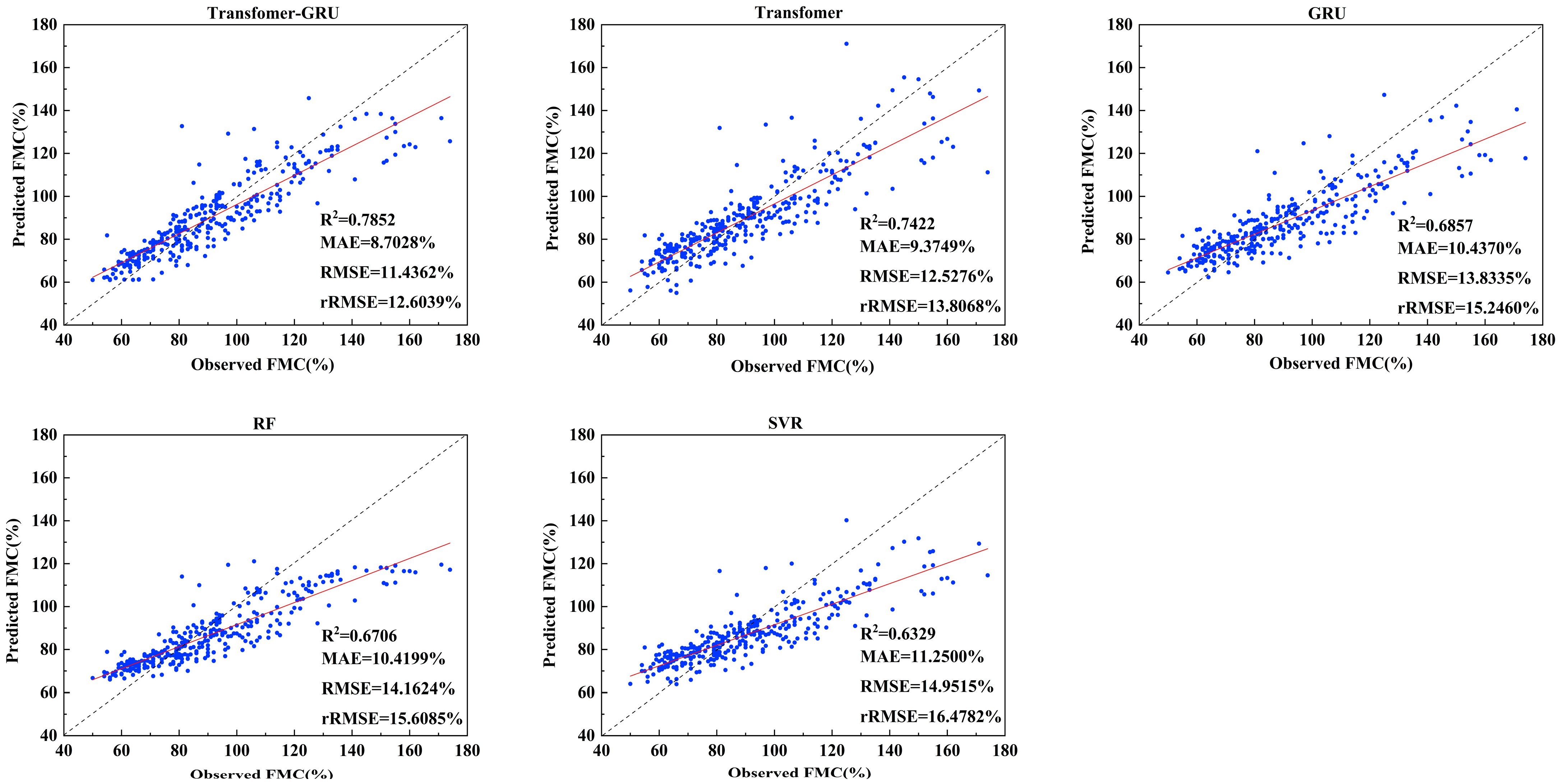
4.2. Model Performance Using Different Methods in FMC Prediction
4.3. Statistical Significance Test of Model Performance
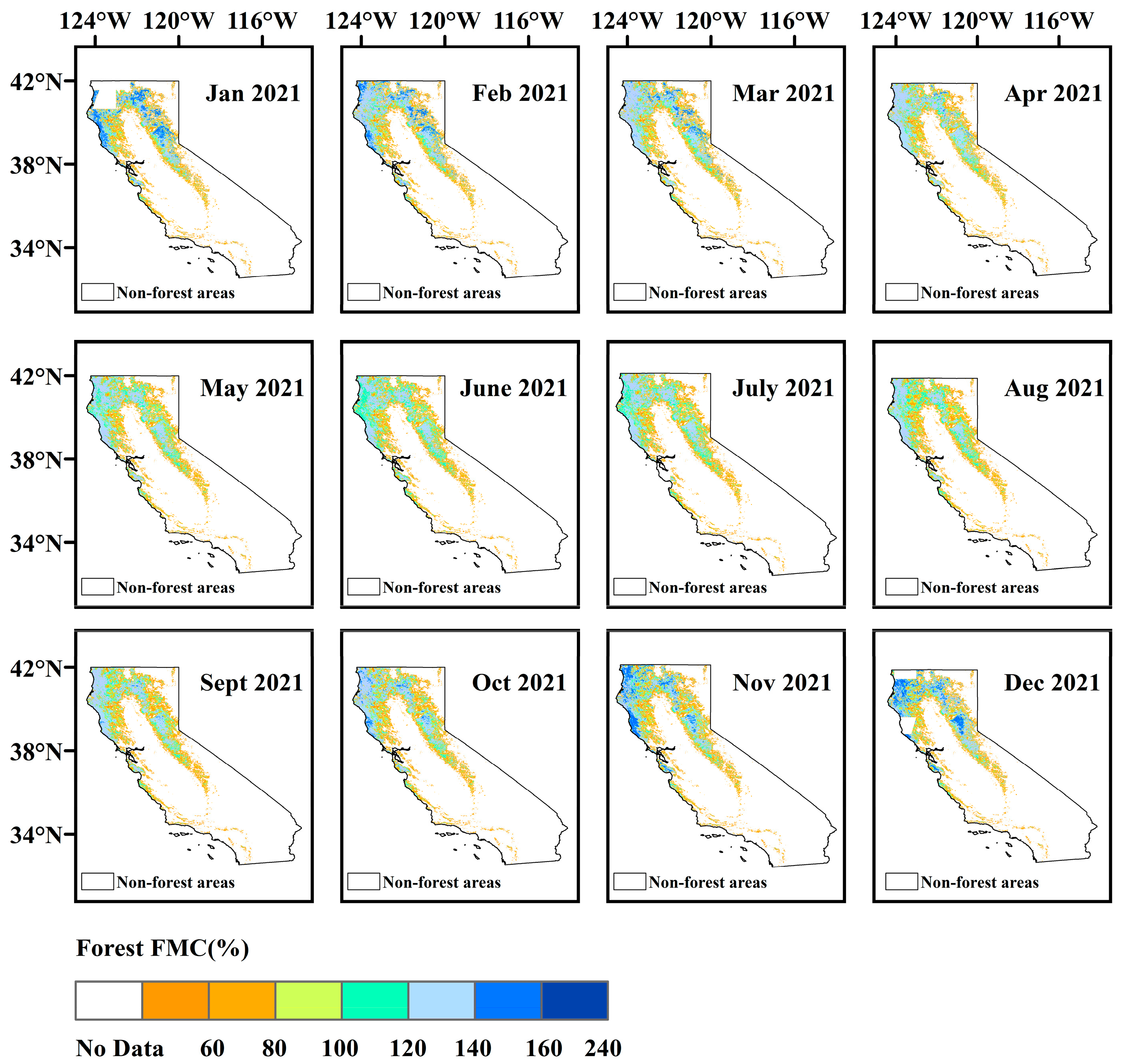
4.4. Spatiotemporal Distribution Pattern of Forest FMC Inversion
5. Discussion
5.1. Multi-Source Remote Sensing Data and Deep Learning in Forest FMC Inversion
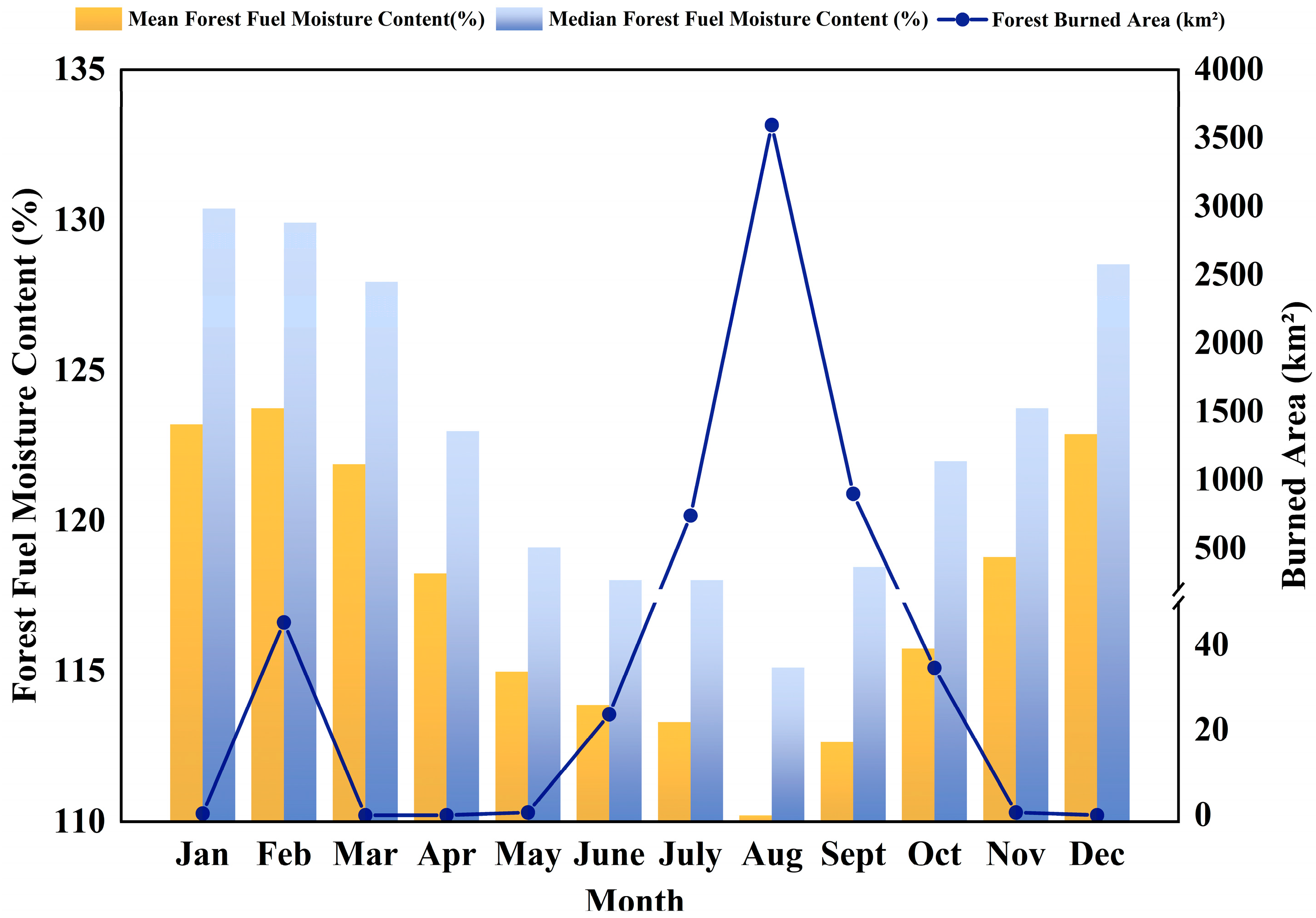
5.2. Correlation Analysis Between Forest Fires and Inversion FMC
5.3. Limitations and Prospects
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pyne, S.J.; Andrews, P.L.; Laven, R.D. Introduction to Wildland Fire; John Wiley and Sons: New York, NY, USA, 1996; ISBN 978-0-471-54913-0. [Google Scholar]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt, E.R.; Danson, F.M.; Qi, Y.; Jurdao, S. A Global Review of Remote Sensing of Live Fuel Moisture Content for Fire Danger Assessment: Moving towards Operational Products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Paltridge, G.W.; Barber, J. Monitoring Grassland Dryness and Fire Potential in Australia with NOAA/AVHRR Data. Remote Sens. Environ. 1988, 25, 381–394. [Google Scholar] [CrossRef]
- Yang, K.; Tang, B.-H.; Fu, W.; Zhou, W.; Fu, Z.; Fan, D. Estimation of Forest Canopy Fuel Moisture Content in Dali Prefecture by Combining Vegetation Indices and Canopy Radiative Transfer Models from MODIS Data. Forests 2024, 15, 614. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Yebra, M.; Yin, C.; Liao, Z.; Li, X. Retrieval of Forest Fuel Moisture Content Using a Coupled Radiative Transfer Model. Environ. Model. Softw. 2017, 95, 290–302. [Google Scholar] [CrossRef]
- Rodriguez-Jimenez, F.; Lorenzo, H.; Novo, A.; Acuña-Alonso, C.; Alvarez, X. Modelling of Live Fuel Moisture Content in Different Vegetation Scenarios during Dry Periods Using Meteorological Data and Spectral Indices. For. Ecol. Manag. 2023, 546, 121378. [Google Scholar] [CrossRef]
- Quan, X.; Chen, R.; Yebra, M.; Riaño, D.; de Dios, V.R.; Li, X.; He, B.; Nolan, R.H.; Griebel, A.; Boer, M.M. Sub-Daily Live Fuel Moisture Content Estimation from Himawari-8 Data. Remote Sens. Environ. 2024, 308, 114170. [Google Scholar] [CrossRef]
- Al-Moustafa, T.; Armitage, R.P.; Danson, F.M. Mapping Fuel Moisture Content in Upland Vegetation Using Airborne Hyperspectral Imagery. Remote Sens. Environ. 2012, 127, 74–83. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil Moisture Retrieval from Active Spaceborne Microwave Observations: An Evaluation of Current Techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Wigneron, J.-P.; Walker, J.; Karbou, F.; Chanzy, A.; Albergel, C. Sensitivity of Passive Microwave Observations to Soil Moisture and Vegetation Water Content: L-Band to W-Band. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1190–1199. [Google Scholar] [CrossRef]
- Leblon, B.; Kasischke, E.; Alexander, M.; Doyle, M.; Abbott, M. Fire Danger Monitoring Using ERS-1 SAR Images in the Case of Northern Boreal Forests. Nat. Hazards 2002, 27, 231–255. [Google Scholar] [CrossRef]
- Tanase, M.A.; Panciera, R.; Lowell, K.; Aponte, C. Monitoring Live Fuel Moisture in Semiarid Environments Using L-Band Radar Data. Int. J. Wildland Fire 2015, 24, 560–572. [Google Scholar] [CrossRef]
- Heffernan, S.; Strimbu, B.M. Estimation of Surface Canopy Water in Pacific Northwest Forests by Fusing Radar, Lidar, and Meteorological Data. Forests 2021, 12, 339. [Google Scholar] [CrossRef]
- Wang, L.; Quan, X.; He, B.; Yebra, M.; Xing, M.; Liu, X. Assessment of the Dual Polarimetric Sentinel-1A Data for Forest Fuel Moisture Content Estimation. Remote Sens. 2019, 11, 1568. [Google Scholar] [CrossRef]
- McCandless, T.C.; Kosovic, B.; Petzke, W. Enhancing Wildfire Spread Modelling by Building a Gridded Fuel Moisture Content Product with Machine Learning. Mach. Learn. Sci. Technol. 2020, 1, 035010. [Google Scholar] [CrossRef]
- Bu, L.; Lai, Q.; Qing, S.; Bao, Y.; Liu, X.; Na, Q.; Li, Y. Grassland Biomass Inversion Based on a Random Forest Algorithm and Drought Risk Assessment. Remote Sens. 2022, 14, 5745. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground Biomass Estimates of Tropical Mangrove Forest Using Sentinel-1 SAR Coherence Data-The Superiority of Deep Learning over a Semi-Empirical Model. Comput. Geosci. 2021, 150, 104737. [Google Scholar] [CrossRef]
- Su, H.; Shen, W.; Wang, J.; Ali, A.; Li, M. Machine Learning and Geostatistical Approaches for Estimating Aboveground Biomass in Chinese Subtropical Forests. For. Ecosyst. 2020, 7, 64. [Google Scholar] [CrossRef]
- Zhu, L.; Webb, G.I.; Yebra, M.; Scortechini, G.; Miller, L.; Petitjean, F. Live Fuel Moisture Content Estimation from MODIS: A Deep Learning Approach. ISPRS J. Photogramm. Remote Sens. 2021, 179, 81–91. [Google Scholar] [CrossRef]
- Perello, N.; Trucchia, A.; D’Andrea, M.; Degli Esposti, S.; Fiorucci, P.; Gollini, A.; Negro, D. An Adaptable Dead Fuel Moisture Model for Various Fuel Types and Temporal Scales Tailored for Wildfire Danger Assessment. Environ. Model. Softw. 2025, 183, 106254. [Google Scholar] [CrossRef]
- Miller, L.; Zhu, L.; Yebra, M.; Rüdiger, C.; Webb, G.I. Projecting Live Fuel Moisture Content via Deep Learning. Int. J. Wildland Fire 2023, 32, 709–727. [Google Scholar] [CrossRef]
- Wen, H.; Guo, Q.; Zeng, Y.; Wu, Z.; Sun, Z. Study on Forest Fire Risk in Conghua District of Guangzhou City Based on Multi-Source Data. Nat. Hazards 2022, 114, 3163–3183. [Google Scholar] [CrossRef]
- Xie, J.; Qi, T.; Hu, W.; Huang, H.; Chen, B.; Zhang, J. Retrieval of Live Fuel Moisture Content Based on Multi-Source Remote Sensing Data and Ensemble Deep Learning Model. Remote Sens. 2022, 14, 4378. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 2017 Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Gillioz, A.; Casas, J.; Mugellini, E.; Abou Khaled, O. Overview of the Transformer-Based Models for NLP Tasks. In Proceedings of the 2020 15th Conference on Computer Science and Information Systems (FedCSIS), Sofia, Bulgaria, 6–9 September 2020; IEEE: Piscataway, NJ, USA; pp. 179–183. [Google Scholar]
- Keeley, J.E.; Syphard, A.D. Twenty-First Century California, USA, Wildfires: Fuel-Dominated vs. Wind-Dominated Fires. Fire Ecol. 2019, 15, 24. [Google Scholar] [CrossRef]
- Brown, P.T.; Hanley, H.; Mahesh, A.; Reed, C.; Strenfel, S.J.; Davis, S.J.; Kochanski, A.K.; Clements, C.B. Climate Warming Increases Extreme Daily Wildfire Growth Risk in California. Nature 2023, 621, 760–766. [Google Scholar] [CrossRef]
- Ma, C.; Johansen, K.; McCabe, M.F. Monitoring Irrigation Events and Crop Dynamics Using Sentinel-1 and Sentinel-2 Time Series. Remote Sens. 2022, 14, 1205. [Google Scholar] [CrossRef]
- Phung, H.-P.; Lam-Dao, N.; Nguyen-Huy, T.; Le-Toan, T.; Apan, A.A. Monitoring Rice Growth Status in the Mekong Delta, Vietnam Using Multitemporal Sentinel-1 Data. J. Appl. Remote Sens. 2020, 14, 014518. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Zheng, H.; Du, P.; Chen, J.; Xia, J.; Li, E.; Xu, Z.; Li, X.; Yokoya, N. Performance Evaluation of Downscaling Sentinel-2 Imagery for Land Use and Land Cover Classification by Spectral-Spatial Features. Remote Sens. 2017, 9, 1274. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product. Usgs Rest. Va Usa 2018, 1, 18. [Google Scholar]
- Yebra, M.; Quan, X.; Riaño, D.; Larraondo, P.R.; Van Dijk, A.I.; Cary, G.J. A Fuel Moisture Content and Flammability Monitoring Methodology for Continental Australia Based on Optical Remote Sensing. Remote Sens. Environ. 2018, 212, 260–272. [Google Scholar] [CrossRef]
- Giglio, L.; Boschetti, L.; Roy, D.P.; Humber, M.L.; Justice, C.O. The Collection 6 MODIS Burned Area Mapping Algorithm and Product. Remote Sens. Environ. 2018, 217, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Long, J.; Zheng, H.; Liu, Z.; Zhang, T.; Wang, Q. Mapping Growing Stem Volume Using Dual-Polarization GaoFen-3 SAR Images in Evergreen Coniferous Forests. Remote Sens. 2023, 15, 2253. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy Near-Infrared Reflectance and Terrestrial Photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep Learning Based Retrieval of Forest Aboveground Biomass from Combined LiDAR and Landsat 8 Data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]
- Long, J.; Lin, H.; Wang, G.; Sun, H.; Yan, E. Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-Based Multivariate Method and Quad-Polarimetric SAR Images. Remote Sens. 2019, 11, 1872. [Google Scholar] [CrossRef]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and Gru Neural Network Performance Comparison Study: Taking Yelp Review Dataset as an Example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; IEEE: Piscataway, NJ, USA; pp. 98–101. [Google Scholar]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A Practical Tutorial on the Use of Nonparametric Statistical Tests as a Methodology for Comparing Evolutionary and Swarm Intelligence Algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Armstrong, R.A. When to Use the BOnferroni Correction. Ophthalmic Physiol. Opt. 2014, 34, 502–508. [Google Scholar] [CrossRef]
- Seager, R.; Cane, M.; Henderson, N.; Lee, D.-E.; Abernathey, R.; Zhang, H. Strengthening Tropical Pacific Zonal Sea Surface Temperature Gradient Consistent with Rising Greenhouse Gases. Nat. Clim. Change 2019, 9, 517–522. [Google Scholar] [CrossRef]
- Underwood, E.C.; Hollander, A.D.; Flint, L.E.; Flint, A.L.; Safford, H.D. Climate Change Impacts on Hydrological Services in Southern California. Environ. Res. Lett. 2018, 13, 124019. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Barbero, R.; Nauslar, N.J. Diagnosing Santa Ana Winds in Southern California with Synoptic-Scale Analysis. Weather Forecast. 2013, 28, 704–710. [Google Scholar] [CrossRef]
- Polade, S.D.; Gershunov, A.; Cayan, D.R.; Dettinger, M.D.; Pierce, D.W. Precipitation in a Warming World: Assessing Projected Hydro-Climate Changes in California and Other Mediterranean Climate Regions. Sci. Rep. 2017, 7, 10783. [Google Scholar] [CrossRef]
- Williams, A.P.; Abatzoglou, J.T.; Gershunov, A.; Guzman-Morales, J.; Bishop, D.A.; Balch, J.K.; Lettenmaier, D.P. Observed Impacts of Anthropogenic Climate Change on Wildfire in California. Earths Future 2019, 7, 892–910. [Google Scholar] [CrossRef]
- Maloney, E.D.; Camargo, S.J.; Chang, E.; Colle, B.; Fu, R.; Geil, K.L.; Hu, Q.; Jiang, X.; Johnson, N.; Karnauskas, K.B. North American Climate in CMIP5 Experiments: Part III: Assessment of Twenty-First-Century Projections. J. Clim. 2014, 27, 2230–2270. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.-M.; Gerber, J.S.; Reddy, V.R. Random Forests for Global and Regional Crop Yield Predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wang, W.; Bai, L.; Chen, N.; Wang, W. Estimation of Aboveground Vegetation Biomass Based on Landsat-8 OLI Satellite Images in the Guanzhong Basin, China. Int. J. Remote Sens. 2019, 40, 3927–3947. [Google Scholar] [CrossRef]
- Taylor, A.H.; Harris, L.B.; Skinner, C.N. Severity Patterns of the 2021 Dixie Fire Exemplify the Need to Increase Low-Severity Fire Treatments in California’s Forests. Environ. Res. Lett. 2022, 17, 071002. [Google Scholar] [CrossRef]
- Araza, A.; De Bruin, S.; Herold, M.; Quegan, S.; Labriere, N.; Rodriguez-Veiga, P.; Avitabile, V.; Santoro, M.; Mitchard, E.T.; Ryan, C.M. A Comprehensive Framework for Assessing the Accuracy and Uncertainty of Global Above-Ground Biomass Maps. Remote Sens. Environ. 2022, 272, 112917. [Google Scholar] [CrossRef]

| Serial Number | Vegetation Type | Forest FMC (%) | Mean (%) | Standard Deviation (%) |
|---|---|---|---|---|
| 1 | Chamise | 42.00–144.00 | 79.69 | 72.12 |
| 2 | Douglas-Fir | 91.00–171.00 | 132.87 | 56.57 |
| 3 | Fir | 92.00–174.00 | 123.5 | 57.98 |
| 4 | Mahogany | 75.00–83.00 | 73.64 | 5.66 |
| 5 | Oak | 58.00–152.00 | 90.15 | 66.47 |
| 6 | Pine | 76.00–151.00 | 112.84 | 53.03 |
| 7 | Tanoak | 90.88–104.66 | 96.13 | 9.75 |
| Serial Number | Feature Name | Calculation Formula | Pearson Correlation Coefficient |
|---|---|---|---|
| 1 | VV (linear) | 0.27 | |
| 2 | VH (linear) | 0.30 | |
| 3 | VV | dB | 0.29 |
| 4 | VH | dB | 0.33 |
| 5 | A1 | 0.35 | |
| 6 | A2 | −0.07 | |
| 7 | A3 | −0.11 | |
| 8 | A4 | 0.15 | |
| 9 | A5 | −0.33 | |
| 10 | A6 | −0.12 | |
| 11 | A7 | −0.12 | |
| 12 | A8 | 0.12 | |
| 13 | A9 | (VV(dB))2 | −0.28 |
| 14 | A10 | (VH(dB))2 | −0.32 |
| 15 | A11 | −0.34 | |
| 16 | A12 | −0.08 | |
| 17 | A13 | −0.09 | |
| 18 | A14 | 0.12 | |
| 19 | A15 | −0.29 | |
| 20 | A16 | 0.14 | |
| 21 | A17 | −0.11 | |
| 22 | A18 | −0.13 | |
| 23 | RVI(Radar) | 0.12 |
| Serial Number | Feature Name | Calculation Formula | Pearson Correlation Coefficient |
|---|---|---|---|
| 1 | Blue | B(Band 2) | 0.04 |
| 2 | Green | G(Band 3) | 0.01 |
| 3 | Red | R(Band 4) | −0.12 |
| 4 | NIR | Band 8 | 0.33 |
| 5 | SWIR1 | Band 11 | −0.33 |
| 6 | SWIR2 | Band 12 | −0.33 |
| 7 | RVI | 0.48 | |
| 8 | NDVI | 0.54 | |
| 9 | EVI | 0.70 | |
| 10 | DVI | 0.65 | |
| 11 | NDII | 0.74 | |
| 12 | NDWI | −0.37 | |
| 13 | NIRV | 0.64 | |
| 14 | GVMI | 0.71 | |
| 15 | SAVI | 0.65 | |
| 16 | OSAVI | 0.58 |
| Model | Number of Features | R2 | MAE (%) | RMSE (%) | rRMSE (%) |
|---|---|---|---|---|---|
| SVR | 39 | 0.63 | 11.25 | 14.95 | 16.48 |
| 38 | 0.63 | 11.34 | 15.05 | 16.58 | |
| 37 | 0.63 | 11.37 | 15.06 | 16.60 | |
| RF | 15 | 0.67 | 10.42 | 14.16 | 15.61 |
| 16 | 0.67 | 10.46 | 14.19 | 15.64 | |
| 14 | 0.67 | 10.50 | 14.20 | 15.65 | |
| GRU | 35 | 0.69 | 10.44 | 13.83 | 15.25 |
| 7 | 0.67 | 10.97 | 14.24 | 15.70 | |
| 30 | 0.65 | 10.90 | 14.50 | 15.98 | |
| Transformer | 26 | 0.74 | 9.37 | 12.53 | 13.81 |
| 4 | 0.73 | 9.12 | 12.76 | 14.06 | |
| 2 | 0.73 | 9.42 | 12.80 | 14.11 | |
| Transformer-GRU | 24 | 0.79 | 8.70 | 11.44 | 12.60 |
| 32 | 0.78 | 8.60 | 11.46 | 12.62 | |
| 20 | 0.78 | 8.90 | 11.49 | 12.66 |
| Model | Mean Rank |
|---|---|
| SVR | 3.55 |
| RF | 2.93 |
| GRU | 3.18 |
| Transformer | 2.81 |
| Transformer-GRU | 2.54 |
| Model Comparison | Bonferroni-Adjusted p-Value | Significance |
|---|---|---|
| Transformer-GRU vs. SVR | 2.38 × 10−13 | Significant |
| Transformer-GRU vs. RF | 8.31 × 10−8 | Significant |
| Transformer-GRU vs. GRU | 2.13 × 10−8 | Significant |
| Transformer-GRU vs. Transformer | 3.26 × 10−4 | Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhou, C.; Zhang, J.; Li, Y.; Chen, Z.; Luo, Y. A Novel Approach for Inverting Forest Fuel Moisture Content Utilizing Multi-Source Remote Sensing and Deep Learning. Forests 2025, 16, 1423. https://doi.org/10.3390/f16091423
Wang W, Zhou C, Zhang J, Li Y, Chen Z, Luo Y. A Novel Approach for Inverting Forest Fuel Moisture Content Utilizing Multi-Source Remote Sensing and Deep Learning. Forests. 2025; 16(9):1423. https://doi.org/10.3390/f16091423
Chicago/Turabian StyleWang, Wenjun, Cui Zhou, Junxiang Zhang, Yuanzong Li, Zhenyu Chen, and Yongfeng Luo. 2025. "A Novel Approach for Inverting Forest Fuel Moisture Content Utilizing Multi-Source Remote Sensing and Deep Learning" Forests 16, no. 9: 1423. https://doi.org/10.3390/f16091423
APA StyleWang, W., Zhou, C., Zhang, J., Li, Y., Chen, Z., & Luo, Y. (2025). A Novel Approach for Inverting Forest Fuel Moisture Content Utilizing Multi-Source Remote Sensing and Deep Learning. Forests, 16(9), 1423. https://doi.org/10.3390/f16091423






