Assessing the Height Gain Trajectory of White Spruce and Hybrid Spruce Provenances in Canadian Boreal and Hemiboreal Forests †
Abstract
1. Introduction
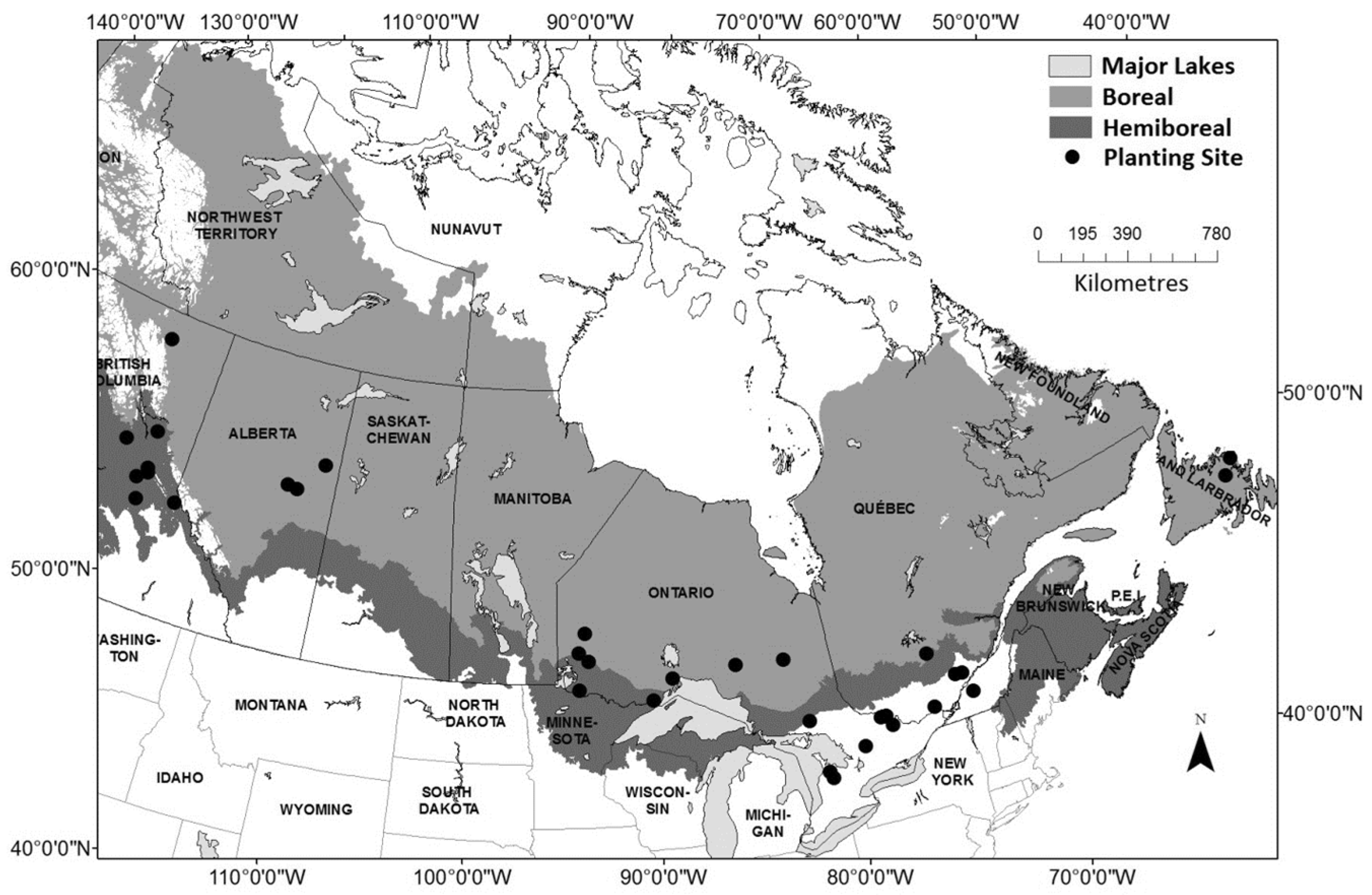
2. Materials and Methods
2.1. Meta-Data and Height Trajectories
2.2. Effects of Age and Definition of Top Performers
2.3. Gain Trajectory Model
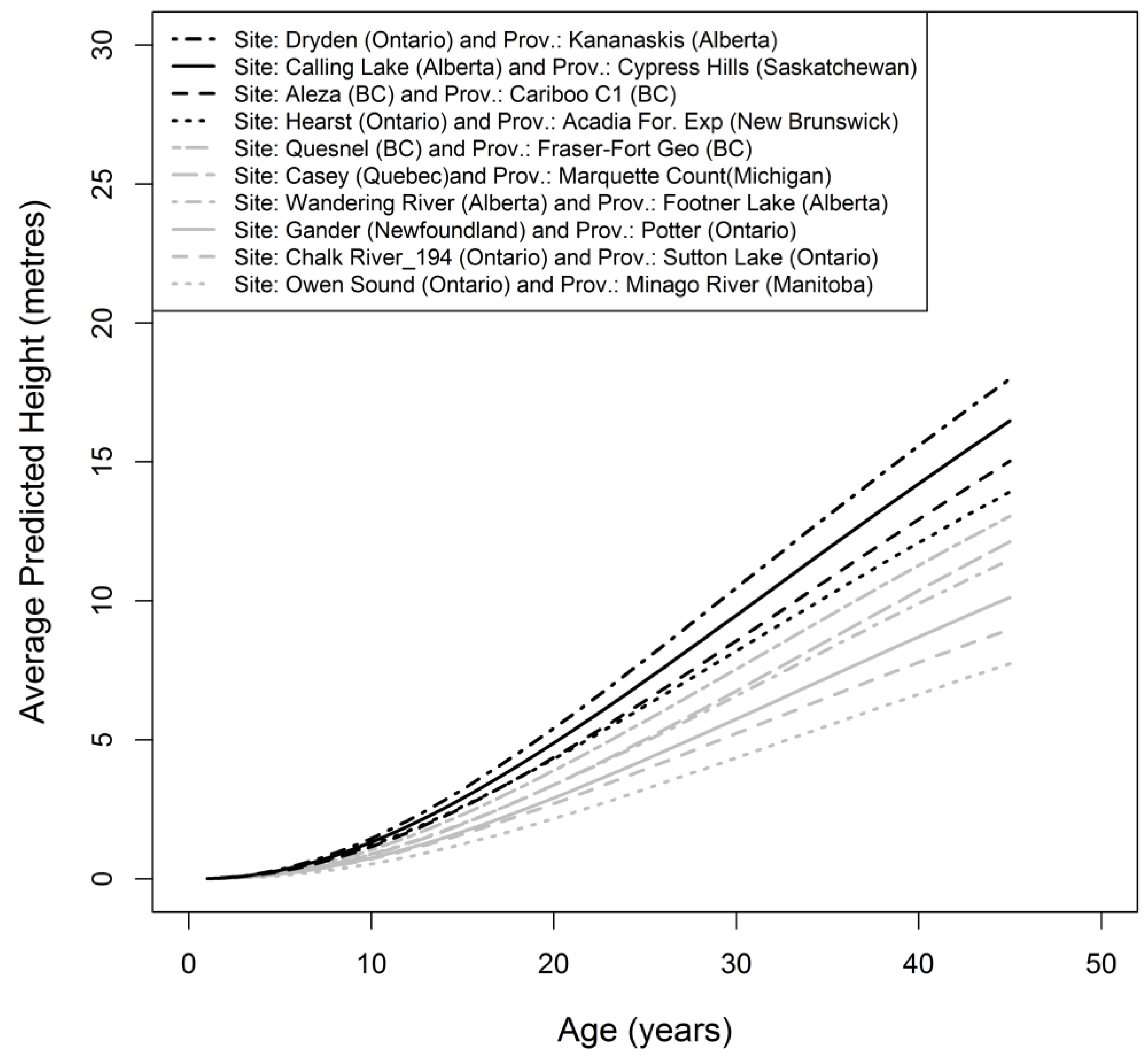
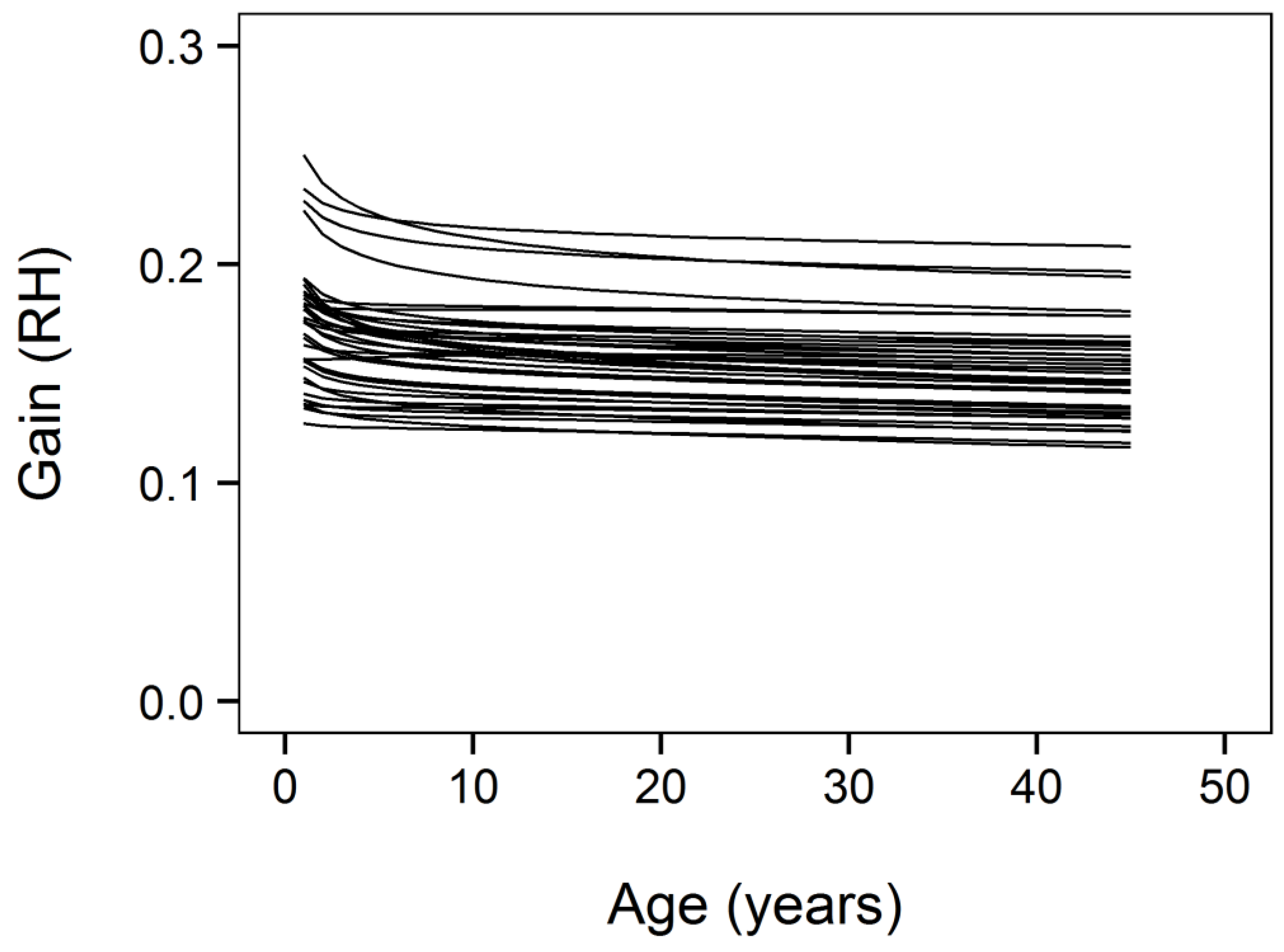
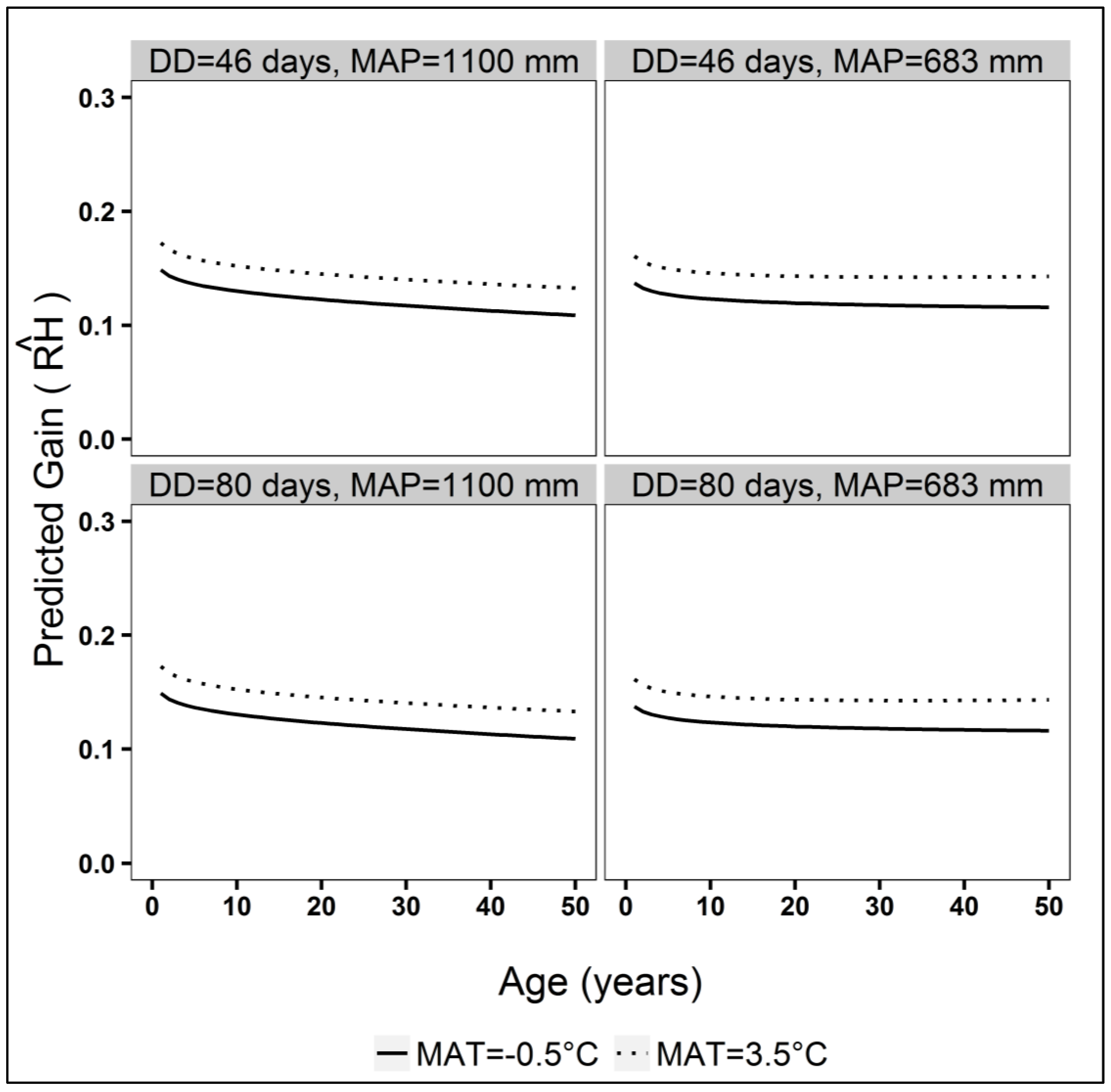
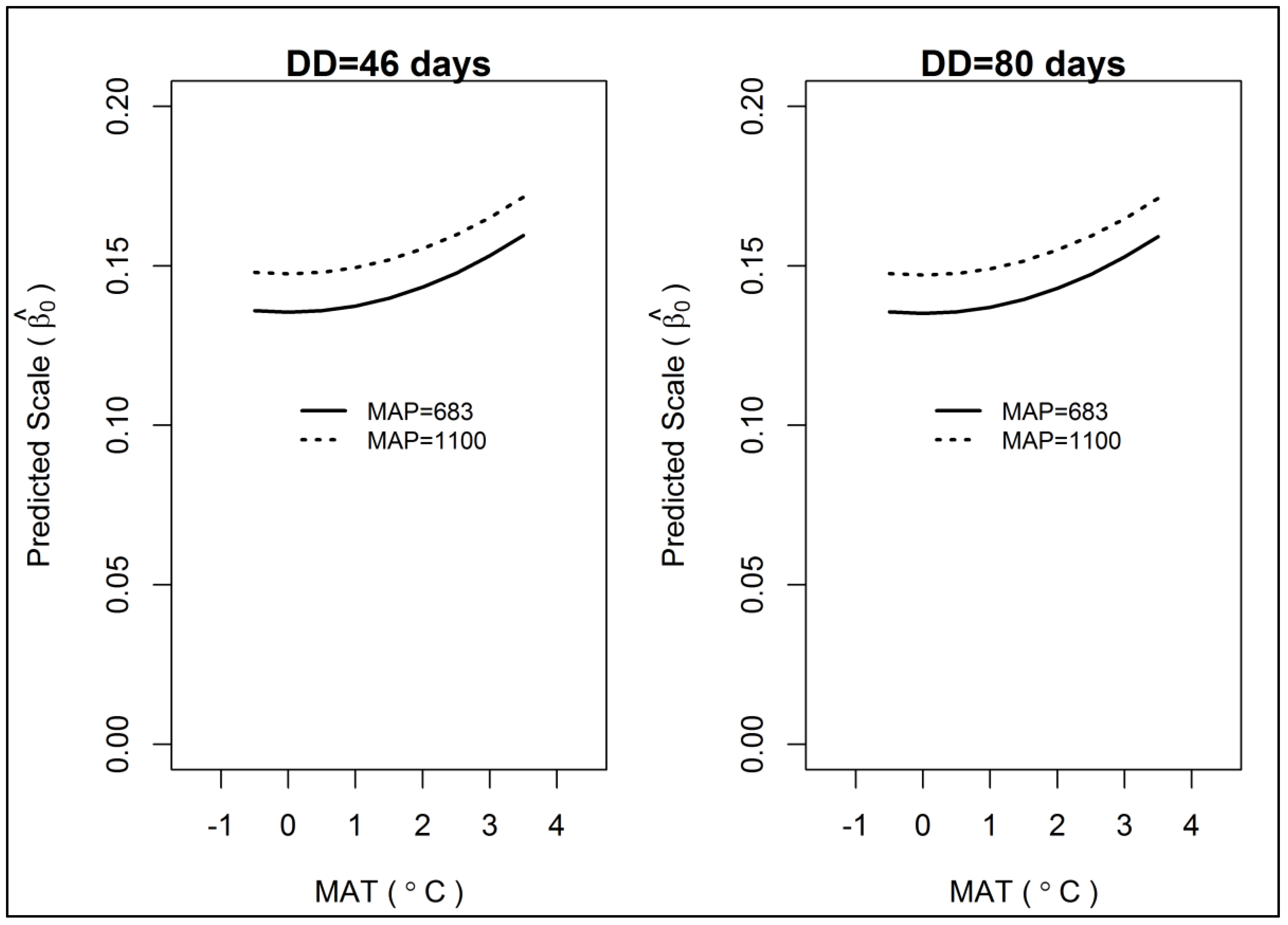
3. Results
3.1. Gain Definition Sensitivity Analysis
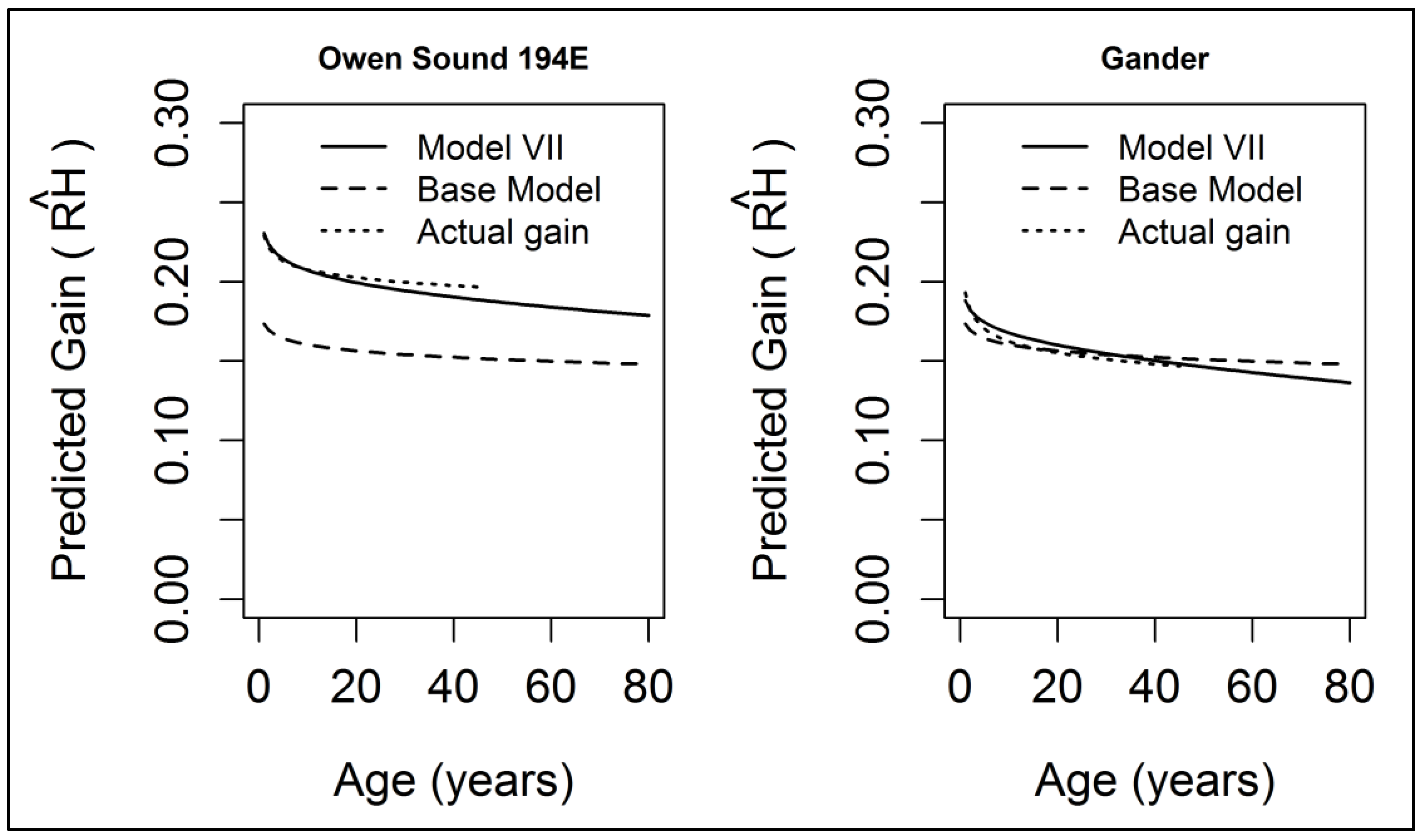
3.2. Gain Trajectory Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fins, L.; Friedman, S.T.; Brotschol, J.V. Handbook of Quantitative Forest Genetics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; 403p. [Google Scholar]
- Zobel, B.; Talbert, J. Applied Forest Tree Improvement; J. Wiley & Sons: New York, NY, USA, 1984; 505p. [Google Scholar]
- White, T.L.; Adams, W.T.; Neale, D.B. Forest Genetics; CABI Publishing: Cambridge, MA, USA, 2007. [Google Scholar]
- Grattapaglia, D. Twelve Years into Genomic Selection in Forest Trees: Climbing the Slope of Enlightenment of Marker Assisted Tree Breeding. Forests 2022, 13, 1554. [Google Scholar] [CrossRef]
- Lebedev, V.G.; Lebedeva, T.N.; Shestibratov, K.A. Genomic Selection for Forest Tree Improvement: Methods, Achievements and Perspectives. Forests 2020, 11, 1190. [Google Scholar] [CrossRef]
- Cappa, E.P.; Chen, C.; Klutsch, J.G.; Sebastian-Azcona, J.; Ratcliffe, B.; Wei, X.; Da Ros, L.; Liu, Y.; Bhumireddy, S.R.; Benowicz, A.; et al. Revealing stable SNPs and genomic prediction insights across environments enhance breeding strategies of productivity, defense, and climate-adaptability traits in white spruce. Heredity 2025, 134, 186–199. [Google Scholar] [CrossRef]
- Cappa, E.P.; Klutsch, J.G.; Sebastian-Azcona, J.; Ratcliffe, B.; Wei, X.; Da Ros, L.; Liu, Y.; Chen, C.; Benowicz, A.; Sadoway, S.; et al. Integrating genomic information and productivity and climate-adaptability traits into a regional white spruce breeding program. PLoS ONE 2022, 17, e0264549. [Google Scholar] [CrossRef] [PubMed]
- Xiang, B.; Chen, Z.-Q.; Chen, J. Integrating evolutionary genomics of forest trees to inform future tree breeding amid rapid climate change. Plant Commun. 2024, 5, 100890. [Google Scholar] [CrossRef]
- Newton, P.F. Systematic review of yield responses of four North American conifers to forest tree improvement practices. For. Ecol. Manag. 2003, 172, 29–51. [Google Scholar] [CrossRef]
- McInnis, B.; Tosh, K. Genetic gains from 20 years of cooperative tree improvement in New Brunswick. For. Chron. 2004, 80, 127–133. [Google Scholar] [CrossRef]
- Petrinovic, J.F.; Gélinas, N.; Beaulieu, J. Benefits of using genetically improved white spruce in Quebec: The forest landowner’s viewpoint. For. Chron. 2009, 85, 571–580. Available online: http://pubs.cif-ifc.org/doi/pdf/10.5558/tfc85571-4 (accessed on 15 April 2017). [CrossRef]
- Nance, W.L.; Wells, O.O. Site index for models for height growth of planted loblolly pine (Pinus taeda L.) seed sources. In Proceedings of the 16th Southern Forest Tree Improvement Conference, Blacksburg, VA, USA, 27–28 May 1981; pp. 86–96. [Google Scholar]
- Hamilton, D.A.; Rehfeldt, G.E. Using individual tree growth projection models to estimate stand-level gains attributable to genetically improved stock. For. Ecol. Manag. 1994, 68, 189–207. [Google Scholar] [CrossRef]
- Stage, A.R. Prognosis Model for Stand Development; USDA Forest Service General Technical Report. INT-137; Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1973. [Google Scholar]
- Wykoff, W.; Crookston, N.L.; Stage, A.R. User’s Guide to the Stand Prognosis Model; USDA Forest Service General Technical Report. INT-133; Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1982. [Google Scholar]
- Magnussen, S.; Yanchuk, A.D. Time trends of predicted breeding values in selected crosses of coastal Douglas-fir in British Columbia: A methodological study. For. Sci. 1994, 40, 663–685. Available online: https://ostrnrcan-dostrncan.canada.ca/entities/publication/cd9de0c8-56a2-4683-90f0-eac7e3d283df (accessed on 15 April 2017). [CrossRef]
- Restrepo, H.I.; Bullock, B.P.; Montes, C.R. Growth and yield drivers of loblolly pine in the southeastern U.S.: A meta-analysis. For. Ecol. Manag. 2019, 435, 205–218. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Ojansuu, R.; Haapanen, M.; Hynynen, J.; Kärkkäinen, K. Financial performance of using genetically improved regeneration material of Scots pine (Pinus sylvestris L.) in Finland. New For. 2012, 43, 335–348. [Google Scholar] [CrossRef]
- Buford, M.A.; Burkhart, H.E. Genetic improvement effects on growth and yield of loblolly pine plantations. For. Sci. 1987, 33, 707–724. Available online: https://research.fs.usda.gov/treesearch/59531 (accessed on 13 April 2017). [CrossRef]
- Carson, S.D.; Garcia, O.; Hayes, J.D. Realized gain and prediction of yield with genetically improved Pinus radiata in New Zealand. For. Sci. 1999, 45, 186–200. Available online: https://academic.oup.com/forestscience/article-abstract/45/2/186/4627556?redirectedFrom=fulltext&login=false (accessed on 13 April 2017). [CrossRef]
- Adams, J.P.; Matney, T.G.; Land, S.B.; Belli, K.L.; Duzan, H.W. Incorporating genetic parameters into loblolly pine growth-and-yield model. Can. J. For. Res. 2006, 36, 1959–1967. [Google Scholar] [CrossRef]
- Gould, P.; Johnson, R.; Marshall, D.; Johnson, G. Estimation of genetic-gain multipliers for modeling Douglas-fir height and diameter growth. For. Sci. 2008, 54, 588–596. Available online: https://www.fs.usda.gov/pnw/pubs/journals/pnw_2008_gould002.pdf (accessed on 13 April 2017). [CrossRef]
- Lu, P.; Charrette, P. Genetic parameter estimates for growth traits of black spruce in northwestern Ontario. Can. J. For. Res. 2008, 38, 2994–3001. [Google Scholar] [CrossRef]
- Gould, P.; Marshall, D. Incorporation of genetic gain into growth projections of Douglas-fir using ORGANON and the forest vegetation simulator. West. J. Appl. For. 2010, 25, 55–61. Available online: https://research.fs.usda.gov/treesearch/37821 (accessed on 13 April 2017). [CrossRef]
- Ahtikoski, A.; Salminen, H.; Ojansuu, R.; Hynynen, J.; Kärkkäinen, K.; Haapanen, M. Optimizing stand management involving the effect of genetic gain: Preliminary results for Scots pine in Finland. Can. J. For. Res. 2013, 43, 299–305. [Google Scholar] [CrossRef]
- Lambeth, C.C. Juvenile-mature correlations in Pinaceae and implications for early selection. For. Sci. 1980, 26, 571–580. [Google Scholar]
- Lambeth, C.; Dill, L.A. Prediction models for juvenile-mature correlations for loblolly pine growth traits within, between and across test sites. For. Genet. 2001, 8, 101–108. [Google Scholar]
- Di Lucca, C.M. TASS/SYLVER/TIPSY: Systems for predicting the impact of silvicultural practices on yield, lumber value, economic return and other benefits. In Stand Density Management Conference: Using the Planning Tools; Bamsey, C.R., Ed.; Clear Lake Ltd.: Edmonton, AB, Canada, 1999; pp. 7–16. [Google Scholar]
- Xie, C.Y.; Yanchuk, A.D. Breeding values of parental trees, genetic worth of seed orchard seedlots, and yields of improved stocks in British Columbia. West. J. Appl. For. 2003, 18, 88–100. Available online: https://academic.oup.com/wjaf/article-abstract/18/2/88/4717963 (accessed on 15 April 2017). [CrossRef]
- Alberta Tree Improvement and Seed Centre. Genetic Test Analysis Report for Region E. White Spruce Tree Improvement 15 Year Results; Technical report ATISC #10-28; Alberta Tree Improvement and Seed Centre: Smoky Lake, AB, Canada, 2011. [Google Scholar]
- Ahmed, S.S. Impacts of Tree Improvement Programs on Yields of White Spruce and Hybrid Spruce in the Canadian Boreal Forest. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2016. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: http://www.R-project.org/ (accessed on 15 April 2017).
- SAS Institute Inc. SAS/STAT 13.2 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2014; 673p. [Google Scholar]
- Johnson, R. Introduction to Forest Genetics. In Proceedings of the Genetics and Growth Workshop, Vancouver, WA, USA, 4−6 November 2003; pp. 20–39. [Google Scholar]
- Xie, C.Y.; Yanchuk, A.D.; Kiss, G.K. Genetics of Interior Spruce in British Columbia: Performance and Variability of Open-Pollinated Families in the East Kootenays; Report no. 07; British Columbia Ministry of Forests Research Program: Victoria, BC, Canada, 1998. [Google Scholar]
- Xie, C.Y. Genotype by environment interaction and its implications for genetic improvement of interior spruce in British Columbia. Can. J. For. Res. 2003, 33, 1635–1643. [Google Scholar] [CrossRef]
- Morgenstern, M. Geographic Variation in Forest Trees: Genetic Basis and Application of Knowledge in Silviculture; UBC Press: Vancouver, BC, Canada, 1996; 224p. [Google Scholar]
- Alberta Tree Improvement and Seed Centre. Genetic Test Analysis Report for Region E White Spruce Tree Improvement; Technical Report ATISC #04-22; Alberta Tree Improvement and Seed Centre: Smoky Lake, AB, Canada, 2004. [Google Scholar]
- Rweyongeza, D.M.; Yang, R.C.; Dhir, N.K.; Barnhardt, L.K.; Hansen, C. Genetic variation and climatic impacts on survival and growth of white spruce in Alberta, Canada. Silvae Genet. 2007, 56, 117–126. Available online: https://ualberta.scholaris.ca/server/api/core/bitstreams/ee1761c2-2237-4a96-8d76-ae14137a66cc/content (accessed on 15 April 2017). [CrossRef]
- Alberta Tree Improvement and Seed Centre. Controlled Parentage Program Plan for the Region G2 White Spruce Tree Improvement Project in the Northwest Boreal Region in Alberta; Technical Report ATISC #07-09; Alberta Tree Improvement and Seed Centre: Smoky Lake, AB, Canada, 2007. [Google Scholar]
- Rweyongeza, D.M.; Barnhardt, L.K.; Hansen, C.R. Patterns of Optimal Growth for White Spruce Provenances in Alberta; Pub. No: Ref. T/255; Alberta Tree Improvement and Seed Centre: Smoky Lake, AB, Canada, 2011. [Google Scholar]
- Pienaar, L.V.; Shiver, B.D. The effect of planting density on dominant height in unthinned slash pine plantations. For. Sci. 1984, 30, 1059–1066. Available online: https://academic.oup.com/forestscience/article/30/4/1059/4656945 (accessed on 15 April 2017).
- Wright, J. Introduction to Forest Genetics; Academic Press: New York, NY, USA, 1976; 463p. [Google Scholar]
- Namkoong, G. Introduction to Quantitative Genetics in Forestry; Technical Bulletin no. 1588; Forest Service, United States Department of Agriculture: Washington, DC, USA, 1979. [Google Scholar]




| Model | Parameter | AIC | ||
|---|---|---|---|---|
| a Scale | Shape 1 | Shape 2 | ||
| Null | Intercept only model | −8124 | ||
| Base (I) | −8206 | |||
| II | −15,298 | |||
| III | −18,684 | |||
| IV | −18,666 | |||
| V | −15,244 | |||
| VI | −18,665 | |||
| VII | −19,136 | |||
| Equation (12) Parameter | Variable a | Parameter Estimate (Standard Error) |
|---|---|---|
(scale) | Intercept | 0.12455 (0.000271) |
| (°C) | 0.0019668 ) | |
| (mm) | ) | |
| DD (days) | −0.000011170 ) | |
| Site elevation (m) | 9.6782 × 10−6 ) | |
(shape 1) | Intercept | −0.051836 (0.00463) |
| ln(density) (stems ha−1) | 0.0010935 (0.000586) | |
(shape 2) | Intercept | 1.0053153 (0.000947) |
| MAT (°C) | 0.00025649 (0.000209) | |
| MAP (mm) | ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; LeMay, V.; Yanchuk, A.; Marshall, P.; Bull, G. Assessing the Height Gain Trajectory of White Spruce and Hybrid Spruce Provenances in Canadian Boreal and Hemiboreal Forests. Forests 2025, 16, 1123. https://doi.org/10.3390/f16071123
Ahmed S, LeMay V, Yanchuk A, Marshall P, Bull G. Assessing the Height Gain Trajectory of White Spruce and Hybrid Spruce Provenances in Canadian Boreal and Hemiboreal Forests. Forests. 2025; 16(7):1123. https://doi.org/10.3390/f16071123
Chicago/Turabian StyleAhmed, Suborna, Valerie LeMay, Alvin Yanchuk, Peter Marshall, and Gary Bull. 2025. "Assessing the Height Gain Trajectory of White Spruce and Hybrid Spruce Provenances in Canadian Boreal and Hemiboreal Forests" Forests 16, no. 7: 1123. https://doi.org/10.3390/f16071123
APA StyleAhmed, S., LeMay, V., Yanchuk, A., Marshall, P., & Bull, G. (2025). Assessing the Height Gain Trajectory of White Spruce and Hybrid Spruce Provenances in Canadian Boreal and Hemiboreal Forests. Forests, 16(7), 1123. https://doi.org/10.3390/f16071123






