Altitudinal Variation in Effect of Climate and Neighborhood Competition on Radial Growth of Picea schrenkiana Fisch. et C.A.Mey. in the Middle Tianshan Mountains, China
Abstract
1. Introduction
2. Materials and Methods
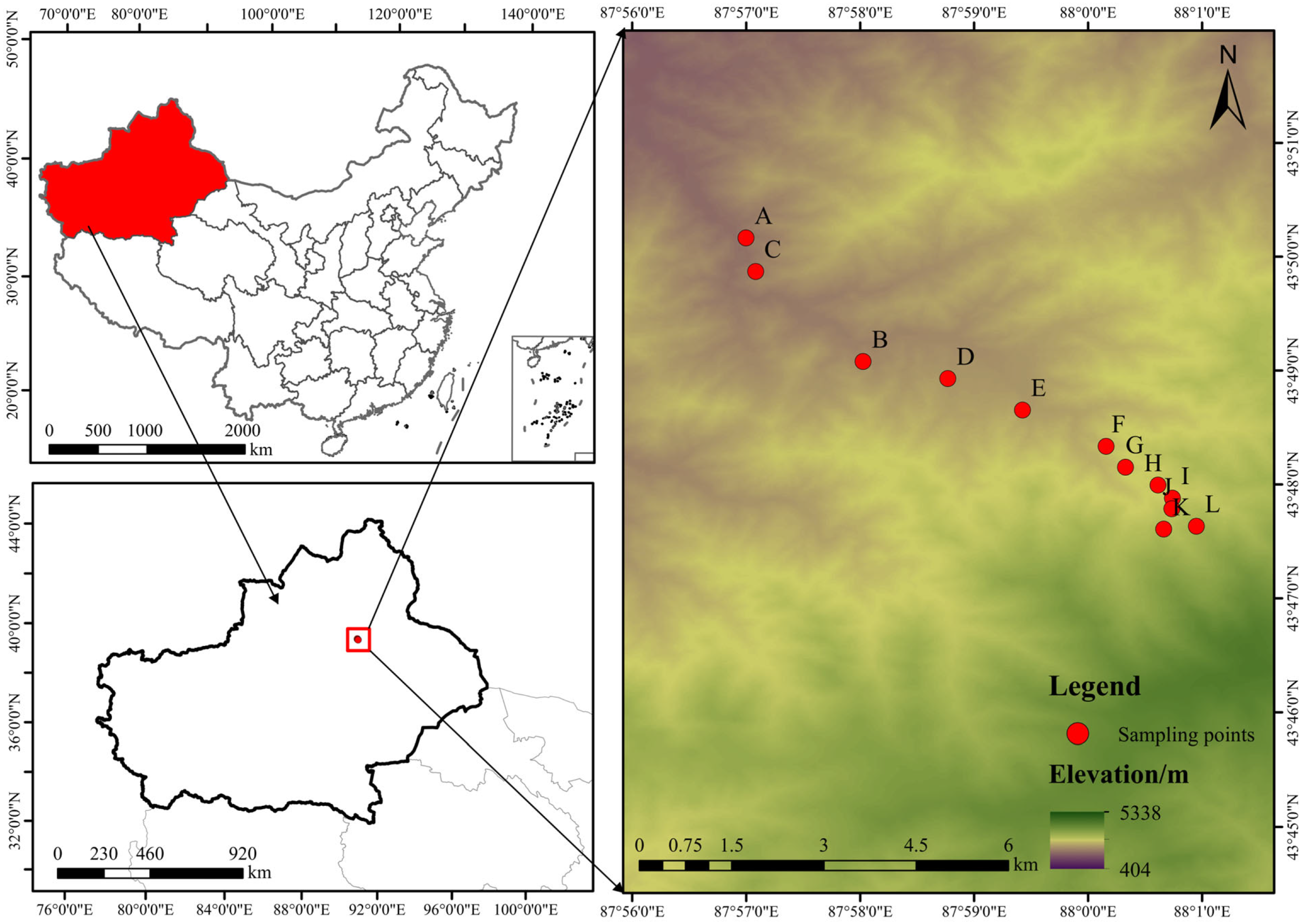
2.1. Study Area
2.2. Collection of Tree Data and Chronology Construction
2.3. Climate Data
2.4. Analysis of the Relationship Between Radial Growth and Climate at Different Altitudes
2.5. Analysis of the Relationship Between Competition and Radial Growth at Different Altitudes
3. Results
3.1. Climate Change and Statistical Characteristics of Chronologies
3.2. Differences in Response of Radial Growth to Climatic Variables at Different Altitudes
3.3. Altitudinal Variation in the Effects of Competition and Other Factors on Growth
4. Discussion
4.1. Altitudinal Variation in Radial Growth
4.2. Altitudinal Variation in the Growth–Climate Relationships
4.3. Altitudinal Variation in the Radial Growth-Competition Relationship
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 1–55. [Google Scholar] [CrossRef]
- Cabon, A.; Peters, R.L.; Fonti, P.; Martínez-Vilalta, J.; De Cáceres, M. Temperature and water potential co-limit stem cambial activity along a steep elevational gradient. New Phytol. 2020, 226, 1325–1340. [Google Scholar] [CrossRef]
- Coomes, D.A.; Flores, O.; Holdaway, R.; Jucker, T.; Lines, E.R.; Vanderwel, M.C. Wood production response to climate change will depend critically on forest composition and structure. Glob. Change Biol. 2014, 20, 3632–3645. [Google Scholar] [CrossRef]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of tree mortality under drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef] [PubMed]
- Begum, S.; Nakaba, S.; Yamagishi, Y.; Oribe, Y.; Funada, R. Regulation of cambial activity in relation to environmental conditions: Understanding the role of temperature in wood formation of trees. Physiol. Plant. 2013, 147, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Adams, H.D.; Zeppel, M.J.B.; Anderegg, W.R.L.; Hartmann, H.; Landhäusser, S.M.; Tissue, D.T.; Huxman, T.E.; Hudson, P.J.; Franz, T.E.; Allen, C.D.; et al. A multi-species synthesis of physiological mechanisms in drought-induced tree mortality. Nat. Ecol. Evol. 2017, 1, 1285–1291. [Google Scholar] [CrossRef]
- Puchi, P.F.; Camarero, J.J.; Battipaglia, G.; Carrer, M. Retrospective analysis of wood anatomical traits and tree-ring isotopes suggests site-specific mechanisms triggering Araucaria araucana drought-induced dieback. Glob. Change Biol. 2021, 27, 6394–6408. [Google Scholar] [CrossRef]
- Pearl, J.; Keck, J.; Tintor, W.; Siekacz, L.; Herrick, H.M.; Meko, M.D.; Pearson, C. New frontiers in tree-ring research. Holocene 2020, 30, 923–941. [Google Scholar] [CrossRef]
- Peng, J.; Li, J.; Li, J.; Li, X.; Cui, J.; Peng, M.; Huo, J.; Yang, L. A Tree-Ring-Based Assessment of Pinus armandii Adaptability to Climate Using Two Statistical Methods in Mt. Yao, Central China during 1961–2016. Forests 2021, 12, 780. [Google Scholar] [CrossRef]
- Körner, C. The use of ‘altitude’ in ecological research. Trends Ecol. Evol. 2007, 22, 569–574. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Zhang, D.; Luo, T.; Wang, X.; Li, X.; Mao, H. Responses of Pinus sylvestris var. mongolica tree ring width to climate factors at different elevations in the Northern Greater Khingan Mountains. Dendrochronologia 2024, 83, 126166. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, Q.; Liu, Y. Altitudinal difference of growth-climate response models in the north subtropical forests of China. Dendrochronologia 2022, 72, 125935. [Google Scholar] [CrossRef]
- Zhou, Y.; Yi, Y.; Liu, H.; Song, J.; Jia, W.; Zhang, S. Altitudinal trends in climate change result in radial growth variation of Pinus yunnanensis at an arid-hot valley of southwest China. Dendrochronologia 2022, 71, 125914. [Google Scholar] [CrossRef]
- Wilmking, M.; Maaten-Theunissen, M.; Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Change Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, X.; Li, J.; Duan, X.; Jin, Y.; Chen, Z. Altitudinal disparity in growth of Dahurian larch (Larix gmelinii Rupr.) in response to recent climate change in northeast China. Sci. Total Environ. 2019, 670, 466–477. [Google Scholar] [CrossRef]
- Sidor, C.G.; Popa, I.; Vlad, R.; Cherubini, P. Different tree-ring responses of Norway spruce to air temperature across an altitudinal gradient in the Eastern Carpathians (Romania). Trees 2015, 29, 985–997. [Google Scholar] [CrossRef]
- Zhou, P.; Huang, J.G.; Liang, H.; Rossi, S.; Bergeron, Y.; Shishov, V.V.; Jiang, S.; Kang, J.; Zhu, H.; Dong, Z. Radial growth of Larix sibirica was more sensitive to climate at low than high altitudes in the Altai Mountains, China. Agric. For. Meteorol. 2021, 304–305, 108392. [Google Scholar] [CrossRef]
- Wang, B.; Chen, T.; Wu, G.; Xu, G.; Zhang, Y.; Gao, H.; Zhang, Y. Qinghai spruce (Picea crassifolia) growth-climate response between lower and upper elevation gradient limits: A case study along a consistent slope in the mid-Qilian Mountains region. Environ. Earth Sci. 2016, 75, 236. [Google Scholar] [CrossRef]
- Yang, B.; He, M.; Melvin, T.M.; Zhao, Y.; Briffa, K.R. Climate control on tree growth at the upper and lower treelines: A case study in the Qilian Mountains, Tibetan Plateau. PLoS ONE 2013, 8, e69065. [Google Scholar] [CrossRef]
- Del Río, M.; Vergarechea, M.; Hilmers, T.; Alday, J.G.; Avdagić, A.; Binderhf, F.; Bosela, M.; Dobor, L.; Forrester, D.I.; Halilović, V.; et al. Effects of elevation-dependent climate warming on intra- and inter-specific growth synchrony in mixed mountain forests. For. Ecol. Manag. 2021, 479, 118587. [Google Scholar] [CrossRef]
- Song, W.Q.; Mu, C.C.; Zhang, Y.D.; Yang, X.X.; Liu, X.P.; Li, X.Q. Moisture-driven changes in the sensitivity of the radial growth of Picea crassifolia to temperature, northeastern Tibetan Plateau. Dendrochronologia 2021, 64, 125761. [Google Scholar] [CrossRef]
- Orešković, M.; Trlin, D.; Anić, I.; Oršanić, M.; Prša, L.; Mikac, S. Climate Sensitivity and Tree Growth Patterns in Subalpine Spruce-Dominated Forests of the North-Western Dinaric Alps. Forests 2024, 15, 1972. [Google Scholar] [CrossRef]
- Collet, C.; Ningre, F.; Barbeito, I.; Arnaud, A.; Piboule, A. Response of tree growth and species coexistence to density and species evenness in a young forest plantation with two competing species. Ann. Bot. 2014, 113, 711–719. [Google Scholar] [CrossRef] [PubMed]
- Anning, A.K.; McCarthy, B.C. Competition, size, and age affect tree growth response to fuel reduction treatments in mixed-oak forests of Ohio. For. Ecol. Manag. 2013, 307, 74–83. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, J.-G.; Cheng, J.; Dawson, A.; Stadt, K.J.; Comeau, P.G.; Chen, H.Y.H. Interspecific variation in growth responses to tree size, competition and climate of western Canadian boreal mixed forests. Sci. Total Environ. 2018, 631–632, 1070–1078. [Google Scholar] [CrossRef]
- Filipescu, C.N.; Comeau, P.G. Aspen competition affects light and white spruce growth across several boreal sites in Western Canada. Can. J. For. Res. 2007, 37, 1701–1713. [Google Scholar] [CrossRef]
- Vayreda, J.; Martínez-Vilalta, J.; Gracia, M.; Retana, J. Recent climate changes interact with stand structure and management to determine changes in tree carbon stocks in Spanish forests. Glob. Change Biol. 2012, 18, 1028–1041. [Google Scholar] [CrossRef]
- Wu, C.; Chen, D.; Sun, X.; Zhang, S. Contributions of competition on Larix kaempferi tree-ring growth were higher than long-term climate in China. Agric. For. Meteorol. 2022, 320, 108967. [Google Scholar] [CrossRef]
- Schurman, J.; Janda, P.; Rydval, M.; Mikolaš, M.; Svoboda, M.; Babst, F. Climate-competition tradeoffs shape the range limits of European beech and Norway spruce along elevational gradients across the Carpathian Mountains. Ecography 2024, 2024, e06715. [Google Scholar] [CrossRef]
- Primicia, I.; Camarero, J.J.; Janda, P.; Čada, V.; Morrissey, R.C.; Trotsiuk, V.; Bače, R.; Teodosiu, M.; Svoboda, M. Age, competition, disturbance and elevation effects on tree and stand growth response of primary Picea abies forest to climate. For. Ecol. Manag. 2015, 354, 281–290. [Google Scholar] [CrossRef]
- Coomes, D.A.; Allen, R.B. Effects of size, competition and altitude on tree growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Deng, H.; Fang, G.; Li, Z. Changes in Central Asia’s Water Tower: Past, Present and Future. Sci. Rep. 2016, 6, 35458. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Yierjiang, B.; Xu, D.; Chen, H. Effects of climate on radial growth of Picea schrenkiana at different altitudes in the central Tianshan Mountains. J. For. Environ. 2024, 44, 530–538. [Google Scholar]
- Zhou, X.D.; Chang, S.L.; Wang, G.Z.; Sun, X.J.; Zhang, Y.T.; Li, X. Altitudinal differentiation of Picea schrenkiana radial growth responses to climate change in the Tianshan Mountains. Sci. Silvae Sin. 2024, 60, 45–56. [Google Scholar]
- Wang, T.; Liang, Y.; Ren, H.; Yu, D.; Ni, J.; Ma, K. Age structure of Picea schrenkiana forest along an altitudinal gradient in the central Tianshan Mountains, northwestern China. For. Ecol. Manag. 2004, 196, 267–274. [Google Scholar] [CrossRef]
- Kang, J.; Liang, H.; Jiang, S.; Zhu, H.; Zhou, P.; Huang, J. Effects of competition and climate on tree radial growth of Pinus sibirica in Altai Mountains, Xinjiang, China. Chin. J. Plant Ecol. 2020, 44, 1195–1202. [Google Scholar] [CrossRef]
- Liang, H.; Huang, J.-G.; Ma, Q.; Li, J.; Wang, Z.; Guo, X.; Zhu, H.; Jiang, S.; Zhou, P.; Yu, B.; et al. Contributions of competition and climate on radial growth of Pinus massoniana in subtropics of China. Agric. For. Meteorol. 2019, 274, 7–17. [Google Scholar] [CrossRef]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–75. [Google Scholar]
- Cook, E.R. A Time Series Approach to Tree-Ring Standardization. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the Average Value of Correlated Time Series, with Applications in Dendroclimatology and Hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B 2011, 73, 3–36. [Google Scholar] [CrossRef]
- Gromping, U. Relative importance for linear regression in R: The package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Zhang, R.; Yuan, Y.; Gou, X.; Zhang, T.; Zou, C.; Ji, C.; Fan, Z.; Qin, L.; Shang, H.; Li, X. Intra-annual radial growth of Schrenk spruce (Picea schrenkiana Fisch. et Mey) and its response to climate on the northern slopes of the Tianshan Mountains. Dendrochronologia 2016, 40, 36–42. [Google Scholar] [CrossRef]
- Jiao, L.; Jiang, Y.; Wang, M.; Zhang, W.; Zhang, Y. Age-Effect Radial Growth Responses of Picea schrenkiana to Climate Change in the Eastern Tianshan Mountains, Northwest China. Forests 2017, 8, 294. [Google Scholar] [CrossRef]
- Jiao, L.; Chen, K.; Wang, S.J.; Liu, X.P. Stability evaluation of radial growth of Picea schrenkiana in different age groups in response to climate change in the eastern Tianshan Mountains. J. Mt. Sci. 2020, 17, 1735–1748. [Google Scholar] [CrossRef]
- Huang, J.G.; Stadt, K.J.; Dawson, A.; Comeau, P.G. Modelling growth-competition relationships in trembling aspen and white spruce mixed boreal forests of Western Canada. PLoS ONE 2013, 8, e77607. [Google Scholar] [CrossRef] [PubMed]
- Bates, D.; Machler, M.; Bolker, B.M.; Walker, S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Rai, S.; Dawadi, B.; Wang, Y.; Lu, X.; Ru, H.; Ram, S. Growth response of Abies spectabilis to climate along an elevation gradient of the Manang valley in the central Himalayas. J. For. Res. 2020, 31, 2245–2254. [Google Scholar] [CrossRef]
- Sun, M.; Li, J.; Cao, R.; Tian, K.; Zhang, W.; Yin, D.; Zhang, Y. Climate-Growth Relations of Abies georgei along an Altitudinal Gradient in Haba Snow Mountain, Southwestern China. Forests 2021, 12, 1569. [Google Scholar] [CrossRef]
- Gou, X.; Chen, F.; Yang, M.; Li, J.; Peng, J.; Jin, L. Climatic response of thick leaf spruce (Picea crassifolia) tree-ring width at different elevations over Qilian Mountains, northwestern China. J. Arid Environ. 2005, 61, 513–524. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, T.; Jiang, S.; Zhang, R.; Qin, L.; Shang, H.; Yang, Y. Tree-ring minimum density chronologies of Picea schrenkiana along an elevation gradient in the Tien Shan Mountains, China. Dendrochronologia 2020, 102, 209–221. [Google Scholar] [CrossRef]
- Wei, X.; Peng, J.; Li, J.; Li, J.; Peng, M.; Li, X.; Liu, Y.; Li, J. Climate-growth relationships of Pinus tabuliformis along an altitudinal gradient on Baiyunshan Mountain, Central China. J. For. Res. 2024, 35, 28–40. [Google Scholar] [CrossRef]
- Lyu, L.; Suvanto, S.; Nöjd, P.; Henttonen, H.M.; Mäkinen, H.; Zhang, Q.B. Tree growth and its climate signal along latitudinal and altitudinal gradients: Comparison of tree rings between Finland and Tibetan Plateau. Biogeosciences 2017, 14, 3083–3095. [Google Scholar] [CrossRef]
- Jiao, L.; Jiang, Y.; Wang, M.; Kang, X.; Zhang, W.; Zhang, L.; Zhao, S. Responses to climate change in radial growth of Picea schrenkiana along elevations of the eastern Tianshan Mountains, northwest China. Dendrochronologia 2016, 40, 117–127. [Google Scholar] [CrossRef]
- Cai, Q.; Liu, Y.; Qian, H.; Liu, R. Inverse effects of recent warming on trees growing at the low and high altitudes of the Dabie Mountains, subtropical China. Dendrochronologia 2020, 59, 125649. [Google Scholar] [CrossRef]
- Jiao, L.; Chen, K.; Liu, X.; Qi, C.; Xue, R. Comparison of the response stability of Siberian larch to climate change in the Altai and Tianshan. Ecol. Indic. 2021, 128, 107823. [Google Scholar] [CrossRef]
- Panthi, S.; Fan, Z.-X.; van der Sleen, P.; Zuidema, P.A. Long-term physiological and growth responses of Himalayan fir to environmental change are mediated by mean climate. Glob. Change Biol. 2020, 26, 1778–1794. [Google Scholar] [CrossRef]
- Li, X.; Liang, E.; Camarero, J.J.; Rossi, S.; Zhang, J.; Zhu, H.; Fu, Y.H.; Sun, J.; Wang, T.; Piao, S.; et al. Warming-induced phenological mismatch between trees and shrubs explains high-elevation forest expansion. Natl. Sci. Rev. 2023, 10, nwad182. [Google Scholar] [CrossRef]
- Gao, S.; Liang, E.; Liu, R.; Babst, F.; Camarero, J.J.; Fu, Y.H.; Piao, S.; Rossi, S.; Shen, M.; Wang, T.; et al. An earlier start of the thermal growing season enhances tree growth in cold humid areas but not in dry areas. Nat. Ecol. Evol. 2022, 6, 397–404. [Google Scholar] [CrossRef]
- Deslauriers, A.; Huang, J.-G.; Balducci, L.; Beaulieu, M.; Rossi, S. The contribution of carbon and water in modulating wood formation in black spruce saplings. Plant Physiol. 2016, 170, 2072–2084. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, Z.; Fang, K.; Cheng, D.; Tang, H.; Ou, T.; Zhang, F.; Chen, D. Summer heat induced the decline of Pinus taiwanensis forests at its southern limit in humid Subtropical China. Agric. For. Meteorol. 2024, 350, 109974. [Google Scholar] [CrossRef]
- Brodribb, T.J.; Powers, J.; Cochard, H.; Choat, B. Hanging by a thread? Forests and drought. Science 2020, 368, 261–266. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, D. Larger diurnal temperature range undermined later autumn leaf senescence with warming in Europe. Glob. Ecol. Biogeogr. 2022, 32, 734–746. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, H.; Ren, J.; Zhan, X.; Cao, S. Tree growth responses to vertical climate gradients in the central Tianshan Mountains. Quat. Res. 2007, 27, 322–331. [Google Scholar]
- Chen, L.; Huang, J.-G.; Stadt, K.J.; Comeau, P.G.; Zhai, L.; Dawson, A.; Alam, S.A. Drought explains variation in the radial growth of white spruce in western Canada. Agric. For. Meteorol. 2017, 233, 133–142. [Google Scholar] [CrossRef]
- Zywiec, M.; Muter, E.; Zielonka, T.; Delibes, M.; Calvo, G.; Fedriani, J.M. Long-term effect of temperature and precipitation on radial growth in a threatened thermo-Mediterranean tree population. Trees 2017, 31, 491–501. [Google Scholar] [CrossRef]
- Reinmann, A.B.; Susser, J.R.; Demaria, E.M.C.; Templer, P.H. Declines in northern forest tree growth following snowpack decline and soil freezing. Glob. Change Biol. 2019, 25, 420–430. [Google Scholar] [CrossRef]
- Lo, Y.-H.; Blanco, J.A.; Seely, B.; Welham, C.; Kimmins, J.P. Relationships between climate and tree radial growth in interior British Columbia, Canada. For. Ecol. Manag. 2010, 259, 932–942. [Google Scholar] [CrossRef]
- Linares, J.C.; Tíscar, P.A. Buffered climate change effects in a Mediterranean pine species: Range limit implications from a tree-ring study. Oecologia 2011, 167, 847–859. [Google Scholar] [CrossRef]
- Feng, X.; Lin, P.; Zhao, W. The physiological constraints of alpine treeline in Qilian Mountains. For. Ecol. Manag. 2022, 503, 119761. [Google Scholar] [CrossRef]
- Xu, G.; Chen, T.; Liu, X.; Wen, T.; Wang, W.; Wang, X.; Yao, Q.; Wu, G.; Zhao, C. Spruce trees have stronger drought sensitivity at low- than high-elevation sites across China’s aridity zones. Glob. Ecol. Conserv. 2024, 53, e03000. [Google Scholar] [CrossRef]
- Torbenson, M.C.A.; Stahle, D.W.; Villanueva Díaz, J.; Cook, E.R.; Griffin, D. The relationship between earlywood and latewood ring-growth across North America. Tree-Ring Res. 2016, 72, 53–66. [Google Scholar] [CrossRef]
- D’Orangeville, L.; Maxwell, J.; Kneeshaw, D.; Pederson, N.; Duchesne, L.; Logan, T.; Houle, D.; Arseneault, D.; Beier, C.M.; Bishop, D.A.; et al. Drought timing and local climate determine the sensitivity of eastern temperate forests to drought. Glob. Change Biol. 2018, 24, 2339–2351. [Google Scholar] [CrossRef] [PubMed]
- Moser, L.; Fonti, P.; Buntgen, U.; Esper, J.; Luterbacher, J.; Franzen, J.; Frank, D. Timing and duration of European larch growing season along altitudinal gradients in the Swiss Alps. Tree Physiol. 2010, 30, 225–233. [Google Scholar] [CrossRef]
- Van der Maaten-Theunissen, M.; Kahle, H.-P.; van der Maaten, E. Drought sensitivity of Norway spruce is higher than that of silver fir along an altitudinal gradient in southwestern Germany. Ann. For. Sci. 2013, 70, 185–193. [Google Scholar] [CrossRef]
- Yao, J.; Mao, W.; Chen, J.; Dilinuer, T. Signal and impact of wet-to-dry shift over Xinjiang, China. Acta Geogr. Sin. 2021, 76, 57–72. [Google Scholar]
- Long, M.; Knox, R.G.; Levine, N.M.; Entekhabi, D.; Swann, A.L. Ecosystem heterogeneity and diversity mitigate Amazon forest resilience to frequent extreme droughts. New Phytol. 2018, 219, 845–847. [Google Scholar] [CrossRef]
- Grime, J.P. Plant Strategies and Vegetation Processes; John Wiley & Sons: Chichester, UK, 1977. [Google Scholar]
- Di Filippo, A.; Biondi, F.; Čufar, K.; De Luis, M.; Grabner, M.; Maugeri, M.; Presutti Saba, E.; Schirone, B.; Piovesan, G. Bioclimatology of beech (Fagus sylvatica L.) in the Eastern Alps: Spatial and altitudinal climatic signals identified through a tree-ring network. J. Biogeogr. 2007, 34, 1873–1892. [Google Scholar] [CrossRef]
- Peñuelas, J. A big issue for trees. Nature 2005, 437, 965–966. [Google Scholar] [CrossRef]
- He, J.N.; Ning, C.W.; Zhang, W.T.; Halik, Ü.; Shen, Z.H. Altitudinal patterns of population structure dynamics of Picea schrenkiana in the northern slope of the eastern Tianshan Mountains. Acta Ecol. Sin. 2024, 44, 5389–5398. [Google Scholar]
- Alados, C.L.; Saiz, H.; Gartzia, M.; Nuche, P.; Escós, J.; Navarro, T.; Pueyo, Y. Plant-plant interactions scale up to produce vegetation spatial patterns: The influence of long- and short-term process. Ecosphere 2017, 8, 233–242. [Google Scholar] [CrossRef]
- Peet, R.K.; Christensen, N.L. Competition and tree death. BioScience 1987, 37, 586–595. [Google Scholar] [CrossRef]
- Fang, Y.; Liang, Z.; Zhang, Y.; Shi, Q.D.; Sun, X.J.; Li, J.M.; Li, X.; Dong, Z.T. Characteristics of altitudinal gradient changes in water retention of Tianshan spruce forest ecosystems. Ecol. Environ. Sci. 2023, 32, 1574–1584. [Google Scholar]
- Xi, L.; Li, S.Y.; Xia, X.Y.; Chen, Y.W.; Wang, J.; Ma, X.L.; Kenijialimu, M.Z.; Maimaiti, A.Y.; Wang, W.X. Effects of altitude, stand age, and canopy density on soil fertility in Picea schrenkiana forest. Chin. J. Ecol. 2023, 42, 2477–2485. [Google Scholar]
- Liu, G.F.; Ding, Y.; Zang, R.G.; Guo, Z.J.; Zhang, X.P.; Cheng, K.W.; Bai, Z.Q.; Ayoufu, B. Distribution patterns of Picea schrenkiana var. tianschanica population in Tianshan Mountains. Chin. J. Appl. Ecol. 2011, 22, 9–13. [Google Scholar]
- Ghotsa Mekontchou, C.; Houle, D.; Bergeron, Y.; Drobyshev, I. Contrasting root system structure and belowground interactions between Black Spruce (Picea mariana (Mill.) B.S.P) and Trembling Aspen (Populus tremuloides Michx) in boreal mixedwoods of Eastern Canada. Forests 2020, 11, 127. [Google Scholar] [CrossRef]









| Plot | Altitude (m) | Core (Tree) | Time Span | MS | SD | AR1 | R | SNR | EPS > 0.85 |
|---|---|---|---|---|---|---|---|---|---|
| A | 1507 | 39 (20) | 1902–2022 | 0.36 | 0.34 | 0.21 | 0.38 | 22.78 | 0.96 (1940) |
| B | 1603 | 40 (20) | 1933–2022 | 0.34 | 0.30 | 0.08 | 0.49 | 32.67 | 0.97 (1938) |
| C | 1703 | 40 (20) | 1886–2022 | 0.35 | 0.40 | 0.37 | 0.61 | 51.00 | 0.98(1908) |
| D | 1807 | 38 (19) | 1897–2022 | 0.29 | 0.34 | 0.17 | 0.38 | 23.41 | 0.96(1924) |
| E | 1900 | 40 (20) | 1894–2022 | 0.27 | 0.37 | 0.40 | 0.47 | 35.62 | 0.97 (1919) |
| F | 2030 | 40 (20) | 1768–2022 | 0.22 | 0.52 | 0.68 | 0.33 | 17.94 | 0.95 (1925) |
| G | 2106 | 39 (20) | 1751–2022 | 0.20 | 0.32 | 0.73 | 0.49 | 33.89 | 0.97 (1890) |
| H | 2221 | 39 (20) | 1731–2022 | 0.17 | 0.38 | 0.86 | 0.50 | 35.29 | 0.97 (1753) |
| I | 2320 | 37 (19) | 1724–2022 | 0.22 | 0.33 | 0.68 | 0.35 | 11.19 | 0.92 (1856) |
| J | 2415 | 31 (17) | 1711–2022 | 0.17 | 0.25 | 0.51 | 0.29 | 11.56 | 0.92 (1839) |
| K | 2530 | 34 (18) | 1701–2022 | 0.19 | 0.42 | 0.72 | 0.45 | 20.49 | 0.95 (1803) |
| L | 2670 | 36 (19) | 1747–2022 | 0.16 | 0.23 | 0.48 | 0.29 | 11.85 | 0.92 (1849) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Gheyret, G. Altitudinal Variation in Effect of Climate and Neighborhood Competition on Radial Growth of Picea schrenkiana Fisch. et C.A.Mey. in the Middle Tianshan Mountains, China. Forests 2025, 16, 948. https://doi.org/10.3390/f16060948
Fan X, Gheyret G. Altitudinal Variation in Effect of Climate and Neighborhood Competition on Radial Growth of Picea schrenkiana Fisch. et C.A.Mey. in the Middle Tianshan Mountains, China. Forests. 2025; 16(6):948. https://doi.org/10.3390/f16060948
Chicago/Turabian StyleFan, Xinchao, and Gheyur Gheyret. 2025. "Altitudinal Variation in Effect of Climate and Neighborhood Competition on Radial Growth of Picea schrenkiana Fisch. et C.A.Mey. in the Middle Tianshan Mountains, China" Forests 16, no. 6: 948. https://doi.org/10.3390/f16060948
APA StyleFan, X., & Gheyret, G. (2025). Altitudinal Variation in Effect of Climate and Neighborhood Competition on Radial Growth of Picea schrenkiana Fisch. et C.A.Mey. in the Middle Tianshan Mountains, China. Forests, 16(6), 948. https://doi.org/10.3390/f16060948






