FS-MVSNet: A Multi-View Image-Based Framework for 3D Forest Reconstruction and Parameter Extraction of Single Trees
Abstract
1. Introduction
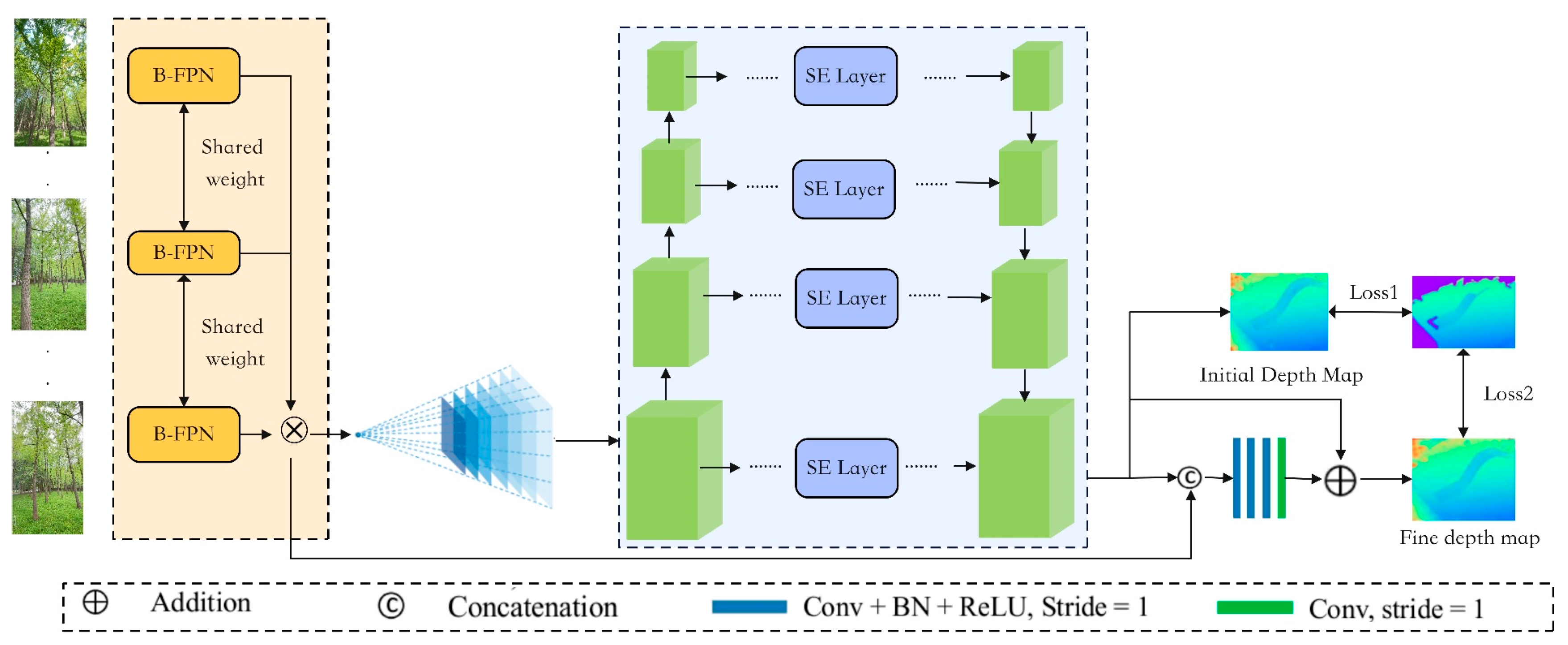
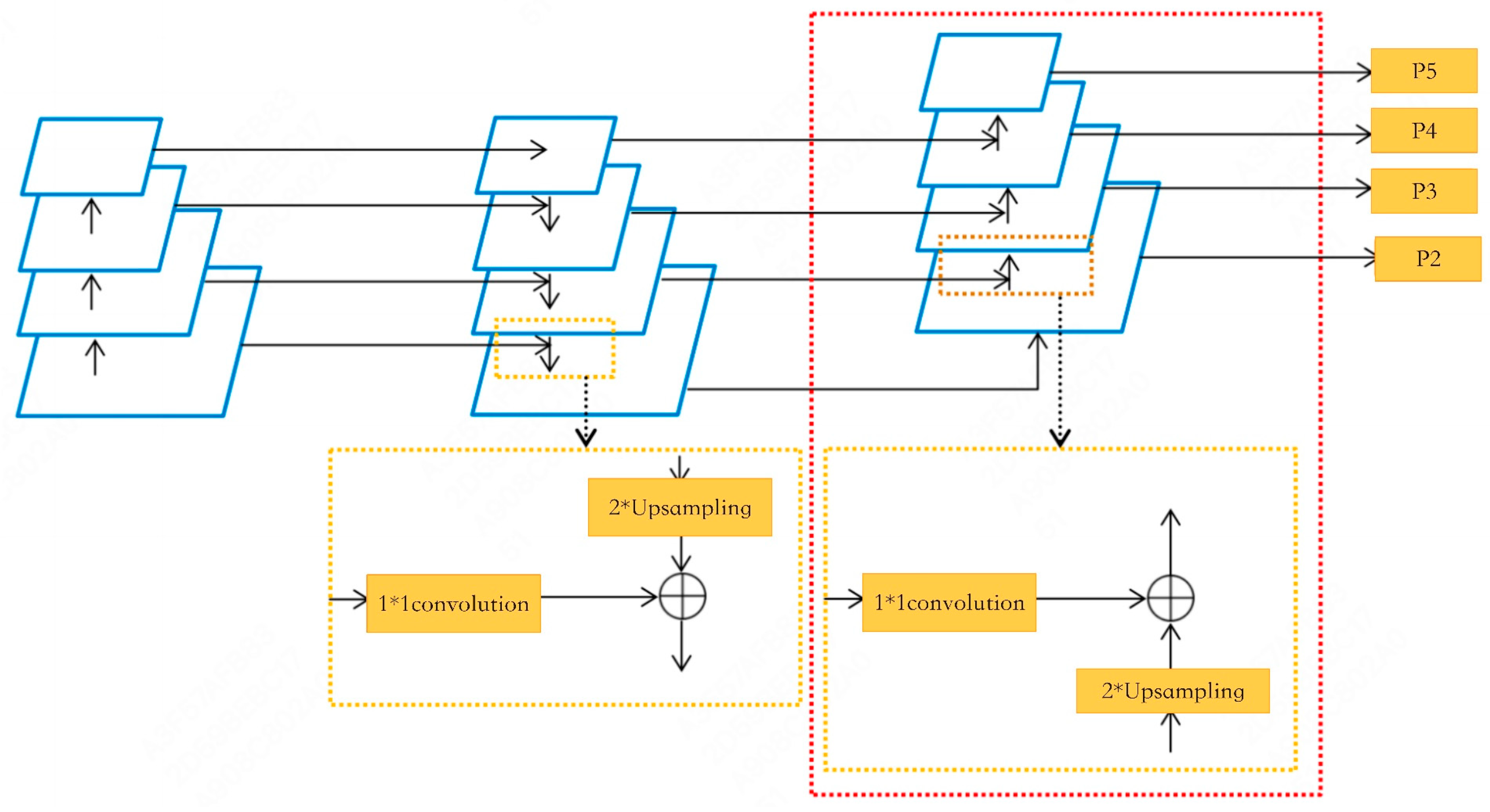
- To overcome the limitation of MVSNet in simultaneously processing multi-scale features such as trunks and canopies during feature extraction, we replace the convolutional backbone with a Bi-directional Feature Pyramid Network (B-FPN) for enhanced multi-scale feature fusion and extraction. B-FPN enhances the network’s capacity to capture texture information across multiple scales by employing a multi-path feature fusion mechanism.
- In response to severe occlusions and lighting variations in forest environments, we introduce a channel attention mechanism—the squeeze-and-excitation (SE) module—during the cost volume regularization stage to enhance the network’s selective focus on critical features. The SE module adaptively recalibrates feature channel weights, thereby optimizing critical information within the cost volume while suppressing irrelevant or redundant features.
- A novel 3D reconstruction framework, FS-MVSNet, integrating B-FPN and SE modules, is proposed and experimentally validated through real-world forest scene modeling. Comparative experiments against the baseline MVSNet and the mainstream SfM-MVS pipeline are conducted to verify the effectiveness of FS-MVSNet in forest 3D reconstruction tasks.
2. Materials and Methods
2.1. Dataset Details
2.1.1. Study Area
2.1.2. Sample Plots Data
2.2. Field Data Collection
2.3. Methodology
2.3.1. FS-MVSNet Architecture Design
- (1)
- B-FPN
- (2)
- Cost Volume Regularization with SE Attention
- (3)
- Hybrid Loss Function
2.3.2. Semi-Automated Single-Tree Parameter Extraction Workflow
- (1)
- Scale Calibration: In multi-view reconstructed point clouds, due to the relative nature of structure recovery, the resulting model lacks a consistent real-world metric scale. To ensure that subsequent geometric estimations are physically meaningful, scale calibration is performed prior to parameter extraction. We adopt a reference object of known length (1 m) placed within the acquisition scene prior to image capture. After reconstruction, two endpoints of the reference marker are manually identified within the point cloud, and their Euclidean distance is measured. The scale factor s is subsequently computed by comparing the measured distance with the actual physical length, formulated as follows:
- (2)
- Ground Point Extraction: Following scale calibration, the next step involves extracting ground points from the 3D point cloud. Ground point extraction aims to eliminate non-ground objects from the forest scene, laying a solid foundation for subsequent individual tree segmentation and DBH (diameter at breast height) estimation. Due to the overlap between ground surfaces and vegetation in multi-view reconstructed point clouds, direct segmentation of ground points remains challenging. To tackle this, we employ the RANSAC-based plane fitting algorithm, renowned for its robustness against outliers, to extract ground points. The RANSAC algorithm is particularly well-suited for estimating ground planes from noisy point clouds with substantial outliers. Its core principle involves randomly sampling minimal point subsets, fitting candidate planes, and optimizing model parameters by evaluating inliers across the point cloud. In ground fitting, the RANSAC model can be mathematically expressed as follows:where (x, y, z) denotes the coordinates of a point, (A, B, C) represents the plane’s normal vector, and d is the intercept. By fitting a plane to the point set and calculating the perpendicular distance from each point to the plane, points are classified as either ground or non-ground. RANSAC iteratively performs random sampling, model fitting, and inlier evaluation, ultimately retaining the plane model that maximizes the number of inliers. To ensure accurate ground extraction, points located within a vertical distance of 2–5 cm from the fitted plane are classified as ground points.
- (3)
- Individual Tree Segmentation: Following scale calibration and ground point extraction, the point cloud typically comprises a mixture of multiple standing trees. To enable accurate extraction of parameters for each individual tree, spatial segmentation at the single-tree level is performed on the point cloud. Theoretically, tree trunks exhibit approximately vertical growth patterns, allowing them to be abstracted using straight-line models. In 3D space, a straight line space can be uniquely determined by a spatial point p = (p1x,p1y,p1z) and a unit direction vector n = (nx,ny,nz) with its parametric form expressed as follows:
- (4)
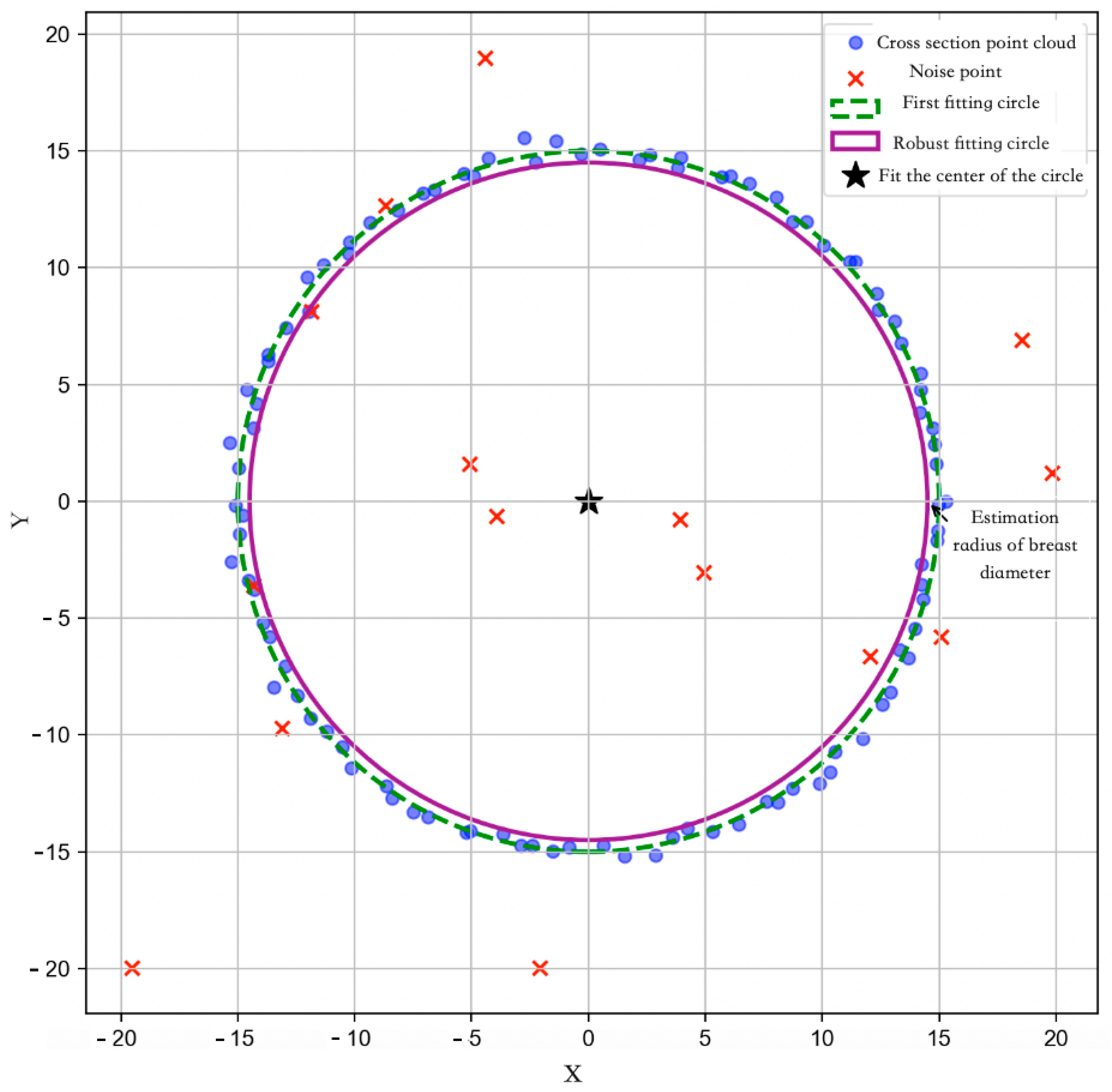
- DBH (Diameter at Breast Height) Extraction: Finally, the DBH of each individual tree is estimated. By isolating trunk points from the 3D point cloud, the DBH for each tree is calculated, thereby completing the individual tree parameter extraction process. Figure 7 illustrates the DBH extraction process based on two-dimensional (2D) circle fitting. In the figure, blue points represent the local cross-sectional point cloud extracted at 1.3 m above ground, serving as candidate points for DBH estimation. Red “×” markers indicate outliers or noisy points, which may arise from branches, reconstruction artifacts, or non-trunk structures. Notably, some red outlier points are located near the center of the trunk cross-section rather than at the periphery. These points are likely the result of 3D reconstruction noise or projection artifacts caused by occluded views, uneven lighting, or insufficient texture in the central trunk region during image capture. Since the reconstruction is image-based, certain internal structures may appear distorted or duplicated due to multi-view matching inconsistencies. Although these points are spatially close to the trunk center, their high residual values relative to the initial circle fitting facilitates their effective exclusion through the residual-based filtering step. First, an initial circle fitting is performed on all cross-sectional points using the least squares method to estimate a preliminary circle center and radius, visualized as a green dashed circle. Although this step provides a coarse DBH estimate, it may be biased by the presence of outliers. To refine the fitting accuracy, the residual distance between each point and the initially fitted circle is computed. Based on the average point spacing of the reconstructed point cloud (approximately 1.5–2.5 cm), a residual threshold of 1.5 cm was empirically selected. This value effectively excludes outlier points while preserving valid trunk boundary data, and aligns with thresholds used in similar forestry studies. Points with residuals smaller than 1.5 cm are retained, while outliers are eliminated. Subsequently, a robust circle fitting is performed on the filtered inlier points. The final fitted circle, represented by the purple solid line in the figure, provides a closer approximation of the actual trunk cross-section. The final circle center is marked by a black pentagram symbol, and the circle diameter d is recorded as the final DBH value. The detailed steps are summarized as follows:
- Point Cloud Preprocessing and Cross-sectional Extraction
- 2.
- Two-Dimensional Cross-sectional Fitting and Initial Estimation
- 3.
- Robust Point Filtering Based on Residuals
- 4.
- Multiple Fittings and Result Fusion
2.4. Evaluation Metrics
3. Experiment and Results
3.1. Experimental Setup
3.1.1. Hardware Environment
3.1.2. Software Environment
3.1.3. Experimental Parameters
3.2. Results and Analysis of Forest Reconstruction
3.2.1. Forest Reconstruction
3.2.2. Trunk and Canopy Fine-Structure Reconstruction Performance
3.2.3. Single-Tree Parameter Extraction
3.3. Experimental Results
3.3.1. DTU Dataset Evaluation Results
3.3.2. Point Cloud Density and Efficiency Analysis
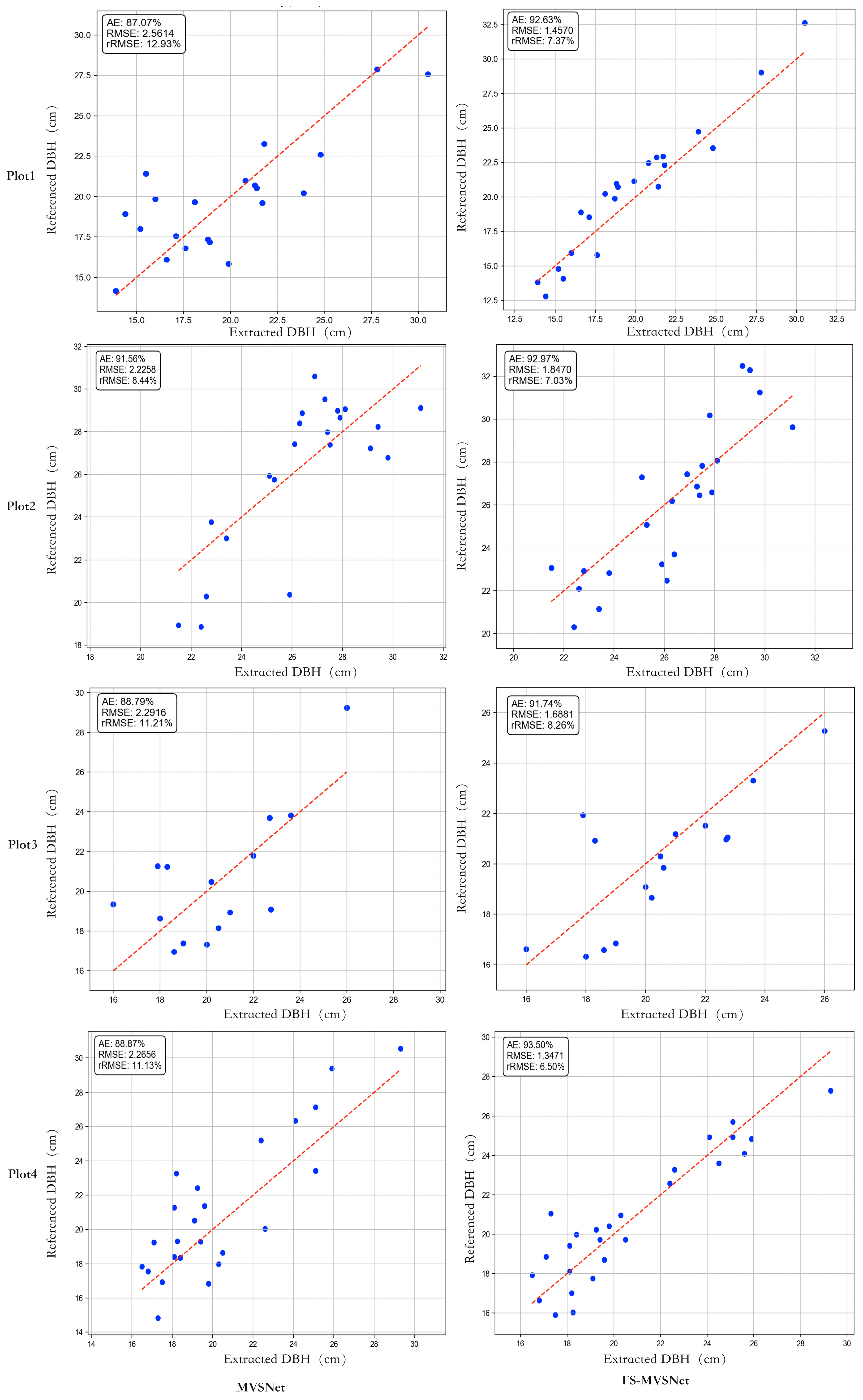
3.3.3. Single-Tree Parameter Extraction Evaluation
3.4. Ablation Study
4. Discussion
- Introduction of a B-FPN to enhance the representation of multi-scale features. The traditional MVSNet architecture typically performs feature extraction at fixed or unidirectional multi-scale levels, limiting its capacity to capture the diverse structural details of large-scale trunks and fine-grained foliage in forested environments. To overcome these limitations, we incorporate a B-FPN during the feature extraction stage, enabling high-level semantic information to flow downward and enhancing low-level features with enriched textures and fine-scale details. Experimental results indicate that the integration of B-FPN significantly increases both the density and completeness of point clouds, particularly in structurally complex regions such as forest canopies and leafy undergrowth. Notably, in dense forest plots with severe occlusions or when focusing on fine-scale canopy reconstruction, the proposed approach yields more continuous and visually coherent reconstructions with minimal fragmentation.
- Integration of a squeeze-and-excitation (SE) attention mechanism into cost volume regularization to enhance matching stability in low-texture and occluded regions. Forest imagery frequently exhibits uneven lighting conditions, localized over-exposure, and extensive shadow regions, all of which hinder stable feature extraction and correspondence matching. To address these challenges, we embed a channel-wise squeeze-and-excitation attention module within the cost volume regularization process, enabling the network to adaptively emphasize informative feature channels while attenuating noise and redundant signals. This mechanism proves particularly effective in challenging regions, including trunk-to-ground transitions and densely interwoven canopy structures, leading to a notable reduction in mismatches.
- A tailored pipeline for extracting the DBH from forest-based multi-view point clouds, demonstrating its feasibility in operational forestry scenarios. Forest-derived point clouds frequently exhibit high noise levels, inconsistent trunk structures, and extensive occlusions within the canopy layer. In contrast to conventional LiDAR-only pipelines, we propose a semi-automated method for directly estimating the DBH from reconstructed point clouds, comprising ground point detection, individual tree segmentation, and circular fitting for trunk diameter estimation. Field evaluations indicate that point clouds generated by FS-MVSNet yield a lower root mean square error (RMSE) and reduced relative error in DBH estimation. In certain plots, the absolute estimation accuracy for the DBH exceeded 93%, with the proposed method out-performing both the baseline MVSNet and conventional SfM-MVS approaches in terms of accuracy and robustness. These results suggest that the enhanced network produces point clouds that are not only visually complete but also sufficiently precise to support the high-accuracy estimation of forestry metrics.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Yu, H.; Zhong, L. Sustainable Futures for Transformational Forestry Resource-Based City: Linking Landscape Pattern and Administrative Policy. J. Clean. Prod. 2025, 496, 145087. [Google Scholar] [CrossRef]
- Sofia, S.; Maetzke, F.; Crescimanno, M.; Coticchio, A.; Veca, D.S.L.M.; Galati, A. The Efficiency of LiDAR HMLS Scanning in Monitoring Forest Structure Parameters: Implications for Sustainable Forest Management. EuroMed J. Bus. 2022, 17, 350–373. [Google Scholar] [CrossRef]
- Geng, J.; Liang, C. Analysis of the Internal Relationship between Ecological Value and Economic Value Based on the Forest Resources in China. Sustainability 2021, 13, 6795. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Wang, H.; Li, D.; Duan, J.; Sun, P. ALS-Based, Automated, Single-Tree 3D Reconstruction and Parameter Extraction Modeling. Forests 2024, 15, 1776. [Google Scholar] [CrossRef]
- Huete, A.R. Vegetation Indices, Remote Sensing and Forest Monitoring. Geogr. Compass 2012, 6, 513–532. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Y.; Zong, J.; Wang, Y.; Cao, X.; Wang, Y.; Cheng, X.; Zhang, W. Remote Sensing Application in Ecological Restoration Monitoring: A Systematic Review. Remote Sens. 2024, 16, 2204. [Google Scholar] [CrossRef]
- Chauhan, J.; Ghimire, S. ‘LiDAR Point Clouds to Precision Forestry. Int J Latest Eng Res Appl 2024, 9, 113–118. [Google Scholar]
- Deng, Y.; Wang, J.; Dong, P.; Liu, Q.; Ma, W.; Zhang, J.; Su, G.; Li, J. Registration of TLS and ULS Point Cloud Data in Natural Forest Based on Similar Distance Search. Forests 2024, 15, 1569. [Google Scholar] [CrossRef]
- Tachella, J.; Altmann, Y.; Mellado, N.; Mccarthy, A.; Mclaughlin, S. Real-Time 3D Reconstruction from Single-Photon Lidar Data Using Plug-and-Play Point Cloud Denoisers. Nat. Commun. 2019, 10, 4984. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Yang, B.; Yang, L.; Liu, F.; Xiong, K. Simulation-Based Correction of Geolocation Errors in GEDI Footprint Positions Using Monte Carlo Approach. Forests 2025, 16, 768. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Karel, W.; Piermattei, L.; Wieser, M.; Wang, D.; Hollaus, M.; Pfeifer, N.; Surovỳ, P.; Koreň, M.; Tomaštík, J.; Mokroš, M. Terrestrial Photogrammetry for Forest 3D Modelling at the Plot Level. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 8–13 April 2018; p. 12749. [Google Scholar]
- Huang, H.; Yan, X.; Zheng, Y.; He, J.; Xu, L.; Qin, D. Multi-View Stereo Algorithms Based on Deep Learning: A Survey. Multimed. Tools Appl. 2024, 84, 2877–2908. [Google Scholar] [CrossRef]
- Tian, G.; Chen, C.; Huang, H. Comparative Analysis of Novel View Synthesis and Photogrammetry for 3D Forest Stand Reconstruction and Extraction of Individual Tree Parameters. arXiv 2024, arXiv:241005772. [Google Scholar] [CrossRef]
- Gallup, D.; Frahm, J.-M.; Mordohai, P.; Yang, Q.; Pollefeys, M. Real-Time Plane-Sweeping Stereo with Multiple Sweeping Directions. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Campbell, N.D.; Vogiatzis, G.; Hernández, C.; Cipolla, R. Using Multiple Hypotheses to Improve Depth-Maps for Multi-View Stereo. In Proceedings of the Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Proceedings, Part I 10. Springer: Berlin/Heidelberg, Germany, 2008; pp. 766–779. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, H.; Weng, L. A Multi-View Matching Method Based on PatchmatchNet with Sparse Point Information. In Proceedings of the 4th World Symposium on Software Engineerig, Xiamen, China, 28–30 September 2022. [Google Scholar] [CrossRef]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively Parallel Multiview Stereopsis by Surface Normal Diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Bayati, H.; Najafi, A.; Vahidi, J.; Jalali, S.G. 3D Reconstruction of Uneven-Aged Forest in Single Tree Scale Using Digital Camera and SfM-MVS Technique. Scand. J. For. Res. 2021, 36, 210–220. [Google Scholar] [CrossRef]
- Dai, L.; Chen, Z.; Zhang, X.; Wang, D.; Huo, L. CPH-Fmnet: An Optimized Deep Learning Model for Multi-View Stereo and Parameter Extraction in Complex Forest Scenes. Forests 2024, 15, 1860. [Google Scholar] [CrossRef]
- Yan, X.; Chai, G.; Han, X.; Lei, L.; Wang, G.; Jia, X.; Zhang, X. SA-Pmnet: Utilizing Close-Range Photogrammetry Combined with Image Enhancement and Self-Attention Mechanisms for 3D Reconstruction of Forests. Remote Sens. 2024, 16, 416. [Google Scholar] [CrossRef]
- Li, Y.; Kan, J. CGAN-Based Forest Scene 3D Reconstruction from a Single Image. Forests 2024, 15, 194. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, Z.; Zhang, X. Forest 3D Reconstruction and Individual Tree Parameter Extraction Combining Close-Range Photo Enhancement and Feature Matching. Remote Sens. 2021, 13, 1633. [Google Scholar] [CrossRef]
- Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; Fang, L. Surfacenet: An End-to-End 3d Neural Network for Multiview Stereopsis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2307–2315. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth Inference for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Quan, L. Recurrent Mvsnet for High-Resolution Multi-View Stereo Depth Inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Luo, K.; Guan, T.; Ju, L.; Huang, H.; Luo, Y. P-Mvsnet: Learning Patch-Wise Matching Confidence Aggregation for Multi-View Stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10452–10461. [Google Scholar]
- Yi, H.; Wei, Z.; Ding, M.; Zhang, R.; Chen, Y.; Wang, G.; Tai, Y.-W. Pyramid Multi-View Stereo Net with Self-Adaptive View Aggregation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 766–782. [Google Scholar]
- Cao, C.; Ren, X.; Fu, Y. MVSFormer: Multi-View Stereo by Learning Robust Image Features and Temperature-Based Depth. arXiv 2022, arXiv:2208.02541. [Google Scholar]
- Liu, T.; Ye, X.; Zhao, W.; Pan, Z.; Shi, M.; Cao, Z. When Epipolar Constraint Meets Non-Local Operators in Multi-View Stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 18088–18097. [Google Scholar]
- Vats, V.K.; Joshi, S.; Crandall, D.J.; Reza, M.A.; Jung, S.H. GC-Mvsnet: Multi-View, Multi-Scale, Geometrically-Consistent Multi-View Stereo. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024. [Google Scholar]
- Murtiyoso, A.; Holm, S.; Riihimäki, H.; Krucher, A.; Griess, H.; Griess, V.C.; Schweier, J. Virtual Forests: A Review on Emerging Questions in the Use and Application of 3D Data in Forestry. Int. J. For. Eng. 2024, 35, 29–42. [Google Scholar] [CrossRef]
- Luo, W.; Lu, Z.; Liao, Q. LNMVSNet: A Low-Noise Multi-View Stereo Depth Inference Method for 3D Reconstruction. Sensors 2024, 24, 2400. [Google Scholar] [CrossRef] [PubMed]
- Barnston, A.G. Correspondence among the Correlation, RMSE, and Heidke Forecast Verification Measures; Refinement of the Heidke Score. Weather Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Gao, Q.; Kan, J. Automatic Forest DBH Measurement Based on Structure from Motion Photogrammetry. Remote Sens. 2022, 14, 2064. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D Lidar Imaging for Detecting and Understanding Plant Responses and Canopy Structure. J. Exp. Bot. 2007, 58, 881–898. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Liu, K.; Shen, X.; Wu, X.; Liu, H. Estimation of Forest Structural Parameters Using UAV-LiDAR Data and a Process-Based Model in Ginkgo Planted Forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4175–4190. [Google Scholar] [CrossRef]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. Patchmatchnet: Learned Multi-View Patchmatch Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 14194–14203. [Google Scholar]
- Gao, S.; Li, Z.; Wang, Z. Cost Volume Pyramid Network with Multi-Strategies Range Searching for Multi-View Stereo. In Proceedings of the Computer Graphics International Conference, Virtual, 12–16 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 157–169. [Google Scholar]
- Yu, Z.; Gao, S. Fast-Mvsnet: Sparse-to-Dense Multi-View Stereo with Learned Propagation and Gauss-Newton Refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1949–1958. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef]
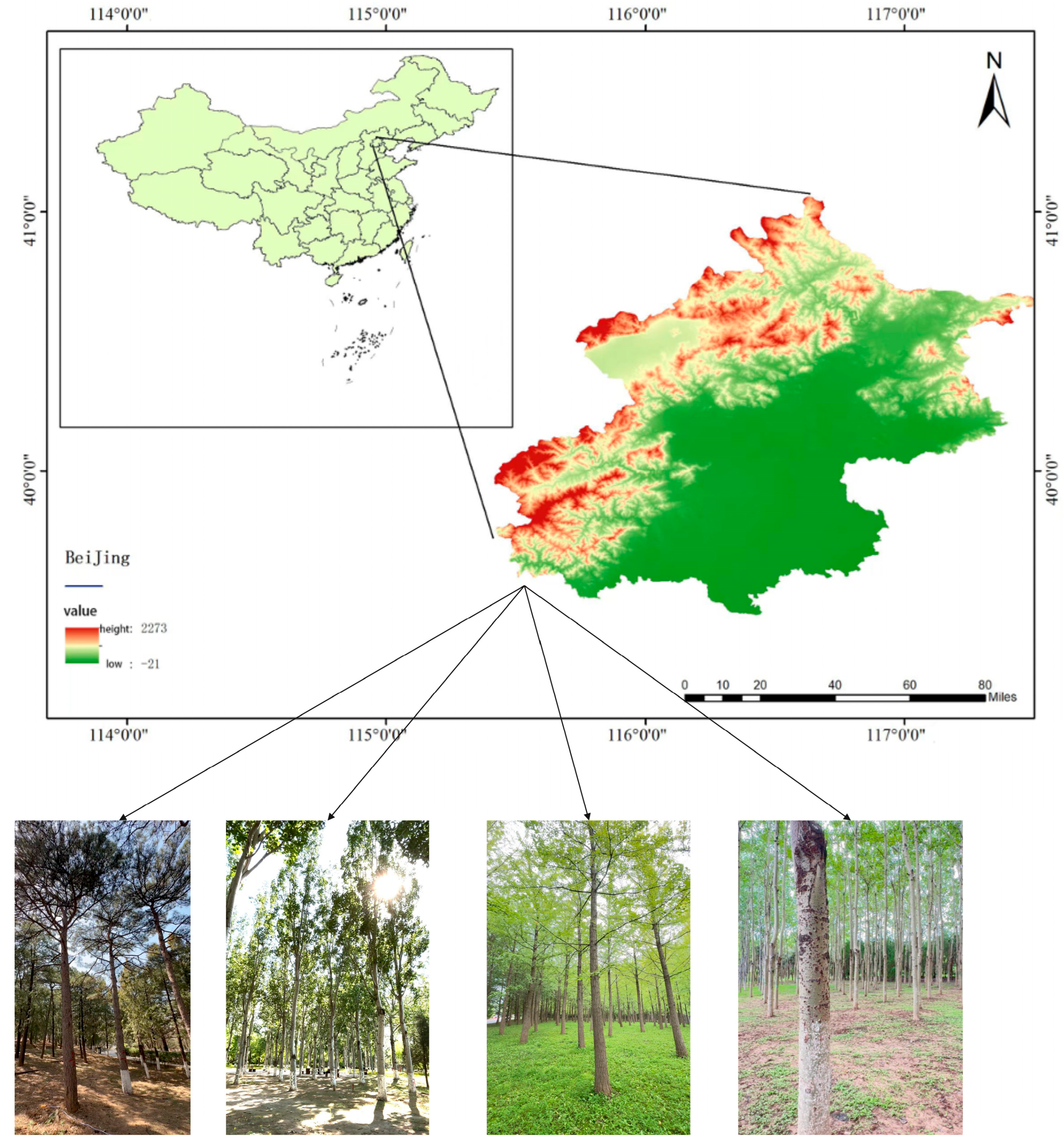






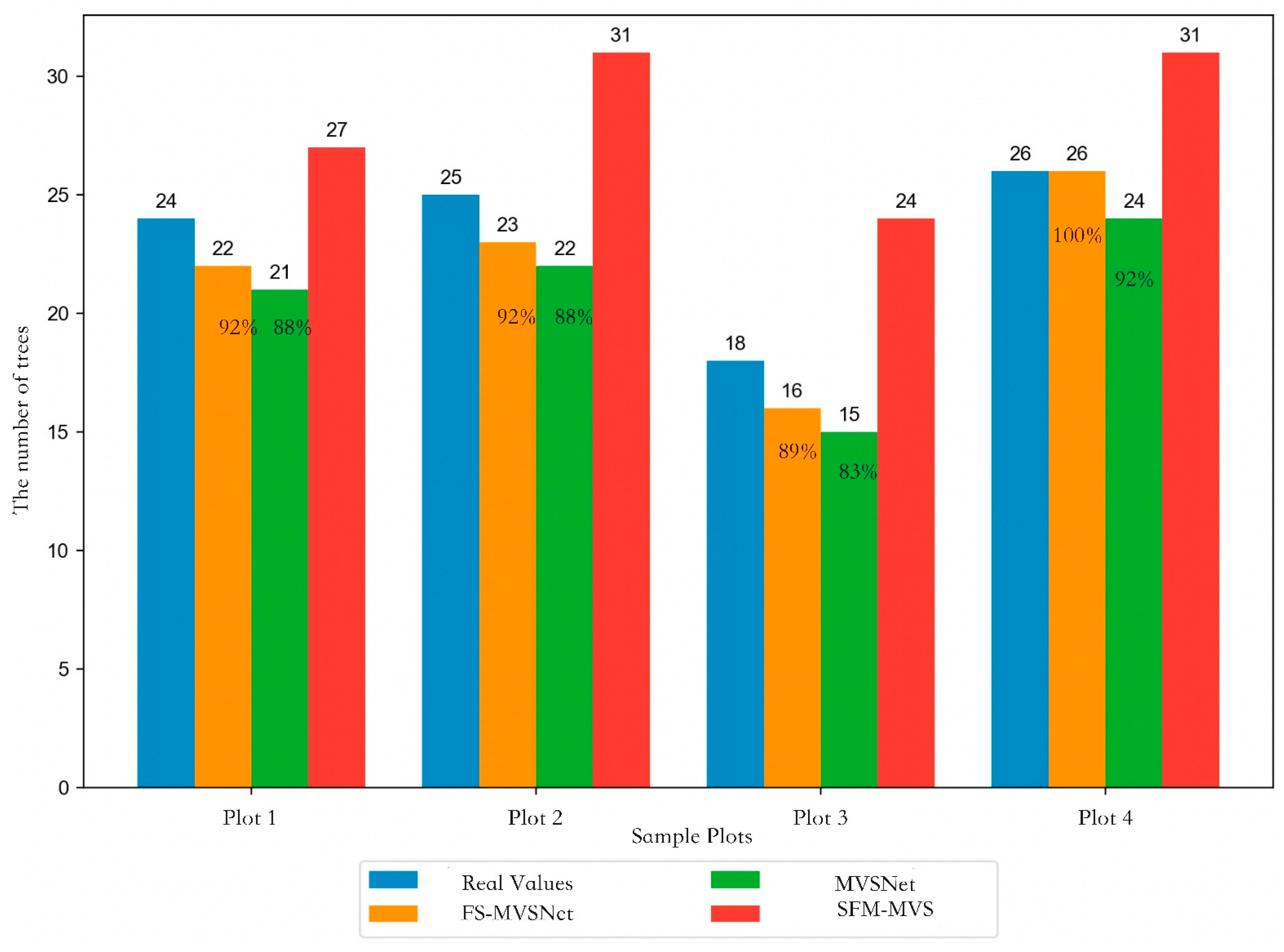
| Plot Name | Number of Trees | Average Tree Height (m) | Average DBH (cm) | Plot Area | Plot Area | Terrain Complexity |
|---|---|---|---|---|---|---|
| Plot 1 | 35 | 12.76 | 21.46 | 15 m × 15 m | Pine | High |
| Plot 2 | 21 | 21.72 | 22.45 | 15 m × 15 m | Poplar | Low |
| Plot 3 | 23 | 21.45 | 20.48 | 15 m × 15 m | Ginkgo | Medium |
| Plot 4 | 26 | 31.45 | 25.47 | 15 m × 15 m | Poplar | High |
| Component | Specification |
|---|---|
| Central Processing Unit (CPU) | 1 × RTX3090 |
| Graphics Processing Unit (GPU) | 24 GB |
| Memory | 128 GB |
| Operating System | Ubuntu 20.04 LTS |
| Software/Tool | Version | Function |
|---|---|---|
| Python | 3.8 | Programming language |
| PyTorch | 1.12 | Neural network construction and custom operations |
| OpenCV | 4.5 | Image preprocessing and enhancement |
| NumPy | 4.5 | Numerical computation and array operations |
| scikit-learn | 0.24 | Dataset partitioning and evaluation metric computation |
| TensorBoard | 2.6 | Visualization and monitoring during training |
| Parameter | Value | Description |
|---|---|---|
| Initial learning rate | 0.001 | Initial learning rate for model training |
| Batch size | 8 | Number of samples fed into the network per training iteration |
| Number of depth hypothesis planes | 192 | Number of depth planes constructed during cost volume building |
| SE compression ratio | 16 | Compression ratio for feature channels in the SE module |
| Attention weight loss coefficient | 0.2 | Loss weight for key feature regions emphasized by attention |
| Multi-scale loss weight coefficient | 0.8 | Loss weight for multi-scale depth supervision |
| Optimization algorithm | Adam | Optimization method for network parameters |
| Number of training epochs | 100 | Total number of training epochs |
| Weight decay | 1 × 10−5 | Regularization coefficient to prevent overfitting |
| Image batch size | 4 | Number of images processed per batch during training |
| Method | Accuracy (mm) | Completeness (mm) | Overall (mm) |
|---|---|---|---|
| FS-MVSNet | 0.352 | 0.392 | 0.372 |
| MVSNet [27] | 0.396 | 0.527 | 0.462 |
| P-MVSNet | 0.406 | 0.434 | 0.420 |
| R-MVSNet | 0.383 | 0.452 | 0.417 |
| CVP-MVSNet | 0.296 | 0.406 | 0.351 |
| Point-MVSNet | 0.342 | 0.411 | 0.376 |
| Fast-MVSNet | 0.336 | 0.403 | 0.370 |
| MSCVP-MVSNet | 0.379 | 0.278 | 0.328 |
| PatchmatchNet | 0.427 | 0.277 | 0.352 |
| CasMVSNet | 0.325 | 0.385 | 0.355 |
| UCSNet | 0.338 | 0.349 | 0.344 |
| VisMVSNet | 0.369 | 0.361 | 0.365 |
| AA-RMVSNet | 0.369 | 0.339 | 0.357 |
| Gipuma | 0.283 | 0.873 | 0.578 |
| Furu | 0.613 | 0.941 | 0.777 |
| Tola | 0.342 | 1.190 | 0.766 |
| COLMAP | 0.400 | 0.664 | 0.532 |
| Plot | Model | Point Cloud Density (Points/m2) | Reconstruction Time (h) |
|---|---|---|---|
| Plot 1 | sfm-mvs [43] | 5.4 × 106 | 6 |
| MVSNet [27] | 11.5 × 106 | 8 | |
| FS-MVSNet | 12.9 × 106 | 8.5 | |
| Plot 2 | sfm-mvs [43] | 4.3 × 106 | 6.5 |
| MVSNet [27] | 9.2 × 106 | 8.5 | |
| FS-MVSNet | 12.4 × 106 | 9.5 | |
| Plot 3 | sfm-mvs [43] | 5.2 × 106 | 7 |
| MVSNet [27] | 10.9 × 106 | 9 | |
| FS-MVSNet | 13.8 × 106 | 10 | |
| Plot 4 | sfm-mvs [43] | 4.2 × 106 | 5.5 |
| MVSNet [27] | 7.3 × 106 | 8.5 | |
| FS-MVSNet | 8.6 × 106 | 9.5 |
| Plot | Model | AE | RMSE | rRMSE |
|---|---|---|---|---|
| Plot 1 | MVSNet [27] | 87.07% | 2.5614 | 12.93% |
| FS-MVSNet | 92.63% | 1.4570 | 7.37% | |
| Plot 2 | MVSNet [27] | 91.56% | 2.2258 | 8.44% |
| FS-MVSNet | 92.97% | 1.8470 | 7.03% | |
| Plot 3 | MVSNet [27] | 88.79% | 2.916 | 11.21% |
| FS-MVSNet | 91.74% | 1.6881 | 8.26% | |
| Plot 4 | MVSNet [27] | 88.87% | 2.656 | 11.13% |
| FS-MVSNet | 93.50% | 1.3471 | 6.50% |
| B-FPN | Cost Volume Regularization (SE) | Loss Function | Density (Point/m2) | Overall |
|---|---|---|---|---|
| √ | √ | √ | 12.9 × 106 | Baseline |
| √ | √ | 11.5 × 106 | ↓1.62 (RMSE), ↓8.45% (rRMSE), ↓89.5% (AE) | |
| √ | √ | 12.1 × 106 | ↓1.551 (RMSE), ↓7.95% (rRMSE), ↓90.2% (AE) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Dai, L.; Wang, D.; Guo, Q.; Zhao, R. FS-MVSNet: A Multi-View Image-Based Framework for 3D Forest Reconstruction and Parameter Extraction of Single Trees. Forests 2025, 16, 927. https://doi.org/10.3390/f16060927
Chen Z, Dai L, Wang D, Guo Q, Zhao R. FS-MVSNet: A Multi-View Image-Based Framework for 3D Forest Reconstruction and Parameter Extraction of Single Trees. Forests. 2025; 16(6):927. https://doi.org/10.3390/f16060927
Chicago/Turabian StyleChen, Zhao, Lingnan Dai, Dianchang Wang, Qian Guo, and Rong Zhao. 2025. "FS-MVSNet: A Multi-View Image-Based Framework for 3D Forest Reconstruction and Parameter Extraction of Single Trees" Forests 16, no. 6: 927. https://doi.org/10.3390/f16060927
APA StyleChen, Z., Dai, L., Wang, D., Guo, Q., & Zhao, R. (2025). FS-MVSNet: A Multi-View Image-Based Framework for 3D Forest Reconstruction and Parameter Extraction of Single Trees. Forests, 16(6), 927. https://doi.org/10.3390/f16060927






