Abstract
With the rapid advancement of smart forestry, 3D reconstruction and the extraction of structural parameters have emerged as indispensable tools in modern forest monitoring. Although traditional methods involving LiDAR and manual surveys remain effective, they often entail considerable operational complexity and fluctuating costs. To provide a cost-effective and scalable alternative, this study introduces FS-MVSNet—a multi-view image-based 3D reconstruction framework incorporating feature pyramid structures and attention mechanisms. Field experiments were performed in three representative forest parks in Beijing, characterized by open canopies and minimal understory, creating the optimal conditions for photogrammetric reconstruction. The proposed workflow encompasses near-ground image acquisition, image preprocessing, 3D reconstruction, and parameter estimation. FS-MVSNet resulted in an average increase in point cloud density of 149.8% and 22.6% over baseline methods, and facilitated robust diameter at breast height (DBH) estimation through an iterative circle-fitting strategy. Across four sample plots, the DBH estimation accuracy surpassed 91%, with mean improvements of 3.14% in AE, 1.005 cm in RMSE, and 3.64% in rRMSE. Further evaluations on the DTU dataset validated the reconstruction quality, yielding scores of 0.317 mm for accuracy, 0.392 mm for completeness, and 0.372 mm for overall performance. The proposed method demonstrates strong potential for low-cost and scalable forest surveying applications. Future research will investigate its applicability in more structurally complex and heterogeneous forest environments, and benchmark its performance against state-of-the-art LiDAR-based workflows.
1. Introduction
As global climate change intensifies goals advance, the accurate monitoring of forest resources has emerged as a pivotal element in national ecological security strategies [1]. Forestry informatization technology encompasses the application of modern information technologies in forestry, primarily aiming to employ advanced techniques for the collection, processing, analysis, and application of forest resource data [2]. The precise acquisition of forest parameters underpins forest conservation, scientific planning, and effective management, offering critical data support and a robust scientific foundation for precision forestry monitoring. Among forest resource monitoring techniques, field-based manual surveys necessitate personnel physically entering forested areas to collect data via direct measurements and recordings [3]. Although this approach can yield relatively accurate data, it is extremely time-consuming and labor-intensive [4], especially in regions characterized by complex terrain or dense vegetation.
By contrast, advanced surveying technologies such as remote sensing and LiDAR demonstrate significant advantages in acquiring forest resource data [5]. Remote sensing, with its capacity for extensive spatial coverage, has become a vital tool for forest monitoring [6]; however, its limited spatial resolution hinders the acquisition of fine-scale 3D structural information. Recent international studies, such as Wang et al., have systematically reviewed the applications of remote sensing in ecological restoration monitoring, highlighting its roles across forests, soil, water, and atmosphere, and proposing multi-dimensional evaluation indicators as well as discussing challenges and future research directions [7]. Similarly, Chauhan and Ghimire (2024) reviewed the global applications of LiDAR technology in precision forestry, 3D landscape modeling, aquatic studies, and environmental monitoring, and noted its emerging use in Nepal for high-resolution mapping and biomass estimation [8]. Although LiDAR actively captures high-precision 3D point cloud data and excels in vegetation structure analysis [9], it is limited by high equipment costs, dependence on flight platforms for data acquisition, and the complexity of post-processing. In particular, the enormous volume of point cloud data necessitates specialized filtering and classification algorithms, rendering the processing workflow cumbersome and time-consuming [10,11]. These constraints have restricted the widespread application of both technologies in forest resource surveys. Consequently, the development of more economical and effective approaches for the 3D modeling of forest structure has emerged as a key research focus in forest resource monitoring [12]. Image-based 3D reconstruction technologies offer a cost-effective and practical alternative for overcoming the limitations of remote sensing and LiDAR [13].
The evolution of multi-view 3D reconstruction technology reflects a transition from traditional geometric methods to deep learning-based approaches. Multi-view 3D reconstruction methods can be broadly categorized into two main classes: traditional geometry-based methods and deep learning-based methods [14]. Traditional approaches, centered on feature extraction and geometric modeling, have given rise to a comprehensive framework represented by Structure-from-Motion (SfM) and Multi-View Stereo methods. As a foundational element of traditional methods, SfM identifies and matches local features across multiple overlapping images, sequentially estimating camera poses and sparse 3D point clouds under geometric constraints [12]. Building upon this, MVS further leverages texture and disparity information from multi-view images to perform dense matching, generating finer and more complete point cloud models [15]. These methods optimize depth estimation and 3D reconstruction by exploiting the geometric relationships among multi-view images, with plane sweeping serving as an early representative technique that estimates optimal depths by projecting reference images onto multiple depth planes and evaluating image consistency [16]. The normalized cross-correlation method proposed by Campbell et al. (2008) markedly improved the robustness of depth estimation [17], subsequently leading to the development of the PMVS (Patch-based Multi-View Stereo) algorithm, which achieves high-quality dense point cloud reconstruction through multi-view feature extraction and patch aggregation [18]. To enhance computational efficiency, Yang et al. introduced the PatchMatch algorithm based on random sampling and patch-based search mechanisms [19], which was further optimized by Galliani et al. through the development of the Gipuma algorithm employing an image propagation strategy [20]. With the rapid development of image-based 3D reconstruction technologies, several studies have explored the application of Structure-from-Motion and Multi-View Stereo methods to practical forestry monitoring tasks. Bayati et al. proposed a ground-based photogrammetric system leveraging SfM and MVS algorithms to address the practical requirements of intelligent rubber plantation monitoring [21]. This system effectively addressed the limitations of traditional monitoring approaches—namely functional inflexibility, bulky equipment, and high operational costs in complex environments—and demonstrated robust performance in field applications, particularly in under-branch height estimation, DBH measurement, and rubber tree volume calculation. Although SfM and MVS methods have been extensively adopted in image-based 3D reconstruction, their strong dependence on handcrafted feature extraction and matching pipelines poses significant challenges in scenarios characterized by weak textures, severe occlusions, or complex illumination conditions [22]. These limitations frequently result in reduced matching accuracy, sparse point clouds, and incomplete reconstruction outcomes [21].
In recent years, multi-view 3D reconstruction technologies based on deep learning have witnessed groundbreaking advancements. In recent years, several researchers have explored the integration of deep learning techniques into forest 3D reconstruction. Yan et al. proposed the SA-PMNet deep learning model, which integrates image enhancement with self-attention mechanisms to facilitate forest 3D reconstruction [23]. Li et al. proposed a method based on conditional generative adversarial networks (cGANs) that enables the efficient and cost-effective reconstruction of complex forest environments from a single image [24]. Nevertheless, existing algorithms continue to encounter significant challenges when applied to complex forest scenes [25]. SurfaceNet, introduced in 2017, pioneered end-to-end voxelized reconstruction by directly predicting surface points within a 3D voxel space, thereby opening new avenues for applying deep learning to 3D reconstruction tasks [26]. Subsequently, the MVSNet framework, proposed in 2018, established the foundational paradigm for deep learning-based 3D reconstruction by constructing a differentiable cost volume and incorporating 3D convolutional regularization, leveraging camera poses estimated via SfM to generate inter-view homographies [27]. With continued research efforts, this technology has achieved notable advancements across multiple dimensions. In terms of computational efficiency, subsequent studies have introduced innovative approaches to address the limitations of traditional 3D convolution operations in deep learning-based reconstruction frameworks. Specifically, researchers have proposed replacing computationally intensive 3D convolutions with recurrent neural networks (RNNs) for cost volume regularizations [28]. This substitution not only reduces the memory footprint but also enables more efficient feature propagation across multiple depth planes. Additionally, residual optimization strategies have been developed, leveraging initial point cloud estimates as priors to iteratively refine depth predictions. These approaches significantly alleviate memory consumption, accelerate inference speed, and improve reconstruction accuracy, particularly in large-scale or resource-constrained environments. Together, these advancements have contributed to making deep learning-based 3D reconstruction methods more practical and scalable for real-world applications.
In terms of feature representation, researchers have developed pyramid feature networks for multi-scale feature fusion [29] and adaptive feature aggregation strategies [30] capable of dynamically adjusting feature weights according to scene complexity, thereby significantly enhancing robustness in weakly textured regions. Regarding network architecture, advancements have shifted from conventional convolutional neural networks to Transformer-based architectures incorporating self-attention mechanisms, as exemplified by MVSFormer [31], thereby further enhancing feature representation capabilities. Recent advances introduced non-local enhancement mechanisms to capture global context through long-range dependencies [32], and geometric consistency constraints to enforce depth map consistency across different views, thereby improving robustness against occlusions and geometric inconsistencies in complex scenes [33]. These advancements have not only improved reconstruction accuracy but also significantly strengthened the reliability and generalization capabilities of the algorithms in real-world applications. These achievements lay a robust technical foundation for the application of 3D reconstruction technologies in critical domains such as autonomous driving environment perception and virtual reality scene modeling, demonstrating the broad application prospects of this technology.
In recent years, despite significant advances of deep learning-based multi-view 3D reconstruction across various domains, numerous unique challenges persist when these technologies are applied to forest environments. First, forests exhibit highly complex geometric structures, comprising coarse, continuous trunks as well as fine, intricate branches and foliage. Existing algorithms generally lack effective cross-scale information fusion during feature extraction, often resulting in the omission of fine details such as branches and leaves when large-scale structures are emphasized. Conversely, an excessive emphasis on small-scale details may induce fractures in trunk structures, thereby compromising the accuracy of individual tree parameter extraction [22]. Second, forest environments are characterized by complex lighting conditions and severe occlusions caused by dense foliage, leading to image artifacts such as texture blurring, discontinuities, and dense leaf regions [34]. Such conditions exacerbate the difficulty of feature matching and frequently lead to mismatches, ultimately resulting in substantial noise within the reconstructed point clouds. Although current forest 3D reconstruction methods have achieved notable improvements in accuracy, efficiency, and applicability, the inherent complexity of forest scenes combined with the limitations of existing algorithms continues to impede comprehensive and accurate 3D data acquisition. Effectively capturing multi-scale structural features while simultaneously addressing challenging lighting and occlusion conditions remains a critical open problem. Meanwhile, deep learning models remain without well-established solutions for effective cross-scale feature fusion under forest scene conditions.
To address the aforementioned challenges, this study proposes and validates a novel multi-view 3D reconstruction framework tailored for forest environments, termed FS-MVSNet. Building upon MVSNet as the baseline, FS-MVSNet innovatively integrates a multi-scale feature pyramid and attention mechanisms to enable the collaborative extraction of large-scale trunk structures and fine-scale branch and foliage details. The specific contributions of this research are outlined as follows:
- To overcome the limitation of MVSNet in simultaneously processing multi-scale features such as trunks and canopies during feature extraction, we replace the convolutional backbone with a Bi-directional Feature Pyramid Network (B-FPN) for enhanced multi-scale feature fusion and extraction. B-FPN enhances the network’s capacity to capture texture information across multiple scales by employing a multi-path feature fusion mechanism.
- In response to severe occlusions and lighting variations in forest environments, we introduce a channel attention mechanism—the squeeze-and-excitation (SE) module—during the cost volume regularization stage to enhance the network’s selective focus on critical features. The SE module adaptively recalibrates feature channel weights, thereby optimizing critical information within the cost volume while suppressing irrelevant or redundant features.
- A novel 3D reconstruction framework, FS-MVSNet, integrating B-FPN and SE modules, is proposed and experimentally validated through real-world forest scene modeling. Comparative experiments against the baseline MVSNet and the mainstream SfM-MVS pipeline are conducted to verify the effectiveness of FS-MVSNet in forest 3D reconstruction tasks.
To further validate the feasibility of FS-MVSNet for practical single-tree parameter extraction, we design a workflow based on reconstructed point cloud data for extracting the tree DBH in forest scenarios. The extracted DBH parameters are quantitatively compared with ground truth field measurements, thereby providing robust evidence for the practical applicability of FS-MVSNet.
2. Materials and Methods
2.1. Dataset Details
2.1.1. Study Area
In this study, three representative forest parks in Beijing were selected as study areas in Figure 1, within which a total of four sample plots were established. A single sample plot was established in Jiufeng National Forest Park and another in Dongsheng Bajia Country Park, designated as Plot 1 and Plot 2, respectively. Two sample plots were established in the Olympic Forest Park, designated as Plot 3 and Plot 4. Jiufeng National Forest Park, situated in the northwest of Haidian District, Beijing, covers an area of approximately 8.3 km2. The park features low mountainous and hilly terrain, with elevations ranging from 200 to 950 m, and is primarily covered by natural secondary forests with complex canopy structures, making it highly representative. Dongsheng Bajia Country Park, located in Dongsheng Town, Haidian District, is an urban country park themed around natural ecology and recreational activities, featuring diverse vegetation types suitable for small- and medium-scale forest structure studies. Olympic Forest Park, situated in Chaoyang District, Beijing, covers a total area of 680 hectares, including 478 hectares of green spaces and 67.7 hectares of water surfaces, with a greening coverage rate of 95.6%. The park is rich in forest resources, dominated by mixed forests of trees and shrubs, and serves as a typical representative of urban forests. Plot 3 and Plot 4 were selected from distinct regions within the Olympic Forest Park.
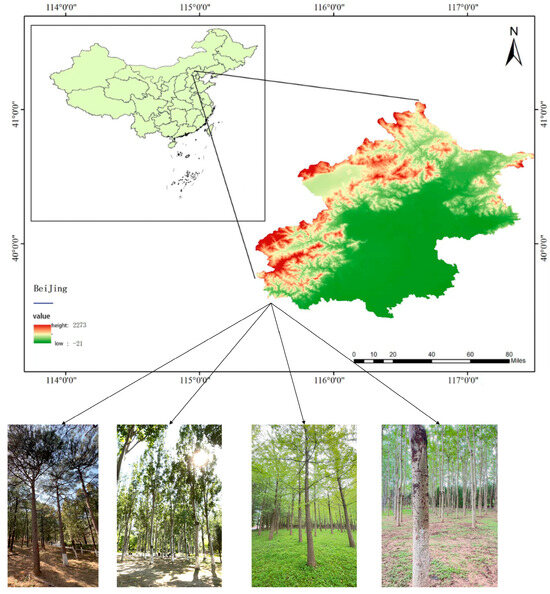
Figure 1.
Location map of the research area.
2.1.2. Sample Plots Data
In this study, a hypsometer, diameter tape, and total station were employed to collect ground truth measurements for all trees within each sample plot. Field data collection procedures are illustrated in Figure 2. Each sample plot covered an area of 15 m × 15 m. The total station was utilized to measure the spatial coordinates of trees, ensuring high positional accuracy. In each sample plot, the tree height, DBH, and relative position of all trees were systematically measured. To minimize measurement errors and enhance data precision, particularly in areas with complex terrain and dense vegetation, all key parameters were measured multiple times and subsequently averaged. Owing to the high degree of canopy overlap in Plot 4, capturing complete tree height images through close-range photography proved challenging. Consequently, image acquisition focused on the DBH regions of trees to facilitate forest reconstruction and DBH extraction under high-overlap conditions. The ground truth measurements collected from the four sample plots are summarized in Table 1.

Figure 2.
Actual data collection site. The photo shows the operator using a laser-based hypsometer to measure tree height at an approximate distance of 12 m from the target tree. During field measurements, a consistent distance of 10–15 m was maintained to ensure canopy visibility and the accurate detection of tree tops. The laser hypsometer provides strong canopy penetration ability and ensures reliable tree height estimation in open park environments.

Table 1.
Statistics of measured plot data.
The data were generated using multi-view images captured via an iPhone 15. Data collection occurred in June 2023 between 10:00 and 14:00 under sunny conditions. One image was extracted every two seconds from stabilized handheld videos. Image registration and 3D reconstruction were conducted using COLMAP (v3.8), employing Structure-from-Motion and Multi-View Stereo modules. The generated point cloud was initially in a relative scale, and scale calibration was applied using a 1 m reference marker visible in each plot. Ground points were extracted using RANSAC-based plane fitting, and height normalization was performed by subtracting ground elevation from all Z-coordinates. The average point spacing was approximately 2–3 cm, sufficient for DBH estimation tasks.
2.2. Field Data Collection
In this study, near-ground imagery was captured using a handheld iPhone 15 smartphone. The device is equipped with a 48-megapixel main camera, capable of capturing high-resolution, detail-rich images that meet the quality requirements for 3D reconstruction, as shown in Figure 3. During image acquisition, the operator followed a slow spiral trajectory from the plot perimeter toward the center, ensuring comprehensive coverage from multiple viewpoints. Throughout the acquisition process, the camera was maintained in a stable posture with a slight forward-downward tilt to ensure sufficient coverage of key areas, including trunks, canopies, and ground surfaces. For the collected video data, one frame was automatically extracted every two seconds to generate a continuous sequence of images. In total, 323, 352, 390, and 310 raw images were collected from the four sample plots, respectively. To ensure high-quality 3D reconstruction, all captured images underwent a rigorous filtering process prior to modeling. Image quality was evaluated using a hybrid approach combining automated analysis and manual inspection. Initially, frames exhibiting substantial motion blur, overexposure, or underexposure were automatically detected and discarded using OpenCV-based image processing scripts. This was followed by a manual review to eliminate images with ambiguous textures, repetitive content, or inadequate lighting conditions. This two-stage filtering strategy ensured that only images meeting the quality criteria were retained for reconstruction. After filtering, the number of valid images per sample plot was 315, 340, 365, and 295, respectively. All retained images were subjected to histogram equalization to mitigate illumination effects [23] and subsequently used for image enhancement and 3D reconstruction analysis.

Figure 3.
Schematic diagram of collection trajectory.
2.3. Methodology
To address the limited reconstruction accuracy of existing 3D reconstruction algorithms in forest environments, this study introduces a novel network architecture, termed FS-MVSNet. First, to accommodate the substantial scale differences between tree trunks and foliage in forest scenes, a multi-scale feature pyramid module is incorporated into the feature extraction stage of the MVSNet backbone. This module facilitates the collaborative extraction of large-scale trunk structures and fine-scale foliage details. Second, to tackle pervasive challenges in forest scenes—such as occlusions and low-texture regions—an attention mechanism is integrated into the cost volume construction stage. This mechanism allows the network to automatically distinguish informative regions from noise, thereby suppressing the influence of irrelevant content. Finally, based on the reconstructed forest point cloud, a semi-automated pipeline for extracting DBH was developed. The pipeline consists of four main stages: scale calibration, ground point extraction, individual tree segmentation, and DBH estimation. This pipeline enables the reliable extraction of single-tree DBH parameters from the reconstructed point cloud data.
2.3.1. FS-MVSNet Architecture Design
Although image enhancement techniques can partially improve data quality, challenges such as complex canopy structures, drastic illumination variations, and severe occlusions continue to hinder the accuracy of forest 3D reconstruction. To address these issues, we propose FS-MVSNet, a novel MVS network, whose overall architecture is illustrated in Figure 4. The framework comprises four core components: (1) feature extraction using a B-FPN, (2) differentiable homography warping, (3) cost volume regularization enhanced by an SE attention module, and (4) multi-scale depth estimation.
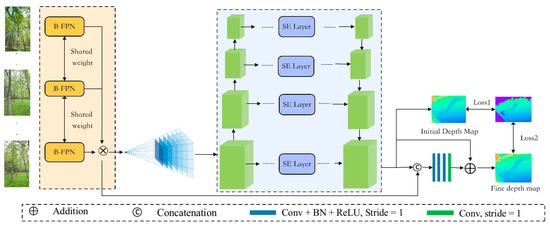
Figure 4.
The architecture of FS-MVSNet.
In the first stage, B-FPN is employed to replace the conventional convolutional neural network (CNN) backbone, enabling efficient multi-scale feature extraction and fusion. Its multi-path fusion mechanism enhances the network’s capacity to capture texture information at various scales, making it well-suited for modeling the complex multi-scale structures typically found in forest environments. Following feature extraction, a differentiable homography warping module aligns the extracted features from multiple views to a common reference frame, ensuring effective cross-view comparison and matching within a unified coordinate system. During the cost volume regularization stage, an SE (squeeze-and-excitation) attention module is incorporated to enhance the model’s ability to selectively emphasize informative features. The SE module adaptively recalibrates channel-wise feature responses, thereby improving cost volume regularization accuracy and suppressing the influence of irrelevant or redundant cues. Upon completing cost volume regularization, depth maps are estimated based on the optimized volume. A multi-scale depth regression strategy is adopted to produce fine-grained, high-precision depth maps, thereby offering robust data support for subsequent single-tree parameter extraction.
- (1)
- B-FPN
In forest environments, the coexistence of coarse tree trunks and fine-grained foliage poses significant challenges for conventional algorithms, which often fail to capture both large-scale structures and fine details simultaneously—leading to fragmented or distorted reconstruction outputs. Traditional Feature Pyramid Networks (FPNs), which rely on a top-down hierarchical structure, often encounter difficulties in concurrently capturing global semantic context and fine-grained spatial details. This limitation becomes especially pronounced in forest scenes, where regions such as shaded tree trunks exhibit low texture, and uneven lighting conditions—such as sunlight filtering through the canopy—further degrade feature consistency and hinder accurate cross-scale representation [32]. To overcome these challenges, we integrate a B-FPN, which enhances the conventional FPN by introducing a bottom-up information pathway alongside the existing top-down flow. This bidirectional design facilitates synergistic interactions between high-level semantic representations and low-level spatial features, thereby substantially improving the network’s ability to encode multi-scale vegetation structures with greater precision and robustness. The B-FPN adopts a three-layer convolutional network as the backbone feature extractor, with each layer composed of a 3 × 3 convolution, batch normalization (BN), and ReLU activation. The overall architecture is illustrated in Figure 5. This hierarchical design progressively expands the receptive field, enabling the extraction of both low-level edge textures and high-level semantic representations. BN alleviates feature distribution shifts caused by uneven illumination within forest scenes, while ReLU activation ensures stable gradient propagation throughout the deep network. Upon base feature extraction, a multi-scale feature pyramid {P5, P4, P3, P2} is constructed, with spatial resolutions increasing progressively from 1/32 to 1/4. Feature fusion is conducted via a bi-directional interaction strategy. In the top-down pathway, high-level features are bilinearly upsampled and fused with lower-level features through element-wise addition. Concurrently, the bottom-up pathway transmits fine-grained spatial details to upper layers via 3 × 3 convolution-based downsampling. This bi-directional fusion enables high-level semantic information to guide the refinement of lower-layer features, while low-level spatial cues enhance the localization accuracy of high-level representations. After each fusion stage, a 1 × 1 convolution is applied to enhance the representation capacity of the merged features. The final multi-scale outputs offer enriched representations of forest vegetation structures across varying scales.
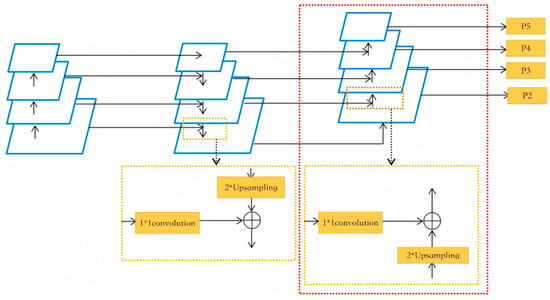
Figure 5.
B-FPN structure.
- (2)
- Cost Volume Regularization with SE Attention
In forest scene reconstruction, the quality of the cost volume plays a critical role in determining the accuracy of depth estimation. Forest scenes typically exhibit uneven illumination, frequent occlusions, and blurred or repetitive textures, leading traditional algorithms to produce erroneous feature correspondences and noisy point clouds. To address these challenges, we propose an attention-enhanced cost volume regularization strategy that dynamically reweights feature channels and significantly improves reconstruction performance (Figure 6). The cost volume, a central data structure in multi-view stereo (MVS), is formulated as a 4D tensor of size H × W × D × F, where H and W denote the spatial dimensions, D represents the number of depth hypotheses, and F denotes the number of feature channels. In complex forest environments, vegetation occlusions and illumination variability hinder accurate estimation of feature channel significance, resulting in biased or inaccurate depth predictions. To mitigate this issue, we integrate an SE attention module into the cost volume regularization pipeline. The attention mechanism enhances cost volume representation via three key stages: global average pooling, adaptive channel weighting, and reweighting of the cost volume. First, global average pooling is applied along the spatial and depth dimensions (H × W × D) to derive a compact channel-wise descriptor:
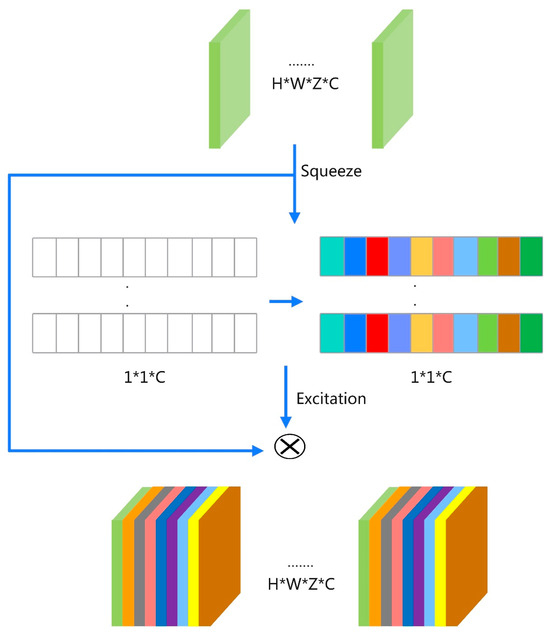
Figure 6.
SE structure.
Here, f denotes the channel index, and Zf represents the global contextual feature for channel f.
Next, the feature vector Z is passed through two fully connected (FC) layers to model inter-channel dependencies and compute attention weights. The first FC layer reduces the dimension by a factor r = 16r = 16r = 16, followed by a ReLU activation. The second FC layer restores the channel dimension, and a sigmoid function is applied to yield the final attention vector:
where W1 and W2 denote the weight matrices of the two FC layers, and ReLU represents the nonlinear activation function.
Finally, the learned attention weights α are applied to the original cost volume C via element-wise multiplication, enhancing informative channels and suppressing noisy or irrelevant ones. The attention-enhanced cost volume significantly improves feature discriminability and enables more accurate depth reconstruction in complex forest environments.
- (3)
- Hybrid Loss Function
To accommodate the feature pyramid structure and attention mechanisms integrated into FS-MVSNet, we design a hybrid loss function that jointly leverages multi-scale supervision and attention-guided optimization, significantly improving the accuracy and robustness of depth predictions. The designed loss function fully accounts for the architectural characteristics of the network, enabling differentiated supervision across multiple feature hierarchies and critical spatial regions. In constructing the overall loss, we first introduce a multi-scale supervision term , formulated as follows:
where S denotes the number of pyramid levels, is the predicted depth at scale s, and is the associated weight factor for each scale.
We define to ensure that coarser scales prioritize global structural consistency while finer scales focus on capturing detailed information. This hierarchical weight decay strategy enables the network to initially prioritize global structural learning and progressively shift attention towards local details throughout the training process. To further exploit attention guidance, we propose an attention-weighted loss term , defined as follows:
where ∈ [0, 1] represents the per-pixel attention weight, derived either from the attention module or from depth gradient magnitudes, emphasizing critical regions such as trunk edges and foliage boundaries. The overall hybrid loss is defined as a weighted linear combination of three terms:
where the hyperparameters are empirically set as λ1 = 1, λ2 = 0.5, and λ3 = 0.2 based on extensive ablation experiments.
This balanced design enables coordinated optimization across multiple feature scales and significantly enhances prediction accuracy, particularly in structurally critical regions.
2.3.2. Semi-Automated Single-Tree Parameter Extraction Workflow
In forest resource surveys and research, commercial software such as LiDAR 360 has been widely employed for individual tree extraction based on airborne or terrestrial LiDAR data. In contrast, the data utilized in this study are derived from point clouds generated via multi-view image-based reconstruction techniques. However, the standard workflows and algorithms of LiDAR 360 are not fully compatible with the structural and quality characteristics of multi-view reconstructed point clouds. During preprocessing, filtering, crown segmentation, and trunk localization stages, discrepancies in point cloud quality and structural properties often lead to reduced identification accuracy and higher false extraction rates.
Therefore, to address these challenges, we design a customized individual tree parameter extraction workflow specifically tailored for multi-view reconstructed point clouds. The DBH estimation was conducted using custom Python 3.8.10 scripts implemented in the Open3D v0.17.0 and NumPy v1.23.5 frameworks. A semi-automated pipeline was developed, in which all trees within each sample plot were segmented and processed automatically based on spatial clustering. For each segmented tree, 2D cross-sectional slices at 1.3 m above ground were extracted, and an iterative circle fitting algorithm was applied. The pipeline included ground filtering, candidate slice extraction, residual-based outlier removal, and multi-round robust fitting. All computations were performed in batch mode, with no manual intervention required. The designed parameter extraction pipeline comprises four key stages:
- (1)
- Scale Calibration: In multi-view reconstructed point clouds, due to the relative nature of structure recovery, the resulting model lacks a consistent real-world metric scale. To ensure that subsequent geometric estimations are physically meaningful, scale calibration is performed prior to parameter extraction. We adopt a reference object of known length (1 m) placed within the acquisition scene prior to image capture. After reconstruction, two endpoints of the reference marker are manually identified within the point cloud, and their Euclidean distance is measured. The scale factor s is subsequently computed by comparing the measured distance with the actual physical length, formulated as follows:
- (2)
- Ground Point Extraction: Following scale calibration, the next step involves extracting ground points from the 3D point cloud. Ground point extraction aims to eliminate non-ground objects from the forest scene, laying a solid foundation for subsequent individual tree segmentation and DBH (diameter at breast height) estimation. Due to the overlap between ground surfaces and vegetation in multi-view reconstructed point clouds, direct segmentation of ground points remains challenging. To tackle this, we employ the RANSAC-based plane fitting algorithm, renowned for its robustness against outliers, to extract ground points. The RANSAC algorithm is particularly well-suited for estimating ground planes from noisy point clouds with substantial outliers. Its core principle involves randomly sampling minimal point subsets, fitting candidate planes, and optimizing model parameters by evaluating inliers across the point cloud. In ground fitting, the RANSAC model can be mathematically expressed as follows:where (x, y, z) denotes the coordinates of a point, (A, B, C) represents the plane’s normal vector, and d is the intercept. By fitting a plane to the point set and calculating the perpendicular distance from each point to the plane, points are classified as either ground or non-ground. RANSAC iteratively performs random sampling, model fitting, and inlier evaluation, ultimately retaining the plane model that maximizes the number of inliers. To ensure accurate ground extraction, points located within a vertical distance of 2–5 cm from the fitted plane are classified as ground points.
- (3)
- Individual Tree Segmentation: Following scale calibration and ground point extraction, the point cloud typically comprises a mixture of multiple standing trees. To enable accurate extraction of parameters for each individual tree, spatial segmentation at the single-tree level is performed on the point cloud. Theoretically, tree trunks exhibit approximately vertical growth patterns, allowing them to be abstracted using straight-line models. In 3D space, a straight line space can be uniquely determined by a spatial point p = (p1x,p1y,p1z) and a unit direction vector n = (nx,ny,nz) with its parametric form expressed as follows:
Based on this, the shortest distance DL from an arbitrary spatial point (x, y, z) to the straight line can be calculated as follows:
where p denotes an arbitrary spatial point and D represents the unit direction vector. This distance metric is utilized to determine whether a given point belongs to the current trunk model.
- (4)
- DBH (Diameter at Breast Height) Extraction: Finally, the DBH of each individual tree is estimated. By isolating trunk points from the 3D point cloud, the DBH for each tree is calculated, thereby completing the individual tree parameter extraction process. Figure 7 illustrates the DBH extraction process based on two-dimensional (2D) circle fitting. In the figure, blue points represent the local cross-sectional point cloud extracted at 1.3 m above ground, serving as candidate points for DBH estimation. Red “×” markers indicate outliers or noisy points, which may arise from branches, reconstruction artifacts, or non-trunk structures. Notably, some red outlier points are located near the center of the trunk cross-section rather than at the periphery. These points are likely the result of 3D reconstruction noise or projection artifacts caused by occluded views, uneven lighting, or insufficient texture in the central trunk region during image capture. Since the reconstruction is image-based, certain internal structures may appear distorted or duplicated due to multi-view matching inconsistencies. Although these points are spatially close to the trunk center, their high residual values relative to the initial circle fitting facilitates their effective exclusion through the residual-based filtering step. First, an initial circle fitting is performed on all cross-sectional points using the least squares method to estimate a preliminary circle center and radius, visualized as a green dashed circle. Although this step provides a coarse DBH estimate, it may be biased by the presence of outliers. To refine the fitting accuracy, the residual distance between each point and the initially fitted circle is computed. Based on the average point spacing of the reconstructed point cloud (approximately 1.5–2.5 cm), a residual threshold of 1.5 cm was empirically selected. This value effectively excludes outlier points while preserving valid trunk boundary data, and aligns with thresholds used in similar forestry studies. Points with residuals smaller than 1.5 cm are retained, while outliers are eliminated. Subsequently, a robust circle fitting is performed on the filtered inlier points. The final fitted circle, represented by the purple solid line in the figure, provides a closer approximation of the actual trunk cross-section. The final circle center is marked by a black pentagram symbol, and the circle diameter d is recorded as the final DBH value. The detailed steps are summarized as follows:
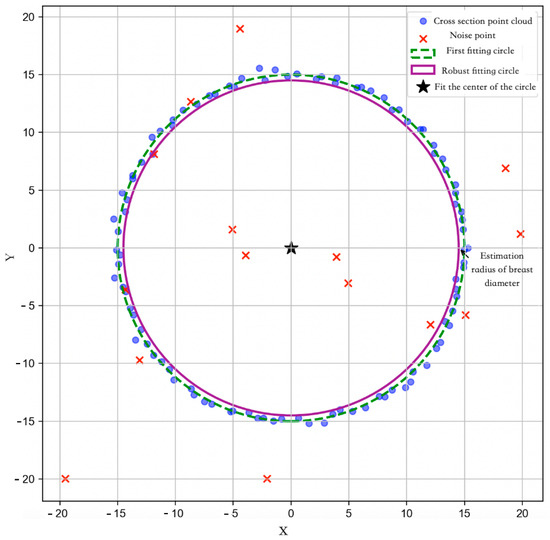 Figure 7. Schematic diagram of chest diameter extraction.
Figure 7. Schematic diagram of chest diameter extraction.
- Point Cloud Preprocessing and Cross-sectional Extraction
First, a local cross-sectional point cloud near 1.3 m above the ground is extracted from the point cloud of each target tree trunk. To suppress interference caused by foliage and other non-trunk structures, vertical stratified filtering is applied to the point cloud, retaining only neighboring points near the target vertical height. To mitigate vertical perturbations introduced by reconstruction artifacts, a fixed-size window (±1.5 cm) is employed to extract a localized point set centered at the desired vertical position, serving as candidate points for DBH estimation.
- 2.
- Two-Dimensional Cross-sectional Fitting and Initial Estimation
A 2D projection is applied to the extracted cross-sectional points, and a circle model is fitted using the least squares method to estimate the center coordinates and radius. The fitting objective function is formulated as follows:
where (xi, yi)are the coordinates of the projected points, (xc, yc) denote the estimated circle center coordinates, and d represents the estimated radius.
- 3.
- Robust Point Filtering Based on Residuals
After the initial circle fitting, a residual-based point filtering mechanism is introduced. The residual is defined as the deviation between the distance from each point to the fitted circle and the estimated mean radius. Points exhibiting an absolute residual less than a predefined threshold (±1.5 cm) are retained for re-fitting, whereas outliers are discarded. The residual error is computed as follows:
- 4.
- Multiple Fittings and Result Fusion
To further enhance fitting stability, multiple rounds of random subsampling and circle fitting are performed on the cross-sectional point cloud. All valid fitting results are recorded, and a weighted fusion is conducted based on the support point ratio and residual distribution. The final DBH estimation is calculated as follows:
where N denotes the number of valid fitting samples, and di represents the radius estimated from the i-th fitting trial. The final DBH value is obtained by doubling the average radius. Fitting results with insufficient support point ratios or abnormally large residual errors are excluded from the final averaging process.
2.4. Evaluation Metrics
To evaluate the accuracy of the single-tree parameter extraction method proposed in this study, the actual measured DBH values were used as reference. Four evaluation metrics were adopted to quantitatively analyze the extraction results, including reconstruction rate (r), root mean square error (RMSE), relative root mean square error (rRMSE), and accuracy evaluation (AE) [23]. The corresponding formulas are as follows:
where n is the number of trees successfully reconstructed and extracted, and m is the total number of trees in the sample plot. The reconstruction rate reflects the model’s ability to comprehensively reconstruct and cover trees within the area [35].
where Textraction denotes the extracted DBH value of the i-th tree, Ttruth denotes the actual measured DBH value of the i-th tree, and n is the number of matched trees. RMSE reflects the average error between the extracted and measured DBH values [36].
where is the mean of all actual measured DBH values. rRMSE measures the magnitude of the extraction error relative to the actual data, expressed as a percentage.
AE = (1 − rRMSE) × 100%
The AE metric is used to evaluate the accuracy and reliability of the extracted data. A higher AE value (closer to 100%) indicates better extraction performance. These metrics are crucial for comparing different methods, different regions, and different data sources, and serve as essential references for verifying the reliability of the extraction method.
3. Experiment and Results
3.1. Experimental Setup
To validate the effectiveness of the proposed FS-MVSNet, a multi-view stereo network enhanced with feature pyramid structures and attention mechanisms, in handling complex 3D reconstruction tasks, a comprehensive experimental setup was established. Additionally, detailed configurations were specified for both the model training and testing processes. The following sections describe the experimental setup in terms of hardware environment, software environment, and experimental parameter settings.
3.1.1. Hardware Environment
To ensure the efficiency of model training and inference, all experiments were conducted on a high-performance computing platform. The specific hardware configurations are summarized in Table 2.

Table 2.
Hardware configuration.
3.1.2. Software Environment
All experiments and developments in this study were conducted under the software environment described above. The tools and library versions used are listed in Table 3.

Table 3.
Software configuration.
3.1.3. Experimental Parameters
To ensure the training stability and convergence performance of the proposed FS-MVSNet in forest 3D reconstruction tasks, the systematic configuration and fine-tuning of key model parameters were performed. In this study, the DTU dataset was selected as the training dataset, while a forest dataset constructed from multi-view imagery of forest plots was used for validation. During the experiments, the input image resolution was uniformly set to 1280 × 720 pixels to guarantee sufficient spatial details for feature extraction and depth estimation. The detailed experimental parameter settings are summarized in Table 4.

Table 4.
Model parameter settings.
3.2. Results and Analysis of Forest Reconstruction
In this study, reconstruction experiments were conducted across four representative sample plots. The proposed FS-MVSNet model was thoroughly compared against the conventional SFM-MVS pipeline and the baseline MVSNet model. The experimental results demonstrate the superior performance of FS-MVSNet in complex forest environments.
3.2.1. Forest Reconstruction
By observing the spatial distribution of point clouds in Figure 8, it was evident that the conventional SfM-MVS method exhibited significant limitations when applied to forest environments. Tree overlap and occlusion made feature point matching challenging, leading to insufficient point cloud generation and frequent discontinuities, especially at tree bifurcations. Such limitations rendered it difficult to distinguish individual trees, resulting in sparse and fragmented point clouds. While MVSNet showed overall improvements compared to SfM-MVS, it still suffered from issues such as blurred local structures and trunk discontinuities. In particular, in areas with weak textures, MVSNet remained vulnerable to occlusions and texture scarcity, resulting in inaccurate matching and missing structures. In contrast, the proposed FS-MVSNet substantially improved point cloud quality through two key innovations. Firstly, the introduction of a multi-scale feature extraction mechanism effectively balanced the capture of both trunk structures and canopy details. By extracting features at multiple scales, FS-MVSNet maintained the clarity of trunk structures while accurately capturing canopy information, thereby significantly enhancing point cloud density and completeness, and avoiding the blurring or fragmentation of tree trunks. Secondly, the incorporation of an attention mechanism further strengthened the model’s ability to focus on critical structural regions. This enhancement was particularly notable in Sample Plot 2, where severe canopy occlusion posed substantial challenges. The attention mechanism enabled better detail preservation for both trunks and canopies under complex forest conditions.

Figure 8.
Three-dimensional point cloud reconstruction effect of the sample plot.
3.2.2. Trunk and Canopy Fine-Structure Reconstruction Performance
As the most central and stable component of forest structure, the quality of tree trunk reconstruction directly impacts the overall topology of the point cloud model and the subsequent accuracy of DBH (diameter at breast height) parameter extraction [37]. Figure 9 illustrate the point cloud reconstruction results for the tree trunk regions using MVSNet, SfM-MVS, and the proposed FS-MVSNet. The SfM-MVS method demonstrated poor performance in trunk reconstruction. The generated point clouds were noticeably sparse and discontinuous, with a large number of holes and fractures on the trunk surface (highlighted in the red boxes). Additionally, the edges of the trunks appeared blurred and lacked precision, making it difficult to recover the continuous structure required for trunk modeling. Although the MVSNet method showed relative improvements compared to SfM-MVS, significant structural defects remained. While the point cloud density was moderately higher, the trunk surfaces and edges still exhibited noticeable noise and fractures, resulting in insufficient continuity and completeness (as shown in the red boxes). In contrast, the proposed FS-MVSNet exhibited clear advantages in trunk reconstruction. The point clouds in the trunk regions were dense and uniformly distributed, with clear and continuous edges. The trunk surfaces appeared smooth and detailed, with no significant noise or missing regions, demonstrating a much higher degree of completeness. These results indicate that FS-MVSNet is capable of accurately and clearly capturing the fine textures of tree trunks, validating the effectiveness of incorporating multi-scale feature pyramids and attention mechanisms for improving the structural reconstruction quality of forest trunks.

Figure 9.
Reconstruction effect of trunk area.
The canopy structure, characterized by its complex geometry and fine-grained branches and leaves, presents one of the major challenges in forest 3D reconstruction [38]. Figure 10 compares the canopy reconstruction results achieved by the three methods. The SfM-MVS method produced sparse and disordered reconstructions in the canopy regions. Most fine details of branches and leaves were missing, and the resulting point clouds exhibited significant fragmentation and discontinuities, failing to accurately reconstruct the intricate structures of the canopy. Given the structural complexity and severe occlusions in the canopy, the limitations of SfM-MVS were particularly evident, rendering it insufficient for capturing detailed canopy structures. The MVSNet method showed some improvements in canopy reconstruction, with relatively higher point cloud density and a rough presentation of major branch structures. However, significant noise, structural blurring, and local disorganization persisted. The fine structures of branches and leaves remained unclear, and the overall detail level was insufficient to accurately represent the geometric features and spatial relationships of the canopy. In contrast, the proposed FS-MVSNet achieved superior performance in canopy reconstruction. The reconstructed canopy point clouds were dense and finely detailed, with distinguishable branch and leaf structures. The branches appeared complete and naturally shaped, and both the overall canopy contours and local structures were well recovered. Even the intricate interwoven features of fine branches and leaves were effectively reconstructed, demonstrating significantly higher completeness. These results further validate that the feature pyramid module effectively captures multi-scale structural features within the canopy, while the attention mechanism enhances the representation of local fine details in key regions.

Figure 10.
Comparison of tree crown detail reconstruction results using different methods.
3.2.3. Single-Tree Parameter Extraction
A series of key operations—including scale calibration, ground point detection, individual tree segmentation, and DBH estimation—were applied to the forest point clouds reconstructed through multi-view 3D modeling. The segmentation results of individual trees across the four sample plots were quantitatively evaluated and compared against ground-truth tree counts.
The bar chart in Figure 11 presents a comparative analysis of reconstructed versus ground-truth tree counts across four experimental plots, using different reconstruction algorithms. Each color in the chart corresponds to a distinct reconstruction method. The blue bars indicate the ground-truth tree counts, orange represents our proposed method, green corresponds to MVSNet, and red denotes SfM-MVS. The SfM-MVS algorithm exhibited substantial overestimation, frequently misinterpreting individual trees as multiple instances. MVSNet consistently produced lower tree counts compared to our method, with a pronounced underestimation observed in Plot 3. Across all four plots, our method yielded the most accurate reconstructions, achieving tree count recovery rates of 92%, 92%, 89%, and 100%, respectively. Notably, in Plots 3 and 4, our approach outperformed MVSNet, achieving reconstruction rate gains of 7% and 8%, respectively.
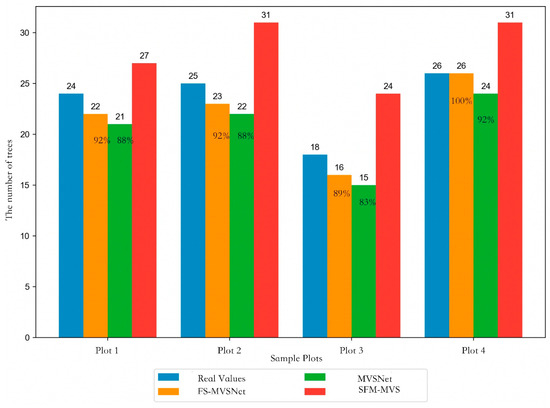
Figure 11.
Comparison of reconstruction rates of different models.
Finally, the DBH was estimated for each segmented individual tree. DBH serves as a critical metric for assessing tree growth dynamics and overall physiological health [39]. Owing to the low-density point clouds produced by the SfM-MVS pipeline, reliable DBH estimation could not be achieved. Therefore, we conducted a comparative analysis of DBH estimation accuracy between MVSNet and FS-MVSNet across multiple forest plots.
The relationship between measured and predicted diameters at breast height in Figure 12 across the four test plots is illustrated. In the plots, blue dots denote ground-truth DBH measurements, while the red dashed line indicates the ideal 1:1 regression line. Absolute error, root mean square error, and relative RMSE are annotated in the upper-right corner of each subfigure. The proposed method exhibits a strong positive correlation between predicted and measured DBH values across all four plots. Overall, the predictions exhibit high accuracy, with the majority of data points tightly clustered around the reference regression line. These findings suggest that the proposed approach yields robust and consistent performance across heterogeneous forest plots.
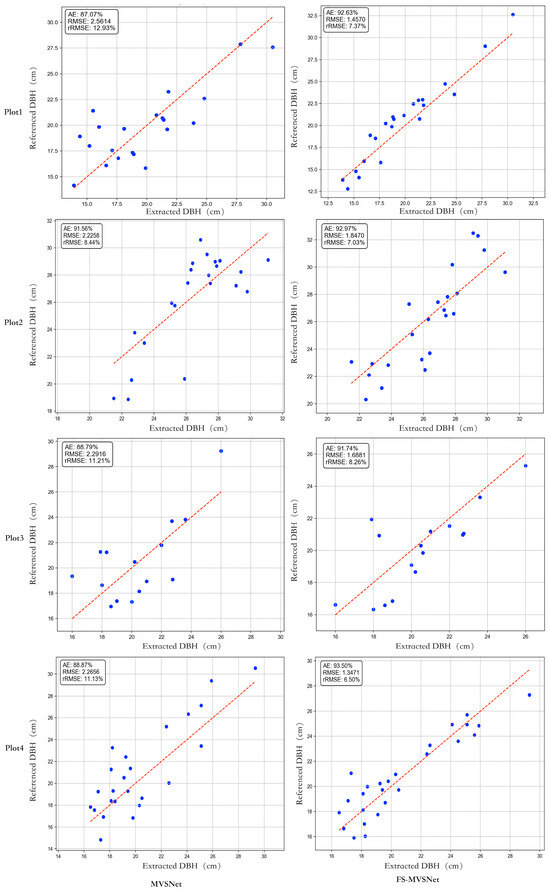
Figure 12.
Comparison of extraction results of diameter at breast height of a single tree using different methods.
3.3. Experimental Results
3.3.1. DTU Dataset Evaluation Results
FS-MVSNet was quantitatively evaluated on the DTU dataset, revealing substantial advantages in 3D reconstruction fidelity (Table 5). To evaluate the effectiveness of the proposed reconstruction method, 22 scenes (e.g., scan1, scan4, scan114) from the DTU benchmark dataset were selected as the test set. In terms of accuracy, FS-MVSNet achieved a mean error of 0.352 mm—lower than P-MVSNet [18], R-MVSNet [28], and most other learning-based counterparts—indicating its superior capacity for recovering fine geometric details. For completeness, FS-MVSNet reported a score of 0.392 mm, slightly exceeding PatchmatchNet [40] and MSCVP-MVSNet [41]. Regarding overall performance, FS-MVSNet attained a score of 0.372 mm, ranking among top-performing approaches and comparable to PatchmatchNet and Fast-MVSNet [42]. These results confirm that FS-MVSNet strikes a favorable balance between geometric accuracy and surface completeness. Compared to the baseline MVSNet, FS-MVSNet improved accuracy by 11.1%, completeness by 25.6%, and overall reconstruction performance by 19.5%.

Table 5.
Quantitative results of different methods on DTU dataset.
3.3.2. Point Cloud Density and Efficiency Analysis
Table 6 presents a comparative evaluation of point cloud density and computational efficiency across four forest plots using SfM-MVS, MVSNet, and the proposed FS-MVSNet. In all test plots, FS-MVSNet consistently produced significantly denser point clouds than both SfM-MVS and MVSNet. Specifically, compared to SfM-MVS, FS-MVSNet yielded density increases of 138.89%, 188.37%, 165.38%, and 104.76% across plots 1 through 4. Relative to MVSNet, FS-MVSNet demonstrated improved point cloud densities of 12.17%, 34.78%, 26.61%, and 17.81% in plots 1 through 4, respectively.

Table 6.
Comparison of reconstruction results of different models.
With respect to reconstruction time, the traditional SfM-MVS method exhibited the shortest processing duration (5.5–7 h across plots 1–4), primarily owing to its lower algorithmic complexity. In contrast, deep learning-based methods such as MVSNet and FS-MVSNet incurred longer runtimes as a result of their computationally intensive architectures. Specifically, MVSNet required 8.0–9.5 h, and FS-MVSNet 8.5–10.0 h across all test plots. Although FS-MVSNet introduces a modest increase in computational overhead, the trade-off is justified by substantial gains in point cloud density and reconstruction fidelity. The method thus remains practically viable for large-scale forest reconstruction tasks. These results indicate that FS-MVSNet achieves an effective balance between algorithmic performance and computational expense. Overall, the performance advantages of FS-MVSNet clearly outweigh the marginal computational cost, reinforcing its applicability in real-world forest scenarios.
3.3.3. Single-Tree Parameter Extraction Evaluation
Table 7 summarizes the quantitative evaluation results for DBH estimation across four representative forest plots. Compared with the original MVSNet model, the proposed method consistently outperformed it across all evaluation metrics. In terms of the absolute error (AE), the proposed method yielded lower error values across all test plots, with notable improvements of 5.56% and 4.63% in plots 1 and 4, respectively. Additionally, the method demonstrated substantial improvements in both the root mean square error (RMSE) and relative RMSE (rRMSE). Specifically, in plots 1 and 4, RMSE values were reduced by 43.1% and 49.3%, while the rRMSE decreased by 5.56% and 4.63%, respectively. These findings indicate that the proposed method offers enhanced accuracy in single-tree DBH estimation and contributes to improved 3D reconstruction fidelity. On average, compared with MVSNet, the proposed method increased the reconstruction rate r by 4%, reduced the AE by 3.14%, RMSE by 1.005 mm, and rRMSE by 3.64%.

Table 7.
Quantitative evaluation results of different models.
3.4. Ablation Study
To gain deeper insights into the individual contributions of each module within FS-MVSNet, we conducted a series of ablation studies. These experiments were designed to systematically remove key components—such as the B-FPN and SE modules—to assess their respective impact on the model’s performance in complex forest scene reconstruction. A baseline model and four comparative variants were constructed for evaluation, as detailed in Table 8.

Table 8.
Model ablation experiment and indicator comparison. “↓” indicates a decrease compared to the baseline model, representing improvement in the corresponding metric. “√” indicates that the corresponding module is included in the model configuration for that experiment.
Plot 1, the most structurally complex site, was selected as the reference dataset for all ablation experiments. Model performance was evaluated using root mean square error (RMSE), relative RMSE (rRMSE), and absolute error (AE) metrics. The experimental results are summarized in the table below.
In the ablation experiments, the full FS-MVSNet model consistently outperformed its ablated variants across all evaluation metrics. These findings underscore the importance of module synergy within the complete model, collectively contributing to substantial performance gains in complex forest scene reconstruction. The experimental results reveal that the B-FPN module is crucial for effective multi-scale feature representation. In complex forest environments, the diverse structural and textural patterns across scales necessitate multi-path feature fusion for effective representation. Removing the B-FPN module impaired the model’s ability to integrate hierarchical features, resulting in a marked decline in both point cloud density and reconstruction accuracy. The SE-based attention mechanism, embedded in cost volume regularization, adaptively reweights feature channels to strengthen focus on key regions such as trunk boundaries and foliage edges. Ablating this mechanism preserved point cloud density to some extent, but significantly degraded the geometric fidelity of reconstructed out-puts. This underscores the mechanism’s role in enhancing feature discriminability under challenging conditions such as severe occlusion and illumination variability. Collectively, the ablation study confirms the necessity and synergistic function of each component within FS-MVSNet. The complete model exhibited superior performance in terms of point cloud density, RMSE, rRMSE, and AE, offering robust and reliable data support for high-fidelity forest reconstruction.
4. Discussion
This study addresses critical limitations in MVS matching accuracy and point cloud quality, which hinder reliable individual tree parameter extraction in complex forest environments. To tackle these challenges, we propose an enhanced FS-MVSNet architecture for 3D reconstruction, enabling the accurate estimation of DBH from the resulting point clouds. Based on comprehensive experimental results and a methodological design, the proposed framework achieves notable advancements and innovations in the following key aspects:
- Introduction of a B-FPN to enhance the representation of multi-scale features. The traditional MVSNet architecture typically performs feature extraction at fixed or unidirectional multi-scale levels, limiting its capacity to capture the diverse structural details of large-scale trunks and fine-grained foliage in forested environments. To overcome these limitations, we incorporate a B-FPN during the feature extraction stage, enabling high-level semantic information to flow downward and enhancing low-level features with enriched textures and fine-scale details. Experimental results indicate that the integration of B-FPN significantly increases both the density and completeness of point clouds, particularly in structurally complex regions such as forest canopies and leafy undergrowth. Notably, in dense forest plots with severe occlusions or when focusing on fine-scale canopy reconstruction, the proposed approach yields more continuous and visually coherent reconstructions with minimal fragmentation.
- Integration of a squeeze-and-excitation (SE) attention mechanism into cost volume regularization to enhance matching stability in low-texture and occluded regions. Forest imagery frequently exhibits uneven lighting conditions, localized over-exposure, and extensive shadow regions, all of which hinder stable feature extraction and correspondence matching. To address these challenges, we embed a channel-wise squeeze-and-excitation attention module within the cost volume regularization process, enabling the network to adaptively emphasize informative feature channels while attenuating noise and redundant signals. This mechanism proves particularly effective in challenging regions, including trunk-to-ground transitions and densely interwoven canopy structures, leading to a notable reduction in mismatches.
- A tailored pipeline for extracting the DBH from forest-based multi-view point clouds, demonstrating its feasibility in operational forestry scenarios. Forest-derived point clouds frequently exhibit high noise levels, inconsistent trunk structures, and extensive occlusions within the canopy layer. In contrast to conventional LiDAR-only pipelines, we propose a semi-automated method for directly estimating the DBH from reconstructed point clouds, comprising ground point detection, individual tree segmentation, and circular fitting for trunk diameter estimation. Field evaluations indicate that point clouds generated by FS-MVSNet yield a lower root mean square error (RMSE) and reduced relative error in DBH estimation. In certain plots, the absolute estimation accuracy for the DBH exceeded 93%, with the proposed method out-performing both the baseline MVSNet and conventional SfM-MVS approaches in terms of accuracy and robustness. These results suggest that the enhanced network produces point clouds that are not only visually complete but also sufficiently precise to support the high-accuracy estimation of forestry metrics.
Compared to existing MVS reconstruction methods, FS-MVSNet incorporates several architectural innovations. First, the bidirectional integration of multi-scale features enables comprehensive representation of textures from tree trunks, foliage, and ground surfaces. Second, the embedded channel-wise attention mechanism enhances correspondence reliability in occlusion-prone and weakly textured areas. Third, a downstream parameter extraction pipeline is tailored to the unique structural properties of forest environments. These innovations are empirically validated, significantly improving both the operational feasibility and geometric accuracy of the reconstruction framework under real-world forest conditions. FS-MVSNet achieves significantly improved reconstruction quality but incurs relatively longer processing times compared to baseline methods. This increased computational load is mainly attributed to the incorporation of multi-scale feature pyramids and attention mechanisms, which enhance spatial detail at the cost of higher inference complexity. To address this limitation, several optimization strategies could be explored. First, model acceleration techniques such as network pruning, lightweight backbone substitution, or tensor quantization could be adopted to reduce computation without compromising accuracy. Second, parallel processing using GPU acceleration or distributed computing across tiles may help scale performance on larger areas. Additionally, reconstruction runtime can be reduced by optimizing image selection—using key-frame sampling or view clustering to minimize redundant inputs while preserving 3D completeness. Such approaches have been successfully applied in recent MVS pipelines to balance accuracy and speed. These strategies offer practical pathways to enhance the efficiency of FS-MVSNet, especially for real-time or large-scale forestry applications.
Our DBH estimation approach shares conceptual similarities with the iterative fitting method described by Panagiotidis et al. [44], who employed terrestrial laser scanning to estimate stem volumes using high-resolution point clouds. However, unlike their TLS-based workflow, our method relies on multi-view image-derived point clouds, which are typically lower in density and more prone to occlusion-induced noise. Despite this, our residual-based multi-fit strategy yielded comparable DBH estimation accuracy, demonstrating that robust fitting can be achieved even with photogrammetrically generated point clouds. While Panagiotidis et al. focused on stem volume reconstruction, our study emphasizes operational DBH extraction under image-only conditions, offering a lightweight and low-cost alternative for forest inventory in data-constrained environments.
In summary, this study presents a novel integration of multi-view stereo reconstruction with individual-tree parameter estimation for forestry applications. The combination of theoretical advancement and empirical validation substantiates the feasibility and superiority of the B-FPN and attention-augmented MVSNet framework in complex forested environments. Looking ahead, integrating multi-source data fusion strategies holds promise for further improving the completeness and precision of reconstructed point clouds.
5. Conclusions
This study introduces a novel semi-automated framework for the 3D reconstruction of forest environments and the extraction of individual tree parameters. For the 3D reconstruction component, we present FS-MVSNet, a deep learning model that integrates a feature pyramid architecture with attention mechanisms. This model improves the capacity to capture multi-scale information while suppressing irrelevant and redundant features within complex forest environments. It effectively addresses the shortcomings of conventional approaches in modeling canopy structures and repeated foliage textures. For parameter extraction, we design a comprehensive workflow to estimate the DBH of individual trees based on the reconstructed point cloud data. The workflow consists of scale calibration, ground point detection, individual tree segmentation, and DBH estimation. This process facilitates the semi-automated estimation of DBH.
The results demonstrate that the proposed semi-automated framework for 3D forest reconstruction and individual tree parameter extraction consistently outperforms existing approaches across a range of evaluation metrics. Regarding 3D reconstruction, experiments conducted across four forest plots indicate that the enhanced algorithm substantially outperforms both the traditional SfM-MVS method and benchmark models. Specifically, relative to the SfM-MVS approach, the point cloud density in plots one through four increased by 138.89%, 188.37%, 165.38%, and 104.76%, respectively. When compared with the benchmark method, point cloud densities improved by 12.17%, 34.78%, 26.61%, and 17.81% in the respective plots. In terms of fine-detail recovery, the proposed method demonstrated clear advantages, particularly in the reconstruction of trunk and canopy structures. By mitigating point cloud discontinuities at bifurcation regions, the enhanced algorithm effectively reconstructs intricate canopy features while preserving tree continuity and structural integrity. Compared to benchmark models, the proposed algorithm yields denser point clouds and more refined structural representations in trunk reconstructions. Furthermore, evaluations on the DTU dataset further corroborate the method’s strong performance. The algorithm achieved respective gains of 11.1%, 25.6%, and 19.5% in accuracy, completeness, and overall performance, further substantiating its superiority in 3D reconstruction applications. In parameter extraction, the proposed method outperformed the benchmark approach in terms of absolute error (AE) across all test plots. Notably, in plots one and four, AE was reduced by 5.56% and 4.63%, respectively. For both the RMSE and relative RMSE (rRMSE), the enhanced method demonstrated notable improvements. For instance, in plots one and four, the RMSE decreased by 43.1% and 49.3%, while the rRMSE was reduced by 5.56% and 4.63%, respectively. These findings underscore the enhanced algorithm’s superiority in estimating the DBH with high accuracy. Although the proposed framework incurs a marginal increase in computation time, the substantial improvements in point cloud quality and reconstruction precision amply justify the trade-off.
The solution proposed in this study demonstrates substantial potential for applications in forest resource monitoring and management, while concurrently offering an innovative technological pathway for ecological conservation and urban green infrastructure planning. By minimizing dependence on costly LiDAR systems and leveraging a cost-efficient alternative for high-precision 3D modeling, the proposed framework offers distinct advantages in large-scale, dynamic forest resource monitoring. More critically, this study establishes a foundational technology for the development of intelligent forest resource supervision systems, bearing significant practical implications for the scientific conservation and sustainable utilization of forest ecosystems.
Author Contributions
L.D. and D.W. completed the experiments and wrote the paper. L.D. and Z.C. designed the specific scheme. L.D. and D.W. completed the result data analysis. Q.G. and R.Z. collected field data. Z.C. modified and directed the writing of the paper. Z.C. provided guidance in planning the experimental design. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China: Intelligent Forest Field Observation Equipment and Precision Extraction Technology for Tree Parameters, grant number 2023YFD2201701.
Data Availability Statement
The data will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, L.; Yu, H.; Zhong, L. Sustainable Futures for Transformational Forestry Resource-Based City: Linking Landscape Pattern and Administrative Policy. J. Clean. Prod. 2025, 496, 145087. [Google Scholar] [CrossRef]
- Sofia, S.; Maetzke, F.; Crescimanno, M.; Coticchio, A.; Veca, D.S.L.M.; Galati, A. The Efficiency of LiDAR HMLS Scanning in Monitoring Forest Structure Parameters: Implications for Sustainable Forest Management. EuroMed J. Bus. 2022, 17, 350–373. [Google Scholar] [CrossRef]
- Geng, J.; Liang, C. Analysis of the Internal Relationship between Ecological Value and Economic Value Based on the Forest Resources in China. Sustainability 2021, 13, 6795. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Wang, H.; Li, D.; Duan, J.; Sun, P. ALS-Based, Automated, Single-Tree 3D Reconstruction and Parameter Extraction Modeling. Forests 2024, 15, 1776. [Google Scholar] [CrossRef]
- Huete, A.R. Vegetation Indices, Remote Sensing and Forest Monitoring. Geogr. Compass 2012, 6, 513–532. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Y.; Zong, J.; Wang, Y.; Cao, X.; Wang, Y.; Cheng, X.; Zhang, W. Remote Sensing Application in Ecological Restoration Monitoring: A Systematic Review. Remote Sens. 2024, 16, 2204. [Google Scholar] [CrossRef]
- Chauhan, J.; Ghimire, S. ‘LiDAR Point Clouds to Precision Forestry. Int J Latest Eng Res Appl 2024, 9, 113–118. [Google Scholar]
- Deng, Y.; Wang, J.; Dong, P.; Liu, Q.; Ma, W.; Zhang, J.; Su, G.; Li, J. Registration of TLS and ULS Point Cloud Data in Natural Forest Based on Similar Distance Search. Forests 2024, 15, 1569. [Google Scholar] [CrossRef]
- Tachella, J.; Altmann, Y.; Mellado, N.; Mccarthy, A.; Mclaughlin, S. Real-Time 3D Reconstruction from Single-Photon Lidar Data Using Plug-and-Play Point Cloud Denoisers. Nat. Commun. 2019, 10, 4984. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Yang, B.; Yang, L.; Liu, F.; Xiong, K. Simulation-Based Correction of Geolocation Errors in GEDI Footprint Positions Using Monte Carlo Approach. Forests 2025, 16, 768. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Karel, W.; Piermattei, L.; Wieser, M.; Wang, D.; Hollaus, M.; Pfeifer, N.; Surovỳ, P.; Koreň, M.; Tomaštík, J.; Mokroš, M. Terrestrial Photogrammetry for Forest 3D Modelling at the Plot Level. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 8–13 April 2018; p. 12749. [Google Scholar]
- Huang, H.; Yan, X.; Zheng, Y.; He, J.; Xu, L.; Qin, D. Multi-View Stereo Algorithms Based on Deep Learning: A Survey. Multimed. Tools Appl. 2024, 84, 2877–2908. [Google Scholar] [CrossRef]
- Tian, G.; Chen, C.; Huang, H. Comparative Analysis of Novel View Synthesis and Photogrammetry for 3D Forest Stand Reconstruction and Extraction of Individual Tree Parameters. arXiv 2024, arXiv:241005772. [Google Scholar] [CrossRef]
- Gallup, D.; Frahm, J.-M.; Mordohai, P.; Yang, Q.; Pollefeys, M. Real-Time Plane-Sweeping Stereo with Multiple Sweeping Directions. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Campbell, N.D.; Vogiatzis, G.; Hernández, C.; Cipolla, R. Using Multiple Hypotheses to Improve Depth-Maps for Multi-View Stereo. In Proceedings of the Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Proceedings, Part I 10. Springer: Berlin/Heidelberg, Germany, 2008; pp. 766–779. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, H.; Weng, L. A Multi-View Matching Method Based on PatchmatchNet with Sparse Point Information. In Proceedings of the 4th World Symposium on Software Engineerig, Xiamen, China, 28–30 September 2022. [Google Scholar] [CrossRef]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively Parallel Multiview Stereopsis by Surface Normal Diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Bayati, H.; Najafi, A.; Vahidi, J.; Jalali, S.G. 3D Reconstruction of Uneven-Aged Forest in Single Tree Scale Using Digital Camera and SfM-MVS Technique. Scand. J. For. Res. 2021, 36, 210–220. [Google Scholar] [CrossRef]
- Dai, L.; Chen, Z.; Zhang, X.; Wang, D.; Huo, L. CPH-Fmnet: An Optimized Deep Learning Model for Multi-View Stereo and Parameter Extraction in Complex Forest Scenes. Forests 2024, 15, 1860. [Google Scholar] [CrossRef]
- Yan, X.; Chai, G.; Han, X.; Lei, L.; Wang, G.; Jia, X.; Zhang, X. SA-Pmnet: Utilizing Close-Range Photogrammetry Combined with Image Enhancement and Self-Attention Mechanisms for 3D Reconstruction of Forests. Remote Sens. 2024, 16, 416. [Google Scholar] [CrossRef]
- Li, Y.; Kan, J. CGAN-Based Forest Scene 3D Reconstruction from a Single Image. Forests 2024, 15, 194. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, Z.; Zhang, X. Forest 3D Reconstruction and Individual Tree Parameter Extraction Combining Close-Range Photo Enhancement and Feature Matching. Remote Sens. 2021, 13, 1633. [Google Scholar] [CrossRef]
- Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; Fang, L. Surfacenet: An End-to-End 3d Neural Network for Multiview Stereopsis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2307–2315. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth Inference for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Quan, L. Recurrent Mvsnet for High-Resolution Multi-View Stereo Depth Inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Luo, K.; Guan, T.; Ju, L.; Huang, H.; Luo, Y. P-Mvsnet: Learning Patch-Wise Matching Confidence Aggregation for Multi-View Stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10452–10461. [Google Scholar]
- Yi, H.; Wei, Z.; Ding, M.; Zhang, R.; Chen, Y.; Wang, G.; Tai, Y.-W. Pyramid Multi-View Stereo Net with Self-Adaptive View Aggregation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 766–782. [Google Scholar]
- Cao, C.; Ren, X.; Fu, Y. MVSFormer: Multi-View Stereo by Learning Robust Image Features and Temperature-Based Depth. arXiv 2022, arXiv:2208.02541. [Google Scholar]
- Liu, T.; Ye, X.; Zhao, W.; Pan, Z.; Shi, M.; Cao, Z. When Epipolar Constraint Meets Non-Local Operators in Multi-View Stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 18088–18097. [Google Scholar]
- Vats, V.K.; Joshi, S.; Crandall, D.J.; Reza, M.A.; Jung, S.H. GC-Mvsnet: Multi-View, Multi-Scale, Geometrically-Consistent Multi-View Stereo. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024. [Google Scholar]
- Murtiyoso, A.; Holm, S.; Riihimäki, H.; Krucher, A.; Griess, H.; Griess, V.C.; Schweier, J. Virtual Forests: A Review on Emerging Questions in the Use and Application of 3D Data in Forestry. Int. J. For. Eng. 2024, 35, 29–42. [Google Scholar] [CrossRef]
- Luo, W.; Lu, Z.; Liao, Q. LNMVSNet: A Low-Noise Multi-View Stereo Depth Inference Method for 3D Reconstruction. Sensors 2024, 24, 2400. [Google Scholar] [CrossRef] [PubMed]
- Barnston, A.G. Correspondence among the Correlation, RMSE, and Heidke Forecast Verification Measures; Refinement of the Heidke Score. Weather Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Gao, Q.; Kan, J. Automatic Forest DBH Measurement Based on Structure from Motion Photogrammetry. Remote Sens. 2022, 14, 2064. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D Lidar Imaging for Detecting and Understanding Plant Responses and Canopy Structure. J. Exp. Bot. 2007, 58, 881–898. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Liu, K.; Shen, X.; Wu, X.; Liu, H. Estimation of Forest Structural Parameters Using UAV-LiDAR Data and a Process-Based Model in Ginkgo Planted Forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4175–4190. [Google Scholar] [CrossRef]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. Patchmatchnet: Learned Multi-View Patchmatch Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 14194–14203. [Google Scholar]
- Gao, S.; Li, Z.; Wang, Z. Cost Volume Pyramid Network with Multi-Strategies Range Searching for Multi-View Stereo. In Proceedings of the Computer Graphics International Conference, Virtual, 12–16 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 157–169. [Google Scholar]
- Yu, Z.; Gao, S. Fast-Mvsnet: Sparse-to-Dense Multi-View Stereo with Learned Propagation and Gauss-Newton Refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1949–1958. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).