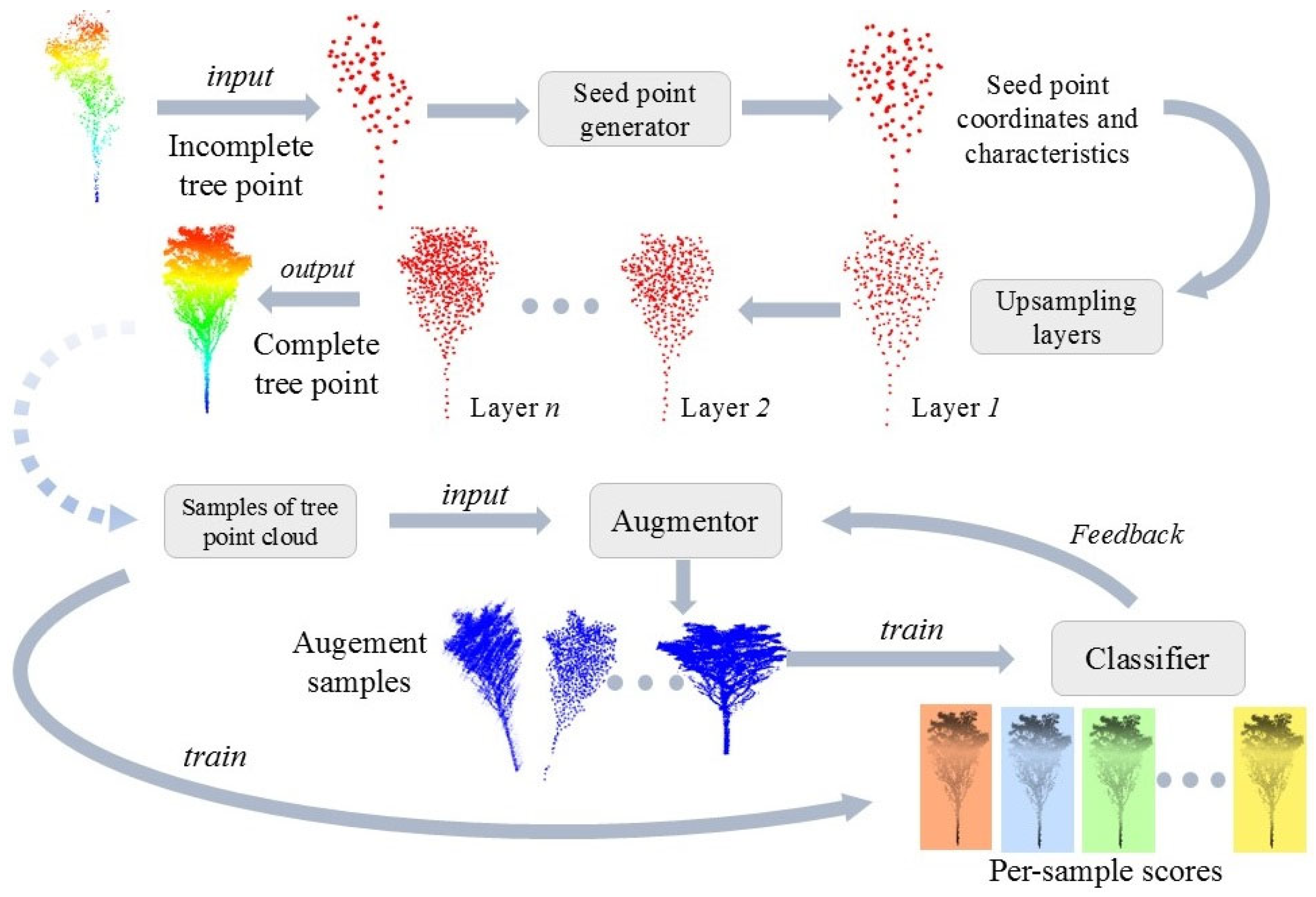
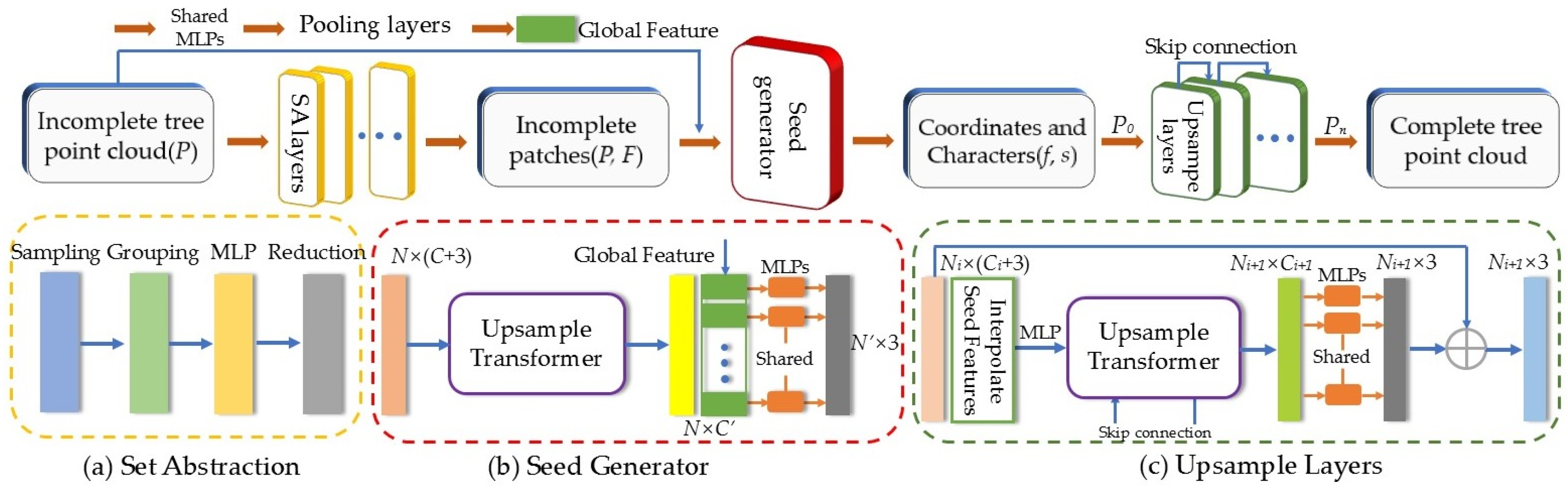
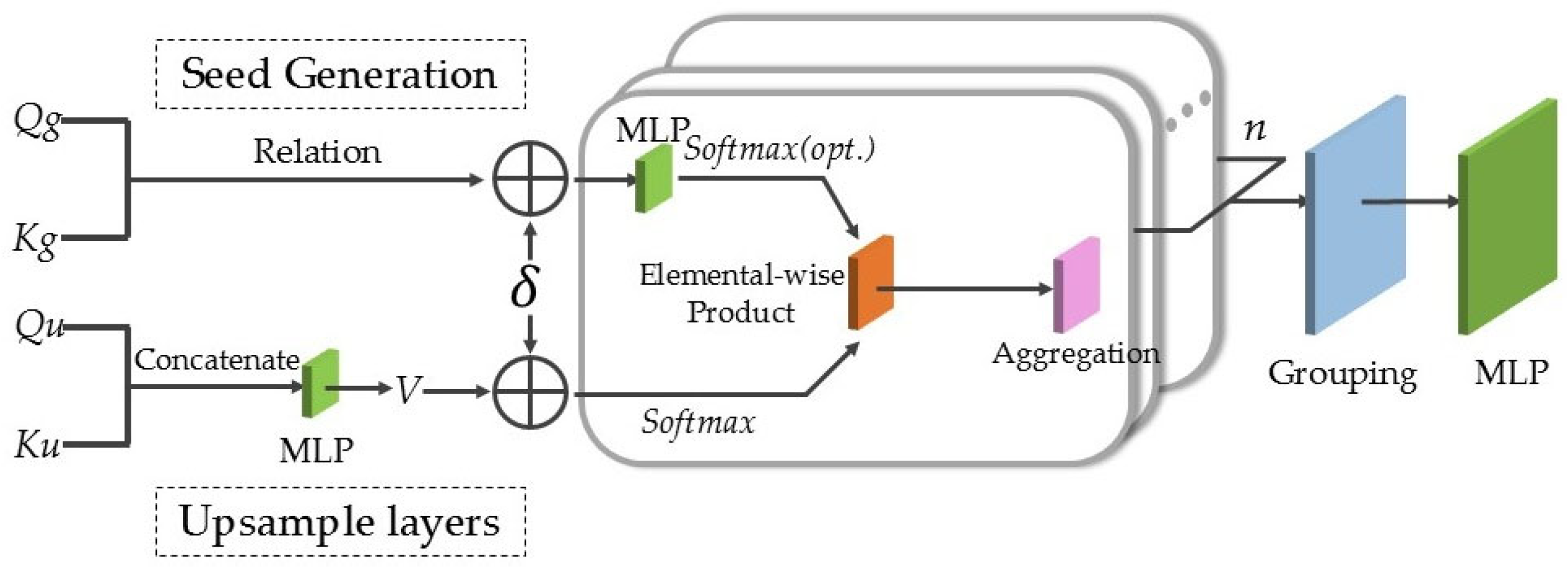
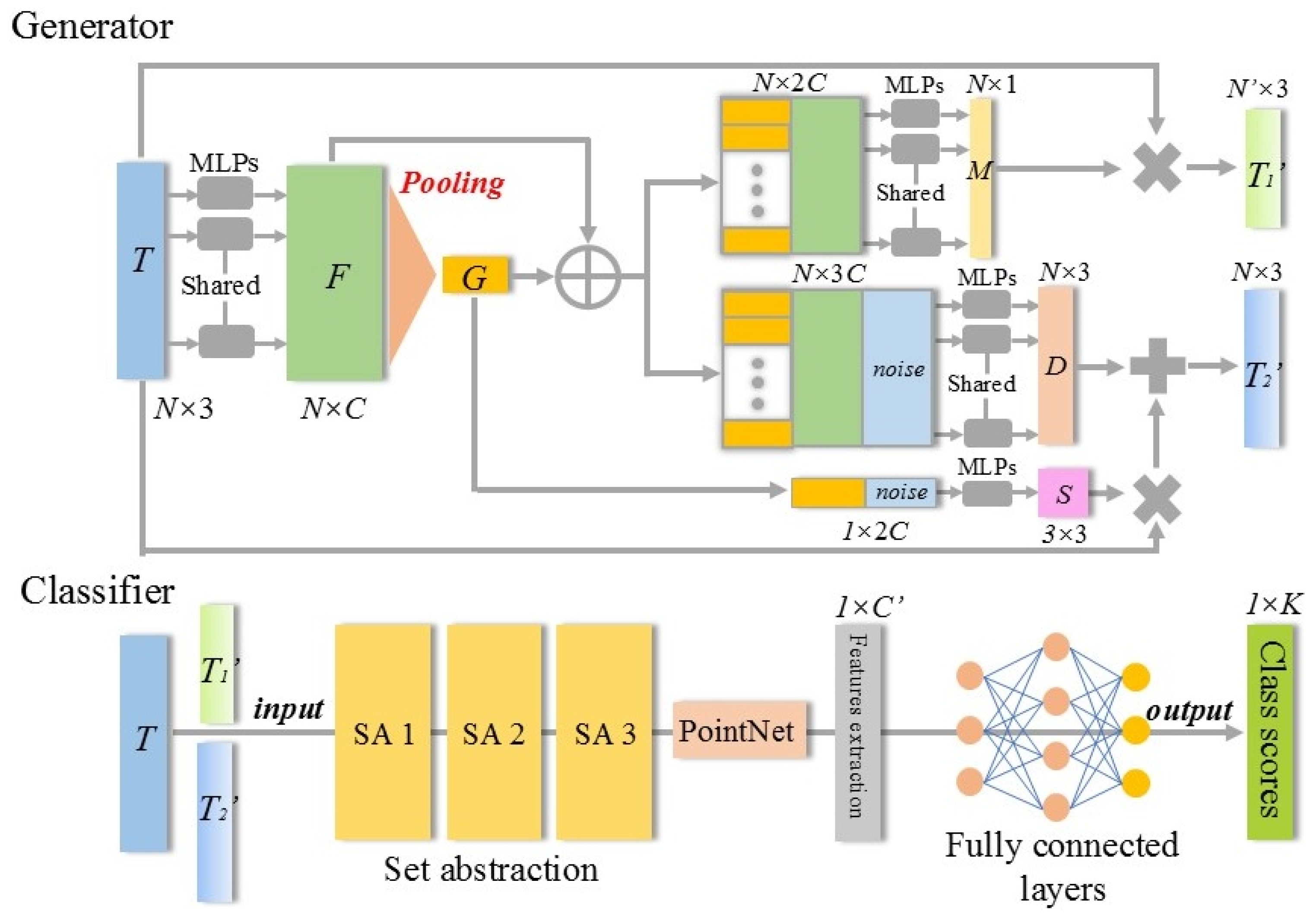
1. Introduction
The rapid development of the LiDAR (light detection and ranging) technology has provided new avenues for forest surveys. As an active remote sensing technology, LiDAR can capture vertical structural information of forests, providing strong support for accurate tree segmentation and parameter extraction [
1,
2]. However, due to limitations such as the acquisition environment and occlusion between trees, the forest point cloud data often suffer from structural deficiencies and sparse point sets, leading to degraded quality [
3,
4]. Additionally, low-quality point clouds may lead to an insufficient number of training samples, negatively impacting subsequent tree species classification and biomass estimation results. Unlike 2D images and videos or 2.5D data (e.g., digital elevation models), 3D point clouds can provide complete spatial coordinates and rich attribute information in volumetric space. They exhibit unordered and discontinuous characteristics. This means that traditional data augmentation methods cannot be directly applied to process them. Therefore, accurately and efficiently implementing point cloud data augmentation has become an urgent issue that needs to be addressed.
Point cloud quality enhancement mainly involves two aspects: point cloud completion and point cloud up-sampling [
5]. Point cloud completion refers to the process of recovering the full point cloud information. Point cloud up-sampling, on the other hand, reconstructs high-resolution point clouds from input low-resolution data [
6,
7,
8]. Traditional methods for point cloud quality enhancement heavily rely on prior knowledge of the point cloud’s structure. These methods can only process data with ground truth templates or point clouds that have accurately calibrated normal vectors [
9,
10]. “Ground truth” refers to the standardized data obtained through manual annotation or reliable measurements, which serve as the benchmark for evaluating model prediction results. However, recent studies have achieved better point cloud quality enhancement performance by leveraging the powerful feature extraction capabilities of deep learning networks. In point cloud completion, Yuan et al. [
11] proposed PCN, which processes raw point clouds without structural assumptions. Huang et al. [
12] introduced PF-Net, an encoder–decoder network that captures multi-resolution data for reconstruction. Compared to convolutional neural networks (CNNs), transformers with attention mechanisms have demonstrated advantages in capturing information from long-distance interactions. PoinTr [
13] uses self-attention to learn local/global structures, while Skeleton-Detail Transformer [
14] refines shapes through coarse-to-fine correlation. For point cloud up-sampling, Yu et al. [
15] developed PU-Net (based on PointNet++), which expands multi-level features but struggles with local details. PU-GAN [
16,
17] employs adversarial training, where a generator produces up-sampled clouds and a discriminator optimizes realism. Similarly, transformers have also shown promise in point cloud up-sampling. PU-Transformer [
18] enhances channel interactions via multi-head attention, and PU-CRN [
19] combines up-sampling/refinement networks with transformer modules for higher-quality outputs. Although point cloud quality enhancement techniques have made significant progress, their application to tree point clouds still requires further validation.
On the other hand, point cloud data augmentation refers to the use of geometric transformation methods—such as rotation, translation, jittering, flipping, and random scaling—to generate new data samples based on the original dataset [
8,
20]. This can enhance the training of neural network models by improving data diversity and volume. With the rapid development of deep learning, research on point cloud data augmentation techniques has expanded. Li et al. [
21] proposed a deep learning network framework named PointAugment for point cloud classification. It used an adversarial learning strategy to jointly optimize the enhancer and classifier networks for automatic sample data augmentation. Chen et al. [
22] introduced the PointMixup augmentation network based on shortest-path interpolation, which creatively performed automatic mixing of object point clouds to generate new sample instances. However, this process can result in the loss of local semantic information. The PA-AUG network proposed by Jaeseok [
23] divides objects into multiple partitions. By randomly applying several augmentation methods to each local region, the network greatly increases the diversity of the newly generated samples. The limitation of this approach is that there should not be excessive overlap between objects. Xiao et al. [
24] introduced two augmentation techniques in their PolarMix model: scene-level and object-level. The scene-level technique achieves data augmentation by swapping regions within the scene point cloud. The object-level technique achieves data augmentation by inserting object point clouds into the scene on a large scale. Zheng et al. [
25] demonstrated the effectiveness of mixing techniques through their SA–DA algorithm, which augments vehicle point clouds via discard, swap, and sparsification operations. However, the structure of tree point clouds is irregular, and transformation methods suitable for regular objects may not be applicable to tree point clouds. Therefore, developing suitable augmentation methods for tree point clouds remains a significant challenge.
In summary, the development of 3D point cloud data augmentation techniques has enhanced the robustness and generalization capabilities of data processing models, while also providing new insights for optimizing 3D point cloud algorithms. Although these advanced data augmentation techniques have yielded significant results, their applications are mainly limited to man-made objects, such as airplanes, cars, and furniture. These objects typically have regular shapes, flat surfaces, and symmetric structures [
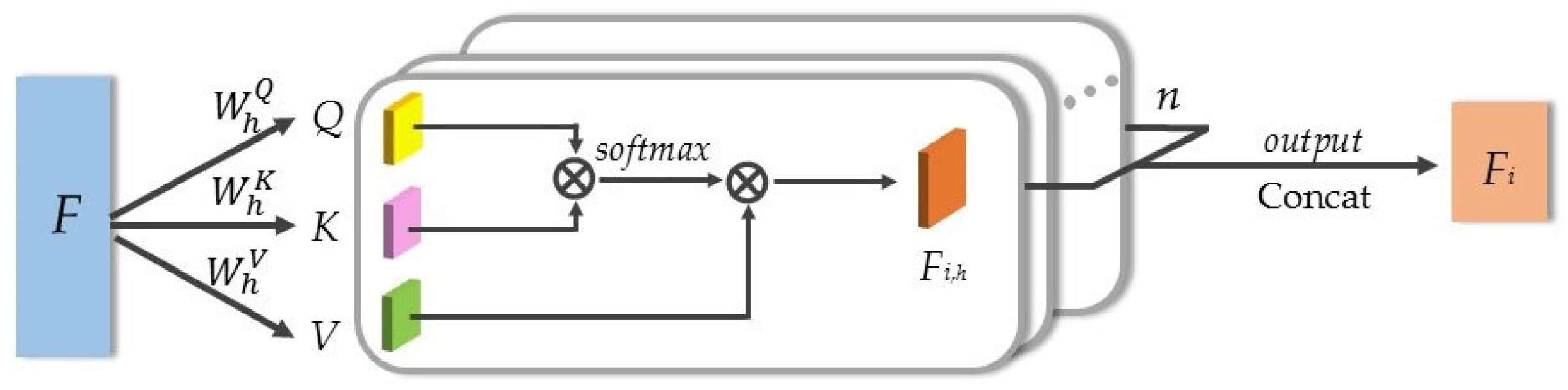
7]. In contrast, tree point clouds have more complex structures with specific regional characteristics, which impose higher demands on augmentation networks. This study selected the Experimental Forest of the Northeast Forestry University in Harbin, Heilongjiang Province, China, as the research area, and proposed a system for tree point cloud enhancement to address the aforementioned issues, which included point cloud completion and sample augmentation networks. The contributions of this study are as follows. (1) To handle the complex structure of tree point clouds, the completion network used a multi-head attention mechanism to extract features and predict missing parts. The sample augmentation network combined several transformation methods suitable for tree point clouds and used an adversarial learning strategy for data augmentation. (2) To address the potential loss of feature information in traditional pooling processes, this study improved the pooling layer with a multi-head self-attention mechanism, enhancing the ability to extract and propagate information. (3) The experimental results demonstrated that the combined network employed in this study can effectively enhance complex tree point clouds, with overall performance surpassing that of other mainstream point cloud augmentation networks.
4. Experiments and Results
4.1. Implementation Details
In this study, all deep learning-based networks were implemented using PyTorch 1.11.0 on a Windows operating system, with Python 3.6 as the programming language. For the point cloud completion network, the coarse point cloud generation network included 3 sets of integrated abstraction layers, while the fine point cloud generation network utilized 3 up-sampling layers. The batch size was set to 8, with 300 epochs per batch. The Adam optimizer was used with an initial learning rate of 0.001. On the other hand, the point cloud augmentation network was trained for 250 epochs with a batch size of 8, also using the Adam optimizer with an initial learning rate of 0.001. Furthermore, all experiments were carried out on a Dell Precision 7550 workstation equipped with an Intel Core i9-10885H CPU processor (Intel Inc., Santa Clara, CA, USA) and an NVIDIA Quadro RTX 4000 GPU (16 GB). The complete training time for the network was approximately 34.2 h, with the completion network training taking about 18.7 h and the augmentation network training taking about 15.5 h. The system exhibited a memory footprint of 12.8 Gb.
For dataset preparation, the 1415 collected original tree point cloud samples were divided into two groups: coniferous and broadleaf. The coniferous group consisted of Pinus sylvestris, Larix gmelinii, and Pinus tabuliformis, while the broadleaf group consisted of Betula platyphylla, Fraxinus mandshurica, and Quercus mongolica. To test the point cloud completion network, uniform sampling was used to extract 12,288 points as the complete ground truth data. Subsequently, partial sampling of the ground truth data was performed to generate inputs of 3072, 6144, and 9216 points, representing varying levels of difficulty. For testing the sample augmentation network, the tree point clouds were reconstructed following the ModelNet10 dataset standard as the initial sample point clouds. The training and test sets were then divided according to the configuration used in PointNet++.
4.2. Tree Point Cloud Completion Results
This study compared several mainstream point cloud completion networks, including PCN [
11], GRNet [
38], PointTr [
13], and SnowflakeNet [
39]. These methods were trained on the tree point cloud dataset using the default configurations provided in the original source code.
Figure 7 showed the completion results of the different networks. In addition, the similarity between the generated completed point clouds and the ground truth was evaluated using the
CD and F-score. The comparison results are shown in
Table 1, where the
CD was multiplied by 1000. As shown, the point cloud completed by the network in this study was more complete, compact, and closer to the ground truth, with fewer random noise points. The quantitative results also demonstrated the strong performance of the network, with the average
CD of 4.84 and the average F-score of 0.90. In contrast, the completion results of PCN were nearly unrecognizable in terms of tree details. Although GRNet restored the geometry of the trunk and branches to some extent, it generated a significant amount of noise. The completion results of SnowflakeNet and PointTr were relatively complete in the overall structure, but their restoration of tree details was not as accurate as those of the network used in this study.
To further assess the robustness of the point cloud completion network in handling incomplete tree point clouds, this study conducted experiments with varying levels of missing data. The input point clouds were divided into three levels of missingness: mild (25%), moderate (50%), and severe (75%), corresponding to 3072, 6144, and 9216 points, respectively.
Figure 8 presents the visualization results of point cloud completion under different levels of missing data.
Table 2 presents the quantitative evaluation results of point cloud completion at different missingness levels. The best completion performance occurred with mild point cloud missingness, where the
avgCD was 4.05. With moderate missingness, the completed canopy showed minimal deformation, and the overall tree structure was well-restored, with an
avgCD of 4.84. At the 75% severe missingness level, although the completion of the canopy showed significant degradation, the basic tree structure was still maintained, with an
avgCD of 6.31. These results demonstrated that the completion network exhibited strong robustness on the tree point cloud dataset, effectively completing point clouds with varying levels of missingness. From the perspective of tree species, coniferous trees generally performed better in completion than broadleaf trees: at the 25% missingness level,
avgCDconiferous = 4.15 <
avgCDbroadleaf = 4.94; at the 50% missingness level,
avgCDconiferous = 4.44 <
avgCDbroadleaf = 5.23; at the 75% level,
avgCDconiferous = 5.89 <
avgCDbroadleaf = 6.73. This difference is mainly attributed to the simpler morphological structure of coniferous trees. In contrast, broadleaf trees generally had larger and more diverse canopies, which posed a challenge to the completion performance of the network. Notably,
Betula platyphylla exhibited the best completion performance among the broadleaf trees (
CD25% = 4.15;
CD50% = 4.94;
CD75% = 6.18). This was mainly due to the smaller canopy size of
Betula platyphylla compared to other broadleaf trees, which reduced the deformation during the completion process.
To validate the reliability of Upsample Transformer in point cloud completion networks, this study conducted comparative experiments with other point cloud generation methods, including the mainstream folding and deconvolution processing. In the ablation study, the Upsample Transformer modules in both the seed generator and the up-sampling layers were replaced with folding and deconvolution modules while maintaining identical network architectures (the point cloud missing ratio was set to 50%). As shown in
Table 3, the Upsample Transformer module demonstrated superior point cloud completion performance compared to the other methods. Among them, the folding operation failed to accurately represent complex structures or model semantic relationships due to its global parameterization, while deconvolution suffered from detail loss owing to the inherent conflict between regular convolution kernels and the irregular nature of point clouds. In contrast, Upsample Transformer employed local attention mechanisms and geometric encoding to achieve semantic-aware feature aggregation and adaptive receptive fields, significantly improving completion accuracy while maintaining computational efficiency.
4.3. Tree Point Cloud Augmentation Results
To evaluate the augmentation effect of the sample augmentation network, this study set up three experimental datasets: samples without augmentation, samples augmented using traditional methods, and samples augmented using the point cloud augmentation network. The traditional augmentation methods involved random rotation, scaling, jittering, and point dropout to increase the training samples [
31]. It was important to note that the number of augmented samples in the traditional method was kept consistent with that produced by the point cloud augmentation network. The effectiveness of the augmentation was assessed based on the average classification accuracy. The quantitative evaluation results are shown in
Table 4.
As shown in
Table 4, the dataset augmented using the sample augmentation network achieved the highest classification accuracy (
avgAP = 90.1%). This represented a 2.9% improvement over the original dataset and a 2% improvement over the dataset augmented using traditional point cloud methods. Furthermore, from the perspective of tree species, the classification accuracy of broadleaf tree samples showed a more significant improvement after network augmentation. The average improvement over the original broadleaf samples was 3.4%. Additionally, there was considerable variation in the augmentation effects among different broadleaf species, with
Fraxinus mandshurica showing the largest improvement in classification accuracy, increasing by 3.9%. These differences were mainly attributed to the diversity in tree morphology. Generally, tree species with more complex canopy structures exhibit greater morphological diversity. Augmenting such species may result in more challenging samples.
To further evaluate the impact of different augmentation methods on classification accuracy, this study conducted ablation experiments, as shown in
Table 5. Model 1 represented the original PointNet++ without the generator structure, with a baseline classification accuracy of 87.2%. Then, models 2, 3, and 4 were constructed by retaining only point displacement (
D), shape transformation (
S), and point drop (
M), respectively. Models 5, 6, and 7 combined any two of these augmentation methods (average accuracy). For tree point clouds, each augmentation method contributed to generating more effective augmented samples. Among them, shape transformation may introduce significant variability, while point displacement and point drop can steadily improve sample classification accuracy.
Additionally, to evaluate the stability of the generated point cloud data, this study simulated real-world tree point cloud acquisition scenarios by introducing natural noise, occlusions, and pose variations. The specific configurations were as follows: (1) random jittering with Gaussian noise within the range of [−1.0, 1.0]; (2) random point removal at a ratio of 0.8; and (3) rotation of ±30° along the central axis. For each type of perturbation, three data augmentation strategies were compared: without data augmentation, conventional data augmentation, and the sample augmentation network in this study.
Table 6 presents the comparative results, including the original test accuracy (without perturbations) as a reference. The results demonstrated that under all perturbation conditions, the sample augmentation network significantly outperformed traditional random augmentation methods. Notably, when compared to the original test accuracy, the proposed network exhibited lower sensitivity to data perturbations, with an average accuracy drop of only 2%. This outcome confirmed the network’s strong robustness in handling real-world data variations.
4.4. Experimental Results of Multi-Head Self-Attention Pooling
In the architectural improvements of this study, we specifically optimized the multi-head self-attention pooling layers in the feature extraction modules of both the point cloud completion network and the point cloud augmentation network. To evaluate the contribution of the multi-head self-attention pooling layers to model performance, this study designed a systematic ablation experimental protocol. While maintaining the original configurations of the network architecture, loss function design, and other critical hyperparameters unchanged, modifications were exclusively made to the pooling layers within the feature extraction modules: (1) replacing the multi-head self-attention pooling layer with a max pooling layer; (2) replacing the multi-head self-attention pooling layer with an average pooling layer; (3) replacing the multi-head self-attention pooling layer with a self-attention pooling layer. Additionally, the point cloud completion network used the dataset with 50% missing points, and performance was evaluated using the
CD and F-score. The sample augmentation network was tested with a mixture of the original and augmented samples, evaluated based on classification accuracy and F-score. The results of the multi-head self-attention pooling ablation experiments are presented in
Table 7.
The results indicated that the point cloud completion network based on multi-head self-attention pooling achieved the highest accuracy, with the CD of 4.84. Similarly, the point cloud augmentation network with multi-head self-attention pooling also achieved the highest classification accuracy, at 90.1%. However, replacing the multi-head self-attention pooling layer with max pooling, average pooling, or self-attention pooling resulted in decreased accuracy. The main reason was that max pooling only selected prominent features, leading to the loss of some key information. Average pooling computed the mean of the feature data, but still struggled to focus on specific regions of interest. Compared to multi-head self-attention, self-attention alone cannot simultaneously focus on different features from multiple perspectives. It was also more susceptible to noise and outliers in the input data. Therefore, multi-head self-attention pooling provided stronger feature extraction capabilities than traditional pooling methods, enhancing the expressive power of the network.
5. Limitations and Conclusions
5.1. Limitations and Future Work
During point cloud completion, the test dataset inadequately simulates potential occlusion and overlapping phenomena in trees. This may lead to performance fluctuations in the completion network, so it is necessary to collect more comprehensive data to support robust network stability testing. In the point cloud augmentation network, the sample generation process may introduce augmentation artifacts, which could lead to biased learning outcomes in the network. In subsequent research, we will impose constraints on the new sample generation using morphological feature parameters and growth orientation metrics across diverse tree species. Additionally, future research will focus on combining point cloud completion and augmentation networks to address additional challenges, such as noise removal, plot-level semantic segmentation, and scene object detection. It is important to note that different tasks may require specific network architectures for optimal performance. For example, in plot-level semantic segmentation, the entire study area will be treated as scene-scale data and employ a semantic segmentation network to classify point clouds into distinct categories: tree points, ground points, object points, and potential aerial noise. Specifically for coniferous and broadleaf tree point cloud clusters within the plots, secondary semantic segmentation will be performed. By integrating point cloud completion networks and point cloud augmentation networks, the precise construction of differentiated tree datasets will be ultimately achieved.
On the other hand, due to limitations in the study area and the available aerial data, the dataset of trees employed in this research exhibits constrained sample size. Future research will focus on evaluating the robustness and transferability of the completion and augmentation networks across diverse tree species, forest types, and LiDAR scanning data. Moreover, the current research on field-collected tree point cloud datasets and their corresponding data-processing networks remains limited, and significant variations exist in tree morphological structures and growth states across different geographical regions. Consequently, the findings of this study cannot represent the optimal performance achievable by deep learning networks in tree point cloud enhancement. Therefore, it is essential to combine more advanced network frameworks, perform comparative analysis of different ability to process high-dimensional feature data, and increase experimental testing of feedback loops.
5.2. Conclusions
This study proposed a joint network for tree point cloud augmentation, consisting of the point cloud completion network and the sample augmentation network. The completion network improved the quality of incomplete tree point clouds, providing sufficient sample sources for the augmentation network. Then, the original samples were applied to the augmentation network to obtain more high-quality tree point clouds. Moreover, the augmented point clouds could be fed back into the joint network, facilitating alternating optimization through the update of learnable parameters. The point cloud completion network adopted a coarse-to-fine point cloud generation strategy. By introducing the Upsample Transformer module to extract seed point coordinates and features from tree point clouds, the network was able to capture the key regional features effectively, which provided the foundation for subsequent point cloud up-sampling. On the other hand, the sample augmentation network used the end-to-end framework, where the generator could be improved based on feedback from the classifier, and the classifier could learn to process a wider range of training samples. The generator processed point cloud samples using three distinct modules: shape transformation, point direction displacement, and point drop, significantly enhancing the efficiency and diversity of point cloud augmentation. Furthermore, this study replaced the traditional max pooling layer in the joint network with the multi-head self-attention-based pooling layer, ensuring the maximum retention of feature information from different sample points. This method effectively enhanced the ability of the network to learn the features of various sample categories in complex scenes.