The Relationships Between Climate and Growth in Six Tree Species Align with Their Hydrological Niches
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites and Tree Species
2.2. Climate Data and Indices
2.3. Field Sampling
2.4. Processing Wood Samples and Ring-Width Data
2.5. Statistical Analyses
3. Results
3.1. Growth Trends and Variability
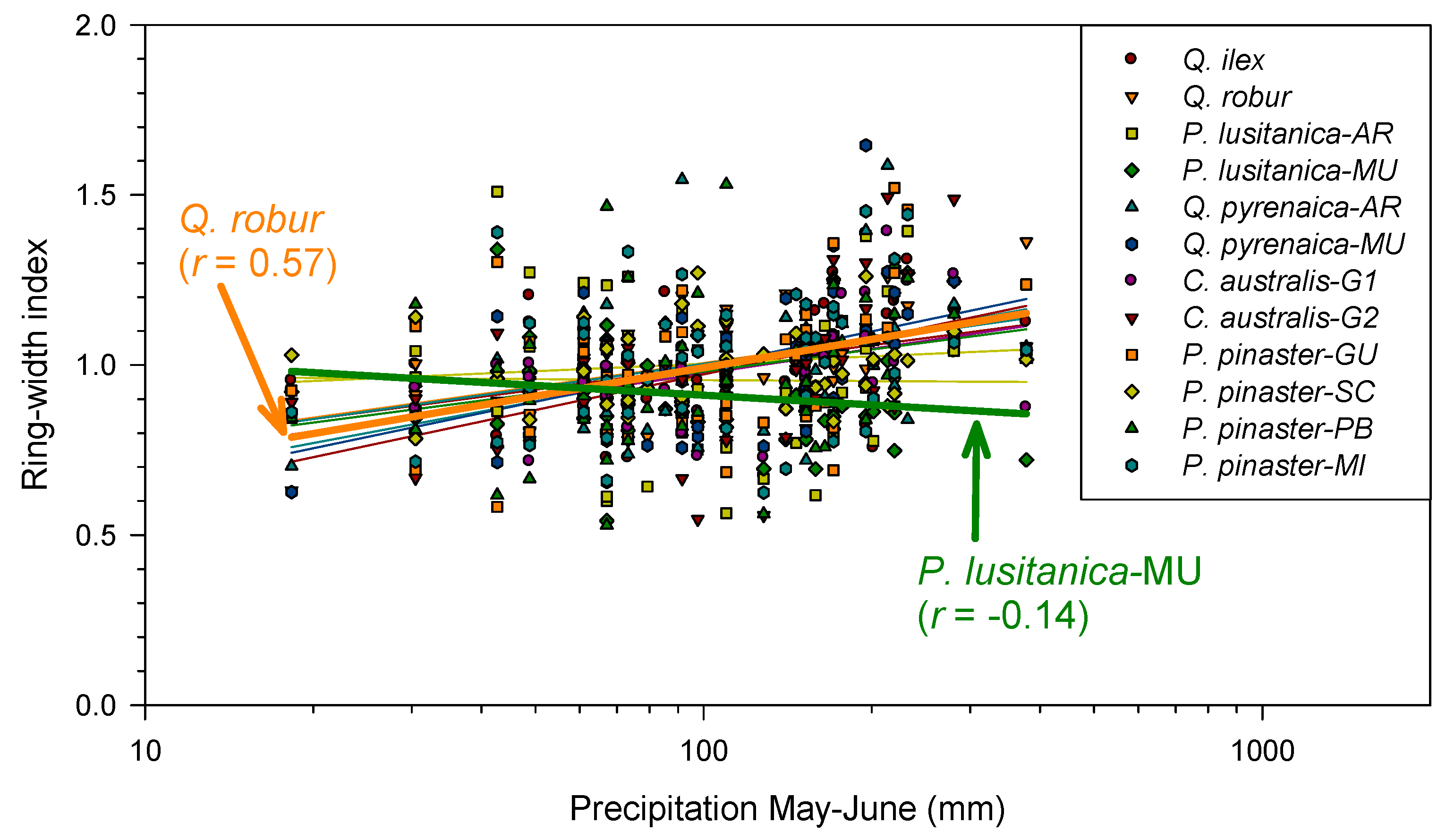
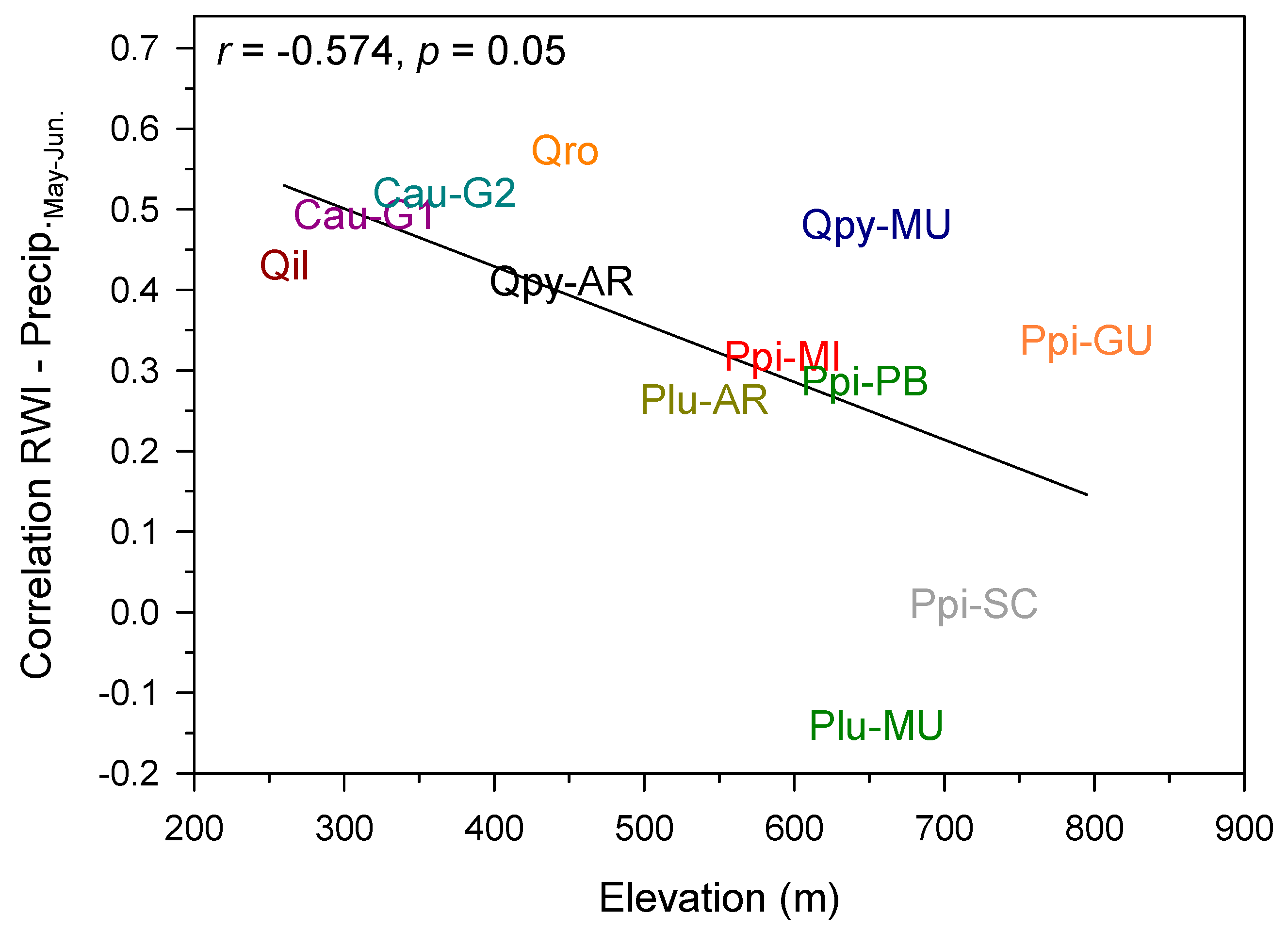
3.2. Correlations Between Climate Variables and Growth Indices
3.3. Climate–Growth Relationships Based on Climwin Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Poulter, B.; Trouet, V.; Girardin, M.P.; Frank, D.C. Twentieth century redistribution in climatic drivers of global tree growth. Sci. Adv. 2019, 5, eaat4313. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Silvertown, J.; Araya, Y.; Gowing, D. Hydrological niches in terrestrial plant communities: A review. J. Ecol. 2015, 103, 93–108. [Google Scholar] [CrossRef]
- Camarero, J.J.; Sánchez-Salguero, R.; Sangüesa-Barreda, G.; Matías, L. Tree species from contrasting hydrological niches show divergent growth and water-use efficiency. Dendrochronologia 2018, 52, 87–95. [Google Scholar] [CrossRef]
- Kunz, J.; Löffler, G.; Bauhus, J. Minor European broadleaved tree species are more drought-tolerant than Fagus sylvatica but not more tolerant than Quercus petraea. For. Ecol. Manag. 2018, 414, 15–27. [Google Scholar] [CrossRef]
- Fuchs, S.; Schuldt, B.; Leuschner, C. Identification of drought-tolerant tree species through climate sensitivity analysis of radial growth in Central European mixed broadleaf forests. For. Ecol. Manag. 2021, 494, 119287. [Google Scholar] [CrossRef]
- López-Sáez, J.A.; Alba-Sánchez, F.; Sánchez-Mata, D.; Luengo-Nicolau, E. Los Pinares de la Sierra de Gredos. Pasado, Presente y Futuro; Institución Gran Duque de Alba: Ávila, Spain, 2019. [Google Scholar]
- Gallardo, J.F.; Cuadrado, S.Y.; González-Hernández, M.I. Suelos Forestales de la Vertiente sur de la Sierra de Gredos; VII Anuario del Centro de Edafología y Biología Aplicada de Salamanca: Salamanca, Spain, 1980; pp. 155–168. [Google Scholar]
- Fernandes, P.M.; Vega, J.A.; Jiménez, E.; Rigolot, E. Fire resistance of European pines. For. Ecol. Manag. 2008, 256, 246–255. [Google Scholar] [CrossRef]
- Tapias, R.; Climent, J.; Pardos, J.A.; Gil, L. Life histories of Mediterranean pines. Plant Ecol. 2004, 171, 53–68. [Google Scholar] [CrossRef]
- Caudullo, G.; Welk, E.; San-Miguel-Ayanz, J. Chorological maps for the main European woody species. Data Brief 2017, 12, 662–666. [Google Scholar] [CrossRef]
- Bogino, S.M.; Bravo, F. Growth response of Pinus pinaster Ait. to climatic variables in central Spanish forests. Ann. For. Sci. 2008, 65, 506. [Google Scholar] [CrossRef]
- Camarero, J.J.; Gazol, A.; Tardif, J.C.; Conciatori, F. Attributing forest responses to global-change drivers: Limited evidence of a CO2-fertilization effect in Iberian pine growth. J. Biogeogr. 2015, 42, 2220–2233. [Google Scholar] [CrossRef]
- Sánchez-Salguero, R.; Camarero, J.J.; Rozas, V.; Génova, M.; Olano, J.M.; Arzac, A.; Linares, J.C. Resist, recover or both? Growth plasticity in response to drought is geographically structured and linked to intraspecific variability in Pinus pinaster. J. Biogeogr. 2018, 45, 1126–1139. [Google Scholar] [CrossRef]
- Hernández-Alonso, H.; Madrigal-González, J.; Silla, F. Differential growth responses in Pinus nigra, P. pinaster and P. sylvestris to the main patterns of climatic variability in the western Mediterranean. For. Ecol. Manag. 2021, 483, 118921. [Google Scholar] [CrossRef]
- Corcuera, L.; Camarero, J.J.; Sisó, S.; Gil-Pelegrín, E. Radial-growth and wood-anatomical changes in overaged Quercus pyrenaica coppice stands: Functional responses in a new Mediterranean landscape. Trees Struct. Funct. 2006, 20, 91–98. [Google Scholar] [CrossRef]
- Moracho, E.; Moreno, G.; Jordano, P.; Hampe, A. Unusually limited pollen dispersal and connectivity of Pedunculate oak (Quercus robur) refugial populations at the species’ southern range margin. Mol. Ecol. 2016, 25, 3319–3331. [Google Scholar] [CrossRef]
- Campelo, F.; Gutiérrez, E.; Ribas, M.; Sánchez-Salguero, R.; Nabais, C.; Camarero, J.J. The facultative bimodal growth pattern in Quercus ilex—A simple model to predict sub-seasonal and inter-annual growth. Dendrochronologia 2018, 49, 77–88. [Google Scholar] [CrossRef]
- Beltrán, R.S. Distribución y autoecología de Prunus lusitanica L. en la Península Ibérica. Investig. Agraria. Sist. Recur. For. 2006, 15, 187–198. [Google Scholar]
- Pardo, A.; Cáceres, Y.; Pulido, F. Rangewide determinants of population performance in Prunus lusitanica: Lessons for the contemporary conservation of a Tertiary relict tree. Acta Oecol. 2018, 86, 42–48. [Google Scholar] [CrossRef]
- Garfi, G. Climatic signal in tree–rings of Quercus pubescens s.l. and Celtis australis L. in South–eastern Sicily. Dendrochronologia 2000, 18, 41–51. [Google Scholar]
- Naumburg, E.; Mata-Gonzalez, R.; Hunter, R.G.; Mclendon, T.; Martin, D.W. Phreatophytic vegetation and groundwater fluctuations: A review of current research and application of ecosystem response modeling with an emphasis on great basin vegetation. Environ. Manag. 2005, 35, 726–740. [Google Scholar] [CrossRef]
- Camisón, A.; Silla, F.; Camarero, J.J. Influences of the atmospheric patterns on unstable climate-growth associations of western Mediterranean forests. Dendrochronologia 2016, 40, 130–142. [Google Scholar] [CrossRef]
- Camarero, J.J.; Sangüesa-Barreda, G.; Montiel-Molina, C.; Seijo, F.; López-Sáez, J.A. Past growth suppressions as proxies of fire incidence in relict Mediterranean black pine forests. For. Ecol. Manag. 2018, 413, 9–20. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Hurrell, J. Decadal trends in North Atlantic Oscillation and relationship to regional temperature and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef]
- Rodó, X.; Baert, E.; Comín, F. Variations in seasonal rainfall in Southern Europe during the present century: Relationships with the North Atlantic Oscillation and the El Niño-Southern Oscillation. Clim. Dyn. 1997, 13, 275–284. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. (Eds.) Methods of Dendrochronology: Applications in the Environmental Sciences; IIASA: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Maxwell, R.S.; Larsson, L.-A. Measuring tree-ring widths using the CooRecorder software application. Dendrochronologia 2021, 67, 125841. [Google Scholar] [CrossRef]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 68–78. [Google Scholar]
- Biondi, F.; Qeadan, F. A theory-driven approach to tree-ring standardization: Defining the biological trend from expected basal area increment. Tree-Ring Res. 2008, 64, 81–96. [Google Scholar] [CrossRef]
- Briffa, K.R.; Jones, P.D. Basic chronology statistics and assessment. In Methods of Dendrochronology: Applications in the Environmental Sciences; Cook, E.R., Kairiukstis, L.A., Eds.; Kluwer: Dordrecht, The Netherlands, 1990; pp. 439–461. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Bunn, A.G. Statistical and visual crossdating in R using the dplR library. Dendrochronologia 2010, 28, 251–258. [Google Scholar] [CrossRef]
- Bunn, A.G.; Korpela, M.; Biondi, F.; Campelo, F.; Mérian, P.; Qeadan, F.; Zang, C. dplR: Dendrochronology Program Library in R. R Package, Version 1.7.8. 2025. Available online: https://cran.r-project.org/web/packages/dplR/index.html (accessed on 21 February 2025).
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.r-project.org/ (accessed on 21 February 2025).
- Oksanen, J.; Simpson, G.; Blanchet, F.; Kindt, R.; Legendre, P.; Minchin, P.R.; O’Hara, R.B.; Solymos, P.; Stevens, M.H.H.; Szoecs, E.; et al. Vegan: Community Ecology Package. R Package Version 2.7-0. 2025. [Google Scholar]
- Zang, C.; Biondi, F. Treeclim: An R package for the numerical calibration of proxy-climate relationships. Ecography 2015, 38, 431–436. [Google Scholar] [CrossRef]
- Bailey, L.D.; van de Pol, M. Climwin: An R Toolbox for Climate Window Analysis. PLoS ONE 2016, 11, e0167980. [Google Scholar] [CrossRef] [PubMed]
- van de Pol, M.; Bailey, L.D.; McLean, N.; Rijsdijk, L.; Lawson, C.R.; Brouwer, L. Identifying the Best Climatic Predictors in Ecology and Evolution. Methods Ecol. Evol. 2016, 7, 1246–1257. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2004; ISBN 978-0-387-95364-9. [Google Scholar]
- Rubio-Cuadrado, A.; Camarero, J.J.; Bosela, M. Applying climwin to dendrochronology: A breakthrough in the analyses of tree responses to environmental variability. Dendrochronologia 2022, 71, 125916. [Google Scholar] [CrossRef]
- Rubio-Cuadrado, Á.; Camarero, J.J. More than Just Chilling and Forcing: Deconstructing the Climate Windows and Drivers of Leaf Emergence and Fall in Woody Plant Species. Forests 2025, 16, 175. [Google Scholar] [CrossRef]
- Kurz-Besson, C.B.; Lousada, J.L.; Gaspar, M.J.; Correia, I.E.; David, T.S.; Soares, P.M.; Trigo, R.M. Effects of recent minimum temperature and water deficit increases on Pinus pinaster radial growth and wood density in southern Portugal. Front. Plant Sci. 2016, 7, 1170. [Google Scholar] [CrossRef]
- Fernández-Blas, C.; Ruiz-Benito, P.; Gazol, A.; Granda, E.; Samblás, E.; Granado-Díaz, I.; Zavala, M.A.; Valeriano, C.; Camarero, J.J. Historical forest use constrains tree growth responses to drought: A case study on tapped maritime pine (Pinus pinaster). Trees For. People 2024, 18, 100699. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Schwalm, C.; Biondi, F.; Camarero, J.J.; Koch, G.; Litvak, M.; Ogle, K.; Shaw, J.D.; Shevliakova, E.; Williams, A.P.; et al. Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models. Science 2015, 349, 528–532. [Google Scholar] [CrossRef]
- Pulido, F.; Valladares, F.; Calleja, J.A.; Moreno, G.; González-Bornay, G. Tertiary relict trees in a mediterranean climate: Abiotic constraints on the persistence of Prunus lusitanica at the eroding edge of its range. J. Biogeogr. 2008, 35, 1425–1435. [Google Scholar] [CrossRef]
- Raposo, M.A.M.; Nunes, L.J.R.; Quinto-Canas, R.; del Río, S.; Pardo, F.M.V.; Galveias, A.; Pinto-Gomes, C.J. Prunus lusitanica L.: An Endangered Plant Species Relict in the Central Region of Mainland Portugal. Diversity 2021, 13, 359. [Google Scholar] [CrossRef]
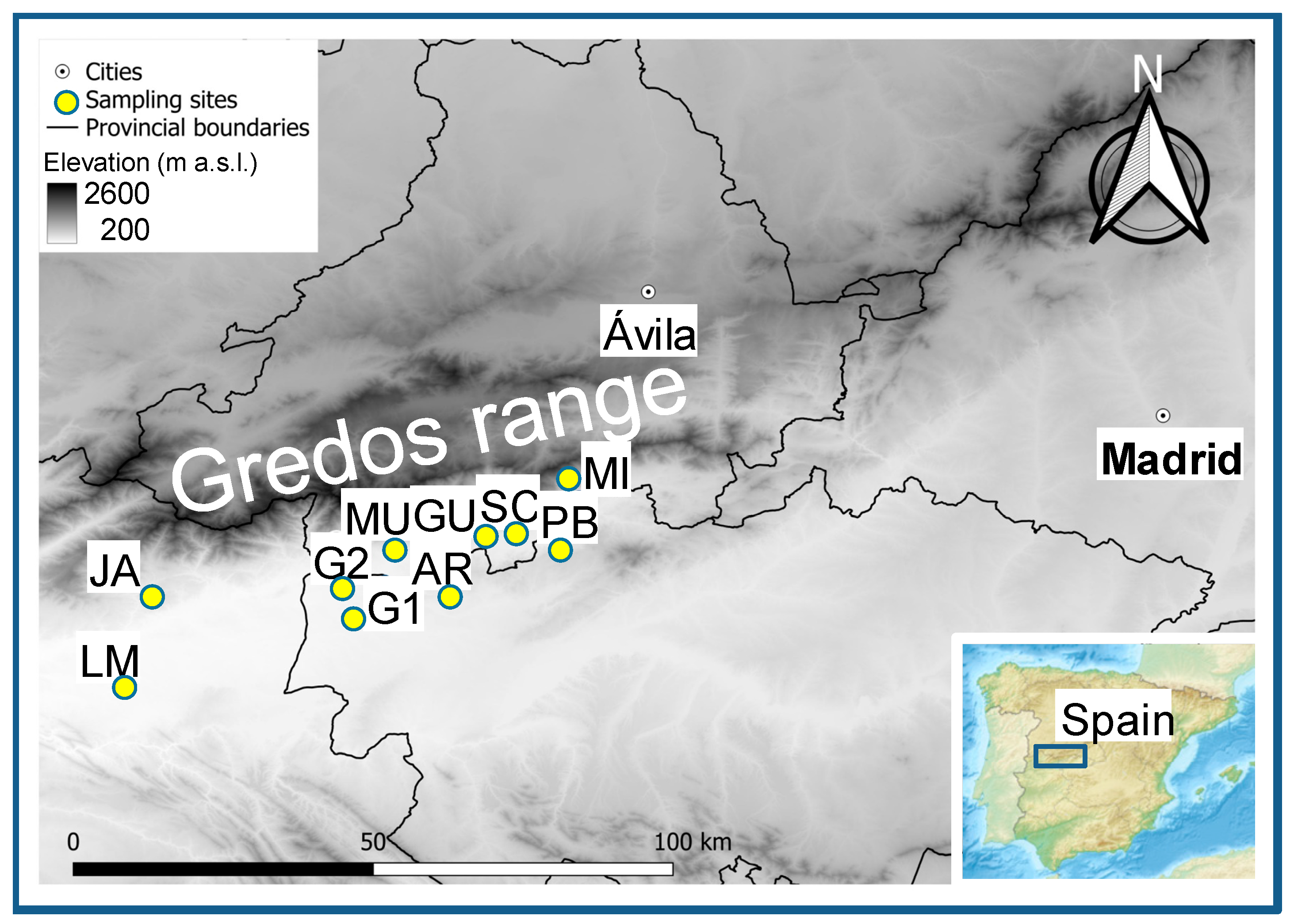
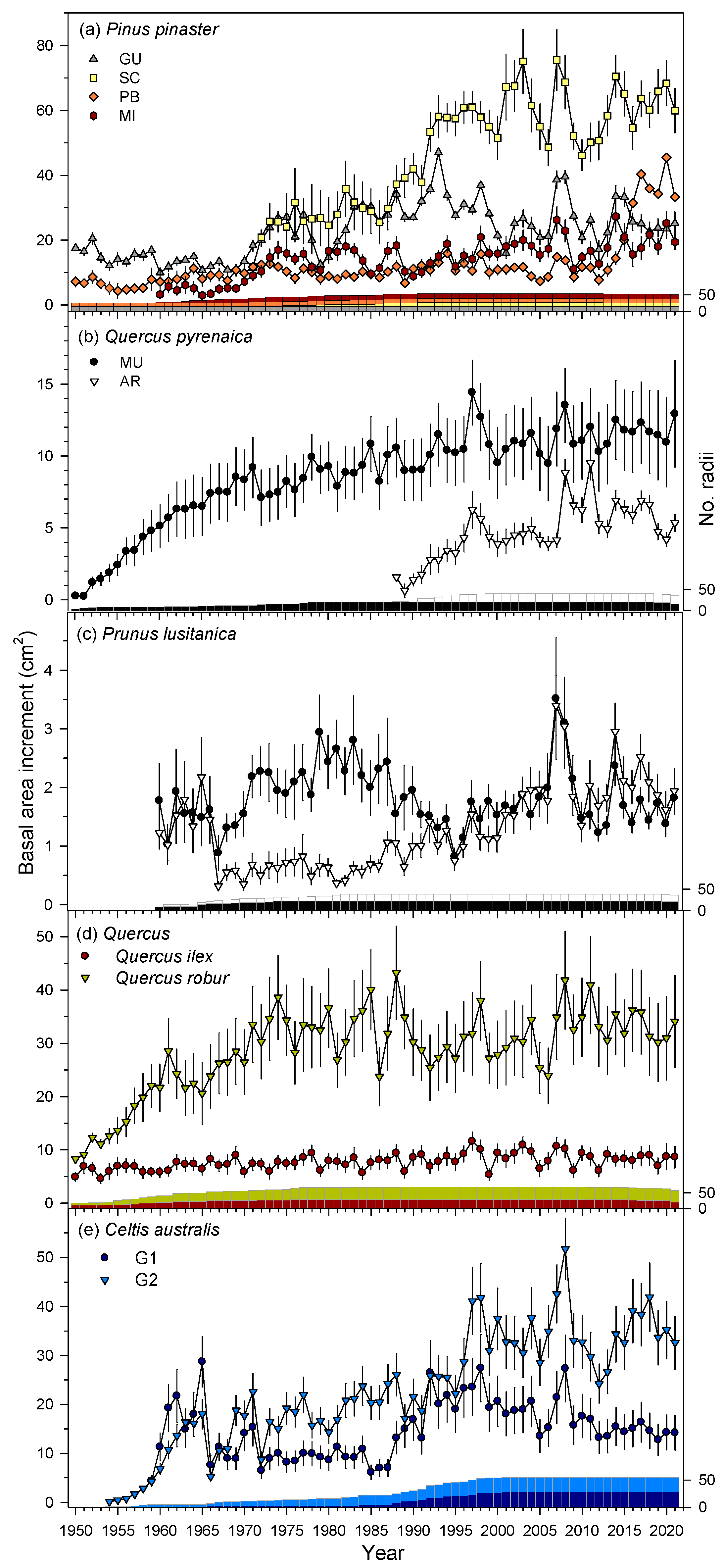
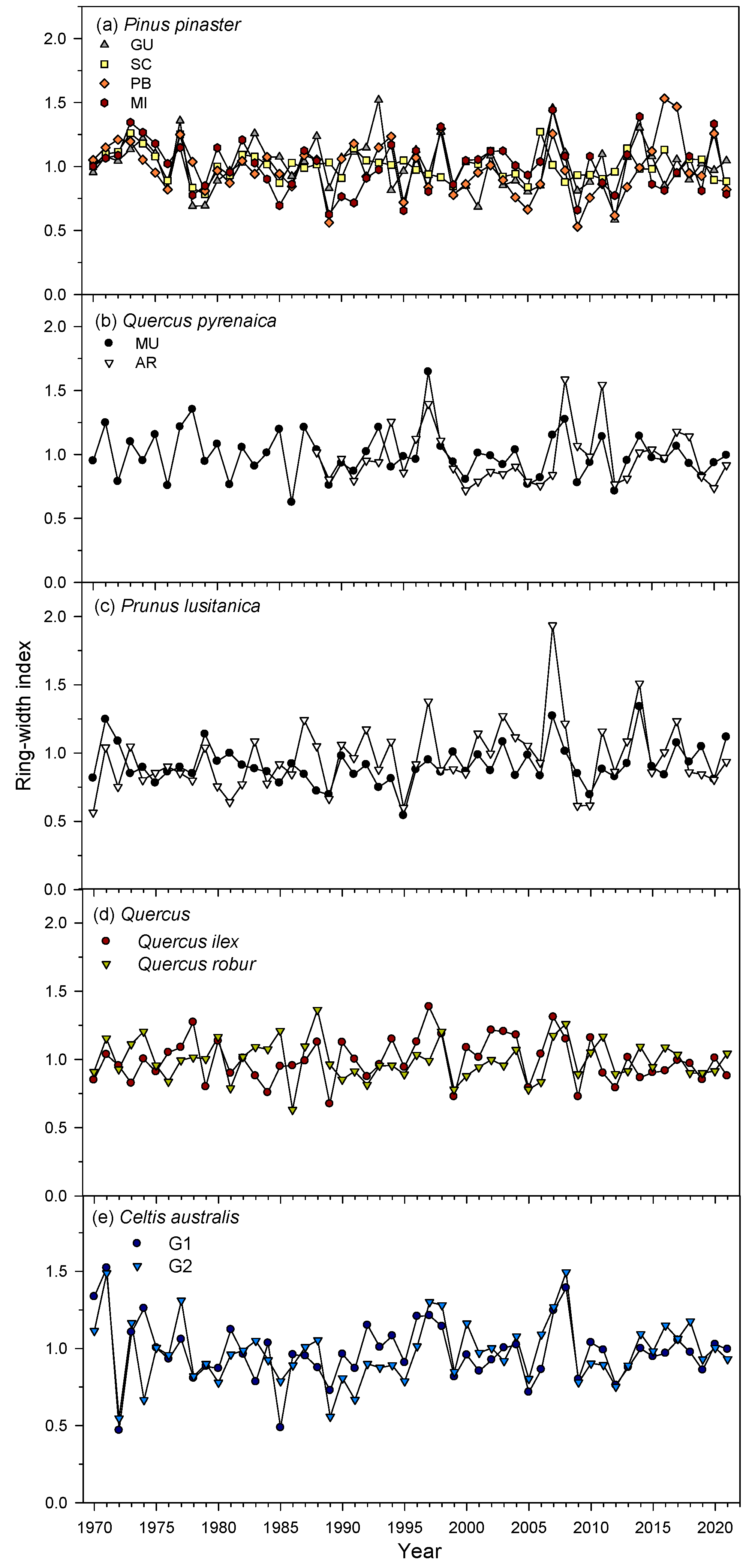

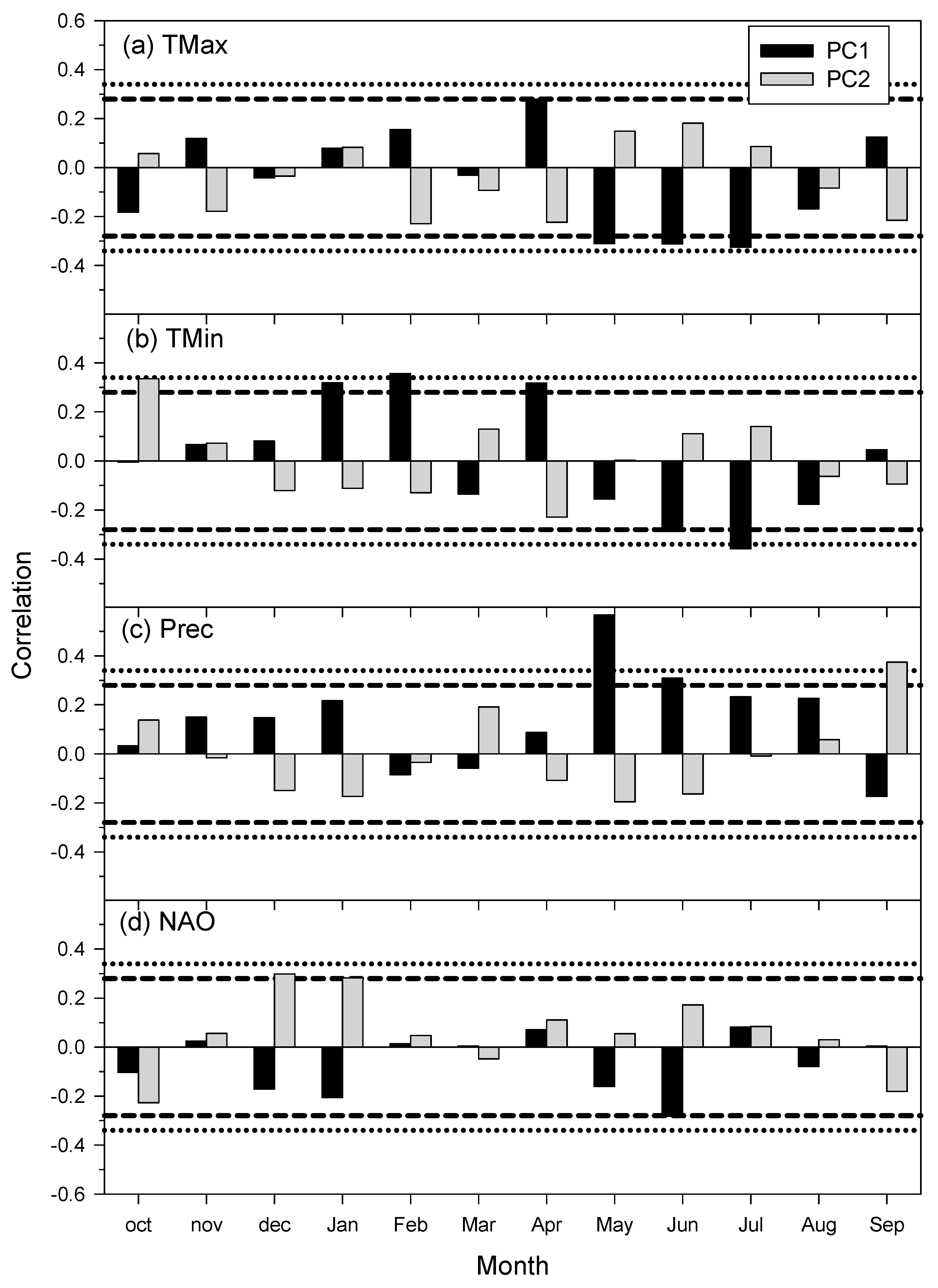
| Tree Species | Site Name | Site Code | Latitude N (°) | Longitude W (°) | Elevation (m a.s.l.) | Sampling Date |
|---|---|---|---|---|---|---|
| Quercus ilex | Majadas del Tiétar | LM | 39.9452 | 5.7683 | 260 | July 2022 |
| Quercus robur | Jaraíz de la Vera | JA | 40.0955 | 5.7690 | 447 | April 2022 |
| Quercus pyrenaica | Río Arbillas | AR | 40.1810 | 5.1497 | 445 | October 2021 |
| Quercus pyrenaica | Río Muelas | MU | 40.1835 | 5.1907 | 655 | October 2021 |
| Prunus lusitanica | Río Arbillas | AR | 40.1810 | 5.1497 | 540 | October 2021 |
| Prunus lusitanica | Río Muelas | MU | 40.1835 | 5.1907 | 655 | October 2021 |
| Celtis australis | Oropesa | G1 | 40.0983 | 5.2110 | 314 | October 2023 |
| Celtis australis | Candeleda | G2 | 40.1396 | 5.2516 | 367 | October 2023 |
| Pinus pinaster | Guisando | GU | 40.2167 | 5.1417 | 795 | January 2022 |
| Pinus pinaster | Santa Cruz del Valle | SC | 40.2083 | 5.0167 | 720 | January 2022 |
| Pinus pinaster | Pedro Bernardo | PB | 40.2165 | 4.9332 | 647 | January 2022 |
| Pinus pinaster | Mijares | MI | 40.2617 | 4.8350 | 592 | January 2022 |
| Species | Site | Dbh (cm) | Time Span | No. Trees/No. Cores | BAI (cm2) | BAI Trend (S) | Tree-Ring Width (mm) | AR1 | MSx | Rbar | EPS |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q. ilex | LM | 48.9 ± 8.4 | 1927–2022 | 13/24 | 8.1 ± 1.4 | 1066 *** | 0.61 ± 0.11 | 0.51 | 0.35 | 0.43 | 0.86 |
| Q. robur | JA | 50.4 ± 14.0 | 1941–2021 | 20/40 | 32.2 ± 4.5 | 1186 *** | 2.94 ± 0.96 | 0.71 | 0.22 | 0.59 | 0.92 |
| Q. pyrenaica | AR | 18.6 ± 3.3 a | 1987–2021 | 10/20 | 4.7 ± 2.0 a | 307 ** | 2.23 ± 0.58 a | 0.57 | 0.31 | 0.63 | 0.92 |
| MU | 26.0 ± 3.4 b | 1941–2021 | 10/20 | 9.7 ± 2.0 b | 2012 *** | 1.63 ± 0.31 b | 0.68 | 0.27 | 0.49 | 0.89 | |
| P. lusitanica | AR | 12.8 ± 2.7 a | 1957–2021 | 11/18 | 1.3 ± 0.7 a | 941 *** | 0.92 ± 0.30 a | 0.56 | 0.40 | 0.33 | 0.79 |
| MU | 15.4 ± 2.9 a | 1942–2021 | 13/23 | 1.9 ± 0.5 a | −133 | 0.94 ± 0.30 a | 0.68 | 0.36 | 0.39 | 0.80 | |
| C. australis | G1 | 19.7 ± 4.8 a | 1958–2023 | 15/29 | 14.9 ± 3.4 a | 423 ** | 2.06 ± 1.11 a | 0.56 | 0.29 | 0.47 | 0.88 |
| G2 | 39.1 ± 9.2 b | 1954–2023 | 15/26 | 27.4 ± 6.3 b | 1674 *** | 3.16 ± 1.29 a | 0.55 | 0.31 | 0.45 | 0.87 | |
| P. pinaster | GU | 66.5 ± 6.9 b | 1912–2021 | 15/31 | 24.0 ± 7.2 a | 994 *** | 2.55 ± 0.77 a | 0.73 | 0.26 | 0.42 | 0.86 |
| SC | 70.0 ± 8.0 b | 1968–2021 | 12/23 | 52.1 ± 9.4 b | 817 *** | 6.44 ± 1.53 b | 0.76 | 0.25 | 0.61 | 0.89 | |
| PB | 49.0 ± 7.9 a | 1883–2021 | 12/24 | 13.1 ± 6.3 a | 1342 *** | 1.82 ± 0.60 a | 0.73 | 0.30 | 0.45 | 0.87 | |
| MI | 47.0 ± 5.0 a | 1956–2021 | 15/24 | 16.0 ± 4.4 a | 1049 *** | 2.80 ± 0.66 a | 0.68 | 0.31 | 0.62 | 0.90 |
| Species | Site | Climate Variable | ∆AICc | Window Open | Window Close | p Value | R2 | p AICc |
|---|---|---|---|---|---|---|---|---|
| Q.ilex | LM | Tmax | −1.71 | Aug (t − 1) | Sep (t − 1) | 0.052 | 0.075 | 0.550 |
| Tmin | −11.36 | Jan | Mar | <0.001 | 0.234 | 0.013 | ||
| Prec | −13.65 | Aug (t − 1) | Sep | <0.001 | 0.268 | 0.006 | ||
| Q.robur | JA | Tmax | −6.91 | May | May | 0.003 | 0.165 | 0.071 |
| Tmin | −12.1 | Jan | Feb | <0.001 | 0.245 | 0.005 | ||
| Prec | −21.08 | May | Jun | <0.001 | 0.367 | <0.001 | ||
| Q. pyrenaica | AR | Tmax | −3.79 | Apr | Apr | 0.016 | 0.112 | 0.287 |
| Tmin | −4.73 | Jul | Jul | 0.010 | 0.128 | 0.224 | ||
| Prec | −8.59 | May | Jun | 0.001 | 0.192 | 0.045 | ||
| MU | Tmax | −14.3 | Jun | Jul | <0.001 | 0.277 | 0.007 | |
| Tmin | −12.63 | Jun | Jul | <0.001 | 0.253 | 0.007 | ||
| Prec | −15.93 | May | Aug | <0.001 | 0.300 | 0.003 | ||
| P. lusitanica | AR | Tmax | −3.59 | Mar | Apr | 0.018 | 0.108 | 0.282 |
| Tmin | −1.71 | Jan | Apr | 0.052 | 0.075 | 0.648 | ||
| Prec | −6.6 | Sep (t − 1) | Sep (t − 1) | 0.004 | 0.160 | 0.160 | ||
| MU | Tmax | −1.95 | Sep (t − 1) | Sep (t − 1) | 0.045 | 0.079 | 0.537 | |
| Tmin | −3.66 | Sep (t − 1) | Sep (t − 1) | 0.018 | 0.110 | 0.328 | ||
| Prec | −0.78 | Jul | Oct | 0.089 | 0.058 | 0.879 | ||
| C. australis | G1 | Tmax | −2.51 | May | Aug | 0.033 | 0.089 | 0.430 |
| Tmin | −4.6 | Jan | Feb | 0.011 | 0.126 | 0.222 | ||
| Prec | −15.38 | May | May | <0.001 | 0.292 | 0.002 | ||
| G2 | Tmax | −2.86 | Jan | Feb | 0.027 | 0.096 | 0.371 | |
| Tmin | −3.96 | Apr | Apr | 0.015 | 0.115 | 0.329 | ||
| Prec | −18.55 | Apr | Aug | <0.001 | 0.335 | 0.001 | ||
| P. pinaster | GU | Tmax | −5.46 | May | Sep | 0.007 | 0.141 | 0.141 |
| Tmin | −11.87 | May | Oct | <0.001 | 0.242 | 0.005 | ||
| Prec | −7.7 | May | Sep | 0.002 | 0.177 | 0.072 | ||
| SC | Tmax | −3.72 | Sep (t − 1) | Mar | 0.017 | 0.111 | 0.263 | |
| Tmin | −4.42 | Sep (t − 1) | Aug | 0.012 | 0.123 | 0.262 | ||
| Prec | −1.7 | Nov (t − 1) | Dec (t − 1) | 0.042 | 0.075 | 0.747 | ||
| PB | Tmax | −4.59 | May | Jun | 0.011 | 0.126 | 0.190 | |
| Tmin | −8.82 | May | Nov | 0.001 | 0.195 | 0.034 | ||
| Prec | −10.78 | Aug (t − 1) | Jul | <0.001 | 0.226 | 0.018 | ||
| MI | Tmax | −1.77 | Jul | Oct | 0.050 | 0.076 | 0.575 | |
| Tmin | −4.99 | Jan | Jan | 0.009 | 0.133 | 0.203 | ||
| Prec | −6.48 | Aug (t − 1) Aug (t − 1) | Sep | 0.004 | 0.157 | 0.132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camarero, J.J.; López Sáez, J.A.; Rubio-Cuadrado, Á.; González de Andrés, E.; Colangelo, M.; Abel-Schaad, D.; Cachinero-Vivar, A.; Pérez-Priego, Ó.; Valeriano, C. The Relationships Between Climate and Growth in Six Tree Species Align with Their Hydrological Niches. Forests 2025, 16, 1029. https://doi.org/10.3390/f16061029
Camarero JJ, López Sáez JA, Rubio-Cuadrado Á, González de Andrés E, Colangelo M, Abel-Schaad D, Cachinero-Vivar A, Pérez-Priego Ó, Valeriano C. The Relationships Between Climate and Growth in Six Tree Species Align with Their Hydrological Niches. Forests. 2025; 16(6):1029. https://doi.org/10.3390/f16061029
Chicago/Turabian StyleCamarero, J. Julio, José Antonio López Sáez, Álvaro Rubio-Cuadrado, Ester González de Andrés, Michele Colangelo, Daniel Abel-Schaad, Antonio Cachinero-Vivar, Óscar Pérez-Priego, and Cristina Valeriano. 2025. "The Relationships Between Climate and Growth in Six Tree Species Align with Their Hydrological Niches" Forests 16, no. 6: 1029. https://doi.org/10.3390/f16061029
APA StyleCamarero, J. J., López Sáez, J. A., Rubio-Cuadrado, Á., González de Andrés, E., Colangelo, M., Abel-Schaad, D., Cachinero-Vivar, A., Pérez-Priego, Ó., & Valeriano, C. (2025). The Relationships Between Climate and Growth in Six Tree Species Align with Their Hydrological Niches. Forests, 16(6), 1029. https://doi.org/10.3390/f16061029











