Stem Profile Estimation of Pinus densiflora in Korea Using Machine Learning Models: Towards Precision Forestry
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Description
2.2. Variable Exponent-Based Model
2.3. Machine Learning-Based Models
2.4. Performance Evaluation of Prediction Models
2.5. Stem Taper Estimation and Visualization
3. Results and Discussion
3.1. Variable Exponent-Based Model Validation
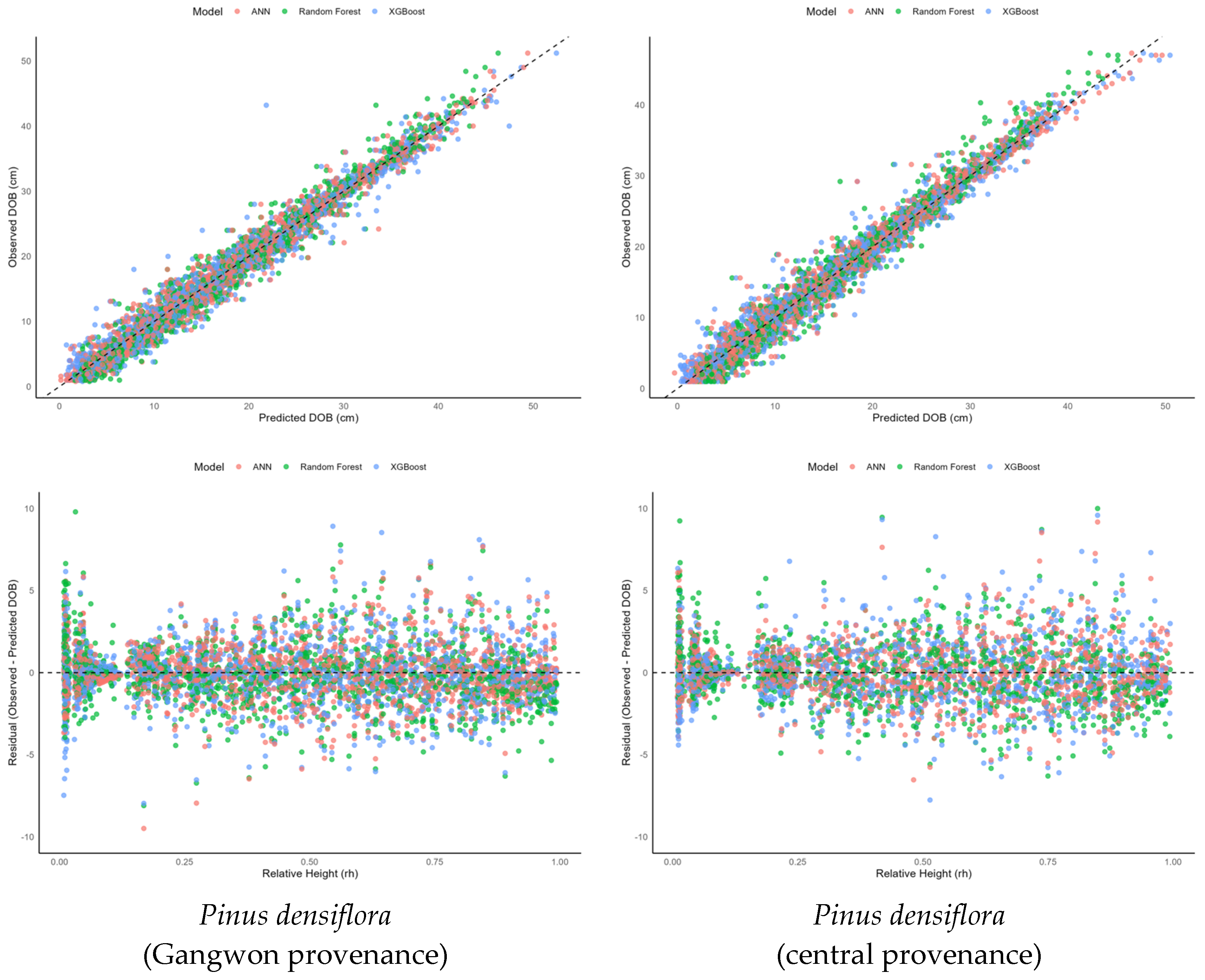
3.2. Comparison of Machine Learning Models’ Performance
3.3. Visualization and Interpretation of Stem Taper Curves
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RF | Random Forest |
| XGBoost | eXtreme Gradient Boosting |
| ANN | Artificial Neural Network |
References
- Kang, J.T.; Son, Y.-M.; Kim, S.W.; Park, H.; Hwang, J.S. Development of Local Stem Volume Table for Larix kaempferi Using Kozak’s Stem Taper Model. J. Agric. Life Sci. 2014, 48, 119–131. [Google Scholar] [CrossRef]
- Tewari, V.P.; Kumar, V.S.K. Construction and Validation of Tree Volume Functions for Dalbergia sissoo Grown under Irrigated Conditions in the Hot Desert of India. J. Trop. For. Sci. 2001, 13, 503–511. [Google Scholar]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar] [CrossRef]
- Hjelm, B. Taper and Volume Equations for Poplar Trees Growing on Farmland in Sweden. Licentiate Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2011. [Google Scholar]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Kang, J.T.; Son, Y.M.; Kim, S.W.; Lee, S.; Park, H. Development of Local Stem Volume Table for Pinus densiflora S. et Z. Using Tree Stem Taper Model. Korean J. Agric. For. Meteorol. (KJAFM) 2014, 16, 327–335. [Google Scholar] [CrossRef]
- Kang, J.T.; Moon, H.S.; Son, Y.M.; An, K.W. An Estimation on the Stem Volume of Cryptomeria japonica in Jeju Using Kozak’s Stem Taper Model. J. Korean Islands (TJOKI) 2015, 27, 145–160. [Google Scholar]
- Kang, J.T.; Son, Y.M.; Kim, H.; Park, H. Developing Optimal Site Prediction Model for Evergreen Broad-Leaved Trees, Machilus thunbergii in Warm Temperate Zone of the Korean Peninsula. J. Agric. Life Sci. 2014, 48, 39–54. [Google Scholar] [CrossRef]
- Son, Y.M.; Kang, J.T.; Jeon, J.H.; Ko, C. The Estimation of Stem Volume for Pinus thunbergii by Coast Using Kozak’s Stem Taper Model in Korea. J. Korean Islands (TJOKI) 2017, 29, 225–244. [Google Scholar] [CrossRef]
- Shin, J.H.; Han, H.; Kim, Y.H.; Yim, J.S.; Chang, Y.S. Uncertainty in Estimating Forest Growing Stock from Volume Estimation of a Standing Tree by Stem Volume Table and the Resulting Bias in Carbon Stock Estimation: A Case Study in Hongcheon-Gun, Republic of Korea. J. Clim. Change Res. 2022, 13, 355–364. [Google Scholar] [CrossRef]
- Kang, J.T.; Ko, C. The Development of a Stem Taper Equation and a Stem Table for Standing Trees of Chamaecyparis obtusa on Jeju Island and in the Southern Regions of South Korea. J. Korean Islands (TJOKI) 2020, 32, 221–233. [Google Scholar] [CrossRef]
- Lee, S.H.; Ko, C.; Shin, J.H.; Kang, J.T. Estimation of Stem Taper for Quercus acutissima Using Machine Learning Techniques. J. Agric. Life Sci. 2020, 54, 29–37. [Google Scholar] [CrossRef]
- Ko, C.; Lee, S.H.; Lee, S.J.; Kim, D.G.; Kang, J.T. Development of a Stem Taper Equation and a Stem Table for Cryptomeria japonica Stands in South Korea. J. Korean Soc. For. Sci. 2020, 109, 461–467. [Google Scholar] [CrossRef]
- Ko, C.; Moon, G.H.; Yim, J.S.; Lee, S.; Kim, D.G.; Kang, J.T. Estimation and Comparison of Stem Volume for Larix kaempferi in South Korea Using the Stem Volume Model. J. Korean Soc. For. Sci. 2019, 108, 592–599. [Google Scholar] [CrossRef]
- Son, Y.M.; Jeon, J.H.; Pyo, J.K.; Kim, K.N.; Kim, S.W.; Lee, K.H. Development of Stem Volume Table for Robinia pseudoacacia Using Kozak’s Stem Profile Model. J. Agric. Life Sci. 2012, 46, 43–49. [Google Scholar]
- Son, Y.M.; Kim, S.W.; Lee, S.; Kim, J.S. Estimation of Stand Yield and Carbon Stock for Robinia pseudoacacia Stands in Korea. J. Korean Soc. For. Sci. 2014, 103, 264–269. [Google Scholar] [CrossRef]
- Son, Y.M.; Kim, H.; Lee, H.Y.; Kim, C.M.; Kim, C.S.; Kim, J.W.; Joo, R.W.; Lee, K.H. Taper Equations and Stem Volume Table of Eucalyptus pellita and Acacia mangium Plantations in Indonesia. J. Korean Soc. For. Sci. 2009, 98, 633–638. [Google Scholar]
- Son, Y.M.; Lee, K.H.; Pyo, J.K. Development of Biomass Allometric Equations for Pinus densiflora in Central Region and Quercus variabilis. J. Agric. Life Sci. 2011, 45, 65–72. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Georgakis, A. Improving European Black Pine Stem Volume Prediction Using Machine Learning Models with Easily Accessible Field Measurements. Forests 2024, 15, 2251. [Google Scholar] [CrossRef]
- Sahin, A. Analyzing Regression Models and Multi-Layer Artificial Neural Network Models for Estimating Taper and Tree Volume in Crimean Pine Forests. iForest 2024, 17, 36–44. [Google Scholar] [CrossRef]
- Habeeb, H.N.; Mustafa, Y.T. Deep Learning-Based Prediction of Forest Cover Change in Duhok, Iraq: Past and Future. Forestist 2025, 75, 1–13. [Google Scholar] [CrossRef]
- Abosuliman, S.S.; Rahman, I.U.; Abdullah, S.; Qadir, A. Selection of third-party logistics in supply chain finance under probabilistic complex hesitant fuzzy sets and distance measures. Heliyon 2024, 10, e36544. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Anees, S.A.; Huang, Q.; Qin, X.; Qin, Z.; Fan, J.; Han, G.; Zhang, L.; Shafri, H.Z.M. Improving Forest Above-Ground Biomass Estimation by Integrating Individual Machine Learning Models. Forests 2024, 15, 975. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R. Estimating and predicting bark thickness for seven conifer species in the Acadian Region of North America using a mixed-effects modeling approach. Eur. J. For. Res. 2011, 130, 219–233. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Trincado, G. Evaluation of potential modeling approaches for Scots pine stem diameter prediction in north-eastern Turkey. Comput. Electron. Agric. 2019, 162, 773–782. [Google Scholar] [CrossRef]
- Shen, J.; Hu, Z.; Sharma, R.P.; Wang, G.; Meng, X.; Wang, M.; Wang, Q.; Fu, L. Modeling height–diameter relationship for poplar plantations using combined-optimization multiple hidden layer back propagation neural network. Forests 2020, 11, 442. [Google Scholar] [CrossRef]
- Scrinzi, G.; Marzullo, L.; Galvagni, D. Development of a neural network model to update forest distribution data for managed alpine stands. Ecol. Model. 2007, 206, 331–346. [Google Scholar] [CrossRef]
- Socha, J.; Netzel, P.; Cywicka, D. Stem taper approximation by artificial neural network and a regression set models. Forests 2020, 11, 79. [Google Scholar] [CrossRef]
- Korea Forest Research Institute. Economic Tree Species 1: Pinus densiflora; Research Report on Korea Forest Research Institute; Korea Forest Research Institute: Seoul, Republic of Korea, 2012. [Google Scholar]
- National Institute of Forest Science (NIFoS). Stem Volume and Biomass, Yield Table; NIFoS: Seoul, Republic of Korea, 2023. [Google Scholar]
- Li, R.; Weiskittel, A.; Dick, A.R.; Kershaw, J.A., Jr.; Seymour, R.S. Regional Stem Taper Equations for Eleven Conifer Species in the Acadian Region of North America: Development and Assessment. North. J. Appl. For. 2012, 29, 5–14. [Google Scholar] [CrossRef]
- Shin, J.H.; Han, H.; Ko, C.; Kang, J.T.; Kim, Y.H. Applying Nonlinear Mixed-Effects Models to Taper Equations: A Case Study of Pinus densiflora in Gangwon Province, Republic of Korea. J. Korean Soc. For. Sci. 2022, 111, 136–149. [Google Scholar] [CrossRef]
- Alo, A.A.; Ogana, F.N. Equations for estimating bark thickness of Gmelina arborea trees in Omo Forest Reserve, Nigeria. J. Agric. Environ. 2018, 14, 153–165. [Google Scholar]
- Li, X.; Du, H.; Mao, F.; Xu, Y.; Huang, Z.; Xuan, J.; Zhou, Y.; Hu, M. Estimation aboveground biomass in subtropical bamboo forests based on an interpretable machine learning framework. Environ. Model. Softw. 2024, 178, 106071. [Google Scholar] [CrossRef]
- Czaplewski, R.L.; Brown, A.S.; Guenther, D.G. Estimating Merchantable Tree Volume in Oregon and Washington Using Stem Profile Models; PNW-RN-459; US Department of Agriculture, Forest Service: Fort Collins, CO, USA, 1989; pp. 1–15. [Google Scholar]
- Jiang, F.; Kutia, M.; Sarkissian, A.J.; Lin, H.; Long, J.; Sun, H.; Wang, G. Estimating the Growing Stem Volume of Coniferous Plantations Based on Random Forest Using an Optimized Variable Selection Method. Sensors 2020, 20, 7248. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H. A Taper and Volume Prediction System for Pinus densiflora in Kangwon Province, Korea. Korea For. Inst. J. For. Sci. 1999, 62, 155–166. [Google Scholar]
- Seo, Y.O. Allometric Equations, Stem Density and Biomass Expansion Factors for Cryptomeria japonica in Mount Halla, Jeju Island, Korea. J. Ecol. Environ. 2014, 37, 177–184. [Google Scholar]
- Son, Y.M.; Lee, K.H.; Kim, R.H. Estimation of Forest Biomass in Korea. J. Korean Soc. For. Sci. 2007, 96, 477–482. [Google Scholar] [CrossRef][Green Version]
- Valverde, J.C.; Rubilar, R.; Medina, A.; Mardones, O.; Emhart, V.; Bozo, D.; Espinoza, Y.; Campoe, O. Taper and individual tree volume equations of Eucalyptus varieties under contrasting irrigation regimes. N. Z. J. For. Sci. 2022, 52, 15. [Google Scholar] [CrossRef]
- Sharma, M.; Zhang, S.Y. Variable-Exponent Taper Equations for Jack Pine, Black Spruce, and Balsam Fir in Eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modeling Stand Density Effects on Taper for Jack Pine and Black Spruce Plantations Using Dimensional Analysis. For. Sci. 2009, 55, 268–282. [Google Scholar] [CrossRef]
- Sandoval, S.; Acuña, E. Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest. Forests 2022, 13, 2143. [Google Scholar] [CrossRef]
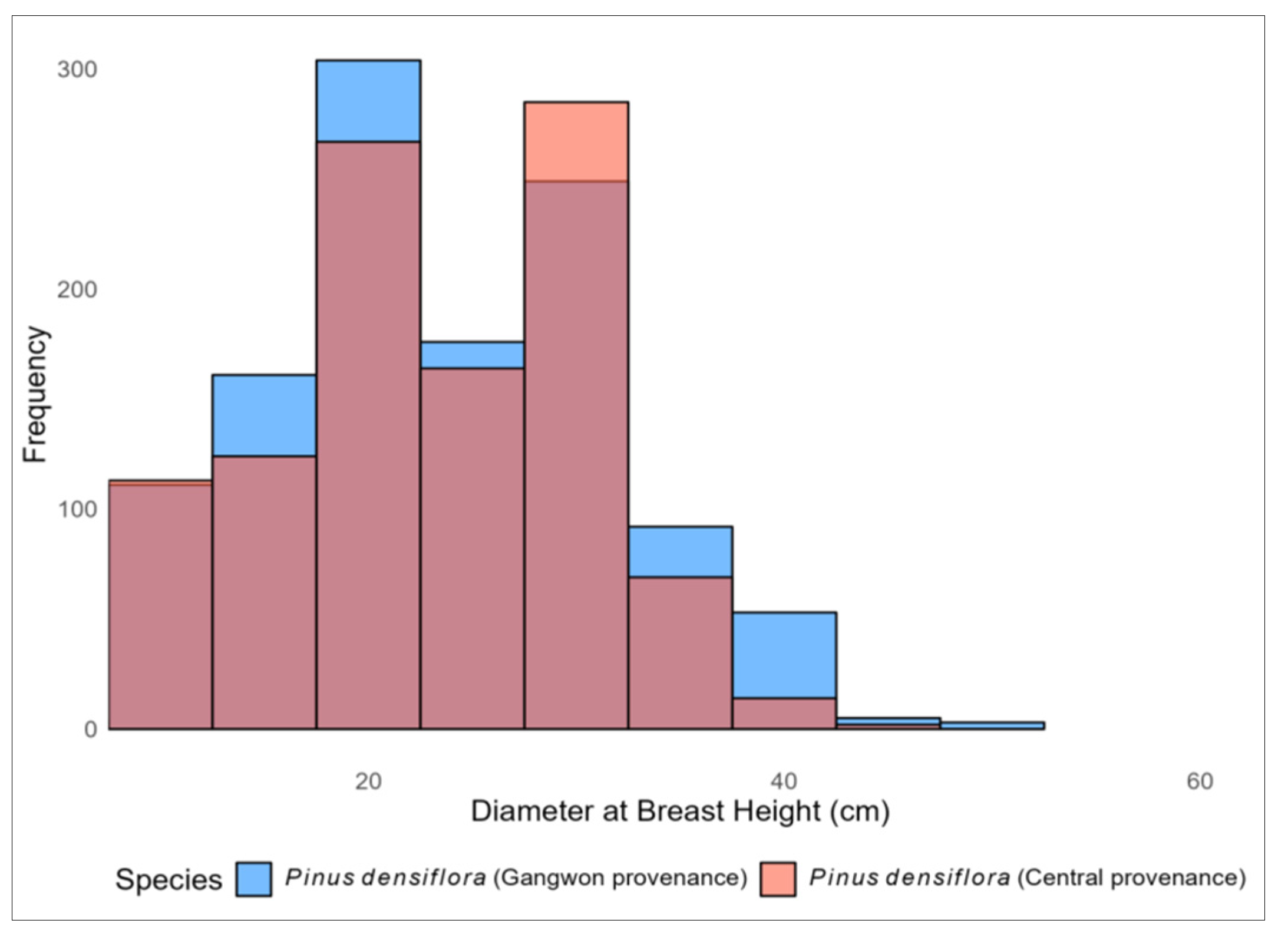
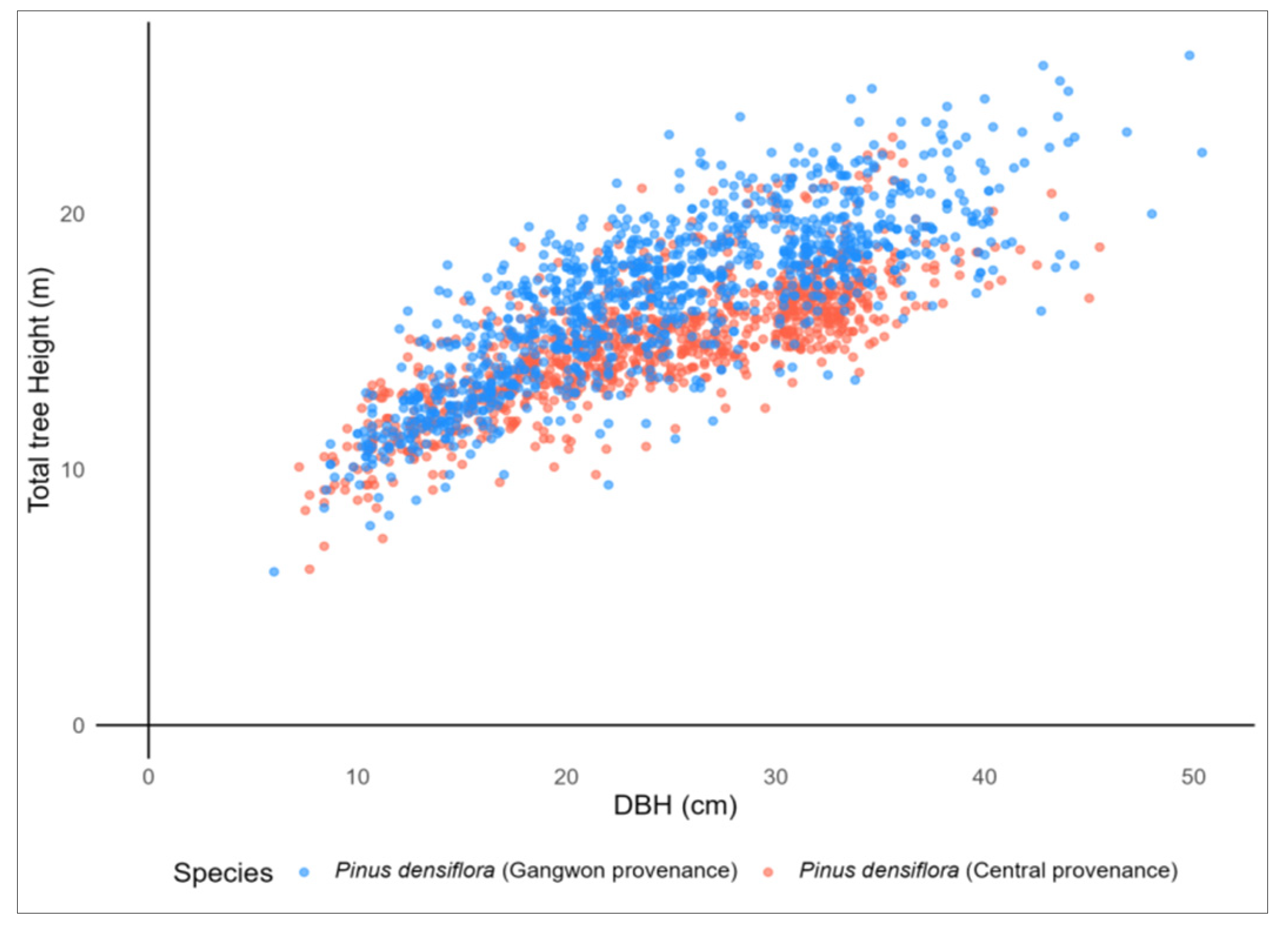


| Species | N | DBH (cm) | TH (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min_ | Max | Mean | SD | Min | Max | ||
| Pinus densiflora (central provenance) | 1042 | 25 | 7.43 | 7.2 | 45.5 | 15.03 | 2.44 | 6.1 | 23 |
| Pinus densiflora (Gangwon provenance) | 1155 | 25.6 | 8.02 | 6 | 50.4 | 16.70 | 3.15 | 6 | 26.2 |
| Model | Taper Equation |
|---|---|
| Kozak (1988) [5] | |
| where Z = relative height (=) X = (p = inflection point) ai, bi = parameters d = diameter (estimated) when h/H |
| Statistic | Calculation Formula |
|---|---|
| Root mean square error (RMSE) | |
| Mean absolute error (MAE) | |
| Coefficient of determination (R2) |
| Parameter | Pinus densiflora (Gangwon Provenance) | Pinus densiflora (Central Provenance) |
|---|---|---|
| a1 | 1.0742 | 1.0046 |
| a2 | 0.8968 | 0.9217 |
| a3 | 1.0013 | 1.0009 |
| b1 | −0.0123 | −0.1732 |
| b2 | −0.1073 | −0.0876 |
| b3 | 0.4714 | 0.4003 |
| b4 | 0.1232 | 0.2271 |
| b5 | −0.0220 | −0.0408 |
| p | 0.3 | 0.3 |
| R2 | 0.9874 | 0.9885 |
| RMSE | 1.1013 | 1.0391 |
| Species | Model | RMSE (cm) | R2 | MAE (cm) |
|---|---|---|---|---|
| Pinus densiflora (central provenance) | Random Forest | 1.824 | 0.968 | 1.304 |
| XGBoost | 1.851 | 0.966 | 1.318 | |
| ANN | 1.616 | 0.974 | 1.147 | |
| Pinus densiflora (Gangwon provenance) | Random Forest | 1.732 | 0.972 | 1.240 |
| XGBoost | 1.803 | 0.969 | 1.225 | |
| ANN | 1.584 | 0.976 | 1.125 |
| Species | Comparison | Test Model | p-Value | Significance (α = 0.05) |
|---|---|---|---|---|
| Pinus densiflora (central provenance) | ANN vs. RF | Wilcoxon signed-rank | 0.0005 | Significant |
| ANN vs. XGBoost | 0.0147 | Significant | ||
| RF vs. XGBoost | 0.959 | Not Significant | ||
| Pinus densiflora (Gangwon provenance) | ANN vs. RF | 0.0000 | Significant | |
| ANN vs. XGBoost | 0.0000 | Significant | ||
| RF vs. XGBoost | 0.597 | Not Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, C.; Kang, J.; Won, H.; Seo, Y.; Lee, M. Stem Profile Estimation of Pinus densiflora in Korea Using Machine Learning Models: Towards Precision Forestry. Forests 2025, 16, 840. https://doi.org/10.3390/f16050840
Ko C, Kang J, Won H, Seo Y, Lee M. Stem Profile Estimation of Pinus densiflora in Korea Using Machine Learning Models: Towards Precision Forestry. Forests. 2025; 16(5):840. https://doi.org/10.3390/f16050840
Chicago/Turabian StyleKo, Chiung, Jintaek Kang, Hyunkyu Won, Yeonok Seo, and Minwoo Lee. 2025. "Stem Profile Estimation of Pinus densiflora in Korea Using Machine Learning Models: Towards Precision Forestry" Forests 16, no. 5: 840. https://doi.org/10.3390/f16050840
APA StyleKo, C., Kang, J., Won, H., Seo, Y., & Lee, M. (2025). Stem Profile Estimation of Pinus densiflora in Korea Using Machine Learning Models: Towards Precision Forestry. Forests, 16(5), 840. https://doi.org/10.3390/f16050840






