Abstract
Urban trees grow in diverse environments where site conditions and human management may influence their growth patterns. However, few allometric equations (AEs) have been developed for urban trees, and the effects of environmental variations across urban land use categories on tree biomass remain largely unexplored. Therefore, this study developed urban land-use-specific AEs for major urban tree species in South Korea. We selected eight major urban tree species groups (at genus level), harvested 201 trees, and non-destructively measured the stem volumes of 1995 trees using a laser dendrometer. Species-specific and generalized AEs to estimate stem volume were developed under three urban land use categories: street trees, urban parks, and others. The results indicated that differences in stem volume across urban land use categories varied by species, with street trees generally showing smaller stem volumes. Furthermore, due to the high variation in stem volume within species, sampling designs that encompass diverse size distributions are necessary when developing AEs for urban trees. Our findings indicate that various factors in urban environments influence tree volume and considering these differences is essential for improving biomass estimation accuracy.
1. Introduction
As urban trees sequester significant amounts of carbon dioxide as they grow, quantifying carbon sequestration by urban trees is critical for global carbon management [1,2,3]. In addition, the Intergovernmental Panel on Climate Change (IPCC) guidelines recommend reporting annual carbon sequestration in urban green spaces (UGSs) under the settlements category for national greenhouse gas inventories [4]. Despite their importance, accurately assessing carbon sequestration by urban trees remains challenging, primarily due to the lack of appropriate allometric equations (AEs) developed for urban trees.
AEs are broadly used to calculate tree biomass using simply measurable values, such as diameter at breast height (DBH) and tree height. Several studies have developed species-specific AEs for urban trees by destructive sampling [5,6,7,8]. However, studies on AEs for urban tree species are still insufficient to address the high species diversity in UGSs. The lack of species-specific AEs leads to the use of non-local AEs, which cannot ensure estimation accuracy [9].
As an alternative for addressing the limited availability of urban-based AEs, IPCC guidelines recommended using a coefficient (0.80) for adjusting forest-based AEs to estimate urban tree biomass [4]. This adjustment accounts for the findings of Nowak [10], who indicated that open-grown trees generally have less biomass than trees in natural forests. However, the differences in biomass allocation between forest and urban trees may not be consistent [11,12]. McHale et al. [13] demonstrated that urban tree biomass may vary by 60%–300% based on the use of forest-based AEs relative to urban-based AEs. Furthermore, inherent differences in species composition between UGSs and forests increase the difficulty of applying forest-derived AEs to urban trees. Therefore, developing species-specific AEs for urban trees is a prerequisite for improving the accuracy of urban tree carbon stock estimates.
The variability in tree biomass across different growing environments must be considered when developing AEs. In forests, the intra- and inter-specific variabilities in biomass relationships are influenced by various factors, such as climate, age, stand characteristics, wood density, specific leaf area, and shade tolerance [14]. However, only a limited number of studies have examined the impact of human management practices, such as pruning, on urban tree biomass [15], and no studies have estimated the carbon sequestration of urban trees by considering the differences in biomass across various urban land use categories.
The traditional method for developing AEs is by harvesting various sizes of trees and measuring their biomass directly [8]. This highly precise method can measure variables that cannot be obtained through non-destructive measurements, such as wood density and root biomass. However, sampling an adequate number of trees in UGSs is challenging due to financial and administrative constraints.
Therefore, non-destructive methods have been used as an alternative to destructive methods. Pillsbury et al. [16] developed AEs for urban trees based on above-ground volume measurements using a Spiegel Relaskop. In South Korea, volumetric AEs for urban tree species were derived using laser dendrometers [17,18,19]. Additionally, progress in terrestrial laser scanning has advanced the development of volumetric-based AEs [20,21,22]. For example, McHale et al. [13] developed AEs for 11 urban tree species in UGSs in Fort Collins, USA, using a Cyrax 2500 LiDAR system. However, inherent uncertainties exist in converting tree volume to biomass because of differences in wood density and moisture content across species, between individual trees, and even within different parts of the same tree [23,24]. Using non-destructive methods allows for estimating tree volume or biomass without causing damage. This approach allows larger sample sizes and facilitates the survey of larger trees that would be too administratively and financially challenging to harvest.
Developing AEs for urban trees is essential for accurately estimating carbon storage and sequestration in UGSs. However, urban-based AEs are rarely available, and there has been limited research on the necessity of a classification system to enhance the accuracy of AEs. The main objective of this study is to develop widely applicable stem volume AEs for major urban tree species in South Korea that encompass a broad DBH range. Additionally, we aimed to develop land use category-specific AEs for five species groups commonly planted across all urban land use categories and to identify the differences between these categories.
We hypothesized that tree stem volume would differ across urban land use categories due to different growing environments and management practices. To test this hypothesis, we divided UGSs into three urban land use categories and derived urban land use-specific AEs. Our methodology consisted of two processes: (1) direct measurements of tree biomass based on harvesting trees and determining species-specific AEs and factors (stem density, root–shoot ratios, and biomass expansion factors) and (2) non-destructive measurements of stem volume using a laser dendrometer and converting them to stem biomass based on stem density values derived from the destructive method. Using these data, we developed AEs for different urban land use categories and generalized AEs for broad-leaf and needle-leaf species to facilitate their application across diverse tree species in UGSs.
2. Materials and Methods
2.1. Study Area
This study was conducted in South Korea, which is classified within the temperate zone. From 2011 to 2020, the mean annual temperature was 13.0 °C, and annual precipitation was 1283.5 mm [25]. The sampling sites were distributed across various UGSs in South Korea (Figure A1). Field measurements were carried out between 2020 and 2023. To account for various management practices and growing environments in UGSs, we categorized UGSs into three urban land use categories: street trees, urban parks, and others (including residential areas, schools, and university campuses).
2.2. Destructive Measurement
For tree harvesting, we selected nine major urban tree species in South Korea and sampled 20–25 trees per species (Table A1). The sampled trees for harvesting were selected according to several criteria: (1) trees planted in open-grown environments, (2) trees representing typical morphologies of each species, and (3) trees subjected to standard urban management practices. The exclusion criterion was trees subjected to severe pruning or other intensive interventions. Some of the tree data used in this study were partially utilized in previous research [26,27,28,29]. We performed an integrated analysis using a uniform methodology to establish species-specific and generalized AEs for estimating above-ground biomass (AGB), above-ground woody biomass (AGWB), and stem biomass. Additionally, we derived stem density and biomass expansion factor (BEF) both including and excluding foliage, which can be used for converting stem volume measured by non-destructive methods to AGWB. Previously published results were cited in the corresponding tables. Detailed information on the sampled trees, field survey methods, and calculation formulas can be found in Appendix A.
2.3. Non-Destructive Measurement
We developed stem volume AEs for each species (Ginkgo biloba L., Metasequoia glyptostroboides Hu & Cheng, Platanus occidentalis L., and Zelkova serrata (Thunb.) Makino) or groups of species (Acer spp., Pinus spp., Prunus spp., and Quercus spp.). The following species were sampled: Acer buergerianum Miq., Acer palmatum Thunb., Pinus densiflora Siebold & Zucc., Pinus koraiensis Siebold & Zucc., Pinus parviflora Siebold & Zucc., Pinus rigida Mill., Pinus strobus L., Pinus thunbergii Parl., Prunus armeniaca L., Prunus jamasakura Siebold ex Koidz., Prunus sargentii Rehder, Prunus × yedoensis Matsum., Quercus acutissima Carruth., Quercus glauca Thunb., Quercus mongolica Fisch. ex Ledeb., Quercus myrsinifolia Blume, Quercus palustris Münchh., Quercus rubra L., and Quercus serrata Murray. Some data were used to develop volumetric AEs [17,30]. However, this study synthesized additional data from the Gyeongsang, Jeolla, and Chungcheong regions to derive AEs at the species level (or genus level by grouping species) and analyzed them by urban land use categories. Although the species composition for each urban land use category was not identical at the genus level, genus-level AEs were developed to enhance model applicability, given the limited number of AEs developed for urban trees and high species diversity in UGSs.
Tree attributes such as the species, DBH of 1.2 m, and height were recorded, and stem volumes were non-destructively estimated. The distributions of the DBH and height of the sampled trees are shown in Figure 1.
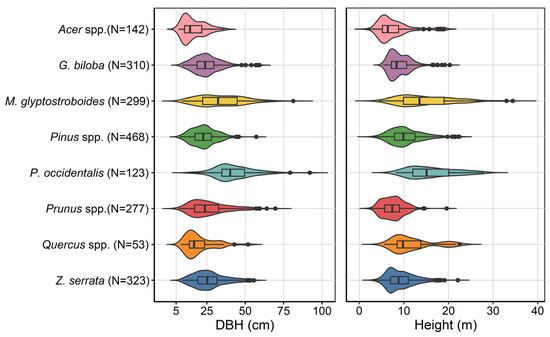
Figure 1.
Violin plot showing the tree size distributions in terms of the diameter at breast height (DBH) of 1.2 m and height. N, number of samples.
The stem volumes (m3) of trees were estimated using the method of Pillsbury et al. [16] with modifications. The stem diameters at different heights (0.2 m, 1.2 m, and 2 m intervals up to the tips) were measured using a laser dendrometer (Criterion RD-1000, Laser Technology Inc., Centennial, CO, USA). The volumes of each stem segment were then calculated using the formulas for the volumes of cylinders and cones. Please refer to Appendix A for more details on the assumptions for calculating stem volumes.
Stem volume measured by non-destructive methods was converted to biomass for the comparison with the AEs developed in previous studies. To convert stem volume to stem biomass and stem biomass to AGWB, we used stem density and the BEF excluding foliage values, respectively (Table A2). Despite wood density being commonly used for volume-to-biomass conversion [31,32,33], the species-specific stem density was used at the genus level to ensure consistency with the non-destructive volume measurement. Both methodologies used the outside bark stem diameter at specific heights to calculate the stem volume. Species-specific stem density and BEF values were developed through the destructive method and applied at the genus level. For Pinus spp., Pinus densiflora values were used for Pinus rigida and Pinus thunbergii, while Pinus strobus values were applied to Pinus parviflora and Pinus koraiensis.
2.4. Data Analysis
For the destructive method, we developed AEs for AGB, AGWB, and stem biomass using either DBH alone or DBH and height as predictor variables (Equations (1)–(4)). For non-destructively sampled trees, we derived AEs for stem volume. Following conventional practice in allometric studies [34,35], we employed log-transformed data fitted to linear regression. The correction factor (CF) was calculated using the methodology described by Sprugel [36], which corrects for bias by back-transforming the logarithm.
where Y represents either above-ground biomass (AGB), above-ground woody biomass (AGWB), stem biomass (kg), or stem volume (m3); DBH is diameter at breast height (cm); H is tree height (m); and a, b, and c are regression coefficients.
Y = a × DBHb
Y = a × DBHb × Hc
ln(Y) = ln(a) + b × ln(DBH)
ln(Y) = ln(a) + b × ln(DBH)+ c × ln(H)
The destructive method was used to develop species-specific AEs without urban land use classifications, while the non-destructive method was used to develop AEs for each urban land use category. Generalized AEs were developed by classifying the target species into broad- and needle-leaf categories. Before the analysis, outlying tree individuals were detected using studentized residuals with a threshold value of 2.5 because AEs are highly sensitive to outliers [37]. The fitting performance of the model was evaluated using the root mean square error (RMSE), mean absolute error (MAE), bias (Equation (5)), and adjusted coefficient of determination (R2adj). All statistical analyses were performed using R software (version 4.2.2).
where Yi and are observed and predicted values, respectively.
Differences in stem volume across urban land use categories were analyzed for five species groups (G. biloba, M. glyptostroboides, P. occidentalis, Prunus spp., and Z. serrata) that are commonly planted across all urban land use categories. An analysis of covariance (ANCOVA) was performed to determine the effect of urban land use categories on stem volume. ln(DBH) was used as a covariate, ln(Stem volume) as the dependent variable, and urban land use category as the grouping variable. The assumptions of normality and homogeneity of variance were verified using Kolmogorov–Smirnov and Levene’s tests, respectively. All data were log-transformed before the analysis. When homogeneity of variance was not satisfied after the log-transformation, the data were weighted using the inverse of the variance for each group [38]. The homogeneity of slopes was tested by examining the interaction between the covariate ln(DBH) and the grouping variable. When the interaction between DBH and the urban land use category was significant (p < 0.05), the interaction term was retained in the final model. Differences in stem volume among urban land use categories were assessed using adjusted means with Tukey’s HSD test. Adjusted means were calculated using the emmeans package in R software [39].
3. Results
3.1. Destructive Method
The BEF, root–shoot ratio, and stem density of each tree species are listed in Table A2. Z. serrata exhibited the highest mean BEF excluding foliage (1.844), followed by P. strobus (1.644), with G. biloba exhibiting the lowest mean value (1.389). A. palmatum had the highest mean root–shoot ratio (0.709), whereas Q. palustris had the lowest (0.332). Stem density varied considerably among the species. Z. serrata had the highest mean value (0.766), and M. glyptostroboides had the lowest value (0.304).
Species-specific AEs were developed based on the biomass data obtained from tree harvesting (Figure A2). For most tree species, including height as an additional variable resulted in higher adjusted R2 values than relying solely on DBH as a variable (Table A3; Table A4). The adjusted R2 values of the generalized AEs between DBH and AGWB were 0.900 and 0.903 for the broad- and needle-leaf species, respectively.
3.2. Comparison Between Destructive and Non-Destructive Methods
The DBH–stem biomass relationship of the destructive method was compared with that of the non-destructive method (Figure 2). G. biloba, P. occidentalis, Prunus spp., and Z. serrata showed similar patterns of DBH–stem biomass relationships between the two methods (Figure 2). In contrast, for Acer spp., destructively measured stem biomass showed a smaller trend than non-destructive estimates. For M. glyptostroboides, Pinus spp., and Quercus spp., both methods produced comparable estimates at smaller DBH values. However, non-destructively estimated stem biomass progressively increased as DBH increased. The DBH–height relationships (Figure A4) also revealed that destructively sampled trees generally had lower height than those in the non-destructive dataset in Acer spp. and Quercus spp. Additionally, M. glyptostroboides and Pinus spp. exhibited a limited height distribution in the destructive dataset compared to the non-destructive dataset (Figure A4).
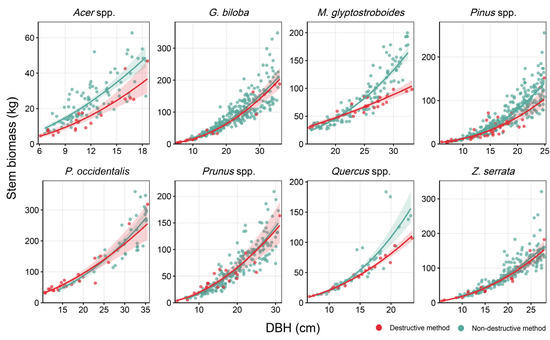
Figure 2.
Comparison of DBH–stem biomass relationships between destructively and non-destructively sampled trees. Shaded areas represent 95% confidence intervals.
3.3. Allometric Equations Developed by the Non-Destructive Method
A regression analysis was conducted for each species group to estimate the stem volume across different urban land use categories using either DBH alone or DBH and height as predictors (Table 1; Table A5). Overall, AEs using height as an additional variable showed higher adjusted R2 values and reduced bias (Table 1; Table A5). The results showed that street trees generally had a lower stem volume than other urban land use categories (Figure 3). Notably, applying AEs (DBH-only) developed for the others category to street trees resulted in overestimations of the mean stem volume of street trees by 35.6% for G. biloba. Meanwhile, applying AEs that include both DBH and height as variables reduced this overestimation to 8.3%.

Table 1.
Allometric equations developed by non-destructive sampling. Regression coefficients, RMSE, MAE, R2adj, Bias, CF, N, and DBH range of allometric equations (ln(Stem volume [m3]) = ln(a) + b × ln(DBH [cm])) developed by each urban land use category.
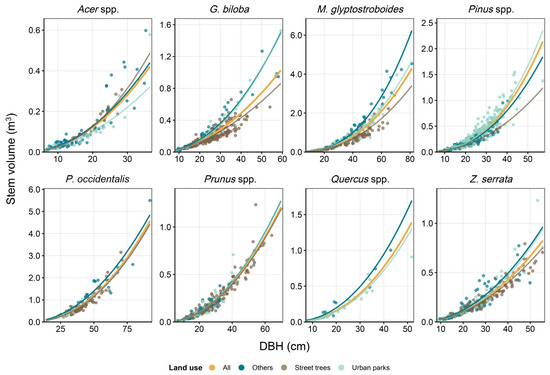
Figure 3.
Regression lines were derived based on the relationship between DBH and stem volume of each species group and urban land use category. The regression lines were extrapolated to compare across different DBH ranges. The yellow line was obtained by aggregating all data for each urban land use category. Street trees AEs for Acer spp. and Pinus spp. were developed solely from A. buergerianum and P. strobus, respectively.
The ANCOVA was conducted across various urban land use categories for five different species (Table 2). Significant interaction effects were observed for G. biloba, M. glyptostroboides, and Z. serrata. For G. biloba, street trees exhibited significantly lower slope coefficients compared to urban parks and others (p < 0.01). However, there was no significant difference between the slopes for urban parks and others (p = 0.811). For M. glyptostroboides, trees in the others category showed significantly steeper slopes than both street trees and urban parks (p < 0.01), while urban parks exhibited higher slope coefficients than street trees, though this difference was marginally significant (p = 0.07). For Z. serrata, street trees demonstrated significantly lower slope coefficients compared to urban parks (p < 0.01), with no significant differences in slopes between the others land use category.

Table 2.
ANCOVA results for stem volume by urban land use categories.
On the other hand, there was no statistical significance among the urban land use categories for Prunus spp., while P. occidentalis showed a lower stem volume in street trees compared to others (Table 2).
3.4. Accuracy of Allometric Equations by Urban Land Use Categories
A comparison of the stem volume estimation accuracy across different classification levels revealed that the highest accuracy was achieved when using AEs that considered both the species group and urban land use category (Figure 4a,b; RMSE = 0.120 m3, R2 = 0.933), followed by species-group-specific AEs (Figure 4c,d; RMSE = 0.136 m3, R2 = 0.909), with the lowest accuracy observed when using generalized AEs that only considered the broad-leaf/needle-leaf classification (Figure 4e,f; RMSE = 0.172 m3, R2 = 0.855). The application of generalized AEs tended to underestimate the volume of larger trees (Figure 4e).
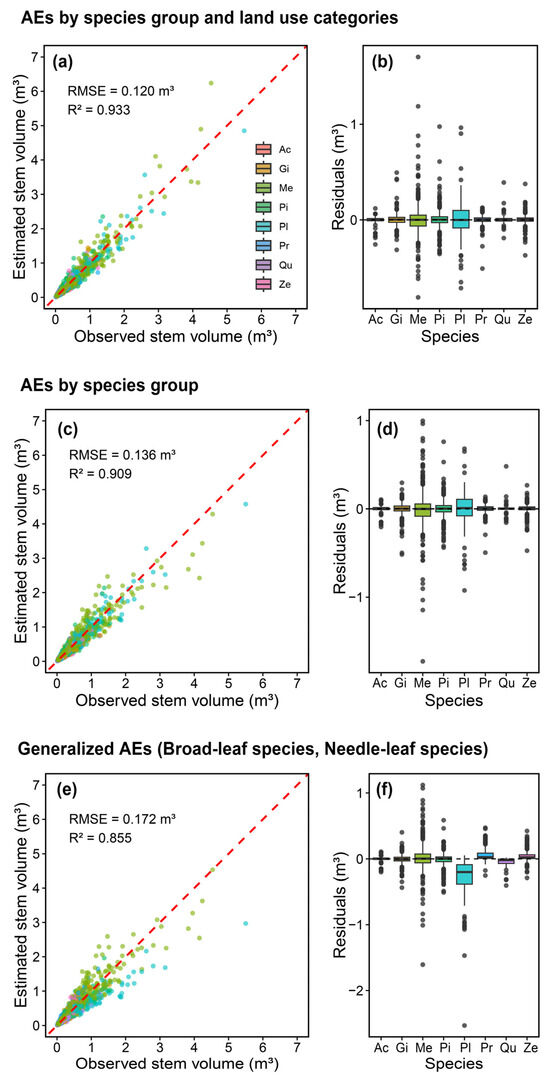
Figure 4.
Comparison of the observed stem volume by non-destructive method and estimated stem volume using different allometric equations (AEs) for (a) by species group and land use categories, (c) by species group, and (e) by generalized AEs for broad-leaf and needle-leaf species. Residuals of stem volume estimation corresponding to each approach for (b) by species group and land use categories, (d) by species group, and (f) by generalized AEs. Generalized AEs were derived by classifying the surveyed tree species into broad-leaf and needle-leaf species. Species abbreviations: Acer spp. (Ac), G. biloba (Gi), M. glyptostroboides (Me), Pinus spp. (Pi), P. occidentalis. (Pl), Prunus spp. (Pr), Quercus spp. (Qu), Z. serrata (Ze).
4. Discussion
4.1. Variability in Stem Volume Between Urban Land Use Categories
Variation in AEs within species reflects the capacity for adjustment to environmental conditions [40,41]. These adaptive responses lead to differences in the DBH–height ratio, biomass allocation, and wood density, which become the primary determinants of variability in AEs [14,40,42,43]. In this study, differences in the DBH–stem volume relationships among urban land use categories exhibited species-specific variations. Generally, street trees had lower stem volume than trees in other urban land use categories. This tendency may be due to their relatively smaller height for a given DBH than trees in other urban land use categories (Figure A4). A major contributing factor could be the intensive pruning of street trees. Speak and Salbitano [15] highlighted that current pruning techniques in Italian cities might reduce the maximum crown volume by 6.5%, while annual pruning can decrease the volume by up to 25%. Although pruning appears to be a major factor, environmental conditions may also play a significant role in the observed differences. Hui et al. [44] reported that roadside trees have a lower height-to-DBH ratio than those growing in open spaces and suggested that this difference could be related to changes in resource allocation. This indicates that the street environment itself, beyond pruning practices, may influence biomass allocation patterns.
Studies have also explored how various environmental factors in forests, such as stand structure, tree age, and climate, affect AEs [14,45,46]. de-Miguel et al. [45] developed AEs based on forest structure (both even-aged and uneven-aged stands) for Pinus brutia and revealed how differences in forest structure influence biomass allocation patterns. Moreover, the factors affecting AEs in UGSs may be more complex than in forests because environmental factors and human influences manifest in more fragmented patterns. Additionally, controlling these factors for research purposes presents inherent difficulties in UGSs. Despite several studies highlighting the variability in tree allometry across UGSs, research incorporating these factors in AE development remains limited [15,44]. While this study developed AEs for different urban land use categories and compared the differences among them, it was unable to identify the factors that influence these differences and the extent of their influence. While this study revealed differences in stem volume across urban land use categories due to complex factors, future research is needed to identify the factors contributing to these differences and their relative influence.
4.2. Improving the Accuracy of Urban Tree Biomass Estimation
Human interventions in urban trees, from planting to management, complicate the generalization of their morphological shapes. Consequently, developing AEs that effectively represent these patterns can be challenging. This study used the harvested tree data of 20 to 25 trees per species. Although this provides a substantial amount of data compared to previous urban studies [6,8], it only covered a limited DBH–height distribution of the surveyed trees (Figure A4). The stem biomass estimated through non-destructive methods exhibited much greater variability than the stem biomass measured using destructive methods (Figure 2). Considering that extrapolating an AE introduces significant uncertainty [47], it is necessary to understand the distribution by species before selecting sample trees in order to cover the diverse growth patterns of urban trees.
Developing urban land-use-specific AEs for key species with distinct stem volume patterns across UGSs is necessary to improve the reliability of estimates. In this study, G. biloba and M. glyptostroboides showed substantial differences in stem volume trends across urban land use categories and exhibited different DBH–height relationships (Figure A4). In contrast, Prunus spp. did not show significant differences in stem volume across urban land use categories, exhibiting similar trends in their DBH–height relationships between each urban land use category (Figure A4). Thus, DBH–height relationships between urban land use categories may serve as effective indicators for evaluating whether distinct AEs are required.
Categorizing urban land use considering the patterns of biomass variation and developing land-use-specific AEs for selected species would be the most reasonable approach. However, if practical considerations require the development of only one representative AE, the sampling process should ensure that selected trees accurately reflect the variability in management intensity. When developing AEs, it is a common practice to exclude trees that have undergone severe disturbances, such as extensive pruning [5,12]. Although this may be a practical approach given the limited research on urban-based AEs, it can introduce uncertainty in biomass estimates. In particular, tree biomass may be overestimated when AEs developed for trees in urban parks or other less-managed environments are applied directly to street trees, as observed in this study.
In addition, forest-based AEs are often applied to estimate urban tree biomass due to the limited availability of urban-specific AEs and the diverse species compositions in UGSs [48,49,50]. Applying forest-based AEs without adjustment may lead to AGWB overestimation. Previous studies have reported that using forest-based AEs may overestimate the AGWB of urban trees [10,51]. Ngo and Lum [12] showed that AEs derived from tropical forests overestimated the AGB of tropical street trees by 33%–324%. In this study, the differences between forest-based AEs and urban-based AEs varied by species (Figure A3). This variation is likely driven by environmental factors that differently influence biomass allocation across species [14,52]. For example, the AGWB of Quercus spp. was smaller than those estimated using forest-based AEs (Figure A3). In contrast, G. biloba and Pinus spp. showed similar patterns. Overall, the differences between forest-based and urban-based AEs by species (or genus) showed varying trends and were difficult to generalize. The extent of these allometric relationship differences between urban and forest trees depends on species characteristics and regional factors. Therefore, when applying AEs developed in different environments, their suitability should be carefully evaluated.
4.3. Practical Considerations for Urban Tree Biomass Estimation
UGSs exhibit diverse tree species richness, even in small areas [53,54], making it impractical to develop species-specific AEs for all tree species. Therefore, when estimating the carbon stock of urban trees at the city or national level, forest-based or urban-based AEs from other regions need to be applied [53]. Generally, AEs are assigned in the order of species, genus, and generalized levels [2]. However, limited research has addressed the uncertainty associated with applying these geographically and environmentally different AEs to urban tree biomass estimation [53].
In this study, generalized AEs (broad-leaf and needle-leaf species) were developed. Our results showed that applying generalized AEs tended to underestimate the stem volume for large trees, which was likely because most of our data were obtained from smaller trees, thus creating a bias when predicting the biomass of larger trees [55]. Aguaron and McPherson [53] derived urban-based generalized AEs for broad-leaf, conifer, and palm trees. When comparing these urban-based AEs with forest-based AEs, they found that the urban AEs produced biomass estimates approximately 25% lower than forest-based equations for hardwood trees with a DBH larger than 35 cm. McHale et al. [13] highlighted that the application of forest-based AEs to urban trees could result in substantial uncertainties in biomass estimation and suggested that using generalized AEs based on a combination of multiple AEs may serve as an alternative approach for reducing such variability. This study developed generalized AEs under two species classifications (broad-leaf and needle-leaf) and three urban land-use categories (street trees, urban parks, and others). However, these generalized AEs present limitations based on the limited number of species and sample size used in their development. Therefore, to improve their accuracy, future research should either increase the sample size of large trees or develop size-class-specific AEs, which will require a consideration of classification systems.
Including height improved the accuracy of estimations because it helps to account for variations in tree architecture and growth patterns that may not be captured by DBH alone, especially in urban environments where trees are subject to various stressors and management practices [56,57]. Our findings indicate that including both DBH and height as variables in AEs improved the estimation accuracy and mitigated the extent of overestimation when applying AEs developed for other urban land use categories to street trees. Given the diverse planting conditions and management regimes found in UGSs, categorizing trees by urban land use categories has inherent limitations. Therefore, supplementary structural or environmental variables that can further enhance biomass estimation accuracy must be identified and incorporated into AEs.
Furthermore, we observed high variations in stem volume in G. biloba and M. glyptostroboides, particularly within street trees (Figure 3). This variability may stem from the various pruning intensities, where some trees receive less pruning while others undergo intensive pruning. These differences make generalizing AEs based solely on land use categories challenging. However, we could not differentiate the individual contributions of each factor to these variations, which requires further investigation. Jo and Cho [58] quantified this management impact, measuring pruned branch weights and deriving average pruning quantities: 11.4 kg (dry weight) for G. biloba street trees with a mean DBH of 22 cm (N = 41) and 34.9 kg for P. occidentalis with a mean DBH of 26 cm (N = 40). The direct quantification of biomass losses from pruning can be used to develop adjustment coefficients that account for management intensity.
4.4. Limitations and Future Research
This study identified stem volume differences across land use categories and demonstrated the need for urban land-use-specific AEs. However, regional differences in species distribution and UGS management practices may result in different patterns of urban land use category differences. This study surveyed a total of 1995 trees; however, when categorized by species and land use categories, insufficient sample sizes were observed in some species groups, such as Pinus spp., P. occidentalis, and Quercus spp. This limited sampling may lead to reduced reliability for the AEs associated with these groups.
There are several uncertainties in the measurement process. While non-destructive volume measurement approach offers a practical and efficient methodology, it presents methodological considerations. The frontal view measurements at specific heights may not fully capture the true diameter due to the three-dimensional nature of tree structures. Furthermore, although we employed Smalian’s formula for non-destructive volume calculations due to computational convenience, this approach requires refinement in future studies. Notably, the stem section between 0.2 m and 1.2 m typically exhibits a neiloid form, especially in M. glyptostroboides, which may lead to overestimation when applying the formulas that assume a paraboloid shape.
Future studies need to adopt advanced technologies such as terrestrial laser scanning to resolve uncertainties in biomass estimates [59,60]. Combining terrestrial laser scanning with partial destructive sampling would further validate the AEs developed in this study. Despite these limitations, this study contributes valuable insights regarding the necessity of developing AEs that reflect the various growth characteristics of urban trees. Furthermore, while this study categorized UGSs into three land use categories and analyzed stem volume differences among them, it did not differentiate and quantify the specific environmental factors affecting biomass changes in urban settings. In forests, stand structure, age, and management may influence biomass allocation patterns [61]. Since the quantification of factors affecting biomass allocation in urban environments has been rarely conducted, we believe future research should investigate the impacts of urban-specific factors such as soil conditions, pruning intensity, and pollution levels on urban tree biomass allocation.
5. Conclusions
This study developed AEs for urban tree species using an approach that combined destructive and non-destructive methods, thereby enhancing their applicability to diverse urban environments. The findings demonstrated variability in stem volume across different urban land use categories. Overall, street trees tended to have lower stem volumes compared to other urban land use categories, which was likely due to intensive management practices and environmental stressors. Our results showed that applying AEs developed for trees with distinct growth characteristics to trees in different environments could lead to significant overestimation or underestimation.
Our findings demonstrated that applying different AEs is crucial for species with distinct management practices among urban land use categories and for species whose biomass is significantly influenced by the planting environment. These results can be applied to more precisely calculate the carbon sequestration potential of UGSs, thereby contributing to improved urban forest carbon accounting while highlighting the need for urban land-use-specific AEs in future research.
Author Contributions
Conceptualization, J.-M.L.; data curation, B.C., J.-Y.J., S.L. and S.-J.L.; formal analysis, J.-M.L.; funding acquisition, Y.S. and W.-K.L.; investigation, J.-M.L. and H.-S.K.; methodology, J.-M.L.; project administration, Y.S. and W.-K.L.; software, J.-M.L.; supervision, Y.S., T.K.Y., C.K. and K.-H.L.; validation, J.-M.L.; visualization, J.-M.L.; writing—original draft, J.-M.L.; writing—review and editing, H.-S.K., H.J., G.K., S.K. and C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a fund from the Ministry of Land, Infrastructure, and Transport and the Korea Agency for Infrastructure Technology Advancement (RS-2020-KA158194), Technology Development Project for Creation and Management of Ecosystem-based Carbon Sinks through KEITI, Ministry of Environment (RS-2023-00218243) and Korea Forest Service (KFS) as ⌈Graduate School specialized in Carbon Sink⌋.
Data Availability Statement
The datasets used in this study are available upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AE | Allometric equation |
| AGWB | Above-ground woody biomass |
| BEF | Biomass expansion factor |
| CF | Correction factor |
| DBH | Diameter at breast height |
| UGSs | Urban green spaces |
Appendix A. Materials and Methods
Appendix A.1. Detailed Methodology for Destructive Analysis
We harvested trees and divided them into several components (stems, branches, leaves, and roots). The fresh weights of each tree component were measured on site. The samples of each component were collected and oven-dried at 85 °C until reaching a constant weight. The dry-to-fresh weight ratios of each part were used to convert the fresh-to-dry weight. To estimate the stem volume (cm3), the stem diameter (cm) was measured at various heights (0.2 m, 1.2 m, and at intervals of 2.0 m up to the tree height). The volumes of each section were calculated based on Huber’s formula (Vstem = M × L, where V = volume, M = cross-sectional area at the midpoint of a section, and L = length of a section). The last section of the stem was assumed to have a conical shape (Vlast part = M × L × 1/3). Stem density (g·cm−3) was calculated by dividing the stem biomass by stem volume (outside the bark).
Consequently, we calculated the species-specific BEF (Equation (A1)), BEF excluding foliage (Equation (A2)), root–shoot ratio (Equation (A3)), and stem density (Equation (A4)).
Biomass expansion factor (BEF) (kg·kg−1) = above-ground biomass (kg) ÷ stem biomass (kg)
BEF excluding foliage (kg·kg−1) = above-ground woody biomass (kg) ÷ stem biomass (kg)
Root–shoot ratio (kg·kg−1) = below-ground biomass (kg) ÷ above-ground biomass (kg)
Stem density (g·cm−3) = stem biomass (g) ÷ stem volume (cm3)
Appendix A.2. Detailed Assumptions for Calculating Stem Volumes
Stem volumes were calculated based on the following assumptions:
- The base segment (0–0.2 m) of the stem was assumed to be cylindrical, and the volume was calculated based on the formula Vstem_bottom = L × A0.2, where A0.2 and L represent the cross-sectional area at 0.2 m and the length of the segment (0.2 m), respectively.
- The tips of the stem were assumed to be conical, and the volumes of these tips were calculated based on the formula Vlast part = L/3 × Atip, where L is the length of the segment, and Atip is the cross-sectional area at the measurement point.
- The intermediate sections between these points were assumed to be a paraboloid frustum, and the volumes of these sections were estimated using the formula Vmiddle = L/2 × (Au + Ab), where L is the length of the section, and Au and Ab are the cross-sectional areas at the upper and lower ends, respectively. For trees with leaning stems, we calculated the section lengths using the leaning angle and height measurements to accurately determine stem volume.
Appendix A.3. Detailed Conversion Processes for Allometric Equations
The following procedures were used to convert the results from various allometric equations (AEs) into above-ground woody biomass (AGWB) for comparison:
- Volume to biomass conversion:
In the AEs developed by Pillsbury et al. [16] and McHale et al. [13], above-ground tree volume was converted to biomass by multiplying the volume by the dry weight density factor (kg·m−3) according to McPherson et al. [56].
- 2.
- Total woody biomass to AGWB conversion:
In the AEs developed by Matsue et al. [8], which included root biomass (excluding leaves), total woody biomass was converted to AGWB using the root–shoot ratio as indicated in their study.
- 3.
- Combining tree part equations:
In the AEs by Son and Kim [62] and KFRI [63], the stem and branch equations were merged into a single AE to estimate the AGWB.

Table A1.
Mean and range of age, DBH, height, above-ground biomass (AGB), and number of sampled trees (N).
Table A1.
Mean and range of age, DBH, height, above-ground biomass (AGB), and number of sampled trees (N).
| Species | Age (yr) | DBH (cm) | Height (m) | AGB (kg) | N |
|---|---|---|---|---|---|
| Acer palmatum | 16.7 (13–26) | 11.7 (6.1–18.6) | 4.9 (2.7–7.5) | 28.1 (7.5–104.2) | 20 |
| Ginkgo biloba | 19.9 (7–45) | 15.0 (5.3–36) | 8.9 (4.3–15.2) | 78.5 (4.4–351.8) | 24 |
| Metasequoia glyptostroboides | 25.0 (15–48) | 25.2 (15.5–33.2) | 12.8 (10.5–15.6) | 115.5 (55.7–175.6) | 25 |
| Pinus densiflora | 17.0 (10–29) | 14.0 (6.1–24.9) | 7.4 (2.9–17.5) | 57.4 (6.5–221.7) | 23 |
| Platanus occidentalis | 26.0 (16–39) | 17.6 (9.9–35.5) | 14.7 (10.3–21.1) | 134.3 (42.4–523.0) | 25 |
| Pinus strobus | 18.7 (7–29) | 14.6 (7.1–20.9) | 6.8 (4.3–8.7) | 52.0 (5.7–111.9) | 20 |
| Prunus yedoensis | 20.0 (6–29) | 16.0 (4.3–31.1) | 9.4 (4.9–12.6) | 86.7 (4.7–365.9) | 24 |
| Quercus palustris | 12.7 (10–15) | 14.3 (6.8–23.4) | 9.3 (7.2–11.6) | 75.8 (13.2–181.8) | 20 |
| Zelkova serrata | 19.1 (12–27) | 16.0 (5.5–27.9) | 8.9 (4.6–14.1) | 125.6 (7.3–483.5) | 20 |
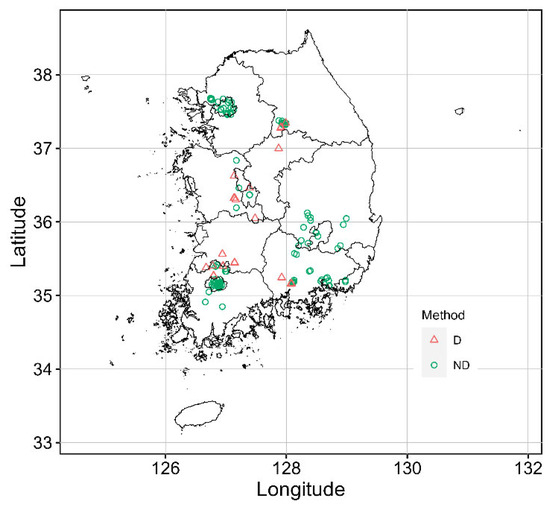
Figure A1.
Location of the study area in South Korea. D, destructive measurement; ND, non-destructive measurement.
Appendix B. Results

Table A2.
Biomass expansion factor (BEF), BEF excluding foliage, root–shoot ratio, and stem density of each species.
Table A2.
Biomass expansion factor (BEF), BEF excluding foliage, root–shoot ratio, and stem density of each species.
| Species | Mean | Median | SD | N | Reference |
|---|---|---|---|---|---|
| BEF | |||||
| Acer palmatum | 1.586 | 1.546 | 0.251 | 20 | |
| Ginkgo biloba | 1.489 | 1.414 | 0.240 | 24 | |
| Metasequoia glyptostroboides | 1.703 | 1.688 | 0.157 | 25 | |
| Pinus densiflora | 1.554 | 1.460 | 0.290 | 23 | |
| Platanus occidentalis | 1.561 | 1.529 | 0.172 | 25 | [27] |
| Pinus strobus | 1.943 | 1.906 | 0.510 | 20 | |
| Prunus yedoensis | 1.715 | 1.612 | 0.376 | 24 | |
| Quercus palustris | 1.617 | 1.619 | 0.145 | 20 | |
| Zelkova serrata | 2.007 | 1.850 | 0.444 | 20 | |
| BEF excluding foliage | |||||
| Acer palmatum | 1.476 | 1.436 | 0.219 | 20 | |
| Ginkgo biloba | 1.389 | 1.316 | 0.228 | 24 | |
| Metasequoia glyptostroboides | 1.527 | 1.509 | 0.126 | 25 | |
| Pinus densiflora | 1.395 | 1.358 | 0.218 | 23 | |
| Platanus occidentalis | 1.397 | 1.360 | 0.130 | 25 | |
| Pinus strobus | 1.644 | 1.602 | 0.335 | 20 | |
| Prunus yedoensis | 1.561 | 1.484 | 0.337 | 24 | |
| Quercus palustris | 1.519 | 1.522 | 0.139 | 20 | |
| Zelkova serrata | 1.844 | 1.689 | 0.406 | 20 | |
| Root–shoot ratio | |||||
| Acer palmatum | 0.709 | 0.740 | 0.183 | 19 | |
| Ginkgo biloba | 0.500 | 0.483 | 0.192 | 16 | |
| Metasequoia glyptostroboides | 0.454 | 0.443 | 0.054 | 25 | |
| Pinus densiflora | 0.413 | 0.390 | 0.141 | 23 | |
| Platanus occidentalis | 0.402 | 0.413 | 0.058 | 25 | [27] |
| Pinus strobus | 0.397 | 0.381 | 0.134 | 17 | |
| Prunus yedoensis | 0.395 | 0.419 | 0.130 | 23 | |
| Quercus palustris | 0.332 | 0.300 | 0.088 | 20 | |
| Zelkova serrata | 0.508 | 0.453 | 0.189 | 20 | |
| Stem density | |||||
| Acer palmatum | 0.591 | 0.554 | 0.145 | 20 | |
| Ginkgo biloba | 0.528 | 0.532 | 0.064 | 24 | |
| Metasequoia glyptostroboides | 0.304 | 0.291 | 0.044 | 25 | |
| Pinus densiflora | 0.518 | 0.524 | 0.109 | 19 | |
| Platanus occidentalis | 0.509 | 0.527 | 0.088 | 25 | [27] |
| Pinus strobus | 0.445 | 0.445 | 0.074 | 20 | |
| Prunus yedoensis | 0.626 | 0.593 | 0.098 | 23 | |
| Quercus palustris | 0.654 | 0.673 | 0.102 | 18 | |
| Zelkova serrata | 0.766 | 0.789 | 0.085 | 20 |
DBH, diameter at breast height; SD, standard deviation; N, number of sampled trees.

Table A3.
Regression coefficients, root mean square error (RMSE), mean absolute error (MAE), adjusted R-square (R2adj), and correction factor (CF) of the allometric equations (ln(Y [dry kg]) = ln(a) + b × ln(DBH [cm])) developed by destructive sampling.
Table A3.
Regression coefficients, root mean square error (RMSE), mean absolute error (MAE), adjusted R-square (R2adj), and correction factor (CF) of the allometric equations (ln(Y [dry kg]) = ln(a) + b × ln(DBH [cm])) developed by destructive sampling.
| Tree Component (Y) | a | b | RMSE | MAE | R2adj | CF | Reference |
|---|---|---|---|---|---|---|---|
| Acer palmatum | [28] | ||||||
| AGB | 0.182 | 1.973 | 0.364 | 0.306 | 0.735 | 1.076 | |
| AGWB | 0.162 | 1.993 | 0.348 | 0.293 | 0.756 | 1.070 | |
| Stem | 0.146 | 1.879 | 0.261 | 0.226 | 0.831 | 1.039 | |
| Ginkgo biloba | |||||||
| AGB | 0.178 | 2.099 | 0.179 | 0.148 | 0.980 | 1.018 | |
| AGWB | 0.151 | 2.135 | 0.169 | 0.145 | 0.983 | 1.016 | |
| Stem | 0.156 | 1.996 | 0.179 | 0.140 | 0.978 | 1.018 | |
| Metasequoia glyptostroboides | |||||||
| AGB | 0.917 | 1.494 | 0.105 | 0.086 | 0.874 | 1.006 | |
| AGWB | 0.789 | 1.507 | 0.102 | 0.086 | 0.882 | 1.006 | |
| Stem | 0.436 | 1.561 | 0.115 | 0.090 | 0.863 | 1.007 | |
| Pinus densiflora | |||||||
| AGB | 0.102 | 2.299 | 0.340 | 0.292 | 0.869 | 1.065 | |
| AGWB | 0.086 | 2.326 | 0.352 | 0.307 | 0.864 | 1.070 | |
| Stem | 0.068 | 2.290 | 0.381 | 0.323 | 0.839 | 1.083 | |
| Platanus occidentalis | |||||||
| AGB | 0.505 | 1.896 | 0.181 | 0.155 | 0.921 | 1.018 | [27] |
| AGWB | 0.468 | 1.884 | 0.186 | 0.158 | 0.916 | 1.019 | |
| Stem | 0.483 | 1.755 | 0.202 | 0.167 | 0.890 | 1.022 | |
| Pinus strobus | |||||||
| AGB | 0.062 | 2.464 | 0.153 | 0.123 | 0.958 | 1.013 | |
| AGWB | 0.039 | 2.579 | 0.150 | 0.124 | 0.963 | 1.013 | |
| Stem | 0.030 | 2.501 | 0.197 | 0.173 | 0.934 | 1.022 | |
| Prunus yedoensis | |||||||
| AGB | 0.252 | 2.045 | 0.235 | 0.192 | 0.934 | 1.031 | |
| AGWB | 0.220 | 2.061 | 0.248 | 0.208 | 0.928 | 1.034 | |
| Stem | 0.310 | 1.775 | 0.300 | 0.260 | 0.867 | 1.050 | |
| Quercus palustris | |||||||
| AGB | 0.271 | 2.077 | 0.117 | 0.097 | 0.971 | 1.008 | [29] |
| AGWB | 0.251 | 2.081 | 0.121 | 0.100 | 0.969 | 1.008 | |
| Stem | 0.226 | 1.964 | 0.086 | 0.074 | 0.982 | 1.004 | |
| Zelkova serrata | |||||||
| AGB | 0.137 | 2.366 | 0.189 | 0.163 | 0.967 | 1.020 | |
| AGWB | 0.117 | 2.395 | 0.192 | 0.172 | 0.966 | 1.021 | |
| Stem | 0.161 | 2.054 | 0.181 | 0.160 | 0.959 | 1.018 | |
| Broad-leaf species | |||||||
| AGB | 0.148 | 2.248 | 0.343 | 0.269 | 0.895 | 1.061 | |
| AGWB | 0.132 | 2.259 | 0.335 | 0.265 | 0.900 | 1.059 | |
| Stem | 0.144 | 2.072 | 0.331 | 0.268 | 0.886 | 1.057 | |
| Needle-leaf species | |||||||
| AGB | 0.216 | 1.977 | 0.268 | 0.216 | 0.906 | 1.038 | |
| AGWB | 0.172 | 2.015 | 0.278 | 0.219 | 0.903 | 1.041 | |
| Stem | 0.132 | 1.967 | 0.311 | 0.233 | 0.876 | 1.051 | |
AGB, above-ground biomass; AGWB, above-ground woody biomass.

Table A4.
Regression coefficients, root mean square error (RMSE), mean absolute error (MAE), adjusted R-square (R2adj), and correction factor (CF) of the allometric equations (ln(Y[dry kg]) = ln(a) + b × ln(DBH [cm]) + c × ln(Height [m])) developed by destructive sampling.
Table A4.
Regression coefficients, root mean square error (RMSE), mean absolute error (MAE), adjusted R-square (R2adj), and correction factor (CF) of the allometric equations (ln(Y[dry kg]) = ln(a) + b × ln(DBH [cm]) + c × ln(Height [m])) developed by destructive sampling.
| Variable | a | b | c | RMSE | MAE | R2adj | CF | Reference |
|---|---|---|---|---|---|---|---|---|
| Acer palmatum | [28] | |||||||
| AGB | 0.050 | 1.572 | 1.435 | 0.247 | 0.198 | 0.871 | 1.036 | |
| AGWB | 0.047 | 1.609 | 1.372 | 0.236 | 0.194 | 0.881 | 1.033 | |
| Stem | 0.065 | 1.630 | 0.892 | 0.202 | 0.180 | 0.893 | 1.024 | |
| Ginkgo biloba | ||||||||
| AGB | 0.104 | 1.932 | 0.447 | 0.155 | 0.129 | 0.984 | 1.014 | |
| AGWB | 0.091 | 1.977 | 0.423 | 0.146 | 0.120 | 0.986 | 1.012 | |
| Stem | 0.084 | 1.805 | 0.514 | 0.147 | 0.112 | 0.984 | 1.012 | |
| Metasequoia glyptostroboides | ||||||||
| AGB | 0.508 | 1.354 | 0.409 | 0.098 | 0.069 | 0.887 | 1.005 | |
| AGWB | 0.411 | 1.353 | 0.451 | 0.092 | 0.066 | 0.900 | 1.005 | |
| Stem | 0.244 | 1.423 | 0.403 | 0.108 | 0.085 | 0.874 | 1.007 | |
| Pinus densiflora | ||||||||
| AGB | 0.119 | 1.862 | 0.518 | 0.275 | 0.230 | 0.910 | 1.044 | |
| AGWB | 0.102 | 1.839 | 0.576 | 0.272 | 0.228 | 0.915 | 1.043 | |
| Stem | 0.085 | 1.665 | 0.739 | 0.253 | 0.217 | 0.926 | 1.037 | |
| Platanus occidentalis | ||||||||
| AGB | 0.213 | 1.733 | 0.494 | 0.166 | 0.138 | 0.930 | 1.016 | |
| AGWB | 0.176 | 1.699 | 0.561 | 0.168 | 0.138 | 0.929 | 1.016 | |
| Stem | 0.151 | 1.536 | 0.665 | 0.177 | 0.135 | 0.911 | 1.018 | |
| Pinus strobus | ||||||||
| AGB | 0.050 | 2.378 | 0.232 | 0.150 | 0.122 | 0.957 | 1.013 | |
| AGWB | 0.026 | 2.420 | 0.433 | 0.140 | 0.113 | 0.966 | 1.012 | |
| Stem | 0.012 | 2.147 | 0.958 | 0.157 | 0.128 | 0.956 | 1.015 | |
| Prunus yedoensis | ||||||||
| AGB | 0.113 | 1.863 | 0.585 | 0.197 | 0.154 | 0.951 | 1.022 | |
| AGWB | 0.094 | 1.868 | 0.616 | 0.208 | 0.170 | 0.947 | 1.025 | |
| Stem | 0.079 | 1.465 | 0.991 | 0.207 | 0.170 | 0.934 | 1.025 | |
| Quercus palustris | ||||||||
| AGB | 0.253 | 2.060 | 0.051 | 0.117 | 0.097 | 0.970 | 1.008 | |
| AGWB | 0.210 | 2.035 | 0.135 | 0.121 | 0.100 | 0.968 | 1.009 | |
| Stem | 0.159 | 1.874 | 0.264 | 0.085 | 0.070 | 0.982 | 1.004 | |
| Zelkova serrata | ||||||||
| AGB | 0.075 | 1.998 | 0.741 | 0.126 | 0.105 | 0.984 | 1.009 | |
| AGWB | 0.063 | 2.023 | 0.749 | 0.130 | 0.109 | 0.984 | 1.010 | |
| Stem | 0.127 | 1.907 | 0.295 | 0.172 | 0.149 | 0.961 | 1.018 | |
| Broad-leaf species | ||||||||
| AGB | 0.080 | 1.857 | 0.751 | 0.243 | 0.204 | 0.947 | 1.031 | |
| AGWB | 0.074 | 1.884 | 0.721 | 0.243 | 0.207 | 0.947 | 1.031 | |
| Stem | 0.074 | 1.647 | 0.816 | 0.201 | 0.169 | 0.958 | 1.021 | |
| Needle-leaf species | ||||||||
| AGB | 0.233 | 1.743 | 0.276 | 0.257 | 0.212 | 0.912 | 1.035 | |
| AGWB | 0.187 | 1.743 | 0.321 | 0.264 | 0.214 | 0.911 | 1.037 | |
| Stem | 0.149 | 1.565 | 0.474 | 0.283 | 0.220 | 0.896 | 1.043 | |
AGB, above-ground biomass; AGWB, above-ground woody biomass.

Table A5.
Allometric equations developed by non-destructive sampling. Regression coefficients, RMSE, MAE, R2adj, Bias, and CF of the allometric equations (ln(stem volume [m3]) = ln(a) + b × ln(DBH [cm]) + c × ln(Height [m])) developed by urban land use category.
Table A5.
Allometric equations developed by non-destructive sampling. Regression coefficients, RMSE, MAE, R2adj, Bias, and CF of the allometric equations (ln(stem volume [m3]) = ln(a) + b × ln(DBH [cm]) + c × ln(Height [m])) developed by urban land use category.
| Land Use | a | b | c | RMSE | MAE | R2adj | Bias | CF | N |
|---|---|---|---|---|---|---|---|---|---|
| Acer spp. | |||||||||
| All | 0.0002035 | 1.758 | 0.512 | 0.247 | 0.194 | 0.927 | −6.5 | 1.032 | 142 |
| Others | 0.0002469 | 1.575 | 0.660 | 0.234 | 0.178 | 0.932 | −5.9 | 1.029 | 77 |
| Street trees * | 0.0001268 | 2.112 | 0.296 | 0.123 | 0.106 | 0.967 | −1.6 | 1.009 | 25 |
| Urban parks | 0.0002920 | 1.661 | 0.396 | 0.226 | 0.169 | 0.927 | −5.5 | 1.028 | 40 |
| Ginkgo biloba | |||||||||
| All | 0.0001164 | 1.804 | 0.741 | 0.163 | 0.120 | 0.949 | −2.7 | 1.014 | 310 |
| Others | 0.0001166 | 1.914 | 0.599 | 0.154 | 0.115 | 0.981 | −2.5 | 1.013 | 43 |
| Street trees | 0.0001440 | 1.742 | 0.730 | 0.158 | 0.115 | 0.931 | −2.5 | 1.013 | 239 |
| Urban parks | 0.0000556 | 1.968 | 0.842 | 0.182 | 0.135 | 0.942 | −3.5 | 1.019 | 28 |
| Metasequoia glyptostroboides | |||||||||
| All | 0.0001110 | 1.944 | 0.610 | 0.170 | 0.133 | 0.977 | −3.0 | 1.015 | 299 |
| Others | 0.0000691 | 2.127 | 0.570 | 0.108 | 0.087 | 0.992 | −1.2 | 1.006 | 63 |
| Street trees | 0.0001556 | 1.946 | 0.457 | 0.167 | 0.127 | 0.965 | −2.9 | 1.014 | 129 |
| Urban parks | 0.0001091 | 1.995 | 0.559 | 0.172 | 0.136 | 0.980 | −3.1 | 1.015 | 107 |
| Pinus spp. | . | ||||||||
| All | 0.0000725 | 2.073 | 0.657 | 0.186 | 0.144 | 0.960 | −3.5 | 1.018 | 468 |
| Others | 0.0000966 | 2.027 | 0.582 | 0.188 | 0.146 | 0.955 | −3.7 | 1.018 | 157 |
| Street trees * | 0.0001899 | 2.657 | −0.763 | 0.107 | 0.092 | 0.916 | −1.3 | 1.007 | 14 |
| Urban parks | 0.0000626 | 2.104 | 0.683 | 0.182 | 0.139 | 0.961 | −3.3 | 1.017 | 297 |
| Platanus occidentalis | . | ||||||||
| All | 0.0001932 | 1.919 | 0.418 | 0.172 | 0.134 | 0.938 | −3.1 | 1.015 | 123 |
| Others | 0.0000808 | 1.873 | 0.795 | 0.157 | 0.122 | 0.949 | −2.7 | 1.015 | 19 |
| Street trees | 0.0002388 | 1.939 | 0.307 | 0.168 | 0.134 | 0.901 | −2.9 | 1.015 | 89 |
| Urban parks | 0.0003068 | 1.557 | 0.684 | 0.124 | 0.097 | 0.972 | −1.7 | 1.010 | 15 |
| Prunus spp. | . | ||||||||
| All | 0.0001902 | 1.746 | 0.543 | 0.178 | 0.131 | 0.963 | −3.2 | 1.016 | 277 |
| Others | 0.0001951 | 1.700 | 0.605 | 0.194 | 0.142 | 0.945 | −3.9 | 1.020 | 50 |
| Street trees | 0.0002428 | 1.661 | 0.572 | 0.150 | 0.114 | 0.967 | −2.2 | 1.011 | 163 |
| Urban parks | 0.0001501 | 1.777 | 0.589 | 0.209 | 0.169 | 0.951 | −4.6 | 1.023 | 64 |
| Quercus spp. | . | ||||||||
| All | 0.0001091 | 1.833 | 0.711 | 0.159 | 0.131 | 0.973 | −2.6 | 1.014 | 53 |
| Others | 0.0000570 | 1.745 | 1.058 | 0.164 | 0.116 | 0.974 | −3.1 | 1.018 | 12 |
| Urban parks | 0.0001348 | 2.050 | 0.350 | 0.138 | 0.114 | 0.977 | −2.0 | 1.010 | 41 |
| Zelkova serrata | |||||||||
| All | 0.0002235 | 1.667 | 0.561 | 0.165 | 0.126 | 0.957 | −2.7 | 1.014 | 323 |
| Others | 0.0001942 | 1.614 | 0.711 | 0.208 | 0.162 | 0.942 | −4.4 | 1.023 | 62 |
| Street trees | 0.0003059 | 1.626 | 0.476 | 0.141 | 0.109 | 0.955 | −2.0 | 1.010 | 177 |
| Urban parks | 0.0001617 | 1.893 | 0.383 | 0.145 | 0.116 | 0.974 | −2.1 | 1.011 | 84 |
| Broad-leaf species | |||||||||
| All | 0.0001497 | 1.750 | 0.674 | 0.207 | 0.161 | 0.958 | −4.4 | 1.022 | 1228 |
| Others | 0.0001409 | 1.747 | 0.710 | 0.225 | 0.173 | 0.965 | −5.3 | 1.026 | 263 |
| Street trees | 0.0001790 | 1.685 | 0.698 | 0.194 | 0.152 | 0.946 | −3.8 | 1.019 | 693 |
| Urban parks | 0.0001427 | 1.792 | 0.615 | 0.207 | 0.160 | 0.959 | −4.4 | 1.022 | 272 |
| Needle-leaf species | |||||||||
| All | 0.0001053 | 1.979 | 0.605 | 0.189 | 0.148 | 0.970 | −3.6 | 1.018 | 767 |
| Others | 0.0000913 | 2.054 | 0.569 | 0.170 | 0.131 | 0.979 | −3.0 | 1.015 | 220 |
| Street trees | 0.0001588 | 1.952 | 0.441 | 0.165 | 0.127 | 0.965 | −2.8 | 1.014 | 143 |
| Urban parks | 0.0000857 | 2.045 | 0.617 | 0.189 | 0.147 | 0.966 | −3.7 | 1.018 | 404 |
DBH, diameter at breast height of 1.2 m; CF, correction factor; N, number of sampled trees. * Street trees AEs for Acer spp. and Pinus spp. were developed solely from A. buergerianum and P. strobus, respectively.
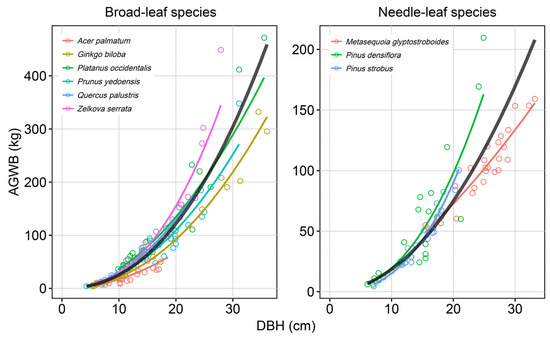
Figure A2.
Relationship between the DBH and AGWB of harvested trees. Black regression lines indicate generalized allometric equations developed by integrating the tree data of each category (broad- and needle-leaf species). AGWB, above-ground woody biomass.
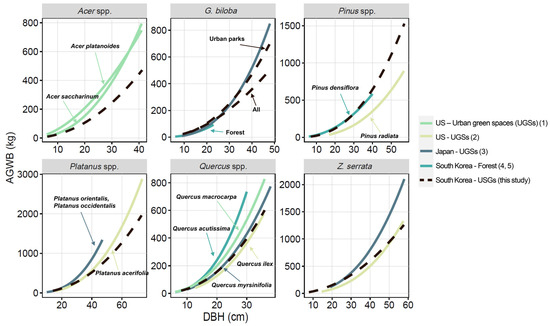
Figure A3.
Model comparison with previously developed allometric equations. All dashed lines represent regression lines derived from integrated data across all urban land use categories. For Ginkgo biloba, an additional regression line for urban parks is also included. (1) McHale et al. [13], (2) Pillsbury et al. [16], (3) Matsue et al. [8], (4) Son and Kim [62], and (5) KRFI [63]. It should be considered that South Korea and Japan AEs are based on a DBH measured at 1.2 m, while the US equations are based on measurements at 1.37 m.
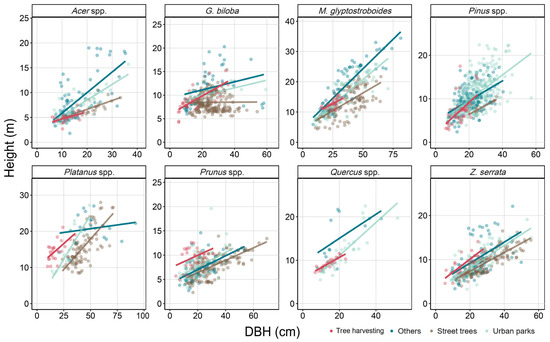
Figure A4.
Relationship between the DBH and height of each species group.
References
- Hardiman, B.S.; Wang, J.A.; Hutyra, L.R.; Gately, C.K.; Getson, J.M.; Friedl, M.A. Accounting for urban biogenic fluxes in regional carbon budgets. Sci. Total Environ. 2017, 592, 366–372. [Google Scholar] [CrossRef]
- Nowak, D.J.; Crane, E.C. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Vaccari, F.P.; Gioli, B.; Toscano, P.; Perrone, C. Carbon dioxide balance assessment of the city of Florence (Italy), and implications for urban planning. Landsc. Urban Plann. 2013, 120, 138–146. [Google Scholar] [CrossRef]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Prepared by the National Greenhouse Gas Inventories Programme; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Eds.; IGES: Hayama, Japan, 2006. [Google Scholar]
- Jo, H.K.; Ahn, T.W. Carbon storage and uptake by deciduous tree species for urban landscape. J. Korean Inst. Landsc. Archit. 2012, 40, 160–168. [Google Scholar] [CrossRef]
- Jo, H.K.; Kim, J.Y.; Park, H.M. Carbon storage and uptake by evergreen trees for urban landscape—For Pinus densiflora and Pinus koraiensis. Korean J. Environ.Ecol. 2013, 27, 571–578. [Google Scholar] [CrossRef]
- Jo, H.K.; Kim, J.Y.; Park, H.M. Carbon reduction effects of urban landscape trees and development of quantitative models—For five native species. J. Korean Inst. Landsc. Archit. 2014, 42, 13–21. [Google Scholar] [CrossRef]
- Matsue, M.; Nagahama, Y.; Iizuka, Y.; Murata, M.; Fujiwara, N. Estimation equations for the amount of CO2 fixed by planted trees in cities in Japan. J. Jpn. Soc. Reveg. Technol. 2009, 35, 318–324. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Herrmann, D.L. A global synthesis of reported urban tree carbon production rates and approaches. Front. Ecol. Evol. 2024, 11, 1244418. [Google Scholar] [CrossRef]
- Nowak, D.J. Atmospheric carbon dioxide reduction by Chicago’s urban forest. In Chicago’s Urban Forest Ecosystem: Results of the Chicago Urban Forest Climate Project; US Department of Agriculture, Forest Service: Washington, DC, USA, 1994; pp. 83–94. [Google Scholar]
- Dahle, G.A.; Gallagher, F.J.; Gershensond, D.; Schäfer, K.V.R.; Grabosky, J.C. Allometric and mass relationships of Betula populifolia in a naturally assembled urban brownfield: Implications for carbon modeling. Urban Ecosyst. 2014, 17, 1147–1160. [Google Scholar] [CrossRef]
- Ngo, K.M.; Lum, S. Aboveground biomass estimation of tropical street trees. J. Urban Ecol. 2018, 4, jux020. [Google Scholar] [CrossRef]
- McHale, M.R.; Burke, I.C.; Lefsky, M.A.; Peper, P.J.; McPherson, E.G. Urban forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosyst. 2009, 12, 95–113. [Google Scholar] [CrossRef]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Speak, A.F.; Salbitano, F. The impact of pruning and mortality on urban tree canopy volume. Urban For. Urban Green. 2023, 79, 127810. [Google Scholar] [CrossRef]
- Pillsbury, N.H.; Reimer, J.L.; Thompson, R.P. Tree Volume Equations for Fifteen Urban Species in California, 7th ed.; Technical Report; Urban Forest Ecosystem Institute, California Polytechnic State University: San Luis Obispo, CA, USA, 1998. [Google Scholar]
- Lee, S.; Lee, S.; Lee, J.; Son, Y.; Yoon, T.K. Estimating aboveground volume of diverse urban tree species: Developing allometric equations for higher taxonomic levels. Urban For. Urban Green. 2024, 94, 128256. [Google Scholar] [CrossRef]
- Park, J.H.; Baek, S.G.; Kwon, M.Y.; Je, S.M.; Woo, S.Y. Volumetric equation development and carbon storage estimation of urban forest in Daejeon, Korea. For. Sci. Technol. 2018, 14, 97–104. [Google Scholar] [CrossRef]
- Yoon, T.K.; Park, C.-W.; Lee, S.J.; Ko, S.; Kim, K.N.; Son, Y.; Lee, K.H.; Oh, S.; Lee, W.-K.; Son, Y. Allometric equations for estimating the aboveground volume of five common urban street tree species in Daegu, Korea. Urban For. Urban Green. 2013, 12, 344–349. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Nemmaoui, A.; Peñalver, A.; Rivas, J.R.; Aguilar, M.A. Developing allometric equations for teak plantations located in the coastal region of Ecuador from terrestrial laser scanning data. Forests 2019, 10, 1050. [Google Scholar] [CrossRef]
- Bornand, A.; Rehush, N.; Morsdorf, F.; Thürig, E.; Abegg, M. Individual tree volume estimation with terrestrial laser scanning: Evaluating reconstructive and allometric approaches. Agric. For. Meteorol. 2023, 341, 109654. [Google Scholar] [CrossRef]
- Stovall, A.E.L.; Vorster, A.; Anderson, R.; Evangelista, P. Developing nondestructive species-specific tree allometry with terrestrial laser scanning. Methods Ecol. Evol. 2022, 14, 280–290. [Google Scholar] [CrossRef]
- Domec, J.C.; Gartner, B.L. How do water transport and water storage differ in coniferous earlywood and latewood? J. Exp. Bot. 2002, 53, 2369–2379. [Google Scholar] [CrossRef]
- Knapic, S.; Louzada, J.L.; Leal, S.; Pereira, H. Within-tree and between-tree variation of wood density components in cork oak trees in two sites in Portugal. Forestry 2008, 81, 465–473. [Google Scholar] [CrossRef]
- Korea Meteorological Administration (KMA). National Climate Data Service System. Available online: https://data.kma.go.kr/tmeta/stn/selectStnList.do?pgmNo=123 (accessed on 15 August 2024).
- Ha, J.; Baek, G.; Choi, B.; Lee, J.; Son, Y.; Kim, C. Development of allometric equations for carbon storage of Ginkgo biloba Linn., Zelkova serrata (Thunb.) Makino. and Prunus × yedoense Matsum. planted in Jinju-City. J. Clim. Chang. Res. 2022, 13, 135–145. [Google Scholar] [CrossRef]
- Jung, J.Y.; Im, S.; Kim, H.J.; Lee, K.H. Development of carbon emission factors and biomass allometric equations for Metasequoia glyptostroboides and Platanus occidentalis in urban forests. Korean Soc. For. Sci. 2023, 112, 127–135. [Google Scholar] [CrossRef]
- Kim, H.; Baek, G.; Choi, B.; Lee, J.; Lee, J.; Son, Y.; Kim, C. Allometric equations for estimating the carbon storage of Maple trees in an urban settlement Area. J. Korean Soc. For. Sci. 2023, 112, 32–39. [Google Scholar] [CrossRef]
- Yoon, T.K.; Lee, S.; Lee, S.; Lee, J.-M.; Son, Y.; Lee, S. Root biomass allocation and carbon sequestration in urban landscaping tree species in South Korea. Forests 2024, 15, 2104. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Han, Y.; Lee, J.; Son, Y.; Yoon, T.K. Determining the aboveground allometric equations of major street tree species in Wonju, South Korea using the nondestructive stem analysis method. J. Korean Soc. For. Sci. 2022, 111, 502–510. [Google Scholar] [CrossRef]
- Fearnside, P.M. Wood density for estimating forest biomass in Brazilian Amazonia. For. Ecol. Manag. 1997, 90, 59–87. [Google Scholar] [CrossRef]
- Nogueira, E.M.; Fearnside, P.M.; Nelson, B.W. Normalization of wood density in biomass estimates of Amazon forests. For. Ecol. Manag. 2008, 256, 990–996. [Google Scholar] [CrossRef]
- Velasco, E.; Chen, K.W. Carbon storage estimation of tropical urban trees by an improved allometric model for aboveground biomass based on terrestrial laser scanning. Urban For. Urban Green. 2019, 44, 126387. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Delcourt, C.J.F.; Veraverbeke, S. Allometric equations and wood density parameters for estimating aboveground and woody debris biomass in Cajander larch (Larix cajanderi) forests of northeast Siberia. Biogeosciences 2022, 19, 4499–4520. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. Camb. Philos. Soc. 2004, 79, 871–889. [Google Scholar] [CrossRef] [PubMed]
- Stanton, M.L.; Thiede, D.A. Statistical convenience vs biological insight: Consequences of data transformation for the analysis of fitness variation in heterogeneous environments. New Phytol. 2005, 166, 319–338. [Google Scholar] [CrossRef] [PubMed]
- Lenth, R. Emmeans: Estimated Marginal Means, aka Least-Squares Means. R Package Version 1.10.7-100002. Available online: https://CRAN.R-project.org/package=emmeans (accessed on 1 March 2025).
- Dutcă, I.; Mather, R.; Blujdea, V.N.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-effects on biomass allometric models for early growth plantations of Norway spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Weiner, J. Allocation, plasticity and allometry in plants. Perspect. Plant Ecol. Evol. Syst. 2004, 6, 207–215. [Google Scholar] [CrossRef]
- Oliveira, G.M.V.; de Mello, J.M.; de Mello, C.R.; Scolforo, J.R.S.; Miguel, E.P.; Monteiro, T.C. Behavior of wood basic density according to environmental variables. J. For. Res. 2021, 33, 497–505. [Google Scholar] [CrossRef]
- Vizcaíno-Palomar, N.; Ibáñez, I.; González-Martínez, S.C.; Zavala, M.A.; Alía, R. Adaptation and plasticity in aboveground allometry variation of four pine species along environmental gradients. Ecol. Evol. 2016, 6, 7561–7573. [Google Scholar] [CrossRef]
- Hui, L.C.; Jim, C.Y.; Zhang, H. Allometry of urban trees in subtropical Hong Kong and effects of habitat types. Landsc. Ecol. 2020, 35, 1143–1160. [Google Scholar] [CrossRef]
- de-Miguel, S.; Pukkala, T.; Assaf, N.; Shater, Z. Intra-specific differences in allometric equations for aboveground biomass of eastern Mediterranean Pinus brutia. Ann. For. Sci. 2014, 71, 101–112. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Zha, T.; Liu, J.; Jia, X.; Wang, X.; Chen, W.; He, G. Patterns of biomass allocation in an age-sequence of secondary Pinus bungeana forests in China. For. Chron. 2014, 90, 169–176. [Google Scholar] [CrossRef]
- Vorster, A.G.; Evangelista, P.H.; Stovall, A.E.; Ex, S. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: The role of allometric equations. Carbon Balance Manag. 2020, 15, 8. [Google Scholar] [CrossRef] [PubMed]
- Davies, Z.G.; Edmondson, J.L.; Heinemeyer, A.; Leake, J.R.; Gaston, K.J. Mapping an urban ecosystem service: Quantifying above-ground carbon storage at a city-wide scale. J. Appl. Ecol. 2011, 48, 1125–1134. [Google Scholar] [CrossRef]
- Lv, H.; Wang, W.; He, X.; Xiao, L.; Zhou, W.; Zhang, B. Quantifying tree and soil carbon stocks in a temperate urban forest in Northeast China. Forests 2016, 7, 200. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Qian, Y.; Zhang, H.; Yao, Y. Estimating aboveground carbon stocks of urban trees by synergizing ICESat-2 LiDAR with GF-2 data. Urban For. Urban Green. 2022, 76, 127728. [Google Scholar] [CrossRef]
- Vonderach, C.; Akontz, A. Learning from forest trees: Improving urban tree biomass functions. Forests 2023, 14, 1473. [Google Scholar] [CrossRef]
- Poorter, H.; Niklas, K.J.; Reich, P.B.; Oleksyn, J.; Poot, P.; Mommer, L. Biomass allocation to leaves, stems and roots: Meta-analyses of interspecific variation and environmental control. New Phytol. 2012, 193, 30–50. [Google Scholar] [CrossRef]
- Aguaron, E.; McPherson, E.G. Comparison of methods for estimating carbon dioxide storage by Sacramento’s urban forest. In Carbon Sequestration in Urban Ecosystems; Springer: Dordrecht, The Netherlands, 2012; pp. 43–71. [Google Scholar]
- Wania, A.; Kühn, I.; Klotz, S. Plant richness patterns in agricultural and urban landscapes in Central Germany—Spatial gradients of species richness. Landsc. Urban Plann. 2006, 75, 97–110. [Google Scholar] [CrossRef]
- Burt, A.; Calders, K.; Cuni-Sanchez, A.; Gómez-Dans, J.; Lewis, P.; Lewis, S.L.; Malhi, Y.; Phillips, O.L.; Disney, M. Assessment of bias in pan-tropical biomass predictions. Front. For. Glob. Chang. 2020, 3, 12. [Google Scholar] [CrossRef]
- McPherson, E.G.; van Doorn, N.S.; Peper, P.J. Urban Tree Database and Allometric Equations; General Technical Report PSW-GTR-253; US Department of Agriculture, Forest Service, Pacific Southwest Research Station: Albany, CA, USA, 2016; 86p. [Google Scholar]
- Rutishauser, E.; Noor’an, F.; Laumonier, Y.; Halperin, J.; Hergoualc’h, K.; Verchot, L. Generic allometric models including height best estimate forest biomass and carbon stocks in Indonesia. For. Ecol. Manag. 2013, 307, 219–225. [Google Scholar] [CrossRef]
- Jo, H.K.; Cho, D.H. Annual CO2 Uptake by Urban Popular Landscape Tree Species. J. Korean Inst. Landsc. Archit. 1998, 26, 38–53. [Google Scholar]
- Demol, M.; Verbeeck, H.; Gielen, B.; Armston, J.; Burt, A.; Disney, M.; Duncanson, L.; Hackenberg, J.; Kükenbrink, D.; Lau, A. Estimating forest above-ground biomass with terrestrial laser scanning: Current status and future directions. Methods Ecol. Evol. 2022, 13, 1628–1639. [Google Scholar] [CrossRef]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- de-Miguel, S.; Mehtätalo, L.; Durkaya, A. Developing generalized, calibratable, mixed-effects meta-models for large-scale biomass prediction. Can. J. For. Res. 2014, 44, 648–656. [Google Scholar] [CrossRef]
- Son, Y.; Kim, H.W. Above-ground biomass and nutrient distribution in a 15-year-old ginkgo (Ginkgo biloba) plantation in Central Korea. Bioresour. Technol. 1998, 63, 173–177. [Google Scholar] [CrossRef]
- KFRI (Korea Forest Research Institute). Carbon Emission Factors and Biomass Allometric Equations by Species in Korea; Report No. 11–1400377-000694-01; Korea Forest Research Institute: Seoul, Republic of Korea, 2014. (In Korean) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).