Abstract
Aboveground biomass models are useful for assessing vegetation conditions and providing valuable information on the availability of ecosystem goods and services, including carbon stock and forest/rangeland products. This study aimed to develop aboveground biomass estimation models for the common woody species found in Borana woodland. Multispecies and species-specific models for aboveground biomass were developed using 114 destructively sampled trees representing five species. The dendrometric variables selected as predictors of the trees’ aboveground dry biomass for both multispecies and species-specific models were diameter at breast height, tree height, wood basic density (ρ), crown area (ca) and crown diameter (cd). The distribution of biomass across trees’ aboveground components was estimated using destructively sampled trees. Most tree biomass is allocated to branches, followed by the stems. The tree diameter, wood basic density, and crown diameter were significant predictors in generic and species-specific biomass models across all tree components. Incorporating wood basic density into the model significantly improved prediction accuracy, while tree height had a minimal effect on biomass estimation. The stem and twig biomasses were the highest and least predictable plant parts, respectively. Compared with the existing models, our newly developed models significantly reduced prediction errors, reinforcing the importance of location-specific models for accurate biomass estimation. Hence, this study fills the geographic and ecological gaps by developing models tailored with the unique conditions of the Borana lowland forest. The accuracy of species-specific biomass models varied among tree species, indicating the need for species-specific models that account for variations in growth architecture, ecological factors, and bioclimatic conditions.
1. Introduction
The estimation of carbon stock sequestered in each ecosystem is a function of plant biomass and reflects the amount of CO2 stored in each vegetation [1,2,3]. A reliable estimate of biomass is crucial for monitoring forest conditions and reporting changes in carbon stocks [4]. Biomass estimations are a function of applied methods and models [2]. Biomass can be calculated by the direct method of destructively harvesting all the trees [5] or the indirect method of using an allometric model [3] and a remote sensing approach [6,7]. The direct method of cutting down trees is costly and time-consuming [2], whereas indirect methods using an allometric model are time-efficient and less expensive [1]. Therefore, different allometric models must be developed for species and forest types to obtain accurate biomass and carbon stock estimates in forests [8].
In Ethiopia, some allometric equations were developed for different trees/shrubs and forests in the northern [4,9,10], northwestern [11,12], central [13], and southern [14,15] regions of the country. All the above-mentioned studies were focused on species-specific biomass models, except for a few cases [4,10,11]. Additionally, wood basic density is rarely used in aboveground biomass prediction in Ethiopia, except for a few studies by [4,10].
The specific biomass prediction models provide a proxy estimate of carbon sequestered in each ecosystem, improve the estimates of carbon stocks in the region, and support the implementation of policies and mechanisms designed to mitigate climate change, like REDD+ [16]. The general multispecies pan-tropical models developed by [17] have been used for the aboveground biomass estimation of different forest types in Africa. However, [4] proves the applicability limitation of the model in Ethiopia. Similarly, [10] tested general multispecies biomass models developed in the drylands of northern Ethiopia and reported significant bias and under-predictions.
Most of the previous studies developed biomass estimation models for different areas, raising uncertainty for the application of the models beyond the area [4,14,17,18,19]. The variability in environmental conditions, such as soil type, climate, and vegetation structure across regions, makes it difficult to generalize the applicability of allometric models. Particularly, the unique ecological conditions of the Borana woodland, which are known for low elevation, dry soil, arid climates, erratic rainfall, and diverse tree species, necessitate the need for developing area-tailored allometric models for accurate carbon stock estimation and vegetation monitoring. Existing allometric models developed for highland areas and/or temperate environments may not account for the stressors and adaptive features of the Borana dryland ecosystem. Thus, developing area-specific allometric models for Borana is crucial for improving the reliability of biomass estimates and ensuring better management of the woodland’s carbon stocks.
The previous biomass models developed for Ethiopian drylands have focused primarily on exclosures and grasslands. Notably, [14,18] developed species-specific allometric models for woody species found in the Borana grassland. However, these studies are limited in scope, as they focus primarily on grassland ecosystems, which differ significantly from the dryland afromontane forests. The species composition, environmental conditions, and vegetation structure in grasslands and afromontane forests are different, which makes the applicability of these grassland-based models less reliable for afromontane forest ecosystems. Although belowground biomass is a critical component of total biomass and is important in carbon stock assessments, it can alternatively be estimated using root-to-shoot ratios derived from other similar ecosystems. Therefore, this study was limited to only aboveground biomass due to the complexity and difficulty of excavating root systems in the rocky mountain of a dryland environment. Hence, our study emphasized aboveground biomass models for tree species of dryland afromontane forests in Borana woodland, located in southern Ethiopia.
Accordingly, the main objective of this study was to develop the aboveground allometric biomass equations for the lowland forest in the Borana woodland of Ethiopia. Specifically, the study aimed to (i) compare the patterns of biomass partitioning to aboveground biomass components within and between tree species; (ii) develop multispecies and species-specific allometric biomass models for predicting the stem, branch, twig, and total tree aboveground biomasses; and (iii) evaluate the prediction performances of previously published multispecies biomass estimation models.
2. Materials and Methods
2.1. Site Description
This study was undertaken in the Gamadu forest in the Borana woodland of Oromia Regional State (hereafter Oromia) in southern Ethiopia (Figure 1). The forest is located at 04°06′ north and 038°06′ east. The study site was selected systematically based on the diversity of agroclimatic zones in the forest cover, with the Gamadu forest block in Borana woodland encompassing the vast area and featuring a range of diverse agroclimatic zones [20].
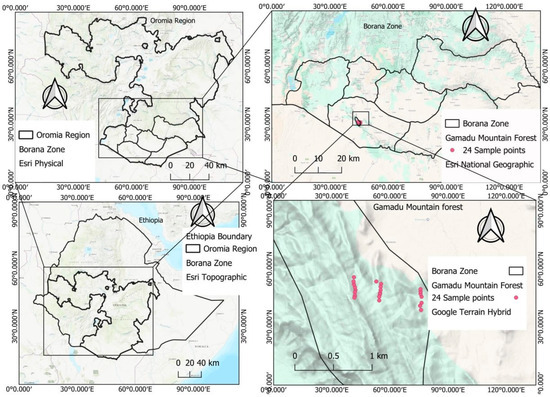
Figure 1.
Map of the study area showing the study location, study forest and sample point distribution in the forest (own sketch).
The main soil texture of the Borana area is 53% red sandy loam soil, 30% black clay and volcanic light-colored silty clay, and 17% silt and vertisols [21]. In Borana, the common land use and land cover types are dense and natural indigenous tree species (woodland), areas dominated by indigenous grass species (grassland), areas neither covered by vegetation nor used for crop production (bare land), and the cultivated areas [22]. Vegetation in the Gamadu forest is dominated by drought-adapted woody species, including Juniperus procera Hochst. ex Endl., Pittosporum viridiflorm Sims, Euclea divinorum Hiern, Teclea nobilis Delile, Olea europaea L., Oncoba spinosa Forssk., Pappea capensis Benth., Commiphora africana (A. Rich.) Engl., Vangueria apiculate K. Schum., and Rytigynia neglecta (Hiern) Robyns, covered with native grass species and herbs. The tree canopy of this forest is typically open to moderately closed, with understory vegetation, which is influenced by grazing intensity and seasonal rainfall. The climate of the Borana woodland is arid to semi-arid with a mean annual precipitation of 580 mm [23]. The area has a bimodal rainfall pattern, with the peak rainy season from March to May and small rain from September to November [23]. Based on data from the nearby weather station, the area receives an average monthly rainfall of 4–5 mm between August and September, up to 121 mm in April, and the average monthly temperature is 17–20 °C.
2.2. Data Collection
For measuring standing trees and shrubs (hereafter referred to as ‘trees’), 24 main plots with 10 m × 10 m were designed, following [24]. First, we crossed the forest by using the narrow road that went through the forest from the foot of the mountain to the top edge, which we utilized as the main transect. While walking along this route, we established three starting points representing low, medium, and high forest disturbance levels. The distance between each site was determined based on variations in the visually detected degree of disturbances.
The degree of forest disturbance level was determined visually by observing canopy cover, density of the trees, dominance of tree stumps, and presence of animal dung and paths, as also used by [25]. Hence, the forest location with a high extent of canopy cover, dense tree stands, and fewer stumps and animal paths was taken as the site of a low disturbance level. Similarly, places with moderate canopy cover, medium tree density, and noticeable signs of some tree stumps and animal paths were considered as sites of medium disturbance. The location with sparse canopy cover, low tree density, frequent tree stumps, and clear signs of animal paths and dung observed was taken as a high-disturbance site. This classification approach was also used in previous ecological studies in Ethiopia [25,26,27].
From the starting points of each site, we made a 1 km transect line to the right and left of the road. In this way, we created six transects from the three starting points, three to the left and three to the right of the road. By taking four main plots, each measuring 100 m2, along each transect, we made 24 main plots, each spaced by 200–300 m based on access to gully passages (Figure 2).
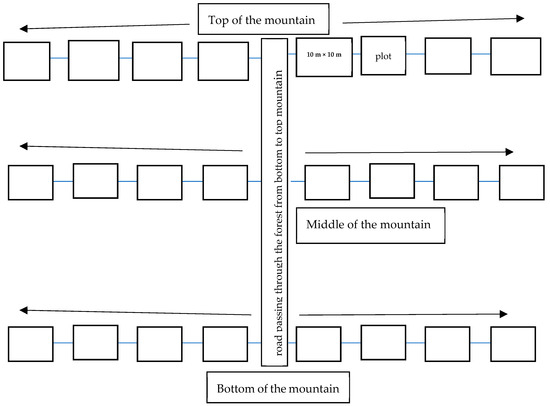
Figure 2.
Study site layout.
Within each main plot, the diameter at stump height (dsh) of all trees was measured at 0.3 m above the ground. Trees with a dsh ≥ 2.5 cm were counted, their species identified, their diameter at breast height (dbh) measured at 1.3 m, and their basal area calculated. Accordingly, the type of plant species included in the destructive sample for developing allometric biomass equations was determined based on the total basal area per hectare of respective species and the relative dominance of the species.
2.2.1. Tree Sampling
The individual tree species in the destructive sample for developing biomass models were selected based on the total basal area per hectare. As the basal area is the circular cross-sectional area of a tree stem at breast height, this was determined from the circle area, which is πr2 [28]. In forest inventory, we usually measure the diameter of a tree, rather than the radius [29], using dbh/2 instead of radius.
where BA = basal area (m2), dbh = diameter at breast height, and π (pi) = 3.14.
The basal area is calculated at the stand level as the total of the values for each live tree, usually expressed as square meters per hectare and commonly measured in centimeters.
The total basal area coverage for each species recorded in the forest was considered to select species to be included in developing allometric biomass models for estimating the biomass of the given forest. The top ten plant species with the highest basal area per ha were Juniperus procera Endl., Pittosporum viridiflorm, Euclea divinorum Hiern., Teclea nobilis Del., Olea europaea Subsp. cuspidata (Wall. Ex G. Don) Cif., Oncoba spinosa Forsk., Pappea capensis, Commiphora africana (A. Rich) Engl., Vangueria apiculate, and Rytigynia neglecta (Hiern) Robyns (Table A1 in Appendix A). However, the large plant species with a mean basal area per tree (BA/tree) greater than 0.01 m2 were excluded from destructive sampling due to the prohibition of felling large trees from the studied forests. Hence, despite their higher total basal area per ha, Juniperus procera, Pittosporum viridiflorm, and Pappea capensis were excluded. Additionally, these species with big trees have a higher demand for wood products and are mostly cut by the local community.
On the other hand, plant species with a total basal area of less than 0.5 m2/ha were also excluded from the sample, because such tree species hold a small fraction of aboveground biomass in forests. Accordingly, five tree species, including Euclea divinorum, Teclea nobilis, Olea europaea, Oncoba spinosa, and Commiphora africana, were included in developing the allometric model.
Among the destructively sampled species, Olea europaea had the highest tree diameter (dbh = 17 cm, dsh = 28.5 cm), wood basic density (ρ = 1.24 g/cm3), and total aboveground biomass (Tagb = 120.89 kg) (Table A2 in Appendix A). On the other hand, the tallest recorded tree is from the Teclea nobilis species, with 8.45 m, and Euclea divinorum is a species with the widest crown area among the samples.
2.2.2. Tree Measurements
Following the identification of tree species to be included in the sample and determination of the sample size, the diameter at stump height, diameter at breast height, tree height, and crown diameters of the selected individual trees were measured. The crown diameter was used to calculate the crown area of the trees [10].
where ca is the crown area, cd1 is the widest crown diameter, and cd2 is its perpendicular crown diameter.
For trees with many stems from the same root at a height of below 1.3 m, the dbh was calculated [30,31].
where dbhc is the computed diameter at breast height, dbhi is the diameter at breast height of individual stems extending from the same root, and i, is the number of stems measured.
The selected trees were cut down by chainsaw and subdivided into stems, branches, and twigs with leaves. Leaves, which might have dropped down during cutting, were carefully collected manually and weighed with the twig component of the trees. All components were immediately weighed separately in the field using a weight balance scale, and the fresh weight of each section was recorded.
Sub-samples were collected from each divided tree component of the harvested plants and weighed for their fresh weight using a digital balance with an accuracy of 0.01 g. The dry weight was determined in the laboratory. Accordingly, from the stem, branch, and twig-leaves components, the sample biomass of 300 g fresh weight was taken by three replications. Stem subsamples were taken at 25%, 50%, and 75% of the total stem length. Similarly, the subsample was taken from large, medium, and small branch sizes. A subsample of the twig-leaves component was taken from a homogeneous mixed sample of the part. An average of three subsamples was used for dry weight determination.
The stem and branch samples were oven-dried at 105 °C, and twig-leaves samples at 70 °C for 48 h, and weighed in the laboratory. The moisture content percentage and dry weight of the stem, branch, and twig leaves were determined. The ratio of sub-sample dry weight to fresh weight was used to convert component fresh weight to dry weight. The total dry weight of each biomass component of each tree was calculated as follows:
The total dry biomass for each sampled plant was obtained by adding the dry biomass of the stem, branches, and twig leaves.
2.3. Data Analysis
A nonlinear regression model was used to develop the biomass allometric model. The dependent variable was tree biomass. For predicting tree biomass, diameter at stump height (dsh at 30 cm), diameter at breast height (dbh at 1.30 m), tree height (th), crown area (ca), crown diameter (cd), and wood basic density (ρ) were used. The relationships between biomass and the predictor variables were determined using Pearson’s correlation before modeling. The correlation matrix plot and correlation coefficients were used to determine the linear relationship of aboveground biomass with predictor variables. Accordingly, different candidate biomass models were generated and evaluated to predict the total aboveground biomass, stem biomass, branch biomass, and twig biomass. All statistical analyses were performed using STATA software version 14.
2.3.1. Linearity Test
The relationships between biomass and each independent variable were examined using a scatterplot. This helps to obtain an insight into the nature of candidate models to be examined for fitness. The linearity test indicates (Figure 3) a nonlinear relationship between aboveground biomass and dendrometric variables.
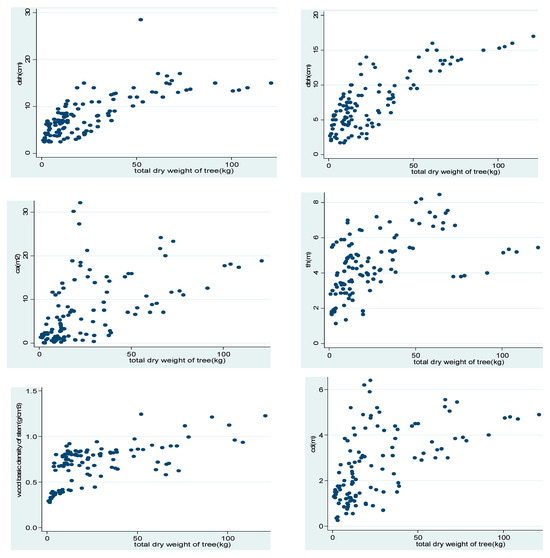
Figure 3.
Scatterplot of dry biomass versus potential predictor variables.
2.3.2. Allometric Equations Development
Following the demonstrated nonlinear relationship between the dry biomass of the trees and the dendrometric variables, a nonlinear exponential form was used to find the best model fit for the data. Accordingly, the nonlinear version of this power function model, which is frequently employed in allometric modeling studies [10,11,32,33,34,35] was fitted using a logarithmic transformation of the biomass and tree biometric data.
where Y is the dry biomass, X is the vector of predictor dendrometric variables, α is the constant, and β is the vector of regression parameters to be estimated.
Total aboveground dry biomasses (i.e., Tagb—total aboveground biomass, Sb—stem biomass, Bb—branch biomass, and Tb—twig biomass) and the probable independent variables were correlated using Pearson’s formula. The tree aboveground dry biomass was significantly correlated with dsh, dbh, th, cd, ca, and ρ (Table A3 in Appendix A).
Tree diameter at breast height had a strong positive and significant correlation with total aboveground dry biomass. This result agrees with previous studies [8,10,17,33,36]. Wood basic density possesses a moderate positive correlation with total aboveground biomass. This result is consistent with several studies [10,37], but contrasts with [17,35,36], who claim that wood density has no significant correlation with the dry biomass of trees. The dsh and ca were eliminated from the model to reduce the issue of multicollinearity.
Considering its strong link with aboveground biomass [8,17,36], different candidate model forms were fitted using dbh as the single predictor and combined with a stepwise inclusion of height, cd, and ρ.
Accordingly, in developing allometric equations, we have divided the model forms into four groups (A, B, C, D) (Table A4 in Appendix A). Group A represents models tested for total aboveground biomass, and groups B, C, and D include models for the biomass of tree compartments, specifically stem, branch, and twig, respectively. A total of 32 model forms, with 8 models in each group, were examined for the accuracy of dry biomass estimation.
The goodness of fit for the biomass equations was analyzed using linear regression models. The post-estimation goodness of fit of each candidate model was assessed using the p-value, adjusted coefficient of determination (), Akaike’s information criterion (AIC), mean prediction error, and relative prediction bias (%).
Adjusted R-squared is an adjustment for the coefficient of determination that considers the number of variables in a data set and is computed as follows:
The Akaike information criterion (AIC) is also an estimator of prediction errors to determine the relative quality of statistical models for given data [38]. AIC is the expected relative distance between the better-fitted and the other candidate model. The general formula to determine AIC is as follows:
where lnL = maximized log-likelihood and k = number of parameters estimated.
AIC = −2lnL + 2k
Accordingly, the model with the best prediction was selected among candidate models based on significant coefficients (p ≤ 0.05), higher adjusted R2, and smaller AIC, MPE, and rBias.
Additionally, as the biomass estimation was made by reversing the logarithmical values into the original units, the transformation might cause a systematic bias. Hence, the bias was adjusted by a correction factor to modify the underestimated biomass. Accordingly, the CF was computed for each selected model using the respective mean square error of the regression.
This CF was used when the back transformation of data to power biomass function was required, at which the calculated CF of the model was then multiplied by the biomass estimated by the model. Hence, the linear model of the form [ln(Y) = α + βln(X)] was then back transformed to a power function in its actual application to determine biomass (Y), as follows:
y = Exp [α + β123ln(x123)] × CF
3. Results
3.1. Distribution of Biomass Along the Tree Compartments
The proportion of tree biomass across the components shows that branches accounted for the largest aboveground biomass, followed by the stem and twigs for the five destructively sampled species (Table 1). Biomass distribution within components across different tree species was shown by ranges. Hence, among the tree components, the branch biomass was found to have the most widely distributed biomass allocation between species. This indicates that the branches are the main plant parts accountable for biomass variability across different plant species. Similarly, stems are found to have the second-highest biomass variability among plant components across species, while twigs have the smallest biomass variability across the species.

Table 1.
Biomass distribution (mean, range) of selected tree species.
3.2. Biomass Models
A comparison of the overall goodness of fit of biomass models for different biomass components shows that the model fitted for stem and twig biomasses had the best and weakest relative values of prediction performance indicators. The model, which combines wood basic density, diameter at stump height, and crown diameter, demonstrated the best prediction performance for estimating total aboveground, stem, and branch biomasses (Table 2). Likewise, despite its relatively poor prediction power, the twig’s dry biomass model was predicted by a combination of tree diameter, tree height, and crown diameter.

Table 2.
Model expressions and parameter estimates for biomass prediction.
The coefficients of determination (R2adjusted) and relative bias of selected multispecies species models for the estimation of tree biomass structure ranged from 0.57 to 0.81 and 3.33% to 4.47%, respectively (Table 2). When the biomass model accuracy among the tree compartments was compared, the stem biomass was the most predictable part, and the twig biomass was the least predictable (Table 3). The coefficient of determination for the models used to determine the biomass of individual species ranged from 0.71 to 0.96 (Table 4).

Table 3.
Generic biomass prediction models for aboveground Components.

Table 4.
Biomass prediction models for selected species.
3.3. Predictive Performance of Previously Developed Models
We have assessed the prediction power of previously reported general multispecies models using the data collected from our study site (Table 5). For this purpose, seven generic models were selected, among which five models from the Ethiopia sample trees [4,10,11,15,39], one model from trees of other African forests [3], and one also from a tree dataset of global pantropical forests [17] were selected. Among the four multispecies models of Ethiopian forests, two were the models developed using sample trees from dryland forests [4,10], which were similar to the ecology of our study area. These selected generic multispecies models were tested by comparing the values of their mean prediction error [40] and relative bias (rBias). The result shows that all tested previous multispecies models [3,4,15,17,39] produced high prediction bias on our data and highly underestimated the biomass of the study area, except [10]. It is not surprising that our model fits the tree and shrub species biomass of the study area and was found to have the least prediction error and the best estimate for aboveground biomass of the studied forest.

Table 5.
Comparison of allometric models for aboveground biomass estimation.
4. Discussion
4.1. Biomass Partition in Tree Components
The study documents that more than half of the tree biomass was allocated to branches, followed by the stem biomass. This result is consistent with [32], which reported that branches contributed two-thirds of the dry aboveground biomass of trees. Other studies, such as [4,41,42], document that branches account for the largest portion of a tree’s biomass. However, [33,43] reported contrasting results where their findings show that the largest fraction of trees’ aboveground biomass was allocated to the stem as compared with branches and leaves. These differences in the allocation of biomass along tree components might be due to the ecological responses of woody plants to environmental factors [32]. Similarly, the biomass allocation can also be determined by factors like climatic conditions and land-use systems.
In arid or semi-arid regions affected by limited rainfall and recurrent droughts, trees may prioritize branching by increasing their canopy size to enhance water retention through lateral growth. Additionally, in open woodlands, characterized by high disturbance, the allocation of greater biomass in branches than stem is common. This is because the trees pruned by grazing and other human activities remain shorter and expand their canopy as a survival strategy. In contrast, in our study area of pastoral land use system, grazing pressure can potentially make trees develop more lateral growth near the ground, which could lead to more biomass being invested in branches than stem. On the other hand, in temperate dense forests where competition for light is intense, trees often allocate more biomass to stems to achieve greater height and access more sunlight. In such an ecosystem, with limited human disturbance, stem biomass often dominates because of the vertical growth strategy adopted by trees to outcompete neighboring vegetation. This could explain why studies like [33,43] find that the stem often make up the largest fraction of the biomass in more temperate or moist environments.
Regarding the variability of biomass across different species, the highest biomass variability was found within branches as compared with stems and twigs. This could be because the size and number of branches vary significantly across the tree species. Similarly, the result shows that the biomass of twigs is less variable compared with stems and branches because twigs are typically smaller, less complex, and more uniform in structure across tree species.
4.2. Multispecies Biomass Estimation Models
The model combining the three-predictor variables produced the greatest possible model fit for biomass estimation of total biomass and biomass of tree compartments (stem, branch, and twig). For the tree biomass estimations, the model with the combination of tree diameter, wood basic density, and crown diameter produced the greatest possible model fit. This result is similar to that found by [10], where more than 95% of the variability in the aboveground biomass of trees was explained by the tree diameter, wood basic density, and crown area as predictors.
Importantly, tree diameter remains an essential predictor of trees’ aboveground biomass. In line with this, [44] documented that 94%–98% of the variation in the aboveground biomass of major woody species in Ethiopia was explained by diameter as a predictor variable. Other studies, such as [9,13,17,30,35,39,45,46], emphasize the importance of tree diameter in dry biomass estimation.
Moreover, our model demonstrates the importance of adding wood basic density to the biomass model in significantly improving its prediction performance when compared with the inclusion of tree height and crown diameter. However, the addition of tree height to the biomass model was found to be statistically not significant (p < 0.05) for total aboveground biomass and biomass of stem, branch, and twig. For instance, in models 3 and 7 of group A (Supplementary Table S1), with the addition of wood basic density to the model, the adjusted R2 for total aboveground biomass increased from 0.58 to 0.78, the AIC decreased from 247.5 to 172, and the MSE decreased from 0.5 to 0.25.
This finding also agrees with that of [47], which states that diameter at breast height is a good predictor for aboveground biomass and that its accuracy increases with the addition of wood basic density and/or crown diameter. Our data demonstrates that the inclusion of total tree height in the model increases the prediction bias of the biomass model and that this variable does not significantly affect the trees’ aboveground biomass. Other studies [10,48] also report that all models that included tree height as a predictor variable had non-significant model parameters. Likewise, [47] documents that the biomass model’s goodness of fit increased by the inclusion of wood basic density data, while no noticeable effect was observed by the addition of height data. More specifically, [49] estimated that adding tree height to the model resulted in a 5% drop in allometric model accuracy. However, this result contrasts with the findings of [11,15,50,51], in which tree height was a preferable predictive variable to wood basic density in estimating aboveground biomass.
On the other hand, [43] concludes that the inclusion of tree height improves the accuracy of the tree biomass model in the wet zone, where tree height is a more important factor in determining biomass. However, for the moist climatic zone, they observed that specific wood density increases model accuracy rather than including tree height. This indicates that, in regions with abundant moisture, the structural characteristics of wood (wood basic density) play a more critical role in biomass estimation than tree height. Additionally, other studies, such as [52,53], document that the relationship between tree diameter and height in estimating the biomass was affected by various environmental factors. More specifically, [50] concludes that the variation of the relationship among predictive biometric variables of trees depends directly on bioclimatic variables. This may explain some of the contradictory findings on the importance of various tree metric variables (i.e., th and ρ) in improving the accuracy of biomass estimating models. Hence, this leads to the realization that the significance of the dendrometric variables in predicting a tree’s aboveground biomass varies depending on the ecological and climatic variations.
This study demonstrates that the prediction accuracy of allometric models is different among biomass components of the tree. The stem biomass was the most predicted plant component, whereas twig biomass was the most unpredictable. This result corroborates the finding by previous studies [11,32,34,54,55,56,57], in which the biomass variation of leaves and tiny branches is less explainable by tree metric variables as compared with that of stems and woody components. Nevertheless, this outcome goes against the claims made by [14,15] that the total aboveground and branch biomasses were predicted more accurately than the stem biomass. According to [2,58], species differences, plant growth conditions, and site characteristics like stand density and availability of light, water, and soil nutrients could all be contributing factors to the variations in predictability in biomass of plant components.
4.3. Species-Specific Biomass Estimation Models
The dominant tree variables in the biomass equations of the five studied species were tree diameter, crown diameter, and wood basic density. Other studies, including [10,57], also used a combination of diameter, crown diameter, and wood basic density to construct the best-fit allometric equations. However, other studies, such as [59], have found the diameter at breast height and total height as the most frequent parameters across their models.
The accuracy of the aboveground biomass models varied among tree species. For example, the total aboveground biomass for Commiphora africana was the most predicted dry biomass. A similar adjusted R2 of 0.93 was reported by [14], while [15] reports an adjusted R2 of 0.47 for the same species. Differences in the predictability level of the same species might be due to the differences in growth architecture and growth stages [47]. The result shows that the combination of tree diameter and crown diameter was the main predictor for the biomass of all tree partitions of Commiphora africana. In line with this, [57] finds diameter at stump height and crown width as the main explanatory variables of dry biomass in Commiphora species. In their generic model, [4] also finds the best-fit equation by combining the diameter at stump height with crown width.
The aboveground biomass of Olea europaea was explained by tree diameter as a single predictor variable. This is consistent with the findings of [36] in biomass models for Olea europaea, which show that the AGB had a substantial correlation with dbh but not with wood basic density or tree height individually. Other studies, such as those of [13,46,50], also corroborate the significance of diameter in predicting tree biomass.
The total aboveground biomass and stem biomass of Oncoba spinosa were better predicted by the model with combinations of the tree height and diameter, but the dry biomasses of its branches and twigs were better explained when the tree diameter and crown diameter were combined. This result shows that, in Oncoba spinosa species, the twig biomass was more predictable than other biomass compartments (i.e., stem and branch). This result is consistent with the findings of [14,15] and contrasts with those documented by [11,57].
The total aboveground biomass of Teclea nobilis was best explained by the combination of tree and crown diameter. Similarly, this result shows that a combination of tree diameter and height typically determines the variation in the dry biomass of the stem. The branch biomass of Teclea nobilis was found to be best predicted by the allometric model with tree diameter and height. Despite the equation with tree diameter, crown diameter, and wood basic density best fit biomass of the twig, the regression constant of the equation was not statistically significant (p > 0.05). This shows the lesser predictability of twig (leaves and tiny branches) biomass than the biomass of the stem and big branches of the tree.
4.4. Performances of Existing Multispecies Models
The model developed by [10] resulted in relatively low differences between mean values of observed and predicted dry weight of aboveground biomass, with the lowest relative prediction bias and relative squared error. The lower prediction error of the model observed by [10] is a result of the model being developed using the sample trees from the dryland afromontane forest, which was found to be similar to the ecology of our study area.
On the contrary, this outcome shows that the general multispecies models developed by [4,39] have proved to underpredict the total aboveground biomass of our data. Like our finding, [10] also confirms the higher prediction bias of [4,39], which significantly underestimated their data by 40.3% and 29.4%, respectively.
Per our data, the commonly used pantropical model of [17] also underpredicted the aboveground biomass. The large prediction errors of the “pan-tropical” model by [17] are documented in several studies [4,60,61]. The multispecies model of [15] also produced a high prediction error on our dataset. This was due to the differences in tree species composition and ecology of the study sites, as their model relied on the majority of sample trees from a single species (i.e., acacia species) in the grassland area, while our sample of trees was from five different plant species in the dryland afromontane forest.
Generally, the high prediction error recorded for the majority of the existing generic allometric equations confirmed the concerns raised by previous studies [4,14,15,17,19] regarding the application of their models outside their study areas. Therefore, the newly developed multispecies model, which has a mean prediction error of 1.01 kg and relative prediction bias of 3.82%, was found to be the model with the best prediction performance to estimate the aboveground biomass of the Borena woodland. This shows the importance and reliability of location-specific biomass estimation models, which is also emphasized by earlier studies [11,39].
5. Conclusions
Multispecies aboveground tree biomass models were developed for Borana woodland, using 114 sample trees from five dominant species in the Gamadu afromontane forest. According to the biomass distribution along the tree compartments of the five species, the branch holds the highest fraction of the aboveground biomass. In generic and species-specific allometric models, tree diameter, wood basic density, and crown diameter were the most significant predictors for biomass across all tree components. The addition of wood basic density to the model significantly improved prediction accuracy, while tree height was found to have a minimal effect on biomass estimation. This further supports the findings of other studies that have emphasized the importance of tree diameter and wood density over tree height for accurate biomass predictions.
The models fitted for the biomass of tree compartments were found to have better statistical prediction than the models of total aboveground biomass of the trees. Among the biomass of tree compartments, the stem and twig biomasses were found to be the most and least predictable plant parts, respectively.
The result affirms that species-specific models possess better prediction performance with minimum errors than the multispecies models. Moreover, the study revealed that there are varying prediction accuracies for different species, with some species, such as Commiphora africana, showing strong predictive power while others, like Euclea divinorum, were poorly explained by dendrometric variables. The results highlight the need for species-specific models that account for variations in growth architecture, ecological factors, and bioclimatic conditions.
Testing existing multispecies biomass models revealed that some models performed well for the study area while others significantly underestimated biomass, confirming concerns about the applicability of generic models across different regions. The newly developed multispecies model, tailored to the study area, demonstrated the best prediction performance, reinforcing the importance of location-specific models for accurate biomass estimation. Hence, this study emphasizes the significance of ecological and species-specific factors in biomass estimation and underscores the importance of developing and applying regionally calibrated models to improve the accuracy of aboveground biomass predictions in different forest ecosystems.
Supplementary Materials
The following supporting information can be available by request: https://www.mdpi.com/article/10.3390/f16050823/s1. Tables: results of all of the candidate allometric models. Table S1: Group A: Multispecies models fitted for total aboveground biomass; Table S2: Group B: Multispecies models fitted for stem biomass; Table S3: Group C: Multispecies models fitted for branch biomass; Table S4: Group D: Multispecies models fitted for twig biomass; Table S5: Commiphora africana (A. Rich) Engl.—models fitted for total aboveground biomass; Table S6: Commiphora africana (A. Rich) Engl.—models fitted for the stem; Table S7: Commiphora africana (A. Rich) Engl.—models fitted for the branch; Table S8: Commiphora africana (A. Rich) Engl.—models fitted for the twig; Table S9: Euclea divinorum Hiern.—models fitted for total aboveground biomass; Table S10: Euclea divinorum Hiern.—models fitted for the stem; Table S11: Euclea divinorum Hiern.—models fitted for the branch; Table S12: Euclea divinorum Hiern.—models fitted for the twig; Table S13: Olea europaea Subsp. cuspidata—models fitted for total aboveground biomass; Table S14: Olea europaea Subsp. cuspidata—models fitted for the stem; Table S15: Olea europaea Subsp. cuspidata—models fitted for the branch; Table S16: Olea europaea Subsp. cuspidata—models fitted for the twig; Table S17: Oncoba spinosa Forsk.—models fitted for total aboveground biomass; Table S18: Oncoba spinosa Forsk.—models fitted for the stem; Table S19: Oncoba spinosa Forsk.—models fitted for the branch; Table S20: Oncoba spinosa Forsk.—models fitted for the twig; Table S21: Teclea nobilis Del.—models fitted for total aboveground biomass; Table S22: Teclea nobilis Del.—models fitted for the stem; Table S23: Teclea nobilis Del.—models fitted for the branch; Table S24: Teclea nobilis Del.—models fitted for the twig.
Author Contributions
Conceptualization, D.J. and E.B.; methodology and software, D.J.; validation, E.B., M.H.U. and T.T.; formal analysis, D.J.; investigation, D.J.; resources, D.J.; data curation, E.B.; writing—original draft preparation, D.J. and E.B.; writing—review and editing, E.B., M.H.U. and T.T.; visualization, D.J.; supervision, E.B.; project administration, E.B.; funding acquisition, D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Mekelle University, through PhD student’s research grant of project number CDANR/PR163350/11.
Data Availability Statement
The research data for this study are available and can be submitted by request.
Acknowledgments
We are thankful to the Arsi University, College of Agriculture and Environmental Sciences, for the provision of the material used for forest measurements. The community in the Dire district of the Borana zone is also acknowledged for their participation and facilitation during the field data collection. We acknowledge the Institute of International Education-Scholars Rescue Fund (IIE-SRF) and Nord University, Faculty of Bioscience and Aquaculture (FBA) for supporting the research stay of Emiru Birhane at Nord University.
Conflicts of Interest
We declare that there are no conflicts of interest. Additionally, we hereby affirm that the funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
Summary of tree species characteristics in the study area.
Table A1.
Summary of tree species characteristics in the study area.
| S/N | Scientific Name | Family Name | Number of Trees per ha | Mean dsh | Mean dbh | Total BA per ha | Mean BA per Tree |
|---|---|---|---|---|---|---|---|
| 1 | Juniperus procera Endl. | Cupressaceae | 188 | 41.76 | 34.82 | 27.454 | 0.146 |
| 2 | Pittosporum viridiflorm | Pittosporaceae | 163 | 31.51 | 24.55 | 9.213 | 0.0565 |
| 3 | Euclea divinorum Hiern. | Ebenaceae | 933 | 6.98 | 5.75 | 2.902 | 0.0031 |
| 4 | Teclea nobilis Del. | Rutaceae | 750 | 6.85 | 6.08 | 2.887 | 0.0038 |
| 5 | Olea europaea Subsp. | Oleaceae | 200 | 13.45 | 9.81 | 1.879 | 0.0094 |
| 6 | Oncoba spinosa Forsk. | Flacourtiaceae | 258 | 9.35 | 8.38 | 1.799 | 0.007 |
| 7 | Pappea capensis | Sapindaceae | 129 | 17.80 | 11.29 | 1.594 | 0.0124 |
| 8 | Commiphora africana (A. Rich) Engl. | Burseraceae | 167 | 6.23 | 6.27 | 0.626 | 0.0037 |
| 9 | Vangueria apiculata | Rubiaceae | 104 | 7.00 | 6.42 | 0.386 | 0.0037 |
| 10 | Rytigynia neglecta (Hiern) Robyns | Rubiaceae | 133 | 6.63 | 5.19 | 0.358 | 0.0027 |
| 11 | Hiddi qaalluu | Hiddi qaalluu | 104 | 7.10 | 4.51 | 0.219 | 0.0021 |
| 12 | Maytenus senegalensis (Lam.) Exell | Celastraceae | 100 | 5.11 | 4.09 | 0.156 | 0.0016 |
| 13 | Ruttya fruticosa Lindau | Acanthaceae | 67 | 4.75 | 3.71 | 0.085 | 0.0013 |
| 14 | Commiphora kua (R.Br.ex Royle) Vollesen | Burseraceae | 71 | 4.70 | 3.49 | 0.082 | 0.0012 |
| 15 | Clausena anisata (Willd.) Benth. | Rutaceae | 54 | 3.95 | 3.58 | 0.059 | 0.0011 |
| 16 | Buuxxee | Buuxxee | 21 | 5.26 | 5.66 | 0.055 | 0.0026 |
| 17 | Buddleja polystachya | Scrophulariaceae | 79 | 3.14 | 2.58 | 0.046 | 0.0006 |
| 18 | Acokanthera schimperi (A. DC.) Schweinf | Apocynaceae | 33 | 4.01 | 3.26 | 0.031 | 0.0009 |
| 19 | Secamone punctulata Decne. | Asclepiadaceae | 42 | 3.73 | 2.88 | 0.030 | 0.0007 |
| 20 | Carissa edulis Vahl | Apocynaceae | 29 | 3.63 | 3.01 | 0.023 | 0.0008 |
| Total | 3625 |
dsh: diameter at stump height, dbh: diameter at breast height; Basal Area (BA): Cross-sectional area of a tree trunk measured at a specific height (m2). Italicized species names follow scientific nomenclature conventions.

Table A2.
Dendrometric variables and dry biomass of trees.
Table A2.
Dendrometric variables and dry biomass of trees.
| Species | Statistic | dsh (cm) | dbh (cm) | th (m) | cd (m) | ca (m2) | ρ (g/cm3) | Sb | Bb | Tb | Tagb |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Commiphora africana (A. Rich) Engl. | Mean | 6.13 | 6.17 | 3.28 | 1.89 | 3.92 | 0.37 | 2.1 | 3.03 | 1.35 | 6.48 |
| Sd | 2.5 | 2.94 | 1.47 | 1.21 | 4.77 | 0.06 | 1.87 | 3.53 | 1.09 | 6.25 | |
| Min | 2.5 | 2.0 | 1.65 | 0.25 | 0.05 | 0.28 | 0.33 | 0.30 | 0.25 | 0.88 | |
| Max | 11.2 | 13.0 | 6.2 | 4.4 | 15.2 | 0.52 | 6.73 | 16.4 | 3.97 | 26.45 | |
| Euclea divinorum Hiern. | Mean | 7.33 | 6.05 | 4.38 | 2.15 | 5.51 | 0.75 | 4.52 | 5.64 | 1.80 | 11.95 |
| Sd | 2.82 | 2.72 | 1.12 | 1.58 | 8.53 | 0.07 | 1.91 | 2.01 | 0.62 | 4.36 | |
| Min | 2.7 | 1.7 | 2.55 | 0.55 | 0.24 | 0.62 | 1.50 | 1.95 | 0.27 | 3.72 | |
| Max | 15.0 | 14.0 | 6.85 | 6.4 | 32.15 | 0.85 | 8.91 | 11.08 | 2.91 | 22.27 | |
| Olea europaea Subsp. Cuspidata | Mean | 12.25 | 10.68 | 4.72 | 4.06 | 12.73 | 0.97 | 16.17 | 30.28 | 8.63 | 55.38 |
| Sd | 5.78 | 4.63 | 1.64 | 0.87 | 4.59 | 0.16 | 10.95 | 24.8 | 6.36 | 39.62 | |
| Min | 2.5 | 2.3 | 1.14 | 2.35 | 4.34 | 0.71 | 1.65 | 1.52 | 0.76 | 3.92 | |
| Max | 28.5 | 17.0 | 7.2 | 5.2 | 18.85 | 1.24 | 40.14 | 71.08 | 21.17 | 120.89 | |
| Oncoba spinosa Forsk. | Mean | 9.48 | 8.37 | 4.92 | 3.25 | 10.62 | 0.65 | 13.55 | 20.42 | 6.50 | 40.47 |
| Sd | 5.43 | 4.55 | 1.87 | 1.78 | 9.18 | 0.05 | 7.16 | 10.11 | 4.01 | 20.26 | |
| Min | 3.0 | 2.3 | 1.65 | 0.9 | 0.64 | 0.56 | 4.02 | 7.85 | 1.92 | 17.97 | |
| Max | 17.0 | 16.0 | 7.4 | 5.55 | 24.18 | 0.72 | 23.22 | 35.91 | 14.93 | 72.89 | |
| Teclea nobilis Del. | Mean | 8.1 | 7.73 | 5.44 | 2.84 | 7.34 | 0.82 | 10.93 | 15.72 | 7.85 | 34.5 |
| Sd | 3.56 | 4.16 | 1.78 | 1.17 | 5.34 | 0.05 | 5.14 | 8.30 | 3.80 | 16.70 | |
| Min | 2.5 | 2.0 | 2.85 | 0.7 | 0.38 | 0.75 | 3.0 | 5.04 | 1.90 | 9.93 | |
| Max | 15.5 | 15.0 | 8.45 | 5.05 | 20.02 | 0.9 | 21.06 | 32.33 | 15.13 | 68.52 | |
| Aggregate of Five Species | Mean | 8.32 | 7.49 | 4.49 | 2.7 | 7.43 | 0.7 | 8.47 | 13.2 | 4.7 | 26.4 |
| Sd | 4.37 | 4.0 | 1.69 | 1.54 | 7.39 | 0.21 | 7.74 | 14.77 | 4.61 | 26.15 | |
| Min | 2.5 | 1.7 | 1.14 | 0.25 | 0.05 | 0.28 | 0.33 | 0.3 | 0.25 | 0.88 | |
| Max | 28.5 | 17.0 | 8.45 | 6.4 | 32.15 | 1.24 | 40.14 | 71.08 | 21.17 | 120.89 |
dsh: Diameter at stump height (cm); dbh: Diameter at breast height (cm); th: Tree height (m); cd: Crown diameter (m); ca: Crown area (m2); ρ: Wood basic density (g/cm3); Sb: Dry biomass of stem; Bb: Dry biomass of branches; Tb: Dry biomass of twig (leaves plus small branches); Tagb: Total aboveground dry biomass of tree.

Table A3.
Correlation between the dry biomass of trees and dendrometry variable of trees.
Table A3.
Correlation between the dry biomass of trees and dendrometry variable of trees.
| Tagb | Sb | Bb | Tb | |
|---|---|---|---|---|
| dsh | 0.7399 * | 0.7419 * | 0.7224 * | 0.634 * |
| dbh | 0.8208 * | 0.8247 * | 0.7938 * | 0.7349 * |
| th | 0.5106 * | 0.532 * | 0.4562 * | 0.5371 * |
| cd | 0.5991 * | 0.5881 * | 0.5565 * | 0.6209 * |
| ca | 0.5607 * | 0.5466 * | 0.5261 * | 0.5731 * |
| wbd | 0.6288 * | 0.623 * | 0.6092 * | 0.5633 * |
Note: Tagb—Total aboveground dry biomass of tree; Sb—dry biomass of stem; Bb—dry biomass of branches; Tb—dry biomass of twig (leaves plus small branches); dbh—diameter at breast height (at 1.3 m); dsh—diameter at stump height (at 0.3 m); ca—crown area; cd—crown diameter; th—tree height; wbd—wood basic density of the stem; and *—the correlation coefficient statistically significant at p < 0.001.

Table A4.
Model groups.
Table A4.
Model groups.
| GROUP A | GROUP B |
| MA1: ln(Tagb) = α + β1ln(dbh) MA2: ln(Tagb) = α + β1ln(dbh) + β2ln(th) MA3: ln(Tagb) = α + β1ln(dbh) + β2ln(cd) MA4: ln(Tagb) = α + β1ln(dbh) + β2ln(wbd) MA5: ln(Tagb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) MA6: ln(Tagb) = α + β1ln(dbh) + β2ln(th) + β3ln(wbd) MA7: ln(Tagb) = α + β1ln(dbh) + β2ln(cd) + β3ln(wbd) MA8: ln(Tagb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) + β4ln(wbd) | MB1: ln(Sb) = α + β1ln(dbh) MB2: ln(Sb) = α + β1ln(dbh) + β2ln(th) MB3: ln(Sb) = α + β1ln(dbh) + β2ln(cd) MB4: ln(Sb) = α + β1ln(dbh) + β2ln(wbd) MB5: ln(Sb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) MB6: ln(Sb) = α + β1ln(dbh) + β2ln(th) + β3ln(wbd) MB7: ln(Sb) = α + β1ln(dbh) + β2ln(cd) + β3ln(wbd) MB8: ln(Sb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) + β4ln(wbd) |
| GROUP C | GROUP D |
| MC1: ln(Bb) = α + β1ln(dbh) MC2: ln(Bb) = α + β1ln(dbh) + β2ln(th) MC3: ln(Bb) = α + β1ln(dbh) + β2ln(cd) MC4: ln(Bb) = α + β1ln(dbh) + β2ln(wbd) MC5: ln(Bb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) MC6: ln(Bb) = α + β1ln(dbh) + β2ln(th) + β3ln(wbd) MC7: ln(Bb) = α + β1ln(dbh) + β2ln(cd) + β3ln(wbd) MC8: ln(Bb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) + β4ln(wbd) | MD1: ln(Tb) = α + β1ln(dbh) MD2: ln(Tb) = α + β1ln(dbh) + β2ln(th) MD3: ln(Tb) = α + β1ln(dbh) + β2ln(cd) MD4: ln(Tb) = α + β1ln(dbh) + β2ln(wbd) MD5: ln(Tb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) MD6: ln(Tb) = α + β1ln(dbh) + β2ln(th) + β3ln(wbd) MD7: ln(Tb) = α + β1ln(dbh) + β2ln(cd) + β3ln(wbd) MD8: ln(Tb) = α + β1ln(dbh) + β2ln(th) + β3ln(cd) + β4ln(wbd) |
Tagb—Total aboveground dry biomass of tree; Sb—dry biomass of stem; Bb—dry biomass of branches; Tb—dry biomass of twig (leaves plus small branches); dbh—diameter at breast height; th—tree height; cd—crown diameter; wbd—wood basic density. α is a constant of the model while β1, β2, β3 and β4 are parameters (regression coefficients) of the model. Tagb = Sb + Bb + Tb.
References
- Vashum, K.T.; Jayakumar, S. Methods to estimate above-ground biomass and carbon stock in natural forests-a review. J. Ecosyst. Ecography 2012, 2, 1–7. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.; Valentini, R.; Bernoux, M.; Saint André, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef]
- Mugasha, W.A.; Eid, T.; Bollandsås, O.M.; Malimbwi, R.E.; Chamshama, S.A.O.; Zahabu, E.; Katani, J.Z. Allometric models for prediction of above-and belowground biomass of trees in the miombo woodlands of Tanzania. For. Ecol. Manag. 2013, 310, 87–101. [Google Scholar] [CrossRef]
- Ubuy, M.H.; Eid, T.; Bollandsås, O.M.; Birhane, E. Aboveground biomass models for trees and shrubs of exclosures in the drylands of Tigray, northern Ethiopia. J. Arid Environ. 2018, 156, 9–18. [Google Scholar] [CrossRef]
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 10. [Google Scholar]
- Wei, X. Biomass estimation: A remote sensing approach. Geogr. Compass 2010, 4, 1635–1647. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote. Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Solomon, N.; Birhane, E.; Tadesse, T.; Treydte, A.C.; Meles, K. Carbon stocks and sequestration potential of dry forests under community management in Tigray, Ethiopia. Ecol. Process. 2017, 6, 20. [Google Scholar] [CrossRef]
- Birhane, E.; Treydte, A.C.; Eshete, A.; Solomon, N.; Hailemariam, M. Can rangelands gain from bush encroachment? Carbon stocks of communal grazing lands invaded by Prosopis juliflora. J. Arid Environ. 2017, 141, 60–67. [Google Scholar] [CrossRef]
- Tetemke, B.A.; Birhane, E.; Rannestad, M.M.; Eid, T. Allometric models for predicting aboveground biomass of trees in the dry afromontane forests of Northern Ethiopia. Forests 2019, 10, 1114. [Google Scholar] [CrossRef]
- Abich, A.; Alemu, A.; Gebremariam, Y.; Mucheye, T.; Gurebiyaw, K.; Kassie, M. Allometric models for predicting aboveground biomass of Combretum-Terminalia woodlands in Amhara, Northwest Ethiopia. Trees For. People 2021, 5, 100122. [Google Scholar] [CrossRef]
- Abich, A.; Mucheye, T.; Tebikew, M.; Gebremariam, Y.; Alemu, A. Species-specific allometric equations for improving aboveground biomass estimates of dry deciduous woodland ecosystems. J. For. Res. 2019, 30, 1619–1632. [Google Scholar] [CrossRef]
- Mulat, A.; Soromessa, T. Species specific allometric model for biomass estimation of Polyscias fulva harms in tumata chirecha agroforestry Gedeo zone of Ethiopia: Implication for sustainable management and climatic change mitigation. J. Energy Technol. Pol. 2016, 6, 12–22. [Google Scholar]
- Hasen-Yusuf, M.; Treydte, A.; Abule, E.; Sauerborn, J. Predicting aboveground biomass of woody encroacher species in semi-arid rangelands, Ethiopia. J. Arid Environ. 2013, 96, 64–72. [Google Scholar] [CrossRef]
- Mulatu, A.; Negash, M.; Asrat, Z. Species-specific allometric models for reducing uncertainty in estimating above ground biomass at Moist Evergreen Afromontane Forest of Ethiopia. Sci. Rep. 2024, 14, 1147. [Google Scholar] [CrossRef]
- Feyisa, K.; Beyene, S.; Angassa, A.; Said, M.Y.; de Leeuw, J.; Abebe, A.; Megersa, B. Effects of enclosure management on carbon sequestration, soil properties and vegetation attributes in East African rangelands. Catena 2017, 159, 9–19. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Feyisa, K.; Beyene, S.; Megersa, B.; Said, M.Y.; Angassa, A. Allometric equations for predicting above-ground biomass of selected woody species to estimate carbon in East African rangelands. Agrofor. Syst. 2018, 92, 599–621. [Google Scholar] [CrossRef]
- Temesgen, H.; Affleck, D.; Poudel, K.; Gray, A.; Sessions, J. A review of the challenges and opportunities in estimating above ground forest biomass using tree-level models. Scand. J. For. Res. 2015, 30, 326–335. [Google Scholar] [CrossRef]
- Dida, H. The Impacts of Development Interventions on Customary Institutions of Forest Resource Management among the Borana Oromo of Southern Ethiopia; Addis Ababa University, Department of Social Anthropology: Addis Ababa, Ethiopia, 2010. [Google Scholar]
- Angassa, A. The Dynamics of Savanna Ecosystems and Management in Borana, Southern Ethiopia; Norwegian University of Life Sciences: As, Norway, 2007. [Google Scholar]
- Teka, H.; Madakadze, C.I.; Botai, J.O.; Hassen, A.; Angassa, A.; Mesfin, Y. Evaluation of land use land cover changes using remote sensing Landsat images and pastoralists perceptions on range cover changes in Borana rangelands, Southern Ethiopia. Int. J. Biodivers. Conserv. 2018, 10, 1–11. [Google Scholar]
- Megersa, B.; Markemann, A.; Angassa, A.; Ogutu, J.O.; Piepho, H.-P.; Zaráte, A.V. Impacts of climate change and variability on cattle production in southern Ethiopia: Perceptions and empirical evidence. Agric. Syst. 2014, 130, 23–34. [Google Scholar] [CrossRef]
- Ellenberg, D.; Mueller-Dombois, D. Aims and Methods of Vegetation Ecology; Wiley: New York, NY, USA, 1974; Volume 547. [Google Scholar]
- Asrat, Z.; Taddese, H.; Ørka, H.O.; Gobakken, T.; Burud, I.; Næsset, E. Estimation of forest area and canopy cover based on visual interpretation of satellite images in Ethiopia. Land 2018, 7, 92. [Google Scholar] [CrossRef]
- Bitew, G.; Tesfaye, A. Patterns of woody species diversity along disturbance gradient in Gumdri Abo natural forest, Dangila District, North Western Ethiopia. J. Nat. Sci. Res. 2017, 9, 32–46. [Google Scholar]
- Hussein, A.; Dejene, S.W.; Aschalew, A. Comparison of woody species diversity and population structure along disturbance gradient in babile elephant sanctuary, ethiopia. J. Landsc. Ecol. 2022, 15, 59–79. [Google Scholar] [CrossRef]
- Philip, M.S. Measuring Trees and Forests; CABI Digital Library: Oxfordshire, UK, 1994. [Google Scholar]
- Bettinger, P.; Boston, K.; Siry, J.P.; Grebner, D.L. Forest Management and Planning; Academic press: Cambridge, MA, USA, 2016. [Google Scholar]
- Giday, K.; Eshete, G.; Barklund, P.; Aertsen, W.; Muys, B. Wood biomass functions for Acacia abyssinica trees and shrubs and implications for provision of ecosystem services in a community managed exclosure in Tigray, Ethiopia. J. Arid Environ. 2013, 94, 80–86. [Google Scholar] [CrossRef]
- Gessesse, T.A. Above-and Belowground Carbon Stocks in Semi-Arid Land-Use Systems under Integrated Watershed Management in Gergera Watershed, Ethiopia; Universitäts-und Landesbibliothek Bonn: Bonn, Germany, 2016. [Google Scholar]
- Balima, L.H.; Nacoulma, B.M.I.; Bayen, P.; Dimobe, K.; Kouamé, F.N.G.; Thiombiano, A. Aboveground biomass allometric equations and distribution of carbon stocks of the African oak (Afzelia africana Sm.) in Burkina Faso. J. For. Res. 2020, 31, 1699–1711. [Google Scholar] [CrossRef]
- Mukuralinda, A.; Kuyah, S.; Ruzibiza, M.; Ndoli, A.; Nabahungu, N.L.; Muthuri, C. Allometric equations, wood density and partitioning of aboveground biomass in the arboretum of Ruhande, Rwanda. Trees For. People 2021, 3, 100050. [Google Scholar] [CrossRef]
- Delcourt, C.J.F.; Veraverbeke, S. Allometric equations and wood density parameters for estimating aboveground and woody debris biomass in Cajander larch (Larix cajanderi) forests of northeast Siberia. Biogeosciences 2022, 19, 4499–4520. [Google Scholar] [CrossRef]
- Egeta, D.; Negash, M.; Alebachew, M.; Eshete, A.; Mulugeta, S.; Lemi, T. Species-Specific Allometric Equations, Biomass Expansion Factor, and Wood Density of Native Tree Species in the Dry Afromontane Forest of Ethiopia. Int. J. For. Res. 2023, 2023, 5572048. [Google Scholar] [CrossRef]
- Kebede, B.; Soromessa, T. Allometric equations for aboveground biomass estimation of Olea europaea L. subsp. cuspidata in Mana Angetu Forest. Ecosyst. Health Sustain. 2018, 4, 1–12. [Google Scholar] [CrossRef]
- Njana, M.A.; Meilby, H.; Eid, T.; Zahabu, E.; Malimbwi, R.E. Importance of tree basic density in biomass estimation and associated uncertainties: A case of three mangrove species in Tanzania. Ann. For. Sci. 2016, 73, 1073–1087. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Mokria, M.; Mekuria, W.; Gebrekirstos, A.; Aynekulu, E.; Belay, B.; Gashaw, T.; Bräuning, A. Mixed-species allometric equations and estimation of aboveground biomass and carbon stocks in restoring degraded landscape in northern Ethiopia. Environ. Res. Lett. 2018, 13, 024022. [Google Scholar] [CrossRef]
- Trumper, K.; Ravilious, C.; Dickson, B. Carbon in Drylands: Desertification, Climate Change and Carbon Finance. 2008. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=cb959da9184a9f4cd60ec6b2b46ccbeca35a927c (accessed on 18 January 2025).
- Goodman, R.C.; Phillips, O.L.; Baker, T.R. The importance of crown dimensions to improve tropical tree biomass estimates. Ecol. Appl. 2014, 24, 680–698. [Google Scholar] [CrossRef] [PubMed]
- Dimobe, K.; Kouakou, J.; Tondoh, J.; Zoungrana, B.; Forkuor, G.; Ouédraogo, K. Predicting the Potential Impact of Climate Change on Carbon Stock in Semi-Arid West African Savannas. Land 2018, 7, 124. [Google Scholar] [CrossRef]
- Henry, M.; Besnard, A.; Asante, W.; Eshun, J.; Adu-Bredu, S.; Valentini, R.; Bernoux, M.; Saint-André, L. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. For. Ecol. Manag. 2010, 260, 1375–1388. [Google Scholar] [CrossRef]
- Sebrala, H.; Abich, A.; Negash, M.; Asrat, Z.; Lojka, B. Tree allometric equations for estimating biomass and volume of Ethiopian forests and establishing a database. Trees For. People 2022, 9, 100314. [Google Scholar] [CrossRef]
- Segura, M.; Kanninen, M. Allometric models for tree volume and total aboveground biomass in a tropical humid forest in Costa Rica 1. Biotropica: J. Biol. Conserv. 2005, 37, 2–8. [Google Scholar] [CrossRef]
- Chave, J.r.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: II. Belowground biomass. Agric. Ecosyst. Environ. 2012, 158, 225–234. [Google Scholar] [CrossRef]
- Hofstad, O. Review of biomass and volume functions for individual trees and shrubs in Southeast Africa. J. Trop. For. Sci. 2005, 17, 151–162. [Google Scholar]
- Phalla, T.; Ota, T.; Mizoue, N.; Kajisa, T.; Yoshida, S.; Vuthy, M.; Heng, S. The importance of tree height in estimating individual tree biomass while considering errors in measurements and allometric models. AGRIVITA J. Agric. Sci. 2017, 40, 131–140. [Google Scholar] [CrossRef]
- Daba, D.E.; Soromessa, T. The accuracy of species-specific allometric equations for estimating aboveground biomass in tropical moist montane forests: Case study of Albizia grandibracteata and Trichilia dregeana. Carbon Balance Manag. 2019, 14, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Petrea, S.; Radu, G.R.; Braga, C.I.; Cucu, A.B.; Serban, T.; Zaharia, A.; Pepelea, D.; Ienasoiu, G.; Petritan, I.C. The role of wood density variation and biomass allocation in accurate forest carbon stock estimation of European beech (Fagus sylvatica L.) mountain forests. Forests 2024, 15, 404. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Cheng, P.; Davis, C.J. Modeling spatial variation in tree diameter–height relationships. For. Ecol. Manag. 2004, 189, 317–329. [Google Scholar] [CrossRef]
- Wang, X.; Fang, J.; Tang, Z.; Zhu, B. Climatic control of primary forest structure and DBH–height allometry in Northeast China. For. Ecol. Manag. 2006, 234, 264–274. [Google Scholar] [CrossRef]
- Sawadogo, L.; Savadogo, P.; Tiveau, D.; Dayamba, S.D.; Zida, D.; Nouvellet, Y.; Oden, P.C.; Guinko, S. Allometric prediction of above-ground biomass of eleven woody tree species in the Sudanian savanna-woodland of West Africa. J. For. Res. 2010, 21, 475–481. [Google Scholar] [CrossRef]
- Berner, L.T.; Alexander, H.D.; Loranty, M.M.; Ganzlin, P.; Mack, M.C.; Davydov, S.P.; Goetz, S.J. Biomass allometry for alder, dwarf birch, and willow in boreal forest and tundra ecosystems of far northeastern Siberia and north-central Alaska. For. Ecol. Manag. 2015, 337, 110–118. [Google Scholar] [CrossRef]
- Dimobe, K.; Goetze, D.; Ouédraogo, A.; Mensah, S.; Akpagana, K.; Porembski, S.; Thiombiano, A. Aboveground biomass allometric equations and carbon content of the shea butter tree (Vitellaria paradoxa CF Gaertn., Sapotaceae) components in Sudanian savannas (West Africa). Agrofor. Syst. 2019, 93, 1119–1132. [Google Scholar] [CrossRef]
- Amanuel, W.; Tadesse, C.; Molla, M.; Getinet, D.; Mekonnen, Z. Allometric equation for estimating aboveground biomass of Acacia-Commiphora forest, southern Ethiopia. J. Ecol. Environ. 2024, 48, 196–206. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Wang, C.; Gower, S. Aboveground and belowground biomass and sapwood area allometric equations for six boreal tree species of northern Manitoba. Can. J. For. Res. 2002, 32, 1441–1450. [Google Scholar] [CrossRef]
- Gebeyehu, G.; Soromessa, T.; Bekele, T.; Teketay, D. Allometric Equations for Aboveground Biomass Estimations of Four Dry Afromontane Tree Species. 2020. Available online: https://www.researchsquare.com/article/rs-102592/v1 (accessed on 20 February 2025).
- Tesfaye, M.A.; Bravo-Oviedo, A.; Bravo, F.; Ruiz-Peinado, R. Aboveground biomass equations for sustainable production of fuelwood in a native dry tropical afro-montane forest of Ethiopia. Ann. For. Sci. 2016, 73, 411–423. [Google Scholar] [CrossRef]
- Ngomanda, A.; Obiang, N.L.E.; Lebamba, J.; Mavouroulou, Q.M.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Iponga, D.M.; Ditsouga, F.K.; Koumba, R.Z. Site-specific versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2014, 312, 1–9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).