MFCPopulus: A Point Cloud Completion Network Based on Multi-Feature Fusion for the 3D Reconstruction of Individual Populus Tomentosa in Planted Forests
Abstract
1. Introduction
- Multi−scale feature fusion combining canopy and trunk structural priors can reduce reconstruction variance by over 20% compared to uniform approaches.
- Hierarchical adversarial learning enables the precise recovery of occluded crown structures, reducing complexity discrepancy by >30%.
- Biologically informed normalization preserves species−specific morphological patterns while optimizing computational efficiency.
2. Related Work
3D Reconstruction of Trees
3. Materials and Methods
3.1. Study Area
3.2. Dataset
3.2.1. UAV Platform and Data Acquisition
3.2.2. Dataset Construction
3.2.3. Dataset Analysis
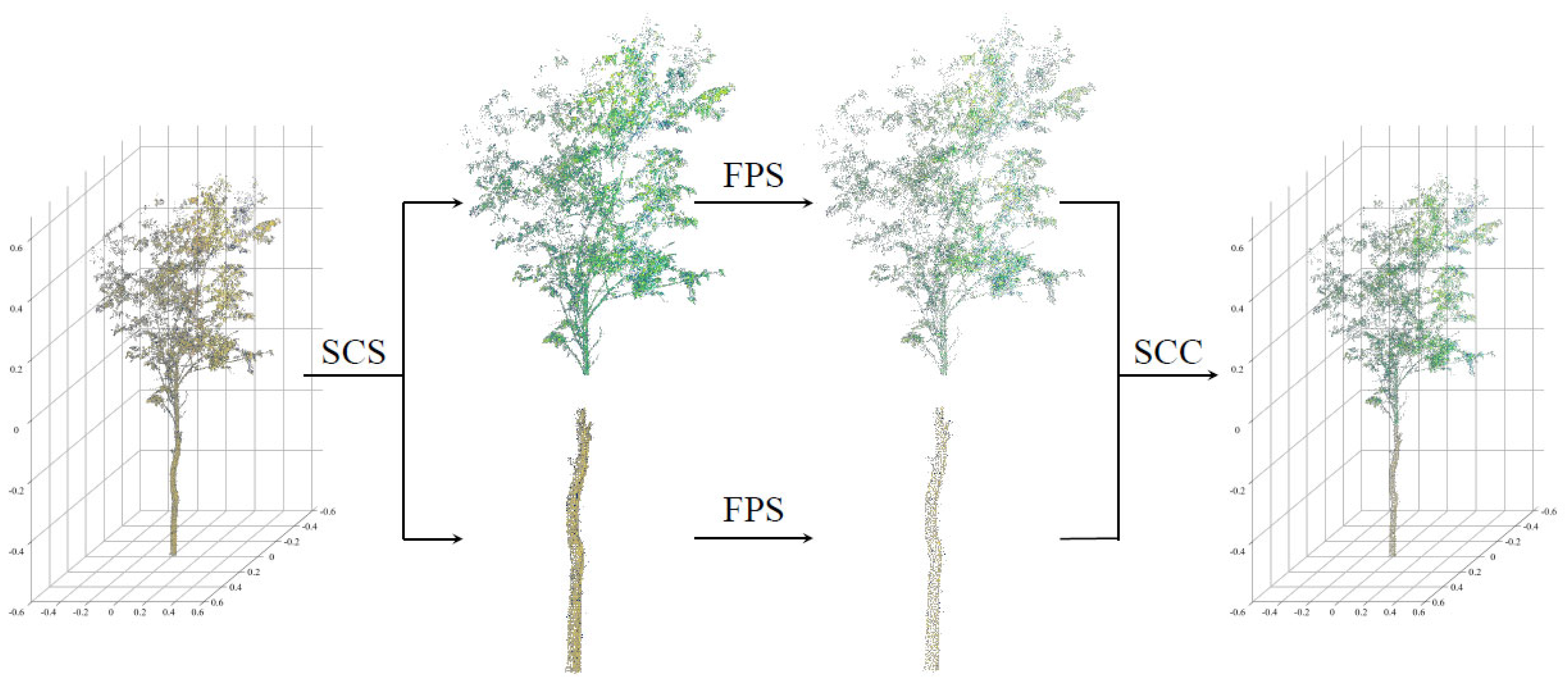
3.3. Sampling of Structural Features
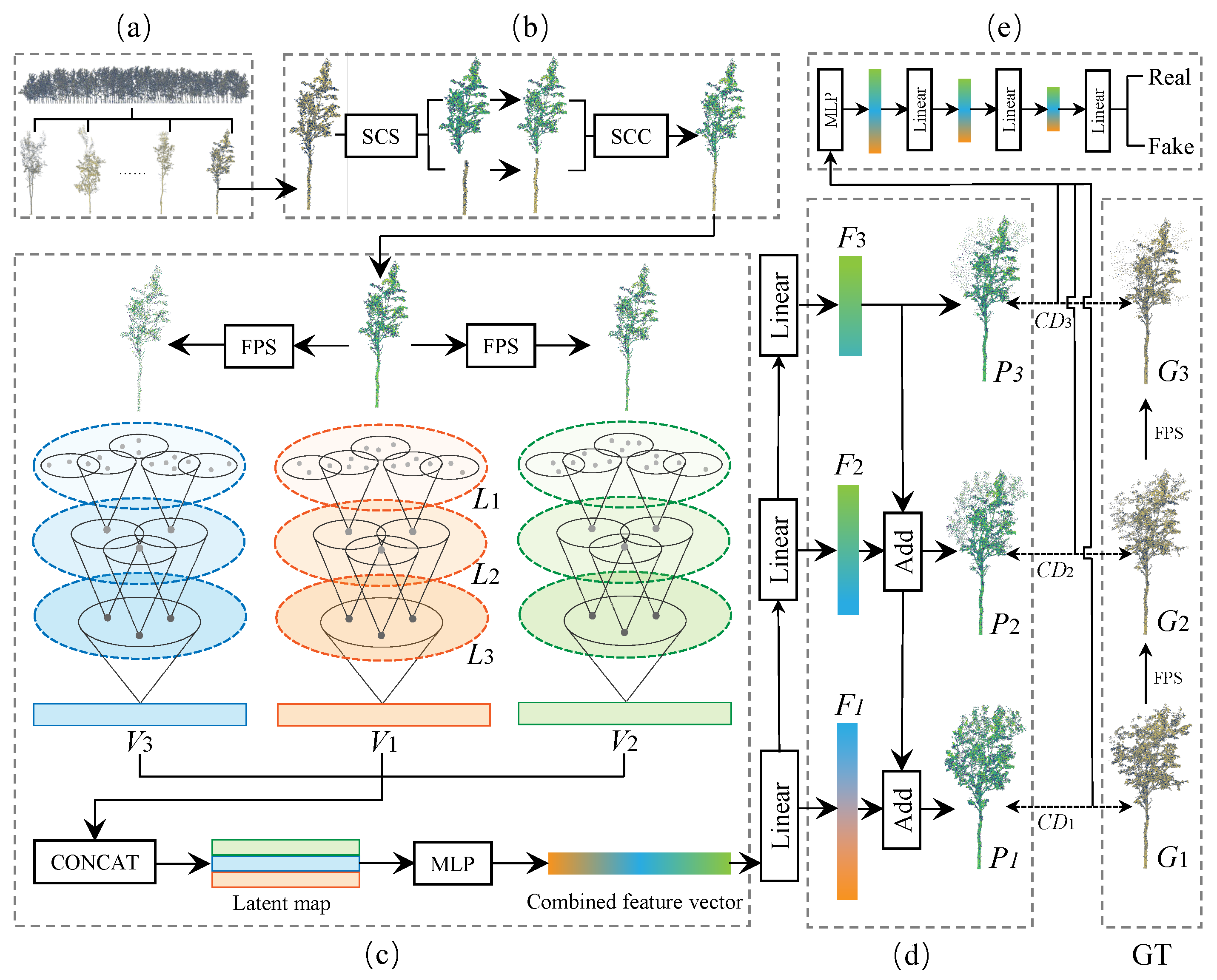
3.4. Multi−Feature Fusion Completion Network
3.4.1. Multi−Scale Feature Fusion with Hierarchical Sampling
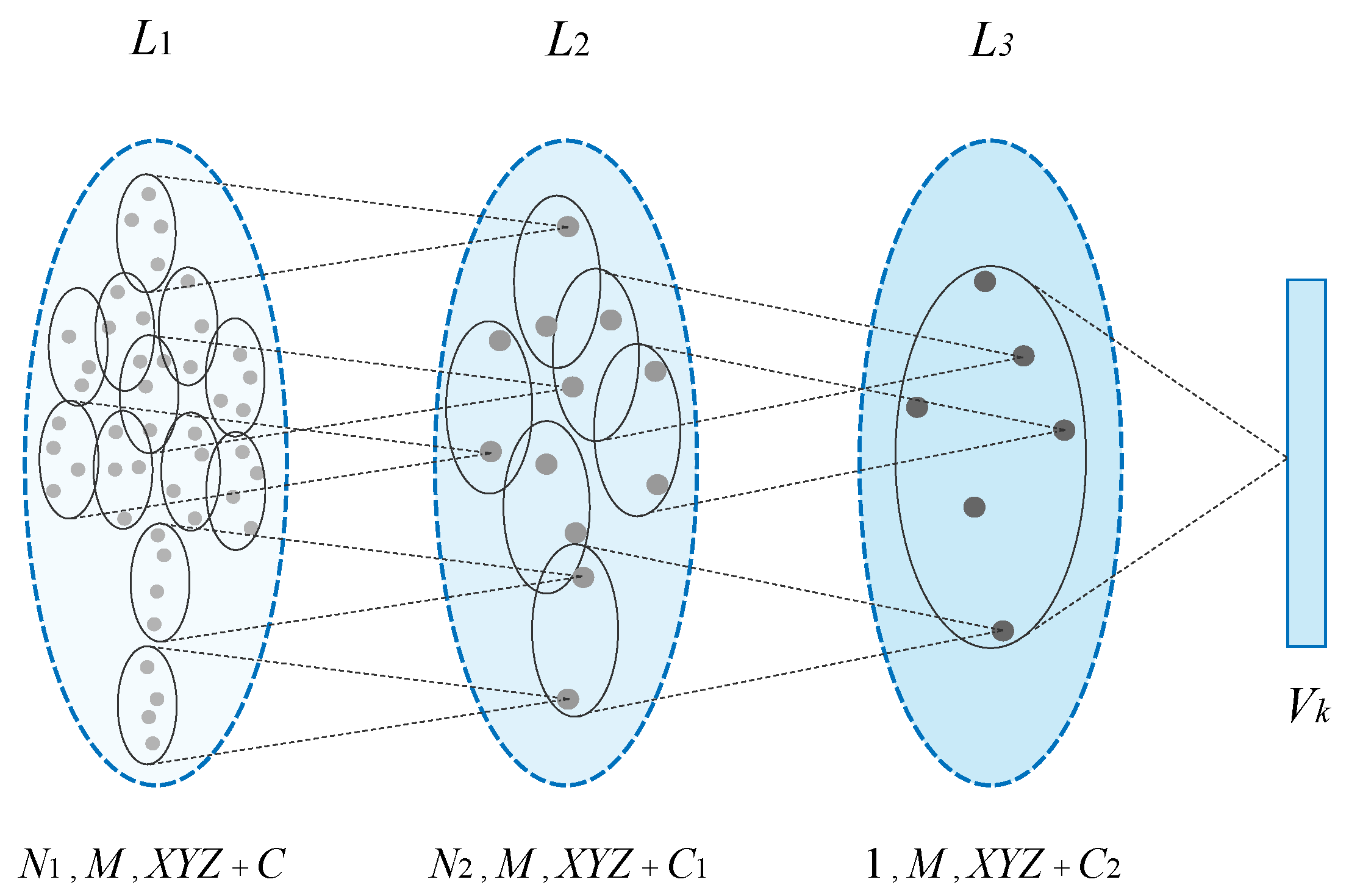
3.4.2. Hierarchical Multi−Sampling
3.4.3. Sampling Centers and Groups
3.4.4. Group Feature Extraction
3.4.5. Feature Fusion
3.5. Generation
3.6. Loss Function
4. Results and Discussion
4.1. Morphological Evaluations of Structural Complexity
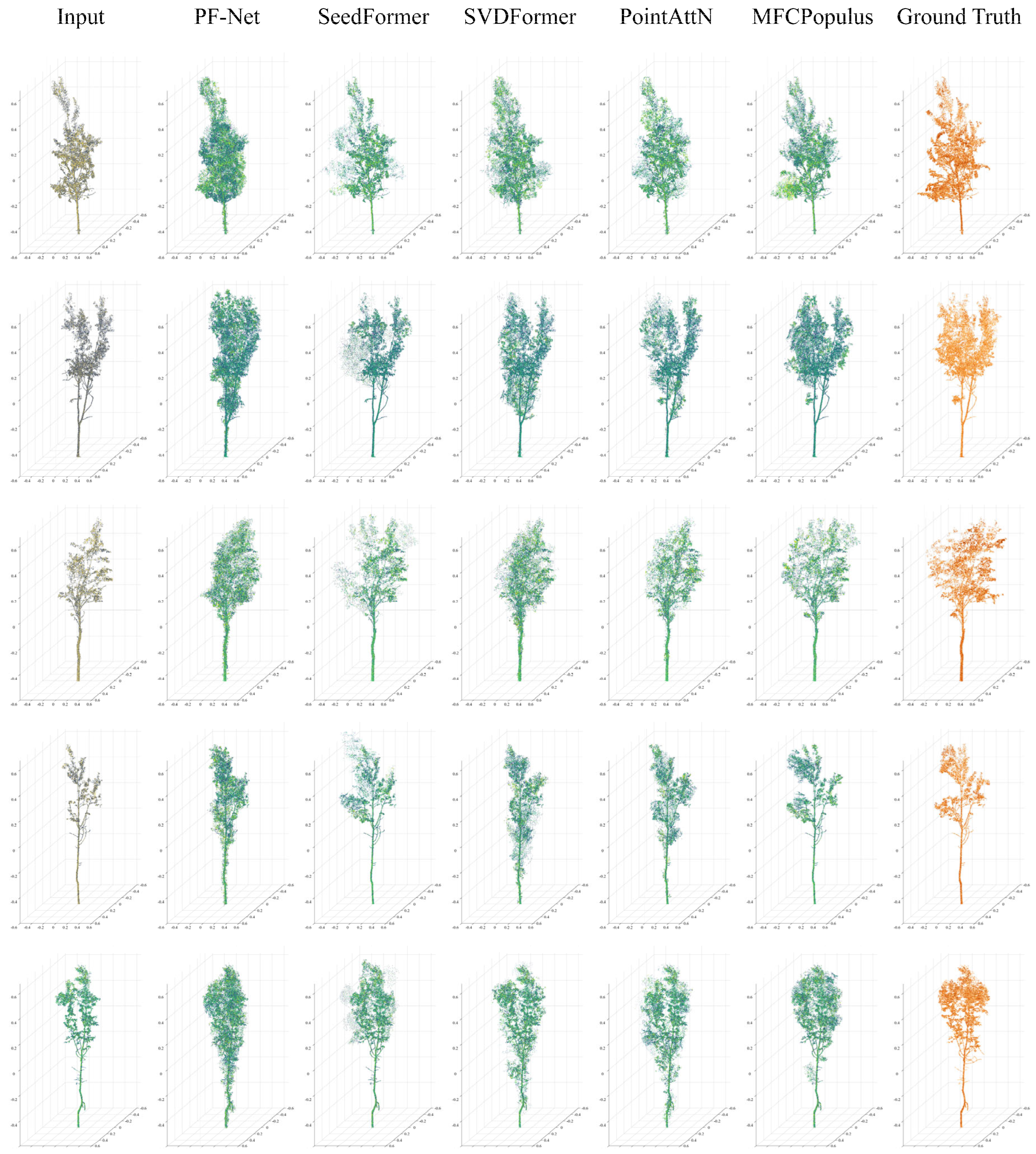
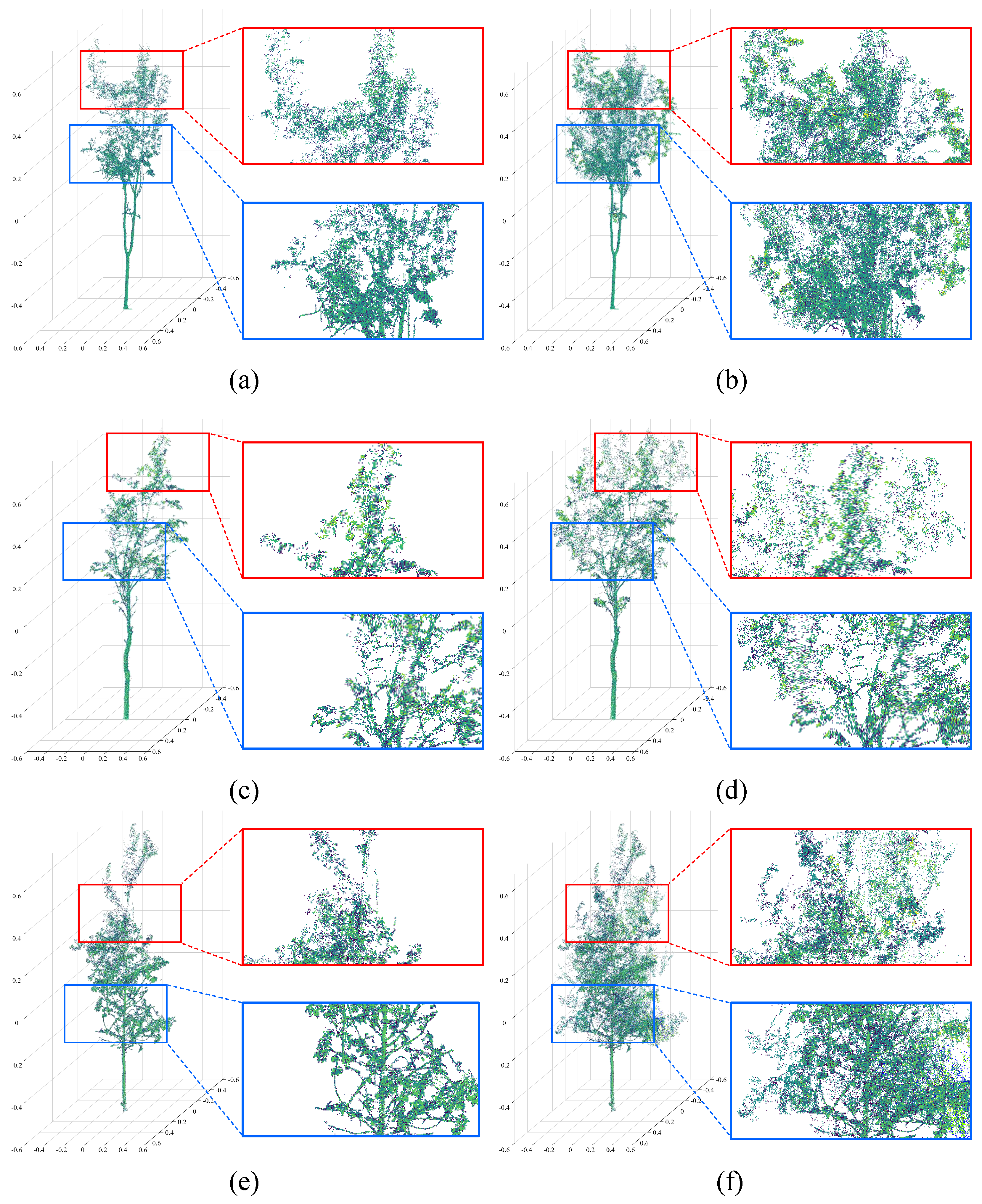
4.2. Visual Evaluations of Representations
4.3. Quantitative Evaluations of Generating Differences
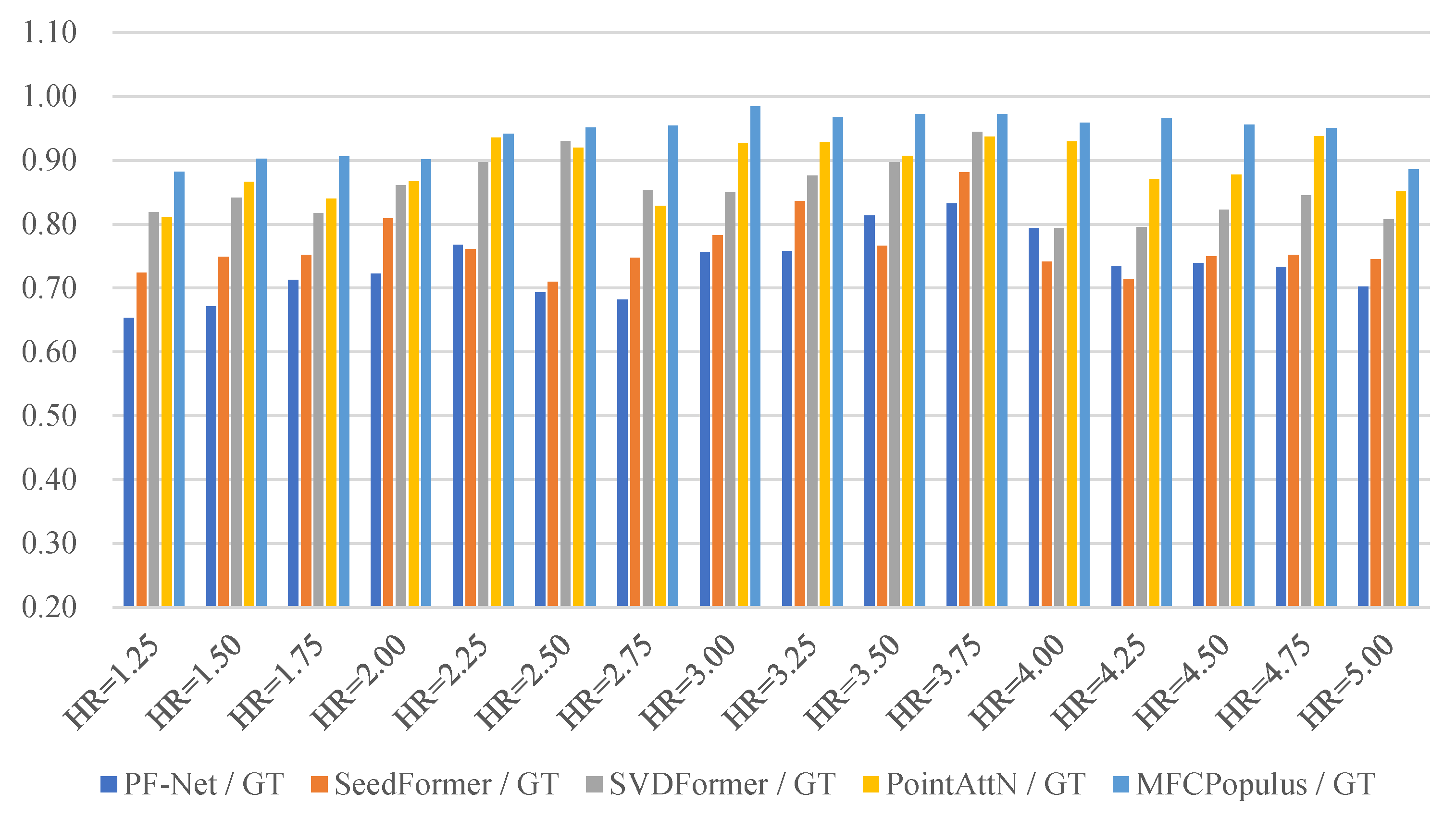
4.4. Point Cloud Utilization Efficiency Analysis
4.5. Model Generalizability and Robustness Analysis
4.5.1. Cross−Species Application Scalability
4.5.2. Sensitivity to Training Dataset Scale
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
- Wang, S.; Kobayashi, K.; Takanashi, S.; Liu, C.P.; Li, D.R.; Chen, S.W.; Cheng, Y.T.; Moriguchi, K.; Dannoura, M. Estimating divergent forest carbon stocks and sinks via a knife set approach. J. Environ. Manag. 2023, 330, 117114. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Wallace, L.; Hillman, S.; Reinke, K.; Hally, B. Non-destructive estimation of above-ground surface and near-surface biomass using 3D terrestrial remote sensing techniques. Methods Ecol. Evol. 2017, 8, 1607–1616. [Google Scholar] [CrossRef]
- Wu, Y.; Sang, M.; Wang, W. A Novel Ground Filtering Method for Point Clouds in a Forestry Area Based on Local Minimum Value and Machine Learning. Appl. Sci. 2022, 12, 9113. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual Tree Crown Segmentation Directly from UAV-Borne LiDAR Data Using the PointNet of Deep Learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Sang, L.; Wang, J. Characterizing Forest Cover and Landscape Pattern Using Multi-Source Remote Sensing Data with Ensemble Learning. Remote Sens. 2022, 14, 5470. [Google Scholar] [CrossRef]
- Du, L.; Pang, Y.; Wang, Q.; Huang, C.; Bai, Y.; Chen, D.; Lu, W.; Kong, D. A LiDAR biomass index-based approach for tree- and plot-level biomass mapping over forest farms using 3D point clouds. Remote Sens. Environ. 2023, 290, 113543. [Google Scholar] [CrossRef]
- Wang, C.; Morgan, G.; Hodgson, M. sUAS for 3D Tree Surveying: Comparative Experiments on a Closed-Canopy Earthen Dam. Forests 2021, 12, 659. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H. Efficient modeling of numerous trees by introducing growth volume for real-time virtual ecosystems. Comput. Animat. Virtual Worlds 2012, 23, 155–165. [Google Scholar] [CrossRef]
- Spadavecchia, C.; Belcore, E.; Piras, M.; Kobal, M. An Automatic Individual Tree 3D Change Detection Method for Allometric Parameters Estimation in Mixed Uneven-Aged Forest Stands from ALS Data. Remote Sens. 2022, 14, 4666. [Google Scholar] [CrossRef]
- Latifi, H.; Valbuena, R.; Silva, C.A. Towards complex applications of active remote sensing for ecology and conservation. Methods Ecol. Evol. 2023, 14, 1578–1586. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Fedorov, N.; Bikbaev, I.; Shirokikh, P.; Zhigunova, S.; Tuktamyshev, I.; Mikhaylenko, O.; Martynenko, V.; Kulagin, A.; Giniyatullin, R.; Urazgildin, R.; et al. Estimation of Carbon Stocks of Birch Forests on Abandoned Arable Lands in the Cis-Ural Using Unmanned Aerial Vehicle-Mounted LiDAR Camera. Forests 2023, 14, 2392. [Google Scholar] [CrossRef]
- Dean, C.; Kirkpatrick, J.; Osborn, J.; Doyle, R.; Fitzgerald, N.; Roxburgh, S. Novel 3D geometry and models of the lower regions of large trees for use in carbon accounting of primary forests. AoB Plants 2018, 10, ply015. [Google Scholar] [CrossRef] [PubMed]
- Okura, F. 3D modeling and reconstruction of plants and trees: A cross-cutting review across computer graphics, vision, and plant phenotyping. Breed. Sci. 2022, 72, 31–47. [Google Scholar] [CrossRef]
- Rengarajan, R.; Schott, J.R. Modeling and Simulation of Deciduous Forest Canopy and Its Anisotropic Reflectance Properties Using the Digital Image and Remote Sensing Image Generation (DIRSIG) Tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4805–4817. [Google Scholar] [CrossRef]
- Mei, J.; Zhang, L.; Wu, S.; Wang, Z.; Zhang, L. 3D tree modeling from incomplete point clouds via optimization and L1-MST. Int. J. Geogr. Inf. Sci. 2017, 31, 999–1021. [Google Scholar] [CrossRef]
- ITAKURA, K.; HOSOI, F. Automatic individual tree detection and canopy segmentation from three-dimensional point cloud images obtained from ground-based lidar. J. Agric. Meteorol. 2018, 74, 109–113. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. 3D point cloud fusion from UAV and TLS to assess temperate managed forest structures. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102917. [Google Scholar] [CrossRef]
- Tai, H.; Xia, Y.; Yan, M.; Li, C.; Kong, X. Construction of Artificial Forest Point Clouds by Laser SLAM Technology and Estimation of Carbon Storage. Appl. Sci. 2022, 12, 10838. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Shi, Y.; Chen, D. Restoration of Individual Tree Missing Point Cloud Based on Local Features of Point Cloud. Remote Sens. 2022, 14, 1346. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G.; Jing, W. A Single-Tree Point Cloud Completion Approach of Feature Fusion for Agricultural Robots. Electronics 2023, 12, 1296. [Google Scholar] [CrossRef]
- Yang, T.; Ye, J.; Zhou, S.; Xu, A.; Yin, J. 3D reconstruction method for tree seedlings based on point cloud self-registration. Comput. Electron. Agric. 2022, 200, 107210. [Google Scholar] [CrossRef]
- Wang, G.; Laga, H.; Xie, N.; Jia, J.; Tabia, H. The Shape Space of 3D Botanical Tree Models. ACM Trans. Graph. 2018, 37, 1–18. [Google Scholar] [CrossRef]
- Tang, S.; Ao, Z.; Li, Y.; Huang, H.; Xie, L.; Wang, R.; Wang, W.; Guo, R. TreeNet3D: A large scale tree benchmark for 3D tree modeling, carbon storage estimation and tree segmentation. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103903. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Han, X.; Li, Z.; Huang, H.; Kalogerakis, E.; Yu, Y. High-Resolution Shape Completion Using Deep Neural Networks for Global Structure and Local Geometry Inference. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Nazir, D.; Afzal, M.Z.; Pagani, A.; Liwicki, M.; Stricker, D. Contrastive Learning for 3D Point Clouds Classification and Shape Completion. Sensors 2021, 21, 7392. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Qi, C.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning representations and generative models for 3d point clouds. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 40–49. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar] [CrossRef]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. PCN: Point Completion Network. In Proceedings of the International Conference on 3D Vision, Verona, Italy, 5–8 September 2018. [Google Scholar] [CrossRef]
- Sarmad, M.; Lee, H.; Kim, Y. RL-GAN-Net: A Reinforcement Learning Agent Controlled GAN Network for Real-Time Point Cloud Shape Completion. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. PF-Net: Point Fractal Network for 3D Point Cloud Completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhou, H.; Cao, Y.; Chu, W.; Zhu, J.; Lu, T.; Tai, Y.; Wang, C. SeedFormer: Patch Seeds Based Point Cloud Completion with Upsample Transformer. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2022; pp. 416–432. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, H.; He, X.; Wang, W.; Qin, J.; Wei, M. SVDFormer: Complementing Point Cloud via Self-view Augmentation and Self-structure Dual-generator. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 14462–14472. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Y.; Guo, D.; Li, J.; Liu, Q.; Shen, C. PointAttN: You Only Need Attention for Point Cloud Completion. Proc. AAAI Conf. Artif. Intell. 2024, 38, 5472–5480. [Google Scholar] [CrossRef]
- Liu, J.; Li, D.; Fernández, J.E.; Coleman, M.; Hu, W.; Di, N.; Zou, S.; Liu, Y.; Xi, B.; Clothier, B. Variations in water-balance components and carbon stocks in poplar plantations with differing water inputs over a whole rotation: Implications for sustainable forest management under climate change. Agric. For. Meteorol. 2022, 320, 108958. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- Kaehler, A.; Bradski, G. Learning OpenCV 3: Computer Vision in C++ with the OpenCV Library; O’Reilly Media: Sebastopol, CA, USA, 2016. [Google Scholar]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Maindonald, J. Pattern Recognition and Machine Learning. J. Stat. Softw. 2015, 17, 1–3. [Google Scholar] [CrossRef]
- Li, C.L.; Zaheer, M.; Zhang, Y.; Póczos, B.; Salakhutdinov, R. Point Cloud GAN. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. J. Jpn. Soc. Fuzzy Theory Intell. Inform. 2017, 177. [Google Scholar] [CrossRef]
- West, G.B.; Enquist, B.J.; Brown, J.H. A general quantitative theory of forest structure and dynamics. Proc. Natl. Acad. Sci. USA 2009, 106, 7040–7045. [Google Scholar] [CrossRef] [PubMed]
- Seidel, D.; Ehbrecht, M.; Dorji, Y.; Jambay, J.; Ammer, C.; Annighöfer, P. Identifying architectural characteristics that determine tree structural complexity. Trees 2019, 33, 911–919. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman Company: New York, NY, USA, 1977. [Google Scholar]
- Sugihara, G.; May, R.M. Applications of fractals in ecology. Trends Ecol. Evol. 1990, 5, 79–86. [Google Scholar] [CrossRef]
- Seidel, D. A holistic approach to determine tree structural complexity based on laser scanning data and fractal analysis. Ecol. Evol. 2018, 8, 128–134. [Google Scholar] [CrossRef]
- Dorji, Y.; Annighöfer, P.; Ammer, C.; Seidel, D. Response of Beech (Fagus sylvatica L.) Trees to Competition—New Insights from Using Fractal Analysis. Remote Sens. 2019, 11, 2656. [Google Scholar] [CrossRef]
- Dorji, Y.; Isasa, E.; Pierick, K.; Cabral, J.; Tobgay, T.; Annighöfer, P.; Schuldt, B.; Seidel, D. Insights into the relationship between hydraulic safety, hydraulic efficiency and tree structural complexity from terrestrial laser scanning and fractal analysis. Trees 2024, 38, 221–239. [Google Scholar] [CrossRef]
- Dorji, Y.; Schuldt, B.; Neudam, L.; Dorji, R.; Middleby, K.; Isasa, E.; Körber, K.; Ammer, C.; Annighöfer, P.; Seidel, D. Three-dimensional quantification of tree architecture from mobile laser scanning and geometry analysis. Trees 2021, 35, 1385–1398. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W.; Seidel, D. Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sens. 2021, 13, 2773. [Google Scholar] [CrossRef]
- Sarkar, N.; Chaudhuri, B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef]
- Seidel, D.; Annighöfer, P.; Stiers, M.; Zemp, C.D.; Burkardt, K.; Ehbrecht, M.; Willim, K.; Kreft, H.; Hölscher, D.; Ammer, C. How a measure of tree structural complexity relates to architectural benefit-to-cost ratio, light availability, and growth of trees. Ecol. Evol. 2019, 9, 7134–7142. [Google Scholar] [CrossRef] [PubMed]
- Koh, N.; Jayaraman, P.K.; Zheng, J. Truncated octree and its applications. Vis. Comput. 2022, 38, 1167–1179. [Google Scholar] [CrossRef]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graph. Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Wang, P.S.; Liu, Y.; Tong, X. Dual Octree Graph Networks for Learning Adaptive Volumetric Shape Representations. ACM Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Mi, Z.; Luo, Y.; Tao, W. SSRNet: Scalable 3D Surface Reconstruction Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Zhang, Y. The D-FCM partitioned D-BSP tree for massive point cloud data access and rendering. ISPRS J. Photogramm. Remote Sens. 2016, 120, 25–36. [Google Scholar] [CrossRef]
- Roth, T.; Weier, M.; Bauszat, P.; Hinkenjann, A.; Li, Y. Hash-Based Hierarchical Caching and Layered Filtering for Interactive Previews in Global Illumination Rendering. Computers 2020, 9, 17. [Google Scholar] [CrossRef]
- Max, N.; Duff, T.; Mildenhall, B.; Yan, Y. Approximations for the distribution of microflake normals. Vis. Comput. 2018, 34, 443–457. [Google Scholar] [CrossRef]
- Schauer, J.; Nüchter, A. Collision detection between point clouds using an efficient k-d tree implementation. Adv. Eng. Inform. 2015, 29, 440–458. [Google Scholar] [CrossRef]
- Teunissen, J.; Ebert, U. Afivo: A framework for quadtree/octree AMR with shared-memory parallelization and geometric multigrid methods. Comput. Phys. Commun. 2018, 233, 156–166. [Google Scholar] [CrossRef]
- Xu, S.; Gao, B.; Lofquist, A.; Fernando, M.; Hsu, M.C.; Sundar, H.; Ganapathysubramanian, B. An octree-based immersogeometric approach for modeling inertial migration of particles in channels. Comput. Fluids 2021, 214, 104764. [Google Scholar] [CrossRef]
- Que, Z.; Lu, G.; Xu, D. VoxelContext-Net: An Octree based Framework for Point Cloud Compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021. [Google Scholar] [CrossRef]
- Gouda, M.; Mirza, J.; Weiß, J.; Ribeiro Castro, A.; El-Basyouny, K. Octree-based point cloud simulation to assess the readiness of highway infrastructure for autonomous vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 922–940. [Google Scholar] [CrossRef]
- Wang, P.S. OctFormer: Octree-based Transformers for 3D Point Clouds. ACM Trans. Graph. 2023, 42, 1–11. [Google Scholar] [CrossRef]
- Puliti, S.; Lines, E.R.; Müllerová, J.; Frey, J.; Schindler, Z.; Straker, A.; Allen, M.J.; Winiwarter, L.; Rehush, N.; Hristova, H.; et al. Benchmarking tree species classification from proximally-sensed laser scanning data: Introducing the FOR-species20K dataset. arXiv 2024, arXiv:2408.06507. [Google Scholar]




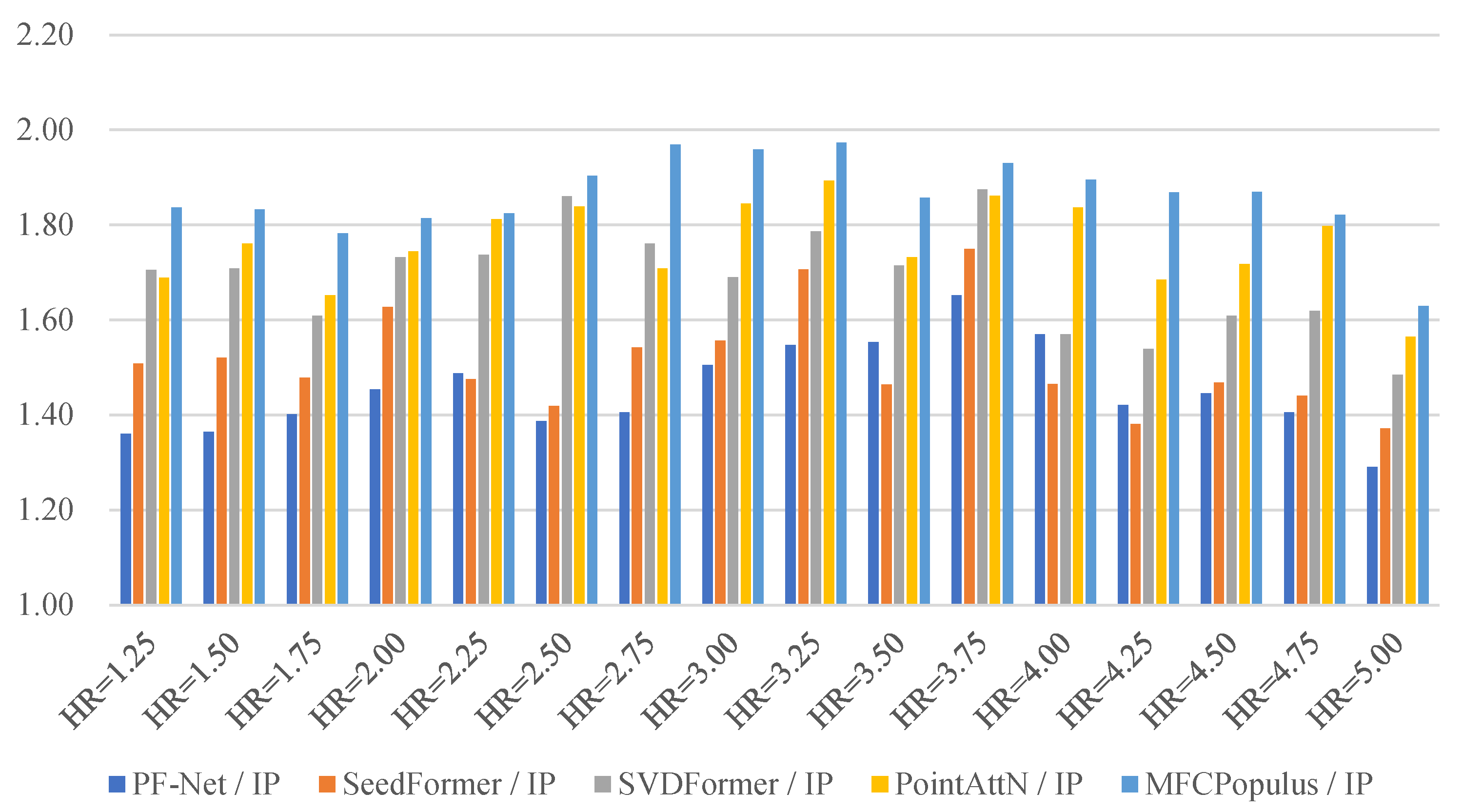
| HR | PF−Net | SeedFormer | SVDFormer | PointAttN | MFCPopulus |
|---|---|---|---|---|---|
| 1.25 | 15.246/4.392 | 14.308/2.496 | 10.556/1.830 | 10.395/1.749 | 9.595/1.197 |
| 1.50 | 11.932/2.879 | 10.060/2.475 | 8.911/1.509 | 9.722/1.107 | 8.238/1.071 |
| 1.75 | 13.251/3.625 | 12.371/2.825 | 9.267/2.448 | 8.302/2.470 | 8.297/2.158 |
| 2.00 | 14.761/3.771 | 11.584/2.243 | 12.344/1.713 | 10.230/1.213 | 9.787/1.308 |
| 2.25 | 10.667/3.770 | 10.134/1.415 | 8.401/1.776 | 6.762/1.002 | 5.953/0.961 |
| 2.50 | 9.810/1.641 | 8.052/1.144 | 9.438/1.221 | 7.516/0.973 | 6.165/0.369 |
| 2.75 | 9.834/2.085 | 10.749/2.229 | 8.699/2.383 | 8.695/1.809 | 7.403/1.097 |
| 3.00 | 10.103/2.368 | 9.870/1.553 | 8.399/1.454 | 9.703/1.462 | 6.221/0.907 |
| 3.25 | 8.902/1.925 | 5.236/2.249 | 5.692/2.031 | 5.972/1.574 | 4.670/1.216 |
| 3.50 | 8.242/2.149 | 6.690/1.802 | 6.824/1.088 | 6.045/1.069 | 5.492/0.687 |
| 3.75 | 9.580/1.801 | 9.531/1.659 | 7.137/1.434 | 12.908/1.816 | 8.472/1.229 |
| 4.00 | 13.139/3.370 | 10.221/2.448 | 7.333/2.603 | 6.871/1.989 | 5.498/1.357 |
| 4.25 | 11.006/3.654 | 11.288/2.505 | 9.118/1.144 | 8.644/0.933 | 6.430/0.769 |
| 4.50 | 15.171/3.483 | 13.961/1.501 | 10.991/2.422 | 10.412/1.062 | 10.229/0.900 |
| 4.75 | 14.645/1.401 | 12.582/1.581 | 12.320/1.597 | 11.601/1.244 | 10.794/1.042 |
| 5.00 | 17.501/3.617 | 13.995/1.680 | 12.721/1.312 | 10.305/1.958 | 11.663/1.077 |
| Mean | 12.112 | 10.665 | 9.259 | 9.005 | 7.807 |
| Methods | Proportion of Crown Point Cloud Volume (%) | ||||
|---|---|---|---|---|---|
| HR = 1.5 | HR = 2.5 | HR = 3.5 | HR = 4.5 | Mean | |
| PF−Net | 66.2 | 77.6 | 62.9 | 56.8 | 65.9 |
| SeedFormer | 79.8 | 73.0 | 73.4 | 74.9 | 75.3 |
| SVDFormer | 87.5 | 80.7 | 76.7 | 79.0 | 81.0 |
| PointAttN | 86.4 | 81.0 | 72.4 | 87.5 | 81.8 |
| MFCPopulus (with out SSF) | 93.1 | 92.0 | 87.3 | 85.6 | 89.5 |
| MFCPopulus (with SSF) | 97.4 | 94.6 | 93.5 | 92.5 | 94.5 |
| Missing Ratio | MFCPopulus/GT | ||||
|---|---|---|---|---|---|
| HR = 1.5 | HR = 2.5 | HR = 3.5 | HR = 4.5 | Mean | |
| 90% | 0.975 | 0.954 | 0.930 | 0.927 | 0.947 |
| 80% | 0.963 | 0.954 | 0.938 | 0.926 | 0.945 |
| 70% | 0.847 | 0.835 | 0.844 | 0.823 | 0.837 |
| 60% | 0.867 | 0.854 | 0.727 | 0.794 | 0.811 |
| 50% | 0.849 | 0.751 | 0.781 | 0.775 | 0.789 |
| 40% | 0.534 | 0.438 | 0.587 | 0.448 | 0.502 |
| 30% | 0.371 | 0.266 | 0.345 | 0.252 | 0.309 |
| Dataset Scale | CD Loss (×1000) | ΔDb | Canopy Coverage Ratio (%) |
|---|---|---|---|
| 100% (1050) | 7.807 | 0.12 | 94.5 |
| 50% (525) | 8.439 | 0.14 | 91.2 |
| 30% (315) | 8.921 | 0.15 | 89.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yang, M.; Xi, B.; Wang, X.; Huang, Q.; Xu, C.; Meng, W. MFCPopulus: A Point Cloud Completion Network Based on Multi-Feature Fusion for the 3D Reconstruction of Individual Populus Tomentosa in Planted Forests. Forests 2025, 16, 635. https://doi.org/10.3390/f16040635
Liu H, Yang M, Xi B, Wang X, Huang Q, Xu C, Meng W. MFCPopulus: A Point Cloud Completion Network Based on Multi-Feature Fusion for the 3D Reconstruction of Individual Populus Tomentosa in Planted Forests. Forests. 2025; 16(4):635. https://doi.org/10.3390/f16040635
Chicago/Turabian StyleLiu, Hao, Meng Yang, Benye Xi, Xin Wang, Qingqing Huang, Cong Xu, and Weiliang Meng. 2025. "MFCPopulus: A Point Cloud Completion Network Based on Multi-Feature Fusion for the 3D Reconstruction of Individual Populus Tomentosa in Planted Forests" Forests 16, no. 4: 635. https://doi.org/10.3390/f16040635
APA StyleLiu, H., Yang, M., Xi, B., Wang, X., Huang, Q., Xu, C., & Meng, W. (2025). MFCPopulus: A Point Cloud Completion Network Based on Multi-Feature Fusion for the 3D Reconstruction of Individual Populus Tomentosa in Planted Forests. Forests, 16(4), 635. https://doi.org/10.3390/f16040635







