Enhanced Climate-Sensitive Crop Planning Models for Multiple Criteria Decision-Making When Managing Jack Pine and Red Pine Forest Types
Abstract
1. Introduction
2. Materials and Methods
2.1. Equation Suites for Predicting End-Product-Based Fibre Attribute Determinates
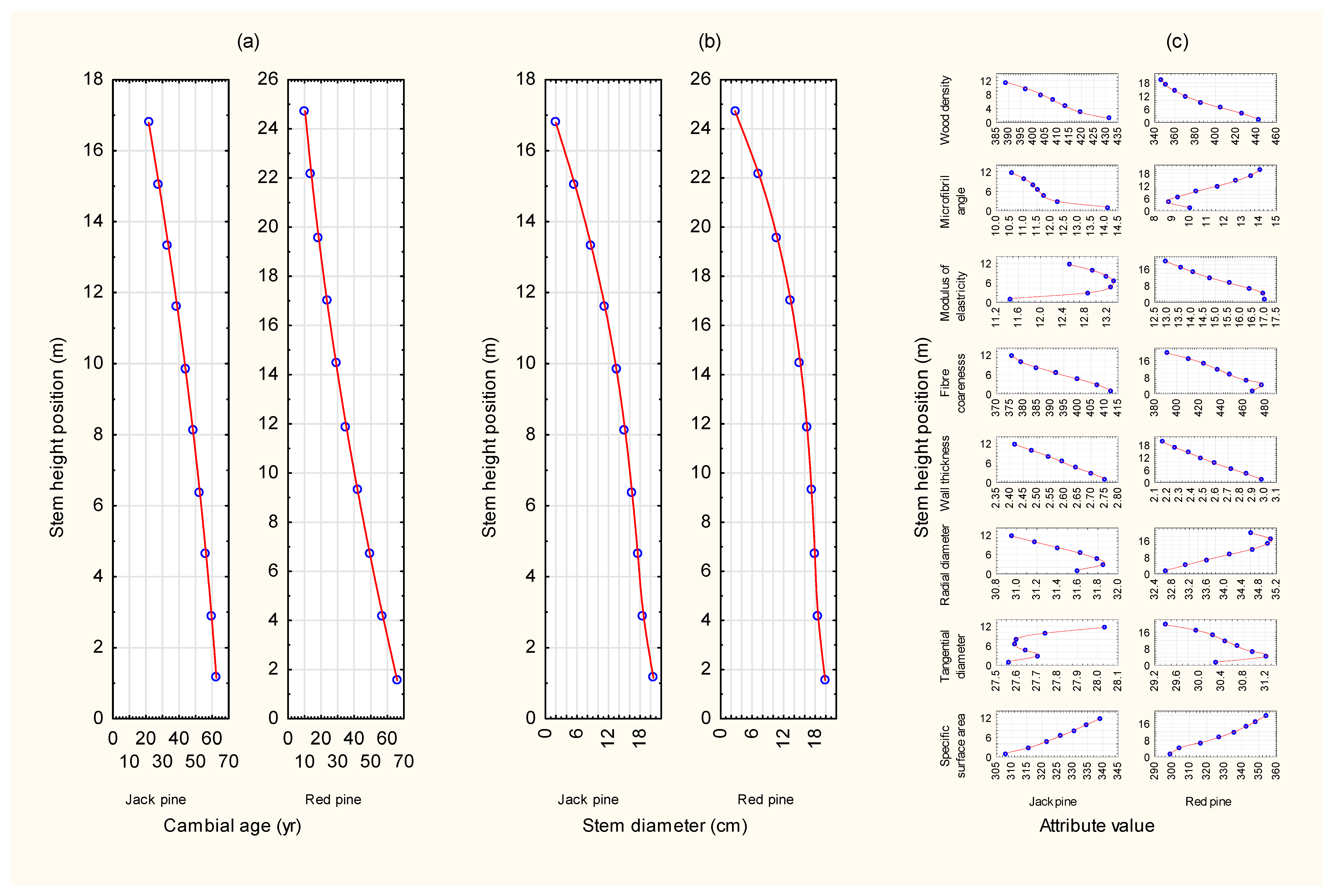
2.2. Development of Whole-Stem Cambial Age Prediction Equations
2.3. Integration of Species-Specific Attribute Equation Suites Within SSDMMs and Resultant Algorithmic Variants
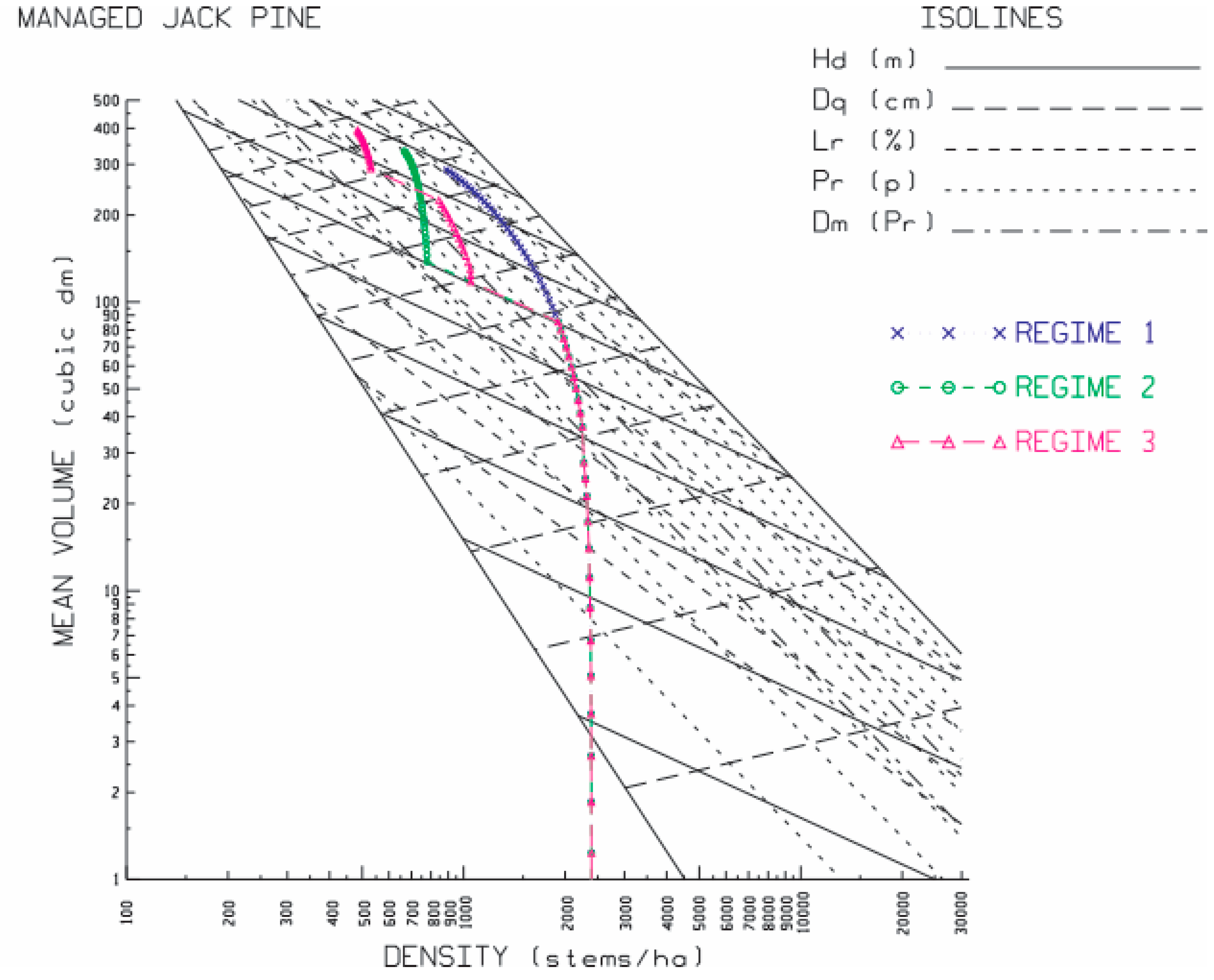
2.4. Exemplifications in Crop Planning Decision-Making
| Parameter (Units) a | Regime 1 | Regime 2 | Regime 3 | |
|---|---|---|---|---|
| (IS) | (IS + 1 CT) | (IS + 2 CTs) | ||
| Planting year | 2024 | 2024 | 2024 | |
| Rotation age (yr): jack pine/red pine | 65/70 | 65/70 | 65/70 | |
| Simulation years: jack pine/red pine | 2024–2089/2094 | 2024–2089/2094 | 2024–2089/2094 | |
| Site index: jack pine/red pine | 18/23 | 18/23 | 18/23 | |
| Initial planting density (stems/ha): jack pine/red pine | 2400/2000 | 2400/2000 | 2400/2000 | |
| Genetic worth (%)/selection age (yr) | Jack pine | 7/20 | 7/20 | 7/20 |
| Red pine | 8/15 | 8/15 | 8/15 | |
| 1st CT: stand age (yr)/basal area removal (%) | Jack pine | - | 30/−35 | 30/−25 |
| Red pine | - | 40/−30 | 40/−20 | |
| 2nd CT: stand age (yr)/basal area removal (%) | Jack pine | - | - | 45/−20 |
| Red pine | - | - | 55/−20 | |
| Operational adjustment factor (%) | 0.01 | 0.01 | 0.01 | |
| Climate change variable settings | ||||
| Scenario (RCP) (Kirkland Lake/Thessalon) | 4.5/4.5 | 4.5/4.5 | 4.5/4.5 | |
| Mean temperature during growing season (°C) (Kirkland Lake/Thessalon) | 2011–2040 | 14.14/14.36 | 14.14/14.36 | 14.14/14.36 |
| 2041–2070 | 14.67/15.05 | 14.67/15.05 | 14.67/15.05 | |
| 2071–2100 | 15.38/15.73 | 15.38/15.73 | 15.38/15.73 | |
| Total precipitation during growing season (mm) (Kirkland Lake/Thessalon) | 2011–2040 | 516.9/586.6 | 516.9/586.6 | 516.9/586.6 |
| 2041–2070 | 579.0/666.8 | 579.0/666.8 | 579.0/666.8 | |
| 2071–2100 | 576.8/635.7 | 576.8/635.7 | 576.8/635.7 | |
| Merchantable Specifications | ||||
| Pulp log length (m) | 2.59 | 2.59 | 2.59 | |
| Pulp log minimum diameter (inside bark; cm) | 10 | 10 | 10 | |
| Sawlog length (m) | 5.03 | 5.03 | 5.03 | |
| Sawlog minimum diameter (inside bark; cm) | 14 | 14 | 14 | |
| Merchantable top diameter (inside bark cm) | 10 | 10 | 10 | |
| Minimum utility pole length (m) | 12.2 | 12.2 | 12.2 | |
| Minimum pole upper diameter (inside bark; cm) | 19.9 | 19.9 | 19.9 | |
| Minimum pole diameter class (outside bark; cm) | 34 | 34 | 34 | |
| Product degrade (%) | 10 | 10 | 10 | |
| Minimum Operability Targets | ||||
| Piece-size (merchantable number of stems per cubic metre of merchantable volume) | 10 | 10 | 10 | |
| Merchantable volumetric stand yield (m3/ha) | 200 | 200 | 200 | |
| Economic Parameters | ||||
| Interest rate (%) | 3 | 3 | 3 | |
| Discount rate (%) | 4 | 4 | 4 | |
| Mechanical site preparation (CAN/ha) | 800 | 800 | 800 | |
| Planting (CAN/seedling) | 1 | 1 | 1 | |
| Costs of 1st CT: variable (CAN/m3 of merchantable volume removed)/fixed (CAN/ha) | - | 75/500 | 75/500 | |
| Costs of 2nd CT: variable (CAN/m3 of merchantable volume removed)/fixed (CAN/ha) | - | - | 65/500 | |
| Rotational harvesting + stumpage + renewal + transportation + manufacturing variable costs (CAN/m3 of merchantable volume harvested) | Jack pine | 75 | 65 | 55 |
| Red pine | 75 | 65 | 55 | |
| Current (2024) net pole value (CAN K/pole) | 0.4 | 0.4 | 0.4 | |
3. Results
3.1. Species-Specific Cambial Age and Whole-Stem Attribute Equation Suites and Their Integration Within Climate-Sensitive SSDMMs
3.2. Crop Planning Exemplifications
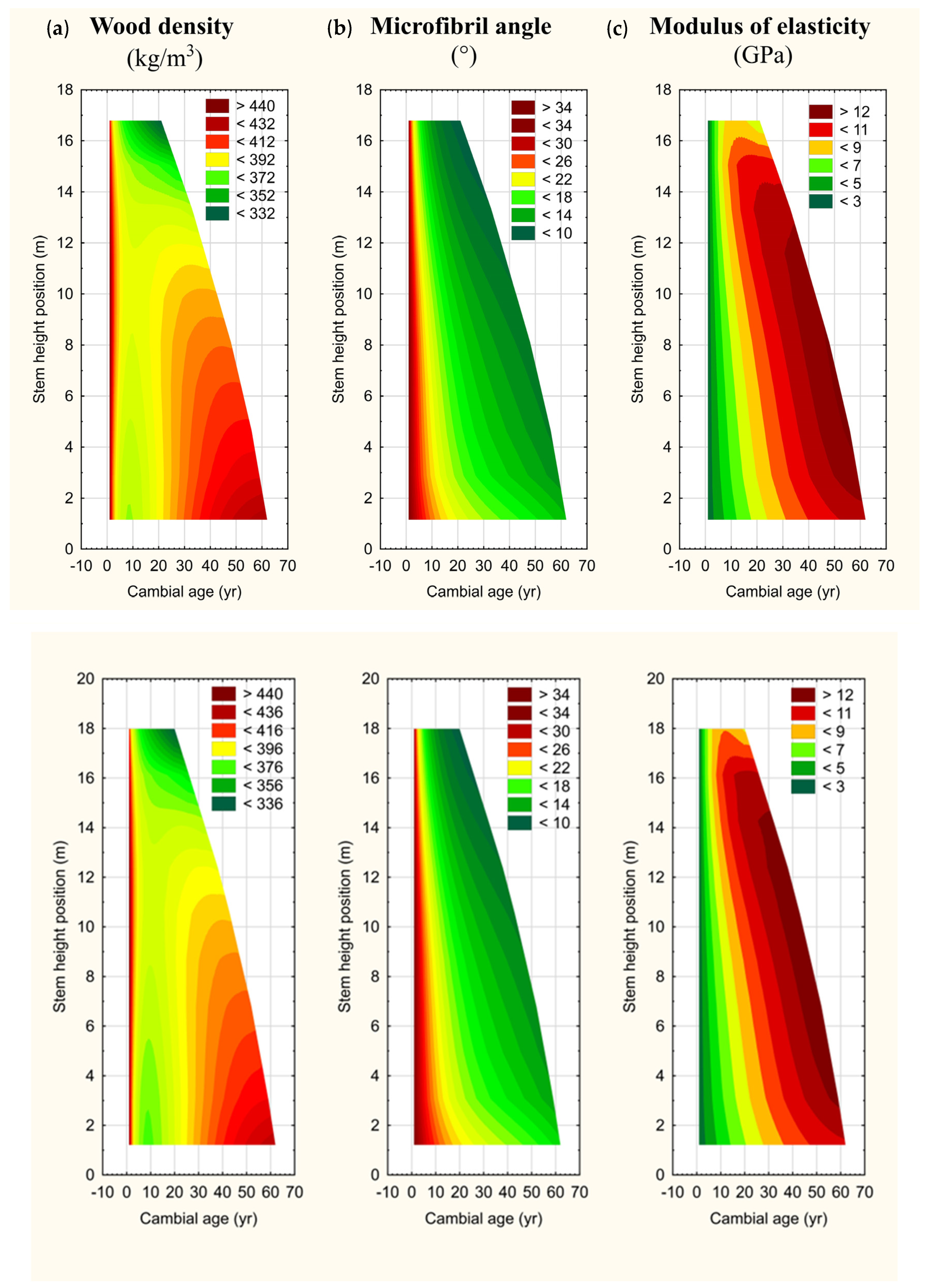
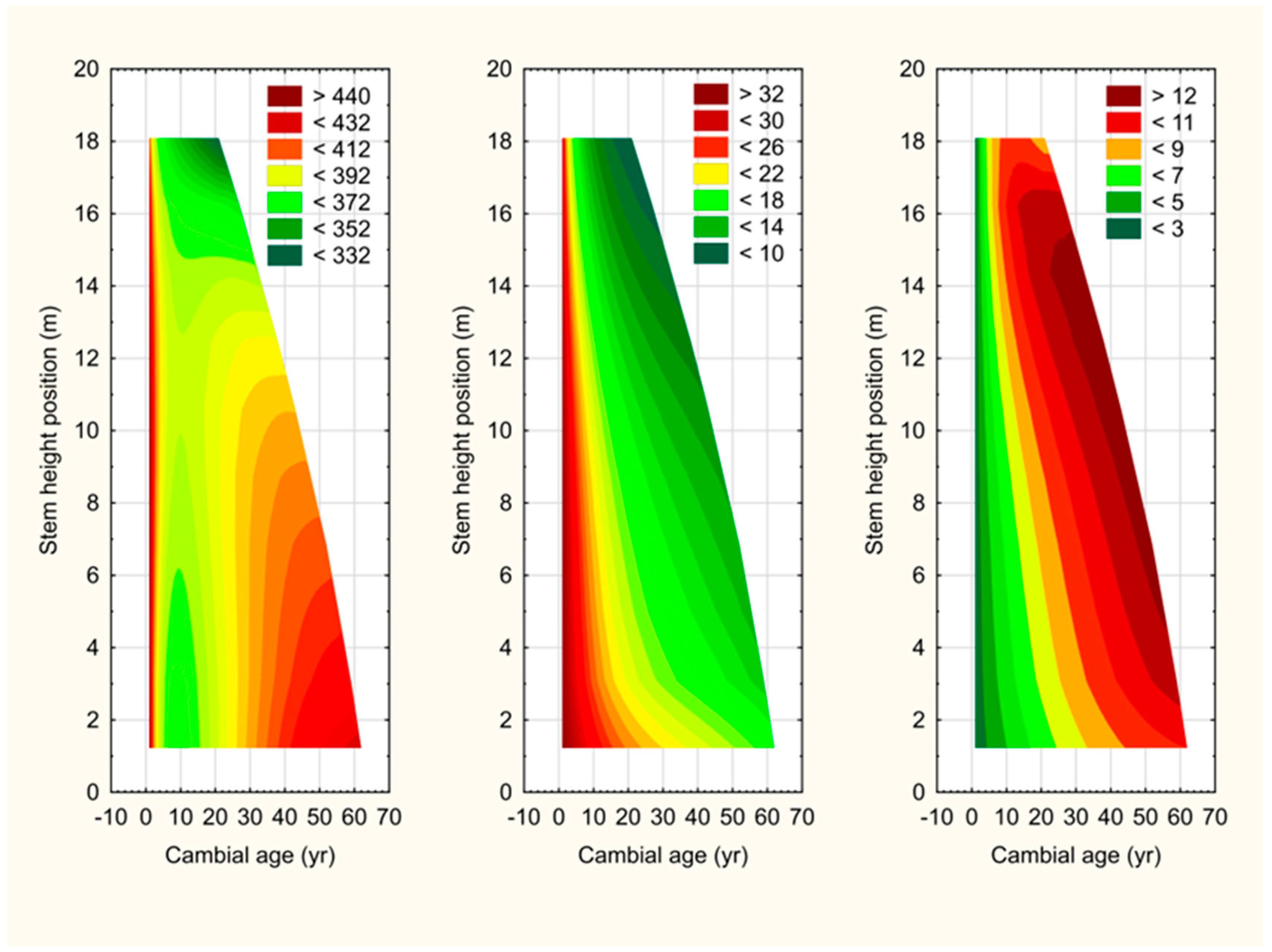
3.3. Whole-Stem Attribute Developmental Maps
4. Discussion
4.1. End-Product Potential (EPP) of HWPs: Concepts, Correlates, and Forecasting
4.2. Tree-Level Fibre Attribute Mapping and Individual Tree HWP Inferences
4.3. Advancing Whole-Tree Attribute Modelling and Evolving Research Opportunities
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walker, W.S.; Gorelik, S.R.; Cook-Patton, S.C.; Baccini, A.; Farina, M.K.; Solvik, K.K.; Ellis, P.W.; Sanderman, J.; Houghton, R.A.; Leavitt, S.M.; et al. The global potential for increased storage of carbon on land. Proc. Natl. Acad. Sci. USA 2002, 119, e2111312119. [Google Scholar]
- Defo, M.; Duchesne, I.; Stewart, J. A Review of the Current State of Wood Quality Modelling and Decision Support Systems in Canada; Information Report FI-X-012; Natural Resources Canada, Canadian Forest Service: Ottawa, ON, Canada, 2016. [Google Scholar]
- Metsaranta, J.M.; Fortin, M.; White, J.C.; Sattler, D.; Kurz, W.A.; Penner, M.; Edwards, J.; Hays-Byl, W.; Comeau, R.; Roy, V. Climate sensitive growth and yield models in Canadian forestry: Challenges and opportunities. For. Chron. 2024, 100, 88–106. [Google Scholar] [CrossRef]
- Ikonen, V.-P.; Peltola, H.; Wilhelmsson, L.; Kilpeläinen, A.; Väisänen, H.; Nuutinen, T.; Kellomäki, S. Modelling the distribution of wood properties along the stems of Scots pine (Pinus sylvestris L.) and Norway spruce (Picea abies (L.) Karst.) as affected by silvicultural management. For. Ecol. Manag. 2008, 256, 1356–1371. [Google Scholar] [CrossRef]
- Newton, P.F. Wood quality attribute models and their utility when integrated into density management decision-support systems for boreal conifers. For. Ecol. Manag. 2019, 438, 267–284. [Google Scholar] [CrossRef]
- Newton, P.F. Development of a climate-sensitive structural stand density management model for red pine. Forests 2022, 13, 1010. [Google Scholar] [CrossRef]
- Newton, P.F. Development of spatiotemporal whole-stem models for estimating end-product-based fibre attribute determinates for jack pine and red pine. Forests 2023, 14, 2211. [Google Scholar] [CrossRef]
- Newton, P.F. Development of an integrated decision-support model for density management within jack pine stand-types. Ecol. Model. 2009, 220, 3301–3324. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Koubaa, A. Softwoods of Eastern Canada: Their Silvics, Characteristics, Manufacturing and End-Uses; Special Publication SP-526E; FPInnovations: Quebec City, QC, Canada, 2008. [Google Scholar]
- Newton, P.F. Quantifying size-dependent developmental trajectories of commercial-relevant fibre attributes within maturing black spruce plantations employing hierarchical linear models. For. Ecol. Manag. 2016, 381, 1–16. [Google Scholar] [CrossRef][Green Version]
- Forrester, D.I. Linking forest growth with stand structure: Tree size inequality, tree growth or resource partitioning and the asymmetry of competition. For. Ecol. Manag. 2019, 447, 139–157. [Google Scholar] [CrossRef]
- Barbour, R.J.; Marshall, D.D.; Lowell, E.C. Managing for wood quality. In Compatible Forest Management; Monserud, R.A., Haynes, R.W., Johnson, A.C., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 299–336. [Google Scholar] [CrossRef]
- Kang, K.-Y.; Zhang, S.Y.; Mansfield, S.D. The effects of initial spacing on wood density, fibre and pulp properties in jack pine (Pinus banksiana Lamb.). Holzforschung 2004, 58, 455–463. [Google Scholar] [CrossRef]
- Watt, M.S.; Zoric, B.; Kimberley, M.O.; Harrington, J. Influence of stocking on radial and longitudinal variation in modulus of elasticity, microfibril angle, and density in a 24-year-old Pinus radiata thinning trial. Can. J. For. Res. 2011, 41, 1422–1431. [Google Scholar] [CrossRef]
- Hoerl, A.E. Fitting curves to data. In Chemical Business Handbook; Perry, J.H., Ed.; McGraw-Hill: New York, NY, USA, 1954; pp. 55–77. [Google Scholar]
- Reynolds, M.R., Jr. Estimating the error in model predictions. For. Sci. 1984, 30, 454–469. [Google Scholar]
- Gribko, L.S.; Wiant, H.V., Jr. A SAS template program for the accuracy test. Compiler 1992, 10, 48–51. [Google Scholar]
- Raudenbush, S.W.; Bryk, A.S.; Cheong, Y.F.; Congdon, R. HLM 8 for Windows; Scientific Software International, Inc.: Skokie, IL, USA, 2019. [Google Scholar]
- Neter, J.; Wasserman, W.; Kutner, M.H. Applied Linear Statistical Models, 3rd ed.; Irwin: Boston, MA, USA, 1990. [Google Scholar]
- NLGA (National Lumber Grades Authority). Special Products Standard for Machine Graded Lumber; NLGA: Surrey, BC, Canada, 2013. [Google Scholar]
- Sharma, M.; Subedi, N.; TerMikaelian, M.; Parton, J. Modeling climatic effects on stand height/site index of plantation-grown jack pine and black spruce trees. For. Sci. 2016, 61, 25–34. [Google Scholar] [CrossRef]
- Ontario Ministry of the Environment, Conservation and Parks. Ontario Provincial Climate Change Impact Assessment. Technical Report No. CL32819. 2023. Available online: https://www.publications.gov.on.ca/CL32819 (accessed on 1 October 2024).
- Sharma, M.; Parton, J. Climatic effects on site productivity of red pine plantations. For. Sci. 2018, 64, 544–554. [Google Scholar] [CrossRef]
- Tong, Q.; Zhang, S.Y.; Thompson, M. Evaluation of growth response, stand value and financial return for pre-commercially thinned jack pine stands in Northwestern Ontario. For. Ecol. Manag. 2005, 209, 225–235. [Google Scholar] [CrossRef]
- Newton, P.F. Systematic review of yield responses of four North American conifers to forest tree improvement practices. For. Ecol. Manag. 2023, 172, 29–51. [Google Scholar] [CrossRef]
- Newton, P.F. Genetic worth effect models for boreal conifers and their utility when integrated into density management decision-support systems. Open J. For. 2015, 5, 105–115. [Google Scholar] [CrossRef]
- Tong, Q.; Zhang, S.Y. Development of lumber recovery correction models for plantation-grown Pinus banksiana trees. Scand. J. For. Res. 2008, 24, 417–424. [Google Scholar] [CrossRef]
- Environment and Climate Change Canada. Second Generation Canadian Earth System Model Online. 2020. Available online: https://www.canada.ca/en/environment-climate-change/services/climate-change/science-research-data/modeling-projections-analysis/centre-modelling-analysis/models/second-generation-earth-system-model.html (accessed on 25 March 2025).
- McKenney, D.; Hutchinson, M.F.; Papadopol, P.; Lawrence, K.; Pedlar, J.; Campbell, K.; Milewska, E.; Hopkinson, R.F.; Price, D.; Owen, T. Customized spatial climate models for North America. Bull. Am. Meteorol. Soc. 2011, 92, 1611–1622. [Google Scholar] [CrossRef]
- Newton, P.F.; Amponsah, I.G. Comparative evaluation of five height-diameter models developed for black spruce and jack pine stand-types in terms of goodness-of-fit, lack-of-fit and predictive ability. For. Ecol. Manag. 2007, 247, 149–166. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis. For. Sci. 2009, 55, 268–282. [Google Scholar] [CrossRef]
- Sharma, M. Incorporating stand density effects in modeling the taper of red pine plantations. Can. J. For. Res. 2020, 50, 751–759. [Google Scholar] [CrossRef]
- OMNRF (Ontario Ministry of Natural Resources and Forestry). Forest Management Guide to Silviculture in the Great Lakes-St. Lawrence and Boreal Forests of Ontario. 2015. Available online: https://www.ontario.ca/page/forest-management-guide-silviculture-great-lakes-st-lawrence-and-boreal-forests-ontario#section-12 (accessed on 8 January 2025).
- Hekkala, A.M.; Jönsson, M.; Kärvemo, S.; Strengbom, J.; Sjögren, J. Habitat heterogeneity is a good predictor of boreal forest biodiversity. Ecol. Ind. 2023, 148, 110069. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Conditions for the start and spread of crown fire. Can. J. For. Res. 1977, 7, 23–34. [Google Scholar] [CrossRef]
- Liu, C.M.; Jiang, Z.H.; Zhang, S.Y. Tree-level models for predicting lumber volume recovery of black spruce using selected tree characteristics. For. Sci. 2006, 56, 694–703. [Google Scholar] [CrossRef]
- NLGA (National Lumber Grades Authority. Standard Grading Rules for Canadian Lumber; NLGA: Surrey, BC, Canada, 2022. [Google Scholar]
- Defo, M. SilviScan-3-A Revolutionary Technology for High-Speed Wood Microstructure and Properties Analysis. Midis de al Foresterie; University of Quebec at Abitibi-Témiscamingue: Témiscamingue, QC, Canada, 22 April 2008. [Google Scholar]
- Downes, G.M.; Harrington, J.J.; Drew, D.M.; Lausberg, M.; Muyambo, P.; Watt, D.; Lee, D.J. A Comparison of Radial Wood Property Variation on Pinus radiata between an IML PD-400 ’Resi’ Instrument and Increment Cores Analysed by SilviScan. Forests 2022, 13, 751. [Google Scholar] [CrossRef]
- Wang, X. Acoustic measurements on trees and logs: A review and analysis. Wood Sci. Technol. 2013, 475, 965–975. [Google Scholar] [CrossRef]
- Legg, M.; Bradley, S. Measurement of stiffness of standing trees and felled logs using acoustics: A review. J. Acoust. Soc. Am. 2016, 139, 588–604. [Google Scholar] [CrossRef]
- Schimleck, L.; Dahlen, J.; Apiolaza, L.A.; Downes, G.; Emms, G.; Evans, R.; Moore, J.; Pâques, L.; Van den Bulcke, J.; Wang, X. Non-destructive evaluation techniques and what they tell us about wood property variation. Forests 2019, 10, 728. [Google Scholar] [CrossRef]
- Wang, X. Recent Advances in Nondestructive Evaluation of Wood: In-Forest Wood Quality Assessments. Forests 2021, 12, 949. [Google Scholar] [CrossRef]
- Drew, D.M.; Downes, G.M.; Seifert, T.; Eckes-Shepard, A.; Achim, A. A Review of Progress and Applications in Wood Quality Modelling. Curr. For. Rep. 2022, 8, 317–332. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J.; Woods, M.; Newton, P.; Penner, M.; Wang, J.; Stinson, A.; Bell, F.W. Ontario’s forest growth and yield modelling program: Advances resulting from the Forestry Research Partnership. For. Chron. 2008, 84, 694–703. [Google Scholar] [CrossRef]
- Burdon, R.D.; Kibblewhite, R.P.; Walker, J.C.F.; Megraw, R.A.; Evans, R.; Cown, D.J. Juvenile versus mature wood: A new concept, orthogonal to corewood versus outerwood, with special reference to Pinus radiata and P. taeda. For. Sci. 2004, 50, 399–415. [Google Scholar] [CrossRef]
- Defo, M.; Goodison, A.; Nelson, U. A method to map within-tree distribution of fibre properties using SilviScan-3 data. For. Chron. 2009, 85, 409–414. [Google Scholar] [CrossRef]
- Schimleck, L.; Antony, F.; Mora, C.; Dahlen, J. Comparison of whole-tree wood property maps for 13- and 22-year-old loblolly pine. Forests 2018, 9, 287. [Google Scholar] [CrossRef]
- Mora, C.R.; Schimleck, L.R. Determination of within-tree variation of Pinus taeda wood properties by near infrared spectroscopy. Part 2: Whole-tree wood property maps. Appita J. 2009, 62, 232–238. [Google Scholar]
- Eberhardt, T.L.; So, C.-L.; Leduc, D.J. Wood property maps showing wood variability in mature longleaf pine: Does getting old change juvenile tendencies. Wood Fibre Sci. 2019, 51, 193–208. [Google Scholar] [CrossRef]
- Schimleck, L.; Dahlen, J.; Mora, C.; Antony, F.; Eberhardt, T.L.; Onakpoma, I. Maps depicting the within-tree wood property variation of some North American conifers: A review. Can. J. For. Res. 2025, 55, 1–14. [Google Scholar] [CrossRef]
- Mäkinen, H.; Jaakkola, T.; Piispanen, R.; Saranpää, P. Predicting wood and tracheid properties of Norway spruce. For. Ecol. Manag. 2007, 241, 175–188. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, L.; Lei, P.; Xiang, W.; Yan, W. Variations of wood basic density with tree age and social classes in the axial direction within Pinus massoniana stems in Southern China. Ann. For. Sci. 2014, 71, 505–516. [Google Scholar] [CrossRef]
- Schimleck, L.; Antony, F.; Mora, C.; Dahlen, J. Whole-tree tracheid property maps for loblolly pine at different ages. Wood Sci. Technol. 2020, 54, 683–701. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. I. The controls of cambial and apical activity in Pinus resinosa Ait. Can. J. Bot. 1953, 31, 471–513. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. II. Specific increments and their relation to the quantity and activity of growth in Pinus resinosa Ait. Can. J. Bot. 1957, 35, 527–572. [Google Scholar] [CrossRef]
- Donaldson, L. Microfibril angle: Measurement, variation and relationships—A review. IAWA J. 2008, 29, 345–386. [Google Scholar] [CrossRef]
- Dahlen, J.; Antony, F.; Schimleck, L.; Daniels, R. Relationships between static mechanical properties and SilviScan measured wood properties in loblolly pine. For. Prod. J. 2018, 68, 37–42. [Google Scholar] [CrossRef]
- Ying, L.; Kretschmann, D.E.; Bendtsen, B.A. Longitudinal shrinkage in fast-grown loblolly-pine plantation wood. For. Prod. J. 1994, 44, 58–62. [Google Scholar]
- Dahlen, J.; Auty, D.; Eberhardt, T.L. Models for predicting specific gravity and ring width for loblolly pine from intensively managed plantations, and implications for wood utilization. Forests 2018, 9, 292. [Google Scholar] [CrossRef]
- Dahlen, J.; Nabavi, M.; Auty, D.; Schimleck, L.; Eberhardt, T.L. Models for predicting the within-tree and regional variation of tracheid length and width for plantation loblolly pine. Forestry 2021, 94, 127–140. [Google Scholar] [CrossRef]
- Emmett, B. Increasing the value of our forest. For. Chron. 2006, 82, 3–4. [Google Scholar] [CrossRef]
- Nilsson, S. Transition of the Canadian forest sector. In The Future Use of Nordic Forests-A Global Perspective; Westholm, E., Lindahl, K.B., Kraxner, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 125–144. [Google Scholar] [CrossRef]
- Brownell, P.H.; Stratton, A.D.H.; Nord-Larsen, T.; Nielsen, A.T.; Schuck, A.; Zudin, S. Including Carbon Accounting in Learning Tools for Sustainable Forest Management. SSRN 2022, 4113099. [Google Scholar] [CrossRef]
- Li, L.; Wei, X.; Zhao, J.; Hayes, D.; Daigneault, A.; Weiskittel, A.; Kizha, A.R.; O’Neill, S.R. Technological advancement expands carbon storage in harvested wood products in Maine, USA. Biomass Bioenergy 2022, 161, 106457. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change). Agriculture, Forestry, and Other Land Uses (AFOLU). In Climate Change 2022: Mitigation of Climate Change, the Working Group III Contribution; Chapter 7, Sixth Assessment Report; IPCC: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Dursky, J. The single tree-based stand simulator SILVA: Construction, application and evaluation. For. Ecol. Manag. 2002, 162, 3–21. [Google Scholar] [CrossRef]
- Hynynen, J.; Ahtikoski, A.; Siitonen, J.; Sievanen, R.; Liski, J. Applying the MOTTI simulator to analyse the effects of alternative management schedules on timber and non-timber production. For. Ecol. Manag. 2005, 207, 5–18. [Google Scholar] [CrossRef]
- Kotze, H.; Malan, F. Further progress in the development of prediction models for growth and wood quality of plantation-grown Pinus patula sawtimber in South Africa. In Proceedings of the Forest Growth and Timber Quality: Crown Models and Simulation Methods for Sustainable Forest Management Conference, Portland, OR, USA, 7–10 August 2007; General Technical Report, PNW-GTR-791. Dykstra, D.P., Monserud, R.A., Eds.; Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2007; pp. 113–123. [Google Scholar]
- Gardiner, B.; Leban, J.-M.; Auty, D.; Simpson, H. Models for predicting wood density of British-grown Sitka spruce. Forestry 2011, 84, 119–132. [Google Scholar] [CrossRef]
- Di Lucca, C.M. TASS/SYLVER/TIPSY: Systems for predicting the impact of silvicultural practices on yield, lumber value, economic return and other benefits. In Proceedings of the Stand Density Management Planning and Implementation Conference, Edmonton, AB, Canada, 6–7 November 1997; Barnsey, C., Ed.; Clear Lake Publishing Ltd.: Edmonton, AB, Canada, 1999; pp. 7–16. [Google Scholar]




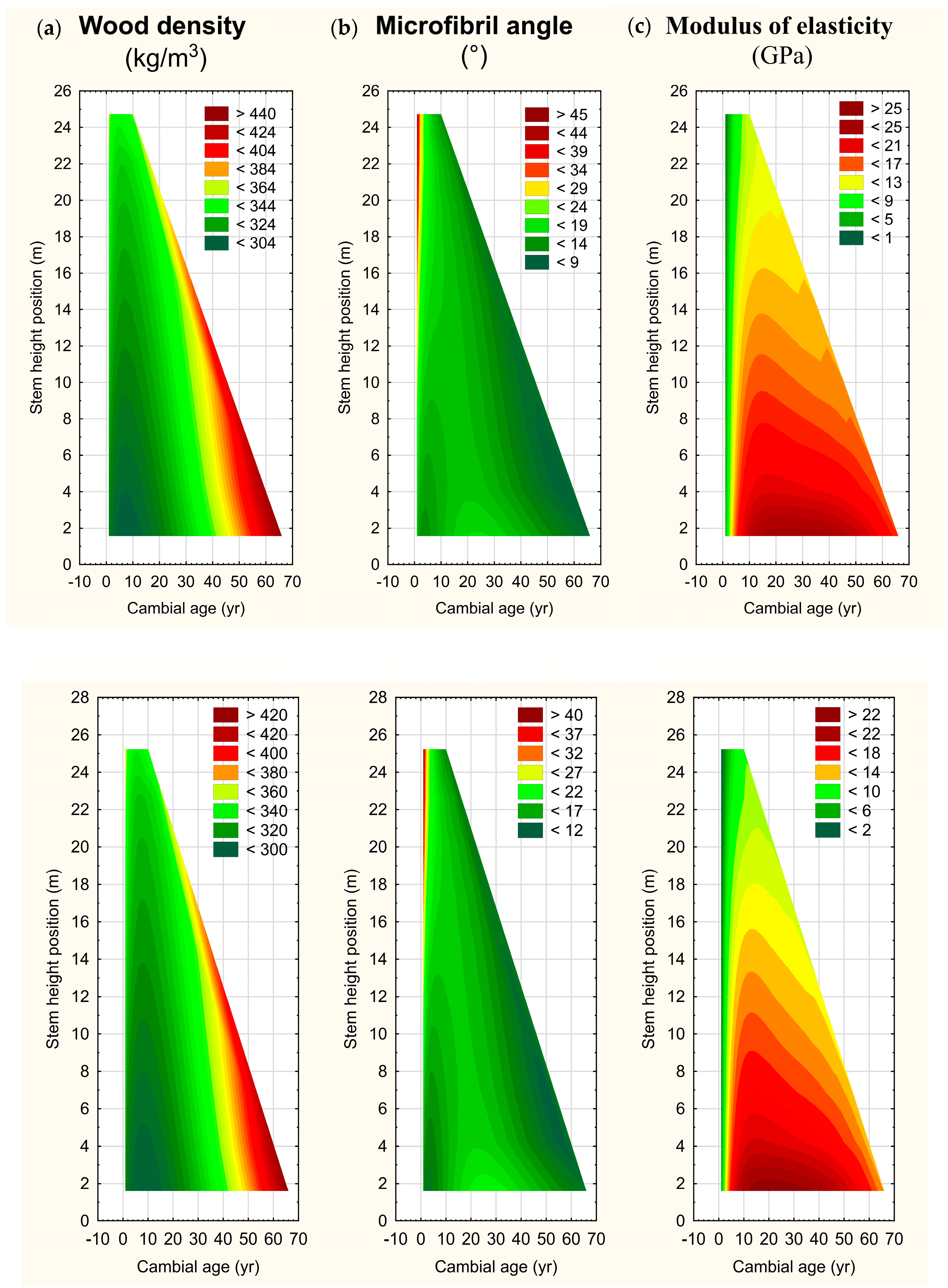
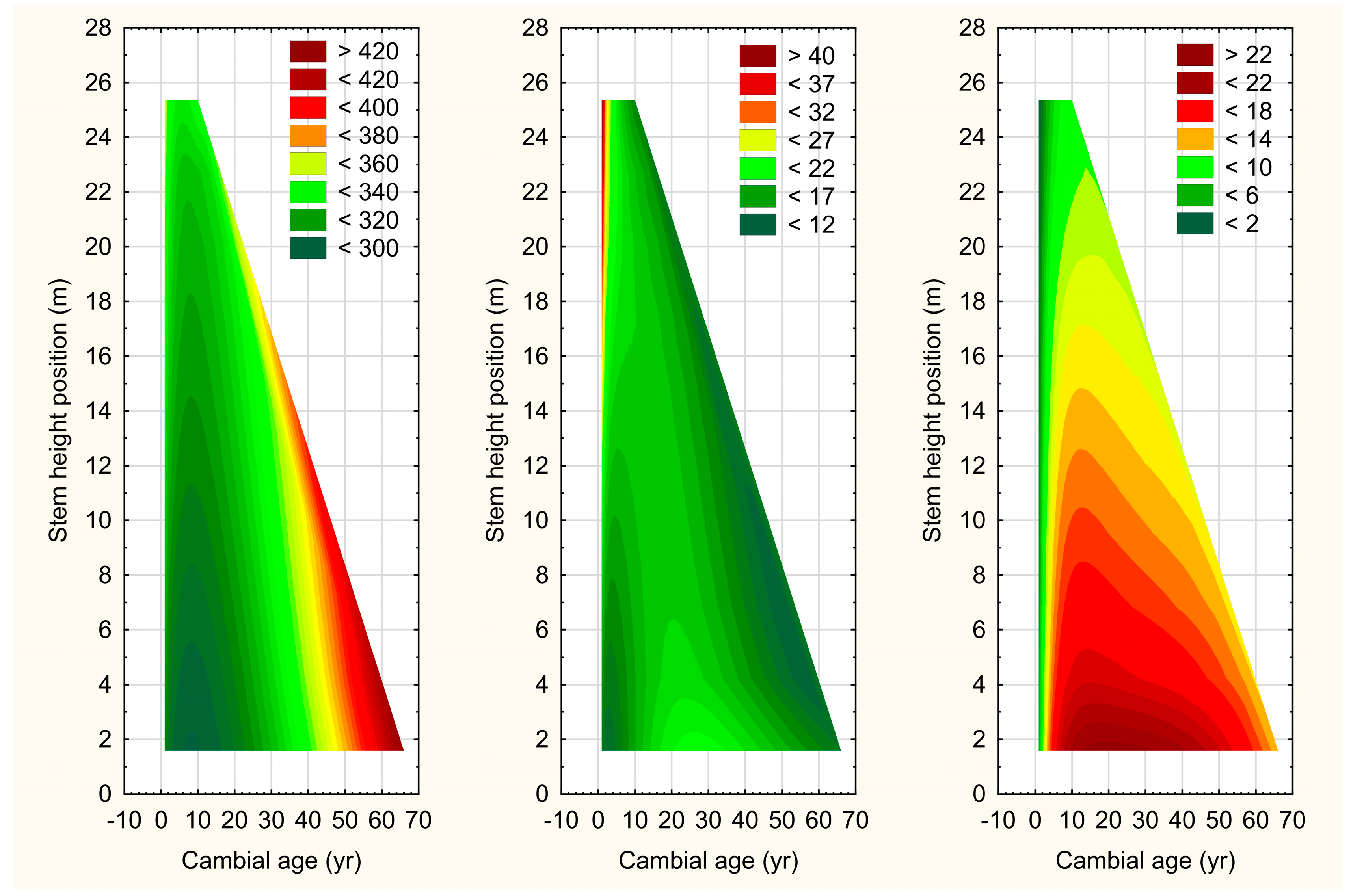
| Parameter or | Variable | Parameter Estimate | |
|---|---|---|---|
| Statistic | Jack Pine | Red Pine | |
| - | −1.277857 | 13.914946 | |
| - | - | ||
| - | 0.135927 | ||
| 1.009610 | 0.772643 | ||
| 0.851887 | −10.766666 | ||
| - | - | ||
| - | - | ||
| −0.034858 | 0.102577 | ||
| −0.267061 | 0.347923 | ||
| 0.001043 | - | ||
| 0.006480 | 0.002460 | ||
| 0.000961 | −0.005243 | ||
| SEE a (yr) | 1.053 | 1.368 | |
| I2 b | 0.995 | 0.996 | |
| Species; Crop Plan [Db (cm); Ht (m)] a | Relative Height (%/100) | Stem Height (m) [H] | Stem Diameter (cm) [D] b | Cambial Age c (yr) [A] | Attribute | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wd d (kg/m3) | Ma d (°) | Me d (GPa) | Co d (µg/m) | Wt d (µm) | Dr d (µm) | Dt d (µm) | Sa d (m2/kg) | |||||
| Jack pine; | 0.07 | 1.2 | 20.5 | 63 | 431.1 | 14.1 | 11.5 | 412.4 | 2.75 | 31.6 | 27.6 | 307.9 |
| Regime 1 | 0.16 | 2.9 | 18.7 | 60 | 419.5 | 12.3 | 12.8 | 407.1 | 2.70 | 31.9 | 27.7 | 315.8 |
| [22; 17.7] | 0.26 | 4.6 | 17.6 | 56 | 413.3 | 11.7 | 13.3 | 399.7 | 2.64 | 31.8 | 27.6 | 321.4 |
| 0.36 | 6.4 | 16.5 | 53 | 408.3 | 11.5 | 13.3 | 392.1 | 2.59 | 31.6 | 27.6 | 326.2 | |
| 0.46 | 8.1 | 15.2 | 48 | 403.2 | 11.3 | 13.2 | 384.9 | 2.54 | 31.4 | 27.6 | 330.5 | |
| 0.56 | 9.8 | 13.5 | 44 | 397.0 | 11.0 | 12.9 | 379.1 | 2.48 | 31.2 | 27.7 | 334.7 | |
| 0.65 | 11.6 | 11.4 | 39 | 388.8 | 10.6 | 12.5 | 375.8 | 2.42 | 31.0 | 28.0 | 338.9 | |
| 0.75 | 13.3 | 8.7 | 34 | 377.5 | 10.0 | 11.8 | 376.5 | 2.36 | 30.8 | 28.5 | 343.5 | |
| 0.85 | 15.1 | 5.6 | 28 | 360.5 | 9.5 | 10.4 | 384.6 | 2.29 | 30.6 | 29.4 | 348.9 | |
| 0.95 | 16.8 | 2.0 | 22 | 326.8 | 9.3 | 6.8 | 420.0 | 2.19 | 30.3 | 31.3 | 356.1 | |
| Jack pine; | 0.06 | 1.2 | 22.3 | 63 | 431.2 | 15.3 | 10.8 | 416.0 | 2.77 | 32.0 | 27.6 | 304.7 |
| Regime 2 | 0.16 | 3.1 | 20.3 | 59 | 420.0 | 13.2 | 12.3 | 409.6 | 2.71 | 32.2 | 27.7 | 312.8 |
| [24; 18.9] | 0.26 | 4.9 | 19.1 | 56 | 414.2 | 12.6 | 12.8 | 401.5 | 2.66 | 32.2 | 27.7 | 318.4 |
| 0.36 | 6.8 | 18.0 | 52 | 409.6 | 12.3 | 13.0 | 393.1 | 2.60 | 32.0 | 27.6 | 323.2 | |
| 0.46 | 8.7 | 16.6 | 48 | 404.8 | 12.1 | 13.0 | 385.1 | 2.55 | 31.7 | 27.6 | 327.5 | |
| 0.56 | 10.5 | 14.8 | 43 | 399.1 | 11.7 | 12.9 | 378.2 | 2.49 | 31.5 | 27.7 | 331.8 | |
| 0.65 | 12.4 | 12.5 | 38 | 391.4 | 11.1 | 12.7 | 373.5 | 2.43 | 31.2 | 28.0 | 336.3 | |
| 0.75 | 14.3 | 9.6 | 33 | 380.7 | 10.3 | 12.3 | 372.1 | 2.37 | 31.0 | 28.4 | 341.4 | |
| 0.85 | 16.1 | 6.1 | 27 | 364.5 | 9.6 | 11.1 | 376.9 | 2.29 | 30.7 | 29.1 | 347.9 | |
| 0.95 | 18.0 | 2.2 | 21 | 332.4 | 9.3 | 7.7 | 405.7 | 2.19 | 30.3 | 30.7 | 356.3 | |
| Jack pine; | 0.06 | 1.22 | 24.13 | 63 | 430.6 | 16.8 | 10.0 | 419.9 | 2.78 | 32.4 | 27.7 | 301.1 |
| Regime 3 | 0.16 | 3.09 | 21.95 | 59 | 420.0 | 14.3 | 11.6 | 412.6 | 2.72 | 32.6 | 27.8 | 309.4 |
| [26; 19.1] | 0.26 | 4.97 | 20.67 | 56 | 414.3 | 13.6 | 12.2 | 404.2 | 2.67 | 32.6 | 27.7 | 315.0 |
| 0.36 | 6.84 | 19.44 | 52 | 409.9 | 13.2 | 12.5 | 395.5 | 2.62 | 32.4 | 27.7 | 319.8 | |
| 0.46 | 8.72 | 17.93 | 48 | 405.3 | 12.8 | 12.6 | 386.9 | 2.56 | 32.1 | 27.7 | 324.3 | |
| 0.56 | 10.59 | 15.97 | 43 | 399.7 | 12.2 | 12.7 | 379.2 | 2.50 | 31.9 | 27.7 | 328.9 | |
| 0.65 | 12.47 | 13.46 | 38 | 392.2 | 11.4 | 12.8 | 373.4 | 2.44 | 31.6 | 27.9 | 334.0 | |
| 0.75 | 14.34 | 10.35 | 33 | 381.6 | 10.5 | 12.6 | 370.8 | 2.37 | 31.3 | 28.3 | 339.9 | |
| 0.85 | 16.22 | 6.63 | 27 | 365.2 | 9.5 | 11.7 | 374.4 | 2.29 | 31.0 | 28.9 | 347.3 | |
| 0.95 | 18.09 | 2.36 | 21 | 331.8 | 9.0 | 8.1 | 402.8 | 2.18 | 30.5 | 30.6 | 357.0 | |
| Red pine; | 0.06 | 1.6 | 19.9 | 66 | 442.1 | 10.0 | 17.0 | 468.0 | 2.98 | 32.6 | 30.3 | 298.4 |
| Regime 1 | 0.16 | 4.1 | 18.6 | 57 | 425.2 | 8.8 | 17.0 | 476.6 | 2.85 | 33.1 | 31.2 | 304.1 |
| [22; 26.0] | 0.26 | 6.7 | 17.9 | 50 | 404.0 | 9.3 | 16.4 | 462.0 | 2.72 | 33.6 | 31.0 | 315.9 |
| 0.36 | 9.3 | 17.3 | 42 | 385.3 | 10.4 | 15.6 | 448.0 | 2.59 | 34.1 | 30.7 | 326.6 | |
| 0.46 | 11.9 | 16.5 | 35 | 370.3 | 11.6 | 14.8 | 436.2 | 2.48 | 34.6 | 30.5 | 335.2 | |
| 0.55 | 14.4 | 15.2 | 29 | 358.9 | 12.7 | 14.1 | 424.6 | 2.37 | 35.0 | 30.3 | 342.1 | |
| 0.65 | 17.0 | 13.4 | 24 | 350.8 | 13.5 | 13.5 | 410.2 | 2.26 | 35.1 | 29.9 | 348.0 | |
| 0.75 | 19.6 | 10.8 | 19 | 346.0 | 14.0 | 13.0 | 390.8 | 2.16 | 34.6 | 29.4 | 353.6 | |
| 0.85 | 22.1 | 7.3 | 14 | 345.4 | 14.2 | 12.3 | 364.2 | 2.06 | 33.5 | 28.6 | 359.6 | |
| 0.95 | 24.7 | 2.8 | 10 | 355.7 | 13.4 | 11.8 | 327.8 | 1.96 | 31.1 | 27.3 | 366.5 | |
| Red pine; | 0.06 | 1.6 | 25.3 | 66 | 434.2 | 13.1 | 13.9 | 480.5 | 2.96 | 33.6 | 30.9 | 295.9 |
| Regime 2 | 0.16 | 4.2 | 23.6 | 57 | 415.6 | 11.1 | 14.4 | 489.1 | 2.84 | 34.2 | 31.7 | 301.8 |
| [28; 26.6] | 0.26 | 6.8 | 22.8 | 49 | 394.1 | 11.6 | 14.2 | 474.3 | 2.72 | 34.7 | 31.4 | 313.7 |
| 0.36 | 9.5 | 22.1 | 42 | 375.8 | 12.6 | 13.7 | 460.2 | 2.60 | 35.3 | 31.1 | 324.3 | |
| 0.46 | 12.1 | 21.0 | 35 | 361.2 | 13.8 | 13.1 | 447.9 | 2.49 | 35.7 | 30.9 | 332.8 | |
| 0.55 | 14.7 | 19.4 | 29 | 350.2 | 14.8 | 12.5 | 435.2 | 2.38 | 36.0 | 30.6 | 339.5 | |
| 0.65 | 17.3 | 17.1 | 23 | 342.2 | 15.5 | 11.9 | 419.2 | 2.28 | 36.0 | 30.3 | 345.2 | |
| 0.75 | 20.0 | 13.8 | 18 | 337.3 | 15.8 | 11.3 | 397.5 | 2.17 | 35.4 | 29.7 | 350.5 | |
| 0.85 | 22.6 | 9.3 | 14 | 336.4 | 15.7 | 10.6 | 368.6 | 2.07 | 34.0 | 28.8 | 356.0 | |
| 0.95 | 25.2 | 3.5 | 11 | 346.2 | 14.4 | 10.0 | 330.0 | 1.97 | 31.4 | 27.6 | 362.0 | |
| Red pine; | 0.06 | 1.6 | 27.1 | 66 | 432.8 | 14.1 | 13.2 | 485.1 | 2.95 | 34.0 | 31.1 | 295.0 |
| Regime 3 | 0.16 | 4.2 | 25.3 | 57 | 413.6 | 11.9 | 13.8 | 493.6 | 2.84 | 34.5 | 31.9 | 301.1 |
| [30; 26.7] | 0.26 | 6.9 | 24.5 | 49 | 391.9 | 12.3 | 13.7 | 478.6 | 2.72 | 35.1 | 31.6 | 313.0 |
| 0.36 | 9.5 | 23.6 | 42 | 373.6 | 13.3 | 13.2 | 464.2 | 2.60 | 35.6 | 31.3 | 323.6 | |
| 0.46 | 12.2 | 22.5 | 35 | 359.1 | 14.5 | 12.7 | 451.7 | 2.49 | 36.1 | 31.0 | 332.0 | |
| 0.55 | 14.8 | 20.8 | 29 | 348.0 | 15.5 | 12.1 | 438.6 | 2.39 | 36.3 | 30.7 | 338.7 | |
| 0.65 | 17.4 | 18.3 | 23 | 340.0 | 16.1 | 11.5 | 422.1 | 2.28 | 36.2 | 30.4 | 344.3 | |
| 0.75 | 20.1 | 14.8 | 18 | 334.9 | 16.4 | 10.9 | 399.7 | 2.18 | 35.6 | 29.8 | 349.5 | |
| 0.85 | 22.7 | 10.0 | 14 | 333.7 | 16.1 | 10.1 | 370.0 | 2.08 | 34.2 | 28.9 | 354.8 | |
| 0.95 | 25.3 | 3.8 | 11 | 343.2 | 14.6 | 9.5 | 330.7 | 1.97 | 31.5 | 27.6 | 360.6 | |
| Index a | Species | |||||
|---|---|---|---|---|---|---|
| (Unit) | Jack Pine | Red Pine | ||||
| IS | IS + 1 CT | IS + 2 CTs | IS | IS + 1 CT | IS + 2 CTs | |
| Dq (cm) | 21.4 | 23.1 | 25.2 | 22.7 | 29.0 | 30.8 |
| G (m2/ha) | 32.1 | 27.8 | 23.4 | 63.4 | 44.4 | 40.7 |
| Vm(t) (m3/ha) | - | 50 | 35 + 35 | - | 100 | 66 + 85 |
| Vm(r) (m3/ha) | 244 | 213 | 183 | 703 | 500 | 460 |
| Vm (m3/ha) | 244 | 263 | 253 | 703 | 600 | 611 |
| Vt(t) (m3/ha) | - | 55 | 76 | - | 104 | 156 |
| Vt(r) (m3/ha) | 256 | 223 | 191 | 722 | 513 | 472 |
| Vt (m3/ha) | 256 | 278 | 267 | 722 | 617 | 628 |
| Vt(ca) (m3/ha) | 198 | 54 | 78 | 106 | 80 | 80 |
| Nb (stems/ha) | 891 | 662 | 478 | 1570 | 675 | 548 |
| Nct (stems/ha) | - | 1122 | 851 + 311 | - | 1050 | 753 + 415 |
| Nca (stems/ha) | 1509 | 616 | 760 | 430 | 275 | 284 |
| (m3/ha/yr) | 3.9 | 4.2 | 4.1 | 10.3 | 8.8 | 9.0 |
| (m3/ha/yr) | 3.0 | 0.8 | 1.2 | 1.5 | 1.1 | 1.1 |
| SS (m/m) | 84 | 77 | 76 | 111 | 90 | 91 |
| RLEV | - | +2 | −5 | - | +33 | +67 |
| Index b | Crop Plan | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Unit) | IS | IS + 1 CT | IS + 2 CTs | |||||||||
| R @ 65 | CT1 @ 30 | R @ 65 | CT1 @ 30 | CT2 @ 45 | R @ 65 | |||||||
| SW | NSW | SW | NSW | SW | NSW | SW | NSW | SW | NSW | SW | NSW | |
| Wd (kg/m3) | 413.4 | 357.5 | 402.1 | 364 | 413.4 | 356.7 | 401.3 | 361 | 409.5 | 364.8 | 414.4 | 360 |
| Ma (°) | 12 | 9.7 | 15.3 | 12 | 12 | 9.7 | 14.8 | 11.7 | 13 | 10.5 | 12.6 | 9.7 |
| Me (GPa) | 12.5 | 9.2 | 10.2 | 8.1 | 12.5 | 9.2 | 10.4 | 7.9 | 11.6 | 9 | 12.2 | 9.8 |
| Co (µg/m) | 399.1 | 402.7 | 378.4 | 398.2 | 399.2 | 403.1 | 378.2 | 405.5 | 387.7 | 403.6 | 401 | 400.2 |
| Wt (µm) | 2.6 | 2.3 | 2.5 | 2.3 | 2.6 | 2.3 | 2.5 | 2.4 | 2.6 | 2.4 | 2.6 | 2.3 |
| Dr (µm) | 31.4 | 30.1 | 32.6 | 31 | 31.4 | 30.1 | 32.4 | 31 | 31.5 | 30.5 | 31.6 | 30.4 |
| Dt (µm) | 27.6 | 29.3 | 28 | 29.9 | 27.6 | 29.3 | 28 | 30.2 | 27.8 | 29.7 | 27.7 | 29.2 |
| Sa (m2/kg) | 320.8 | 346.4 | 323 | 342.9 | 320.8 | 346.4 | 324.9 | 343.5 | 326.1 | 344.5 | 318.6 | 345.7 |
| Grade | L | - | L | - | L | - | L | - | L | - | L | - |
| Percent of volume production (m3/ha) | 78 | 22 | 8 | 92 | 80 | 20 | 5 | 95 | 58 | 42 | 79 | 21 |
| Index b | Crop Plan | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Unit) | IS | IS + 1 CT | IS + 2 CTs | |||||||||||
| R @ 70 | CT1 @ 40 | R @ 70 | CT1 @ 40 | CT2 @ 55 | R @ 70 | |||||||||
| SW | NSW | SW | NSW | SW | NSW | SW | NSW | SW | NSW | P | SW | NSW | ||
| Wd (kg/m3) | 422.7 | 448 | 362.2 | - | 331.5 | 423.2 | 354.8 | - | 331.5 | - | 340.2 | 376.5 | 424.3 | 352.8 |
| Ma (°) | 9.3 | 8.1 | 12.6 | - | 14.2 | 11.9 | 14.3 | - | 14.2 | - | 16.6 | 15.4 | 12.6 | 14.6 |
| Me (GPa) | 17 | 20.2 | 13.8 | - | 21.6 | 14.4 | 12.1 | - | 21.6 | - | 14.7 | 11.9 | 13.9 | 11.8 |
| Co (µg/m) | 469.8 | 461.8 | 404.2 | - | 402.4 | 483.3 | 415.5 | - | 402.4 | - | 385.7 | 469.5 | 486.8 | 414.3 |
| Wt (µm) | 2.8 | 3 | 2.3 | - | 2.1 | 2.9 | 2.3 | - | 2.1 | - | 2.2 | 2.6 | 2.9 | 2.3 |
| Dr (µm) | 33.1 | 32 | 34 | - | 40.6 | 33.9 | 34.8 | - | 40.6 | - | 36.5 | 36 | 34.1 | 34.9 |
| Dt (µm) | 31 | 30.1 | 29.6 | - | 29.6 | 31.3 | 30 | - | 29.6 | - | 28.9 | 31.4 | 31.4 | 30 |
| Sa (m2/kg) | 307.3 | 301.6 | 345.1 | - | 389.2 | 300.3 | 340.9 | - | 389.2 | - | 375.1 | 319.4 | 298.5 | 340.9 |
| Lumber grade | L | M | - | - | - | L | - | - | - | - | - | - | L | - |
| Percent of volume production (m3/ha) | 9 | 32 | 59 | - | 100 | 34 | 66 | - | 100 | - | 100 | 9 | 30 | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, P.F. Enhanced Climate-Sensitive Crop Planning Models for Multiple Criteria Decision-Making When Managing Jack Pine and Red Pine Forest Types. Forests 2025, 16, 610. https://doi.org/10.3390/f16040610
Newton PF. Enhanced Climate-Sensitive Crop Planning Models for Multiple Criteria Decision-Making When Managing Jack Pine and Red Pine Forest Types. Forests. 2025; 16(4):610. https://doi.org/10.3390/f16040610
Chicago/Turabian StyleNewton, Peter F. 2025. "Enhanced Climate-Sensitive Crop Planning Models for Multiple Criteria Decision-Making When Managing Jack Pine and Red Pine Forest Types" Forests 16, no. 4: 610. https://doi.org/10.3390/f16040610
APA StyleNewton, P. F. (2025). Enhanced Climate-Sensitive Crop Planning Models for Multiple Criteria Decision-Making When Managing Jack Pine and Red Pine Forest Types. Forests, 16(4), 610. https://doi.org/10.3390/f16040610






