Comparative Analysis of Drought-Driven Water-Use Strategies in Mangroves and Forests

Abstract

Mangroves grow in high-salinity environments with low soil water potential (Ψ_s), where high light intensity and strong winds increase the vapor pressure deficit (VPD), causing physiological drought and high transpiration demand (Δw), which limits carbon dioxide (carbon gain) for photosynthesis. This study explored how mangroves optimize their carbon-gain-to-water-loss ratio (water-use strategies) to maximize carbon gain during both dry and rainy seasons. We also calculated the relative costs of key leaf traits and compared them with those of terrestrial forests under the carbon gain optimization model. The results revealed that (1) with increasing Δw, terrestrial forests primarily adjusted leaf hydraulic conductance (K_leaf), while mangroves altered the difference in water potential (ΔΨ); (2) as Ψ_s decreased, π_tlp of both terrestrial forests and mangroves increased; (3) terrestrial forests developed a more balanced distribution of leaf trait costs between osmotic pressure (46.7 ± 0.2%) and stomata (43.3 ± 1.2%), whereas mangroves had the highest cost in osmotic pressure (49.04 ± 0.03%) and the lowest cost in stomata (11.08 ± 3.00%) during the rainy season; and (4) although mangroves showed differences in trait values between dry and rainy seasons, their responses to drought stress remained consistent. These findings provided new theoretical insights into how mangroves maintain high carbon gain and water-use efficiency under extreme environmental conditions, which is important to improve mangrove conservation efforts and contribute to climate mitigation policies.

1. Introduction

Mangroves predominantly inhabit tropical and subtropical intertidal zones [1,2,3,4,5,6]. Despite abundant water availability, the low osmotic potential and extremely negative water potential in high-salinity soils make water absorption unfavorable and lead to the occurrence of physiological drought [7]. Environmental stressors, such as high light, high temperature, strong winds, tide inundation, and high VPD, are predicted to increase transpiration demand [8,9], exacerbating water loss and stress. In response, mangroves typically extract water by maintaining extremely low xylem water potentials, high xylem tension, and elevated cellular osmotic pressure [10], thereby conserving water through structural and physiological adaptations such as enhanced water-use efficiency [11,12] and reduced transpiration rates [13,14]. This conservative water-use strategy enables mangroves to maintain high productivity [1,11,15] and greater capacity for carbon sequestration than adjacent terrestrial forests, thereby enhancing their role in carbon storage [16,17,18,19].

Under high VPD and salinity stress, plants typically close their stomata to limit water loss [13,20,21,22], thereby conserving water but simultaneously reducing CO₂ uptake and net photosynthesis [23,24,25,26,27]. Despite such constraints, mangroves maintain relatively high photosynthetic capacity [17,28,29] by employing advanced salt management—such as root ultrafiltration, salt glands, ion sequestration in vacuoles, and the production of compatible solutes for osmotic regulation [10,30,31]—while maintaining xylem water transport under low water potential by improving water-use efficiency, adjusting leaf structure, and regulating osmotic balance, thereby sustaining cell turgor [32,33,34,35,36,37]. However, the water and salt balance of mangroves remains sensitive to seasonal fluctuations and climate change, underscoring the importance of these adaptations for ensuring resilience in extreme environments [38,39,40,41]. In global climate models, these adaptive mechanisms can represent mangrove resilience in the face of climate change. By incorporating these physiological adaptations into carbon sequestration models, we can more accurately predict their carbon absorption capacity under future climate conditions.

In the unique environment of mangroves, leaves serve as crucial organs for gas exchange and energy conversion [42]. Leaf water potential (Ψ_leaf), transpiration rate (E), stomatal conductance (g_sat), leaf hydraulic conductance (K_leaf), and CO₂ assimilation rate (A_sat) are closely interconnected and significantly affected by osmotic pressure [43,44]. The turgor loss point (π_tlp) has been identified as a reliable predictor of species’ capacities for osmotic adjustment [45,46,47]. Plants with lower π_tlp values typically exhibit stronger drought tolerance [48], enabling them to preserve turgor pressure and endure prolonged dry periods. The variation in π_tlp also accounts for species distribution, where species with lower π_tlp values are adapted to arid or saline environments [49]. Collectively, these traits, which balance leaf-level water uptake, transport, and loss, are key adaptations to high-salinity intertidal environments and facilitate efficient carbon gain [2,50]. Under both high vapor pressure deficit (VPD) and elevated salinity, mangroves need to optimize their leaf water-use strategies to maximize carbon gain and enhance survival [51,52].

The optimization hypothesis provided a critical theoretical framework for understanding the coordinated mechanisms among traits, suggesting that plants were subject to natural selection to achieve maximal net carbon gain [53,54]. The pioneering model by Cowan and Farquhar [55] suggested that the function of stomata is to minimize water loss while maintaining photosynthesis. Later, Farquhar et al. [56] proposed the FvCB model, which clarifies how photosynthesis functions under water and CO₂ constraints. Building on the optimization hypothesis, numerous studies have further advanced photosynthetic modeling [57], particularly regarding nitrogen allocation [58] and leaf carbon gain and associated costs [53,59,60]. Collectively, these studies highlight the central role of the optimization hypothesis in plant photosynthesis and physiological adaptation, providing valuable insights into how plants cope with various environmental stresses and optimize resource use.

Given the above context, this study hypothesized that under the dual stress of high VPD and salinity, mangrove leaves would optimize water-use traits to maximize carbon gain and enhance adaptability. Our research investigated mangrove species in subtropical China during both the dry and rainy seasons, assessing net photosynthetic rates, gas exchange, and hydraulic traits. Although these mangrove species differ in their salt-exclusion strategies, the existing evidence suggests that such distinctions did not fundamentally alter their water relations [50]. Here, we applied a carbon-gain optimization model to explore how osmotic regulation, leaf water potential control, and stomatal optimization enable mangroves to balance water use and carbon uptake, thereby attaining maximal carbon gain. We further quantified the relative costs of key leaf functional traits and compared them with those of terrestrial forests. From the perspective of maximizing carbon gain, this study aimed to elucidate the water management and carbon acquisition strategies of mangroves in extreme environments, providing new insights and theoretical foundations for the conservation and management of mangrove ecosystems in response to climate change.

2. Materials and Methods

2.1. Study Area and Materials

In this study, we focused on four key functional traits of mangroves that were closely related to water stress responses. The goal of examining these traits was to gain deeper insight into how mangroves optimize their physiological functioning under elevated VPD (denoted as Δw) and high salinity (denoted as Ψ_s), ultimately maximizing carbon gain. We assessed these traits across different seasonal conditions through fieldwork in several major mangrove conservation areas in Hainan Province: the Dongzhaigang Mangrove Reserve (Haikou), the Xinying Mangrove Reserve (Danzhou), the Qinglangang Mangrove Reserve (Wenchang), and along the Linchun River and the Yuya salt field (Sanya). Measurements were taken on dominant mangrove species during both the dry season (March) and the rainy season (August). Species were selected based on their ecological significance, abundance, and functional roles in maintaining ecosystem stability in mangroves. We prioritized species that contribute significantly to primary productivity, exhibit strong adaptations to varying salinity and hydrological conditions, or play key roles in nutrient cycling and habitat structure. Data were also collected from additional mangrove species exhibiting the same traits (see

Table 1. Details of the mangrove species sampled for optimization model.

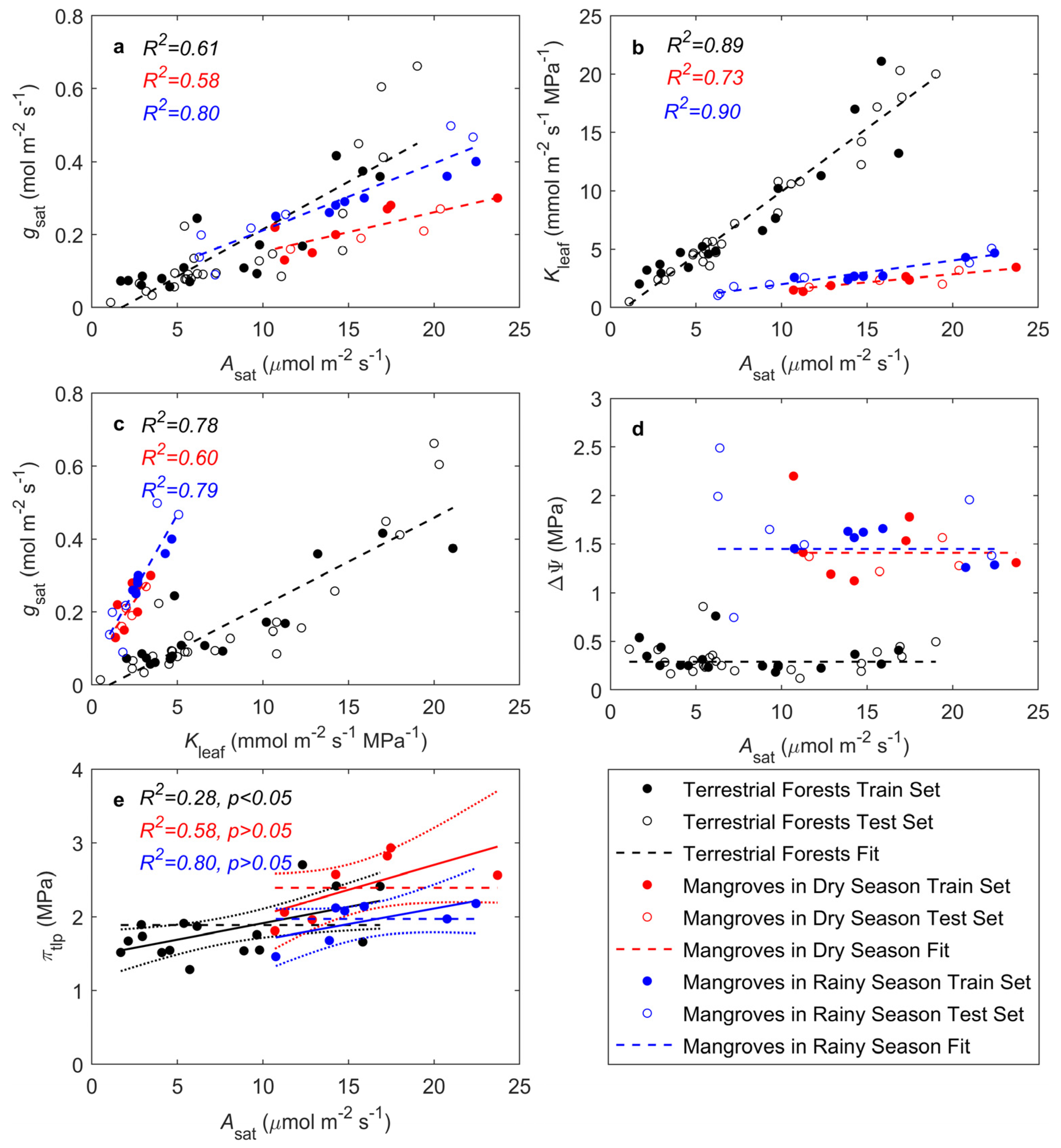
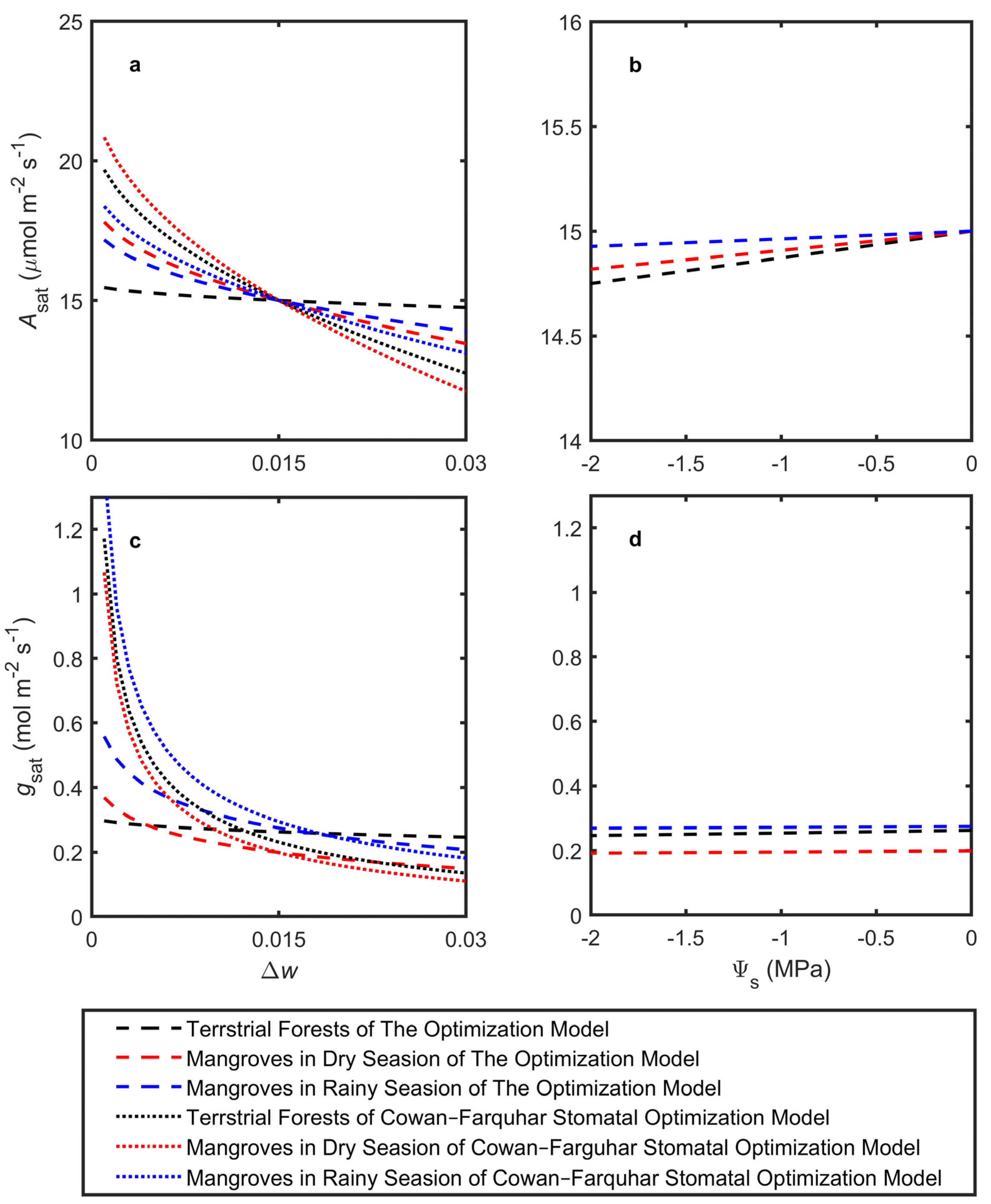
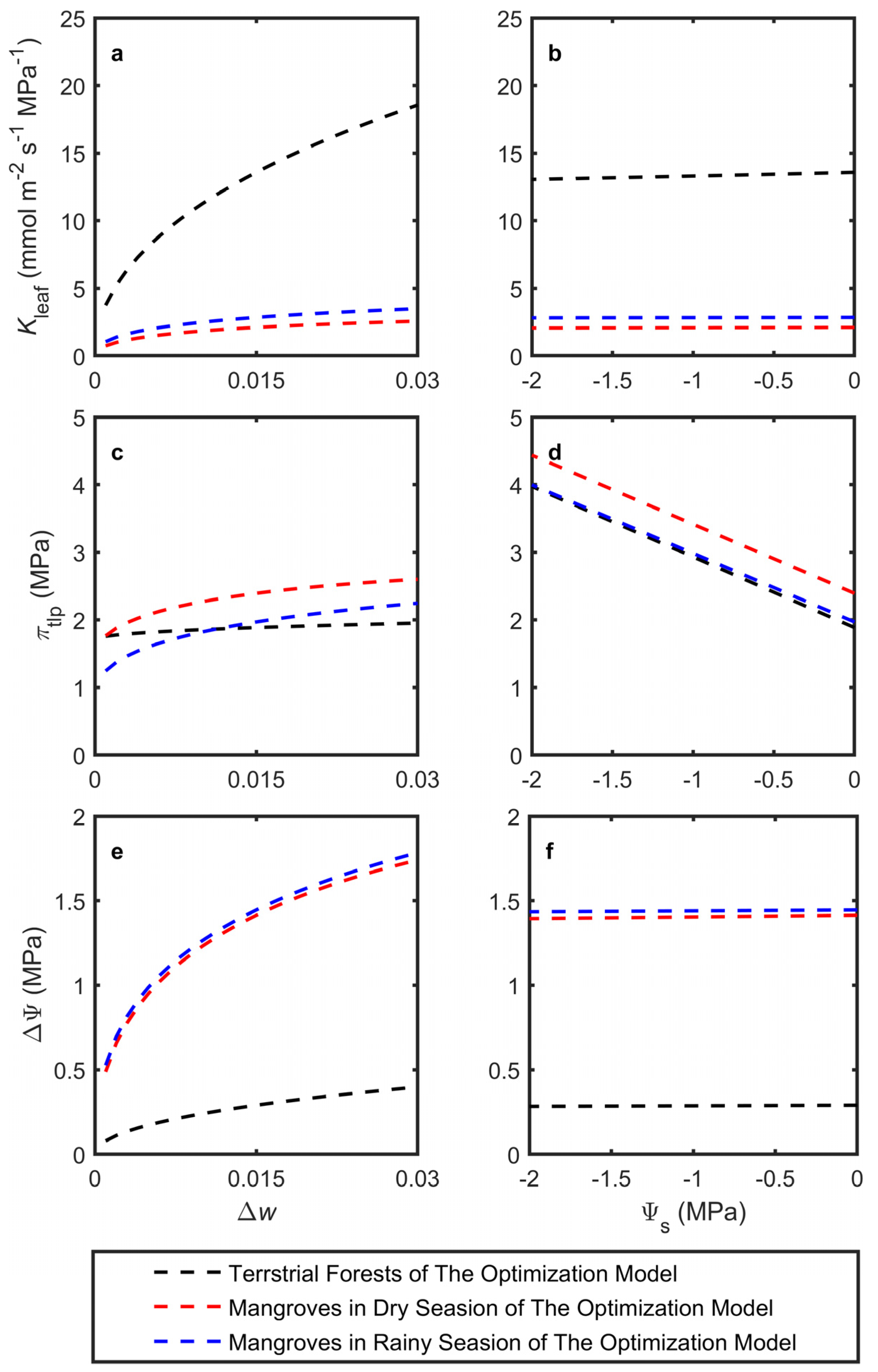
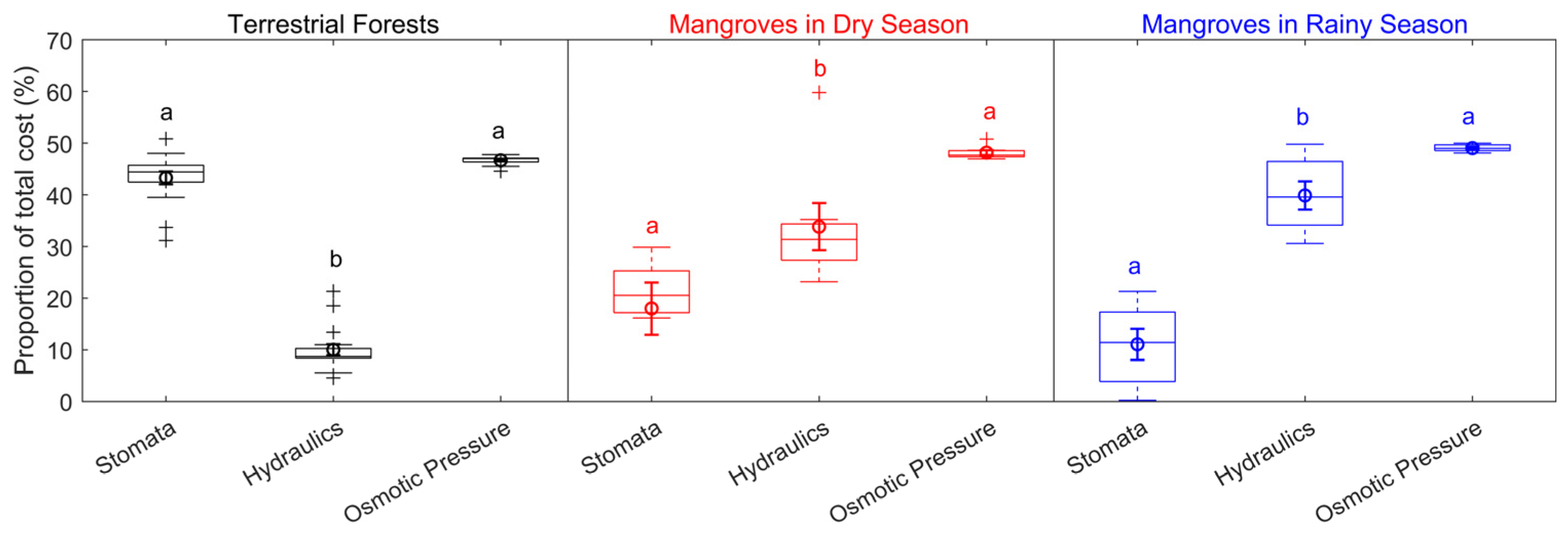
Season		Species	Family	Type	Salt Management	Asat	Kleaf	gsat	πtlp	Source
Arid	1	Rhizophora stylosa	Rhizophoraceae Pers.	True mangrove	Salt exclusion	15.73	2.34	0.19	1.87	This study
	2	Rhizophora apiculata	Rhizophoraceae Pers.	True mangrove	Salt exclusion	12.88	1.89	0.15	1.96	This study
	3	Avicennia marina	Acanthaceae	True mangrove	Salt diluting	17.27	2.64	0.27	2.82	This study
	4	Ceriops tagal	Rhizophoraceae Pers.	True mangrove	Salt diluting	11.26	1.38	0.13	2.06	This study
	5	Bruguiera gymnorrhiza	Rhizophoraceae Pers.	True mangrove	Salt diluting	11.61	1.75	0.16	1.79	This study
	6	Aegiceras corniculatum	Myrsinaceae	True mangrove	Salt excretion	17.47	2.36	0.28	2.93	This study
	7	Xylocarpus granatum	Meliaceae Juss.	True mangrove	Salt diluting	10.7	1.5	0.22	1.81	This study
	8	Sonneratia caseolaris	Sonneratia caseolaris (L.) Engl.	True mangrove	Salt diluting	20.37	3.17	0.27	1.85	[61]
	9	Heritiera littoralis	Malvaceae	Semi-mangrove	Salt excretion	14.25	2.67	0.2	2.57	[61]
	10	Sonneratia alba	Sonneratia caseolaris (L.) Engl.	True mangrove	Salt diluting	19.4	2.01	0.21	2.92	[61]
	11	Hibiscus tiliaceus	Malvaceae	Semi-mangrove	Salt diluting	23.71	3.44	0.3	2.56	[61]
Rain	1	Rhizophora stylosa	Rhizophoraceae Pers.	True mangrove	Salt exclusion	14.25	2.68	0.28	2.12	This study
	2	Rhizophora apiculata	Rhizophoraceae Pers.	True mangrove	Salt exclusion	20.76	4.29	0.36	1.97	This study
	3	Avicennia marina	Acanthaceae	True mangrove	Salt diluting	22.45	4.67	0.4	2.18	This study
	4	Ceriops tagal	Rhizophoraceae Pers.	True mangrove	Salt diluting	13.88	2.39	0.26	1.68	This study
	5	Aegiceras corniculatum	Myrsinaceae	True mangrove	Salt diluting	15.92	2.71	0.3	2.14	This study
	6	Xylocarpus granatum	Meliaceae Juss.	True mangrove	Salt diluting	10.75	2.58	0.25	1.46	This study
	7	Bruguiera gymnorrhiza	Rhizophoraceae Pers.	True mangrove	Salt diluting	14.78	2.68	0.29	2.08	This study
	8	Sonneratia caseolaris	Sonneratia caseolaris (L.) Engl.	True mangrove	Salt excretion	20.98	3.82	0.498	-	[62]
	9	Hibiscus tiliaceus	Malvaceae	Semi-mangrove	Salt diluting	22.28	5.07	0.467	-	[62]
	10	Dolichandron spathacea	Bignoniaceae	Semi-mangrove	Salt diluting	9.3	1.98	0.218	-	[62]
	11	Acrostichum aureum	Acrostichaceae	True mangrove	Salt excretion	6.39	1.2	0.199	-	[62]
	12	Acrostichum speciosum	Acrostichaceae	True mangrove	Salt diluting	6.28	1.04	0.138	-	[62]
	13	Bruguiera sexangula	Rhizophoraceae Pers.	True mangrove	Salt exclusion	11.33	2.56	0.255	-	[62]
	14	Kandelia obovata	Rhizophoraceae Pers.	True mangrove	Salt exclusion	7.21	1.81	0.090	-	[63]

(1) Parameters include the average maximum leaf hydraulic conductance (K_leaf, mmol·m⁻²·s⁻¹·MPa⁻¹), the average maximum stomatal conductance (g_sat, in mmol·m⁻²·s⁻¹), the average maximum instantaneous CO₂ assimilation rate (A_sat, μmol·m⁻²·s⁻¹), and the average turgor loss point (π_tlp, MPa). Note that the table presents absolute values of π_tlp. (2) True mangroves: Fully adapted to saltwater and tidal zones, with specialized salt tolerance mechanisms. Semi-mangroves: Tolerate some salt but are not as specialized and can grow in a wider range of conditions. (3) “-” represents no experimental data.

). To facilitate comparison, information on terrestrial species exhibiting these four traits was obtained from Deans et al. [53].

2.2. Photosynthetic Rate and Gas Exchange

We measured the maximum net photosynthetic rate (A_sat), average maximum transpiration rate (E), and average maximum stomatal conductance (g_sat) on three sunlit canopy leaves from three individuals of each species using a Li-Cor 6800 portable photosynthesis system (Li-Cor Inc., Lincoln, NE, USA). Prior to measurement, the leaves were exposed to 1800 μmol·m⁻²·s⁻¹ for 10 min. The photosynthetic photon flux density in the leaf chamber was set to 1200 μmol·m⁻²·s⁻¹. The chamber temperature was maintained at 26 °C. A CO₂-filled steel cylinder controlled the leaf chamber CO₂ concentration at 400 ppm. The flow rate was set to 500 μmol·m⁻²·s⁻¹. The relative humidity was maintained at 55%.

2.3. Leaf Hydraulic Conductance

Healthy mangrove branches were collected before dusk; the cut ends were wrapped in wet paper towels and enclosed in black plastic bags with moist towels. The samples were then sealed and transported to the lab. Under water, each branch was re-cut and placed vertically (simulating natural growth) to submerge the petiole. The branches were wrapped in black plastic bags and rehydrated overnight to restore leaf water potential to near-saturation.

Following Xiong et al. [64], we used the evaporation flux method (EFM) to determine the mean maximum leaf hydraulic conductance (K_leaf max). During measurement, a target leaf with a 5–10 cm sheath was first cut underwater and trimmed in the target water tank. Next, the trimmed leaf was placed in darkness for 30 min to saturate. We then used the LI-6800 photosynthesis system (LI-COR Biosciences Inc., Lincoln, NE, USA) to measure the transpiration rate (E) under a PPFD of 1200 μmol·m⁻²·s⁻¹ and a temperature of 28 °C, which were favorable for transpiration. The leaf was immediately placed into a sealed bag with moist paper towels in the dark for about 30 min to equilibrate. Leaf water potential (Ψ_leaf) was then measured using a WP4C device. Five replicates per treatment were measured. Leaf hydraulic conductance (K_leaf) was calculated using the following formula:

$$K_{leaf}={\displaystyle \frac{E}{{\mathsf{\Psi }}_{water}-{\mathsf{\Psi }}_{leaf}}}$$

(1)

where ${\mathsf{\Psi }}_{water}$ = 0 for distilled water in this study.

2.4. Leaf Osmotic Pressure at the Turgor Loss Point

We collected fully rehydrated leaves (as described above) and quickly removed any remaining surface water. Using an 8 mm hole punch, we extracted a leaf disk from the area between the main vein and the leaf edge. The leaf disk was tightly wrapped in aluminum foil and rapidly frozen in liquid nitrogen (five replicates per species). During measurement, we punctured the frozen leaf disk 10–15 times with sharp tweezers to facilitate water vapor movement through the cuticle and reduce equilibrium time [65]. The disk was immediately placed into a vapor pressure osmometer (VAPRO 5600; Wescor, Logan, UT, USA) chamber. Prior to measurements, the osmometer was calibrated using three standard solutions (290, 1000, 100 mmol/kg) in sequence. Measurements were taken without opening the sample chamber until the final two readings had a deviation below 5 mmol/kg. The recorded value was the saturated osmotic potential (${\mathsf{\pi }}_{100}$), and the mean of each sample was calculated and converted to MPa (1000 mmol/kg = 2.5 MPa). The turgor loss point ${\pi }_{tlp}$ was calculated from ${\pi }_{100}$, using the biophysical calibration equation by [66], which was based on 30 species from different climate zones:

$${\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}=0.832\times {\mathsf{\pi }}_{100}-0.631$$

(2)

2.5. Carbon-Gain Optimization Model

We followed [53] in using a carbon-gain optimization model. In this model, net carbon gain is calculated by integrating the CO₂ assimilation rate and trait parameters associated with photosynthesis, stomatal conductance, and leaf water relations:

$$\begin{array}{c}F={\displaystyle \frac{\mathrm{k}\left({\mathrm{C}}_{\mathrm{a}}-{\mathsf{\Gamma }}^{\mathrm{*}}\right)\mathsf{\chi }{\mathrm{K}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}\left({\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}+{\mathsf{\Psi }}_{\mathrm{s}}\right)}{1.6\mathrm{k}\left[{\mathrm{K}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}\left(1+\frac{{\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}}{\mathsf{\epsilon }}\right)+\mathsf{\chi }∆\mathrm{w}\right]+\mathsf{\chi }{\mathrm{K}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}\left({\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}+{\mathsf{\Psi }}_{\mathrm{s}}\right)}}\\ -{\mathsf{\mu }}_{\mathsf{\chi }}\chi -{\mathsf{\mu }}_{\mathrm{k}}{\mathrm{K}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}-{\displaystyle \frac{{\mathsf{\mu }}_{\mathsf{\pi }}}{\mathsf{\upsilon }}}{\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}\mathrm{k}\end{array}$$

(3)

where $\mathrm{k}$ is the biochemical photosynthetic capacity of the leaf, ${\mathsf{\Gamma }}^{\mathrm{*}}$ is the CO₂ compensation point without respiration, ${\mathrm{C}}_{\mathrm{a}}$ is the ambient CO₂ concentration, $\mathsf{\epsilon }$ is the light-saturated respiration rate, $∆\mathrm{w}$ is the atmospheric evaporative demand, ${\mathsf{\Psi }}_{\mathrm{s}}$ is the water potential at the petiole, $\mathsf{\chi }$ is the light-saturated stomatal conductance, ${\mathrm{K}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}$ is leaf hydraulic conductance, ${\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}$ is the osmotic potential at the turgor loss point, ${\mathsf{\mu }}_{\mathsf{\chi }}$ is the cost parameter for stomata, ${\mathsf{\mu }}_{\mathrm{k}}$ is the cost parameter for hydraulic traits, and ${\displaystyle \frac{{\mathsf{\mu }}_{\mathsf{\pi }}}{\mathsf{\upsilon }}}$ is the cost parameter for ${\mathsf{\pi }}_{\mathrm{t}\mathrm{l}\mathrm{p}}$. These parameters collectively determine both the CO₂ assimilation rate and net carbon gain. Here, $\mathsf{\epsilon }$ = 10 MPa, ${\mathsf{\Gamma }}^{*}$ = 48.4 μmol mol⁻¹, ${\mathrm{C}}_{\mathrm{a}}$ = 400μμmol mol⁻¹, $∆\mathrm{w}$ = 0.015, and ${\mathsf{\Psi }}_s$ = 0 MPa.

2.6. Model Validation

We used a dataset of species with known A_sat, g_sat, K_leaf, and π_tlp values to solve for the unknown cost parameters and fit the model. Each species was treated as a unique sample, and the model was further validated using species data with only A_sat, g_sat, and K_leaf. In this study, the focus was solely on recording and analyzing species trait data values (such as A_sat and g_sat) in the context of the optimization model, with no comparisons made between groups (such as between different species or seasons). We performed the Kruskal–Wallis test and two-sided multiple comparison testing to examine the relative costs of stomatal, hydraulic, and osmotic traits between terrestrial forests and mangrove groups. Our goal was to determine whether the model explained the cross-species trends in osmotic adjustment, stomatal conductance, and leaf hydraulic conductance, as well as to estimate the relative costs of these traits. The model and terrestrial plant data were from [53].

3. Results

3.1. Relationships Among Leaf Photosynthesis, Stomata, and Hydraulic Conductance

The analysis of A_sat, g_sat, and K_leaf in mangroves during both the dry and rainy seasons showed strong correlations between these three parameters in both terrestrial forests and mangroves (Figure 1a–c), although there were notable differences. Compared to terrestrial forests, mangroves particularly during the dry season, had lower g_sat (Figure 1a) and K_leaf (Figure 1b) as a response to drought stress, thereby reducing water loss while maintaining a certain level of CO₂ assimilation. Additionally, g_sat in mangroves was more sensitive to changes in K_leaf (Figure 1c), suggesting a more adaptable water regulation mechanism. The seasonal analyses also indicated that mangroves adjusted their physiological responses based on the availability of water throughout the seasons.

The results from the optimization model showed that ΔΨ is independent of A_sat in both terrestrial forests and mangroves. The observed ΔΨ across species did not significantly differ from the predicted values of the model. The model predicted an optimal ΔΨ = 0.29 MPa (p = 0.27) for terrestrial forests, ΔΨ = 1.41 MPa (p = 0.52) for mangroves in the dry season, and ΔΨ = 1.45 MPa (p = 0.34) for mangroves in the rainy season (Figure 1d). The observed ΔΨ values in mangroves during the dry and rainy seasons were higher than predicted, possibly because the model did not fully consider the adaptive mechanisms of mangroves under extreme conditions. Mangroves efficiently utilize water during drought through mechanisms such as osmotic adjustment, root adaptations, and stomatal regulation, which may not be fully captured by the model. Compared to terrestrial forests, mangroves need to maintain a higher ΔΨ under high salinity or periodic water shortages in order to draw water from saline environments. In the rainy season, characterized by more variable water and salinity, ΔΨ showed relatively large variations. In contrast, during the dry season, limited water supply resulted in a more stable ΔΨ compared to the rainy season.

For terrestrial forests, π_tlp showed a weak but significant correlation with A_sat, (R² = 0.28, p = 0.021), whereas π_tlp in mangroves during both the dry and rainy seasons exhibited a weak but non-significant correlation with A_sat (dry season: R² = 0.37, p = 0.08; rainy season: R² = 0.28, p = 0.13; Figure 1e). The model predicted an optimal π_tlp = 1.54 MPa for terrestrial forests, π_tlp = 2.39 MPa for mangroves in the dry season, and π_tlp = 1.97 MPa for mangroves in the rainy season (Figure 1e). In the rainy season, increased freshwater availability brought the π_tlp of mangroves closer to that of terrestrial forests.

3.2. Changes in Leaf Traits Under Atmospheric and Soil Drought

The model was used to estimate optimal A_sat, g_sat, K_leaf, π_tlp, and ΔΨ in response to changes in Δw and Ψ_s, simulating adaptation to mean atmospheric dryness and leaf petiole water potential, respectively (Figure 2). The latter integrated soil dryness (salinity) and other resistances to water flow. The simulations utilized the average trait cost parameters across species, assuming a given biochemical photosynthetic capacity k. All model predictions were based on a photosynthetic capacity expected for a plant with an A_sat of 15 μmol m⁻² s⁻¹ at Δw = 0.015 and Ψ_s = 0 MPa (Figure 2a,c). Both terrestrial forests and mangroves generally showed trends consistent with the Cowan–Farquhar model in terms of A_sat and g_sat, although with weaker sensitivity. Notably, mangroves were more sensitive to changes in Δw for both A_sat and g_sat (Figure 2a,c). Under drier atmospheric conditions, the model predicted that terrestrial forests would significantly increase K_leaf while only slightly raising ΔΨ to support higher transpiration, whereas π_tlp showed minimal changes. On the other hand, mangroves displayed a substantial increase in ΔΨ with only minor changes in K_leaf and π_tlp (Figure 3a,c,e).

Under drier water-source conditions (Ψ_s more negative; Figure 2b,d), both terrestrial forests and mangroves reduced π_tlp (i.e., more negative π_tlp), while the model predicted relatively stable K_leaf and ΔΨ (Figure 3b,d,f).

3.3. Relative Cost Contributions of Key Traits

The carbon-gain optimization model provided a method to estimate the individual costs of hydraulic, stomatal, and osmotic pressure relative to the combined cost of these three traits. For terrestrial forests, leaf hydraulics were estimated to contribute 10.0 ± 1.1% of the total cost, while stomata costs made up 43.3 ± 1.2%, and osmotic pressure made up 46.7 ± 0.2%. In mangroves during the dry season, leaf hydraulics contributed 33.84 ± 4.56% of the total cost, while stomata contributed 18.00 ± 5.05%, and osmotic pressure made up 48.16 ± 0.49%. During the rainy season, mangroves showed a higher contribution from leaf hydraulics at 39.88 ± 2.74%, with stomata contributing 11.08 ± 3.00%, and osmotic pressure accounting for 49.04 ± 0.026% (Figure 4). The statistical tests, including Kruskal–Wallis and two-sided multiple comparison tests, revealed significant differences between terrestrial forests and mangroves in the allocation of costs between hydraulic and stomatal traits. However, no significant difference in cost allocation was found in osmotic traits.

4. Discussion

By integrating field observations with a carbon-gain optimization model, we measured and analyzed key functional traits (i.e., g_sat, K_leaf, π_tlp, and A_sat) in mangrove leaves and investigated how mangroves optimize water-use strategies under the dual stresses of declining Ψ_s and rising Δw. Additionally, we systematically compared these strategies with those of terrestrial forests. Our study revealed the following key findings: (1) the differences in water-use strategies between mangroves and terrestrial forests enhance our understanding of plant ecohydrology; (2) mangroves adapt to drought and salinity stress by adjusting ΔΨ and π_tlp, enabling them to survive in high VPD and high salinity environments, thereby providing new insights into plants might respond to future climate change; and (3) by highlighting the shared role of osmotic adjustment in drought tolerance, this study enriched the theoretical framework of plant water-use strategies.

4.1. Differences in Water-Use Strategies Under Drought Stress Between Mangroves and Terrestrial Forests

Our results showed that as Δw increased, mangroves significantly raised ΔΨ while keeping K_leaf relatively stable. In contrast, terrestrial forests increased K_leaf with only minor changes in ΔΨ. This pattern was consistent with previous studies, which found that under extreme conditions, drought-adapted species sharply reduced g_sat while maintaining stable K_leaf [67], protecting leaves from rapid water potential declines and preventing hydraulic failure [68]. Under favorable external conditions, mangroves’ g_sat can reach levels comparable to other tropical forests [69]. However, under high VPD, mangroves swiftly close their stomata [70,71,72] to minimize water loss and limit salt intake, preventing excessive dehydration and salt accumulation. Such high stomatal sensitivity enables mangroves to respond rapidly to changing VPD and optimize water-use efficiency, though it can lead to more frequent stomatal closure events. Similar to other halophytes, mangroves exhibited fast stomatal movements, which may have been an adaptive mechanism to manage salinity [73]. By regulating stomatal conductance, mangroves maintained water balance and minimized salt uptake in saline environments [74]. This response was particularly important under extreme conditions. When high temperatures and VPD increased the transpiration rate [75], increased water flux across leaves could have led to hydraulic conductivity loss [76]. To maintain water balance and sustain A_sat comparable to those in tropical plants [62], mangroves accumulated osmolytes via osmotic adjustment, reducing cell Ψ_leaf and regulating ΔΨ. This process ensured a continuous water supply to leaves and prevented drought-induced hydraulic dysfunctions [77]. As a result, K_leaf remained relatively stable [50], allowing mangroves to sustain adequate A_sat [53,78] and survive in harsh environments.

In terrestrial forests, g_sat was less sensitive to VPD, leading to less frequent stomatal closure. This facilitated more stable photosynthesis under varying VPD but increased the risk of water stress under high VPD conditions. When Ψ_leaf was sufficient, terrestrial forests did not necessarily maintain a constant K_leaf or decrease it as E rose. Instead, they may have increased K_leaf alongside higher E to minimize changes in ΔΨ, thereby maximizing Ψ_leaf [43]. Additionally, ΔΨ remained relatively stable during leaf desiccation [79]. By enhancing K_leaf, terrestrial forests effectively transported limited water to support both transpiration and photosynthesis. This strategy helped maintain ΔΨ within a safe range and prevented excessive reliance on ΔΨ for water transport, preserving the integrity of the water transport system.

4.2. The Overarching Importance of Osmotic Adjustment in Drought Tolerance Across Species

Our findings showed that under the stress of declining Ψ_s, both mangrove and terrestrial forests exhibited more negative π_tlp values. Additionally, the optimization model predicted that osmotic pressure incurred the highest cost in both forest groups. This suggested that despite biochemical differences, both groups relied on similar osmotic adjustments under drought [80]. Specifically, they maintained a more negative osmotic potential at full turgor, which allowed cells to retain a larger water content when dehydrated to the turgor loss point [34]. Such osmoregulation involves cytoplasmic adjustments [81] and cell wall reinforcement to increase rigidity [80,82]. Both mechanisms required carbon that would otherwise support growth [50,83]. While the carbon costs at the single-leaf level might have been small, their cumulative impact at the canopy scale could have been substantial [50]. Additionally, maintaining osmotic gradients between mesophyll cells and the leaf apoplast required continuous metabolic energy. Over a leaf’s lifetime, this ongoing energy demand likely contributed further to the overall carbon cost of osmoregulation [53].

4.3. Changes in the Relative Importance of Stomatal and Hydraulic Traits in Mangroves During the Dry and Rainy Seasons

Our study revealed significant differences between terrestrial forests and mangroves in the carbon investment for hydraulic and stomatal traits. These differences could be explained by construction, maintenance, and metabolic costs. In saline environments, mangroves typically had low stomatal density and small, often sunken stomata [62]. The high sensitivity of g_sat to VPD enabled rapid responses that minimized water loss and salt intake, reducing the construction and maintenance costs with stomatal traits. Some studies indicated that under arid conditions, certain mangroves absorbed moisture from air, rain, dew, or fog through leaf stomata [35,40,84,85] to maintain leaf hydration [34,86] as an important water acquisition strategy [35], which may further lead to lower stomatal-related carbon costs [87].

In contrast, salt deposits and air emboli in the xylem significantly restricted mangrove K_leaf [88], limiting water transport capacity. Improving leaf water uptake capacity necessitated considerable construction costs, such as increasing vein diameter and density [89]. Furthermore, high salinity and periodic flooding demanded continuous maintenance of hydraulic system stability to prevent vessel blockage and cavitation, leading to higher maintenance costs for hydraulic traits.

Seasonal differences in mangrove trait cost allocation showed that during the rainy season—when plant growth peaks—mangroves allocated more resources to leaf development and hydraulic structures, such as vessel diameter and density, to support the rapid expansion of leaves, shoots, and roots. A higher K_leaf was essential for efficient water and nutrient transport, which sustained photosynthesis and metabolism [50]. In regions with abundant rainfall, mangroves often formed taller canopies and stored more carbon than those in arid areas [90,91]. In contrast, during the dry season, limited rainfall and higher salinity stress [40] reduced mangrove metabolism [41]. Studies on sea level rise suggested that rising salinity could further stress mangroves, making it more difficult to maintain physiological functions, especially during the dry season with reduced freshwater input [15]. This, in turn, affected their ability to sequester carbon [92].

5. Conclusions

This study explained how mangroves optimize their water-use strategies to maximize carbon gain under the dual stress of high salinity and atmospheric dryness. Unlike terrestrial forests, mangroves primarily adjust π_tlp and ΔΨ, while keeping K_leaf relatively stable. This unique trait allocation and water management mechanism enabled mangroves to maintain high carbon gain and physiological function in extreme environments. It highlighted their specialized adaptations to high salinity and high VPD. Understanding these mechanisms is important for developing carbon trading policies and green economic strategies, as mangroves play a significant role in the global carbon cycle and serve as vital carbon sinks with significant ecological value.

For policymakers and conservationists, these findings emphasized the importance of protecting mangrove ecosystems, particularly in areas at risk of sea level rise and increased salinity. Supporting mangrove resilience not only helps preserve local biodiversity but also contributes to global climate mitigation efforts. Policymakers should prioritize mangrove habitat conservation and integrate their unique water-use strategies into environmental management frameworks.

However, the carbon gain model had limitations. It did not fully account for trait adaptability under extreme conditions, the variation in trait costs among different species, or the lack of independent dataset validation. Future research could focus on including spatial variability across different salinity gradients and climate conditions in mangrove ecosystems to gain a deeper understanding of their carbon sequestration potential. Expanding the model to include other species would also provide valuable insights into water-use strategies across plant groups, enhancing our ability to predict and manage carbon storage in the context of climate change.