Abstract
Inferring forest properties is crucial for the timber industry, enabling efficient monitoring, predictive analysis, and optimized management. Nondestructive testing (NDT) methods have proven to be valuable tools for achieving these goals. Recent advancements in data analysis, driven by machine learning (ML) algorithms, have revolutionized this field. This study analyzed 492 eucalyptus trees (Eucalyptus sp.), aged 3 to 7 years, planted in São Paulo, Brazil. Data from forest inventories were combined with results from ultrasound, drilling resistance, sclerometric impact, and penetration resistance tests. Seven machine learning algorithms were evaluated to compare their generalization capabilities with conventional statistical methods for predicting basic wood density. Among the models, extreme gradient boosting (XGBoost) achieved the highest accuracy, with a coefficient of determination (R2) of 89% and a root mean square error (RMSE) of 10.6 kg·m−3. In contrast, the conventional statistical model, using the same parameters, yielded an R2 of 33% and an RMSE of 26.4 kg·m−3. These findings highlight the superior performance of machine learning in the nondestructive inference of wood properties, paving the way for its broader application in forest management and the timber industry.
1. Introduction
Despite advances in genetic engineering and cloning, the properties of wood are still influenced by factors related to the growing of trees as climate, soil, altitude, tree spacing, silvicultural treatments, etc., [1,2,3,4,5,6,7]. These influences result in significant variability in the wood produced in the forest, making it difficult to establish important reference values for the production line of forest companies linked to pulp and paper, wood-based products (fiberboards and particleboards), as well as roundwood or processed wood used in solid or engineered forms (glued laminated timber or cross-laminated timber) in construction.
The prediction of tree properties in forests has been a recurring topic in publications, with non-destructive techniques being a viable alternative to this challenge [8,9,10,11,12]. By not affecting the material, these techniques allow tests to be repeated during the tree’s growth. They can be performed directly on standing trees [13,14], and since no sampling or tree cutting is required, they are more economical, simpler, and faster, enabling increased sampling. Thus, several research groups have been developing studies using various nondestructive techniques aimed at inferring properties such as wood density (basic or apparent) and stiffness [15,16,17,18,19,20,21,22,23,24]. These nondestructive methods include those that use wave propagation (ultrasound and stress waves), resistance to drilling, resistance to penetration, and mass spectrometry, among others. Regardless of the type of equipment or technique used, the focus of the research is to correlate the measured parameters in trees with wood properties, with statistical modeling being the tool typically used to obtain the relationship between variables to predict results. Classical statistical tools are no longer the most suitable when the volume of data are very large, and machine learning algorithms are currently recommended for such cases.
The adoption of non-destructive techniques as a tool for evaluating the quality of wood produced in forests stems from the possibility of obtaining correlations between the responses of these methods and the physical and mechanical properties of the fibers, which are used for the selection and classification of forest products. Thus, the adoption of such techniques in the wood production chain represents a fast and effective means of assessing wood quality, with the potential to enhance inference models already employed by companies in the forestry sector [25,26,27].
The literature review indicated that, in Brazil, studies related to machine learning are more strongly focused on estimating tree volume [28,29,30,31,32]. In other countries we found researchers [33,34] whose objectives were closer to ours, directed to study different machine learning algorithms in inferring density, and presenting superior results to those obtained using classical multiple regression. In this research [33,34], field trials used dendrometric measurements of trees (height and diameter at breast height (DBH), NDT techniques (stress wave propagation and resistance to drilling [33]), and extracted cores with an increment borer for density measurement using X-ray densitometry.
The main objective of this research was to evaluate whether machine learning algorithms, utilizing data collected from standing trees (forest inventory and non-destructive inspections), can provide accurate predictions of wood basic density compared to conventional statistics methods.
2. Materials and Methods
The sampling comprised 491 eucalyptus trees (Eucalyptus sp.) planted in the state of São Paulo, Brazil, aged between 3 and 7 years. In addition to the data collected in the conventional inventory of the partnering company Suzano S.A. (Salvador, Brazil) (diameter at breast height, total height, and pylodin (Pylodin 6J Standard, FBK, Germany) penetration), data from ultrasonic wave propagation tests (USLab, Valora Madeira, Brazil) in the longitudinal and radial directions, drilling resistance (PD500, IML, Germany), sclerometric impact (Silver Schimidt, Proceq, Switzerland), and sample retrieval with the Pressler probe (Increment Borer 5, 15 mm, Sweeden) were added (Figure 1). From each plot, 3 trees were chosen according to their DBH class (1: 8 ± 4 cm, 2: 12 ± 4 cm, 3: 16 ± 4 cm) and cut for determination of basic density in the laboratory of the partnering company. The data were compiled into a single database, containing the inventory results and additional tests, to which 7 machine learning algorithms were applied, selected with the aim of predicting basic density from the other variables, following a sequence of steps (Figure 2). The basic density of the trees that were not cut was estimated using a model adopted by the partnering company.

Figure 1.
Ultrasonic wave propagation test in the longitudinal direction (a), drilling resistance test (b), sclerometric impact test (c), and sample retrieval by Pressler probe (d).

Figure 2.
Sequence of steps performed during the modeling of machine learning algorithms.
The ultrasound test consists of emitting an electrical signal, which is converted into a mechanical signal through the piezoelectric effect of a crystal or ceramic element embedded in a transducer. After passing through the material, the signal is received by another transducer, which, using the same piezoelectric effect, converts the mechanical signal back into an electrical signal. The wave travel time is measured by the equipment, and with the known travel distance, the velocity is calculated. In ultrasound testing, it is possible to control the wave frequency by adjusting the cutting angle of the transducer’s crystal/ceramic element. Established results in the literature indicate a correlation between wave propagation velocity and the material’s elastic parameters. The resistance-to-drilling test measures the torque required to maintain the feed rate and rotational speed of a needle, approximately 2 mm in diameter, as it penetrates the wood. The equipment allows obtaining amplitude graphs of drilling resistance along the drilling path, and according to the literature, this amplitude is primarily correlated with the material’s density. The impact sclerometric test evaluates the amount of energy returned to the equipment after the release of a plunger propelled by a spring with known properties. For the ultrasonic wave propagation test, a pre-drilling procedure at a 45-degree angle is required. In the case of the impact sclerometric test, the tree bark must be removed before testing.
The process of splitting the data into training and testing sets was carried out to ensure that the models were trained with distinct datasets in each training round. This approach increases their generalization capacity and reduces the likelihood of overfitting. The chosen proportion was 70/30, in which 70% of the dataset was used to train the models, and 30% was used during the prediction phase of the algorithms. The normalization step was critical to prevent dimensional differences between variables from being incorporated into the models. Moreover, some algorithms operate more effectively with normalized data, enhancing their performance.
It is important to clarify that the machine learning algorithms applied in our study did not exclude any data points identified as outliers. Instead, the algorithms internally adjusted the weight of each observation based on its contribution to the overall model performance. This process allows the models to automatically reduce the influence of extreme values—without removing them—by focusing on the trends that are most representative of the complete dataset.
The feature selection process aimed to identify the most relevant variables for predicting basic density in eucalyptus forests, optimizing model performance and reducing data dimensionality. Initially, the ExtraTreeRegressor algorithm was used to calculate feature importance based on the variance reduction provided by tree splits. Subsequently, other methods, such as Random Forest and Extreme Gradient Boosting (XGBoost), were applied to validate the results and ensure robustness in the selection process. The most relevant variables were then selected to form the final set of features used in training the predictive models.
To prevent data leakage and ensure model reliability, the feature importance analysis was conducted exclusively on the training set after splitting the data. Only the variables selected based on the training data were used in the testing set. This approach ensures that model evaluation reflects the performance of truly unseen data, simulating practical application scenarios [35].
All data mining methods were configured following the guidelines of [36,37,38] for hyperparameter tuning. Individual adjustments were made for each model to mitigate the risks of overfitting and underfitting. During hyperparameter optimization, different seeds were used for initializing evaluations, allowing the assessment of varying model behaviors. A 10-fold cross-validation strategy (cv = 10) was also employed. Overfitting occurs when a model fits the training data exceptionally well but fails to generalize to new data. Conversely, underfitting happens when the model cannot capture relationships between the variables in the training set, causing the process to terminate prematurely, even before testing [38].
The variables selected by machine learning algorithms were also evaluated using conventional statistical software (Statgraphics Centurion XV 15.1.02) to identify the best model for inferring wood basic density. This process involved applying classical statistical modeling techniques, such as multiple regression and models automatically suggested by the software, aiming to maximize the coefficient of determination (R2) and minimize the root mean square error (RMSE).
After the prediction step, each model was evaluated using the following metrics: coefficient of determination (R2), adjusted coefficient of determination (adjusted R2), mean absolute error (MAE), and root mean squared error (RMSE).
3. Results
3.1. Laboratory and Field Results
The mean values, standard deviation, coefficient of variation, skewness, and kurtosis of the numerical variables evaluated in this research are presented in Table 1. As mentioned previously, we can notice the difference between the scales of the variables and that is why it is important to carry out the normalization step.

Table 1.
Mean values, standard deviation, coefficient of variation, skewness, and kurtosis of the parameters.
From Table 1, it can be observed that there are differences between the density obtained by the partner company (BdSU) and by the borer (BdV), which is due to the way they were obtained. The density provided by the partner company was determined according to ABNT—ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS NBR 11941/2003 standard [39]. From this standard, the selected trees are sectioned at different heights along the stem, corresponding to 0% (base); DBH (diameter at breast height); 25%; 50%; 75%; and 100% of the total height. From each section, 1 m-long logs are extracted, identified, and subsequently chipped. The wood chips are immersed in water until fully saturated, weighed by immersion, and then oven-dried to a constant mass for further analysis. On the other hand, the density obtained from the extracted cores was determined by measuring the green volumes and oven-dried masses of either the complete cores or their segments. These core samples were collected using an increment borer from the diameter at breast height (DBH) region.
3.2. Feature Selection
During the feature selection stage, the following variables were selected: DBH, H, VL, DR, AGE, and IMATCC. AGE, DBH, H, and IMATCC are already part of the inference models employed by companies. Conversely, VL and DR stood out as the non-destructive methods with the highest levels of importance within the models. It is also well-known that the individual use of DBH and H in models can lead to autocorrelation issues, as observed in Table 2. Variance inflation factors (VIF) were calculated for each variable, and although there is no definitive consensus on acceptable VIF limits, we adopted the criterion that values exceeding five should be excluded or transformed. To address multicollinearity, these variables were combined (H/DBH).

Table 2.
Variance inflation factors of the variables, before and after the creation of a new variable.
3.3. Hyperparameter Optimization
The hyperparameter tuning process was conducted using multiple random seeds to initialize the evaluations and a 10-fold cross-validation strategy (cv = 10) (Table 3). The coefficient of variation (CV) for the evaluation metrics—mean absolute error (MAE), root mean squared error (RMSE), coefficient of determination (R2), and adjusted coefficient of determination (R2 adj)—reached up to 21% across different random seeds (Table 4).

Table 3.
Optimized hyperparameters for each algorithm evaluated.

Table 4.
Mean and coefficient of variation in the evaluation metrics for the algorithms.
3.4. Classical Statistics Results
The model obtained by classical statistics (Equation (1)) was evaluated by parametrical statistics (Statgraphics Centurion XV 15.1.02), using the same variables previously selected (1).
BbSU = 300.823 + 6.11588 × AGE + 4.89593 × H/DBH + 0.0170558 × VL + 0.0270439 × DR − 0.832398 × IMATCC
R2 = 33.6%; R2 adjusted = 32.9%; RMSE = 26.4 and MAE = 21.7
R2 = 33.6%; R2 adjusted = 32.9%; RMSE = 26.4 and MAE = 21.7
The p-value = 0.0000 for AGE, VL, DR and IMATCC and p-value = 0.5028 for H/DBH, so the parameter H/DBH is not significant and can be removed from the model. However, the removal of this variable, despite being non-significant, did not impact the model’s coefficient of determination or errors (2). Therefore, it was retained to allow for a comparison between models containing all variables selected during the feature selection stage.
BbSU = 305.752 + 6.4629 × AGE + 0.0177836 × VL + 0.0259805 × DR − 0.823152 × IMATCC
R2 = 33.5%; R2 adjusted = 33%; RMSE = 26.4 and MAE = 21.7
R2 = 33.5%; R2 adjusted = 33%; RMSE = 26.4 and MAE = 21.7
3.5. Optimal Metrics Results
Table 5 presents the best values obtained by the algorithms evaluated in this research with respect to the assessment metrics.

Table 5.
Evaluation metrics of the best assessed algorithms.
In addition to the metrics (Table 5), two graphs were generated for each model. The first graph (Figure 3) displays the dispersion of predicted versus observed values, where the points are concentrated around the 45° line, indicating a strong agreement between the estimated and actual values. The second graph (Figure 4) illustrates the residuals, which are randomly distributed, suggesting that the model is effectively capturing the relationship between the variables.
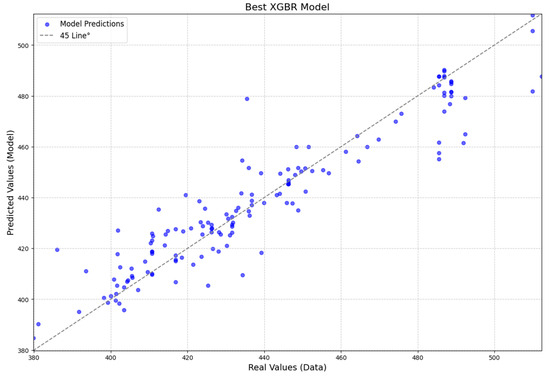
Figure 3.
Results predicted (model) vs. observed (data) graph for the extreme gradient boosting algorithm.
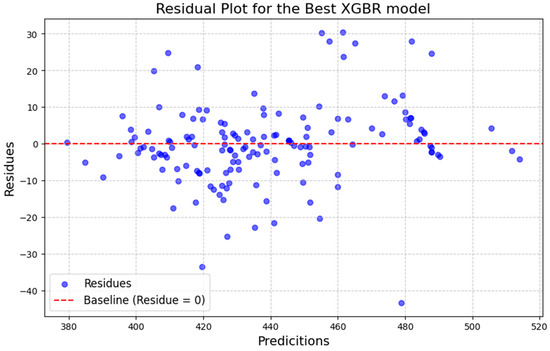
Figure 4.
Residuals graph for the extreme gradient boosting algorithm.
4. Discussion
4.1. Laboratory and Field
Some parameters do not follow a normal distribution because their skewness and/or kurtosis values fall outside the typical range of −2 to 2 expected for a normal distribution. (Table 1). For evaluations involving conventional parametric statistics, it is sometimes necessary to attempt transformations, as, for example, in the case of statistics related to mean comparisons. In the case of multiple linear regressions, normality must be present in the residuals (errors) of the model, but not necessarily in the independent or dependent variables [40,41].
4.2. Hyperparameter Optimization Evaluation
During the hyperparameter optimization stage, we observed that the maximum coefficient of variation was 21% among all evaluated seeds. This result indicates moderate variability in the model’s performance, suggesting that random initialization and variations in data splits may have a noticeable, though not critical, impact. Nonetheless, the CV values are within an acceptable range, indicating that the models provide reasonably consistent outcomes. This variability emphasizes the importance of using multiple seeds and cross-validation to ensure reliable and generalizable results. Overall, the models remain suitable for the proposed task of basic density prediction in eucalyptus forests [38].
4.3. Classical Statistics
The use of predictive models evaluated through classical statistical techniques is a well-established method. Thus, to confirm the hypothesis of this research, we obtained Equations (1) and (2). This approach aligns with methodologies employed in other studies. For instance, Ref. [42] evaluated Eucalyptus camaldulensis samples using ultrasound and developed density inference models with a determination coefficient of 34%. Similarly, Ref. [43] assessed three conifer species using drilling resistance, which is also one of the methods evaluated in this research, achieving basic density inference models with determination coefficients ranging from 25% to 52%.
Results as good as those obtained in this study using machine learning were achieved with conventional statistics [20], using only the DR variable (R2 = 0.77–0.89). However, it is important to note that direct comparison is difficult because only part of the sample used by the authors [20] consisted of young trees, like those in our research, while the most part of the trees were significantly older. Additionally, the authors’ sampling involved drilling resistance tests conducted near the locations where increment borer samples were taken, increasing the likelihood of obtaining significant correlations. It is also important to emphasize that, in our study, the adoption of multiple parameters was not only aimed at improving the inference models for density, but also at incorporating aspects related to fiber quality into the model.
In the literature, discrepancies are observed in the correlations obtained between density and drilling resistance, depending on how the density was measured. In a study with eucalyptus clones aged 3.5 and 4.5 years, Ref. [44] reported correlations between drilling resistance and density ranging from 54% to 67% when basic density was determined considering the entire tree, and from 72% to 82% when density was measured only at breast height (DBH). On the other hand, Ref. [45] a study with 3-year-old eucalyptus clones found a correlation of 20% when density was obtained from DBH disks, and 74% when density was measured for the entire tree using wood chips. Additionally, the correlation results appear to be influenced by tree age, with higher correlation values observed in older trees [46]. These findings suggest that incorporating different parameters obtained from the tree and its planting site can lead to more robust models for inferring wood properties.
4.4. Optimal Metrics
Comparing the MAE to the mean laboratory value of basic density contextualizes the error, highlighting its practical relevance and confirming the model’s robustness in handling the natural variability of basic density. Evaluating the MAE as a percentage of the mean basic density obtained from laboratory tests, values ranged from 1.61% to 4.90% (Table 5). These results indicate low estimation errors relative to the coefficient of variation in basic density. Such findings suggest that the model effectively captures the variability of the data and provides accurate predictions that align with the observed dispersion of actual values.
When modeling a variable in relation to others, it is essential to always consider the composition of the dataset, its size, and how the variables within the dataset relate to each other. It is important to highlight that this study utilized a dataset consisting of trees planted at varying spacings and locations—factors that significantly influence density. However, these variables were not explicitly modeled in this phase of the research. While the model could potentially be improved by adding these factors to the dataset, this was not the objective of this paper, which aims to compare conventional techniques and machine learning approaches in modeling data for density inference.
When graphically analyzing the dispersion of predicted versus actual data (Figure 3), where the intersection of the data are concentrated near the 45-degree line dividing the graph, it suggests that the model is capable of generalizing the data effectively and predicting new data with efficiency. Furthermore, the residuals are randomly distributed and do not show a trend (Figure 4). This indicates that the model does not exhibit bias, overfitting, or underfitting issues, further supporting its robustness and reliability [37].
The research developed by [32] presented predicted vs. observed plots and residual analyses that were comparable to those obtained in this study (Figure 3 and Figure 4). Although their study utilized a database approximately 4.5 times larger than ours—resulting in a more robust training dataset—and included additional variables such as basal area and number of stems per hectare, it did not incorporate nondestructive testing results. Despite working with a smaller database, our study achieved metrics of a similar magnitude, demonstrating the effectiveness of the selected variables and modeling approaches.
For species different than those examined in this research (e.g., Douglas-fir, fir hybrids, acacias, and species from the Brazilian Cerrado), with tree ages ranging from 32 to 50 years, the literature reports R2 values between 50% and 80%. These studies employed various algorithms and architectures such as artificial neural networks (ANN), classification and regression trees (CART), and support vector machines (SVM) [33,34,47,48]. These performance ranges are closer to those obtained in the present study, where R2 values ranged from 19% to 89% (Table 2 and Table 3).
The results from the literature make it clear that the database size and variable selection significantly impact model performance, and that the incorporation of nondestructive testing methods provides a novel contribution of this study to the field. In addition to enhancing predictive accuracy, nondestructive testing data introduce information about the quality of the fiber produced, which is not captured by traditional models based solely on mass and volumetric variables [25,26,27]. This added dimension positions nondestructive methods as valuable tools for advancing wood quality assessments, addressing the gaps in current modeling approaches.
The integration of non-destructive testing (NDT) data into machine learning models enhances accuracy, robustness, and predictive performance in forestry management. By incorporating NDT-derived variables, models provide a more comprehensive representation of tree properties, enabling the better estimation of key factors, like wood density and timber quality. This improves field operations by reducing the need for frequent visits and optimizing resource allocation. Additionally, the insights gained from NDT tests allow for more tailored management strategies, aligning with both economic and environmental goals. Ultimately, this approach supports sustainable forest management and enhances the competitiveness of the forestry sector.
Although the results indicate the superiority of machine learning methods, some limitations must be considered. Despite the database including trees of different dimensions and ages, all were planted in the same Brazilian state. Factors such as tree spacing, soil type, and the genetic identification of clones were not evaluated, even though they may significantly influence basic density. These aspects will be explored in future studies within this research. Additionally, the interpretation of the models depends on the algorithms used. To better understand the relationships between variables, it is essential to employ specific techniques that allow extracting insights from models that might otherwise be considered black boxes.
From a practical perspective, the importance of our results for forestry management and industry applications lies in the development and analysis of a tool that enables the creation of models incorporating a diverse range of parameters, leading to more robust inferences. Additionally, some of these parameters are already collected by forestry companies in their inventories, allowing for the expanded use of these data for other purposes. Beyond the ability to analyze large datasets, machine learning models can manage the influence of outliers, enhancing both the accuracy and generalization capacity of the results, thereby making them more reliable for practical applications. Since these models are more comprehensive and not derived from limited or biased datasets, they enable the sector to make more confident and informed decisions.
5. Conclusions
Machine learning algorithms, when applied to databases derived from measurements on standing trees and enhanced with data from nondestructive techniques, enable the development of suitable models for accurately inferring the basic density of wood.
This study highlighted the superior performance of machine learning models compared to those derived from classical statistical approaches. While classical methods offer simplicity and interpretability, machine learning models demonstrated significantly higher predictive accuracy and better generalization. Moreover, integrating data from nondestructive methods into the models not only improved performance, but also incorporated valuable information about fiber quality, an aspect overlooked by traditional mass and volumetric models.
These findings underscore the importance of leveraging advanced modeling techniques in conjunction with robust datasets and interpretable frameworks. Such an approach enhances confidence in machine learning applications and supports their integration into forest management and industrial decision-making, offering a pathway toward more efficient and sustainable use of timber resources.
Author Contributions
Conceptualization, R.G.M.L. and R.G.; methodology, R.G.M.L. and R.G.; software, R.G.M.L.; validation, R.G.M.L. and R.G.; formal analysis, R.G.M.L.; investigation, R.G.M.L.; resources, R.G.; data curation, R.G.M.L.; writing—original draft preparation, R.G.M.L. and R.G.; writing—review and editing, R.G.M.L. and R.G.; visualization, R.G.M.L.; supervision, R.G.; project administration, R.G.M.L.; funding acquisition, R.G.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the São Paulo Research Foundation (FAPESP), grant number 2022/14731-6 and the publication supported by Federal Agency for Support and Evaluation of Graduate Education (CAPES), grant number SCBA 2049/2023/88881.907381/2023-01.
Data Availability Statement
The datasets presented in this article are not readily available due to a confidentiality agreement signed with the partner company. This agreement restricts the disclosure of certain proprietary and sensitive data belonging to the company. Requests to access the datasets should be directed to rafael@valoramadeira.com, and access will be evaluated on a case-by-case basis in compliance with the confidentiality terms.
Acknowledgments
We thank the pulp and paper company Suzano S.A. (Salvador, Brazil) for their logistical support and supply of eucalyptus clones for this research, and the Laboratory of Nondestructive Testing—LabEND (FEAGRI/UNICAMP) for their assistance with field and laboratory trials.
Conflicts of Interest
Author Rafael Gustavo Mansini Lorensani was employed by the company Valora Madeira Classificação e Inspeção Ltda. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Topaloglu, E.; Nurgül, A.Y.; Altun, L.; Serdar, B. Effect of altitude and aspect on various wood properties of Oriental beech (Fagus orientalis Lipsky) wood. Turk. J. Agric. Forestry 2016, 40, 397–406. [Google Scholar] [CrossRef]
- Mauri, R.; Oliveira, J.T.S.; Filho, M.T.; Rosado, A.M.; Paes, J.B.; Calegario, N. Wood density of clones of Eucalyptus urophylla × Eucalyptus grandis in different conditions of growth. Rev. Floresta 2015, 45, 193–202. [Google Scholar] [CrossRef]
- Alves Ferreira, D.H.A.; Leles, P.S.S.; Machado, E.C.; Abreu, A.H.M.; Abilio, F.M. Crescimento de clone de Eucalyptus urophylla × E. grandis em diferentes espaçamentos. Rev. Floresta 2014, 44, 431–440. [Google Scholar] [CrossRef]
- Lasserre, J.P.; Mason, E.; Watt, M.S.; Moore, J.R. Influence on initial planting spacing and genotype on microfibril angle, wood density, fibre properties and modulus of elasticity in Pinus radiata D. Don corewood. For. Ecol. Manag. J. 2009, 258, 1924–1931. [Google Scholar] [CrossRef]
- Merlo, E.; Zas, R.; Piñeiro, G.; Pedras, F. Variabilidad de parámetros de calidad de madera entre y dentro de procedencias de Pseudo Tsugamenziesii. Cuad. Soc. Esp. Cie. Forestales 2008, 24, 262–266. [Google Scholar]
- Roth, B.E.; Li, X.; Huber, D.A.; Peter, G.F. Effects of management intensity, genetics and planting density on wood stiffness in a plantation of juvenile loblolly pine in the southeastern USA. For. Ecol. Manag. 2007, 246, 155–162. [Google Scholar] [CrossRef]
- Wilkins, A.P.; Horne, R. Wood density variation of young plantation grown Eucalyptus grandis in response to silvicultural treatments. Forest Ecol. Manag. 1991, 40, 39–50. [Google Scholar] [CrossRef]
- Lorensani, R.G.M.; Alves, C.S.; Gonçalves, R. Prediction of basic density using parameters measured on trees. In Proceedings of the 19th International Nondestructive Testing and Evaluation of Wood Symposium, Rio de Janeiro, Brazil, 22–25 September 2015; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015. [Google Scholar]
- Wang, X.; Carter, P.; Ross, R.J.; Brashaw, B.K. Acoustic assessment of wood quality of raw forest materials—A path to increased profitability. Forest Prod. J. 2007, 57, 6–14. [Google Scholar]
- Wang, X.; Ross, R.J.; Carter, P.; Harvey, C.H. Acoustic evaluation of wood quality in standing trees. Part I. Acoustic wave behavior. Wood Sci. Technol. 2007, 39, 28–38. [Google Scholar]
- Goncalves, R.; Batista, F.A.F.; Lorensani, R.G.M. Selecting eucalyptus clones using ultrasound test on standing trees. For. Prod. J. 2013, 63, 112–118. [Google Scholar] [CrossRef]
- Goncalves, R.; Pedroso, C.B.; Massak, M.V. Acoustic bending properties in Pinus elliottii beams obtained from trees of different ages. J. Wood Sci. 2013, 59, 127–132. [Google Scholar] [CrossRef]
- Gonçalves, R.; Lorensani, R.G.M.; Ruy, M.; Veiga, N.S.; Müller, G.; da Silva Alves, C.; Martins, G.A. Evolution of acoustical, geometrical, physical, and mechanical parameters from seedling to cutting age in Eucalyptus clones used in the pulp and paper industries in Brazil. For. Prod. J. 2019, 69, 5–16. [Google Scholar] [CrossRef]
- Gonçalves, R.; Lorensani, R.G.M.; Merlo, E.; Santaclara, O.; Touza, M.; Guaita, M.; Lario, F.J. Modeling of wood properties from parameters obtained in nursery seedlings. Can. J. For. Res. 2018, 48, 621–628. [Google Scholar] [CrossRef]
- Gendvilas, V.; Downes, G.M.; Neyland, M.; Hunt, M.; Jacobs, A.; O’Reilly-Wapstra, J. Friction correction when predicting wood basic density using drilling resistance. Holzforschung 2021, 75, 508–516. [Google Scholar] [CrossRef]
- Nickolas, H.; Williams, D.; Downes, G.; Harrison, P.A.; Vaillancourt, R.E.; Potts, B.M. Application of resistance drilling to genetic studies of growth, wood basic density and bark thickness in Eucalyptus globulus. Aust. For. 2020, 83, 172–179. [Google Scholar] [CrossRef]
- de Pádua, F.A.; Tomeleri, J.O.P.; Franco, M.P.; da Silva, J.R.M.; Trugilho, P.F. Recommendation of non-destructive sampling method for density estimation of the Eucalyptus wood. Maderas-Cienc. Tecnol. 2019, 21, 565–572. [Google Scholar] [CrossRef]
- Kharrat, W.; Koubaa, A.; Khlif, M.; Bradai, C. Intra-ringwood density and dynamic modulus of elasticity profiles for black spruce and jack pine from X-ray densitometry and ultrasonicwave velocity measurement. Forests 2019, 10, 569. [Google Scholar] [CrossRef]
- Liu, F.; Xu, P.; Zhang, H.; Guan, C.; Feng, D.; Wang, X. Use of time-of-flight ultrasound to measure wave speed in poplar seedlings. Forests 2019, 10, 682. [Google Scholar] [CrossRef]
- Downes, G.M.; Lausberg, M.; Potts, B.M.; Pilbeam, D.L.; Bird, M.; Bradshaw, B. Application of the IML Resistograph to the infield assessment of basic density in plantation eucalypts. Aust. For. 2018, 81, 177–185. [Google Scholar] [CrossRef]
- Fundova, I.; Funda, T.; Wu, H.X. Non-destructive wood density assessment of Scots pine (Pinus sylvestris L.) using Resistograph and Pilodyn. PLoS ONE 2018, 13, e0204518. [Google Scholar] [CrossRef]
- Carrillo, I.; Valenzuela, S.; Elissetche, J.P. Comparative evaluation of Eucalyptus globulus and E. nitens wood and fibre quality. IAWA J. 2017, 38, 105–116. [Google Scholar] [CrossRef]
- Soriano, J.; da Veiga, N.S.; Martins, I.Z. Wood density estimation using the sclerometric method. Eur. J. Wood Wood Prod. 2015, 73, 753–758. [Google Scholar] [CrossRef]
- Sandoz, J.L. Standing Tree Quality Assessments Using Ultrasound. Acta Hortic. 1999, 496, 269–278. [Google Scholar] [CrossRef]
- Proto, A.; Macrì, G.; Bernardini, V.; Russo, D.; Zimbalatti, G. Acoustic evaluation of wood quality with a non-destructive method in standing trees: A first survey in Italy. iForest Biogeosci. For. 2017, 10, 700–706. [Google Scholar] [CrossRef]
- Ondrejka, V.; Gergeľ, T.; Bucha, T.; Pástor, M. Innovative methods of non-destructive evaluation of log quality. For. J. 2020, 67, 3–13. [Google Scholar] [CrossRef]
- Jones, G.; Liziniewicz, M.; Lindeberg, J.; Adamopoulos, S. Non-Destructive Evaluation of Downy and Silver Birch Wood Quality and Stem Features from a Progeny Trial in Southern Sweden. Forests 2023, 14, 2031. [Google Scholar] [CrossRef]
- Aragão, M.D.E.A.; Santos, J.S.; Da Silva, M.L.M. Técnica de mineração de dados aplicada a estimação de volume de árvores de eucalyptus. In Proceedings of the 5a Semana de Engenharia Florestal da Bahia, Vitória da Conquista, Brazil, 14–16 March 2018. [Google Scholar]
- Lima, E.D.S.; De Souza, Z.M.; Montanari, R.; Oliveira, S.R.D.M.; Lovera, L.H.; Farhate, C.V.V. Classification of the initial development of eucalyptus using data mining techniques. Cerne 2017, 23, 201–208. [Google Scholar] [CrossRef]
- Cordeiro, M.A.; Pereira, N.N.d.J.; Binoti, D.H.B.; Binoti, M.L.M.d.S.; Leite, H.G. Estimativa do volume de Acacia mangium utilizando técnicas de redes neurais artificiais e máquinas vetor de suporte. Pesqui. Florest. Bras. 2015, 35, 255–261. [Google Scholar] [CrossRef][Green Version]
- da Silva Binoti ML, M.; Binoti DH, B.; Leite, H.G.; Garcia SL, R.; Ferreira, M.Z.; Rode, R.; da Silva, A.A.L. Redes neurais artificiais para estimação do volume de árvores. Revista Árvore 2014, 38, 283–288. [Google Scholar] [CrossRef]
- Leite, H.G.; Binoti, D.H.B.; Neto, R.R.d.O.; Lopes, P.F.; de Castro, R.R.; Paulino, E.J.; Binoti, M.L.M.d.S.; Colodette, J.L. Redes Neurais artificiais para a estimação da densidade básica da madeira. Sci. For. 2016, 44, 149–154. [Google Scholar] [CrossRef][Green Version]
- Demertzis, K.; Iliadis, L.; Avramidis, S.; El-Kassaby, Y.A. Machine learning use in predicting interior spruce wood density utilizing progeny test information. Neural Comput. Appl. 2017, 28, 505–519. [Google Scholar] [CrossRef]
- Iliadis, L.; Mansfield, S.D.; Avramidis, S.; El-Kassaby, Y.A. Predicting Douglas-fir wood density by artificial neural networks (ANN) based on progeny testing information. Holzforschung 2013, 67, 771–777. [Google Scholar] [CrossRef]
- Nassar, O. Data Leakage in Machine Learning. 2023. Available online: https://www.researchgate.net/publication/378434451_Data_Leakage_in_Machine_Learning (accessed on 31 October 2024).
- Plas, J.V. Python Data Science Handbook. 2016. ISBN 9781491912058. Available online: https://jakevdp.github.io/PythonDataScienceHandbook/ (accessed on 9 September 2024).
- McKinney, W. Python for Data Analysis, 3rd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2012; ISBN 978-1-098-10403-0. [Google Scholar]
- Goldschimidt, R.; Passos, E. Data Mining: Um Guia Prático; Gulf Professional Publishing: Houston, TX, USA, 2005. [Google Scholar] [CrossRef]
- NBR 11941/2003; Madeira—Determinação da Densidade Básica. ABNT—Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2003.
- Sainani, K.L. Dealing With Non-normal Data. PM&R 2012, 4, 1001–1005. [Google Scholar] [CrossRef]
- Chowdhury, S.; Lin, Y.; Liaw, B.; Kerby, L. Evaluation of Tree Based Regression over Multiple Linear Regression for Non-normally Distributed Data in Battery Performance. In Proceedings of the 2022 International Conference on Intelligent Data Science Technologies and Applications (IDSTA), San Antonio, TX, USA, 5–7 September 2022; pp. 17–25. [Google Scholar]
- de Melo, R.R.; Barbosa, K.T.; Beltrame, R.; Acosta, A.P.; Pimenta, A.S.; Mascarenhas, A.R.P. Ultrasound to determine physical-mechanical properties of Eucalyptus camaldulensis wood. Wood Mater. Sci. Eng. 2020, 16, 407–413. [Google Scholar] [CrossRef]
- Yao, J.; Zhao, Y.; Lu, J.; Liu, H.; Wu, Z.; Song, X.; Li, Z. Research on the Wood Density Measurement in Standing Trees though the Micro Drilling Resistance Method. Forests 2024, 15, 175. [Google Scholar] [CrossRef]
- Couto, A.M.; Trugilho, P.F.; Neves, T.A.; Protásio, T.d.P.; de Sá, V.A. Modeling of basic density of wood from Eucalyptus grandis and Eucalyptus urophylla using nondestructive methods. Cerne 2013, 19, 27–34. [Google Scholar] [CrossRef]
- Gouvêa, A.d.F.G.; Trugilho, P.F.; Gomide, J.L.; da Silva, J.R.M.; Andrade, C.R.; Alves, I.C.N. Determinação da densidade básica da madeiras de Eucalyptus por diferentes métodos não destrutivos. Rev. Arvore 2011, 35, 349–358. [Google Scholar] [CrossRef]
- Oliveira, J.T.d.S.; Wang, X.; Vidaurre, G.B. Assessing specific gravity of young Eucalyptus plantation trees using a resistance drilling technique. Holzforschung 2017, 71, 137–145. [Google Scholar] [CrossRef]
- Iglesias, C.; Santos, A.J.A.; Martínez, J.; Pereira, H.; Anjos, O. Influence of heartwood on wood density and pulp properties explained by machine learning techniques. Forests 2017, 8, 20. [Google Scholar] [CrossRef]
- Silva, J.P.M.; Cabacinha, C.D.; Assis, A.L.; Monteiro, T.C.; Júnior, C.A.A.; Maia, R.D. Redes neurais artificiais para estimar a densidade básica de madeiras do cerrado. Pesqui. Florest. Bras. 2018, 38, e201701656. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).