Empirical Relationships of the Characteristics of Standing Trees with the Dynamic Modulus of Elasticity of Japanese Cedar (Cryptomeria japonica) Logs: Case Study in the Kyoto Prefecture
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
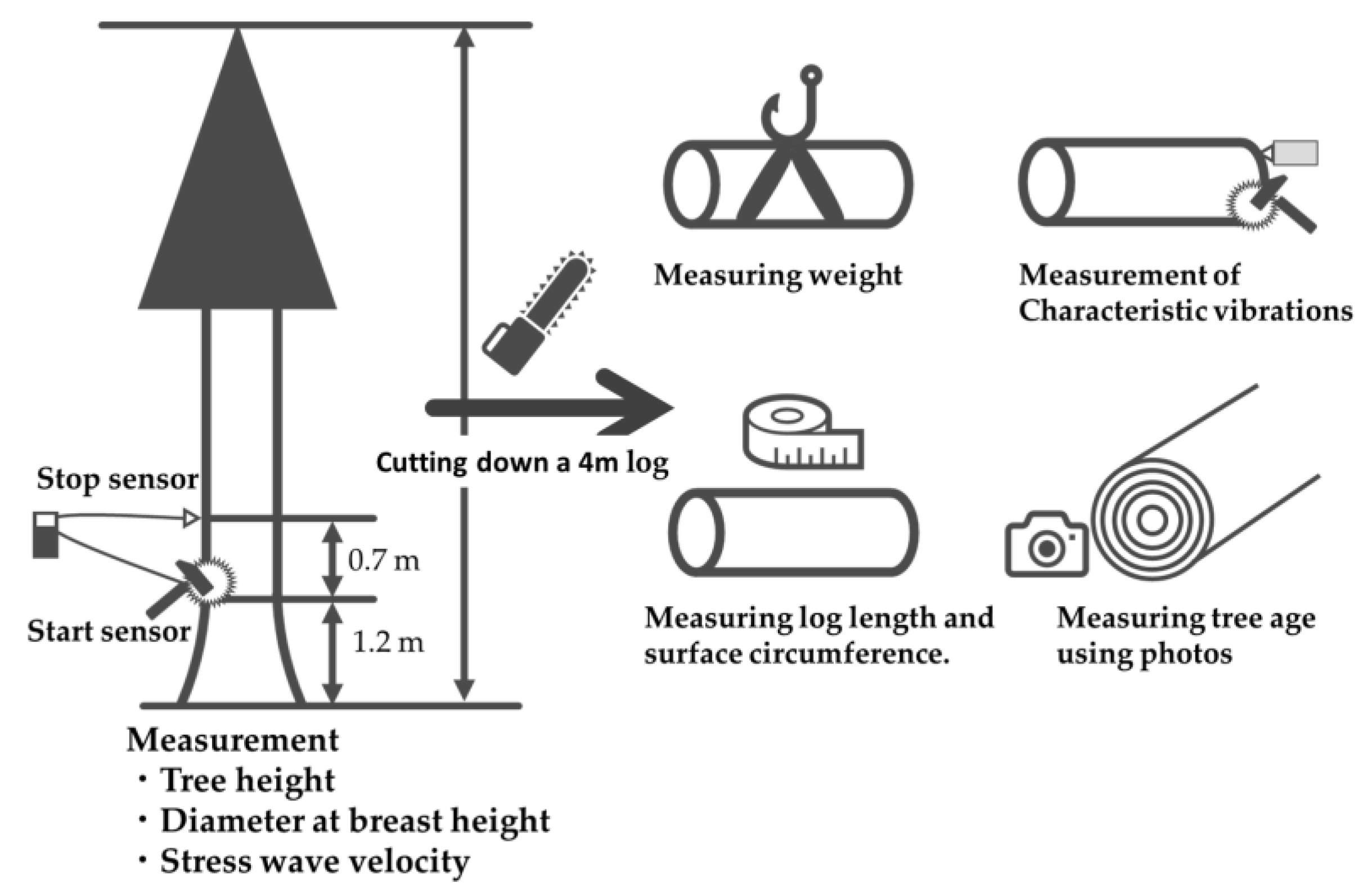
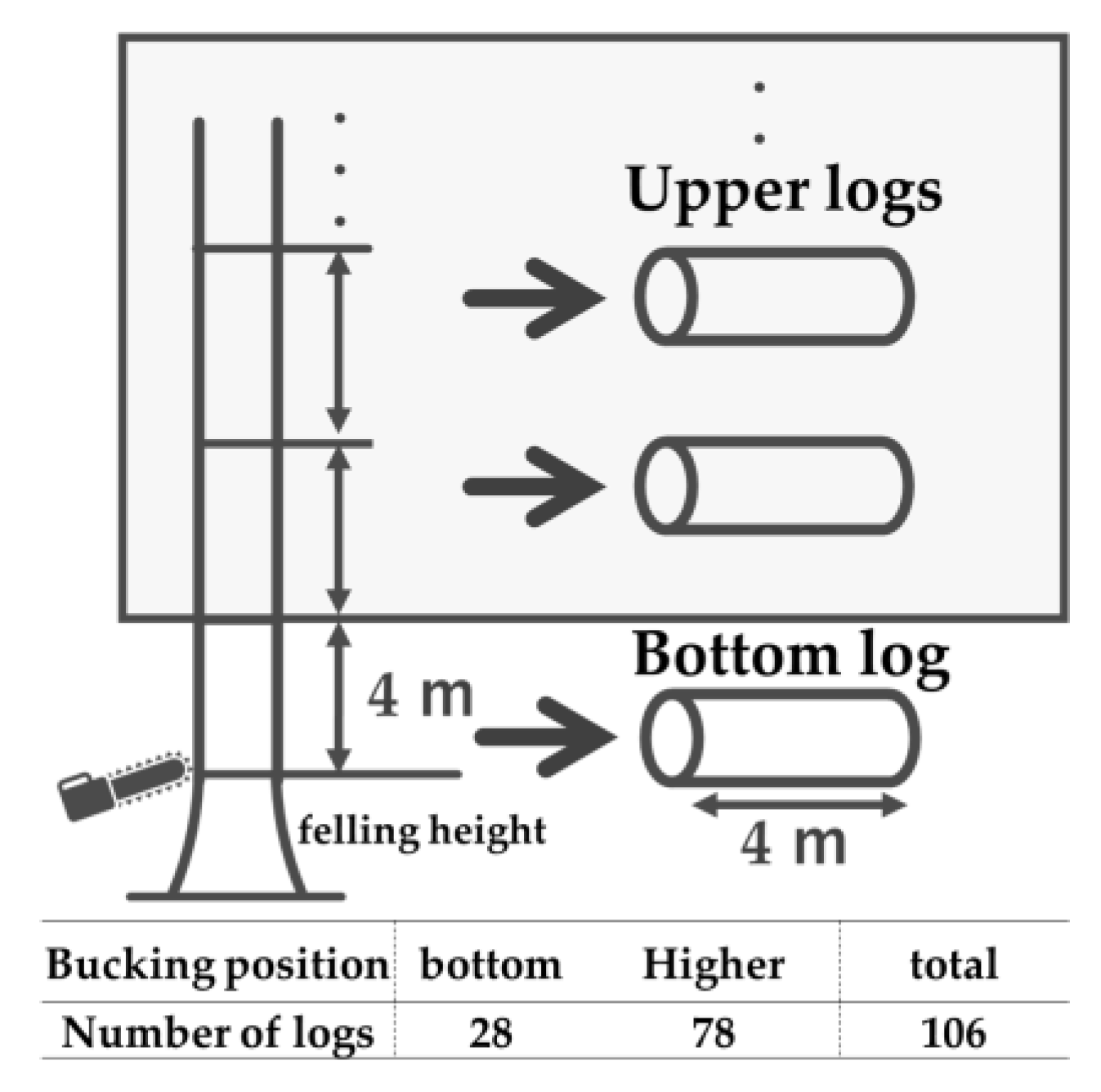
2.2. Sampling and Data Collection
2.3. Data Analyses
2.3.1. Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
2.3.2. Multiple Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
3. Results
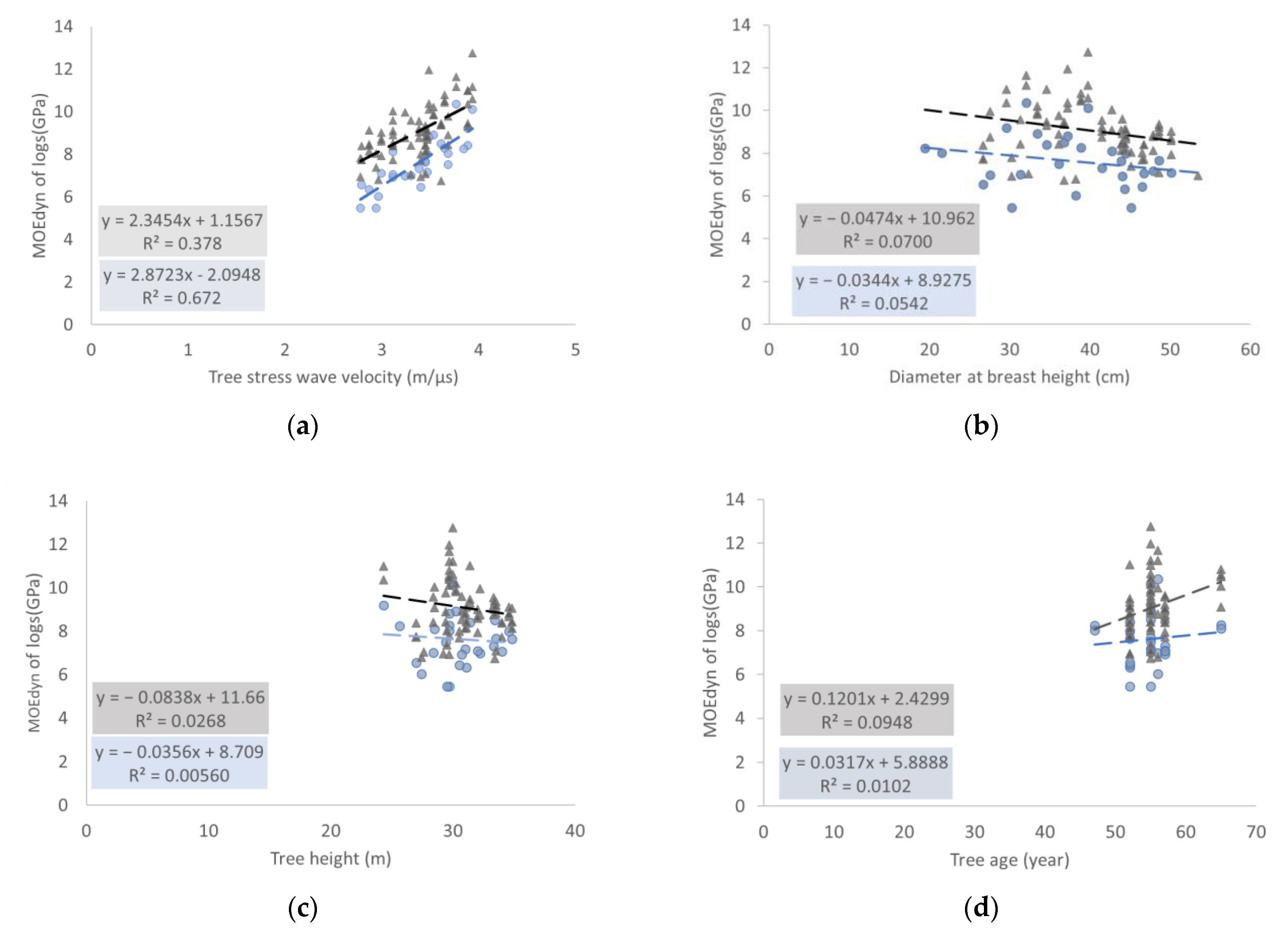
3.1. Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
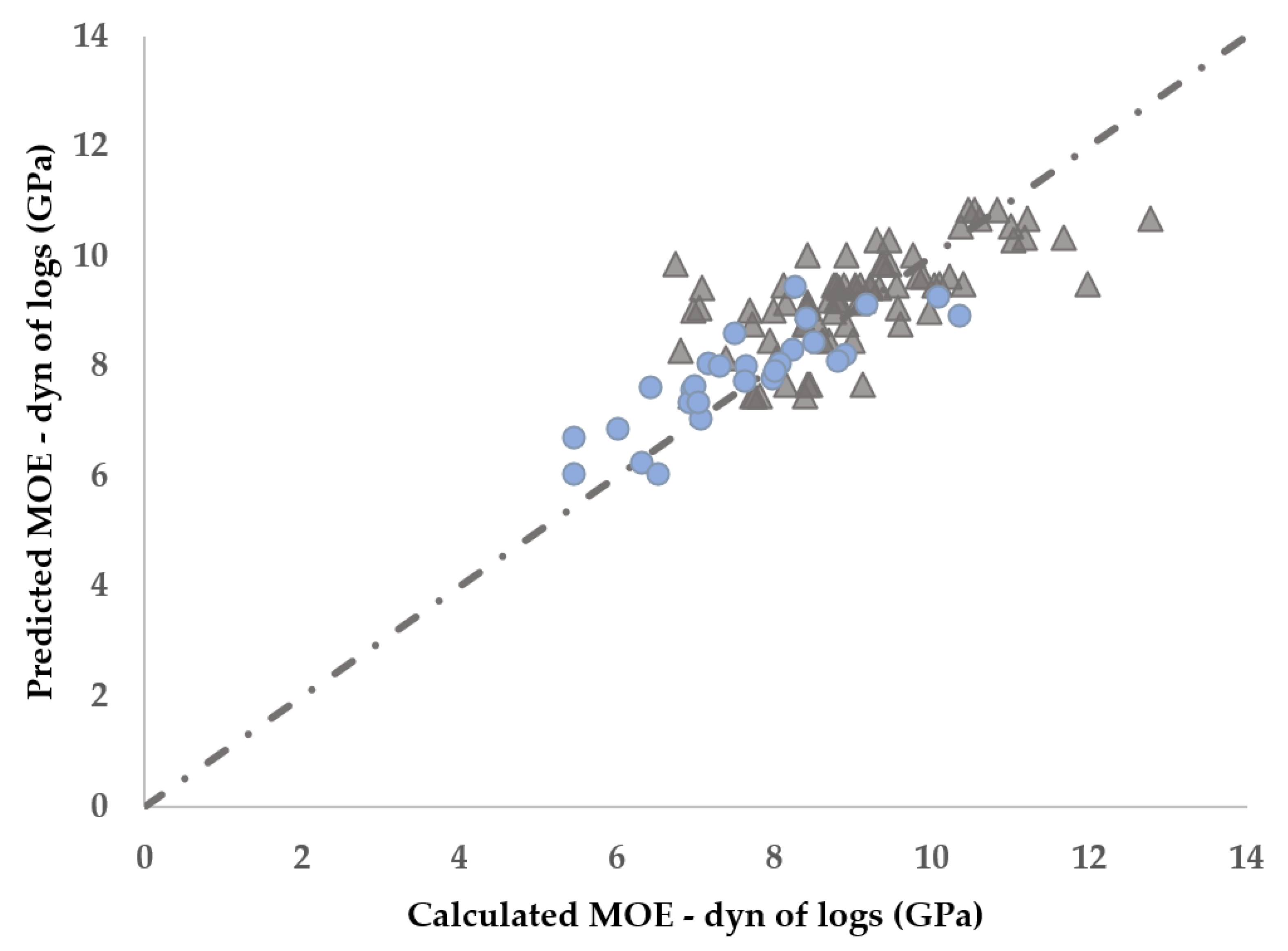
3.2. Multiple Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
4. Discussion
4.1. Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
4.2. Multiple Relationships Between the of the Cut Logs and the Characteristics of Standing Trees
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loss, C.; Tannert, T.; Tesfamariam, S. State-of-the-art review of displacement-based seismic design of timber buildings. Constr. Build. Mater. 2018, 191, 481–497. [Google Scholar] [CrossRef]
- González-Retamal, M.; Forcael, E.; Saelzer-Fuica, G.; Vargas-Mosqueda, M. From trees to skyscrapers: Holistic review of the advances and limitations of multi-storey timber buildings. Buildings 2022, 12, 1263. [Google Scholar] [CrossRef]
- Barrette, J.; Achim, A.; Auty, D. Impact of intensive forest management practices on wood quality from conifers: Literature review and reflection on future challenges. Curr. For. Rep. 2023, 9, 101–130. [Google Scholar] [CrossRef]
- Ikeda, K.; Arima, K. Quality evaluation of standing trees by a stress-wave propagation method and its application II. Evaluation of sugi stands and application to production of sugi (Cryptomeria japonica D. Don) structural square sawn timber. JWRS 2000, 46, 189–196. [Google Scholar]
- Moore, J.R.; Lyon, A.J.; Searles, G.J.; Lehneke, S.A.; Ridley-Ellis, D.J. Within- and between-stand variation in selected properties of Sitka spruce sawn timber in the UK: Implications for segregation and grade recovery. Ann. For. Sci. 2013, 70, 403–415. [Google Scholar] [CrossRef]
- Butler, M.A.; Dahlen, J.; Eberhardt, T.; Montes, C.; Antony, F.; Daniels, R. Acoustic evaluation of loblolly pine tree- and lumber-length logs allows for segregation of lumber modulus of elasticity, not for modulus of rupture. Ann. For. Sci. 2017, 74, 20. [Google Scholar] [CrossRef]
- Schimleck, L.; Dahlen, J.; Apiolaza, L.A.; Downes, G.; Emms, G.; Evans, R.; Moore, J.; Pâques, L.; Van den Bulcke, J.; Wang, X. Non-destructive evaluation techniques and what they tell us about wood property variation. Forests 2019, 10, 728. [Google Scholar] [CrossRef]
- Wessels, C.B.; Malan, F.S.; Rypstra, T. A review of measurement methods used on standing trees for the prediction of some mechanical properties of timber. Eur. J. For. Res. 2011, 130, 881–893. [Google Scholar] [CrossRef]
- Bucur, V. A Review on Acoustics of Wood as a Tool for Quality Assessment. Forests 2023, 14, 1545. [Google Scholar] [CrossRef]
- Tumenjargal, B.; Ishiguri, F.; Takahashi, Y.; Nezu, I.; Baasan, B.; Chultem, G.; Aiso-Sanada, H.; Ohshima, J.; Yokota, S. Predicting the bending properties of Larix sibirica lumber using nondestructive-testing methods. Int. Wood Prod. J. 2020, 11, 115–121. [Google Scholar] [CrossRef]
- Tsushima, S.; Koga, S.; Oda, K.; Shiraishi, S. Effects of initial spacing on growth and wood properties of Sugi (Cryptomeria japonica) cutting cultivars. JWRS 2006, 52, 196–205. [Google Scholar] [CrossRef]
- Justin, E.; Anton, K.; David, M.; Drew, C.; Brand, W. The effect of planting spacing on Pinus patula stem straightness, microfibril angle and wood density. For. Int. J. For. Res. 2018, 91, 247–258. [Google Scholar] [CrossRef]
- Teraoka, Y.; Takata, K.; Koga, S. Use of trunk-MOE of Japanese cedar as forestry management information. JFP 2001, 35, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Kijidani, Y.; Kitahara, R. Variation of wood properties with height position in the stems of Obi-Sugi cultivars. JWRS 2009, 55, 198–206. [Google Scholar] [CrossRef][Green Version]
- Tsushima, S.; Koga, S.; Oda, K.; Shiraishi, S. Growth and wood Properties of Sugi (Cryptomeria japonica) cultivars planted in the Kyushu region. JWRS 2005, 51, 394–401. [Google Scholar] [CrossRef]
- Hiraiwa, T.; Ishiguri, F.; Endo, R.; Takeyama, F.; Tanabe, J.; Kameyama, Y.; Ohno, H.; Takashima, Y.; Iizuka, K.; Yokota, S. Wood properties of Sanbu-Sugi Cultivar of Sugi (Cryptomeria japonica D. Don) planted in Chiba Prefecture. Japan. J. Soc. Mater. Sci. 2014, 63, 635–640. [Google Scholar] [CrossRef][Green Version]
- Japan Meteorological Agency Transport and Tourism. Annual Climate Data for Kyoto Prefecture for the Year 2023. Available online: https://www.data.jma.go.jp/obd/stats/etrn/view/annually_s.php?prec_no=61&block_no=47759&year=2023&month=&day=&view= (accessed on 16 July 2024).
- Wang, X. Acoustic measurements on trees and logs: A review and analysis. Wood Sci. Technol. 2013, 47, 965–975. [Google Scholar] [CrossRef]
- Gallego, A.; Ripoll, M.A.; Timbolmas, C.; Rescalvo, F.; Suarez, E.; Valverde, I.; Rodríguez, M.; Navarro, F.B. Modulus of elasticity of I-214 young poplar wood from standing trees to sawn timber: Influence of the age and stand density. Eur. J. Wood Prod. 2021, 79, 1225–1239. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 1974. [Google Scholar] [CrossRef]
- Lindström, H.; Reale, M.; Grekin, M. Using non-destructive testing to assess modulus of elasticity of Pinus sylvestris trees. Scand. J. For. Res. 2009, 24, 247–257. [Google Scholar] [CrossRef]
- Arriaga, F.; Wang, X.; Íñiguez-González, G.; Llana, D.F.; Esteban, M.; Niemz, P. Mechanical Properties of Wood: A Review. Forests 2023, 14, 1202. [Google Scholar] [CrossRef]
- Watanabe, H.; Tsutsumi, J.; Kojima, K. Studies on juvenile wood. II: Distribution of specific compressive strength and specific compressive Young’s modulus in Sugi (Cryptomeria japonica D. Don) stems. J. Soc. Mater. Sci. 1964, 10, 125–130. [Google Scholar]
- Wang, X. Recent advances in nondestructive evaluation of wood: In-forest wood quality assessments. Forests 2021, 12, 949. [Google Scholar] [CrossRef]
- Nakatani, H.; Kato, A.; Hasegawa, M.; Aiura, H.; Iijima, Y. Structural mechanics study on the damage of tree stems caused by accumulating in the Crown III. Distribution of mechanical properties in tree stem. J. Toyama For. For. Prod. Res. Cent. 1988, 1, 25–33. [Google Scholar]
- Mitsuda, Y.; Ito, S.; Sakamoto, S. Predicting the site index of sugi plantations from GIS-derived environmental factor in Miyazaki Prefecture. J. For. Res. 2007, 12, 177–186. [Google Scholar] [CrossRef]
- Antony, F.; Jordan, L.; Schimleck, L.R.; Clark, A., III; Souter, R.A.; Daniels, R.F. Regional variation in wood modulus of elasticity (stiffness) and modulus of rupture (strength) of planted loblolly pine in the United States. Can. J. For. Res. 2011, 41, 1522–1533. [Google Scholar] [CrossRef]
- Nagashima, K. Forest management based on site suitability: A case study of Odai Town, Mie Prefecture. In Landscape Ecology for Sustainable Society; Hong, S.K., Nakagoshi, N., Eds.; Springer: Tokyo, Japan, 2017; pp. 181–196. [Google Scholar]
- Kuprevicius, A.; Auty, D.; Achim, A.; Caspersen, J. Quantifying the influence of live crown ratio on the mechanical properties of clear wood. Forestry 2013, 86, 361–369. [Google Scholar] [CrossRef]
- Amarasekara, H.; Denne, M.P. Effects of crown size on wood characteristics of Corsican pine in relation to definitions of juvenile wood, crown formed wood and core wood. Forestry 2002, 75, 51–61. [Google Scholar] [CrossRef]
- Diószegi, G.; Molnár, V.E.; Nagy, L.A.; Enyedi, P.; Török, P.; Szabó, S. Testing treecbh in Central European forests: An R package for crown base height detection using high-resolution aerial laser-scanned data. Forestry 2024, 31, cpae044. [Google Scholar] [CrossRef]
- Lim, W.; Park, H.-C.; Park, S.; Seo, J.-W.; Kim, J.; Ko, D.W. Modeling Tree Mortality Induced by Climate Change-Driven Drought: A Case Study of Korean Fir in the Subalpine Forests of Jirisan National Park, South Korea. Forests 2025, 16, 84. [Google Scholar] [CrossRef]
- Auty, D.; Achim, A. The relationship between standing tree acoustic assessment and timber quality in Scots pine and the practical implications for assessing timber quality from naturally regenerated stands. Forestry 2008, 81, 475–487. [Google Scholar] [CrossRef]
- Madhoushi, M.; Daneshvar, S. Predicting the static modulus of elasticity in eastern cottonwood (Populus deltoides) using stress wave non-destructive testing in standing trees. Eur. J. Wood Prod. 2016, 74, 885–892. [Google Scholar] [CrossRef]
| Mean ± SE | Range | ||
|---|---|---|---|
| Tree | Stress-wave velocity (m/μs) | 3.38 ± 0.34 | 2.78–3.93 |
| DBH (cm) | 37.8 ± 8.13 | 19.5–50.2 | |
| Tree height (m) | 30.4 ± 2.51 | 24.3–34.8 | |
| Tree age (year) | 54.8 ± 3.82 | 47.0–65.0 | |
| Log | (GPa) | 8.47 ± 0.86 | 5.46–12.8 |
| ) | 736 ± 70.3 | 574–914 | |
| Characteristic vibration (Hz) | 412 ± 29.1 | 336–478 |
| Model Rank | AIC | ΔAIC | Estimated Coefficients (Standard Error) | ||||
|---|---|---|---|---|---|---|---|
| Intercept | Tree Stress-Wave Velocity | Tree Age | DBH | Tree Height | |||
| A | 285 | 0.00 | −5.06 ** (1.74) | 2.56 ** (0.248) | 0.0870 ** (0.0246) | ||
| B | 288 | 3.00 | −2.79 (2.07) | 2.57 ** (0.145) | 0.0826 ** (0.0243) | −0.0668 * (0.0334) | |
| C | 288 | 3.10 | −4.16 * (1.76) | 2.42 ** (0.248) | 0.0991 ** (0.0245) | −0.0286 * (0.0116) | |
| D | 290 | 4.37 | −0.299 (1.16) | 2.56 ** (0.262) | |||
| E | 292 | 6.42 | 2.03 (1.56) | 2.58 ** (0.257) | −0.0772 (0.0349) | ||
| F | 294 | 9.18 | −3.41 (2.10) | 2.46 ** (0.253) | 0.0948 ** (0.0254) | −0.0228 (0.0146) | −0.0275 (0.0416) |
| G | 296 | 10.87 | 0.74 (1.34) | 2.48 ** (0.266) | −0.0192 (0.0122) | ||
| H | 300 | 14.86 | 2.06 (1.58) | 2.55 ** (0.268) | −0.00595 (0.0147) | −0.0674 (0.0427) | |
| I | 353 | 68.03 | 4.27 (2.00) | 0.112 ** (0.0339) | −0.0526 ** (0.0157) | ||
| Fixed Effects | Random Effects | ||||||
|---|---|---|---|---|---|---|---|
| Top Model | AIC | R2 Fix. | R2 Ran. | Estimated Coefficients (Standard Error) | |||
| Intercept | Tree Stress-Wave Velocity | Tree Age | SD | ||||
| A | 285 | 0.314 | 0.723 | −5.06 ** (1.74) | 2.56 ** (0.248) | 0.0870 ** (0.0246) | 0.720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harada, K.; Nakata, Y.; Nakazawa, M.; Kojiro, K.; Nagashima, K. Empirical Relationships of the Characteristics of Standing Trees with the Dynamic Modulus of Elasticity of Japanese Cedar (Cryptomeria japonica) Logs: Case Study in the Kyoto Prefecture. Forests 2025, 16, 244. https://doi.org/10.3390/f16020244
Harada K, Nakata Y, Nakazawa M, Kojiro K, Nagashima K. Empirical Relationships of the Characteristics of Standing Trees with the Dynamic Modulus of Elasticity of Japanese Cedar (Cryptomeria japonica) Logs: Case Study in the Kyoto Prefecture. Forests. 2025; 16(2):244. https://doi.org/10.3390/f16020244
Chicago/Turabian StyleHarada, Kiichi, Yasutaka Nakata, Masahiko Nakazawa, Keisuke Kojiro, and Keiko Nagashima. 2025. "Empirical Relationships of the Characteristics of Standing Trees with the Dynamic Modulus of Elasticity of Japanese Cedar (Cryptomeria japonica) Logs: Case Study in the Kyoto Prefecture" Forests 16, no. 2: 244. https://doi.org/10.3390/f16020244
APA StyleHarada, K., Nakata, Y., Nakazawa, M., Kojiro, K., & Nagashima, K. (2025). Empirical Relationships of the Characteristics of Standing Trees with the Dynamic Modulus of Elasticity of Japanese Cedar (Cryptomeria japonica) Logs: Case Study in the Kyoto Prefecture. Forests, 16(2), 244. https://doi.org/10.3390/f16020244







