Analysis of the Changes in the Mechanical Properties of Branches of Salix Energy Plants After Shearing
Abstract
1. Introduction
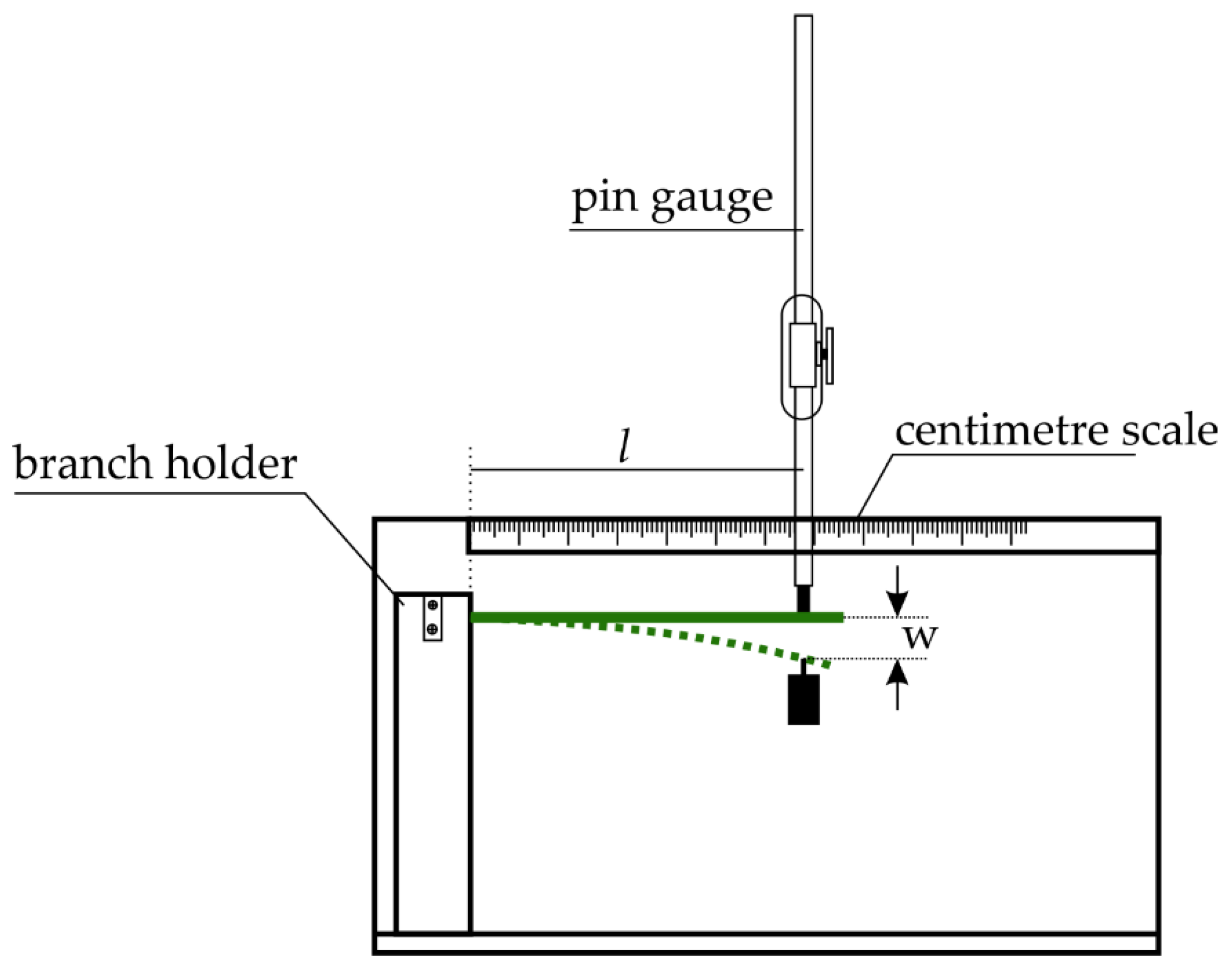
2. Materials and Methods
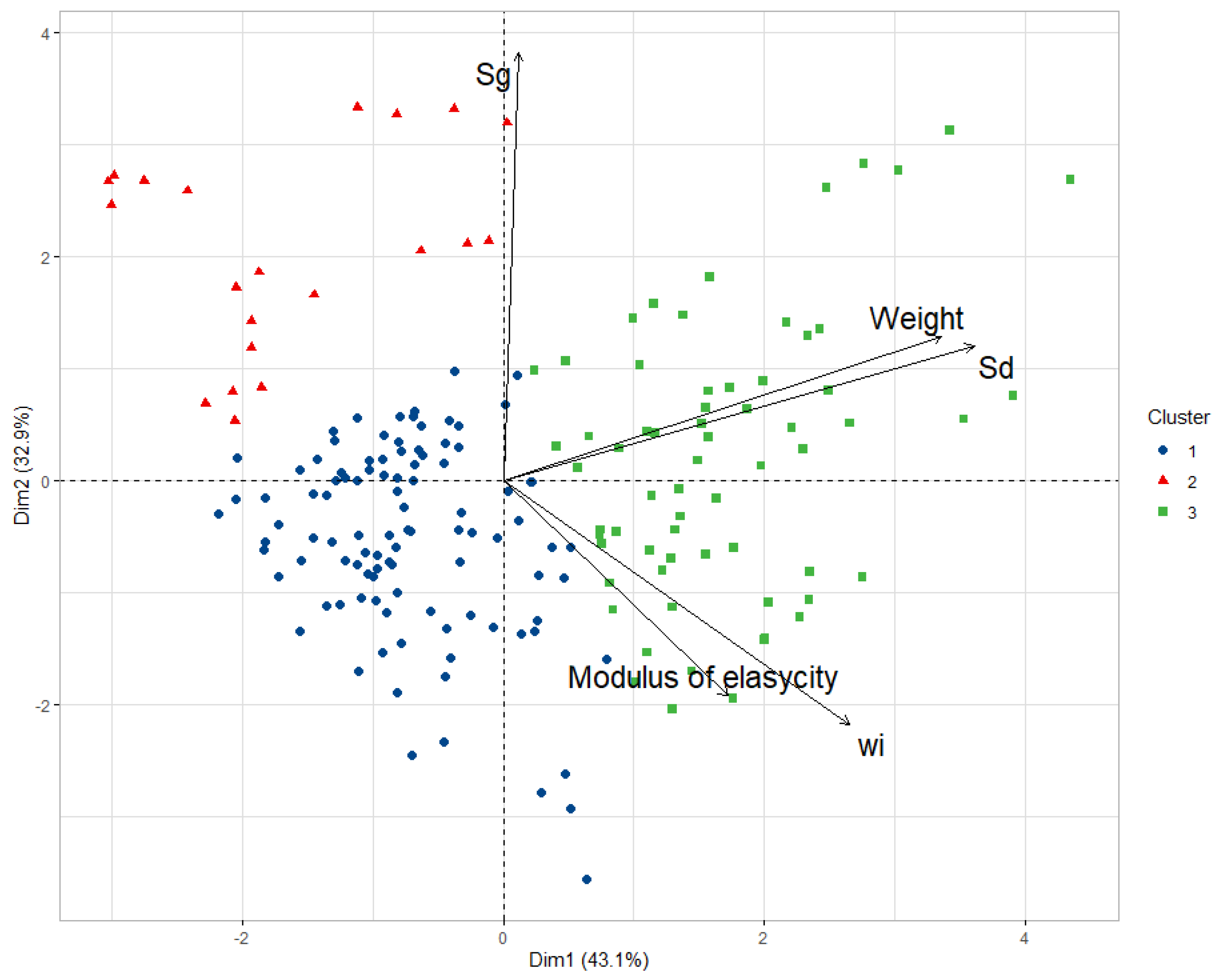
3. Results and Discussion
3.1. Diameters
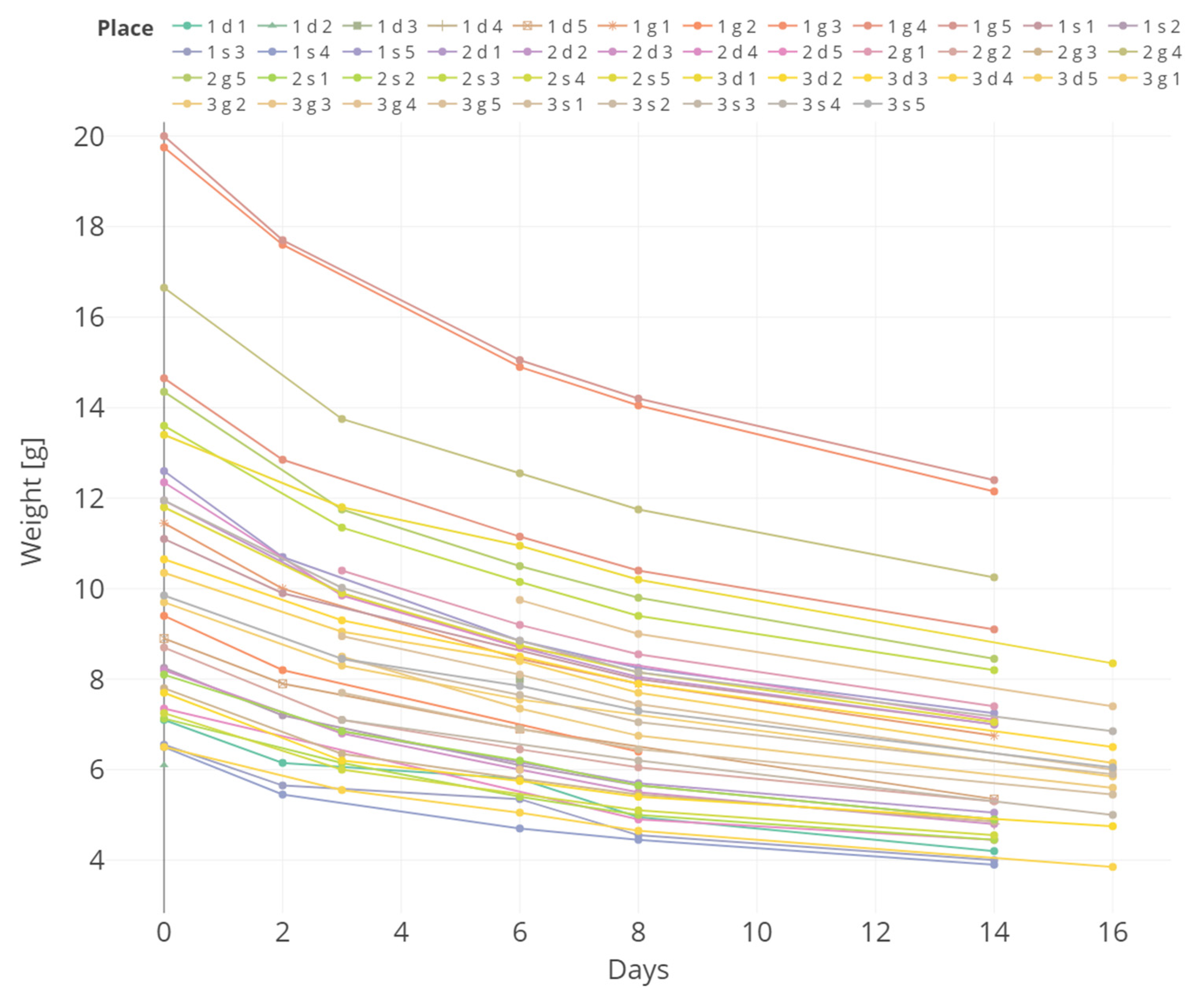
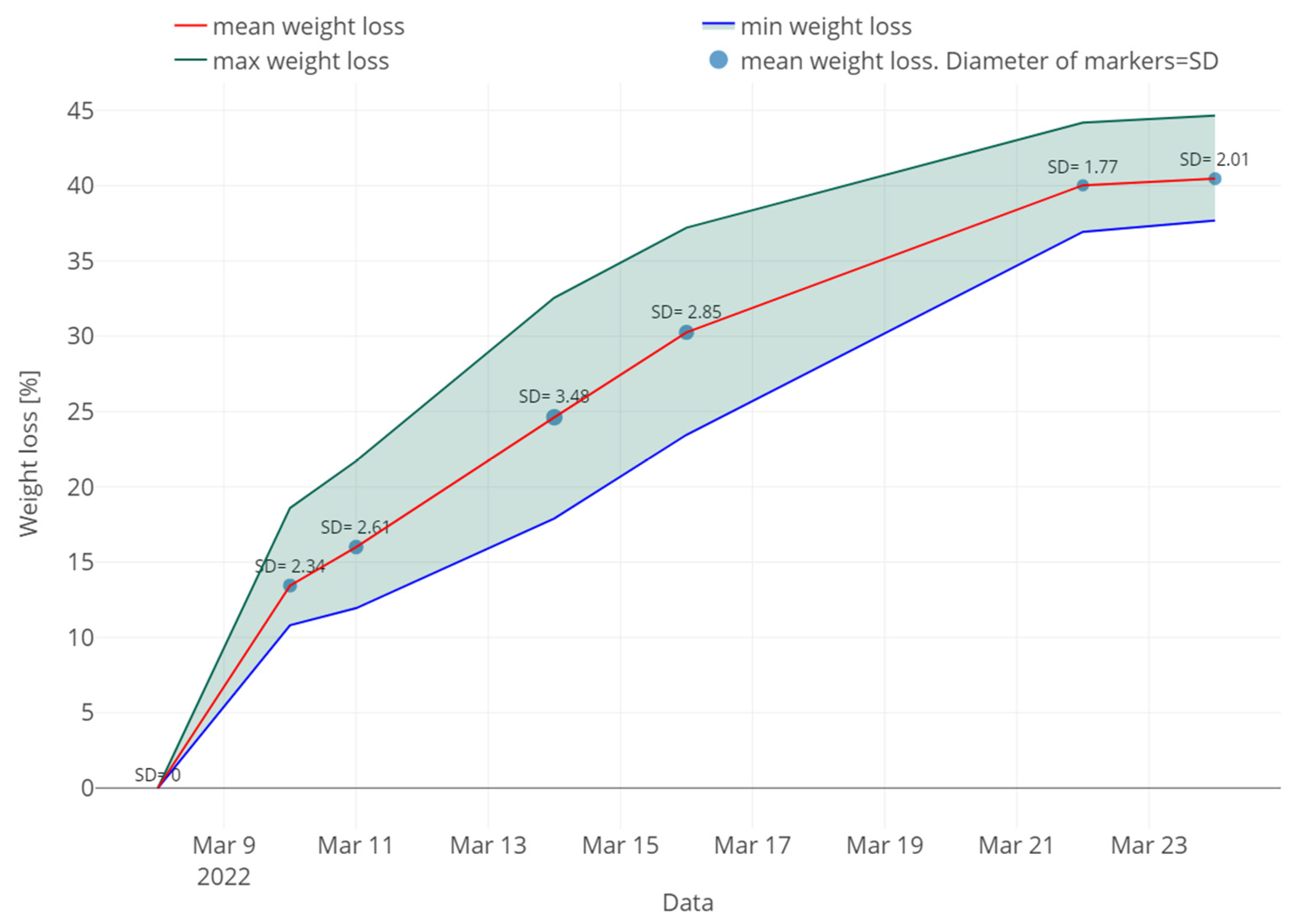
3.2. Weight
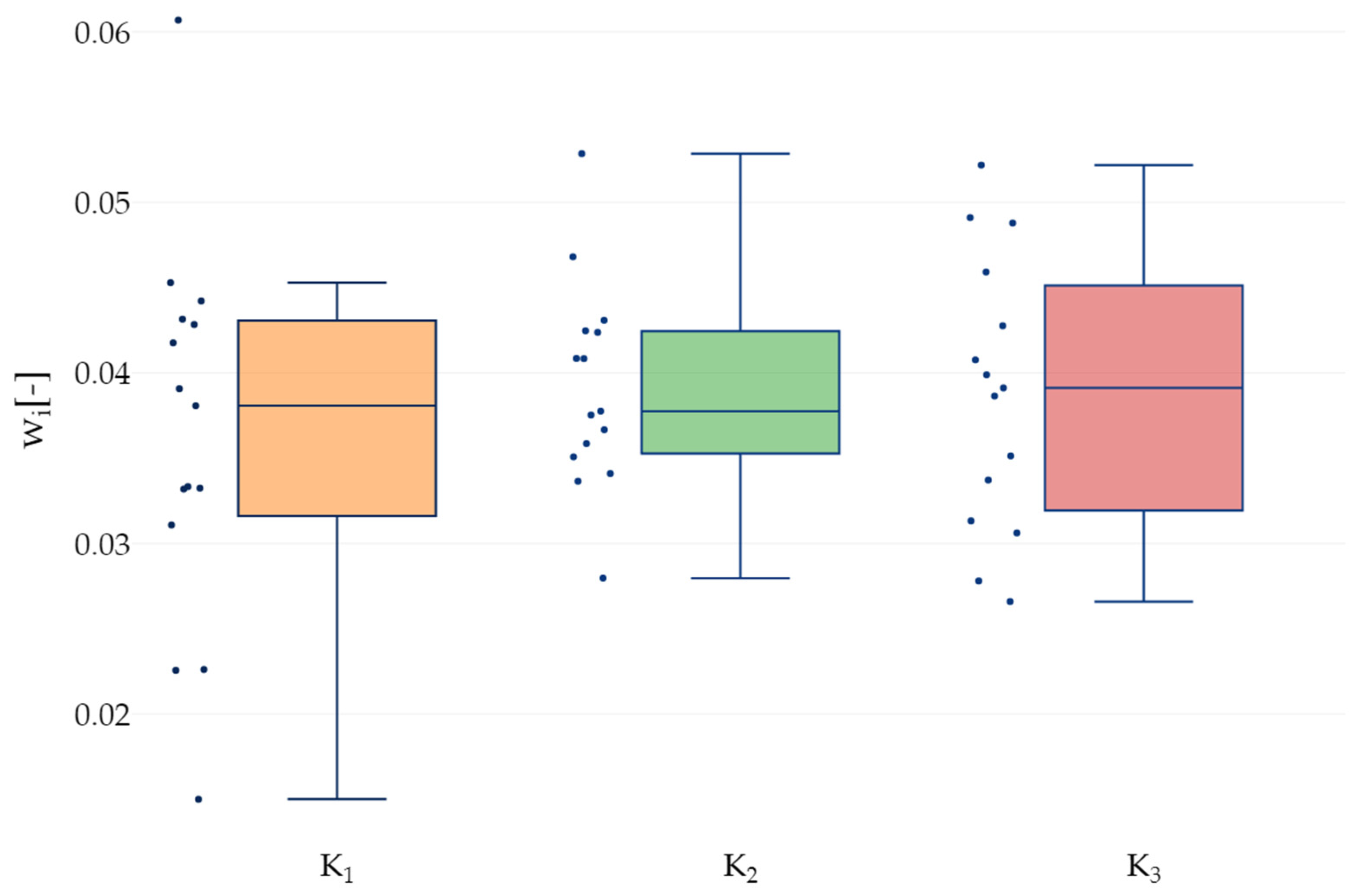
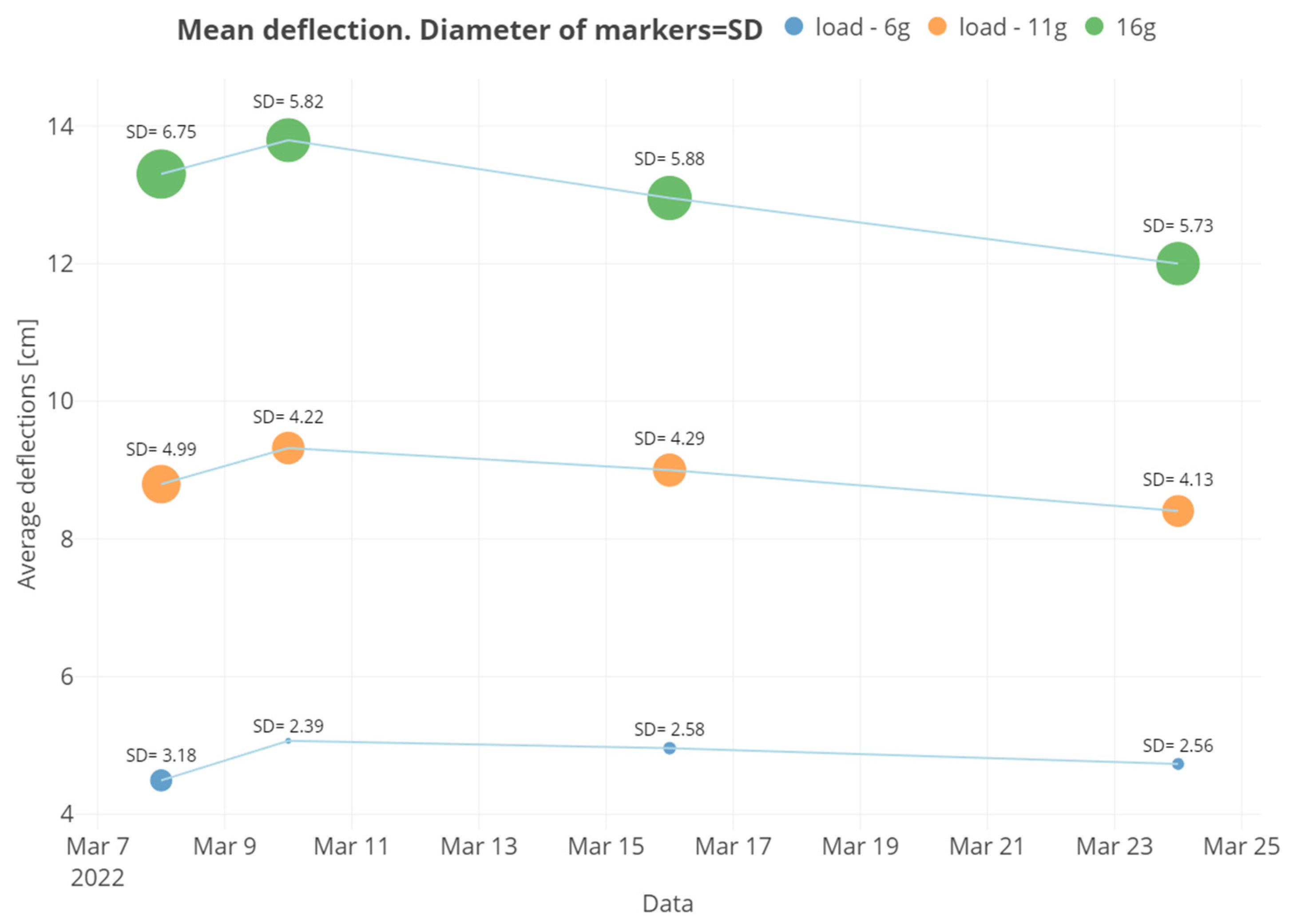
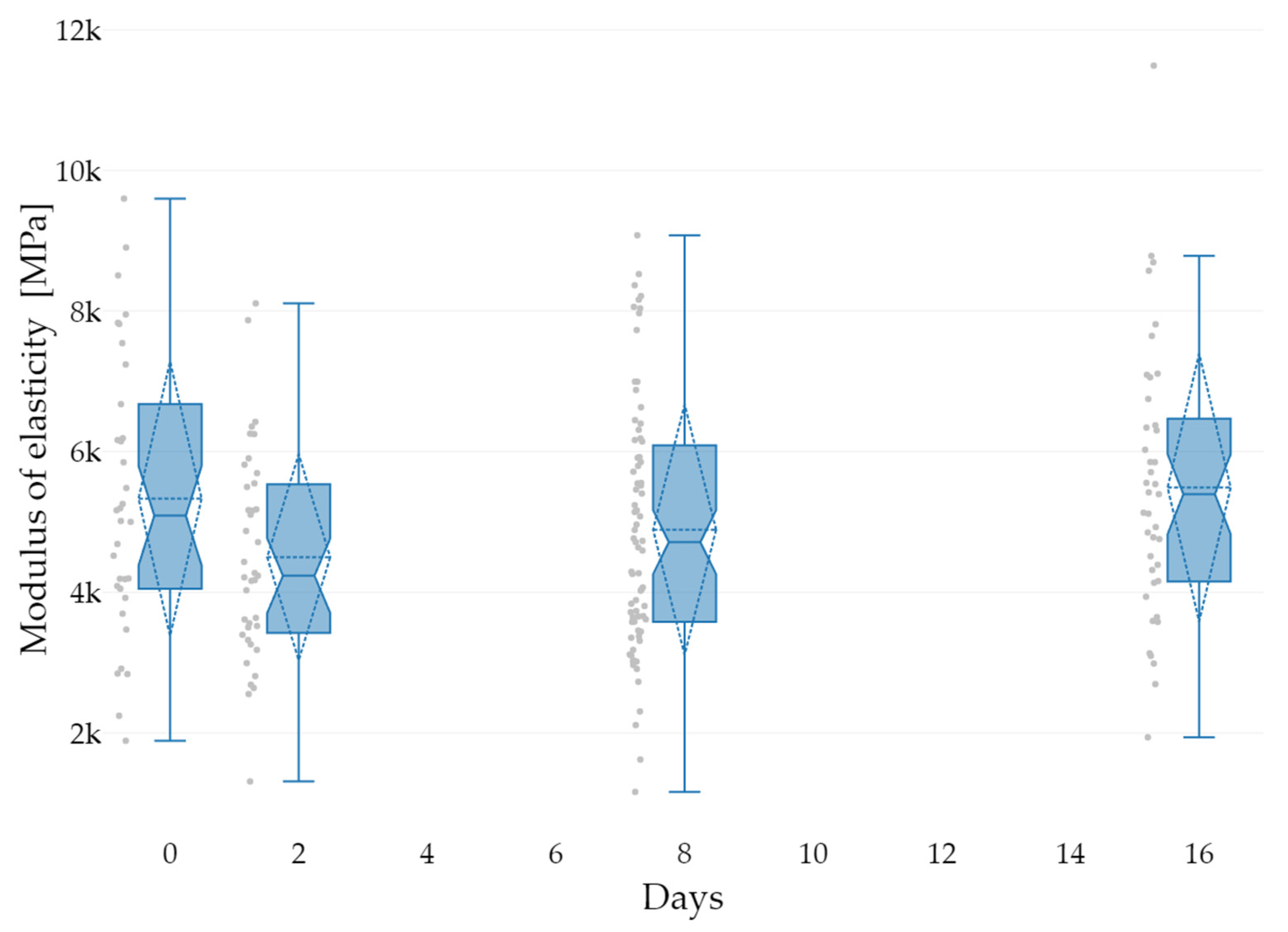
3.3. Deflections and Moduli of Elasticity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ISBN 978-92-9260-537-7; Renewable Energy Statistics 2023. International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2023.
- World Bioenergy Association. Annual Report 2023; World Bioenergy Association: Stockholm, Sweden, 2023. [Google Scholar]
- Słupska, M.; Dyjakon, A.; Stopa, R. Determination of Strength Properties of Energy Plants on the Example of Miscanthus × giganteus, Rosa multiflora and Salix viminalis. Energies 2019, 12, 3660. [Google Scholar] [CrossRef]
- Roman, K.; Roman, M.; Szadkowska, D.; Szadkowski, J.; Grzegorzewska, E. Evaluation of Physical and Chemical Parameters According to Energetic Willow (Salix viminalis L.) Cultivation. Energies 2021, 14, 2968. [Google Scholar] [CrossRef]
- González-García, S.; Mola-Yudego, B.; Dimitriou, I.; Aronsson, P.; Murphy, R. Environmental Assessment of Energy Production Based on Long Term Commercial Willow Plantations in Sweden. Sci. Total Environ. 2012, 421, 210–219. [Google Scholar] [CrossRef]
- Tiebel, K.; Leinemann, L.; Hosius, B.; Schlicht, R.; Frischbier, N.; Wagner, S. Seed Dispersal Capacity of Salix caprea L. Assessed by Seed Trapping and Parentage Analysis. Eur. J. For. Res 2019, 138, 495–511. [Google Scholar] [CrossRef]
- Gramlich, S.; Sagmeister, P.; Dullinger, S.; Hadacek, F.; Hoerandl, E. Evolution in Situ: Hybrid Origin and Establishment of Willows (Salix L.) on Alpine Glacier Forefields. Heredity 2016, 116, 531–541. [Google Scholar] [CrossRef]
- Shrivastava, P.; Kumar, R. Soil Salinity: A Serious Environmental Issue and Plant Growth Promoting Bacteria as One of the Tools for Its Alleviation. Saudi J. Biol. Sci. 2015, 22, 123–131. [Google Scholar] [CrossRef]
- Mirck, J.; Zalesny, R.S. Mini-Review of Knowledge Gaps in Salt Tolerance of Plants Applied to Willows and Poplars. Int. J. Phytoremediation 2015, 17, 640–650. [Google Scholar] [CrossRef]
- Martin, P.J.; Stephens, W. Willow Growth in Response to Nutrients and Moisture on a Clay Landfill Cap Soil. I. Growth and Biomass Production. Bioresour. Technol. 2006, 97, 437–448. [Google Scholar] [CrossRef][Green Version]
- Albertsson, J.; Verwijst, T.; Hansson, D.; Bertholdsson, N.-O.; Åhman, I. Effects of Competition between Short-Rotation Willow and Weeds on Performance of Different Clones and Associated Weed Flora during the First Harvest Cycle. Biomass Bioenergy 2014, 70, 364–372. [Google Scholar] [CrossRef]
- Sage. Weed Competition in Willow Coppice Crops: The Cause and Extent of Yield Losses. Weed Res. 1999, 39, 399–411. [Google Scholar] [CrossRef]
- Albertsson, J.; Hansson, D.; Bertholdsson, N.; Åhman, I. Site-related Set-back by Weeds on the Establishment of 12 Biomass Willow Clones. Weed Res. 2014, 54, 398–407. [Google Scholar] [CrossRef]
- Kulig, B.; Gacek, E.; Wojciechowski, R.; Oleksy, A.; Kołodziejczyk, M.; Szewczyk, W.; Klimek-Kopyra, A. Biomass Yield and Energy Efficiency of Willow Depending on Cultivar, Harvesting Frequency and Planting Density. Plant Soil Environ. 2019, 65, 377–386. [Google Scholar] [CrossRef]
- Dragusanu, V.; Lunguleasa, A.; Spirchez, C.; Scriba, C. Some Properties of Briquettes and Pellets Obtained from the Biomass of Energetic Willow (Salix viminalis L.) in Comparison with Those from Oak (Quercus Robur). Forests 2023, 14, 1134. [Google Scholar] [CrossRef]
- Stolarski, M.J.; Krzyżaniak, M.; Warmiński, K.; Załuski, D.; Olba-Zięty, E. Willow Biomass as Energy Feedstock: The Effect of Habitat, Genotype and Harvest Rotation on Thermophysical Properties and Elemental Composition. Energies 2020, 13, 4130. [Google Scholar] [CrossRef]
- Bala-Litwiniak, A.; Musiał, D. Computational and Experimental Studies of Selected Types of Biomass Combustion in a Domestic Boiler. Materials 2022, 15, 4826. [Google Scholar] [CrossRef]
- Dudits, D.; Cseri, A.; Török, K.; Vankova, R.; Dobrev, P.I.; Sass, L.; Steinbach, G.; Kelemen-Valkony, I.; Zombori, Z.; Ferenc, G. Manifestation of Triploid Heterosis in the Root System after Crossing Diploid and Autotetraploid Energy Willow Plants. Genes 2023, 14, 1929. [Google Scholar] [CrossRef]
- Manzone, M.; Balsari, P. Planters Performance during a Very Short Rotation Coppice Planting. Biomass Bioenergy 2014, 67, 188–192. [Google Scholar] [CrossRef]
- Pacaldo, R.S.; Volk, T.A.; Briggs, R.D. Greenhouse Gas Potentials of Shrub Willow Biomass Crops Based on Below- and Aboveground Biomass Inventory Along a 19-Year Chronosequence. Bioenergy Res. 2013, 6, 252–262. [Google Scholar] [CrossRef]
- Heller, M.C.; Keoleian, G.A.; Volk, T.A. Life Cycle Assessment of a Willow Bioenergy Cropping System. Biomass Bioenergy 2003, 25, 147–165. [Google Scholar] [CrossRef]
- Keoleian, G.A.; Volk, T.A. Renewable Energy from Willow Biomass Crops: Life Cycle Energy, Environmental and Economic Performance. Crit. Rev. Plant Sci. 2005, 24, 385–406. [Google Scholar] [CrossRef]
- Dimitriou, I.; Aronsson, P. Willows for Energy and Phytoremediation in Sweden. Unasylva 2005, 56, 47. [Google Scholar]
- Börjesson, P. Produktionsförutsättningar För Biobränslen Inom Svenskt Jordbruk. IMES/EESS Rapp. 2007, 61. Available online: https://portal.research.lu.se/files/5617156/609151.pdf (accessed on 20 January 2025).
- Dimitriou, I.; Baum, C.; Baum, S.; Busch, G.; Schulz, U.; Köhn, J.; Lamersdorf, N.; Leinweber, P.; Aronsson, P.; Weih, M. The Impact of Short Rotation Coppice (SRC) Cultivation on the Environment. Landbauforsch. Vti Agric. For. Res. 2009, 59, 159–162. [Google Scholar]
- Börjesson, P. Environmental Effects of Energy Crop Cultivation in Sweden—I: Identification and Quantification. Biomass Bioenergy 1999, 16, 137–154. [Google Scholar] [CrossRef]
- Nordborg, M.; Cederberg, C.; Berndes, G. Modeling Potential Freshwater Ecotoxicity Impacts Due to Pesticide Use in Biofuel Feedstock Production: The Cases of Maize, Rapeseed, Salix, Soybean, Sugar cane, and Wheat. Environ. Sci. Technol. 2014, 48, 11379–11388. [Google Scholar] [CrossRef]
- Hanley, S.J.; Karp, A. Genetic Strategies for Dissecting Complex Traits in Biomass Willows (Salix spp.). Tree Physiol. 2014, 34, 1167–1180. [Google Scholar] [CrossRef]
- Isebrands, J.G.; Richardson, J. (Eds.) Poplars and Willows: Trees for Society and the Environment, 1st ed.; CABI: Wallingford, UK, 2014; ISBN 978-1-78064-108-9. [Google Scholar]
- Kuzovkina, Y.A.; Volk, T.A. The Characterization of Willow (Salix L.) Varieties for Use in Ecological Engineering Applications: Co-Ordination of Structure, Function and Autecology. Ecol. Eng. 2009, 35, 1178–1189. [Google Scholar] [CrossRef]
- Stanturf, J.A.; Oosten, C.V. Operational Poplar and Willow Culture. In Poplars and Willows: Trees for Society and the Environment; Isebrands, J.G., Richardson, J., Eds.; CABI: Wallingford, UK, 2014; pp. 200–257. ISBN 978-1-78064-108-9. [Google Scholar] [CrossRef]
- Perttu, K.L. Environmental Justification for Short-Rotation Forestry in Sweden. Biomass Bioenergy 1998, 15, 1–6. [Google Scholar] [CrossRef]
- Dimitriou, I.; Baum, C.; Baum, S.; Busch, G.; Schulz, U.; Köhn, J.; Lamersdorf, N.; Leinweber, P.; Aronsson, P.; Weih, M. Quantifying Environmental Effects of Short Rotation Coppice (SRC) on Biodiversity, Soil and Water; IEA Bioenergy Task 43, Report 2011:01; International Energy Agency: Paris, France, 2011; Volume 43, p. 1. Available online: https://www.ieabioenergy.com/wp-content/uploads/2018/01/IEA_Bioenergy_Task43_TR2011-01.pdf (accessed on 20 January 2025).
- Klang-Westin, E.; Eriksson, J. Potential of Salix as Phytoextractor for Cd on Moderately Contaminated Soils. Plant Soil 2003, 249, 127–137. [Google Scholar] [CrossRef]
- Pučka, I.; Lazdiņa, D. Review about Investigations of Salix spp. in Europe. In Proceedings of the Annual 19th International Scientific Conference Proceedings, Latvia University of Agriculture, Jelgava, Latvia, 15 May 2013; Volume 2, p. 13. [Google Scholar]
- Murphy, F.; Devlin, G.; McDonnell, K. Energy Requirements and Environmental Impacts Associated with the Production of Short Rotation Willow (Salix sp.) Chip in Ireland. GCB Bioenergy 2014, 6, 727–739. [Google Scholar] [CrossRef]
- Warmbier, K.; Wilczyński, A.; Danecki, L. Properties of One-Layer Experimental Particleboards from Willow (Salix viminalis) and Industrial Wood Particles. Eur. J. Wood Wood Prod. 2013, 15, 1–6. [Google Scholar] [CrossRef][Green Version]
- Yermakov, S.; Hutsol, T.; Gerasymchuk, I.; Fedirko, P.; Dubik, V. Study of the Unloading and Selection Process of Energy Willow Cuttings for the Creation a Planting Machine. In Proceedings of the International Scientific and Practical Conference, Rezekne, Latvia, 14–15 June 2023; Volume 3, pp. 271–275. [Google Scholar]
- Scriba, C.; Lunguleasa, A.; Spirchez, C.; Ciobanu, V. Influence of INGER and TORDIS Energetic Willow Clones Planted on Contaminated Soil on the Survival Rates, Yields and Calorific Value. Forests 2021, 12, 826. [Google Scholar] [CrossRef]
- Żabowski, B.; Wronka, A.; Kowaluk, G. Selected Physical and Mechanical Properties of Particleboards Manufactured from Plantation Willow and Poplar Wood. Materials 2024, 17, 4069. [Google Scholar] [CrossRef] [PubMed]
- Baker, P.; Charlton, A.; Johnston, C.; Leahy, J.J.; Lindegaard, K.; Pisano, I.; Prendergast, J.; Preskett, D.; Skinner, C. A Review of Willow (Salix spp.) as an Integrated Biorefinery Feedstock. Ind. Crops Prod. 2022, 189, 115823. [Google Scholar] [CrossRef]
- Wilkinson, J.M.; Evans, E.J.; Bilsborrow, P.E.; Wright, C.; Hewison, W.O.; Pilbeam, D.J. Yield of Willow Cultivars at Different Planting Densities in a Commercial Short Rotation Coppice in the North of England. Biomass Bioenergy 2007, 31, 469–474. [Google Scholar] [CrossRef]
- Amichev, B.Y.; Hangs, R.D.; Van Rees, K.C. A Novel Approach to Simulate Growth of Multi-Stem Willow in Bioenergy Production Systems with a Simple Process-Based Model (3PG). Biomass Bioenergy 2011, 35, 473–488. [Google Scholar] [CrossRef]
- Mleczek, M.; Rutkowski, P.; Rissmann, I.; Kaczmarek, Z.; Golinski, P.; Szentner, K.; Strażyńska, K.; Stachowiak, A. Biomass Productivity and Phytoremediation Potential of Salix alba and Salix viminalis. Biomass Bioenergy 2010, 34, 1410–1418. [Google Scholar] [CrossRef]
- Mleczek, M.; Gąsecka, M.; Waliszewska, B.; Magdziak, Z.; Szostek, M.; Rutkowski, P.; Kaniuczak, J.; Zborowska, M.; Budzyńska, S.; Mleczek, P. Salix viminalis L.-A Highly Effective Plant in Phytoextraction of Elements. Chemosphere 2018, 212, 67–78. [Google Scholar] [CrossRef]
- Stelte, W.; Holm, J.K.; Sanadi, A.R.; Barsberg, S.; Ahrenfeldt, J.; Henriksen, U.B. A Study of Bonding and Failure Mechanisms in Fuel Pellets from Different Biomass Resources. Biomass Bioenergy 2011, 35, 910–918. [Google Scholar] [CrossRef]
- Vlăsceanu, G.; Nicolae, F.; Petculescu, N.; Nicolae, M. Principles of Circular Economy Applied to Energy Plants in Culture. The Correlation of Soil Quality with the Valuation Potential of Willow by-Products. In Proceedings of the E3S Web of Conferences, Dushanbe, Tajikistan, 11–13 December 2023; Volume 436, p. 04004. [Google Scholar]
- Chahal, A.; Ciolkosz, D.; Puri, V.; Jacobson, M.; Liu, J. Mechanical Characteristics of Wood-Bark Interface of Shrub Willow. Ind. Crops Prod. 2021, 162, 113236. [Google Scholar] [CrossRef]
- Joardder, M.U.H.; Brown, R.J.; Kumar, C.; Karim, M.A. Effect of Cell Wall Properties on Porosity and Shrinkage of Dried Apple. Int. J. Food Prop. 2015, 18, 2327–2337. [Google Scholar] [CrossRef]
- Beismann, H.; Wilhelmi, H.; Baillères, H.; Spatz, H.-C.; Bogenrieder, A.; Speck, T. Brittleness of Twig Bases in the Genus Salix: Fracture Mechanics and Ecological Relevance. J. Exp. Bot. 2000, 51, 617–633. [Google Scholar] [CrossRef] [PubMed]
- Jiao, H.; Tang, A.; Ma, C.; Li, Y.; Wang, L.; Li, C. Modelling and Numerical Simulation of a Concentrated Mass-Based Branch Vibration. Sci. Hortic. 2024, 330, 113028. [Google Scholar] [CrossRef]
- Tymiński, T.; Rembeza, L.; Kałuża, T. Analysis of Impact of Flexible Vegetation on Hydraulic Conditions of Flow in Vegetated Channels. Part 1: Mechanical Properties of Elastic Plants; Uniwersytet Przyrodniczy we Wrocławiu: Poland, Wrocław, 2008; ISBN 978–83–60574–18–8. (In Polish) [Google Scholar]
- Monteoliva, S.; Senisterra, G.; Marlats, R. Variation of Wood Density and Fibre Length in Six Willow Clones (Salix spp.). Iawa J. 2005, 26, 197–202. [Google Scholar] [CrossRef]
- Chahal, A.; Ciolkosz, D.; Puri, V.; Liu, J.; Jacobson, M. Factors Affecting Wood-Bark Adhesion for Debarking of Shrub Willow. Biosyst. Eng. 2020, 196, 202–209. [Google Scholar] [CrossRef]
- Walczak, N.; Walczak, Z.; Ficner, T. Determination of the Variation of the Geometric and Dynamic Parameters of the Floodplain Vegetation. Water 2022, 14, 1274. [Google Scholar] [CrossRef]
- Vilkovskỳ, P.; Vilkovská, T.; Klement, I.; Čunderlík, I. The Analysis Effect of Selected Factors on the Shear Strength of Woodbark at Different Wood Species. Forests 2022, 13, 637. [Google Scholar] [CrossRef]
- Hofstetter, K.; Hinterstoisser, B.; Salmén, L. Moisture Uptake in Native Cellulose—the Roles of Different Hydrogen Bonds: A Dynamic FT-IR Study Using Deuterium Exchange. Cellulose 2006, 13, 131–145. [Google Scholar] [CrossRef]
- Butler, D.W.; Gleason, S.M.; Davidson, I.; Onoda, Y.; Westoby, M. Safety and Streamlining of Woody Shoots in Wind: An Empirical Study across 39 Species in Tropical Australia. New Phytol. 2012, 193, 137–149. [Google Scholar] [CrossRef]
- Sutili, F.J.; Denardi, L.; Durlo, M.A.; Rauch, H.P.; Weissteiner, C. Flexural Behaviour of Selected Riparian Plants under Static Load. Ecol. Eng. 2012, 43, 85–90. [Google Scholar] [CrossRef]
- Vargas, C.A.; Nascimento, M.B.; de Muñiz, G.I.B.; Nisgoski, S. Physical and Mechanical Properties of Four Salix Species. Rev. Ciência Da Madeira (Braz. J. Wood Sci.) 2012, 3, 10–12953. [Google Scholar] [CrossRef]


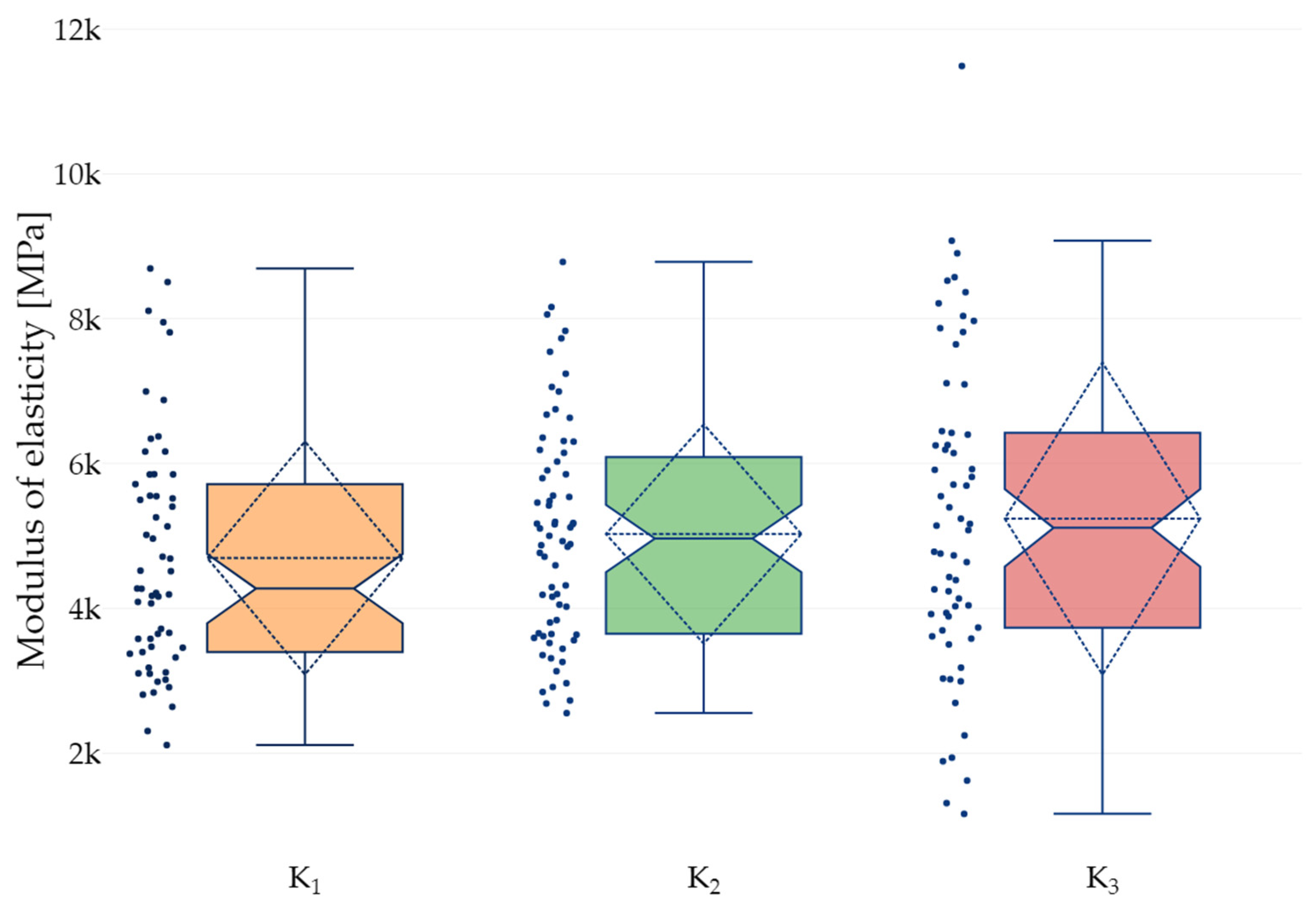
| Groups | K1 | K2 | K3 |
|---|---|---|---|
| Num of observations | 30 | 30 | 30 |
| Minimum | 1.43 | 1.63 | 1.35 |
| Maximum | 7.03 | 6.32 | 5.97 |
| Range | 5.6 | 4.69 | 4.62 |
| ) | 4.08 | 3.76 | 3.66 |
| Standard Deviation (SD) | 1.67 | 1.60 | 1.65 |
| Q1 | 2.42 | 2.2 | 2.23 |
| Median | 4.07 | 3.72 | 3.77 |
| Q3 | 5.26 | 5.17 | 5.25 |
| Interquartile range | 2.84 | 2.97 | 3.02 |
| Normality (Shapiro–Wilk Test, α = 0.05) | 0.103 | 0.0012 | 0.00063 |
| Coefficient of variation CV [%] | 41.06 | 42.55 | 44.96 |
| Groups | K1 | K2 | K3 |
|---|---|---|---|
| Minimum | 0.00150 | 0.00280 | 0.00266 |
| Maximum | 0.00607 | 0.00529 | 0.00522 |
| Range | 0.00457 | 0.00249 | 0.00256 |
| ) | 0.00364 | 0.00392 | 0.00388 |
| Standard Deviation (SD) | 0.00112 | 0.00060 | 0.00080 |
| Q1 | 0.00321 | 0.00355 | 0.00325 |
| Median | 0.00381 | 0.00378 | 0.00391 |
| Q3 | 0.00430 | 0.00424 | 0.00443 |
| Interquartile range | 0.00109 | 0.00070 | 0.00118 |
| Coefficient of variation CV [%] | 30.73 | 15.37 | 20.52 |
| Date | Mean | SD | Min | Max | Q1 | Q3 | CV |
|---|---|---|---|---|---|---|---|
| 8 March 2022 | 5202 | 1858 | 1890 | 8903 | 4051 | 6189 | 35.7 |
| 10 March 2022 | 4498 | 1482 | 1312 | 8108 | 3449 | 5522 | 32.9 |
| 16 March 2022 | 4890 | 1791 | 1164 | 9076 | 3581 | 6032 | 36.6 |
| 24 March 2022 | 5489 | 1929 | 1939 | 11,491 | 4160 | 6373 | 35.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walczak, N.; Walczak, Z. Analysis of the Changes in the Mechanical Properties of Branches of Salix Energy Plants After Shearing. Forests 2025, 16, 206. https://doi.org/10.3390/f16020206
Walczak N, Walczak Z. Analysis of the Changes in the Mechanical Properties of Branches of Salix Energy Plants After Shearing. Forests. 2025; 16(2):206. https://doi.org/10.3390/f16020206
Chicago/Turabian StyleWalczak, Natalia, and Zbigniew Walczak. 2025. "Analysis of the Changes in the Mechanical Properties of Branches of Salix Energy Plants After Shearing" Forests 16, no. 2: 206. https://doi.org/10.3390/f16020206
APA StyleWalczak, N., & Walczak, Z. (2025). Analysis of the Changes in the Mechanical Properties of Branches of Salix Energy Plants After Shearing. Forests, 16(2), 206. https://doi.org/10.3390/f16020206







